L'article précédent était assez pessimiste et peut-être même un peu rébarbatif, avec cette liste des instructions du 6502. On était arrivé à la conclusion que les possibilités de ce processeur étaient finalement assez limitées : opérations seulement sur 8 bits, pas de multiplications ni de divisions, pas de nombre à virgule, très très peu de registres utilisables (A, X et Y).
Aujourd'hui, nous allons commencer à contourner ces limitations, notamment pour ce qui concerne l'arithmétique entière.
1. Les modes d'adressage, la vraie puissance du 6502
Le 6502 ne dispose que de 56 opcodes (instructions), mais beaucoup de ces opcodes peuvent avoir un paramètre et ce paramètre peut à son tour avoir plusieurs formes. Cette forme est appelée mode d'adressage. En effet, le paramètre est généralement une donnée 8 bits stockée quelque part en mémoire et donc, à une certaine adresse, et le 6502 offre une multitude de façons d'indiquer l'adresse en question.
1.1 Les modes directs, simples
Le mode le plus évident à comprendre est probablement le mode immédiat. Dans ce cas-là, la donnée est fournie immédiatement (d'où le nom, c'est bien fichu, hein ?) après l'opcode. Une donnée immédiate est forcément sur 8 bits. Elle peut donc aller de 0 à 255 (ou de -128 à 127 si l'on veut indiquer une donnée signée). On indique qu'on veut utiliser ce mode avec le caractère #, de cette façon :
Cela place immédiatement la valeur 22 dans le registre A.
Un mode encore plus simple, mais auquel on ne pense pas vraiment comme à un mode d'adressage est le mode implicite. Dans ce cas, on n'a simplement pas d'adresse à indiquer, car l'opcode n'en a pas besoin ! Par exemple :
Donc, si on ne met aucun nombre, il s'agit du mode implicite, et si on met un nombre précédé d'un dièse, il s'agit d'une donnée immédiate. Mais que se passe-t-il si on écrit un nombre sans ce # ? Et bien, il s'agit du mode absolu. Le nombre est considéré comme une adresse (sur 16 bits, donc), et la donnée à manipuler est alors celle présente à cette adresse. Si l'adresse est inférieure à 256, elle tient sur 8 bits, dans ce cas, l'instruction sera légèrement plus rapide, car il y a un octet de moins à traiter pour créer l'adresse. C'est pourquoi les 256 premiers octets des machines qui utilisent un 6502 sont souvent nommés « mémoire rapide ». Ce n'est pas vraiment la mémoire qui est rapide, c'est la manière d'y accéder. L'adressage absolu utilisant cette zone mémoire, celle dont les 8 bits de poids forts sont à 0 est appelée ZP (pour Zero Page).
Ces quatre modes d'adressage sont de loin les plus utilisés. On les retrouve d'ailleurs dans la plupart des microprocesseurs. Et ils vont suffire à détailler quelques algorithmes.
Par exemple, voici comment réaliser une simple addition :
Deux petites remarques sur ce bout de code : Premièrement, l'opcode ADC (ADdition with Carry) réalise une addition avec retenue et il n'existe pas d'opcode permettant de faire une addition sans retenue. Il faut donc systématiquement penser à remettre la retenue à zéro avant une addition. D'autre part, l'exemple cité n'est pas très intéressant, on aurait pu faire l'addition de tête et directement utiliser ceci : LDA #95 / STA resultat.
Additionner deux nombres est nettement plus intéressant lorsqu'il ne s'agit pas de constantes, et c'est là que l'adressage absolu (ou l'adressage ZP) intervient :
On notera que le choix du mode d'adressage entre absolu et absolu ZP est réalisé automatiquement par l'assembleur qu'on utilise.
Les valeurs en mémoire RAM se comportent comme des variables et il est même possible d'effectuer certaines opérations directement sur celles-ci, sans passer par un registre. On peut par exemple incrémenter, décrémenter, multiplier par deux ou diviser par deux une valeur en mémoire en utilisant l'adressage absolu ou ZP (et d'autres que nous allons voir bientôt). Même si toute la RAM peut être utilisée de cette façon, on préfère souvent utiliser les 256 premiers octets pour cela, puisque l’instruction est alors 50 % plus rapide en moyenne.
Les utilisateurs chevronnés du 6502 s'accordent à dire que chaque octet de la mémoire, et plus particulièrement les 256 premiers, sont autant de registres disponibles, on est donc loin de la limite des 3 registres en tout. Les opérations sur les « vrais » registres restent toutefois nettement plus rapides.
Cependant, afin que le code soit plus facile à lire, on aime bien donner des noms aux différentes adresses que l'on utilise. Suivant l'assembleur que vous utilisez, cela se fera de différentes manières. Souvent ce genre de code fonctionnera :
Cependant, si vous utilisez l'assembleur en ligne [1] comme je le conseille pour cette série, il faudra utiliser la syntaxe suivante :
C'est la syntaxe que j'utiliserai dans mes exemples pour que vous puissiez facilement les tester.
1.1.1 Addition et soustraction de nombres de 16 bits
Le fait de toujours devoir se soucier de la retenue à chaque addition peut paraître lourd. Mais cela devient un avantage lorsque l'on veut manipuler des données de 16 bits.
En effet, même si le 6502 est incapable de manipuler autre chose que des données de 8 bits, rien ne nous empêche d'en associer deux pour les considérer comme une seule de 16 bits. Et de la même façon que nous réalisons des additions à la main en base dix en commençant par les unités, puis les dizaines, les centaines, etc. tout en reportant la retenue, le 6502 va nous permettre de réaliser des additions en base 256, avec une retenue éventuelle.
On stocke généralement les données 16 bits comme deux octets consécutifs en mémoire, en commençant par la partie des « unités ». Par exemple, si on veut stocker 520, qui est 2*256+8, on stockera 8 à une certaine adresse, et 2 à l'adresse suivante. C'est juste une convention, mais c'est celle que le 6502 utilise dans certains cas. Et comme on commence par le « petit bout » de la donnée (8 est plus petit que 2*256), on dit que les données sont en « petit-boutiste », ou little-endian en anglais.
Ainsi, le bout de code suivant permettra d'ajouter la valeur 16 bits stockée aux adresses val1 et val1 + 1 à la valeur 16 bits stockée aux adresses val2 et val2 + 1 et stocke le résultat dans resultat et resultat + 1. Dans cet exemple, on considérera que val1 contient 480 (soit 224, 1) et que val2 contient 806 (soit 38, 3).
À l'issue de ce code, resultat contient (6, 5), soit 5*256+6=1286, ce qui est bien la somme de 480 et de 806.
Pour la soustraction, cela marche de la même manière, mais en positionnant la retenue avec SEC (SEt Carry) au lieu de CLC (CLear Carry), car le 6502 gère la retenue à l'envers pour les soustractions.
Il peut arriver d'avoir envie d'utiliser des nombres entiers de plus de 16 bits, 24 ou 32 par exemple. Il suffit alors de continuer de la même manière, avec la retenue qui se propage petit à petit.
1.2 L'adressage relatif
Pour aller plus loin et faire des choses plus intéressantes, nous allons avoir besoin de tests et de sauts conditionnels.
Certains opcodes comme CMP, CPX et CPY sont spécialisés dans le test de valeur contenue respectivement dans A, X ou Y. Mais la plupart des opcodes modifient les drapeaux du 6502 (registre P) suivant le résultat de leur opération. On peut ensuite tirer parti de l'état de ses drapeaux pour effectuer un saut dans le programme suivant, si un drapeau est positionné ou pas. La destination du saut est donnée par un décalage par rapport à l'endroit actuel. Ce décalage est compris entre -128 et +127 et cette donnée est appelée adressage relatif.
L'adressage relatif n'est utilisé que par les opcodes de branchement conditionnels, Bxx.
Voici un exemple d'utilisation de cela :
La mémoire adressable par un 6502 peut aller jusqu’à 64 Ko, mais on vient de voir que les opcodes Bxx ne permettaient pas de se déplacer de plus de 128 octets, ce qui est très peu. Aussi, si l'on veut effectuer un saut plus grand, on utilisera le saut inverse, associé à l'opcode JMP comme ceci :
L'opcode JMP utilise donc généralement le mode d'adressage absolu ; il peut aussi utiliser un autre mode d'adressage : l'adressage indirect, qui lui est d'ailleurs réservé.
L'adressage indirect s'utilise ainsi :
place étant un endroit en mémoire où l'on trouve l'adresse à laquelle cette instruction va sauter.
1.2.1 Incrémentation et décrémentation sur 16 bits
Maintenant que l'on a dans notre arsenal les sauts conditionnels, on va pouvoir implémenter les incrémentations et les décrémentations sur 16 bits. En effet, les opcodes INC (incrémentation d'une valeur en mémoire) ou DEX (décrémentation du registre X) par exemple, n'utilisent pas du tout la retenue (C). On ne peut donc pas réutiliser l'astuce des additions et des soustractions. Mais ils positionnent le flag Z si la nouvelle valeur est 0.
On peut donc implémenter l'incrémentation sur 16 bits ainsi :
La décrémentation sur 16 bits est un poil plus complexe, mais pas tant que ça :
1.3 L'adressage absolu avec index
Les modes d'adressages que l'on a vus jusqu'à maintenant sont présents sur la grande majorité des microprocesseurs, même ceux de l'époque. Là où le 6502 se distingue, c'est avec les trois restants.
Chacun de ses modes utilise à la fois une adresse et l'un des registres X ou Y. Le premier de ces modes est l'adressage absolu avec index. Il peut s'utiliser par exemple comme ceci :
La position de la valeur est donnée par l'addition d'une valeur (comme pour l'adressage absolu) et du contenu d'un registre. Et cela peut être utilisé par beaucoup d'opcodes, pratiquement partout où l'on peut utiliser le mode d'adressage absolu !
Et comme il est facile d'incrémenter ou de décrémenter X ou Y, il devient très facile de faire des boucles. Par exemple, le bout de code suivant permet d'additionner les dix éléments du tableau tab1 aux éléments correspondants de tab2 et de stocker le résultat dans les éléments de tab3.
Cela correspondrait à ce code C : for (x = 0; x < 10; x++) { tab3[x] = tab[1] + tab[2]; }. Qui a dit que l'assembleur était beaucoup plus compliqué que le C ?
Comme il est très fréquent de devoir faire des boucles, le mode d'adressage absolu avec index est très très répandu en programmation 6502.
1.4 Adressage indexé indirect
Le mode d'adressage indexé indirect est un dérivé du précédent. Il est un peu plus complexe à comprendre, mais aussi beaucoup plus puissant. Il s'utilise par exemple ainsi :
La valeur concernée par l'opération est celle trouvée à l'endroit dont on trouve l'adresse en adr, auquel on ajoute la valeur de Y. Deux restrictions cependant : seul Y peut être utilisé comme registre d'index dans ce mode, et pas X, et adr doit être inférieur à 255.
Afin d'en comprendre l'utilité, voyons comment utiliser ce mode d'adressage dans un exemple concret. Il arrive souvent que l'on veuille copier un ensemble de données d'un endroit vers un autre. Évidemment, si la zone de départ et la zone d'arrivée sont tout le temps les mêmes, ce n'est pas très intéressant et on peut utiliser le mode d'adressage précédent pour cela. Dans notre exemple, on va paramétrer la copie en indiquant dans le registre A quelle zone doit être copiée :
Ce bout de code implémente une fonction Copie, qui va copier une zone de 40 caractères vers la zone mémoire dest. La zone copiée pourra au choix commencer à $0100, $0248 ou $390, suivant la valeur du registre A (0, 1 ou 2) avant l'appel à cette fonction. Notez que les DC.B ne sont pas des opcodes, mais une syntaxe permettant d'insérer des données directement à côté du code, sans avoir à les placer là par une série interminable de LDA #donne / STA adresse. Malheureusement, l'émulateur en ligne [1] ne supporte pas cette syntaxe, qui est tout de même très fréquente sur pratiquement tous les assembleurs comme ASM6 ou AS65. On peut convertir ce bout de code pour qu'il fonctionne tout de même sur [1], mais je vous laisse faire cela à titre d'exercice.
1.5 Adressage indirect indexé
Le dernier mode d'adressage du 6502 est nommé « indirect indexé ». Il est un peu le pendant du précédent. Voyons comment il s'utilise :
On a cette fois-ci un mode d'adressage qui nécessite l'utilisation du registre X. La valeur à charger/modifier est trouvée en commençant par additionner l'adresse (ou plutôt la table d'adresses) fournie et X, puis en regardant à l'adresse ainsi obtenue. Cela permet de considérer une zone mémoire comme un tableau d'adresses de variables, ce qui peut être très puissant dans certains cas. Ce mode d'adressage est toutefois nettement moins utilisé que les deux précédents.
J'ai donné des exemples d'opcodes utilisant certains modes d'adressage. Nous n'avons évidemment pas vu toutes les combinaisons possibles, et toutes ne sont d'ailleurs pas disponibles. Il n'est pas toujours évident de savoir ce qu'on a le droit de faire ou pas et les documentations sont souvent longues et rébarbatives. Je conseille donc l'infographie [2] qui regroupe sur une même page tous les opcodes, la liste des modes d'adressage utilisables pour chacun de ces opcodes, ainsi que les drapeaux que ces opcodes peuvent éventuellement modifier.
2. Multiplication
Après ce tour assez complet des modes d'adressage du 6502, nous allons nous intéresser quelques instants à un algorithme fondamental en arithmétique : la multiplication.
Le 6502 ne propose pas d'opcode pour les multiplications. Nous allons donc devoir les réaliser « à la main ». La manière la plus simple pour faire ça maintenant que nous disposons des boucles est de transformer une multiplication du genre 4x6 en 6+6+6+6.
Par exemple, on peut multiplier la valeur 8 bits en $00 par la valeur 8 bits en $01 et mettre le résultat dans $02 avec le bout de code suivant :
Les avantages de cette façon de faire sont qu'elle est très simple et facile à adapter pour des données 16 bits. Mais l'inconvénient majeur est que c'est hyper lent, on doit pouvoir faire mieux.
Dans certains cas particuliers, on peut aller beaucoup plus vite. Par exemple, pour multiplier par 2 ou une puissance de deux, on peut utiliser l'opcode ASL (Arithmetic Shift Left) une ou plusieurs fois. En effet, comme dans notre base 10, on multiplie par 10 en décalant un nombre d'un chiffre vers la gauche, en binaire, on multiplie par deux en décalant d'un bit vers la gauche. On peut donc aussi multiplier par 4 en décalant deux fois, par 8 en décalant 3 fois, etc.
On peut même étendre cette idée pour multiplier assez rapidement par n'importe quelle constante. Par exemple, pour multiplier une valeur par 9, on peut simplement (et rapidement) multiplier par 8, puis ajouter la valeur initiale, pour multiplier par 15 on multipliera par 16 et on enlèvera une fois la valeur, etc.
Mais si on ne connaît pas par avance la valeur par laquelle on veut multiplier, il va falloir être plus inventif. Plus exactement, il va falloir revenir au primaire, du temps où l'on apprenait à faire des multiplications à la main.
Cela ressemblait à ça :
C'est-à-dire que l'on multipliait la première valeur par chacun des chiffres de la seconde, en décalant chaque nouvelle ligne vers la gauche avant de tout additionner.
Faire ça en binaire est en fait encore plus simple :
On voit que chacune des lignes que l'on ajoute à la fin est soit 0 (si le chiffre du multiplicateur est un 0), soit la valeur de départ décalée vers la gauche.
Cela va être facile à implémenter (ADC pour additionner, ASL pour décaler vers la gauche), il reste juste à tester chacun des chiffres pour savoir s'il est à 0 ou à 1. Pour cela, on va utiliser LSR (Logical Shift Right) qui place le chiffre le plus à droite dans la retenue (C) et décale vers la droite.
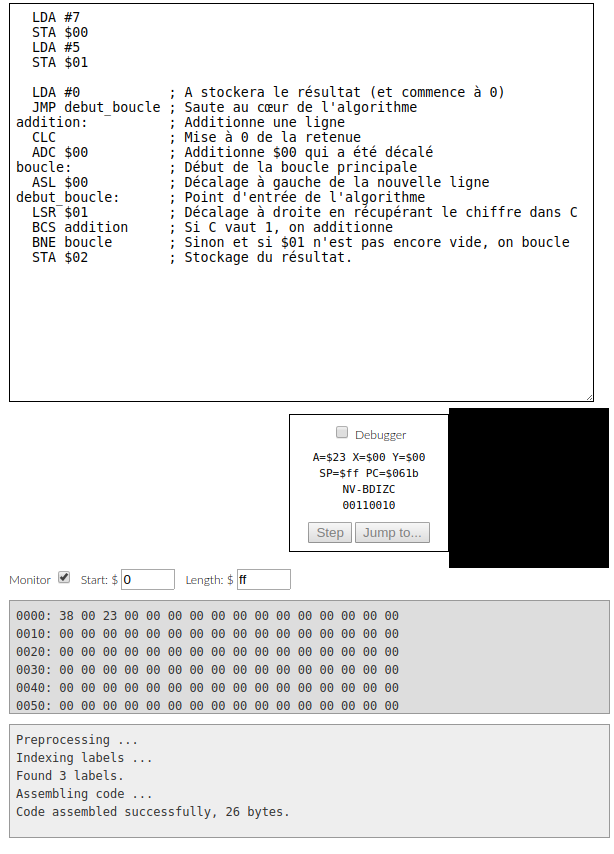
Voici une implémentation possible, que j'ai adaptée d'un exemple récupéré sur [3] qui multiplie assez rapidement la valeur présente en $00 par la valeur présente en $01 et stocke le résultat en $02. Ce code est très court (18 octets une fois compilé) et fait les choses dans un ordre pas forcément naturel, mais permet de gérer tous les cas sans avoir de duplication de code.
Note : ce code modifie aussi $00 et $01.
Voyons comment cela fonctionne par exemple pour multiplier 7 (en $00) par 5 (en $01). 5 est représenté par %101 en binaire. On commence par mettre A à zéro, puis on saute à debut_boucle.
Je vous encourage à tester ce code avec différentes valeurs et à l'exécuter pas-à-pas grâce à l'émulateur en ligne [1]. Vous pouvez voir une exécution de la multiplication de 7 par 5 sur la figure 1 justement. Notez les valeurs de $00 ($38 = 56 en décimal), $01 (0) et $02 ($23 = 35 en décimal) qui sont bien celles que l'on attendait.
Notez qu'il existe plein d'autres méthodes pour faire des multiplications rapidement. On peut par exemple précalculer les résultats, mais cela prend une place folle, et on doit alors se limiter par exemple a un maximum de 16 fois 16. Une astuce que je trouve assez géniale consiste à ne précalculer que les carrés (1x1, 2x2, 3x3, etc.) et à utiliser la formule suivante : a x b = ((a+b)/2)^2-((a-b)/2)^2. Cela permet de faire une multiplication avec seulement une addition, deux soustractions, deux décalages et deux lectures dans une table, quels que soient les nombres à multiplier !
On peut vérifier facilement que 7 x 5 = ((7+5)/2)^2-((7-5)/2)^2 = (12/2)^2-(2/2)^2 = 6^2 - 1^2 = 36 - 1 = 35.
Ce n'est pas très difficile à implémenter et les plus courageux d'entre vous peuvent largement le faire avant le prochain article !
3. La prochaine fois
Dans le prochain article, on continuera d'utiliser astucieusement les quelques opcodes du 6502 pour faire des choses de plus en plus complexes. On verra par exemple comment réaliser des divisions par 2, 4, 3, 5 ou même n'importe quelle valeur. On abordera aussi la représentation des nombres à virgule afin de faire des opérations dessus et même, un peu de trigonométrie. Avouez que ce n'est pas mal pour un processeur qui est a priori tout juste capable de faire une addition entière sur 8 bits !
Références
[1] https://skilldrick.github.io/easy6502/ assembleur/émulateur en ligne.
[2] https://raw.githubusercontent.com/camsaul/nesasm/master/beagle_bros_6502_reference.png résumé en une seule page de tous les opcodes et modes d’adressage du 6502.
[3] https://codebase64.org/doku.php plein d’exemples de code.
[4] http://www.6502.org/ qui regorge d'informations, d'archives et d'astuces.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture