De nos jours, l'informatique et la simulation numérique prennent une place de plus en plus importante dans la recherche scientifique, ainsi que le développement technologique. L'ENIAC, le premier ordinateur conçu, avait pour but le calcul scientifique, puisqu'il était utilisé pour calculer des trajectoires d'artillerie. En effet, un ordinateur permet d'automatiser bien des tâches, dont les tâches de calcul, et d'explorer systématiquement les problèmes scientifiques.
Python dispose de nombreux modules de calcul scientifique permettant d'aborder efficacement un problème scientifique. C'est un langage très riche et des outils interactifs permettent de le transformer en un environnement de travail complet et facile d'utilisation pour l'informatique scientifique.
De façon générale, un problème de recherche et développement se présente comme un modèle que l'on veut étudier et comprendre. Le modèle peut aussi bien être un modèle théorique qu'un système modèle fait d'expériences ou une maquette. Pour développer son intuition, l'idéal est de pouvoir interagir le plus possible avec le modèle. Ainsi, depuis l'antiquité, les mathématiciens utilisent des dessins et des calculs pour formuler leurs hypothèses, mais la généralisation des ordinateurs, il y a vingt ans, a conduit à l'apparition des mathématiques dites « expérimentales », s'appuyant sur l'utilisation systématique de l'informatique. Dans l'industrie, par exemple, lors de la conception d'un nouveau produit, la simulation numérique permet de tester systématiquement de nombreuses solutions géométriques ou des matériaux différents de manière relativement pratique, plutôt que de construire de nombreuses maquettes à grand coût. L'informatique scientifique a pour but premier de faciliter cette exploration du problème. Ses outils, que le scientifique doit apprendre et maîtriser, ne sont que des barrières pour l'utilisateur entre son problème et lui-même. Par ailleurs, dans le domaine de la recherche, il est inévitable que les problèmes soient souvent mal posés, et changent en permanence au fur et à mesure que l'on progresse. C'est pourquoi, il faut que les solutions utilisées soient aussi souples et agiles que possible.
Pour répondre aux exigences d'interactivité et de souplesse de développement, les outils de l'informatique scientifique se sont éloignés des langages compilés utilisés traditionnellement pour s'orienter vers des environnements interactifs spécialisés dotés de leur propre langage interprété, comme Matlab ou Mathematica. Cependant, la limite de ces outils est qu'ils sont spécialisés. L'un des problèmes épineux que j'ai eu à résoudre plusieurs fois pour mon travail de recherche est le contrôle par ordinateur d'une expérience de physique compliquée, avec de nombreux appareils à commander et synchroniser, et des données à traiter et à afficher. J'ai exploré beaucoup de solutions. Mon expérience a montré que les environnements scientifiques spécialisés ne sont pas satisfaisants du tout pour la création d'interfaces graphiques, la gestion des couches réseau ou le contrôle de matériel scientifique. Les langages généralistes et bas niveau comme le C peuvent se révéler désastreux dans les labos, car ils forcent l'utilisateur à s'occuper de problèmes qui ne l'intéressent pas, comme la gestion de mémoire, et ne proposent pas de façon transparente les outils standards dont le scientifique à besoin pour faire ses calculs, traiter ses données, et visualiser les résultats. Il y a quelques années, je me suis jeté à l'eau, et j'ai décidé d'utiliser Python pour développer une infrastructure de contrôle d'expérience, malgré les réticences de mes collègues qui ne connaissaient pas le langage et ne voulaient pas apprendre un nouvel outil. Le résultat a été remarquable : non seulement, j'ai pu rapidement construire l'infrastructure dont j'avais besoin, mais, en plus,, le code était propre et facile à étendre [1]. Mes collègues m'ont avoué qu'ils préféraient cette solution à celles que nous avions déployées jusqu'ici, car, avec celle-ci, ils avaient l'impression de comprendre la base de code.
Depuis cette expérience positive, je suis convaincu que Python n'est pas seulement un langage que j'apprécie personnellement beaucoup, mais aussi une bonne réponse au problème récurrent de l'informatique scientifique. La rapidité avec laquelle le langage se répand dans les laboratoires de recherche semble le confirmer. Techniquement, Python possède beaucoup d'atouts qui en font un outil idéal. En effet, c'est un langage très clair à lire, même pour un non initié comme un scientifique dont le corps de métier n'est pas l'informatique. De plus, il est possible d'utiliser le langage de façon interactive, comme une calculatrice, ce qui est nécessaire pour une approche exploratoire d'un problème. Le langage est conçu pour faciliter la réutilisation de code et les cycles de développement courts ; il ne cherche pas à imposer les techniques de programmation nécessaires à un gros projet, tout en les permettant. Finalement, Python n'est pas un langage spécialisé, ce qui lui permet de bénéficier d'une grosse masse de développeurs, et d'excellentes bibliothèques pour les tâches non spécifiquement scientifiques, par exemple pour coupler les résultats d'une expérience à une base de données.
Le potentiel de Python dans un environnement scientifique a été perçu depuis longtemps. Dès le milieu des années 90, des pionniers développaient des modules de calcul scientifique. Ces dernières années ont cependant vu l'utilisation scientifique de Python s'accélérer grandement et de nombreux modules scientifiques sont maintenant disponibles. Dans cet article, j'aimerais prendre le temps de présenter les outils majeurs de l'informatique scientifique en Python, ainsi qu'illustrer leur utilisation.
Contrôler une expérience d'optique atomique
J'ai fait ma thèse en physique atomique. J'ai travaillé sur plusieurs grosses expériences qui mélangent une quantité effroyable d'équipements. Le cœur de l'expérience est une chambre sous ultra-vide dans laquelle on introduit une petite quantité d'atomes. On utilise alors une combinaison de champs magnétiques, d'ondes radio et micro-ondes et de lasers pour manipuler les atomes. Les différents appareils (certains commerciaux, d'autres maisons) sont synchronisés à l'aide d'un ordinateur, qui s'occupe aussi d'acquérir des données par l'intermédiaire d'oscilloscopes et de caméras. Les données sont traitées en temps réel et affichées pour que l'opérateur puisse ajuster l'expérience. De plus, nous programmons souvent l'expérience en séquences pendant lesquelles des paramètres sont variés automatiquement pendant des heures, si possible sans intervention humaine. Au cours de ces prises de données, tous les paramètres et les résultats expérimentaux sont stockés pour être analysés plus tard.
Bien que le logiciel de contrôle soit un logiciel scientifique, avec une partie de traitement de données, les problèmes contre lesquels je me suis le plus heurté sont des problèmes d'interface graphique, de flux de données, de communication asynchrone sur différents bus ou d'appel direct au matériel. J'ai pu constater que la polyvalence de Python est un atout majeur pour ce genre de travail [1]. Il est nettement plus agréable d'implémenter un serveur TCP/IP pour parler à un système de contrôle embarqué en Python qu'en MatLab. Malheureusement, une grande partie du code contrôlant les expériences sur lesquelles j'ai travaillé était en MatLab.
1. Calcul vectoriel avec numpy
1.1 Tableaux et matrices
Le fer de lance des applications scientifiques en Python est le module numpy qui introduit deux nouveaux types de données : tableaux et matrices. Les tableaux numériques multidimensionnels sont un élément essentiel d'un langage pour faire du calcul numérique. Fortran est le seul langage non spécialisé intégrant ce type numérique et cela explique son succès dans la communauté scientifique. En effet, on est souvent amené à faire les mêmes opérations numériques sur un ensemble de nombres. Si on les range dans un tableau numpy, on peut effectuer ces opérations simultanément sur tout l'ensemble. Voici un exemple illustrant comment élever au carré une série de nombres avec numpy :
>>> import numpy
>>> a = numpy.array([1, 2, 4, 8, 16])
>>> a**2
array([ 1, 4, 16, 64, 256])
numpy fournit des fonctions mathématiques de base s'appliquant à ces tableaux, telles que sinus ou exponentielle, mais aussi des fonctions pour les manipuler, les redimensionner, les concaténer. Ces fonctions sont implémentées directement en C, et sont donc très rapides sur de gros tableaux. Une bonne règle à suivre pour faire du code efficace et lisible avec numpy est de bannir les boucles for et de manipuler un tableau comme un tout.
Les tableaux fournis par numpy sont des objets très riches avec des moyens optimisés de les parcourir, dans une direction ou une autre, selon un pas variable ou avec un jeu particulier d'indices, ce qui permet d'implémenter des fonctions optimisées pour le cache du processeur. De plus, il est possible d'extraire une vue d'une partie d'un tableau. Cette vue se comporte comme un tableau à part entière, mais ce n'est pas une copie du tableau d'origine et les modifications qui lui sont faites s'appliquent aussi au tableau parent. L'API C de numpy permet de contrôler en détail la structure interne des tableaux, pour, par exemple, la passer à des fonctions implémentées en Fortran ou en C [2]. Toute cette richesse est cependant transparente sous Python, et le code ressemble à une suite d'opérations mathématiques, ce qui permet au scientifique de se concentrer sur celles-ci, plutôt que sur les structures de données ou la gestion de la mémoire.
Un autre type numérique important pour les scientifiques est la matrice. numpy définit la notion de « matrices », qui se comportent comme des tableaux, à part que la multiplication de deux matrices n'est pas une multiplication éléments par éléments, comme pour les tableaux, mais la multiplication matricielle.
1.2 Vectoriser les boucles pour la performance
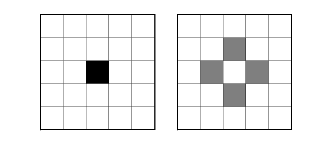
Remplacer une boucle for sur une liste par une opération sur tableau entraîne un important gain de performance, mais cela peut aussi demander de reformuler le problème. C'est ce qu'on appelle vectoriser le code. Si, par exemple, on a un tableau numérique bi-dimensionnel I, une image peut-être, auquel on désire appliquer la transformation suivante : I2[i, j] = 0.25*(I[i-1, j] + I[i+1, j] + I[i, j-1] + I[i, j+1]), qui peut être visualisé ainsi :
Image avant et après application du laplacien
Cette transformation peut être utilisée pour ajouter du flou à une image, mais, de façon plus générale, en termes mathématiques, elle consiste à prendre le laplacien du tableau. Une implémentation en Python pur, sans l'utilisation de numpy, peut s'écrire, pour un tableau I de taille n x n :
I = [[0 for j in range(n)] for i in range(n)]
I[n/2][n/2] = 1
from copy import deepcopy
I2 = deepcopy(I)
for i in range(1, n-1):
for j in range(1, n-1):
I2[i][j] = (I[i-1][j] + I[i+1][j] +
I[i][j-1] + I[i][j+1])*0.25
Lorsqu'on utilise numpy, l'opération se formule à l'aide d'opérations globales sur les tableaux, en utilisant de l'indexage par slices pour créer des vues décalées du tableau I :
from numpy import zeros
I = zeros((n, n))
I[n/2, n/2] = 1
I[1:-1, 1:-1] = (I[:-2, 1:-1] + I[2:, 1:-1] +
I[1:-1, :-2] + I[1:-1, 2:])*0.25
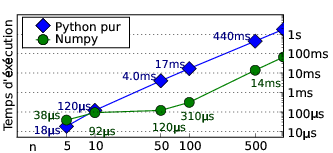
Cet exemple illustre bien une des notions-clés de numpy : la création de vues à partir d'un tableau par de l'indexage par intervalle ou slice en termes de Python. La première chose qui saute aux yeux en comparant les deux implémentations est que l'implémentation avec numpy est plus concise. Pour un regard entraîné au calcul vectoriel, elle est aussi plus claire. Les opérations vectorielles globales sur un tableau sont par ailleurs très rapides. Mesurons le temps d'exécution de l'opération pour différentes valeurs de n :
Temps d'exécution de la transformation pour différentes tailles de tableau
On peut voir que, sur cet exemple très simple, pour des petits tableaux, le temps de création du tableau numpy surpasse le gain en vitesse sur les opérations vectorielles. Cependant, dès que les tableaux contiennent plus de 100 éléments, il est plus efficace de passer par numpy, car le temps d'initialisation du tableau devient négligeable. Lorsque le nombre d'éléments croît, le temps d'exécution en Python pur croît aussi vite qu'en utilisant numpy, et le gain apporté par numpy se stabilise à un facteur 30.
On a donc tout intérêt à remplacer les boucles avec des opérations sur un ensemble uniforme de nombres par des manipulations sur des vues d'un tableau numpy. Dans l'exemple ci-dessus, les vues étaient prises décalées afin d'avoir des opérations mélangeant différentes cases d'un tableau. Une autre opération de vectorisation courante est d'effectuer une opération conditionnelle sur un tableau en utilisant un masque : on applique la condition au tableau pour créer un tableau de booléens, que l'on utilise pour sélectionner les indices des cases du tableau sur lesquelles on veut agir, en opérant sur une vue de ce tableau extraite par indexage. Ainsi, si on veut remplacer par zéro tous les nombres pairs d'un tableau, la condition s'écrit (a % 2) == 0, car % retourne le reste de la division entière en Python, et l'opération sur tout le tableau s'écrit ainsi :
>>> a = numpy.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> masque = ((a % 2) == 0)
>>> a[masque] = 0
>>> a
array([0, 1, 0, 3, 0, 5, 0, 7, 0, 9])
Notons qu'il n'est pas vraiment nécessaire de créer le tableau masque si on ne le réutilise pas en dehors de ce code. L'opération peut se réduire à a[(a % 2) == 0] = 0.
Prendre en compte les incertitudes dans le calcul numérique Jayant Sen Gupta, EADS
Une simulation numérique consiste à évaluer une grandeur à partir d'un jeu de paramètres physiques qui alimente un modèle de calcul. Par exemple, la charge subie par la coiffe d'Ariane 5 peut être calculée à partir de ses caractéristiques mécaniques et des conditions de vent lors du vol. Or, ces paramètres sont souvent méconnus ou naturellement aléatoires.
Pour faire face au besoin grandissant dans l'industrie de prendre en compte les incertitudes dans la simulation, OpenTURNS, une plateforme libre de modélisation et de propagation d'incertitudes (voir www.openturns.org) a été développée conjointement par EADS IW, EDF R&D et Phimeca. Cet outil, composé d'une bibliothèque C++ de plus de 300 classes, est utilisé sous la forme d'un module Python. L'interfaçage entre C++ et Python a été grandement facilité par l'utilisation de SWIG. L'utilisation du langage Python permet de manipuler dans un cadre unifié les objets spécialisés dans la propagation d'incertitudes (algorithmes de Monte Carlo, lois de probabilités multivariées, tests statistiques,...) et les objets plus généraux par une interaction efficace avec d'autres modules, notamment matplotlib et rpy.
1.3 Un exemple grandeur nature
Intéressons-nous maintenant à l'implémentation d'un problème concret avec numpy : l'étude de l'ensemble de Mandelbrot. L'ensemble de Mandelbrot est une bizarrerie mathématique : un fractal ; c'est non seulement un objet mathématique fascinant, mais aussi fort joli. On peut en obtenir une représentation considérant un ensemble de points complexes c qui forment un carré dans le plan complexe. On itère la transformation z = z**2 + c en prenant z initialement nul et on arrête l'itération lorsque le module de z, abs(z), dépasse un seuil que nous prendrons à 10. Le tableau qui nous intéresse est la carte qui donne l'itération à partir de laquelle abs(z) franchit le seuil pour les différentes valeur de c. Une implémentation non vectorisée de cet algorithme consiste juste à le traduire en Python : il faut parcourir la grille de valeurs de c qui nous intéressent, et pour chacune de ces valeurs itérer la transformation et noter à partir de quand abs(z) franchit le seuil :
from numpy import zeros, linspace
divergence = zeros((500, 500))
for c_x in linspace(-1.5, 0.5, 500):
for c_y in linspace(-1, 1, 500):
c = c_x + c_y*1j
z = 0
for i in range(50):
z = z**2 + c
if (abs(z) > 10):
divergence[(c_x+1.49)*250,
(c_y+0.99)*250] = 50 - i
break
Si on cherche à vectoriser cet algorithme, on peut noter que les deux boucles for extérieures sont des parcours d'indices d'un tableau, et peuvent donc être remplacées par des opérations globales sur le tableau. On peut alors stocker les valeurs successives de c_x et c_y dans deux tableaux qui forment une grille comme créée par la fonction numpy ogrid. La boucle interne, elle, est une itération, et se traduit donc bien par une boucle. Finalement, il nous faut remplacer la condition par un masque et une opération sur tout le tableau :
from numpy import ogrid, zeros, ones, abs
c_x, c_y = ogrid[-1.5:0.5:500j, -1:1:500j]
c = c_x + c_y * 1j
divergence = zeros((500, 500))
z = zeros((500, 500))
masque = ones((500, 500), dtype=bool)
for i in range(50):
z[masque] = z[masque]**2 + c[masque]
masque = (abs(z) > 10)
divergence += masque
Cet algorithme se prête mal à la vectorisation, car le seuil est atteint pour différentes valeurs de c au bout d'un nombre d'itérations très différentes. Appliquer les mêmes opérations à l'ensemble du tableau conduit à faire des itérations superflues pour certaines cases du tableau. C'est pourquoi on utilise un masque qui nous permet de ne pas itérer sur les valeurs ayant dépassé le seuil. Notons que si nous itérions sans le masque, il faudrait faire attention à la divergence rapide de z : certains nombres ne pourraient être représentés par des float et apparaîtrons comme des nan après avoir dépassé le seuil. Il est alors nécessaire d'en tenir compte lors des comparaisons.
Les temps d'exécution de la version non vectorisée et de la version vectorisée sont 0.5s et 26s. Une version vectorisée, mais sans masque met 8s à s'exécuter. On peut donc voir que, dans ce cas mal adapté à la vectorisation, celle-ci ne nous fait gagner qu'un facteur 15 en temps d'exécution. La vectorisation est un art, et certains algorithmes se vectorisent nettement moins bien. Nous verrons qu'il existe d'autres solutions.
2. Tracé de courbes avec MatPlotLib
Pour explorer efficacement des problèmes scientifiques, il est indispensable de pouvoir visualiser ses résultats. Cela fait partie intégrante du processus de développement. Python excelle à ce jeu, car il dispose d'un excellent module de visualisation 2D, matplotlib [4]. Avoir des méthodes de visualisation intégrées au langage, sans faire appel à des outils extérieurs comme gnuplot, est un grand gain, car il n'est plus nécessaire de maîtriser un environnement hétérogène et de traduire les types de données. De plus, la visualisation et le traitement de données sont deux problèmes difficilement séparables.
matplotlib propose une interface appelée pylab qui s'inspire fortement des fonctions d'affichage de Matlab. pylab fournit un ensemble de fonctions très simples permettant d'afficher des courbes, des images, ou des champs de vecteurs à partir des tableaux numpy. Les détails fins d'affichage peuvent être réglés grâce à l'emploi d'arguments optionnels. L'ensemble de Mandelbrot calculé au paragraphe précédent peut être facilement visualisé :
>>> from pylab import imshow, cm
>>> imshow(divergence, cmap=cm.spectral,
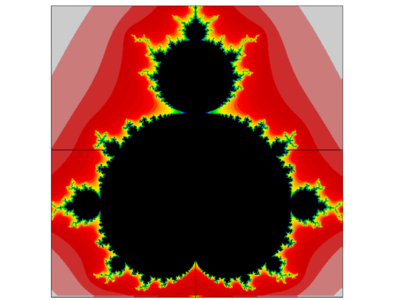
extent=(-1, 1, -1, 1))
L'ensemble de Mandebrot, visualisé avec MatPlotLib
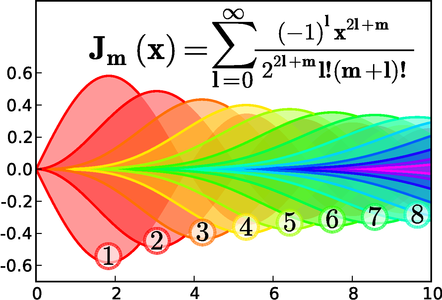
Les figures peuvent être exportées sous forme de fichiers en de nombreux formats raster, mais aussi vectoriels. De plus, MatPlotLib fournit des interfaces pour les différentes API graphiques (Tk, Wx, Qt, ...). Leur structure interne est orientée objet et se prête bien à l'inclusion dans un grand programme interactif. L'utilisateur peut zoomer sur les graphes, et les objets graphiques savent émettre des événements lorsqu'ils sont sélectionnés.
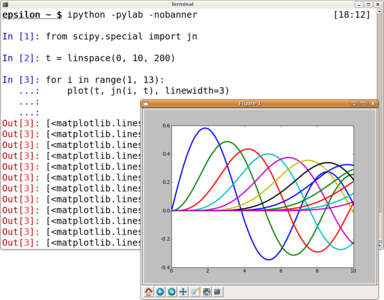
Tracé des fonctions de Bessel avec MatPlotLib. Cette figure montre à quel point MatPlotLib permet de contrôler les détails fins de l'affichage de courbes mathématiques. En plus des courbes, il est possible d'afficher des régions remplies, et du texte. MatPlotLib dispose aussi d'un moteur de rendu des équations.
3. scipy : une bibliothèque d'algorithmes
Le module scipy fournit une collection d'algorithmes numériques courants utilisant les tableaux et matrices numpy comme types de base. Beaucoup de ces algorithmes utilisent des algorithmes disponibles dans les bibliothèques scientifiques standards implémentées en C ou en Fortran, telles que LAPACK, LSODE, MINPACK et bien d'autres. En effet, les problèmes de bases rencontrés en calcul numérique sont souvent les mêmes. Malheureusement, les scientifiques ont tendance à perpétuellement réinventer la roue, car les types de données utilisées par les différentes bibliothèques en C ou en Fortran ne sont pas toujours les mêmes, ou bien parce qu'ils ne maîtrisent pas bien l'utilisation de bibliothèques avec des langages compilés.
Parmi les nombreux algorithmes disponibles dans scipy, on peut entre autres trouver des algorithmes d'optimisation, qui recherchent le minimum d'une fonction, des méthodes d'interpolation, des fonctions de traitement du signal, des procédures d'intégration numérique, de traitement d'images, de statistiques... La bibliothèque est vaste et grandit régulièrement. L'intérêt d'une telle bibliothèque généraliste est de fournir un point d'accès unique aux scientifiques pour trouver les outils dont ils ont besoin, mais aussi de permettre de construire des algorithmes élaborés qui nécessitent d'utiliser plusieurs classes d'algorithmes standards. scipy a récemment été complété par un ensemble de scikits, des petits modules qui accueillent des algorithmes dont le code ne peut aller dans scipy, parce qu'il n'est pas assez mûr ou pour des problèmes de licence.
>>> def f(x):
... return x**3 - x**2 -10
...
>>> from scipy import optimize
>>> optimize.fsolve(f, 1)
2.54451152839
Exemple de recherche du zéro d'une fonction avec scipy
4. Le travail interactif avec IPython
En recherche, l'angle d'attaque d'un problème est rarement connu à l'avance. L'algorithme s'affine au fur et à mesure que l'on explore le problème. C'est pour cela qu’un environnement interactif pour afficher les données, les traiter, essayer différentes approches est au cœur de la méthodologie scientifique moderne. Le projet IPython fournit cet environnement riche. En plus de la ligne de commande interactive de Python, IPython dispose de fonctionnalités puissantes d'édition de ligne, comme la complétion de code, le rappel d'historique, ainsi que des possibilités de sauvegarde de sessions, et bien plus.
Je développe souvent un algorithme en travaillant simultanément sous IPython, où je teste et je mets au point chaque étape, ainsi qu’avec un éditeur de fichier, dans lequel j'inscris l'algorithme pour pouvoir le réutiliser. L'outil dont je me sers le plus sous IPython est la commande %run mon_fichier.py, qui permet d'exécuter un script Python. Après l'exécution du script, les variables qu'il a définies sont accessibles dans IPython et je peux les explorer, soit en les affichant directement dans IPython, soit à l'aide de MatPlotLib. Cela me permet d'introspecter facilement l'algorithme.
De plus, si je lance IPython avec la commande ipython -pylab, le module pylab est directement importé dans IPython pour une visualisation interactive des résultats. En effet, je peux utiliser les commandes d'affichage fournies par pylab pour afficher les différents tableaux que je manipule ; elles créent alors des fenêtres MatPlotLib qui apparaissent au fur et à mesure que je travaille sous la ligne de commande IPython, sans la bloquer. Je peux interagir avec elles, par exemple en agrandissant les parties qui m'intéressent, tout en continuant à travailler sous IPython. La couche graphique de MatPlotLib tourne alors dans un différent thread que la ligne de commande IPython, mais tout ceci est transparent pour l'utilisateur.
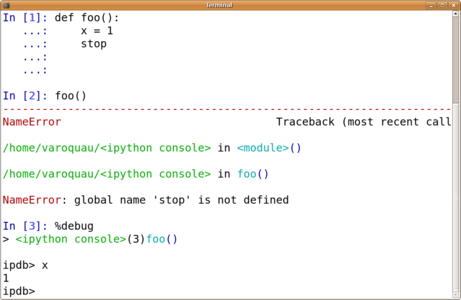
IPython m'aide aussi à comprendre les erreurs dans mon code. Lorsqu'une commande ou un script exécuté sous IPython contient une erreur, IPython affiche en couleur un traceback détaillant la pile d'appel au moment de l'erreur. La commande %debug permet de lancer le débogueur sur la dernière erreur. L'environnement interactif contient alors les variables locales de la fonction dans laquelle s'est produite l'erreur. Je peux utiliser les commandes up et down pour naviguer dans la pile d'appels et explorer les valeurs des différentes variables.
Si je traite des données, je suis amené à effectuer en plus des opérations mathématiques sur des tableaux de la manipulation de fichier. IPython introduit des raccourcis pour des actions courantes, comme les commandes système, que l'on précède alors d'un « ! », ou rappeler le résultat de la nième commande, ou encore éditer le code source correspondant à une fonction avec la commande %edit fonction. Par ailleurs, la commande %timeit m'est très utile pour mesurer la rapidité d'exécution d'une fonction, afin de guider ses choix d'optimisation. Tout ces petits détails en font un outil central pour mon travail. Finalement, IPython propose un mode spécial physique, lancé avec la commande ipython -p physics dans lequel la syntaxe de Python est modifiée pour permettre de définir facilement des grandeurs dimensionnées ; c'est mon outil favori pour faire un calcul au laboratoire :
In [1]: d = 1 m
In [2]: t = 1 s
In [3]: v = d/t
In [4]: v
Out[4]: 1 m/s
5. Visualisation 3D interactive avec Mayavi
Si MatPlotLib fournit une excellente réponse pour le tracé de courbe en 2D, ce module ne cherche pas à répondre au problème de la visualisation de données dans l'espace. Le programme Mayavi, créé à l'origine pour permettre une visualisation facile de résultats de simulations de mécanique des fluides, a beaucoup été utilisé pour visualiser des données en 3D en le scriptant en Python. Il s'appuie grandement sur la bibliothèque de visualisation VTK écrite en C++, mais est lui-même écrit en Python. Une version 2 du programme a été récrite à partir de zéro pour lui permettre d'être aussi utilisé comme une bibliothèque de visualisation 3D au sein de scripts ou de plus gros projets.
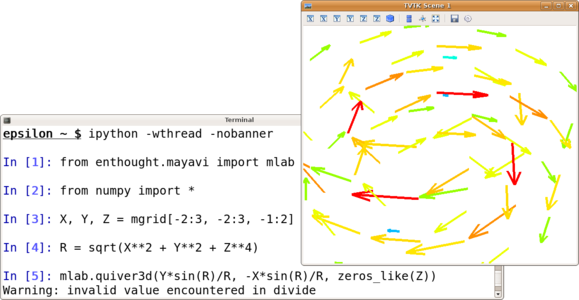
Une des difficultés rencontrées lorsqu'on veut afficher des données en 3D est de décrire comment les données sont agencées et comment on veut les visualiser : est-ce un nuage de points, une surface, un champ de vecteur ? Pour cela, les données sont traditionnellement mises dans un format dédié à VTK, mais Mayavi fournit aussi une interface simplifiée similaire à pylab qui décrit les données par des tableaux numpy. Elle peut être utilisée dans IPython pour afficher les données en 3D alors que l'on travaille interactivement.
Les objets affichés en 3D sont souvent compliqués, et il est important de pouvoir interagir avec eux, par exemple en changeant l'angle de vue ou en affichant des coupes. Mayavi permet de modifier tous les paramètres de la visualisation, soit par des boites de dialogues, soit par son API orientée objet. Par ailleurs, l'application permet à l'utilisateur avancé d'utiliser pleinement la puissance de VTK, car elle lui expose un jeu de classes Python qui correspondent aux classes de la bibliothèque C++ VTK. Il est possible par exemple de rajouter des filtres pour faire du post-traitement des données pour la visualisation, comme de la simplification de grille.
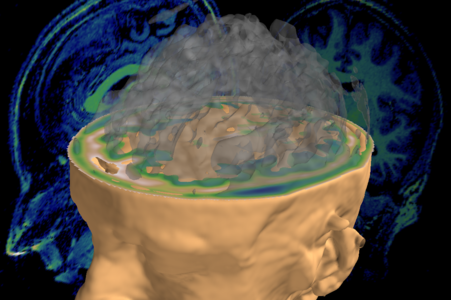
Données d'IRM du cerveau visualisées avec Mayavi
Comprendre le cerveau
Les scanneurs IRM modernes ouvrent la porte à la compréhension des mécanismes du cerveau. Cependant, le cerveau est un objet très compliqué et les données expérimentales sortant des scanneurs sont bruitées et difficiles à interpréter. Une partie de la recherche en neuro-imagerie contemporaine consiste à traiter les séquences d'images tridimensionnelles acquises sur différents sujets avec des algorithmes quantitatifs, pour extraire par exemple l'évolution temporelle de l'activité neuronale des sujets et la corréler avec leurs actions lors de l'acquisition.
Les difficultés liées à ce traitement de données sont non seulement les algorithmes qu'il faut développer, mais aussi la visualisation, et finalement l'organisation des données. Pour ce dernier problème, Python excelle, car il permet de définir des objets riches ou de se connecter à des bases de données. En effet, il faut conserver les informations sur les différents algorithmes appliqués, l'expérience menée sur le sujet, ses mouvements, etc., tout en permettant une analyse systématique sur un ensemble d'expériences et de sujets en faisant varier les différents paramètres. Python est déjà beaucoup utilisé dans la communauté de neuro-imagerie, et le projet NiPy vise à développer un module cohérent réunissant les outils spécifiques dont les chercheurs ont besoin.
6. Interfaces avec d'autres langages
L'utilisation de Python est un grand gain en rapidité de développement et en facilité de maintenance du code par rapport aux langages compilés, comme le C ou le Fortran, mais il faut avouer que malgré les optimisations de numpy et de scipy, le code compilé reste plus rapide. De plus, il existe une grande quantité de codes scientifiques écrits dans ces langages qu'il est important de pouvoir réutiliser. Soyez rassurés, il est très facile de mêler Fortran, C et Python. C'est même l'une des grandes forces de Python par rapport à d'autres langages scientifiques de haut niveau comme Matlab ou Mathématica, qui n'ont que des interfaces rudimentaires avec les langages compilés.
6.1 Inclure du C avec weave
Tout d'abord, il est possible d'inclure des bouts de code C++ directement dans le code Python sous forme de chaîne de caractères en utilisant le module scipy.weave. Celui-ci compile le bout de code lorsqu'il est appelé pour la première fois et s'occupe de faire le passage d'arguments de Python au C++. On peut donc récrire le code étudié plus haut pour prendre le laplacien d'un tableau :
from numpy import zeros_like
from scipy import weave
def laplace(I):
I2 = zeros_like(I)
nx, ny = I.shape
weave.inline("""
for (int i=1; i<nx-1; ++i) {
for (int j=1; j<ny-1; ++j) {
I2(i, j) = (I(i-1, j) +
I(i+1, j) +
I(i, j-1) +
I(i, j+1))*0.25;
} }""",
['I', 'I2', 'nx', 'ny'],
type_converters=weave.converters.blitz)
return I2
Grâce aux blitz converters, les tableaux I et I2 sont passés sous forme d'un objet blitz I(i, j) au code C++, qui permet d'accéder à leurs éléments et de les modifier. Le code C++ modifie donc le tableau I2 et, comme il s'agit de la même plage mémoire en C++ et en Python, celui-ci est aussi modifié dans la couche Python.
Une bonne règle à suivre, lorsqu'on mélange du code C et du code Python, est de laisser Python faire la gestion mémoire. Ainsi, au lieu de créer un tableau en C, on peut en passer en vide, créé en Python, comme je l'ai fait pour I2 dans l'exemple ci-dessus. Ainsi, on n’a pas à se préoccuper d'allouer ou de libérer la mémoire, Python s'en charge.
6.2 Cython
Le projet le plus ambitieux et le plus prometteur pour ce qui est de mélanger langages compilés et Python, c'est-à-dire un langage dynamique, est Cython. Ce projet, qui descend du projet Pyrex, introduit un nouveau langage qui ressemble comme deux gouttes d'eau à Python, mais permet de spécifier des informations supplémentaires, comme des déclarations de type. Le code Cython est transformé en du code C, qui est compilé en langage machine, mais qui forme une bibliothèque liée à la machine virtuelle Python. La machine virtuelle Python est utilisée pour exécuter les parties typées dynamiquement, qui ne s'exécuteront pas plus vite que du code Python normal ; cependant, les opérations pour lesquels Cython peut déterminer les types de toutes les variables seront aussi rapides que du code C normal. L'exemple du laplacien peut être aussi écrit en Cython. Comme dans la plupart des cas, transformer le code Python en code Cython consiste simplement à rajouter les informations de types :
cimport numpy
cimport cython
@cython.boundscheck(False)
def blur_cython(numpy.ndarray[double, ndim=2] I):
cdef numpy.ndarray[double, ndim=2] I2
I2 = I.copy()
cdef int i, j
for i in range(1, I.shape[0]-1):
for j in range(1, I.shape[1]-1):
I2[i, j] = (I[i-1, j] + I[i+1, j] +
I[i, j-1] + I[i, j+1])*0.25
return I2
Pour pouvoir exécuter cet exemple, il me faut le compiler. Pour cela, le plus simple est de créer un fichier setup.py contenant :
from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext
ext_modules=[Extension("exemple", ["exemple.pyx"])]
setup( cmdclass = {'build_ext': build_ext},
ext_modules = ext_modules)
que l'on exécute en appelant python setup.py build_ext --inplace.
Le support des tableaux multidimensionnels dans Cython a été implémenté cet été, grâce au support de Google et d’Enthought. Le décorateur boundscheck peut être utilisé pour indiquer à Cython de ne pas vérifier les bornes des tableaux, lors de leur indexage. Le code résultant est plus rapide, mais court aussi le risque de « segfaulter ». Une erreur courante avec Cython est d'oublier de déclarer le type d'une variable, comme une variable peu importante, i ou j dans notre exemple. Le code fonctionne alors sans erreur, mais la variable est typée dynamiquement et ralentit grandement l'exécution. Malgré ces limitations, je préfère écrire du code Cython que du code C, car la syntaxe est plus proche de Python et je bénéficie des objets Python, que je peux utiliser en payant un coût en performance.
Cython est un projet très dynamique et cherche au maximum la facilité d'utilisation. Ainsi, lorsqu'une erreur se produit pendant l'exécution d'une bibliothèque Cython, Python génère des tracebacks qui montrent la pile d'appel dans le code Cython d'origine, tout comme lors de l'exécution de code Python normal. Finalement, Cython est très bien documenté [7].
6.3 Rapidité d'exécution
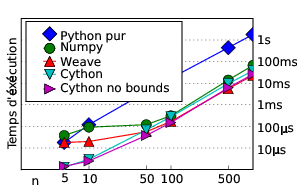
Armé de ces deux nouveaux outils, nous pouvons chiffrer le temps d'exécution de notre routine test, le calcul du laplacien d'un tableau.
Temps d'exécution du calcul du laplacien pour différentes tailles de tableau.
Sur l'exemple du laplacien, pour des grands tableaux, Weave ou Cython apportent un gain en vitesse d'exécution d'un facteur 2 par rapport au code numpy, soit un facteur 60 par rapport au code Python.
Le gain en rapidité d'exécution par rapport à du code numpy bien écrit n'est donc pas foudroyant, tout du moins sur l'exemple du laplacien qui se vectorise très bien. L'effort pour produire et maintenir le code est cependant beaucoup plus important. Il convient donc de limiter au maximum cette utilisation de code compilé. La règle à suivre est de chercher d'abord à développer un algorithme qui marche, en cherchant à bien le comprendre et l'analyser grâce aux outils interactifs comme IPython, MatPlotLib ou Mayavi ; une fois satisfait par l'approche générale, il faut d'abord chercher à bien optimiser l'algorithme, sa vectorisation, à utiliser des bibliothèques numériques déjà écrites comme scipy, tout en mesurant en continu les gains en performance (par exemple en utilisant %timeit sous IPython). Je ne considère l'utilisation de code compilé que comme un dernier recours, et uniquement aux quelques endroits critiques au sein du projet scientifique. Le but d'un code scientifique n'est généralement pas de tourner le plus vite possible, mais de produire des résultats scientifiques.
6.4 L'ensemble de Mandelbrot
Le calcul du laplacien se vectorise extrêmement bien, et il ne semble pas justifiable d'employer des langages compilés pour ce problème. Cependant, nous avons vu que le calcul de l'ensemble de Mandelbrot se prêtait beaucoup moins bien à la vectorisation. Regardons la performance des versions Weave et Cython. Dans les deux cas, nous devons utiliser trois boucles for, comme dans l'implémentation en pur Python, ce qui nous permet d'interrompre l'itération dès que le seuil de divergence est atteint, et donc d'éviter les calculs superflus. Il nous faut aussi implémenter les calculs sur des nombres complexes à la main. En Weave, les calculs sont simplement les opérations sur les éléments des tableaux, et on peut s'inspirer de l'implémentation pur Python pour la traduire en C :
from numpy import zeros
from scipy import weave
divergence = zeros((500, 500))
weave.inline(r"""
float x, y, x_buffer, c_x, c_y ;
for (c_x=-1.5; c_x<0.5; c_x=c_x+0.004) {
for (c_y=-1; c_y<1; c_y=c_y+0.004) {
x = 0; y = 0;
for (int i=0; i<50; i++) {
x_buffer = x*x - y*y + c_x ;
y = 2*x*y + c_y;
x = x_buffer ;
if ((x*x + y*y) > 100) {
divergence(
(int) ((c_x+1.5)*250),
(int) ((c_y+1)*250)
) = 50 - i;
break;
}
}
}
}""",
['divergence'],
type_converters=weave.converters.blitz)
Le code étant du code C, il faut bien entendu faire attention à la conversion de type, par exemple dans l'indexage des tableaux. À trop faire du Python, on finit par oublier ces détails importants du C.
En Cython, le code ressemble fortement au code Python correspondant, au détail près qu'il nous faut effectuer à la main les opérations sur les nombres complexes :
cimport numpy
from numpy import zeros
cdef numpy.ndarray[double, ndim=2] divergence
divergence = zeros((500, 500))
cdef float x, y, x_buffer, c_x, c_y
cdef int i, j, n
c_x = -1.5
for i in range(500):
c_y = -1
for j in range(500):
c_y += 0.004
x = 0; y = 0
for n in range(50):
x_buffer = x*x - y*y + c_x
y = 2*x*y + c_y
x = x_buffer
if (x*x + y*y > 100):
divergence[i, j] = 50 - n
break
c_x += 0.004
Nous pouvons à nouveau nous intéresser à la performance de ces implémentations. Pour mémoire, l'implémentation Python pur prend 26s et celle en numpy prend 0.5s. Passer à du code compilé nous permet de gagner encore un ordre de grandeur : l'implémentation en Weave prend 64ms et celle en Cython 59ms. On gagne donc beaucoup en vitesse à passer à du code compilé pour cet exemple, mais encore faut-il que les besoins scientifiques justifient l'excès en complexité pour que cela soit rentable. Je dois avouer que je n'ai presque jamais utilisé du code compilé au sein de mon code Python pour mes projets de recherche, mais de savoir que j'ai cette possibilité si j'ai des besoins particuliers de performance me permet d'utiliser Python sans douter de mon choix de langage.
6.5 Réutiliser des bibliothèques Fortran ou C
Si l'on a une grande quantité de code à écrire en C, il peut être plus pratique de compiler des bibliothèques C. De même, on peut vouloir utiliser des bibliothèques C existantes, dont on n’a pas forcément le code source. Le module ctypes permet de charger des bibliothèques C sous Python et de définir la signature des fonctions qu'elles contiennent pour pouvoir les utiliser de façon transparente à partir de Python. De plus, les tableaux numpy savent exposer leur structure interne sous forme d'un tableau C dont on récupère l'adresse mémoire pour la passer aux fonctions de la bibliothèque en C.
Par ailleurs, il existe une grande quantité de code scientifique écrit en Fortran. Il est important de pouvoir le réutiliser, pour pouvoir bâtir les efforts de recherche actuels sur des résultats passés. Du code Fortran peut facilement être chargé dans Python. Pour cela, on utilise le script f2py qui sait compiler un programme Fortran en un module que l'on importe dans Python de façon transparente. Chaque fonction en Fortran est automatiquement importée, car f2py sait analyser les signatures des fichiers Fortran.
Finalement, si l'on veut interfacer une grosse bibliothèque C++, par exemple avec des diagrammes de classes compliqués, SWIG est un système puissant d'analyse de code qui sait interpréter du C++ pour générer du code Python l'appelant. On peut même spécifier toute une logique de conversion de types et de templates de C++ vers Python. C'est cependant un outil avancé, à l'utilisation plus délicate.
6.6 Interagir avec d'autres environnements scientifiques
Il est important de pouvoir réutiliser le code déjà écrit dans des langages compilés, mais il peut aussi être important de pouvoir bénéficier du travail écrit dans d'autres langages dynamiques, tels que Matlab. Ainsi, bien que je trouve le langage de statistiques R nettement moins agréable que Python, il existe une grande quantité d'algorithmes de statistiques implémentés en R. Le module rpy permet ainsi d'accéder aux fonctionnalités du langage R sous Python en appelant directement les fonctions C sous-jacentes et en exposant les objets R en Python. Pour pouvoir faire une interface aussi élégante, il faut cependant pouvoir appeler l'environnement que l'on veut réutiliser comme une bibliothèque. Malheureusement, tous ne se prêtent pas à cela.
Plus généralement, on peut utiliser des pipes pour communiquer avec des processus. Le module PyMat crée ainsi une instance de MatLab, avec laquelle il communique pour exécuter du code Matlab. De même, le module gnuplot permet de faire de la visualisation avec Gnuplot en lui envoyant les données par l'intermédiaire de la fonction pipe du module os. Ceci peut être utile pour réutiliser des scripts Python existants, mais fait perdre bien des avantages de Python, même en utilisant le module gnuplot. En effet, il y a un fort surcoût en mémoire et en temps d'exécution à transférer les variables d'un processus à l'autre. De plus, les structures de données riches et la bonne gestion d'erreur de Python sont perdus. Je n'ai recours à ces solutions que si un module Python natif ne me permet pas de faire ce dont j'ai besoin, mais, encore une fois, c'est rassurant de savoir qu'elles existent.
Concevoir des ailes
Au centre de recherche d'Airbus, à Bristol en Angleterre, plus de 2000 ingénieurs travaillent à concevoir et tester des ailes d'avion. Une grande partie du travail de conception se fait à l'aide de simulations très complexes déployées sur de gros clusters. Le cœur dur numérique de ces simulations sont principalement écrites en C et en Fortran, mais depuis quelques années Airbus utilise Python pour guider les simulations.
En plus du code qui tourne sur les clusters pendant la simulation, les ingénieurs utilisent une application interactive développée en Python pour mieux comprendre les résultats d'une simulation et préparer les suivantes. Cette application combine conception et dessin des profils des ailes avec le traitement et la visualisation de données, utilisant entre autres Mayavi2.
7. Au-delà du calcul numérique : networkX et sympy
Tous les problèmes scientifiques ne se résument pas à des manipulations de nombres. Ainsi, en génétique, l'exploration des filiations entre espèces se fait naturellement en représentant les données sur des arbres, qui ne sont que des cas particuliers de graphes. Les graphes sont une structure mathématique formée de sommets connectés entre eux par des arrêtes. Ils peuvent servir à décrire les réseaux, souvent de connectivité complexe, que l'on rencontre en chimie, en étudiant de grandes molécules, en informatique théorique, en économie ou encore en sociologie.
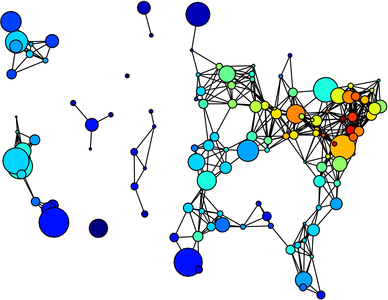
Un graphe des principales villes américaines avec leur population, et la circulation sur les autoroutes le reliant, représenté à l'aide de NetworkX et MatPlotLib
networkX est un module Python optimisé pour décrire, représenter et étudier les graphes. Il dispose d'algorithmes standards, en théorie des graphes, permettant par exemple de trouver la distance la plus courte entre deux sommets donnés (problème dit « de percolation sur graphe »), d'isoler des sous-ensembles non connectés, d'étudier les propriétés de transport, comme sur un réseau informatique ou les propriétés statistiques du réseau. Je peux par exemple utiliser networkX pour trouver le moyen le plus rapide d'aller de Paris à Austin, connaissant les temps de vols entre les différents aéroports :
In [1]: import networkx as NX
In [2]: G = NX.XGraph()
In [3]: G.add_edges_from((
...: ('Paris', 'Dallas', 10),
...: ('Dallas', 'Austin', 1),
...: ('Paris', 'NY', 7),
...: ('NY', 'Dallas', 5)))
In [4]: NX.draw_graphviz(G, prog='fdp')
In [5]: NX.dijkstra_path(G, 'Paris', 'Austin')
Out[5]: ['Paris', 'Dallas', 'Austin']
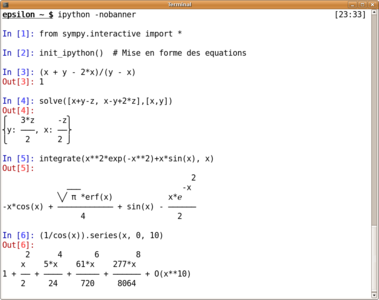
Le module sympy définit des expressions symboliques sous Python. Ces objets permettent du calcul formel en Python lorsqu'ils sont manipulés avec les opérateurs standards comme l'addition ou la multiplication. De plus sympy fournit un ensemble de fonctions de calcul, comme la dérivation, l'intégration ou la recherche de solution à des équations. sympy est assez jeune et ne peut encore être considéré comme un système de calcul formel complet. Cependant, il est très intéressant de pouvoir manipuler des expressions symboliques dans un programme où l'on utilise des tableaux numpy pour faire du calcul numérique. En effet, simplifier une expression ou la dériver peut grandement accélérer un calcul numérique.
Une session sympy sous ipython. Les variables x, y et z sont définies dans sympy.interactive.
Sage : un environnement pour les mathématiques fondamentales
La recherche en mathématiques pures utilise l'informatique à la fois pour automatiser les travaux systématiques dans des démonstrations et pour des expériences virtuelles avec des objets mathématiques, pour développer l'intuition, et conduire à des conjectures qui pourront alors être démontrées de façon formelle.
Pour cela, le chercheur a besoin d'un environnement qui lui permette de manipuler les objets abstraits mathématiques, de définir et d'appliquer des opérations dessus, et de les visualiser. Il existe de nombreuses bibliothèques permettant de faire cela pour différents domaines des mathématiques, mais elles ne sont généralement accessibles que par l'intermédiaire d'un langage compilé, et ne fournissent pas un environnement très propice à l'exploration. De plus, il est difficile de les combiner. Sage est un projet qui utilise Python comme langage pour construire un environnement combinant les différentes bibliothèques en un ensemble homogène. Sage peut être utilisé en ligne sur http://sagenb.org.
8. Des outils intégrés, une plate-forme non spécialisée
J'espère que l'énumération ci-dessus de modules scientifiques disponibles sous Python vous a convaincu que c'est une plate-forme très riche pour le calcul scientifique, même si je n'ai fait qu'explorer la surface de ce monde. Ses outils, qui sont souvent basés sur des bibliothèques existantes en langages compilés, forment beaucoup plus qu'un jeu de programmes indépendants : ils partagent entre autres le langage, l'interpréteur, les types de données ou la gestion d'erreur. J'ai utilisé par le passé des jeux de scripts shell appelant toute sorte de programmes scientifiques, comme Gnuplot ou Octave, ainsi que des bouts de codes compilés. Non seulement, il faut apprendre un nouveau mini-langage pour chaque outil, mais en plus une bonne partie du temps et de l'énergie est gâchée à faire parler un programme avec un autre. Les modules listés ci-dessus sont tous basés sur les mêmes types de données, car Python fournit des types de bases riches, qui sont complétés par numpy. On peut mêler de façon transparente les modules et espérer construire un programme cohérent, par exemple avec une interface graphique, et une bonne gestion d'erreur, des possibilités intégrées de débogage ou de profiling... De plus, le langage n'est pas un langage spécialisé au domaine scientifique, et l'on peut bénéficier d'excellents modules développés par d'autres communautés. Ainsi, l'un de mes collègues développe un appareil intégré d'analyse spectroscopique de l'air qui sera déployé sur le terrain ; il contrôle son appareil et visualise les données à l'aide d'une interface web, développée avec le module de développement web Django, en combinaison avec MatPlotLib.
Bien entendu, tout n'est pas parfait et l'informatique scientifique avec Python souffre aussi de problèmes. Tout d'abord, on peut noter que la qualité de la documentation laisse beaucoup à désirer. La communauté est très consciente de ce problème, et maintenant que les différentes bibliothèques ont mûri, un sérieux effort de documentation est en court : le site http://docs.scipy.org permet non seulement d'accéder à la documentation distribuée avec numpy et scipy, mais aussi de l'améliorer, à la manière de Wikipédia. Par ailleurs, les différentes bibliothèques dépendent souvent de codes numériques difficiles à compiler, comme ATLAS ou VTK. L'installation peut donc être un problème. Je pense que la solution à ce problème peut être trouvée grâce à des distributions formées de l'ensemble de binaires de ces modules. Ainsi, l'Enthought Python Distribution (http://www.enthought.com/epd/) est une distribution multiplateforme supportée commercialement, tandis que PythonXY (http://pythonxy.com) est une distribution libre, mais uniquement sous Windows. Sous Linux, la proportion de ces modules offerts par les distributions varie, Ubuntu et Debian offrant la meilleure couverture.
La combinaison d'un langage très agréable à utiliser, d'une communauté dynamique et d'un ensemble d'outils scientifiques très complet fait de Python un environnement idéal pour le travail scientifique qui se détache comme le langage scientifique du futur. Si, il y a quelques années, le langage était méconnu dans la communauté scientifique, je rencontre aujourd'hui un nombre grandissant de collègues ayant franchi le pas. Mes collègues d'Airbus m'ont confié qu'ils incitaient les universités à ce que les étudiants apprennent Python. Et ce n'est qu'un début ! Le langage est très jeune pour la communauté scientifique et les progrès sont en train de s'emballer en ce moment même.
Bibliographie
[1] VAROQUAUX, (G.), « Agile Computer Control of a Complex Experiment », Computing in Science & Engineering, vol. 10, p. 55 ; 2008.
[2] Oliphant, Guide to NumPy, Tregol publishing, 2005
[3] BRUCHER (M.), « Python : Les fondamentaux du langage – La programmation pour les scientifiques », ENI Ressources Informatiques, 2008.
[4] HUNTER, DALLE (D.), Guide de l'utilisateur de matplotlib,
http://matplotlib.sourceforge.net/
[5] Documentation en ligne de scipy et numpy : http://docs.scipy.org
[6] RAMACHANDRAN, VAROQUAUX (G.), Guide de l'utilisateur de Mayavi2,
http://code.enthought.com/projects/mayavi
[7] Documentation en ligne de Cython : http://docs.cython.org/
[8] VAROQUAUX (G.), VAUGHT (T.), MILLMAN (J.), « Proceedings of the 7th Python in Science conference », 2008.
http://conference.scipy.org/proceedings/SciPy2008/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture