Accélération de Python avec Numba

Plusieurs solutions sont possibles pour accélérer Python ([1] et [2]). Numba, l'une de ces solutions, propose un bon compromis entre la complexité d’utilisation et l'amélioration des performances. Numba utilise LLVM pour compiler « à la volée » (Just In Time) des portions de code Python afin d’accélérer les programmes. Il est aussi possible de compiler du code CUDA pour profiter des performances des cartes NVIDIA. Dans cet article, plusieurs optimisations vont être proposées afin d’améliorer grandement les temps de calcul de Python.

1. Configuration de la machine de test

La machine utilisée a été assemblée fin 2014, elle n’est donc pas équipée des toutes dernières technologies, mais l’exemple proposé va montrer que de telles machines peuvent encore avoir de très bonnes capacités de calcul.

1.1 Processeur principal

Le processeur principal est un AMD FX-8320 comprenant 8 cœurs cadencés à 3,5 GHz. La mémoire principale du système est de 16 Gio (ce qui ne sera pas un facteur limitant pour nos programmes).

1.2 Carte graphique

La carte graphique est équipée d'un processeur NVIDIA GeForce GTX 970 (architecture Maxwell) avec 4096 Mio de mémoire vidéo. Elle est cadencée à 1050 MHz. Ce processeur contient 1664 cœurs CUDA pouvant être utilisés pour le calcul parallèle.

L’architecture Maxwell correspond à la version 5 des capacités de calcul (Compute capabilities). Les cartes les plus modernes sont équipées de processeurs compatibles avec la version 7.5.

1.3 Installation des différents éléments

Les premières versions de CUDA avaient souvent mauvaise presse sous GNU/Linux. Les pilotes propriétaires n’étaient pas disponibles dans les paquets des principales distributions. Les drivers devaient être installés à la main et souvent l’environnement graphique ne redémarrait pas à la suite de cette installation.

Depuis quelques années, les pilotes NVIDIA sont proposés par la plupart des distributions. Sur la distribution utilisée pour rédiger cet article (Linux Mint 19.3 basée sur une Ubuntu 18.04), les paquets nvidia-driver-440 et cuda (en version 10.2.89) suffisent pour profiter de CUDA.

Python est utilisé en version 3 et Numba a été installé avec le gestionnaire de paquet pip :

Numba est normalement opérationnel et peut utiliser CUDA.

2. CUDA

La technologie CUDA de NVIDIA permet de programmer les cartes graphiques pour accélérer des calculs « ordinaires ». CUDA propose une abstraction du matériel NVIDIA, quelle que soit la génération de la carte (à partir de la série GeForce 8 de fin 2006).

CUDA permet d’écrire un programme sans connaître toutes les caractéristiques physiques de la carte. La répartition des processus sur les différents cœurs équipant la carte se fera automatiquement en fonction des paramètres choisis par le programmeur.

2.1 Processus

Les processus exécutés dans le processeur NVIDIA sont nommés threads dans la terminologie CUDA. Le programme exécuté par les threads est appelé kernel. Plusieurs langages peuvent être utilisés pour écrire les kernels ; NVIDIA propose un compilateur C/C++ ou Fortran. Dans cet article, nous allons utiliser le compilateur Numba qui permet d’écrire les kernels en Python. Sur ces langages, les kernels sont écrits comme des fonctions n’ayant pas de valeur de retour.

Les threads sont regroupés dans des blocs. Tous les threads composant un bloc sont considérés comme exécutés en même temps (même si ce n’est pas forcément le cas physiquement). Ils peuvent partager de la mémoire, mais en veillant à éviter les problèmes de concurrence des opérations de lecture/écriture.

L’ensemble des blocs forme la grille de calcul. Les blocs (et donc la grille) peuvent avoir une, deux ou trois dimensions. Le nombre de blocs composant la grille et le nombre de threads dans les blocs doivent être spécifiés lors de l’appel du kernel. À l’intérieur du kernel, il est possible de connaître le numéro de bloc et le numéro de thread.

2.2 Mémoires

Chaque thread dispose d’une quantité limitée de mémoire dédiée très rapide : les registres. Les cartes actuelles proposent 256 registres de 32 bits par thread.

Les groupes de threads peuvent utiliser de la mémoire partagée avec un temps d’accès un peu plus élevé que celui des registres. Selon la carte, la mémoire partagée est comprise entre 48 et 96 KB.

La mémoire globale est accessible par tous les threads, mais avec un très mauvais temps d’accès. Sur la carte utilisée, cette mémoire est de 4 Gio, c’est la quantité de mémoire communiquée par le fabricant de la carte.

Pour des données en lecture seule, la mémoire constante permet d’avoir des temps d’accès proches de la mémoire partagée. Quel que soit le modèle de carte, la mémoire constante est de 64 KB.

Enfin, l’API C de CUDA permet d’accéder à un autre type de mémoire non utilisé par Numba, la mémoire texture optimisée pour des accès dans des zones mémoires proches.

3. Calculs de distances

3.1 Présentation

Différentes implémentations d’un même programme vont être comparées pour apprécier la complexité de l’écriture et les performances. Les comparaisons de performances seront faites à la fin de cette section après avoir présenté les différentes implémentations.

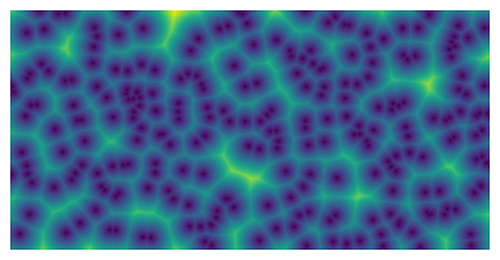
Des points sont choisis aléatoirement dans un tableau bidimensionnel comme germes pour générer une image. Pour chaque point de l’image, la distance avec tous les germes est calculée et la plus petite des distances est assignée au point, puis en utilisant un dégradé de couleurs pour afficher les distances, l’image de la figure 1 est construite.

Ce programme est dérivé des diagrammes de Voronoï. Dans les diagrammes de Voronoï, ce sont les limites entre les zones d’influences des germes qui sont tracées.

3.2 Programme de référence en Python

En Python « ordinaire », le programme s’écrit assez simplement. Pour rechercher la distance minimale, il est nécessaire de remplir une variable avec une valeur suffisamment grande :

L’algorithme a une complexité en O(n²) si le nombre de germes est faible devant la dimension de l’image.

3.3 Réécriture avec NumPy

Le programme précédent ne profite pas des optimisations de NumPy. Il comporte 3 boucles imbriquées qui ralentissent le programme. La bibliothèque NumPy permet d’accélérer des calculs s’ils peuvent être écrits de manière vectorielle.

Pour éviter les boucles sur les dimensions de l’image, la fonction mgrid est utilisée pour construire deux tableaux bidimensionnels contenant les coordonnées des points. Un tableau tridimensionnel est initialisé avec des zéros pour contenir les distances entre les points et les germes.

Une seule boucle reste pour calculer les distances de tous les germes avec chaque point. Les distances minimales sont calculées avec la méthode min en passant en argument l’indice de la dimension à utiliser pour la recherche du minimum (ici, la dernière). Le résultat est ensuite copié dans le tableau de destination.

3.4 Optimisation avec Numba

L’utilisation de Numba sur le CPU est extrêmement simple, un décorateur permet de spécifier si une fonction doit être accélérée sur le CPU. Il existe deux décorateurs @jit ou @njit (qui correspond à l’option nopython=True pour @jit).

Le décorateur @jit est le plus laxiste : il tente d’abord une compilation sans utiliser l’API C de Python et en cas d’échec, il basculera sur l’utilisation de l’API C de Python ; dans ce cas, les performances seront peu différentes de l’implémentation Python. En utilisant l’option nopython=True, Numba provoquera une exception si le programme nécessite l’API C de Python.

Le programme est inchangé par rapport à l’implémentation Python de référence, seul le décorateur est ajouté.

L’option cache=True permet d’éviter une nouvelle compilation à chaque appel de la fonction, ce qui permet de gagner du temps en cas d’appels multiples.

3.5 Optimisation avec Numba et CUDA

La fonction est peu modifiée pour être utilisée sur la carte graphique. Le décorateur @cuda.jit est ajouté pour cibler la compilation sur la carte graphique. Les cordonnées dans le tableau sont calculées directement par la fonction grid (qui peut être utilisée pour des coordonnées dans un tableau 1D, 2D ou 3D). Ces coordonnées sont calculées à partir de la configuration d’appel du kernel (détaillée dans la fonction suivante). Il est nécessaire de vérifier la validité des coordonnées obtenues (x et y), car un débordement est possible. Le reste du code est identique à la fonction Python initiale.

Pour utiliser un kernel, il faut préciser une configuration lors de l’appel. Cette configuration doit spécifier le nombre de threads par blocs et le nombre de blocs composant la grille de calcul. Les blocs (et donc la grille) peuvent avoir une, deux ou trois dimensions.

Puisque le problème est bidimensionnel, le mieux est d’utiliser une configuration à deux dimensions (il est tout à fait possible d’utiliser une configuration différente et ensuite de faire des décalages d’indices, c’est simplement moins naturel…). La configuration est composée du nombre de threads par blocs et du nombre de blocs utilisés. Le nombre de threads et la taille des données à traiter fixent le nombre de blocs (en divisant la taille par le nombre de threads par blocs et en arrondissant au supérieur, d’où la vérification dans le kernel).

Le kernel est ensuite appelé avec la notation dédiée (propre à Numba, proche de celle de CUDA en C) qui nécessite le nombre de blocs dans la grille et le nombre de threads par blocs. Le nombre maximum de threads dans un bloc est de 1024, quelle que soit la topologie retenue. Puisque nous avons retenu des blocs bidimensionnels, une configuration de 32 threads par 32 threads permet d’utiliser les 1024 threads possibles. Il n’est pas nécessaire que la disposition des threads soit carrée (la configuration de 64 par 16 aurait tout à fait été possible).

3.6 Amélioration du programme CUDA

Pour optimiser le programme, il est possible de changer le tableau contenant les germes, car il n’est pas modifié par le kernel. Sans spécification particulière, les données sont dans la mémoire générale de la carte graphique, qui est très peu performante. La mémoire constante est très performante en lecture, mais il n’est pas possible d’y écrire depuis les kernels. Elle est donc tout à fait indiquée pour le stockage des coordonnées des germes.

La fonction array_like est utilisée pour accéder à un élément en mémoire constante. Le reste du kernel est inchangé, ainsi que l’appel du kernel (qui n’est pas repris ici).

3.7 Résultats

La figure 2 présente l’évolution du temps de calcul en fonction de la taille de l’image générée. L’algorithme ayant une complexité en O(n²), une représentation logarithmique des temps de calcul a été retenue. Cette représentation est d’autant plus efficace que les temps de calcul sont très différents selon l’implémentation retenue.

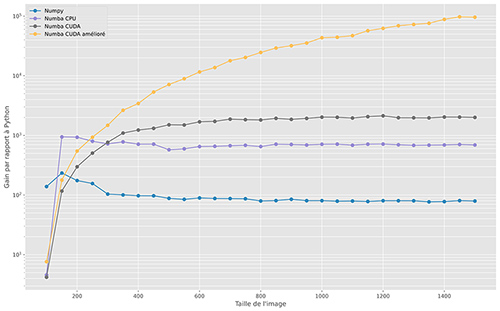
L’accélération des différentes implémentations par rapport à l’implémentation initiale en Python est présentée dans la figure 3 (comme pour la figure précédente, une échelle semi-logarithmique est utilisée). Plusieurs constats peuvent être faits :

• NumPy permet une accélération quasiment constante, avec un code 80 fois plus rapide que l’implémentation Python initiale ;
• le code Python compilé par Numba est presque 700 fois plus rapide que le Python (et donc presque 100 fois plus rapide que le code NumPy) ;
• l’implémentation CUDA élémentaire nécessite des images conséquentes pour que l’accélération soit optimale. Dans ce cas, le programme s’exécute presque 2000 fois plus rapidement que le code Python ;
• l’utilisation de la mémoire constante pour le stockage des germes améliore grandement les performances de l’implémentation sur la carte graphique.

3.8 Découpage du problème

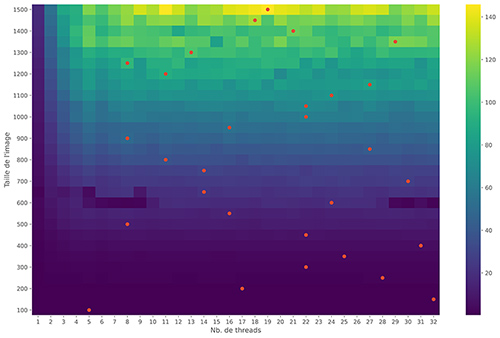
Lors de l’appel du kernel CUDA, le nombre de processus a été arbitrairement fixé au maximum possible, sans aucune réflexion. Afin d’apprécier les conséquences du nombre de threads utilisés sur la vitesse d’exécution, le gain en temps de calcul en fonction du nombre de threads et de la taille de l’image a été calculé. Pour chaque taille d’image, le gain en temps en calcul maximum a été marqué par un point rouge sur la figure 4.

Le maximum de performance n’est pas nécessairement obtenu pour le nombre maximum de threads possible (il n’y a que pour une taille d’image de 1300 de côté que l’on profite du nombre maximum de threads possible). Optimiser le nombre de threads pour un problème donné est assez délicat. NVIDIA propose une feuille de calcul (CUDA Occupancy Calculator) qui peut être utilisée afin de rechercher les performances optimales. Il est par contre nécessaire de bien connaître la mémoire utilisée par son kernel en utilisant le débogueur de Numba. Ces optimisations sortent du cadre de cet article, elles ne seront pas traitées ici. Si le problème travaille sur des données de taille constante, la solution la plus simple et de réaliser des mesures de performance comme ici.

4. Le jeu de la vie

4.1 Présentation

Le jeu de la vie est la base des automates cellulaires ([3][4]). Il a été proposé par J.H. Conway (disparu récemment).

On considère un monde représenté par une grille à deux dimensions, rempli aléatoirement de valeurs binaires (les cellules). Le principe du jeu est de faire évoluer les valeurs des cellules selon les règles suivantes :

• une cellule naît (passe de 0 à 1) s’il y a juste 3 cellules vivantes dans son voisinage (les 8 cellules qui l’entourent) ;
• une cellule reste vivante si elle est entourée de 2 ou 3 cellules vivantes dans son entourage.

Dans tous les autres cas, s’il y a une cellule dans la case, elle meurt. Par rapport à la règle initiale du jeu de la vie, nous avons retenu la règle suivante :

• si le nombre de cellules vivantes entourant la cellule est de 3 ou 4, la cellule est maintenue en vie ;
• si une case vide est entourée de 3 ou 4 cellules vivantes, une nouvelle cellule apparaît.

Cette modification conduit à un code un peu plus simple, pour éviter des listings trop longs.

Afin de construire une animation, l’intégralité des générations va être conservée ainsi que l’âge des cellules (il est incrémenté à chaque génération). Les données sont placées dans un tableau à trois dimensions, la première étant la génération, les deux autres étant les dimensions spatiales. L’initialisation remplit le tableau de zéros.

La génération initiale est remplie aléatoirement de valeurs 0 ou 1 avec une probabilité fixée par la variable seuil.

Comme précédemment, les différentes implémentations seront présentées et les performances seront discutées dans le paragraphe dédié.

4.2 Programme de référence en Python

L’écriture du programme Python est l’application directe des règles du jeu de la vie. La boucle la plus extérieure parcourt les générations, les deux autres boucles parcourent la grille. Les données de la génération t-1 sont utilisées pour calculer la génération t.

Les cellules composant la bordure de la grille ne sont pas prises en compte par la boucle, pour éviter d’avoir à gérer les cas particuliers des bords (certaines implémentations du jeu de la vie considèrent un monde rebouclé sur les deux dimensions).

4.3 Optimisation avec Numba

L’optimisation avec Numba se fait simplement en ajoutant le décorateur @njit(cache=True) avant la déclaration de fonction. Le reste est identique à la fonction précédente.

4.4 Portage sur la carte graphique

Le portage en CUDA se fait comme précédemment avec un kernel exécuté sur la carte graphique et une fonction qui l’appellera pour le calcul de chaque génération.

L’écriture du kernel reprend les grandes lignes du programme Python. Comme précédemment, la fonction grid permet d’obtenir les coordonnées du kernel dans la grille de calcul, et donc de la cellule. Le reste est identique.

4.5 Utilisation de la mémoire graphique

Sans modifier le kernel, la fonction d’appel est modifiée pour accéder directement à la mémoire graphique. La fonction cuda.to_device permet d’allouer de la mémoire graphique et éventuellement de copier en même temps des données de la mémoire principale. Réciproquement, la fonction cuda.copy_to_host permet de copier le contenu de la mémoire graphique vers la mémoire principale. Ainsi, il n’y a qu’un seul cycle de copie de la mémoire principale vers la mémoire graphique et de la mémoire graphique vers la mémoire principale dans cette implémentation. Précédemment, ces opérations étaient réalisées de manière implicite par Numba à chaque appel du kernel.

4.6 Utilisation de la mémoire partagée

Lors du calcul de la nouvelle valeur d’une cellule, les valeurs des 8 cellules environnantes sont lues. Les accès en mémoire principale (la mémoire graphique de la carte) sont très lents. Par ailleurs lors du calcul de la nouvelle valeur, chaque thread a plusieurs valeurs communes avec les threads qui lui sont adjacents. Les accès en mémoire sont donc multipliés.

Un bloc de mémoire partagée est déclaré avec une taille correspondant au bloc plus les bordures, puisque les cellules entourant les threads de bordures doivent être lues. La taille (le nombre de threads dans le bloc plus deux pour chaque dimension) est déclarée avec des valeurs numériques (en C, on aurait utilisé un #define). Depuis peu, il est possible de faire de l’allocation dynamique de la mémoire partagée dans les kernels avec Numba [6].

Le remplissage de la mémoire partagée est fait par tous les threads en même temps. Chaque thread remplit une case de la mémoire temporaire, certains threads remplissant aussi les éléments de bordure. Avant d’utiliser ces données, il faut s’assurer que tous les threads aient terminé leurs accès à la mémoire principale. Pour cela, la fonction syncthreads bloque l’exécution du kernel tant que tous les threads ne sont pas arrivés à ce point du programme.

Le reste du kernel est identique au kernel précédent, avec comme différence l’utilisation de la mémoire partagée à la place de la mémoire principale.

4.7 Résultats

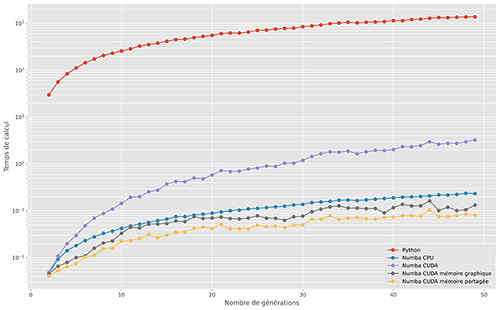
Les temps de calcul pour un monde de 1000 par 1000 pendant 50 générations ont été mesurés. Comme précédemment, ils sont présentés sur un diagramme (figure 5) semi-logarithmique (les écarts sont tels qu’ils auraient été illisibles sur un repère linéaire).

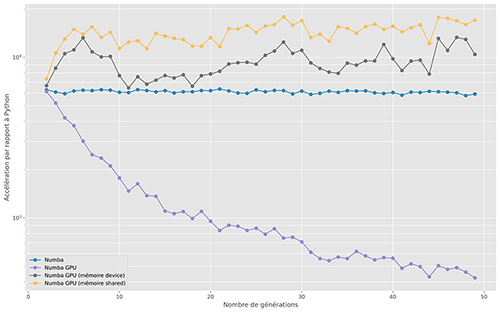
Sur la figure 6, l’accélération vis-à-vis de l'implémentation Python de référence est représentée :

• Numba permet d’accélérer le code Python d’un facteur supérieur à 6000 (!), sans aucune réécriture du code ;
• sur la première implémentation GPU, les performances sont moins bonnes que Numba. Les échanges entre la mémoire principale du processeur et la mémoire graphique sont très nombreux. On le constate d’ailleurs dans la décroissance de la courbe d’accélération. Ce sont les transferts mémoire qui représentent une grosse partie des temps de calcul ;
• ce problème de transfert mémoire est résolu en allouant de la mémoire graphique, ce qui permet d’avoir un code 12 500 fois (en moyenne) plus rapide que le code Python. Les temps de calcul sont divisés par deux, par rapport à la version Numba ;
• enfin, l’utilisation de la mémoire partagée permet d’accélérer le code GPU d’un facteur 1,4 en moyenne.

Cet exemple a permis d’illustrer les différentes mémoires des cartes graphiques et les interactions entre la mémoire principale et la mémoire graphique. Il est nécessaire de regrouper les calculs pour profiter de la carte graphique. Les échanges entre la mémoire principale et la mémoire graphique étant lents (relativement aux performances de calcul), seules des quantités de données conséquentes gagneront à être traitées par la carte graphique.

4.8 Distribution de l’âge des cellules

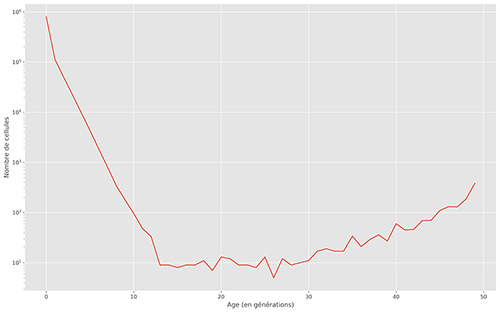
À partir du programme précédent, la distribution de l’âge des cellules dans la dernière génération va être calculée. Cette information peut, par exemple, être utilisée pour voir si des structures stables apparaissent rapidement dans le jeu de la vie et voir les conséquences des règles sur cette distribution. Avec les règles utilisées dans cet article, la distribution de la figure 7 est obtenue.

4.8.1 Écriture avec Numba

Le programme est suffisamment simple pour être écrit directement et optimisé avec Numba. Deux boucles parcourent la dernière génération (donc l’indice -1 en Python) du monde et la case correspondante est incrémentée dans le tableau représentant l’histogramme.

4.8.2 Écriture « naïve » sur la carte graphique

À partir des programmes précédents, il est assez simple d’écrire un kernel qui remplit l’histogramme. Chaque thread prend en charge une cellule et incrémente la case associée dans l’histogramme.

Lorsque l’on exécute ce programme, la compilation sur la carte graphique a lieu sans problème particulier (ni erreur ni avertissement...). Par contre, le résultat est faux ! Ces erreurs proviennent de l’accès concurrent aux données. Tous les threads d’un même bloc accèdent plus ou moins en même temps aux données contenues dans l’histogramme. Certains sont en train de lire la valeur pour l’incrémenter, alors que d’autres sont en train d’écrire la valeur qu’ils viennent de calculer.

4.8.3 Utilisation des opérations atomiques

Pour éviter les accès concurrents sur des opérations arithmétiques, CUDA propose plusieurs opérations atomiques (qui garantissent l’unicité de l’opération dans un même bloc). Numba en reprend quelques-unes. Dans notre cas, il suffit de remplacer la ligne histogramme[monde[x,y]] += 1 dans le kernel par cuda.atomic.add(histogramme, monde[x,y], 1) pour que le résultat soit correct.

Attention, seuls les types int32, float32 et float64 sont utilisables avec cette opération. Ce qui explique pourquoi un int32 a été retenu alors qu’un uint32 aurait été plus judicieux pour un histogramme (puisque les valeurs négatives sont impossibles).

4.8.4 Optimisation avec la mémoire partagée

Dans un même bloc, de nombreux accès au tableau stockant l’histogramme se produisent. L’histogramme est stocké en mémoire principale, très lente. Comme nous l’avons précédemment montré, il est judicieux dans ce cas d’utiliser de la mémoire partagée.

Les premiers threads du bloc initialisent la mémoire partagée. Il faut donc que le nombre de threads soit supérieur à la taille de l’histogramme (sinon chaque thread prend en charge 2,3,4… éléments de la mémoire partagée). Les threads sont synchronisés par la fonction syncthreads, pour être sûr que l’initialisation soit terminée avant de commencer le remplissage. Comme précédemment, il faut utiliser une opération atomique pour éviter les conflits d’accès mémoire. Enfin, les premiers threads mettent à jour la mémoire principale en ajoutant le contenu de la mémoire partagée.

4.8.5 Résultats

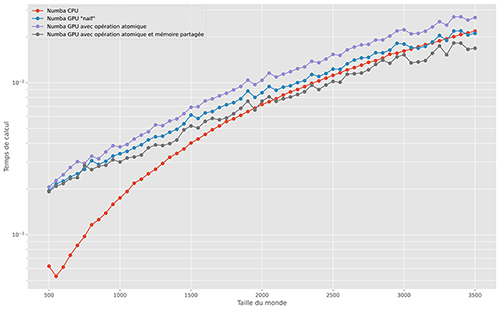
Les temps de calcul des différentes solutions proposées sont comparés sur la figure 8.

Les conclusions suivantes peuvent être déduites de cette figure :

• l’utilisation des opérations atomiques ralentit le GPU. Ce qui s’explique (en partie) par le fait que les threads doivent attendre pour pouvoir accéder aux données sans conflit ;
• la mémoire partagée permet d’accélérer le programme en réduisant les accès à la mémoire principale ;
• pour de petites tailles de monde, le processeur principal est plus performant que la carte graphique. Le transfert en mémoire graphique des données prend plus de temps que le calcul sur le CPU. Il est donc important de grouper les opérations GPU.

4.9 Enchaînement des kernels

Sur cet exemple du jeu de la vie, deux kernels ont été écrits, l’un pour le remplissage du monde, l'autre pour le calcul de l’histogramme. Si le but final du programme était le calcul de l’histogramme, il est plus efficace de maintenir les données dans la mémoire graphique, comme présenté ci-dessous :

La fonction to_device permet de copier explicitement sur le GPU les données avant d’appeler le kernel. Seules les données de l’histogramme sont renvoyées vers la mémoire principale avec la fonction copy_to_host.

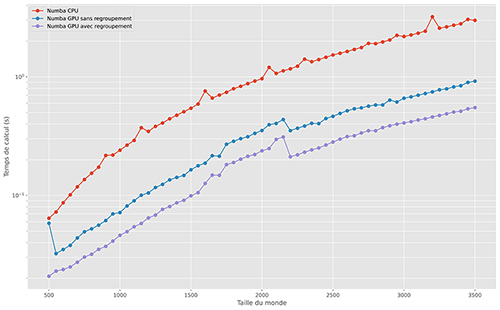
Cette optimisation permet de diminuer les échanges entre les mémoires processeur et graphique et donc d’accélérer les temps de calcul, comme présentés dans la figure 9.

Sur cet exemple, les performances de la carte graphique sont moins spectaculaires que sur le calcul des distances, mais il faut garder à l’esprit que l’algorithme du jeu de la vie nécessite beaucoup moins d’opérations arithmétiques.

Conclusion

Numba (avec ou sans l’utilisation de CUDA) propose un compromis intéressant pour les développeurs Python. L’ajout d’un simple décorateur peut permettre de diviser le temps de calcul de manière significative. Cette solution est plus simple que l’utilisation de Cython, puisqu’il n’est pas nécessaire de modifier le programme de base.

L’utilisation de CUDA augmente encore les performances, mais il nécessite de connaître un peu le fonctionnement des cartes graphiques NVIDIA et surtout les différents types de mémoire, pour profiter de cette technologie. Il est aussi important de regrouper les calculs pour que les temps de transfert entre la mémoire du processeur principale et la mémoire graphique soient minimisés.

Références

[1] T. COLOMBO, « Algorithmes de tri et impacts des choix d'implémentation sur les performances », GNU/Linux Magazine no176, novembre 2014 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-176/Algorithmes-de-tri-et-impacts-des-choix-d-implementation-sur-les-performances

[2] T. COLOMBO, « Optimisation de code Python : des fractales au pays des serpents », GNU/Linux Magazine no179, février 2015 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-179/Optimisation-de-code-Python-des-fractales-au-pays-des-serpents

[3] T. COLOMBO, « Le jeu de la vie de Conway : implémentation et petites adaptations », GNU/Linux Magazine no205, juin 2017 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-205/Le-jeu-de-la-vie-de-Conway-implementation-et-petites-adaptations

[4] Wikipédia, « Le jeu de la vie » : https://fr.wikipedia.org/wiki/Jeu_de_la_vie

[5] Numberphile, interview de John Conway, « Inventing Game of Life » : https://youtu.be/R9Plq-D1gEk

[6] Stackoverflow, « Numba CUDA shared memory size at runtime ? » : https://stackoverflow.com/questions/30510580/numba-cuda-shared-memory-size-at-runtime