Format WAV : des sons de plus en plus complexes

Dans l'article précédent, nous nous étions arrêtés à la synthèse d'un son sinusoïdal pur à l'aide du programme synthe.c. Nous allons maintenant voir comment nous pouvons créer des sons plus intéressants et explorer différents aspects des théories acoustiques et musicales, en tapant finalement très peu de code supplémentaire. Les sons étudiés dans cet article sont disponibles sur la page [1] au format audio Ogg Vorbis.

Nous allons aborder la synthèse additive en sommant des harmoniques puis, nous verrons comment synthétiser un accord majeur. Nous nous intéresserons ensuite à l'enveloppe des sons et à son influence sur le timbre des instruments et nous verrons également comment spatialiser le son. Nous aborderons la modulation de fréquence, qui permet d'obtenir très facilement des sons très complexes. Enfin, nous évoquerons d'autres méthodes de synthèse sonore.

1. Synthèse additive

Rappelons que tout signal périodique peut être décomposé en une somme de sinusoïdes (séries de Fourier) [2] : la première correspond à la fréquence fondamentale f, ou harmonique de rang 1, les suivantes correspondent aux harmoniques dont les fréquences sont des multiples de f. Lorsque l'on joue une note sur un instrument réel, un grand nombre d'harmoniques sont générés et ils vont avoir un rôle important dans la formation du timbre de l'instrument. Enfin, en règle générale, plus les harmoniques sont de rang élevé plus ils s'amortissent rapidement.

Dans la procédure mon_signal(), remplacez le signal sinusoïdal par cette boucle qui somme un fondamental et ses six premiers harmoniques, avec de plus des facteurs d'amortissement dépendant de l'ordre j de l'harmonique (la fonction mathématique pow(t,j) renvoie t à la puissance j) :

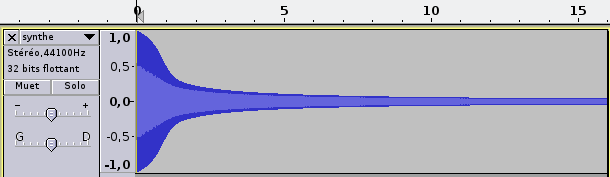
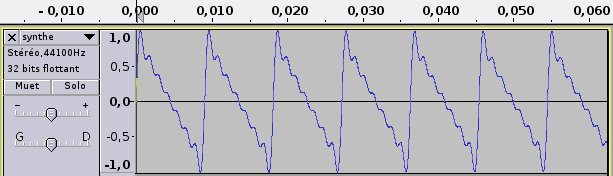
Dans le programme principal, réglez la fréquence à 110 Hz. Après compilation et exécution, ouvrez le fichier synthe.wav dans Audacity. Vous obtiendrez la forme d'onde, avec le temps en abscisse et l'amplitude en ordonnée (figure 1), pour les deux voix qui sont ici identiques. À l'échelle de la seconde, vous ne voyez que l'enveloppe du signal. Si vous zoomez à l'échelle de la dizaine de millisecondes, vous voyez le signal lui-même, qui est ici proche d'un signal en dents de scie descendantes (augmentez le nombre d'harmoniques et vous vous en approcherez encore plus). Mais cette forme de visualisation nous apprend finalement peu de choses sur le son que nous percevons.

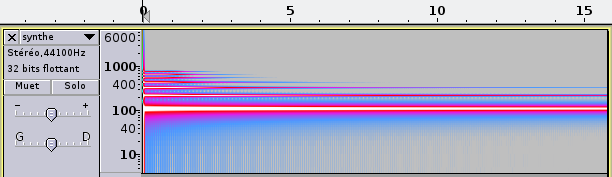
Le sonagramme (figure 2), ou sonogramme, va nous en apprendre beaucoup plus [3]. L'abscisse représente toujours le temps, mais l'ordonnée est ici la fréquence du signal et son intensité est codée par une palette de couleurs. Dans Audacity, il suffit de cliquer sur le petit menu déroulant présent en haut à gauche de la fenêtre contenant la piste sonore et de choisir Spectre logarithmique décimal au lieu de Forme d'onde. À noter que dans la version 2.0.6 que j'ai utilisée, il semble y avoir un bug au niveau de l'échelle des fréquences, qui est fausse quand on passe dans ce mode. Mais il suffit de zoomer puis de dézoomer sur cette échelle pour obtenir une échelle correcte. Dans ce sonagramme, nous voyons clairement les six harmoniques et le fondamental à 110 Hz, et leur décroissance d'autant plus rapide qu'ils sont de rang élevé.

Audacity permet également d'afficher un simple spectrogramme, grâce au menu Analyse > Tracer le spectre…, où vous lisez cette fois l'intensité en décibels associée à chaque fréquence, sans la dimension temporelle.

Si vous vous limitez aux harmoniques impairs, en incrémentant j de deux unités à chaque itération, vous obtiendrez un signal carré. Vous pouvez bien sûr écrire des procédures générant directement des formes d’onde de types dents de scie (montantes ou descendantes), triangle, carré, rectangle, impulsion, bruit, etc. Ce sont les principaux générateurs d'ondes dont disposent les synthétiseurs.

2. Un accord majeur

Si vous jouez un accord de plusieurs notes, d'après la théorie de Helmholtz [2] le fait que certains de leurs harmoniques soient très proches va être déterminant pour la qualité de l'accord (majeur, mineur, etc.). Dans le cas d'un accord do-mi-sol, on voit par exemple dans le tableau suivant que l'harmonique 3 du do est à moins de 1 Hz de l'harmonique 2 du sol et que l'harmonique 4 du sol est à moins de 2 Hz de l'harmonique 6 du do :

Quand les harmoniques sont trop proches, ils sont d'ailleurs confondus dans le sonagramme d'Audacity. Par contre, votre oreille sera capable de percevoir certains battements résultants.

Voici le bout de code qui vous permettra, en s'arrêtant ici à l'harmonique de rang 7, de créer un bel accord parfait majeur, sachant que le mi est quatre demi-tons au-dessus du do et le sol sept demi-tons au-dessus :

Veillez bien à écrire 4/12.0 ou 4/(double)12 pour éviter que le compilateur ne code une division euclidienne, dont le résultat serait bien sûr nul !

3. Enveloppe

3.1 Percussions

Les sons que nous venons d'aborder commencent brutalement pour décroître ensuite en suivant une loi mathématique du type 1/(j+pow(t,j)), où j est le rang de l'harmonique. Vous pouvez essayer d'autres formules comme t/(j+pow(t,j)) ou exp(-j*t). Le sinus cardinal donne également un résultat intéressant, ressemblant à une percussion :

Voilà déjà de quoi programmer une petite boîte à rythmes à l'aide de quelques boucles ! Si vous descendez en dessous de 150 Hz, vous remarquerez néanmoins qu'il vaut mieux avoir des enceintes correctes ou un casque. Le sonagramme montrerait que durant les trois premiers dixièmes de seconde le spectre est très large et continu, ce qui est caractéristique des bruits.

Notez que le son perçu différera sensiblement selon la valeur de la phase phi choisie. Pour phi=0, on entend un clic désagréable au tout début. Vous pouvez essayer différents multiples de PI, positifs ou négatifs.

3.2 Enveloppe ADSR

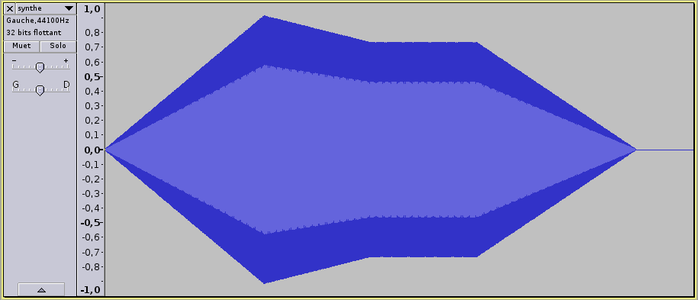
Pierre Schaeffer avait dans ses expérimentations mis en évidence l'importance de l'attaque dans le timbre de l'instrument et sa reconnaissance par l'auditeur. Une attaque brutale correspond bien aux instruments frappés ou pincés (percussions, guitare, piano, etc.). Pour les instruments à vent ou à cordes frottées, une attaque longue est nécessaire. Il est très courant en synthèse sonore d'utiliser le modèle ADSR (figure 3), implémenté dans notre programme par la procédure generateur_enveloppe(). L’enveloppe est appliquée à la piste sonore entre les instants t1 et t2 et comprend quatre paramètres :

• l'attaque (attack) donnée en pourcentage de la durée t2-t1 ;
• le déclin (decay) donné en pourcentage de la durée t2-t1 ;
• le maintien (sustain) donné en pourcentage par rapport à la valeur pic de l'amplitude (la durée du maintien peut être déduite des trois autres paramètres) ;
• le relâchement (release) donné en pourcentage de la durée t2-t1.

Chaque partie de l'enveloppe ADSR est traitée par une boucle, après calcul des indices nécessaires :

Essayez par exemple dans la procédure mon_signal(), de remplacer votre sinusoïde par ce son ne contenant que des harmoniques impairs :

Puis dans le programme principal, appelez cette procédure pour créer un son de trois secondes à 220 Hz et appliquez ensuite une enveloppe :

Le résultat évoque une clarinette. Si au lieu d'appliquer cette enveloppe ADSR, vous faites décroître au cours du temps le niveau en multipliant le signal par un facteur exp(-sqrt(j)*t), vous remarquerez que votre son n'est plus perçu comme ressemblant à une clarinette.

À noter également que notre procédure applique l'enveloppe à l'ensemble du signal, alors que les pionniers de la synthèse sonore s'étaient rendu compte qu'il pouvait être nécessaire d'avoir une enveloppe différente pour chaque harmonique afin de synthétiser correctement en particulier les instruments à vent ou à cordes frottées.

3.3 Trémolo

On utilise beaucoup dans les synthétiseurs des oscillateurs basses fréquences (LFO, pour Low Frequency Oscillator) pour faire varier certaines grandeurs. Faire varier par exemple l'amplitude du son avec une fréquence de 5 à 10 Hz produira un trémolo :

Ici, on module l'amplitude du signal déjà existant dans le canal gauche avec une pulsation lente omegaLFO et une profondeur AmpLFO (par exemple 0,1). En théorie du signal, c'est de la modulation d'amplitude (AM), le son de départ jouant le rôle de porteuse dont on module l'enveloppe.

Attention, si la fréquence de modulation est beaucoup plus élevée, cette modulation sera perçue par l'oreille d'une façon très différente, avec l'apparition de signaux aux deux fréquences éloignées du fondamental de cette valeur, conformément à la formule de trigonométrie sin(a)*sin(b)=(cos(a-b)-cos(a+b))/2.

3.4 Spatialisation du son

Dans tous les exemples donnés jusqu'ici, nous nous sommes contentés d'assigner au canal droit les mêmes valeurs qu'au canal gauche. Mais le programme est conçu pour que vous puissiez aussi jouer de la stéréo. Faire par exemple tournoyer le son n'est pas plus difficile que de moduler le signal à l'aide d'un cosinus d'un côté et d'un sinus de l'autre, afin que le signal soit maximum d'un côté quand il est minimum de l'autre :

Ici omegaLFO est la pulsation du tournoiement, par exemple 2*PI*f avec f=0,5 Hz, et AmpLFO la profondeur de modulation entre 0 et 1. La phase phi permet de régler le point de départ.

En améliorant le programme pour travailler avec plus de canaux dans le fichier WAV, par exemple en 5.1, on pourrait facilement déplacer le son dans l'espace et étudier nous aussi, comme Stockhausen, la spatialisation du son.

4. Modulation de fréquence ou de phase

Quand on parle de modulation de fréquence (FM), il s'agit souvent en fait d'une modulation de phase (PM) [2]. En modulant la phase de la sinusoïde à une fréquence d'environ 4 Hz, vous obtiendrez un effet de vibrato :

Mais si la modulation se fait à des fréquences similaires à celles des signaux acoustiques, vous rentrerez dans le domaine de la synthèse dite FM. Voici par exemple un son de type bourdonnement :

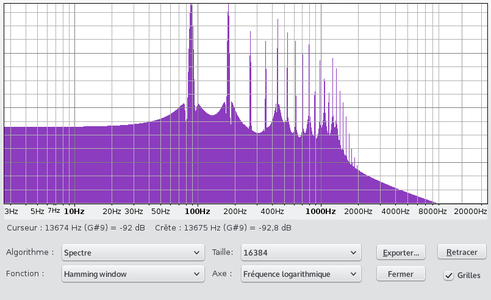
La synthèse FM a pour effet de faire apparaître un large spectre de fréquences (figure 4).

À vous d'imaginer des formules mathématiques générant des sons intéressants, comme (à faire durer au moins 50 secondes) :

Vous pouvez aussi moduler véritablement la fréquence :

L'effet est souvent contre-intuitif : dans cet exemple, la profondeur de modulation n'est que d'un millième, mais l'effet sur le son devient au fil des secondes de plus en plus énorme ! Et en remplaçant le facteur 50 par 500, vous obtenez un son très intéressant, qui mériterait une enveloppe ADSR bien ficelée pour le mettre en valeur. Passez maintenant d'un facteur 500 à un facteur 5000 et vous voilà avec un son dont les premières secondes évoquent un gong.

N'hésitez pas à moduler la modulation (et pourquoi pas la modulation de la modulation !) :

Vous comprenez que le terrain de jeu est infini ! La synthèse FM a été la grande révolution du début des années 80 avec le synthétiseur Yamaha DX7 qui a connu un énorme succès sur la scène pop de l'époque [2].

5. Autres méthodes de synthèse sonore

La synthèse soustractive consiste à sculpter le son en filtrant un signal riche en harmoniques à l'aide par exemple de filtres passe-bas, passe-haut, passe-bande, etc. Mais ces filtres nécessitent des méthodes mathématiques particulières telles que les transformées de Fourier et dépassent le cadre de cet article.

La synthèse physique consiste à modéliser les vibrations d'un objet à l'aide d'équations physiques, par exemple une corde vibrante ou même un instrument complet comme une guitare ou un piano.

Concernant les instruments à cordes pincées, vous pouvez plus simplement vous intéresser à l'étonnant algorithme de Karplus et Strong (1983) qui en à peu près huit lignes de code génère des sons de guitare très convaincants [2]. Il consiste à générer un signal aléatoire au début, la suite étant calculée à l'aide d'une relation de récurrence ayant pour effet de faire disparaître progressivement les fréquences élevées.

Conclusion

Nous avons vu comment, à partir d'un court programme et d'une simple sinusoïde, il est possible de créer des sons plus ou moins complexes, en sommant des sinusoïdes, en modifiant l'enveloppe des sons, en modulant certains paramètres de l'onde, et comment l'on pouvait même jouer sur sa spatialisation.

Vous pouvez maintenant vous lancer sur les pas d’Éliane Radigue [4], grande exploratrice de la musique drone, musique qui se caractérise par l'usage de bourdons (drone en anglais), sons continus évoluant très lentement au cours de morceaux souvent assez longs (typiquement une heure). Ou tenter de reproduire des illusions acoustiques telles que le glissando de Shepard-Risset [5, 6], série de glissandos entrant et sortant continûment du spectre audible pour donner l'illusion d'une ascension ou d'une descente éternelle, sorte d'équivalent acoustique des escaliers d'Escher.

Pour les plus enthousiastes, l'étape suivante pourrait être de s'attaquer au langage de création sonore Csound [7], logiciel libre initialement développé au MIT…

Références

[1] Écoutez les sons de l'article : http://magnin.plil.net/spip.php?article131

[2] BENSON D., « Music: A Mathematical Offering », 2008, livre téléchargeable en PDF sur son site : http://www.maths.abdn.ac.uk/∼bensondj/html/maths-music.html

[3] Sonagramme : https://fr.wikipedia.org/wiki/Sonagramme

[4] Émission sur Eliane Radigue : http://www.francemusique.fr/emission/le-jour-d-avant/2013-2014/eliane-radigue-ou-l-experience-electronique-11-10-2013-00-00

[5] Glissando de Shepard-Risset : https://en.wikipedia.org/wiki/Shepard_tone

[6] RISSET J.-C., « COMPUTER MUSIC: WHY ? », https://www.utexas.edu/cola/france-ut/_files/pdf/resources/risset_2.pdf

[7] Langage de création musicale Csound : http://csound.github.io/