Nous avons vu dans l'épisode précédent comment décoder le code convolutif par algorithme de Viterbi, pour passer des symboles radiofréquences de la modulation QPSK aux bits. Nous sommes restés sur un échec de décodage, que nous allons corriger ici pour aboutir à la restitution des images issues du décodage JPEG, en passant par les diverses couches protocolaires de la liaison numérique.
Nous avons attaqué le problème du décodage des images transmises par protocole LRPT de Meteor-M2. Tout comme l’utilisateur d’un browser web qui désire afficher une image transmise par HTML avec, pour seul outil, une sonde d’oscilloscope branchée sur un câble Ethernet, nous devons remonter petit à petit les couches OSI pour passer de la couche matérielle à la couche applicative. L’étude précédente nous avait permis de retrouver, à partir des mesures de phases, la constellation QPSK et des bits déconvolués par algorithme de Viterbi. Nous avions échoué à trouver le mot de synchronisation des trames dans cette séquence de bits. Poursuivons donc l’exploration pour aller jusqu’au décodage des images JPEG, dont on affichera le contenu pour avoir une vue de l’espace.
1. Rotation de la constellation
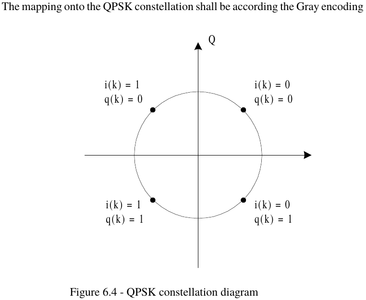
Fig. 1 : Constellation QPSK : chaque état possible de phase encode 2 bits. L’assignation de chaque symbole vers les paires de bits sera l’objet d’une partie du travail de décodage. Cette figure est issue de [1, Fig. 6.4, p.16].
L’absence de corrélation observée à l’issue de l’étude précédente indique que nous ne comprenons pas comment les bits sont encodés dans le message acquis, sous réserve que le mot de synchronisation encodé par convolution soit correct, hypothèse que nous ferons compte tenu des informations fournies sur [2]. Lorsque nous avions étudié la modulation en phase binaire (BPSK – Binary Phase Shift Keying), nous avions vu que deux cas pouvaient se produire [3][4] : soit le signal acquis était en phase avec l’oscillateur local, et les bits issus de la comparaison de la phase entre le signal reçu et la reproduction locale de la porteuse (boucle de Costas) étaient ceux attendus, soit le signal était en opposition de phase et les bits étaient inversés par rapport à la valeur attendue. Dans les deux cas, la corrélation avec le mot de synchronisation accumule de l’énergie le long de la séquence de bits et se traduit, en prenant la valeur absolue, par un pic de corrélation, que nous ayons la bonne séquence dans la trame acquise ou son opposé. Ce cas simple se complique dans le cas de QPSK (Quadrature Phase Shift Keying) [5], dans lequel la phase prend quatre états possibles qui encodent chacun une paire de bits (figure 1). L’assignation entre la valeur de la phase et la paire de bits correspondante n’est pas évidente, mais surtout toute erreur dans l’assignation symbole-paire de bits se traduit par une séquence erronée, qui ne corrèle pas avec le mot recherché. À titre d’exemple, si nous attribuons 0° à la paire de bits 10 et 90° à 11 (code de Gray, dans lequel seul 1 bit change entre deux valeurs adjacentes de la phase) alors une séquence 0-90° se traduit par 1011, alors que l’assignation 0° à 11 et 90° à 01 interprète la même séquence de phases par 1101 : les deux messages issus de la même séquence de phases mesurées sont complètement différents et n’ont aucune chance d’accumuler l’énergie nécessaire au pic de corrélation, lors de la comparaison avec le motif de synchronisation de référence. On notera, en comparant la figure 1 à la dernière figure de la première partie de cet article, que nous avions placé la paire de bits 00 sur la mauvaise valeur de phase (voir figure 7 de la section 5 de l’article précédent, pour l’assignation entre chaque symbole et chaque paire de bits dans le Constellation Soft Decoder – digital.constellation_calcdist(([-1-1j, -1+1j, 1+1j, 1-1j]), ([0, 1, 3, 2]), 4, 1).base(), et l’analyse que nous proposons ici en figure 2). Par ailleurs, le code de Gray peut évoluer dans le sens horaire ou trigonométrique, induisant encore un risque d’erreur. Il ne semble pas y avoir de façon d’identifier l’assignation phase-paire de bits autre que la force brute, dans laquelle toutes les combinaisons de codes possibles sont testées, tel que nous l’enseigne le contenu de m.c.patts[][] de medet.dpr dans meteor_decoder :
1111110010100010101101100011110110110000000011011001011110010100
0101011011111011110100111001010011011010101001001100000111000010
0000001101011101010010011100001001001111111100100110100001101011
1010100100000100001011000110101100100101010110110011111000111101
1111110001010001011110010011111001110000000011100110101101101000
0101011000001000000111001001011100011010101001110011110100111110
0000001110101110100001101100000110001111111100011001010010010111
1010100111110111111000110110100011100101010110001100001011000001
Ceci donne toutes les combinaisons possibles de paires de bits dans le mot encodé par convolution, et la corrélation du message acquis se fait avec toutes les déclinaisons de ce code.
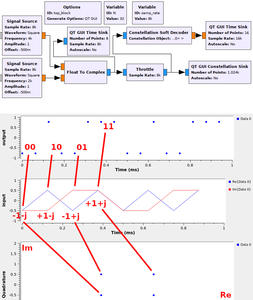
Fig. 2 : Exemple de signaux synthétiques permettant d’analyser la configuration du Constellation Soft Decoder par digital.constellation_
calcdist(([-1-1j, -1+1j, 1+1j, 1-1j]), ([0, 1, 3, 2]), 4, 1).base(). Nous constatons que l’assignation des symboles aux paires de bits ne correspond pas à la norme (figure 1).
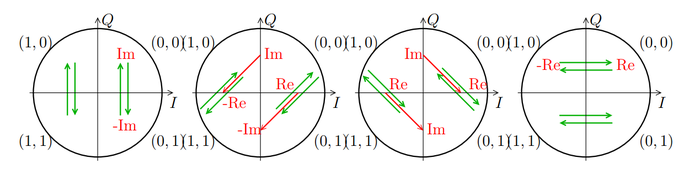
Cependant, nous avons encore un problème : ces inversions de bits se font facilement sur des valeurs binaires du mot de référence en inversant 1 et 0, mais que faire avec les soft bits qui encodent chaque phase reçue dans le message acquis avec une valeur continue codée sur 8 bits ? Sommes-nous obligés de décider maintenant de la valeur attribuée à chaque phase (soft→ hard bits), ou pouvons-nous manipuler les valeurs brutes ? Il nous faut interpréter les échanges de bits comme des opérations de rotation ou de symétrie de la constellation (figure 3). Nous constatons qu’échanger des bits correspond à des opérations entre partie réelle et partie imaginaire, soit de rotation, soit de symétrie le long d’un des axes du plan complexe. Ainsi, en manipulant la partie réelle et imaginaire des données acquises, nous pouvons atteindre le même résultat que l’échange des bits, mais en conservant les valeurs continues des soft bits et en repoussant l’attribution de chaque bit (0 ou 1) à chaque valeur de phase au décodage par l’algorithme de Viterbi.
Fig. 3 : Rotations et symétries de la constellation, et le résultat correspondant sur les axes réel et imaginaire (I et Q) des données brutes acquises.
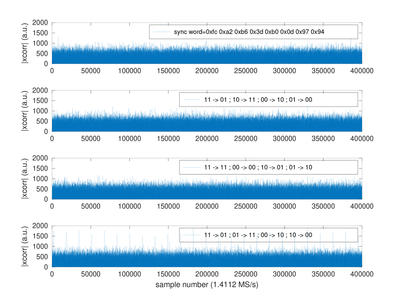
L’identification de la correspondance entre les 4 états QPSK dans le diagramme de constellation (I en abscisse, Q en ordonnée) et les paires de bits correspondantes nécessite donc une attaque brute, dans laquelle tous les cas possibles sont testés. La corrélation des phases des signaux acquis avec les diverses permutations possibles du code d’en-tête de trame encodé par convolution est illustrée en figure 4. Une seule condition d’attribution des symboles aux paires de bits fournit une séquence périodique de pics de corrélation (figure 4, bas) : il s’agit de la bonne correspondance, que nous exploiterons pour la suite du décodage.
Fig. 4 : Corrélation pour les 4 cas possibles de rotation de la constellation QPSK avec le code connu de début de trame. Nous constatons que seul le quatrième cas – en bas – fournit des pics périodiques de corrélation représentatifs du début de trame. C’est donc cette attribution des 4 symboles de QPSK aux paires de bits correspondants qui est correcte.
Cette permutation sera désormais appliquée à tous les couples I/Q du message acquis, car nous savons que nous retrouverons alors la séquence de bits émise par le satellite, lors du décodage par algorithme de Viterbi appliqué aux soft bits résultants.
1.1 Des bits aux phrases : mise en œuvre du décodage par algorithme de Viterbi
Nous avons maintenant une séquence de phases comprises dans l’ensemble [0;π/2;π;3π/2] convenablement organisée pour devenir une séquence de bits dans laquelle nous retrouvons le mot de synchronisation, et nous n’avons qu’une unique attribution des divers symboles {00;01;11;10} à chaque phase qui fournit une solution présentant cette corrélation. Il nous reste à décoder pour retirer l’encodage par convolution, puis appliquer aux bits résultants (qui étaient donc les bits encodés par le satellite avant convolution) une séquence de XOR (OU exclusif) avec un polynôme garantissant de rendre la séquence aussi aléatoire que possible, pour éviter tout risque de répétition trop long du même état de bit.
Nous avons mentionné la disponibilité de libfec, implémentant efficacement le décodage des signaux encodés par code de convolution. Nous étendons ici l’exemple simple au cas pratique de la trame complète.
Notre première idée a consisté à décoder d’un coup l’ensemble du fichier acquis. De cette façon, nous cachons le problème de l’initialisation et de la fin du décodage du code de convolution par l’algorithme de Viterbi. Cela fonctionne, puisque nous vérifions après décodage que, tous les 1024 octets, nous retrouvons le code de synchronisation 0x1ACFFC1D.
Nous avons rencontré un problème d’erreur d’accès à un segment mémoire (segmentation fault), en allouant le tableau permettant de charger l’ensemble du fichier. En effet, le fichier contenant les octets en soft bits fait 11,17 MB, donc nous avions alloué un tableau statique, comme le ferait tout bon développeur sur système embarqué qui n’a pas accès à l’allocation dynamique de mémoire malloc, gourmande en ressources. Cependant, ce faisant nous plaçons le tableau sur la pile, et GNU/Linux impose par défaut une pile de 8192 kB, tel que nous le dit ulimit -s : 8192. Plutôt qu’imposer une limite de taille de pile plus importante, nous nous autorisons sur notre système d’exploitation une allocation dynamique de mémoire, pour placer le tableau sur le tas et non sur la pile, libérant ainsi la contrainte de place mémoire occupée.
01: #include <stdio.h> // from libfec/vtest27.c
02: #include <stdlib.h> // gcc -o demo_libfec demo_libfec.c -I./libfec ./libfec/libfec.a
03: #include <fcntl.h>
04: #include <unistd.h> // read
05: #include <fec.h>
06: #define MAXBYTES (11170164/16) // file size /8 (bytes-> bits) /2 (Viterbi)
07:
08: #define VITPOLYA 0x4F
09: #define VITPOLYB 0x6D
10: int viterbiPolynomial[2] = {VITPOLYA, VITPOLYB};
11:
12: int main(int argc,char *argv[]){
13: int i,framebits,fd;
14: unsigned char data[MAXBYTES],*symbols;
15: void *vp;
16:
17: symbols=(unsigned char*)malloc(8*2*(MAXBYTES+6)); // *8 for bytes->bits & *2 Viterbi
18: // root@rugged:~# ulimit -a
19: // stack size (kbytes, -s) 8192
20: // -> static allocation (stack) of max 8 MB, after requires malloc on the heap
21: fd=open("./extrait.s",O_RDONLY); read(fd,symbols,MAXBYTES*16); close(fd);
22:
23: for (i=1;i<MAXBYTES*16;i+=2) symbols[i]=-symbols[i]; // I/Q constellation rotation
24: framebits = MAXBYTES*8;
25: set_viterbi27_polynomial(viterbiPolynomial);
26: vp=create_viterbi27(framebits);
27: init_viterbi27(vp,0);
28: update_viterbi27_blk(vp,&symbols[4756+8],framebits+6);
29: chainback_viterbi27(vp,data,framebits,0);
30: for (i=0;i<20;i++) printf("%02hhX",data[i]);
31: printf("\n");
32: fd=open("./sortie.bin",O_WRONLY|O_CREAT,S_IRWXU|S_IRWXG|S_IRWXO);
33: write(fd,data,framebits);
34: close(fd);
35: exit(0);
36: }
L. Teske nous informe cependant que cette approche n’est pas optimale, car elle impose de charger tout le fichier en mémoire d’un coup. Nous savons que les blocs de 1024 octets (2048 octets après encodage) sont encodés individuellement, donc au lieu de décoder tout le fichier, nous pouvons nous contenter de chercher le code de synchronisation encodé, et décoder les 2048 octets qui suivent à partir de ce point. Pour plus de sécurité et pour laisser le décodeur s’initialiser, on prendra soin de prendre quelques valeurs avant et après le bloc à décoder. La partie main du code résultant est de la forme suivante :
01: fdi=open("./extrait.s",O_RDONLY);
02: fdo=open("./sortie.bin",O_WRONLY|O_CREAT,S_IRWXU|S_IRWXG|S_IRWXO);
03: read(fdi,symbols,4756+8); // offset
04: framebits = MAXBYTES*8;
05:
06: do {
07: res=read(fdi,symbols,2*framebits+50); // prend un peu plus
08: lseek(fdi,-50,SEEK_CUR); // revient en marche arrière
09: for (i=1;i<2*framebits;i+=2) symbols[i]=-symbols[i]; // I/Q constellation rotation
10: set_viterbi27_polynomial(viterbiPolynomial);
11: vp=create_viterbi27(framebits);
12: init_viterbi27(vp,0);
13: update_viterbi27_blk(vp,symbols,framebits+6);
14: chainback_viterbi27(vp,data,framebits,0);
15: write(fdo,data,MAXBYTES); // résultat du décodage
16: } while (res==(2*framebits+50)); // ... tant qu'il y a des data à lire
17: close(fdi); close(fdo);
Cette approche de traitement par blocs de données permettra en plus d’appréhender le code correcteur d’erreur par bloc de Reed Solomon. L’utilisation de ce code correcteur par blocs est optionnel : les blocs de données issus du décodage par l’algorithme de Viterbi sont utilisables en l’état et dans un premier temps, nous passerons le code correcteur d’erreur de Reed Solomon sous silence, en n’exploitant que les premiers 1024-4-128=892 octets dans chaque bloc (après avoir rejeté donc les 4 octets du mot de synchronisation, en début de bloc et les 128 octets de code correcteur, en fin de bloc).
Alternativement, le lecteur qui préfère se cantonner à GNU/Octave au lieu de passer au C pourra exploiter le code fourni sur https://github.com/Filios92/Viterbi-Decoder/blob/master/viterbi.m, qui fonctionne lui aussi parfaitement avec :
01: f=fopen("extrait.s"); % soft bits generated from GNURadio
02: d=fread(f,inf,'int8'); % read file
03: d(2:2:end)=-d(2:2:end); % rotation constellation
04: phrase=(d<0)'; % soft -> hard bits
05: [dv,e]=viterbi([1 1 1 1 0 0 1 ; 1 0 1 1 0 1 1 ],phrase,0);
06: data=(dv(1:4:end)*8+dv(2:4:end)*4+dv(3:4:end)*2+dv(4:4:end));
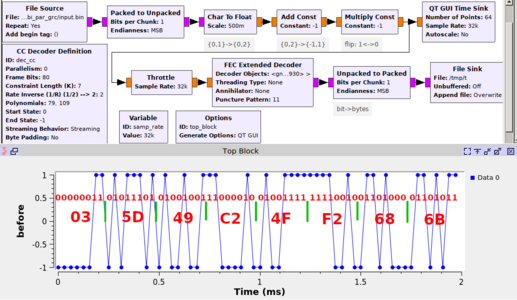
Finalement, le lecteur désireux de poursuivre son exploration de Meteor-M2 exclusivement par GNU Radio n’est pas en reste : les codes correcteurs d’erreur et libfec sont implémentés dans gr-satellite de github.com/daniestevez/gr-satellites et décrits en détail dans le blog de D. Estévez sur destevez.net. Sous sa direction lors de divers échanges de courriers électroniques, nous avons fini par faire aboutir le décodage du mot de synchronisation par son bloc de déconvolution par algorithme de Viterbi, selon le schéma de traitement proposé en figure 5. Partant d’un fichier binaire contenant le mot encodé fca2b63db00d9794, par exemple généré par echo -e -n "\xfc\xa2\xb6\x3d\xb0\x0d\x97\x94" > input.bin, nous visons à retrouver le mot de synchronisation 1acffc1d qui démontrerait notre compréhension du décodeur. Attention : le point qui nous a bloqués n’est pas la configuration du décodeur, qui reprend exactement la notation de libfec, mais le format des données en entrée. En effet, GNU Radio s’attend, tel que décrit au détour de la page d’aide de fec_decode_ccsds_27_fb (bloc GNU Radio Companion Decode CCSDS 27) de gr-fec, à recevoir une entrée comprise entre -1 et +1 (et non 0 à +1 comme nous nous y serions attendus pour une représentation de bits : il s’agit ici de soft bits, compris entre exp(jπ)=-1 et exp(j0)=+1et non de hard bits). Nous prenons donc les bits issus de la lecture du fichier contenant le mot encodé, multiplions par 2 (donc facteur d’homothétie inverse de 0,5, valeur à renseigner dans ), retranchons 1 et éventuellement, échangeons les valeurs des bits (multiplication par -1) pour atteindre le bon résultat et non son opposé. Nous vérifions sur la sortie graphique de la figure 5 que la lecture du fichier est fonctionnelle, et en observant la sortie de ce flux de traitement (par xxd par exemple), nous trouvons :
$ xxd result.bin | cut -d: -f2
1acf fc1d 1acf fc1d 0334 53c0 1acf fc1d .........4S.....
Ceci n’est pas parfait, mais ressemble bien à nos attentes. Nous trouvons bien la séquence 1acffc1d, mais parfois une séquence erronée 033453c0 se glisse, du fait d’une mauvaise initialisation du décodeur de Viterbi. En effet, Viterbi fait l’hypothèse d’une initialisation avec tous les éléments du registre à décalage à 0, ce qui n’est pas nécessairement le cas ici lors d’une lecture répétitive du mot encodé. D. Estévez présente sur destevez.net/2017/01/coding-for-hit-satellites-and-other-ccsds-satellites/ les diverses déclinaisons sur la configuration du décodeur pour respecter les diverses déclinaisons de la norme du CCSDS.
Fig. 5 : Flux de traitement dans GNU Radio Companion, exploitant gr-satellite et le bloc généraliste de décodage du code de convolution par Viterbi, FEC Extended Decoder configuré pour respecter la norme du CCSDS pour démontrer le décodage du mot de synchronisation. L’entrée se généralisera donc au fichier enregistré et contenant les soft bits de Meteor-M2. Le mot annoté sur le graphique du bas est l’opposé du mot fourni dans le fichier d’entrée 0xFCA2B63DB00D9794, issu de l’encodage du code de synchronisation pour que la sortie réponde à nos attentes : l’inversion de bits est prise en charge par la multiplication par -1, juste avant l’affichage en haut à droite du flux de traitement.
Nous prétendons avoir décodé les messages venant du satellite, mais sommes nous certains de la validité de ces bits ? Afin de chercher rapidement une séquence connue de bits, nous reprenons le cas proposé au début de cet article, à savoir rechercher par corrélation un motif connu. Or il se trouve que, sans rien connaître à l’encodage des paragraphes qui formera l’objet de la suite de ce texte, la description du protocole a inclus dans son Appendice A une description de la trame de télémétrie, censée contenir la date à bord du satellite, et cette trame est identifiée par le code PRS-64 formé de la séquence "2 24 167 163 146 221 254 191". Sommes-nous capables de trouver cette séquence d’octets dans les trames décodées ? Ayant obtenu des bits que nous supposons avoir stocké dans le tableau dv, nous les concaténons sous GNU/Octave en quartets, puis en octets (tableau data) et en trames (matrice fin ci-dessous) :
01: % data est le tableau d'octets issus de Viterbi tel que vu auparavant
02: for k=1:24 % on analyse les 24 premiers blocs
03: d(:,k)=data(1+(k-1)*2048:k*2048); % trames de 2048 quartets
04: dd(:,k)=d(1:2:end,k)*16+d(2:2:end,k); % quartets -> octets
05: fin(:,k)=dd(5:end,k); % retire l'en-tête de synchro de chaque paquet
06: fin(:,k)=[bitxor(fin(1:255,k)',pn) bitxor(fin(1+255:255+255,k)',pn) ...
07: bitxor(fin(1+255*2:255+255*2,k)',pn) bitxor(fin(1+255*3:255+255*3,k)',pn)];
08: end
Nous constatons que nous avons dû appliquer un code pn, qui a été conçu pour rendre la séquence de bits aussi aléatoire que possible (et donc distribuer l’information) par masquage bijectif (XOR). Cette structure aléatoire des trames évite de longues séquences de la même valeur de bits, rendant la récupération de l’horloge compliquée. La séquence de pn longue de 255 éléments est fournie sur https://www.teske.net.br/lucas/2016/11/goes-satellite-hunt-part-4-packet-demuxer/ et nous nous contentons de l’appliquer à nos octets, regroupés par paquets de 255 (les 4 octets d’en-tête, qui ne subissent pas cette transformation, ont déjà été retirés).
Finalement, ces trames sont analysées pour y rechercher l’occurrence de la séquence magique PRS-64, représentative de la trame de télémétrie. L’obtention de cette séquence prouve que notre procédure est cohérente, car non seulement nous identifions la séquence d’octets indicatrice de la télémesure – séquence qui n’a à peu près aucune chance d’apparaître par hasard – mais en plus l’analyse de la télémesure fournit un résultat cohérent avec les conditions d’acquisition et le décodage par meteor_decoder (Onboard time: 11:48:33.788), sous la forme :
date_header=final(589:589+7,9)' % on a trouvé la date dans CADU 9 (sur les 24 traitées)
date=final(589+8:589+11,9)'
ans =
11
48
33
197
Nous avons réussi à trouver l’heure qu’il était à bord du satellite au moment de la capture de l’image, validant la procédure d’obtention des octets à partir du flux de données I/Q. Maintenant que nous sommes confiants sur la séquence de bits, le reste de l’analyse n’est plus que de l’assemblage de trame et du décodage d’images, une activité plus classique d’informatique que de traitement du signal.
1.2 Des phrases aux paragraphes
La séquence de bits respecte la norme décrite dans les documents techniques, nous avons donc fini notre travail de décodage. Pas tout à fait... le satellite transmet une image, et nous avons obtenu une date. C’est un peu maigre comme résultat. Pouvons-nous aller plus loin ?
C’est là que les couches de la norme OSI apparaissent. Une image est une somme conséquente d’informations, trop grosse pour être contenue dans un unique paquet transmis depuis le satellite. Pire, le satellite envoie au moins 3 bandes spectrales (selon que nous soyons le jour ou la nuit, ces bandes changent... c’est quoi le jour ou la nuit au Spitsberg, avec ses 3 mois de jour et 3 mois de nuit complets ?!) qui sont interlacées entre les divers paquets. Nous comprenons mieux pourquoi la norme OSI sépare les divers niveaux d’abstraction : une image est une entité découpée en couches de couleurs, qui sont elles-mêmes découpées en blocs (codage JPEG), qui sont eux-mêmes découpés en paquets qui sont transmis vers le sol, avec toute l’artillerie de correction d’erreurs et de redondance pour maximiser les chances que le récepteur reçoive un flux de données intègre. J’ai bien écrit JPEG dans la phrase précédente : pour quelqu’un qui a été élevé avec tous les méfaits des compressions à perte d’images et des artefacts induits par la compression JPEG, est-il possible que les images transmises par satellites soient codées ainsi ? Le compromis tient probablement entre le débit de données accessible sur une liaison relativement basse fréquence et la masse de données à transmettre pour récupérer une image haute résolution : on prendra évidemment soin, lors du traitement de telles images, de ne pas s’apitoyer sur les artefacts de codage des blocs de 8x8 pixels, qui vont être l’objet de la discussion qui va suivre.
Le point, fort peu clair dans la documentation, tient sur la définition du Minimum Code Unit (MCU) : nous apprenons que chaque MCU comporte 196 zones adjacentes d’une image, chacune formée de 14 imagettes de 8x8 pixels. Le point qui ne nous était pas apparu clair dans la documentation est que les MCU successifs sont indépendants les uns des autres. Ainsi, une ligne d’image est formée de 14 MCU, chacune contenant 14 imagettes de 8x8 pixels : 14 x 14 = 196 et 14 x 14 x 8 = 1568 pixels est bien la largeur d’une image issue de Meteor-M2. Donc, notre objectif est de décoder des imagettes de 8x8 pixels encodées en JPEG, de les concaténer, et ce, jusqu’à former une ligne d’une image dans une composante spectrale. La procédure se répète pour les deux autres bandes spectrales, avant de recommencer suite à une trame de maintenance (identifiant 70 fourni dans le champ APID, APplication IDentifier – les images ont quant à elles des identifiants APID compris entre 64 et 69 ). Par ailleurs, un paquet MCU peut ne pas entrer complètement dans la charge utile de la couche protocolaire M-PDU : il se peut que la charge utile d’un M-PDU contienne plusieurs MCU successifs (par exemple, lorsque les imagettes compressées en JPEG sont petites, tel que lors de la transmission d’une zone de couleur uniforme) ou bien qu’un MCU soit distribué entre deux M-PDU. Ainsi, l’en-tête du paquet VCDU contient un pointeur qui nous informe de l’indice auquel le prochain M-PDU démarre. Avant ce pointeur, nous obtiendrons la fin du paquet M-PDU précédent.
Nous avions placé dans la matrice fin les diverses trames successives, décodées après application de l’algorithme de Viterbi et derandomization : nous affichons le contenu des premières lignes de cette matrice, pour constater la cohérence d’un certain nombre de motifs – en-tête des paquets – avant d’atteindre la charge utile, qui sera elle aléatoire. Le document qui nous est apparu le plus limpide pour décoder les trames est [7].
octave:28> fin(1:16,:) % voir 20020081350.pdf NASA p.9 du PDF
64 64 64 64 64 64 64 64 64 64 64 64 64 64 Version
5 5 5 5 5 5 5 5 5 5 5 5 5 5 Type
140 140 140 140 140 140 140 140 140 140 140 140 140 140 \
163 163 163 163 163 163 163 163 163 163 163 163 163 163 - counter
43 44 45 46 47 48 49 50 51 52 53 54 55 56 /
0 0 0 0 0 0 0 0 0 0 0 0 0 0 sig. field
0 0 0 0 0 0 0 0 0 0 0 0 0 0 VCDU insert
0 0 0 0 0 0 0 0 0 0 0 0 0 0 ... zone
0 0 2 1 0 0 0 0 0 0 0 0 2 0 5 bits @ 0
18 142 28 54 18 130 78 226 0 20 70 28 82 32 M_PDU header
77 166 239 222 73 82 83 199 8 28 232 247 165 183 M_PDU...
133 188 229 42 24 23 220 94 68 117 92 151 87 203 ... 882 bytes
75 177 221 215 0 48 49 128 13 166 8 218 126 212
42 138 254 87 12 32 249 87 34 172 247 107 9 142
146 238 236 80 215 96 143 121 0 124 12 89 86 191
179 227 64 144 89 59 240 105 105 251 46 43 0 199
^
Nous analysons ceci comme suit, de la première à la dernière ligne, en commençant par le VCDU Primary Header de 6 octets :
- 64 correspond à la version constante de 01, suivie de 6 zéros pour les bits de poids fort du VCDU Id (S/C id). Ainsi, les 8 premiers bits sont 0100 0000 ;
- suit l’identifiant du satellite qui transmet (champ Type de VCDU Id) : ce champ est renseigné dans [6] comme valant 5, si l’instrument est présent et 63, si l’instrument est absent. Ici, une valeur de 5 est un bon présage pour la suite du décodage des images. Par ailleurs, [8, p. 149] indique qu’un VCDU Id de 5 (AVHRR LR) sera associé aux canaux APID 64..69, que nous identifierons plus tard ;
- le VCDU Counter de 3 octets s’incrémente à chaque paquet, tel que nous l’observons avec le décompte sur le dernier octet (140 163 43..56) du triplet d’octets, correspondant au compteur de trame ;
- tous les champs suivants (signaling field) sont renseignés comme nuls, pour indiquer la transmission de données en temps réel, tout comme les champs VCDU Insert zone et l’absence de cryptographie [8, p. 150] ;
- enfin, les deux derniers octets de l’en-tête fournissent un pointeur, qui nous indique à quel emplacement se trouvera le début du premier paquet contenu dans cette trame. Cette information est probablement la plus importante, car un paquet M_PDU a toutes les chances de se partager entre plusieurs trames et donc, savoir où commence le premier paquet M_PDU contenu dans la trame permet de synchroniser le début du décodage d’une nouvelle image. Les 5 premiers bits sont toujours nuls, tandis que les 11 derniers bits donnent l’adresse, dans la trame, du début du premier paquet utile. Dans la séquence proposée ici, le pointeur se calcule comme :
- x=fin(9,:)*256+fin(10,:)+12 = 30 154 552 322 30 142 90 238 12 32 82 40 606 44
- les 882 octets qui suivent sont la charge utile M-PDU, contenant les champs du canal virtuel (Virtual channel field). Nous pourrons nous convaincre que la position de l’en-tête, identifiée ci-dessus, est correcte par for k=1:length(x);fin(x(k),k),end, qui renvoie 64 64 64 64 65 65 65 65 68 64 64 64 64 65 qui est la liste des identifiants des canaux virtuels que nous analyserons ci-dessous, c.-à-d les diverses longueurs d’onde observées pour former les images (APID compris entre 64 et 69 [6]) ;
- la 9e colonne est un peu spéciale, car elle contient le premier paquet de la séquence de transmissions du canal d’APID 68, donc un en-tête d’offset par rapport à la fin de l’en-tête du VCDU, qui permet de commencer à appréhender le format de la charge utile M_PDU, sans avoir à en rechercher le début. Nous verrons ainsi que 8=0000 1000 est la version (ID=000/Type Indicator=0/Secondary Header 1=present/000 APID), puis APID=68 est un des canaux de mesure et finalement, la longueur du paquet (en octets) est fournie par {0 105}.
2. Que de texte... des images maintenant
Nous avons identifié comment décoder la trame VCDU, maintenant il reste à analyser la charge utile qu’est le M_PDU. Plusieurs M_PDU peuvent se regrouper dans une même trame VCDU (par exemple, lorsque la charge utile qu’est une imagette JPEG est fortement compressée) et un M_PDU peut se distribuer entre deux VCDU successifs – il n’y a aucune raison pour que la taille de la charge utile M_PDU soit multiple de la taille d’une trame VCDU.
Nous avons identifié auparavant les pointeurs, dans l’en-tête du VCDU, de l’adresse de début de chaque paquet M_PDU contenu dans le VCDU. Si nous affichons les premiers octets de chaque M_PDU, nous observons un motif cohérent :
8 8 8 8 8 8 8 8 8 8 8
68 68 68 68 68 68 68 70 64 64 64
13 13 13 13 13 13 13 205 77 13 13
34 35 36 37 38 39 40 41 42 43 44
0 0 0 0 0 0 0 0 0 0 0
105 47 49 69 81 107 57 57 97 77 79
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
2 2 2 2 2 2 2 2 2 2 2
136 136 136 136 136 136 136 136 136 136 136
181 181 181 181 181 181 181 181 186 186 186
124 124 124 124 124 124 124 124 76 76 76
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
98 112 126 140 154 168 182 2 0 14 28
0 0 0 0 0 0 0 24 0 0 0
0 0 0 0 0 0 0 167 0 0 0
255 255 255 255 255 255 255 163 255 255 255
240 240 240 240 240 240 240 146 240 240 240
77 77 77 77 77 77 77 221 77 79 81
243 186 210 178 136 175 242 154 173 238 235
197 41 160 177 253 120 216 191 166 148 77
60 194 210 146 236 9 151 11 88 100 166
240 156 80 106 84 81 201 48 42 228 208
105 41 5 65 152 245 135 33 131 208 9
254 104 41 23 193 172 56 197 38 210 28
91 52 20 205 1 233 249 0 62 115 118
Nous allons analyser ceci dans le cas particulier de la première colonne :
- 68 est l’identifiant (packet identifier) de l’instrument à bord du satellite qui transmet l’information, APID. Comme une image d’un instrument s’étalera sur plusieurs paquets successifs, il est normal que nous retrouvions plusieurs fois de suite le même APID. Un cas intéressant est l’APID 70 de la colonne 8, qui indique une trame de télémesure qui nous avait permis auparavant de trouver l’heure à bord du satellite, au moment de la prise de vue.
- “13 34” est formé de deux premiers bits, indiquant s’il s’agit du premier paquet d’une séquence (01) ou la suite d’une transmission (00), suivie du compteur de paquets, sur 14 bits, qui nous servira à savoir si nous avons perdu une imagette dans une ligne. Nous constatons bien que l’octet de poids faible s’incrémente à chaque nouveau M_PDU.
- Les deux octets qui suivent indiquent la longueur du paquet M_PDU, ici 105 octets.
- Suit la date codée sur 64 bits, soit un jour sur deux octets “0 0”, un nombre de millisecondes dans la journée codé sur 32 bits “2 136 181 124”, valable pour tous les paquets d’une même image et finalement, un complément de date en microsecondes codé sur 16 bits et fixé, pour Meteor-M2, à “0 0”.
- La description du champ de données indique l’indice du premier MCU (Minimum Code Unit), imagette dont l’assemblage formera une ligne de l’image finale. Cet indice de MCU s’incrémente de 14 entre deux paquets successifs, ici 98 112 126, puisque les imagettes sont regroupées par paquets de 14, pour améliorer la compression.
- Finalement, l’en-tête de l’image contient 16 bits fixés à 0 (Scan Header suivi du Segment Header contenant un indicateur de présence de facteur de qualité sur 16 bits, fixé à 0xFF 0xF0 ou 255 240 suivi de la valeur de ce facteur de qualité, qui interviendra dans la quantification de l’imagette JPEG – dans notre cas 77, mais variable le long d’une ligne de l’image finale).
- Suivent les données des 14 MCU successifs formant 14 imagettes de 8x8 pixels, ou 64 octets successifs dans la nomenclature (dans le cas de la première trame, cette charge utile commence par 243 197).
Cette description un peu fastidieuse est nécessaire pour bien comprendre le lien entre les VCDU et les M_PDU, qui finalement représentent deux abstractions du flux de données, à deux niveaux différents des couches OSI. Une fois cette distinction assimilée, l’assemblage des imagettes JPEG, pour former une ligne, n’est plus que question de rigueur dans le suivi de la norme. Sous GNU/Octave, les octets représentant chaque MCU, composé de 14 imagettes, sont regroupés dans des fichiers individuels suivant le bout de programme :
01: for col=1:23 % numéro de colonne = numéro de frame VCDU
02: first_head=fin(9,col)*256+fin(10,col) % 70 pour colonne 11
03: fin([1:first_head+1]+9,col)';% début de la ligne 11 : 1er header en 70
04: fin([1:22]+first_head+11,col)';% début du MCU de la ligne 11
05:
06: clear l secondary apid m
07: l=fin(first_head+16-1,col)*256+fin(first_head+16,col); % vector of packet lengths
08: secondary=fin(first_head+16-5,col); % initialise la liste des en-têtes
09: apid=fin(first_head+16-4,col); % initialise la liste des APIDs
10: m=fin([first_head+12:first_head+12+P],col);
11: k=1;
12: while ((sum(l)+(k)*7+first_head+12+P)<(1020-128))
13: m=[m fin([first_head+12:first_head+12+P]+sum(l)+(k)*7,col)];
14: secondary(k+1)=fin(first_head+16+sum(l)+(k)*7-5,col);
15: apid(k+1)=fin(first_head+16+sum(l)+(k)*7-4,col);
16: l(k+1)=fin(first_head+16-1+sum(l)+(k)*7,col)*256+fin(first_head+16+sum(l)+(k)*7,col);
17: % 16=offset from VDU beginning
18: k=k+1;
19: end
20: for k=1:length(l)-1 % sauvegarde dans un fichier des octets de chaque MCU
21: jpeg=fin([1:l(k)]+first_head+12+19+sum(l(1:k-1))-1+7*(k-1),col);
22: f=fopen(['jpeg',num2str(apid(k),'%03d'),'_',num2str(col,'%03d'),'_',num2str(k,'%03d'),'.bin'],'w');
23: fwrite(f,jpeg,'uint8');
24: fclose(f);
25: end
26:
27: k=length(l); % dernier paquet incomplet
28: jpeg=fin([1+first_head+12+19+sum(l(1:k-1))-1+7*(k-1):end],col);
29: first_head=final(9,colonne+1)*256+final(10,col+1); % cherche dans VCDU suivant
30: jpeg=[jpeg ; final([1:first_head]+10,col+1)];
31: % on annonçait 79 octets dans le dernier paquet : il en manque 925-892=33
32: f=fopen(['jpeg',num2str(apid(k),'%03d'),'_',num2str(col,'%03d'),'_',num2str(k,'%03d'),'.bin'],'w');
33: fwrite(f,jpeg,'uint8');
34: fclose(f);
35: end
Ayant sauvé dans des fichiers individuels jpeg*.bin les MCU, nous devons aborder le problème d’interpréter leur contenu comme des images. Ceci nécessite de réimplémenter le décodage de Huffman, RLE puis transformée en cosinus discrète pour convertir chaque imagette au format JPEG en une matrice de pixels affichable. En particulier, le décodage de Huffman est pénible à implémenter par sa manipulation des données par paquets de bits qui ne sont pas multiples de 8, mais dépend de la taille de chaque information dans l’arbre binaire d’encodage. Nous nous contentons dans un premier temps de lire et comprendre le code source du décodeur de meteor_decoder, traduit en C++ sur github.com/infostellarinc/starcoder/blob/master/gr-starcoder/lib/meteor, et à l’intégrer dans un petit bout de code, pour valider le contenu des paquets de bits issus du traitement précédent et que nous affirmons encoder des imagettes au format JPEG, pour aborder plus en détail cette séquence de traitement dans la section qui va suivre. Cette fois, la séquence d’encodage (et donc de décodage) est très bien décrite dans [9]. Le fait que le décodeur de meteor_decoder accepte nos MCU comme valides et en déduise des imagettes cohérentes qui s’assemblent convenablement prouve que notre décodage des VCDU, puis MCU a été correct.
01: #include "meteor_image.h"
02: using namespace gr::starcoder::meteor;
03:
04: int main(int argc,char **argv)
05: {int fd,len,k,quality=77; // quality fixe
06: unsigned char packet[1100]; // sera arg plus tard
07: imager img=imager();
08: if (argc>1) quality=atoi(argv[1]);
09: fd=open("jpeg.bin",O_RDONLY);
10: len=read(fd, packet, 1100);
11: close(fd);
12: img.dec_mcus(packet, len, 65,0,0,quality);
13: }
Ceci se linke sur meteor_image.cc et meteor_bit_io.cc de l’archive GitHub citée précédemment. En exploitant ce programme, à qui nous fournissons en format binaire la charge utile qu’est chaque MCU, nous obtenons en sortie une matrice de 14x64 éléments que nous nommerons imag, chaque ligne de 64 octets étant elle-même une imagette de 8x8 pixels. En réorganisant sous GNU/Octave ces 64 éléments par m=[];for k=1:size(imag)(1) a=reshape(imag(k,:),8,8); m=[m a'];end, nous obtenons une matrice de 112x8 pixels que nous affichons par imagesc(m) pour visualiser l’image, telle que présentée en figure 6 (gauche). Cette procédure est répétée pour les 14 MCU qui forment une ligne de l’image finale : la figure 6 illustre la concaténation de la première série d’imagettes (gauche) avec une seconde série, démontrant la continuité des motifs. Cette séquence se poursuit pour toute une ligne d’images acquise à une longueur d’onde donnée par un instrument donné (donc une valeur d’APID donnée), avant de reprendre pour un nouvel APID et ainsi former, en parallèle, plusieurs images acquises à plusieurs longueurs d’onde. On notera l’excellent facteur de compression de JPEG sur ces zones relativement homogènes : il ne faut qu’une soixantaine d’octets pour encoder ces images de 14x64=896 pixels. Les zones les plus structurées nécessitent tout de même des MCU de plusieurs centaines d’octets, voire jusqu’à 700 octets.
Fig. 6 : Décodage d’un MCU (haut) formé de 14 imagettes de 8x8 pixels successives, et concaténation avec le MCU suivant (bas) pour former une image de 28x8=224 pixels de large et 8 pixels de haut. L’image complète finale sera ainsi assemblée petit à petit par morceaux de MCU. Cet exemple porte sur l’APID 68.
Le résultat de l’assemblage des images décompressées de JPEG vers des matrices de 8x8 pixels est illustré en figure 7 pour l’instrument d’APID 68. Nous commençons à entrevoir une séquence cohérente d’images, mais clairement il manque quelques vignettes sur chaque ligne, car quelques paquets étaient corrompus et n’ont pas pu donner lieu à un décodage (figure 7).
Fig. 7 : Haut : résultat du décodage des imagettes JPEG et assemblage sans tenir compte du compteur. Nous observons clairement un décalage du motif lorsque des paquets manquent, résultant dans une image à peine exploitable. Bas : si le compteur de paquet n’atteint pas la valeur attendue de 14 imagettes/MCU, alors de faux paquets manquants sont insérés : cette fois, l’image est convenablement alignée. Ici, l’APID est 68.
Nous pallions à ce dysfonctionnement, au moins provisoirement, en dupliquant chaque image manquante comme indiqué par le compteur de MCU : à défaut de retrouver l’information perdue, nous arrivons au moins à aligner selon la verticale de l’image des vignettes adjacentes et ainsi, obtenir une image reconnaissable (figure 8). Dans cet exemple, nous n’avons pas utilisé l’indice de qualité, qui modifie les facteurs de quantification de la compression JPEG en fonction de la nature de l’image, et des discontinuités sur les tons de gris restent visibles.
Fig. 8 : Résultat du décodage de l’APID 65, avec exploitation du compteur pour identifier les imagettes manquantes, mais sans exploitation de l’information de qualité du code JPEG. Les caractéristiques géographiques sont visibles, mais de forts contrastes existent au sein de l’image, la rendant peu esthétique.
En intégrant le facteur de qualité comme argument passé au décodeur d’imagettes de meteor_decoder sur lequel nous lions notre programme, les tons de gris s’homogénéisent pour donner un résultat convaincant (figure 9), proche de la référence qu’est l’image entièrement décodée par meteor_decoder (figure 10). On notera qu’il s’agissait d’un passage du satellite loin de l’optimal lors d’une écoute depuis la France, puisque sont clairement visibles l’Istrie, les Alpes italiennes et autrichiennes ainsi que le lac Balaton en Hongrie (structure allongée à l’abscisse 1050, environ en milieu d’image), laissant penser à un passage s’approchant de l’horizon Est.
Fig. 9 : Résultat du décodage de l’APID 65, avec exploitation du compteur pour identifier les imagettes manquantes, et de l’information de qualité du code JPEG. Les imagettes individuelles sont maintenant à peine visibles et les tons de gris évoluent continuellement sur l’image.
Fig. 10 : Résultat du décodage de l’APID 65 par medet, servant de référence pour comparaison avec la figure 9.
3. Décodage des images JPEG
Nous avons exploité gr-starcoder, sans en comprendre le contenu. Cela ne saurait nous satisfaire : nous devons comprendre, par quelle magie, des coefficients de Fourier ont été convertis en une imagette d’intensité lumineuse de pixels dans le domaine spatial (nous sommes en tons de gris, donc nous oublions le concept de couleur : seule l’intensité lumineuse, ou luminance, importe dans ce traitement).
Nous désirons comprendre comment, à partir du MCU fourni par le décodage des trames, retrouver une imagette au format JPEG de 8 par 8 pixels. Nous savons qu’il y a un codage sans pertes de Huffman, avec éventuellement élimination des redondances en copiant une valeur qui se répète (RLE – Run Length Encoding), pour finalement convertir les coefficients de Fourier dans le domaine spatial par une transformée en cosinus discrète.
Le principal point de friction tient en la définition de la table de Huffman. Tout le monde pourra visiter les multiples pages décrivant [10, section 2.2, p.111] le calcul de l’arbre binaire, permettant de trouver une représentation des données minimisant le nombre de bits nécessaires à représenter les informations les plus fréquentes, quitte à augmenter le nombre de bits nécessaires à représenter les informations les moins fréquentes : statistiquement, le fichier s’en trouvera souvent réduit en taille (c’est pourquoi la compression d’un fichier texte, avec beaucoup de redondance, est très efficace alors que la compression d’un exécutable binaire, où tous les octets sont à peu près équiprobables, ne donne que des résultats médiocres). Un point qui peut rendre le fichier compressé plus volumineux que le fichier original est le fait de transmettre la table de correspondance entre séquences de bits et données décodées. Dans le cas de LRPT, le choix est fait d’exploiter une table fixe, standardisée après analyse de suffisamment d’images pour avoir une distribution statistiquement représentative du nombre d’apparition de chaque symbole. La norme LRPT nous explique simplement de consulter [9]... un raccourci quelque peu grossier, puisque nous n’avons identifié qu’une unique page utile, sur les 186 que compte la norme ! Les tables qui permettront de retrouver les arbres de décodage (pour les composantes DC – fréquences nulles – et AC – fréquences non nulles – de la transformée de Fourier de l’image) se trouvent en page 158. Nous allons donc nous efforcer, grâce aux explications de https://www.impulseadventure.com/photo/jpeg-huffman-coding.html et imrannazar.com/Let's-Build-a-JPEG-Decoder (section 3), de comprendre comment lire ces tables, nommées DHT pour Define Huffman Table.
On nous explique que le nombre de codes composé de N bits est :
X’00 02 01 03 03 02 04 03 05 05 04 04 00 00 01 7D’
Et que l’assignation de la valeur à chacun de ces codes suit la séquence :
X’01 02 03 00 04 11 05 12 21 31 41 06 13 51 61 07' ...
Notez que ces séquences sont celles visibles dans huffman.pas de meteor_decoder (premières lignes du tableau t_ac_0). La partie implicite est comment former lesdits codes ! La première table nous informe qu’il y a 0 code de 1 bit, 2 codes de 2 bits, 1 code de 3 bits, 3 codes de 4 bits, 3 codes de 5 bits, 2 codes de 6 bits... Il nous faut donc former cette séquence de bits. L’opération consiste à compter en binaire, et lorsque nous incrémentons le nombre de bits nécessaires à continuer la séquence, nous partons de la séquence précédente que nous complétons d’un 0 (en rouge ci-dessous). Cela donne en pratique
00 : premier code de deux bits
01 : second code de deux bits
10 : unique code de 3 bits
101 : premier code de 4 bits
1011 : deuxième code de 4 bits
1100 : troisième code de 4 bits
1101 : premier code de 5 bits
11011 : deuxième code de 5 bits
11100 : troisième code de 5 bits
11101 : premier code de 6 bits
111011 : second code de 6 bits
111100 : premier code de 7 bits
...
Et la table qui suit nous informe de la valeur associée à chacun de ces codes
00 = 1
01 = 2
100 = 3
1010 = 0
1011 = 4
1100 = 0x11 = 17
11010 = 5
11011 = 0x12 = 18
11100 = 0x21 = 33
111010 = 0x31 = 49
111011 = 0x41 = 65
1111000 = 6
1111001 = 0x13 = 19
...
On se rassurera en constatant que la somme des éléments de la première table vaut 162, qui est bien le nombre d’éléments dans la seconde table : il y aura donc bien une valeur pour chaque code. Bien que les valeurs soient comprises entre 0 et 255, nous constatons que 125 de ces éléments nécessiteront 16 bits pour être codés au lieu de 8. Néanmoins, comme la majorité des valeurs se regroupe autour des quelques éléments, ces valeurs codées sur 16 bits apparaissent suffisamment peu souvent pour qu’en moyenne, la compression soit rentable.
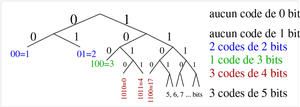
Une façon élégante, même si peu utile, pour se raccrocher aux arbres binaires bien connus du codage de Huffman, est de représenter le code tel que proposé sur la figure 11.
Fig. 11 : Représentation en arbre binaire de la table du code de Huffman, proposé dans [9].
Le problème est le même, mais plus simple pour la composante DC qui contient beaucoup moins de valeurs :
X’00 01 05 01 01 01 01 01 01'
Le contenu est ici séquentiel de 0 à 0xb = 11. Ici encore, nous ne constatons aucun code de 1 bit, 1 code de 2 bits, 5 codes de 3 bits, puis 1 code de 4 à 9 bits. Cette séquence s’écrit donc :
00 = 0
010 = 1
011 = 2
100 = 3
101 = 4
110 = 5
1110 = 6
11110 = 7
111110 = 8
...
Nous voici maintenant équipés pour décoder une image JPEG. Si nous observons la séquence binaire du début d’un MCU issu des décodages précédents, nous obtenons :
$ xxd -b jpeg.bin | head -2
00000000: 11111011 01010011 11000111 11110110 11110000 11101000 .S....
00000006: 10011111 10110011 00011111 10001101 00111110 00100000 ....>
Ceci commence par la composante DC de la transformée en cosinus discrète de l’image, suivi des 63 composantes AC (la transformée de Fourier est bijective, donc les 64 pixels de l’imagette de 8 par 8 pixels donnent 64 coefficients de Fourier, avec éventuellement un certain nombre de valeurs nulles). À chaque fois, nous aurons le couple “nombre de bits” suivi de “valeur”. En suivant à partir du début jusqu’à atteindre le premier code DC valable, nous constatons que nous obtenons 111110 (premier 0 atteint), soit la valeur 8 dans la seconde table qui nous venons d’exposer. Cela signifie que la valeur de la composante DC est codée sur les 8 bits qui suivent, soit 11 010100=212 en décimal. Nous verrons plus bas si cette valeur est correcte. Suit le premier des 63 coefficients AC : ici encore, nous lisons la séquence de bits jusqu’à atteindre le premier code valable dans la première table exposée ci-dessus : 11 11000 est le premier code valable que nous rencontrons, qui est associé à la valeur 6. Le premier coefficient AC est donc codé par les 6 bits qui suivent, soit 111 111=63 en décimal. Continuons pour découvrir une autre subtilité de l’assignation des codes aux séquences de bits : nous poursuivons où nous nous étions arrêtés dans la lecture des bits pour trouver 1011, qui correspond à la valeur 4 et indique que nous lisons les 4 bits qui suivent, soit 0 111 pour connaître la valeur du coefficient suivant. Et là, une simple conversion binaire ne convient plus, puisque la représentation n’est pas en complément à 2, mais séquentielle, avec le codage du nombre signé composé uniquement de 0s, représentant la valeur minimum de l’intervalle et le codage formé de 1s, la valeur maximale. Donc 0 111 ne vaut pas +7 comme le ferait un bête convertisseur binaire vers décimal, mais -8 puisque sur 4 bits, nous pouvons représenter de -15 à +15 en excluant l’intervalle de -7 à +7, qui aurait été codé avec moins de bits. Ceci est résumé dans le tableau F1 de la page 89 de [9] (ou Table 5 de www.impulseadventure.com/photo/jpeg-huffman-coding.html que nous reproduisons ici dans le tableau suivant, montrant la correspondance entre le nombre de bits affectés à une valeur, la séquence de bits et la valeur elle-même (on notera que l’intervalle pris en charge par un nombre inférieur de bits est exclu de l’intervalle représenté par un nombre de bits donné) :
|
Longueur |
|
|
|
|
|---|---|---|---|---|
|
0 |
|
|
0 |
|
|
1 |
0 |
1 |
-1 |
1 |
|
2 |
00,01 |
10,11 |
-3, -2 |
2,3 |
|
3 |
000,001,010,011 |
100,101,110,111 |
-7,-6,-5.-4 |
4,5,6,7 |
|
4 |
0000,...,01111 |
1000,...,1111 |
-15,...,-8 |
8,...,15 |
|
5 |
00000,...,011111 |
10000,...,11111 |
-31,...,-16 |
16,...,31 |
|
6 |
000000,... |
...,111111 |
-63,...,-32 |
32,...,64 |
|
7 |
0000000,... |
...,1111111 |
-127,...,-32 |
32,...,64 |
|
8 |
00000000,... |
...,11111111 |
-255,...,-128 |
128,...,255 |
|
... |
... |
... |
... |
... |
Suit ensuite le code 100 qui vaut 3 et dont les 3 bits qui suivent valent 00 1 soit -6, et nous continuons ainsi pour décoder tous les coefficients de Fourier ou rencontrer la valeur 0 pour le nombre de bits, signifiant la fin du MCU avec tous les autres coefficients nuls.
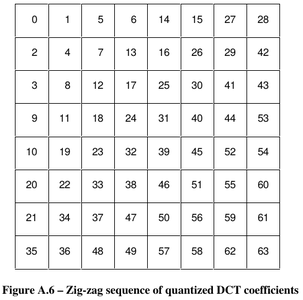
Une fois les coefficients obtenus, ils sont réorganisés selon le motif de zigzag décrit en p.16 (figure 5) de [9] ou explicité avec l’indice de chaque case de la matrice en p.30 (figure 12), et la transformée en cosinus discrète est effectuée, pour passer du domaine spectral au domaine spatial.
Fig. 12 : Assignation de la position de chaque coefficient dans le codage en zigzag des coefficients, maximisant d’avoir les coefficients importants en début de séquence et d’éliminer bon nombre de coefficients de fréquence élevée (vers la droite et le bas) lors de la quantification.
Nous pouvons nous convaincre de la validité de l’analyse, en modifiant légèrement meteor_image.cc de github.com/infostellarinc/starcoder/blob/master/gr-starcoder/lib/meteor pour afficher les coefficients avant réorganisation et transformée en cosinus : nous affichons le contenu (nombres à virgule flottante !) de zdct[], juste avant la boucle dct[i] = zdct[ZIGZAG[i]] * dqt[i]; qui réorganise les coefficients selon le motif de zigzag. Ce faisant, nous obtenons :
212 63 -8 -6 -27 -156 52 65 -2 10 3 -1 21 -1 -4 6 -14 0 6 2 4 1 0 2 4 5 0 16 1 -12 3 -1 0 -3 0 17 3 -2 1 0 2 7 -8 -4 3 -1 -1 1 -5 -1 0 -1 1 5 1 -1 -2 1 -1 -1 -1 1 1 0
Ceci commence bien par la séquence que nous avons identifiée pour se poursuivre avec les 64 coefficients. Après réorganisation selon le motif de zigzags et application du facteur d’homothétie qui a permis d’annuler un certain nombre de coefficients lors de la compression, nous obtenons un vecteur que nous nommerons coefficients :
1484 315 -780 364 -44 108 368 28 -48 -162 390 -9 -168 0 -336 -200 -36 -12 147 0 90 78 224 -104 60 -8 60 52 -23 80 111 145 24 20 34 0 0 -50 47 35 44 0 -75 29 -37 -48 -52 -42 23 0 -72 40 0 -112 -55 46 561 126 -220 -45 52 -46 47 0
Ce sont les 64 coefficients dans le domaine spectral sur lesquels s’applique la transformée en cosinus discrète (fonction idct2 de la signal processing toolbox de GNU/Octave – page 27 de [9]) :
avec C = 1 / √2 et Ck≠ = 1 et S la matrice des coefficients de Fourier.
Après l’iDCT, le décodeur fournit la séquence de 64 valeurs, que nous nommerons image :
410 299 332 320 292 508 307 222 304 189 185 283 95 353 290 160 252 474 370 552 558 497 273 109 149 261 215 264 328 340 226 -4 417 289 641 512 644 510 245 95 282 56 407 255 466 390 160 -33 418 131 613 569 551 572 96 59 371 47 498 416 460 478 -45 78
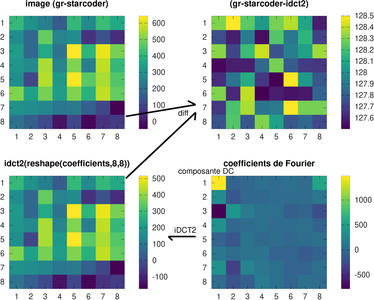
Nous la réorganisons en imagette de 8x8 pixels et vérifions qu’à la constante de 128 près ajoutée par gr-starcoder (tel que préconisé par la norme), nous obtenons le même résultat entre
idct2(reshape(coefficients,8,8)) et reshape(image,8,8) (figure 13).
Fig. 13 : Une fois la séquence de coefficients de Fourier obtenue, la fin du traitement est triviale : réorganisation le long du motif en zigzag, application du facteur d’homothétie définissant la qualité de l’image, puis finalement transformée en cosinus discrète inverse. Partant des coefficients de Fourier (en bas à droite, en vérifiant que la composante continue du signal est bien en coordonnées (1,1) en haut à gauche de la matrice), nous comparons (en haut à droite) le calcul effectué par gr-starcoder et celui obtenu par transformée en cosinus discret 2D inverse (idct2 de GNU/Octave). Nous constatons que l’erreur est à peu près constante et égale à 128 – constante ajoutée par gr-starcoder, après calcul de l’iDCT (en haut à droite).
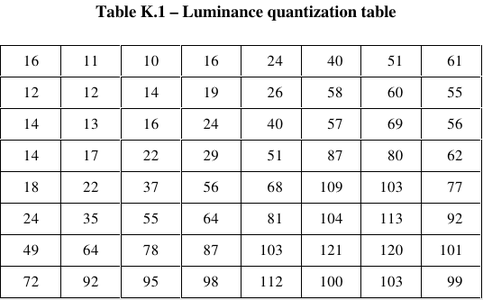
Le facteur d’homothétie de chaque coefficient, qui est la source par quantification de la perte dans l’algorithme de compression JPEG, s’est déduit comme suit. Partant de la table de quantification HTK des coefficients de Fourier fournie en Table K.1 page 143 de [9] (figure 14), un facteur de qualité Q est fourni avec chaque MCU pour indiquer le facteur de compression de l’image. De ce facteur de qualité Q, nous déduisons F=5000/Q si 20<Q<50 et F=200-2xQ si 50<Q<100. Ce facteur de quantification pondère la table de quantification originale par PTK=F/100xHTK et finalement, chaque coefficient transmis Sq est le résultat de l’arrondi à l’entier le plus proche des coefficients de Fourier S, normalisés par la table de quantification ajustée Sq=S/PTK.
Fig. 14 : Table de quantification fournie dans [9, p.143].
Conclusion
Cette exploration du protocole LRPT des liaisons numériques entre les satellites et le sol a été l’opportunité d’appréhender l’ensemble des couches OSI, de la couche physique (fréquence de transmission) au codage (QPSK et code de convolution) aux paquets (mots) et images (phrases) contenus dans le message. Cette présentation avait pour vocation d’illustrer la puissance pédagogique de la radio logicielle : chacune des étapes de traitement fait appel à un principe physique ou mathématique incroyablement ennuyeux, si appréhendé de façon purement théorique, mais qui prend tout son sens dans les étapes du jeu qui doit se conclure par le décodage d’une image.
Ainsi, nous avons découvert, par la pratique, la subtilité de la modulation QPSK et les diverses solutions à l’assignation de chacun des 4 états de phase possible à une paire de bits – problème qui nous avait échappé dans l’étude d’un signal modulé en BPSK – puis mis en œuvre le décodage du code de convolution par algorithme de Viterbi. Ayant identifié la cohérence des séquences de bits issues de la déconvolution, nous avons provisoirement négligé le codage par blocs de Reed Solomon, pour dépiler les diverses couches du protocole encapsulant les imagettes formant l’image finale, après assemblage. Le lecteur le plus perspicace pourra conclure sur la réimplémentation du décodage JPEG, que nous avons simplement implémenté ici sans en reprendre les fondements théoriques. Finalement, le décodage du code correcteur par blocs de Reed Solomon est mis en œuvre et son bon fonctionnement validé, malgré un bénéfice relativement mineur dans le cas qui nous a intéressés ici. M. Braun [11] citait au cours de son exposé au FOSDEM sur les codes correcteurs d’erreur le théorème de Shannon, tel que décrit dans son article [12] (figure 15), que « tout système de codage suffisamment complexe est susceptible d’atteindre le débit de transfert optimal dans un canal de communication bruité » : le concept de « suffisamment complexe » devient plus clair à l’issue de cette étude d’un mode de liaison avec un émetteur spatial, et fournit les bases pour aborder des modulations plus complexes encore, telles qu’utilisées par exemple dans la télévision numérique terrestre (DVB-T).
Fig. 15 : Extrait de l’article de Shannon sur le débit de communication dans un canal bruité.
Ces fondements doivent fournir les bases pour décoder multitude d’autres télémesures spatiales, tel que démontré par la richesse du blog de D. Estévez, qui met en œuvre ses compétences sur une multitude de satellites sur destevez.net/, par exemple destevez.net/2017/01/ks-1q-decoded/. Un dépôt sur github.com/jmfriedt/meteor-m2 regroupe les divers fichiers de données et scripts utilisés au cours des deux parties de cet article.
Remerciements
L. Teske et D. Estévez ont répondu à mes demandes de compléments d’information par courrier électronique. M. Addouche (Univ. de Franche-Comté à Besançon) m’a présenté le décodage du code de convolution par algorithme de Viterbi. Tous les ouvrages et références qui ne sont pas librement disponibles sur le Web ont été obtenus auprès de Library Genesis sur gen.lib.rus.ec, une ressource d’une valeur inestimable pour nos recherches.
Références
[1] A. BOISSIN et al., « Single space segment – HRPT/LRPT direct broadcast services specification », ESA EUMETSAT EPS/METOP MO-DS-ESA-SY-0048 rev. 5, 1998.
[2] L. TESKE, « GOES Satellite Hunt » : www.teske.net.br/lucas/satcom-projects/satellite-projects/.
[3] J.-M FRIEDT et G. CABODEVILA, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », Open Silicium n°15, juillet-septembre 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-015/Decodage-des-signaux-de-satellites-GPS-recus-par-recepteur-de-television-numerique-terrestre-DVB-T.
[4] J.-M FRIEDT, « Radio Data System (RDS) – analyse du canal numérique transmis par les stations radio FM commerciales, introduction aux codes correcteurs d’erreur », GNU/Linux Magazine France n°204, mai 2017 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-204/Radio-Data-System-RDS-analyse-du-canal-numerique-transmis-par-les-stations-radio-FM-commerciales-introduction-aux-codes-correcteurs-d-erreur.
[5] H. BOEGLEN et L. MURA, « Les bases des communications numériques avec GNU Radio », GNU/Linux Magazine France n°225, avril 2019 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-225/Les-bases-des-communications-numeriques-avec-GNU-Radio.
[6] « Structure of Meteor-M 2 satellite data transmitted through VHF-band in direct broadcast mode » : planet.iitp.ru/english/spacecraft/meteor_m_n2_structure_2_eng.htm.
[7] W. FONG et al., « Low Resolution Picture Transmission (LRPT) Demonstration System – Phase II Report », Version 1.0, 2002 : https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20020081350.pdf .
[8] P. GHIVASKY et al., « MetOp Space to Ground Interface Specification », doc. MO-IF-MMT-SY0001 rev. 07C, EADS/ASTRIUM/METOP, 29 mars 2004 : http://web.archive.org/web/20160616220044/http://www.meteor.robonuka.ru/wp-content/uploads/2014/08/pdf_ten_eps-metop-sp2gr.pdf. Le site www.meteor.robonuka.ru a servi d’inspiration tout au long de cette étude, mais a malheureusement disparu : seule archive.org conserve trace des documents introuvables par ailleurs.
[9] « Information technology – Digital compression and coding of continuous-tone still images – requirements and guidelines », ITU CCITT recommandation T.81, 1993 : www.w3.org/Graphics/JPEG/itu-t81.pdf.
[10] J.-G. DUMAS, J.-L. ROCH, É. TANNIER et S. VARRETTE, « Théorie des codes – Compression, cryptage, correction », Dunod, 2007 et en.wikipedia.org/wiki/Huffman_coding sont limpides sur la construction de l’arbre.
[11] M. BRAUN, « Protect your bits: Introduction to gr-fec », FOSDEM Free Software Radio devroom, 2019.
[12] C.E. SHANNON, « Communication in the Presence of Noise », Proc. IRE 37(1), 10–21, 1949.