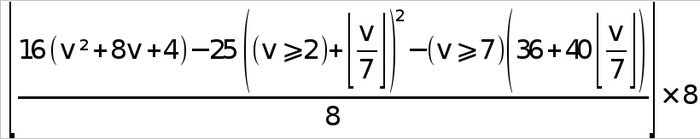Une fois que l'on sait déchiffrer un code QR [1], il faut le décoder... et il y a encore du travail avant de pouvoir lire son contenu.
Nous allons décortiquer le code QR petit à petit pour en extraire les informations utiles à la lecture de son contenu. Le code et les fichiers utiles sont sur GitHub [2].
Je me suis servi des informations données sur Wikiversity [3] pour la rédaction de cet article.
1. Formats
Nous allons enfin pouvoir lire le contenu du message caché dans la bouillie de pixels de la figure 1. Pour cela, il faut lire le format (niveau de correction et masque) dans la petite zone dédiée. Ensuite, une fois l’image démasquée, on en extrait le message brut : les données en clair et de quoi le corriger. La partie en clair contient en son début les informations précises nécessaires à son interprétation.
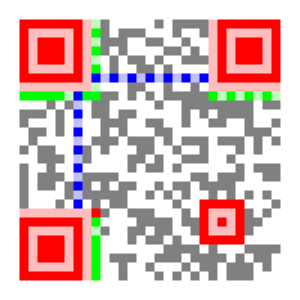
Fig. 1 : Le code QR à décoder.
1.1 Lecture du format
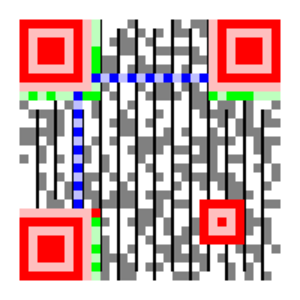
On commence par lire (voir figure 2) les deux zones de bits verts dans form[0] (celle en haut à gauche) et form[1] (celle coupée en deux morceaux en bas et à droite).
Fig. 2 : Les quatre différentes zones d’un code QR.
La couleur rouge caractérise les cibles d’alignement, le bleu les pointillés, en vert les deux zones de format et en gris les données.
Je renuméroterai le code à partir de 01 à chaque section.
01: def formats(self):
02: if self.esttourne is None:
03: self.placeim()
04: self.form=[None,None]
05: self.form[0]=self.qr[8][:6]+self.qr[8][7:9]+[self.qr[7][8]]
06: for i in range(5,-1,-1):
07: self.form[0].append(self.qr[i][8])
08: self.form[0]=[i^j for (i,j) in zip(self.form[0],masquef)]
09: self.form[1]=[self.qr[-i-1][8] for i in range(7)]
10: self.form[1]=self.form[1]+self.qr[8][-8:]
11: self.form[1]=[i^j for (i,j) in zip(self.form[1],masquef)]
Les formats, après lecture, valent 111110110101010, qui n’est pas interprétable directement. On a besoin du masque binaire masquef (qui est dans qrcodestandard.py) pour les décoder bit à bit avec un simple ^ (ou exclusif).
masquef=[int(i) for i in "101010000010010"]
En effet :
111110110101010
^101010000010010
----------------
010100110111000
Notre zone de format est donc 010100110111000.
masquef est créé à partir de la chaîne que j’avais la flemme de convertir à la main en une liste. La fonction zip de la ligne 11 regroupe en parallèle les éléments de types itérables. Par exemple, zip([1,2],[3,4],(5,6)) retourne [(1, 3, 5), (2, 4, 6)]. Mathématiquement, zip retourne la matrice transposée de celle dont les lignes sont en argument et permet de démasquer bit à bit la zone de format. J’aurais pu convertir en entiers chaînes et listes pour utiliser l’opérateur pythonique ^ qu’on emploiera plus loin.
1.2 Vérification du format
On se contente pour le moment de vérifier que form[0] et form[1] sont identiques, la vérification complète et son code correcteur seront détaillés dans un article ultérieur.
01: def verifformat(self):
02: if self.form is None:
03: self.formats()
04: if self.form[0]!=self.form[1]:
05: print("Formats différents.",file=stderr)
06: exit(1)
07:
08: self.formatok=True
Et on dit qu’on est content, chantons sous la pluie...
Dans les images suivantes, la zone verte sera démasquée.
1.3 Démasquage des données
1.3.1 Masque binaire
La partie grise et blanche ne contient pas tout à fait les données brutes, il faut composer avec un masque binaire pour les obtenir.
01: def demasque(self):
02: if self.formatok is None:
03: self.verifformat()
04:
05: self.nivcor=niveaucorrection[tuple(self.form[0][:2])]
06: self.masque=masques[tuple(self.form[0][2:5])]
Les deux premiers bits du format donnent le niveau de correction des erreurs, du niveau L qui corrige le moins d’erreurs au niveau H qui en corrige le plus (les lettres signifient Low, Medium, Quality et High [4]). Ici, notre image utilise le niveau L. niveaucorrection et masques sont dans qrcodestandard.py :
niveaucorrection={(0,1):"L",(0,0):"M",(1,1):"Q",(1,0):"H"}
masques={(0,0,0):lambda i,j:(i+j)%2==0,
(0,0,1):lambda i,j:i%2==0,
(0,1,0):lambda i,j:j%3==0,
(0,1,1):lambda i,j:(i+j)%3==0,
(1,0,0):lambda i,j:(i//2+j//3)%2==0,
(1,0,1):lambda i,j:(i*j)%2==0 and (i*j)%3==0,
(1,1,0):lambda i,j:((i*j)%3+i*j)%2==0,
(1,1,1):lambda i,j:((i*j)%3+i+j)%2==0
}
Le masque est donné par les trois bits suivants. masques est un dictionnaire où les clés sont des tuples (les bits de rang 2 à 4 de la zone de format) et les valeurs des fonctions anonymes créées ad hoc. Oui, Python permet ça tout naturellement. Dans notre cas, masque est le troisième de la liste (voir le premier article de cette série [5] pour le dessin des huit masques ou la fin de cet article pour le nôtre), il inverse les valeurs des colonnes d’abscisse divisibles par 3, c’est une fonction à deux variables qui retourne un booléen ; True s’il faut inverser le bit à la position idoine et False sinon.
08: self.dim=len(self.qr)
09: self.version=(self.dim-17)//4
On calcule le nombre de modules en hauteur (et donc en largeur), on en déduit la version. Il s’agit bien de la version du code qui commence à 1 s’il contient 21 modules et augmente de 1 à chaque quadruplet de modules supplémentaires en hauteur et en largeur. Il n’y a donc pas de code QR de dimension paire ou de 23×23 modules.
1.3.2 Création de la zone à masquer
10: self.gris=griser(self.dim,self.version)
La fonction griser est dans qrcodestandard.py ; elle retourne un tableau de mêmes dimensions que le code QR qui indique la zone dont on doit démasquer le contenu :
def griser(dimension,version):
tablegris=[[False for _ in range(9)]+[True for _ in range(dimension-17)]+\
[False for _ in range(8)] for _ in range(6)]
tablegris=tablegris+[[False for _ in range(dimension)]]
tablegris=tablegris+[[False for _ in range(9)]+[True for _ in range(dimension-17)]+\
[False for _ in range(8)] for _ in range(2)]
tablegris=tablegris+[[True for _ in range(6)]+[False]+\
[True for _ in range(dimension-7)] for _ in range(dimension-17)]
tablegris=tablegris+[[False for _ in range(9)]+\
[True for _ in range(dimension-9)] for _ in range(8)]
Les trois premières lignes ajoutent les deux cibles du haut et la zone entre elles deux (la deuxième est la zone de pointillés horizontale). La suivante construit les lignes entre les cibles et la dernière les lignes inférieures avec la cible inférieure à gauche.
Quand gris[i][j] vaut True, on est dans la zone de données en blanc et gris (et non entre gris clair et gris foncé...). On a commencé par les grandes cibles, les pointillés et les zones de format. Le code aurait été moins lourd en utilisant la multiplication des listes par un scalaire (où 2*[[4,1]] vaut [[4,1],[4,1]]) ; sauf que des copies comme précédemment ou dans [[]]*2=[[],[]] sont comme des liens unix, modifier l’une des listes internes modifie l’autre ce qu’on veut éviter s’il y a des mini-cibles.
for ci in minicibles[version]:
for cj in minicibles[version]:
if (ci,cj) not in {(6,6),(6,max(minicibles[version])),(max(minicibles[version]),6)}:
for i in range(ci-2,ci+3):
tablegris[i][cj-2:cj+3]=[False]*5
Pour les petites cibles de 5 modules de côté, le dictionnaire minicibles contient les abscisses et les ordonnées de leurs centres en fonction de la version du code QR [6]. Il faut veiller à ne pas faire se chevaucher les mini-cibles et les grandes d’où le test au milieu de ce code.
Voici le début du dictionnaire minicibles, lui aussi dansqrcodestandard.py :
minicibles={1:[],
2:[18],3:[22],4:[26],5:[30],6:[34],
7:[6,22,38],8:[6,24,42],9:[6,26,46],10:[6,28,50],11:[6,30,54],12:[6,32,58],13:[6,34,62],
...
}
Et ainsi de suite jusqu’à 40, vous comprenez pourquoi je coupe, le chef et la PAO aussi.
La suite de la fonction griser :
if version>=7:
for i in range(6):
tablegris[i][-11:-8]=[False]*3
for i in range(3):
tablegris[-11+i][0:6]=[False]*6
Il s’agit des deux rectangles de 3×6 modules placés entre les pointillés, à gauche contre la cible de droite et au-dessus contre la cible du bas. Ils n’existent que pour les codes QR de version supérieure ou égale à 7.
return tablegris
1.3.3 Démasquage
12: for i in range(self.dim):
13: for j in range(self.dim):
14: if self.gris[i][j]:
15: self.qr[i][j]^=self.masque(i,j)
Et enfin, on démasque bit à bit, le résultat est dans la figure 3 (la partie verte est démasquée, observez en bas et en haut 01010 c’est-à-dire 01 suivi de 010, voir section 1.1).
Fig. 3 : La partie grisée est démasquée.
Vous vous dites qu’on pourrait démasquer tout le tableau sans se soucier du gris et vous avez raison. Seulement, le gris est nécessaire lors de l’extraction des données brutes puisqu’on ne doit pas lire de bit dans les zones colorées et autant anticiper s’il faut déboguer.
2. Lecture des données
2.1 Extraction des données binaires
2.1.1 L’extraction
Il est temps d’extraire de la zone grise le message binaire et sa correction.
01: def messagebrut(self):
02: if None in [self.version,self.masque,self.dim,self.gris,self.nivcor]:
03: self.demasque()
04: i,j=self.dim-1,self.dim-1
05: self.code=[]
06: direction=-1
La suite de bits, en-tête, message et correction des deux, est dans code, on le découpera plus tard, car ils y sont mélangés.
08: limite=(16*(4+self.version*(8+self.version))-25*(self.version>=2+self.version//7)**2-(self.version>=7)*(36+self.version//7*40))//8*8
limite est le nombre maximum de bits (message et correction) que peut contenir un code QR de la version donnée. Dans notre cas, il peut contenir au maximum 560 bits, soit 70 octets. La formule vient du complément [7] et tient compte de la taille des pointillés, du nombre de mini-cibles et de la présence éventuelle des zones de format. Si v est la version, la voici plus lisible (les crochets incomplets en haut signifient qu’on ne conserve que la partie entière du quotient comme dans version//7 en Python 3) :
Comme d’habitude en Python, un test vaut 1 s’il est vrai et 0 s’il est faux. Vous pouvez vous amuser à retrouver la raison de chaque terme dans cette formule, vous avez tout ce qu’il faut ici.
09: while len(self.code)<limite:
10: if self.gris[i][j]:
11: self.code.append(self.qr[i][j])
12: i,j,direction=suivant(i,j,direction,self.dim)
Bon, je vais vous aider à démontrer cette formule, appelons v la version.
On a au total 4v + 17 modules en longueur et en hauteur donc (4v+17)² modules en tout, ce à quoi il faut soustraire les trois cibles de 8 × 8 = 64 modules, les deux zones de format de 15 modules chacune, le module toujours noir et les pointillés bleus. On a donc, sans compter les mini-cibles et les zones complémentaires de 3 × 6 :
(4v+17)²−3×64−2×15−1−2×(4v+17−2×8)=16v²+128v+64=16(v²+8v+4).
La seconde expression compte le nombre de modules pris par les mini-cibles qui ne rencontrent pas les pointillés. Elles sont de 5 × 5, apparaissent à partir de la version 2 et on en ajoute à chaque version divisant 7.
Enfin, 36 compte les modules pris dans les deux rectangles de 3 × 6, 40 vient des mini-cibles qui chevauchent les pointillés bleus, donc qui prennent 2 × (25 − 5) = 40 modules supplémentaires.
On compte le nombre d’octets, on divise par 8 (euclidiennement) et j’ai remultiplié par 8 pour obtenir le nombre de bits.
Remarquez que dans notre cas, il reste 7 modules puisque la formule donne bien 560 alors que29×29−3×64−2×15−1−2×13−25=567.
On stocke le bit s’il est bien dans le gris. La fonction suivant, dans qrcodestandard.py, donne les coordonnées du bit suivant celui de coordonnées i,j selon la direction et la dimension du code QR et la direction (utile si elle a changé) :
Et voici la partie délicate. On commence par le bit tout en bas à droite puis on remonte de droite à gauche une colonne de deux bits de largeur.
def suivant(i,j,direction,dimension):
j-=1
On commence par reculer d’un module vers la gauche.
if j%2!=(dimension%2+(j<6))%2:
j+=2
i+=direction
Si on a reculé deux fois, on change de ligne et on avance de deux modules pour rester dans la colonne.
if i==-1:
j-=2
i=0
direction=1
Une fois arrivé en haut, on redescend la colonne suivante de deux modules de largeur, toujours de droite à gauche.
if i==dimension:
j-=2
i=dimension-1
direction=-1
Et arrivé en bas, on remonte.
if j==6:
j=5
return i,j,direction
À un détail près : on saute la septième colonne (d’indice 6) qui contient le segment pointillé bleu vertical. La variable direction indique si on monte (-1) ou si on descend (+1). Il suffit de suivre le labyrinthe de la figure 4 en partant du coin inférieur droit.
On peut remarquer que la fonction suivant ne se préoccupe pas du gris sauf pour la colonne bleue.
On lira donc la suite de bits suivante pour la première colonne, en montant : 0100001001010100110001101001011100110110. La deuxième, descendante, commence par 0101011110.
Fig. 4 : Comment lire les données brutes.
2.1.2 L’entrelacement des blocs
Pour qu’un petit dessin n’empêche pas la lecture du message d’un code QR, les données sont en fait entrelacées dès qu’un code QR est assez grand selon le tableau suivant :
|
Niveau de correction |
Low |
Medium |
Quality |
High |
|
Entrelacement à partir de la version |
6 |
4 |
3 |
3 |
On le voit par exemple plus bas dans le dictionnaire tableau de qrcodestandard.py où tableau[5]["L"] vaut "(134,108)" alors que tableau[6]["L"] vaut "2×(86,68)".
Les octets des blocs en clair puis correcteurs sont mélangés et donc distribués partout dans l’image. Dans notre cas, on a un seul bloc de 55 octets de données suivis de 15 octets correcteurs. Dans le cas dela version 5 et niveau de correction H ("2×(33,11),2×(34,12)"), on a deux blocs de données de 11 octets suivis de deux de douze octets suivis de quatre blocs de correction de 22 octets. On écrit les octets des quatre blocs dans un tableau comme ci-dessous :
|
Bloc |
Octets |
|||||||||||
|
n°0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
n°1 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
|
n°2 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
|
n°3 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
Le bloc n°0 contient les 11 premiers octets soit les octets 0 à 10, une case vide signifie qu’il faut la sauter et passer à la suivante. La partie en clair est construite orthogonalement : on lit le tableau de haut en bas d’abord puis de gauche à droite, il s’agit en quelque sorte du tableau transposé de celui-ci en sautant les cases vides. Ainsi, la partie en clair entrelacée contient les octets , 11, 22, 34, 1, 12, 23, …, 9, 20, 31, 43, 10, 21, 32, 44, 33, 45.
On fait la même chose pour les octets des blocs correcteurs qui ont tous la même taille.
14: posclair,lonredondant,lonclair,nbbloc=court2vf(tableau[self.version][self.nivcor])
On récupère, dans le tableau (qui est un dictionnaire de dictionnaires), la chaîne qui nous intéresse "(70,55)" et on la transforme en son équivalent qui ne contient que des coordonnées absolues (plus un zéro initial). Les données en clair et leurs corrections sont regroupés en blocs pas trop grands pour des raisons de temps de calcul. Par exemple, pour le niveau de correction Q de la version 3, les données sont en deux blocs de 35 octets dont les 17 premiers contiennent la partie en clair (il reste donc 18 octets pour la correction dans chacun).
Voici le début du contenu de tableau, stocké dans qrcodestandard.py :
tableau={1:{"L":"(26,19)","M":"(26,16)","Q":"(26,13)","H":"(26,9)"},
2:{"L":"(44,34)","M":"(44,28)","Q":"(44,22)","H":"(44,16)"},
3:{"L":"(70,55)","M":"(70,44)","Q":"2×(35,17)","H":"2×(35,13)"},
4:{"L":"(100,80)","M":"2×(50,32)","Q":"2×(50,24)","H":"4×(25,9)"},
5:{"L":"(134,108)","M":"2×(67,43)","Q":"2×(33,15),2×(34,16)","H":"2×(33,11),2×(34,12)"},
6:{"L":"2×(86,68)","M":"4×(43,27)","Q":"4×(43,19)","H":"4×(43,15)"},
Et ainsi de suite jusqu’à 40. J’ai graissé les trois niveaux de correction illustrés dans cette section.
2.1.3 Le code qui détricote
Plutôt que de transformer à la main les informations données dans [8], j’ai préféré créer des fonctions ad hoc qui le font à ma place, elles aussi dans qrcodestandard.py :
def blocs(l):
return list(eval(l.replace("×","*").replace("),",")+")))
On remplace les × par * et les séparateurs ), par )+ pour que Python transforme tout ça en une seule liste via eval. Dans notre cas, blocs retourne [70,55] et pour le niveau de correction Q, elle retourne [35,17,35,17]. Oui, la multiplication est toujours prioritaire sur l’addition, même pour les listes.
Comme la manière initiale, relative,n’est pas très utilisable, je l’ai convertie, à l’aide de la fonction court2vf en des True/False dans le tableau transposé :
def court2vf(l):
l1=blocs(l)
clair=l1[1::2]
M=max(clair)
m=min(clair)
s1=M*len(l1)//2
s2=sum(clair)
l2=[True]*m*len(clair)
l2+=[False]*(M-m)*l1.count(m)
l2+=[True]*(M-m)*l1.count(M)
l3=sum(l1[2*i]-l1[2*i+1] for i in range(len(clair)))
return l2,l3,s1,len(l1)//2
Cette fonction retourne, dans le niveau de correction L de la version 3, [True]*55,15,55,1 et pour le niveau de correction Q, [True]*34,36,34,2. Dans le cas où les blocs en clair n’ont pas tous la même longueur comme dans la version 5 et niveau de correction H ("2×(33,11),2×(34,12)"), elle retourne[True]*11*4+[False]*2+[True]*2,46,88,4.
15: self.clair=[[] for _ in range(nbbloc)]
16: self.redondant=[[] for _ in self.clair]
Pour le moment, clair et redondant contiennent autant de listes vides que de blocs de données dans le code QR.
17: j=0
18: for i in range(lonclair):
19: if posclair[i]:
20: self.clair[i%nbbloc]+=self.code[j*8:j*8+8]
21: j+=1
22: for i in range(lonredondant):
23: self.redondant[i%nbbloc]+=self.code[(i+j)*8:(i+j+1)*8]
posclair[i] vaut True s’il faut stocker le bit. i est le numéro du bit dans le tableau transposé remis à plat, sans tenir compte des longueurs éventuellement différentes des blocs. j est le numéro du bit, mais en en tenant compte, il sert aussi à déterminer le début des blocs correcteurs.
Dans notre cas (version 3 et niveau de correction L), les données ne sont pas coupées et on a au maximum 70 octets de données dont 55 de message.
Voici le contenu hexadécimal de la partie en clair 4254c6973657a20474e552f4c696e7578206d6167617a696e65204672616e63652e20f09f98830ec11ec11ec11ec11ec11ec11ec11ec11 et de la correction 0b1622eb6e2c152a08d34a2dd8c788. Observez le bourrage à la fin, on le voit sur la figure 5 juste après la pièce de Tetris blanche au milieu de la zone haute ; et le peu d’erreurs que l’on pourra corriger. Akala jingle bells toutes ces couleurs.
Fig. 5 : Le découpage du message.
Les barres noires délimitent les zones importantes : l’en-tête, les données (avec bourrage), la correction et le supplément inutilisé. Les octets ou quadruplets sont délimités par les barres magenta.
2.2 Vérification de la correction du message
On va se contenter de dire que tout va bien, le développement de la correction d’erreurs se fera plus loin après des préliminaires de rigueur.
01: def messagecorr(self):
02: if None in [self.clair,self.redondant]:
03: self.messagebrut()
04: compte=0
05: if self.corrige:
06: for i in range(len(self.clair)):
07: self.clair[i],self.redondant[i],c=corrige(self.clair[i],self.redondant[i])
08: compte+=c
09: clair=[]
10: for l in self.clair:
11: clair+=l
12: self.clair=clair
13: redondant=[]
14: for l in self.redondant:
15: redondant+=l
16: self.redondant=redondant
17: if compte:
18: self.messageok=compte
19: else:
20: self.messakeok=True
Ligne 04, la variable compte décompte le nombre total d’erreurs corrigées, qu’on corrige si le drapeau des options de ligne de commandes corrige est égal à 1. Ensuite, on regroupe les blocs de la partie en clair puis ceux de la partie redondante.
2.3 Décodage final
Enfin ! On va pouvoir savoir ce que contient notre exemple de code QR.
01: def decodeqr(self):
02: if self.messageok is None:
03: self.messagecorr()
05: self.mode=3-self.code[:4].index(1)
06: self.longueur=longbin(self.version,self.mode)
La sélection du mode se fait selon la position du premier 1 dans les quatre premiers bits (qui sont 0100, observer le carré en bas à droite de la figure 5). Ici, on utilise le mode Byte, le 1 est en effet en deuxième position (donc d’indice 1) et mode vaut 2.
Voici la fonction longbin, présente dansqrcodestandard.py :
def longbin(version,mode):
if version<=9:
return {0:10,1:9,2:8,3:8}[mode]
elif version<=26:
return {0:12,1:11,2:16,3:10}[mode]
return {0:14,1:13,2:16,3:12}[mode]
Selon le mode et la version, varie le nombre de bits du champ qui donne le nombre exact de caractères du message final et non le nombre d’octets, la nuance est importante pour les formats numérique, alphanumérique et kanji. Celui-ci est écrit en base 2, le champ de longueur contient 8 bits dans notre cas, c’est le rectangle de 2 × 4 sous le trait noir.
La fonction suivante, bin2dec stockée dans qrcodeoutils.py, calcule la valeur décimale d’une suite de et de 1 stockée dans une liste.
def bin2dec(n):
s=0
for b in n:
s*=2
s+=b
return s
Cette fonction utilise l’algorithme de Horner (William George, pas Yvette), rapide et simple à mettre en œuvre.
(c’est l’écriture de n en base 2, chaque bi vaut ou 1), on peut écrire que n=b7 27+b6 26+b5 25+b4 24+b3 23+b2 22+b1 21+b 2 =(((((((0×2+b7)×2+b6)×2+b5)×2+b4)×2+b3)×2+b2)×2+b1)×2+b.
Pourquoi diable ? Pour économiser le nombre de multiplications effectuées. On a 29 multiplications par le calcul naïf en comptant le calcul des puissances (en O(n²), en gros proportionnel au carré du nombre de bits) et 8 par la méthode de Horner (en O(n), proportionnel au nombre de bits). La technique fonctionne aussi si on veut évaluer un polynôme (on remplace 2 par x), on la réutilisera plus loin.
20: self.longclair=bin2dec(self.clair[4:4+self.longueur])
On calcule donc la longueur exacte du message qui est, dans notre cas, de 37 caractères puisque les huit bits du champ sont 00100101 soit 32 + 4 + 1.
Suivent les fonctions des quatre modes. Le message est lu immédiatement après les bits de longueur, donc au treizième bit dans notre cas.
22: def numeric():
23: n=""
24: fin=self.longclair%3
25: self.longclair-=fin
26: i=4+self.longueur
27: while len(n)<self.longclair:
28: n=n+str(bin2dec(self.clair[i:i+10]))
29: i+=10
30: if fin==1:
31: n=n+str(bin2dec(self.clair[i:i+4]))
32: elif fin==2:
33: n=n+str(bin2dec(self.clair[i:i+7]))
34: return int(n)
Le format numérique ne permet de stocker que des nombres entiers positifs, par exemple de très grands nombres premiers. Comme 999<210=1024, il suffit de dix bits pour stocker trois chiffres en base 10, ce qui est bien mieux que 24 bits en ASCII. Que se passe-t-il si le nombre de chiffres n’est pas un multiple de 3 ? Si le nombre contient 3n + 1 chiffres, le dernier est codé sur 4 bits ligne 31 (car 23<9<24) et s’il en contient 3n + 2, les deux derniers sont codés sur 7 bits ligne 33 (car 26<99<27).
36: def alphanumeric():
44: ch=""
45: fin=self.longclair%2
46: self.longclair-=fin
47: i=4+self.longueur
48: while len(ch)<self.longclair:
49: n=bin2dec(self.clair[i:i+11])
50: q,r=divmod(n,45)
51: ch=ch+alphanum[q]+alphanum[r]
52: i+=11
53: if fin==1:
54: ch=ch+alphanum[bin2dec(self.clair[i:i+6])]
55: return ch
Le format alphanumérique permet d’écrire des URL ou du texte simple. Il contient 45 symboles : de 0 à 9, les chiffres, de 10 à 35, les lettres et enfin neuf symboles supplémentaires de 36 à 44 : alphanum (stocké dans qrcodestandard.py) est la chaîne de caractères "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ $%*+-./:" avec un espace après le Z et pas de lettre minuscule.
En fait, deux symboles sont codés sur 11 bits : le quotient et le reste de la division par 45 puisque 210<45²=2025<211. Si le nombre de symboles est impair, le dernier est codé sur 6 bits ligne 54 (car 25<45<26).
57: def byte():
58: return bytes([bin2dec(self.clair[i:i+8]) for i in range(4+self.longueur,4+self.longueur+self.longclair*8,8)]).decode("utf-8")
Là, c’est simple : chaque octet est lu tel quel, mais nous supposons ici que le message est encodé en utf-8, ce qui n’est pas le cas en général, les codes QR acceptent d’autres encodages. Notre message commence par 0x4c 0x69 0x73 0x65 ce qui donne Lise. J’ai utilisé le type bytes, qui est la manière élégante en Python 3 d’effectuer des manipulations sur un flux d’octets. Il s’agit en gros d’une chaîne de caractères (d’octets en fait, immuable) sans encodage. Ainsi, afficher un byte affiche la liste des valeurs décimales de ses éléments, c’est le format idéal pour la manipulation de flux de caractères. La méthode decode permet de le traduire en une chaîne de caractères encodée, ici en utf-8. Mon précédent code essayait de sortir le message sans se soucier de son encodage.
63: def kanji():
Je ne connais rien aux kanjis donc j’ai préféré m’abstenir d’écrire un code faux même si j’ai déjà joué avec une Casio FX-850P.
66: self.message={0:numeric,1:alphanumeric,2:byt,3:kanji}[self.mode]()
Python permet ce genre de syntaxe concise et efficace. Le numéro du mode est remplacé par la fonction idoine, qui n’a pas d’argument.
2.4 Affichage
Testons notre travail :
if __name__=="__main__":
essai=qrdecode()
essai.decodeqr()
print(essai)
On initialise essai, on applique la méthode qui décode qui, par poupées russes, fait tout le travail et voici la sortie de la méthode __str__ au grand complet :
> ./qrdecode.py glmf3.png -a 1
Fichier : glmf3.png
Niveau de correction : Low
Masque :
█ █
█ █
█ █
█ █
█ █
█ █
Dimensions : 29×29
Version : 3
Mode : Byte
Longueur du message : 37
Message :
Lisez GNU/Linux magazine France. :D
Et voilà, avec le beau sourilaid bien interprété, certains lecteurs transforment les sourilaids en une image.
Conclusion
Nous pouvons maintenant lire n’importe quel code QR bien carré, mais pas ceux munis d’un logo. Pour cela, il faut un détour par les mathématiques des corps finis et ça, ce sera pour un prochain article.
Références
[1] PATROIS N., « Déchiffrer un code QR », GNU/Linux Magazine n°193, p. 28 à 31.
[2] Le code et les exemples sont présents ici : https://github.com/GLMF/GLMF194.
[3] « Reed–Solomon codes for coders » https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders et le complément plus précis https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders/Additional_information. Le code QR utilisé dans cet article a été créé sur le site https://www.the-qrcode-generator.com/, car le code de création n’existait pas à ce moment.
[4] http://www-igm.univ-mlv.fr/~dr/XPOSE2011/QRCode/workflows.html.
[5] PATROIS N., « Expliquer un code QR », GNU/Linux Magazine n°193, p. 22 à 26.