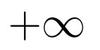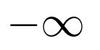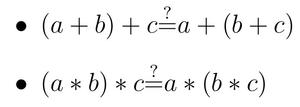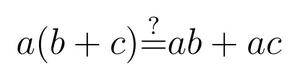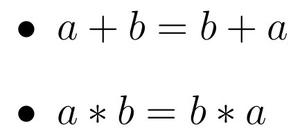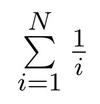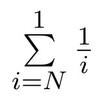Nous avons vu le mois dernier comment étaient représentés les réels sur ordinateur. Il est temps maintenant d'utiliser ces réels (les flottants) pour calculer. Quels sont les mécanismes mis en œuvre lors de chaque opération ? À quelle(s) étape(s) des erreurs de précision peuvent-elles apparaître ? L'ordre des calculs a-t-il une importance sur la qualité des résultats ? Vous trouverez les réponses à toutes ces questions (et bien d'autres) dans les pages de cet article.
Après avoir expliqué comment les réels étaient représentés sur ordinateur, nous allons montrer dans les détails comment se déroulent deux opérations (l'addition et la soustraction). Ainsi, nous verrons les causes des erreurs de précision et quelles sont les pistes pour les contenir. Nous regarderons ensuite ce qui se passe avec les autres opérations et conclurons.
La lecture de la première partie de cet article vous a convaincu (si besoin était) que les résultats des calculs sur ordinateur n'étaient que des approximations (plus ou moins bonnes) des vraies valeurs. Maintenant que nous savons comment sont stockés ces réels, nous allons pouvoir les utiliser pour calculer !
Calculer sur ordinateur, c'est d'abord arrondir, c'est-à-dire choisir un représentant (dans le monde des flottants) pour chaque réel. Je présenterai, au début de cet article, les outils permettant d'arrondir puis je détaillerai les mécanismes de deux opérations (l'addition et la soustraction) en indiquant les situations dans lesquelles le résultat est inexact, voire aberrant. Je montrerai aussi comment, en réordonnant l'ordre des opérations, la précision peut être améliorée. Enfin, j'évoquerai plus globalement le comportement de toutes les opérations et la norme IEEE-754 qui a permis de limiter les dérives.
1. Le besoin d'arrondir
Nous avons vu que tous les nombres réels n'étaient pas représentables en machine. Lors de chaque opération (ou presque) on devra arrondir la vraie valeur par un nombre représentable proche, appelé l'arrondi. Les réels représentables sur ordinateur sont appelés réels flottants (ou simplement les flottants).
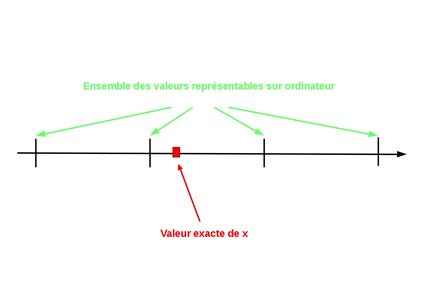
La première opération qui est concernée est l'affectation. En effet, il est probable que, dès l'affectation, on soit obligé de choisir un flottant proche de la vraie valeur pour la représenter, et ainsi, de commettre une première erreur de précision. La figure 1 représente les choix qui s'offrent pour stocker un réel (non représentable exactement sur ordinateur).
Fig. 1 : Comment choisir le meilleur représentant pour une valeur x, non représentable sur ordinateur ?
Pour effectuer ce choix, la norme IEEE-754 propose quatre modes d'arrondi :
- vers
(noté RU pour Round Up) permet de choisir le flottant le plus proche en se dirigeant vers
- vers
(RD : Round Down) permet de choisir le flottant le plus proche en se dirigeant vers
- vers (RZ : Round towards Zero) permet de choisir le flottant le plus proche en se dirigeant vers .
- au plus proche (RN : Round to Nearest) permet de choisir le flottant le plus proche. C'est le mode d'arrondi par défaut.
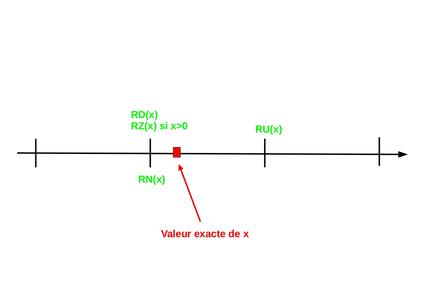
Ces quatre modes d'arrondis sont schématisés par la figure 2.
Fig. 2 : Les quatre modes d'arrondis pour représenter x, réel positif.
On dispose ainsi d'un premier outil pour choisir comment on peut arrondir un réel lors de n'importe quelle opération. À titre d'exemple, le programme arrondi_affectation.cpp (ci-dessous) permet de vérifier l'effet d'un changement de mode d'arrondi pour l'affectation.
#include <iomanip>
#include <iostream>
#include <fenv.h>
void affectation(){
float a;
std::cout<<"Entrer la valeur de a"<<std::endl;
std::cin>>a;
std::cout<<" a : "<<a<<std::endl;
}
int main(){
std::cout<<std::setprecision(10);
std::cout<<"mode d'arrondi RD"<<std::endl;
std::cout<<"-----------------"<<std::endl;
fesetround(FE_DOWNWARD);
affectation();
std::cout<<std::endl<<"mode d'arrondi RU"<<std::endl;
std::cout<<"-----------------"<<std::endl;
fesetround(FE_UPWARD);
affectation();
std::cout<<std::endl<<"mode RN"<<std::endl;
std::cout<<"-------"<<std::endl;
fesetround(FE_TONEAREST);
affectation();
return 0;
}
Le changement du mode d'arrondi s'effectue avec l'appel à std::fesetround().
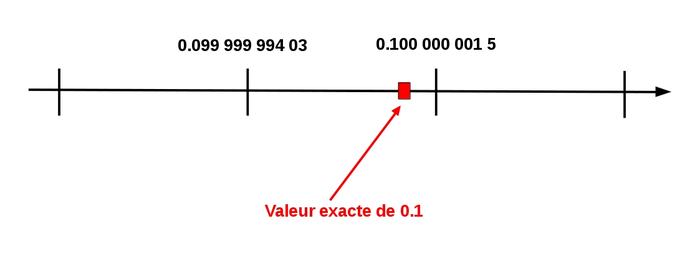
L'exécution de ce programme avec la valeur a=0,1 donne les résultats ci-dessous, conformes aux attentes, compte tenu des représentations possibles pour cette valeur sur ordinateur (schématisées par la figure 3).
mode d'arrondi RD
-----------------
Entrer la valeur de a
0.1
a : 0.09999999403
mode d'arrondi RU
-----------------
Entrer la valeur de a
0.1
a : 0.1000000015
mode RN
-------
Entrer la valeur de a
0.1
a : 0.1000000015
Fig. 3 : Arrondis pour représenter 0,1 sur ordinateur.
2. Additionner des réels
2.1 Principes
L'addition de deux réels A et B (dont le résultat est un réel S) se décompose en 3 étapes :
- alignement des mantisses si les exposants de A et B sont différents ;
- addition des mantisses ainsi alignées ;
- renormalisation de la mantisse de S si elle n’est pas normalisée (et gestion du bit implicite).
2.2 Exemple : 9,5 + 1,75
Nous allons maintenant détailler le mécanisme d'addition de deux réels représentables sur ordinateur : 9,5 et 1,75. Ces nombres sont représentés en simple précision selon la figure 4.
Fig. 4 : Représentation (simple précision) des nombres 9,5 et 1,75 sur ordinateur avec le bit de signe (en rouge), les bits représentant l'exposant décalé (en vert) et la mantisse (en bleu).
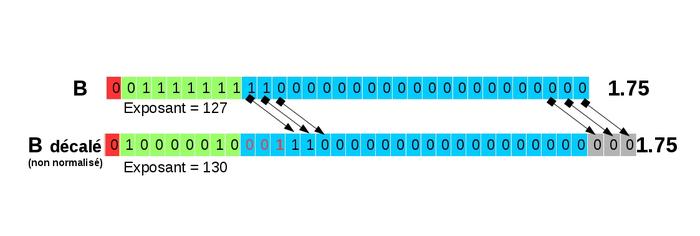
La première étape consiste à aligner les mantisses pour que les exposants soient les mêmes. On réécrit donc le nombre le plus petit (ici 1,75) pour que son exposant soit le même que celui du plus grand (130). Il faut donc ajouter 3 à l'exposant et décaler vers la droite la mantisse de 1,75. Lors de ce décalage (représenté sur la figure 5) :
- il ne faut pas oublier de réintroduire le bit implicite (qui a pour valeur 1) ;
- après avoir réintroduit le 1 (bit implicite), on introduit des .
Ce décalage a pour conséquence de faire « sortir » des bits de la mantisse. Ces bits sont perdus ; on peut donc perdre de l’information à ce stade.
Il faut bien noter que, sous cette écriture, 1,75 n'est plus sous sa forme normalisée.
Fig. 5 : Décalage lors de l'alignement des mantisses. Les bits qui sortent (et qui sont donc perdus) sont représentés en gris.
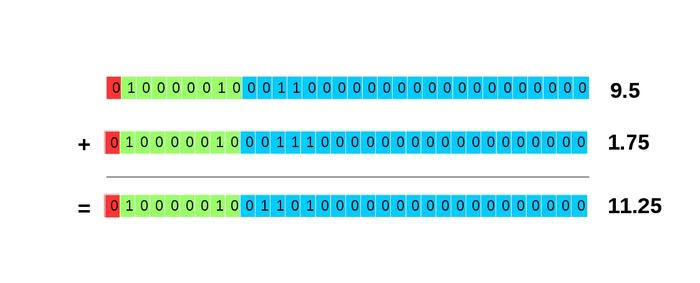
Ainsi réécrit, l'exposant de 1,75 est le même que celui de 9,5. Il ne nous reste plus qu'à additionner les mantisses. Il s'agit simplement d'une addition en binaire schématisée par la figure 6.
Fig. 6 : Somme des mantisses.
Ce calcul mène donc à l'écriture 0 10000010 01101000000000000000000, qui correspond bien à 11,25. Ce calcul est donc juste...
Le bit implicite est géré dans le cas de l'addition de 9,5+1,75 de manière transparente : le bit implicite de la somme est la somme des bits implicites (1 pour 9,5 et pour 1,75 après décalage) ; il vaut donc bien 1 et le résultat est bien écrit sous sa forme normalisée avec un bit implicite (qui vaut 1). Ce n'est pas le cas lors de l'addition de nombres proches qui nécessite alors un traitement supplémentaire.
2.3 Perte de précisions
Lors de l'alignement des mantisses, nous avons vu que des bits « sortent » (on ne stocke que 23 bits de mantisse en simple précision). Dans le cas précédent, c'est sans conséquence, car tous ces bits valaient . En revanche, si certains de ces bits n'étaient pas nuls, ce décalage provoquerait une perte de précision.
Pour s'en convaincre, nous allons effectuer l'addition de 9,5 avec le nombre juste supérieur à 1,75, soit 1,7500001192092896 (dont le bit de poids faible de la mantisse est 1) représenté par la figure 7.
Fig. 7 : Représentation des nombres 9,5 et 1,7500001192092896.
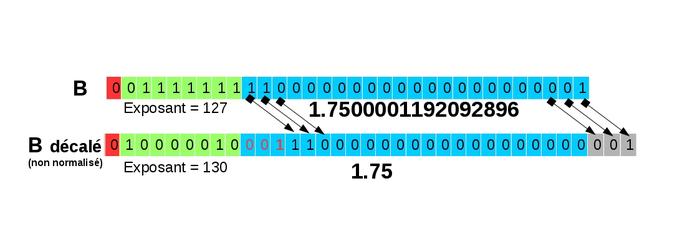
En alignant les mantisses (voir figure 8), la valeur du bit de poids faible (1) est perdue. Le nombre ainsi représenté (sous une forme non normalisée) correspond à 1,75 et non plus à 1,7500001192092896 !
Fig. 8 : Décalage lors de l'alignement des mantisses : 1,7500001192092896 devient 1,75 !
L'addition se termine comme celle de 9,5 et de 1,75 et l'on obtient : 9,5 + 1,7500001192092896 = 11,25.
Il est important toutefois de noter que 11,25 est la meilleure (la plus proche) représentation de la vraie valeur (11,2500001192092896) qui n'est pas représentable sur ordinateur.
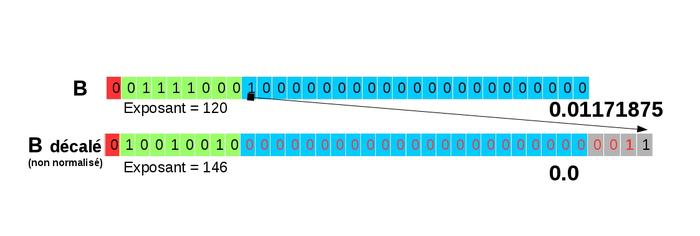
Voici donc le premier exemple de perte de précision lors d'une addition. On peut alors facilement comprendre que cette perte peut être beaucoup plus importante si de nombreux bits valant 1 sortent lors du décalage. Cette situation peut se rencontrer lorsque l'on additionne deux réels d'ordres de grandeur très différents. On peut même arriver au cas extrême où toute l'information du plus petit des deux nombres est perdue : c'est l'absorption que nous allons illustrer sur l'addition de 1 000 000 et de 0,01171875 (représentés sur la figure 9).
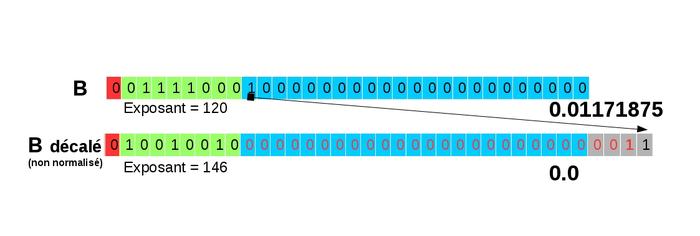
Fig. 9 : Représentation des nombres 1 000 000 et de 0,01171875.
Lors de l'alignement des mantisses (décalage de 26 bits vers la droite), tous les bits de la mantisse sortent et toute l'information est perdue comme le montre la figure 10.
Fig. 10 : Décalage lors de l'alignement des mantisses : 0,01171875 devient 0 !
La conséquence est alors prévisible : on réalise (voir figure 11) l'addition de 1 000 000 avec .
On obtient donc : 1 000 000 + 0,01171875 = 1 000 000 !
Fig. 11 : Addition de 1 000 000 et 0.
3. Soustraire des réels
3.1 Principes et exemple
Pour réaliser une soustraction entre deux réels, le principe est identique à celui de l'addition : alignement des mantisses, soustraction des mantisses et éventuellement renormalisation du nombre ainsi obtenu.
Prenons l'exemple de 9,875 − 1,75. Ces deux nombres sont représentés selon la figure 12.
Fig. 12 : Représentation des nombres 9,875 et 1,75.
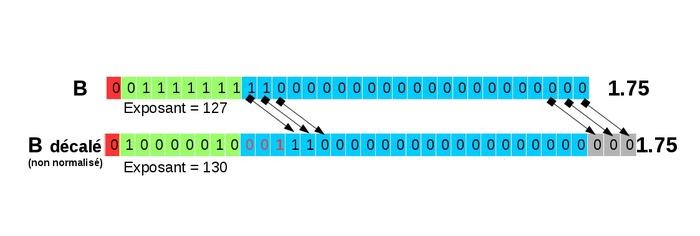
La première étape (alignement des mantisses) conduit à réécrire 1,75 pour que son exposant soit le même que celui de 9,875, soit 130 (voir figure 13).
Fig. 13 : Décalage pour aligner les mantisses.
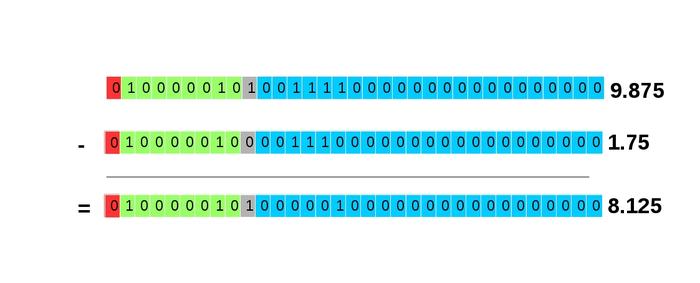
On réalise ensuite la soustraction des mantisses (voir figure 14).
Fig. 14 : Soustraction : 9,875 − 1,75.
Dans ce cas (sans perte de précision) on obtient la valeur exacte lors du calcul soit 9,875 − 1,75 = 8,125.
3.2 Perte de précisions
La soustraction, comme l'addition, est susceptible de provoquer des pertes de précision. C'est le cas lorsque l'on soustrait deux nombres proches. Nous allons tout d'abord traiter un exemple (9,75 - 9,5) pour lequel il est inutile d'aligner les mantisses puisque les exposants sont identiques (voir figure 15).
Fig. 15 : Représentation des nombres 9,75 et 9,5.
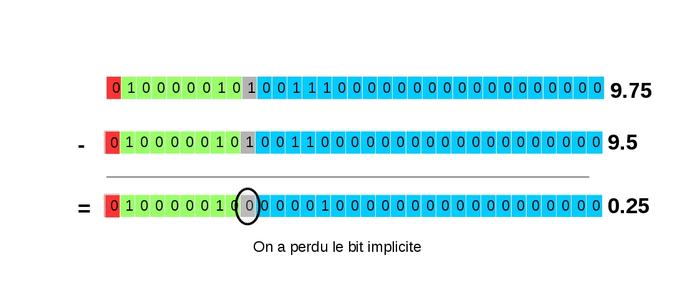
Dans ce cas, il suffit de soustraire les mantisses pour obtenir le résultat comme le montre la figure 16. Cette figure fait également apparaître la gestion du bit implicite : contrairement au cas précédent où cette gestion était transparente (on avait 1 pour le bit implicite du plus grand nombre et pour le plus petit), ici le bit implicite est 1 pour les deux nombres (puisque l'on n'a pas réalisé de décalage). Le bit implicite du résultat est donc égal à .
Fig. 16 : Soustraction des mantisses laissant apparaître un 0 à la place du bit implicite.
Le résultat obtenu est juste, mais il n'est pas sous son écriture normalisée (avec un bit implicite égal à !). Il convient donc de le normaliser pour faire réapparaître en gris le bit implicite (1) en décalant la mantisse vers la gauche pour que le premier bit non nul prenne la place du bit implicite. Lors de ce décalage, on a besoin d'introduire des bits (par la droite) pour remplacer ceux qui sont partis à gauche. La valeur de ces bits est inconnue, et arbitrairement considérée comme étant nulle.
Dans notre exemple (voir figure 17), on a besoin de décaler la mantisse de 5 bits vers la gauche et donc de soustraire 5 à la valeur de l'exposant pour avoir un nombre à l'écriture normalisée.
Fig. 17 : Renormalisation avec introduction de valeurs arbitraires.
Lors de ce calcul, on obtient bien : 9,75 − 9,5 = 0,25. Mais alors d'où peuvent venir les pertes de précision ?
Des pertes de précision peuvent apparaître lorsque le vrai résultat n'est pas représentable sur ordinateur. En effet, rappelons que la soustraction (comme l'addition) de deux nombres représentables sur ordinateur peut être un nombre non représentable sur ordinateur.
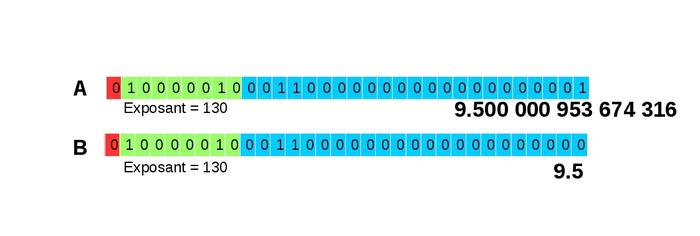
Pour bien comprendre ce cas de figure, nous allons prendre un nouvel exemple avec la soustraction de deux « voisins » (deux nombres qui se suivent dans le monde des flottants) : 9,5 - 9,500000953674316. La représentation de ces deux nombres ne diffère que sur la valeur du bit de poids faible de la mantisse comme illustré sur la figure 18.
Fig. 18 : Représentation des nombres 9,5 et 9,500000953674316.
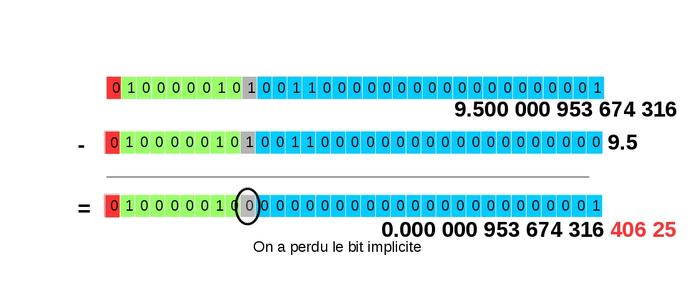
Lors de la soustraction des mantisses (voir figure 19), comme dans l'exemple précédent, on a perdu le bit implicite. De plus, la valeur représentée n'est pas le résultat exact de la soustraction, car celui-ci n'est pas représentable. Il est cependant le meilleur représentant (le plus proche).
Fig. 19 : Soustraction des mantisses, perte du bit implicite. Les chiffres en rouge indiquent l'erreur de précision lors de cette opération.
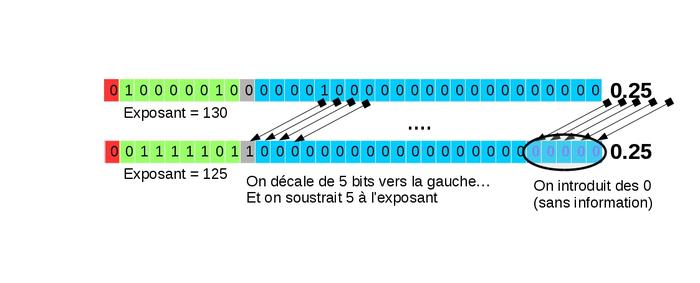
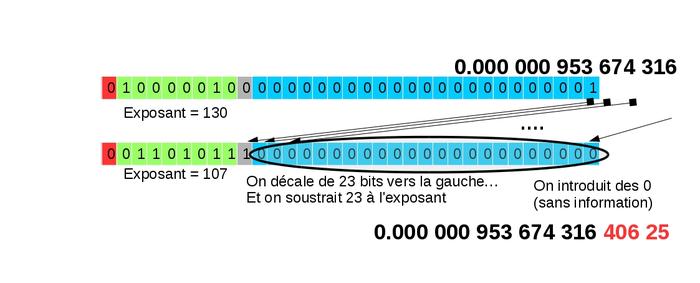
La renormalisation de ce nombre (figure 20) produit un décalage de 23 bits vers la gauche.
Fig. 20 : Renormalisation.
La perte de précision lors de la soustraction de deux nombres proches est appelée cancellation.
4. Cancellation et absorption : le duo explosif
Lors d’une cancellation, on introduit arbitrairement des dans la mantisse (car on ne dispose pas de plus de précision sur les opérandes). Si les opérandes sont issus d’un calcul précédent, ils ont pu subir une perte de précision (en cas d’absorption par exemple). Cette perte de précision va alors être réintégrée et amplifiée. Dans ce cas, les bits arbitrairement introduits (des ) ne sont pas les bons.
Ainsi une absorption suivie d'une cancellation peut conduire à des pertes de précision très importantes et à des résultats très surprenants (et faux).
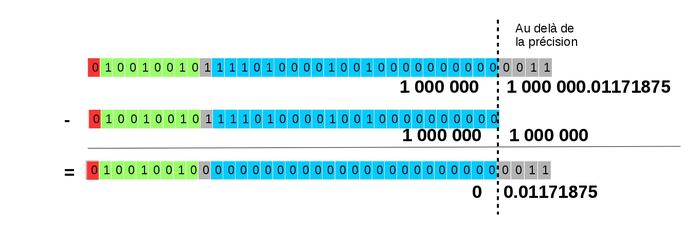
On se propose de calculer : (1 000 000 + 0,01171875) − 1 000 000.
On commence donc par l'addition de 1 000 000 et de 0,01171875 représentés selon la figure 21.
Fig. 21 : Représentation des nombres 1 000 000 et 0,01171875.
Lors de l'alignement des mantisses (voir figure 22), toute l'information de la mantisse de 0,01171875 est perdue. Le nombre ainsi représenté n'est plus 0,01171875 mais !
Fig. 22 : Alignement des mantisses et perte de toute l'information.
L'addition des mantisses (figure 24) conduit donc naturellement au résultat 1 000 000 + 0,01171875 = 1 000 000. Sur cette figure on a également représenté en gris les bits qui ont été perdus lors de l'étape précédente. On remarque donc que si l'on disposait de quatre bits supplémentaires pour la mantisse, le calcul serait exact.
Fig. 23 : Addition des mantisses.
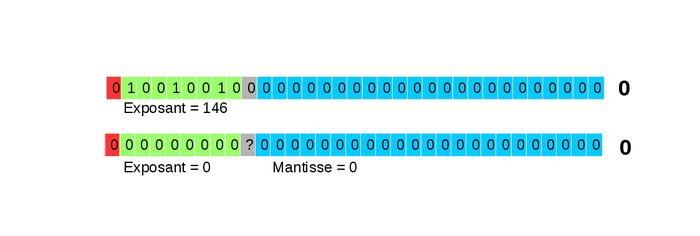
Ensuite, nous procédons à la soustraction de 1 000 000 (figure 24) puis à la renormalisation du nombre représenté (figure 25).
Fig. 24 : Soustraction des mantisses.
Fig. 25 : Renormalisation.
Au final, le nombre obtenu est alors qu'avec quatre bits supplémentaires le calcul aurait été juste.
On arrive donc à ce résultat étonnant : (1 000 000 + 0,01171875) − 1 000 000 = 0 !
Ce résultat est bien évidemment faux mais, conduit différemment, ce calcul aurait pu donner le bon résultat. En effet, le calcul (1 000 000 - 1 000 000) + 0,01171875 donne bien 0,01171875.
5. Propriétés algébriques, impact de l'ordre des opérations
5.1 Propriétés algébriques
L'exemple précédent montre que certaines propriétés algébriques ne sont pas assurées en arithmétique flottante :
- L’associativité n’est pas respectée (en général) ni pour l’addition, ni pour la multiplication :
- La distributivité n’est pas respectée (en général) entre la multiplication et l’addition :
Seule la commutativité est respectée pour l’addition et la multiplication :
Cette différence essentielle entre l'arithmétique sur des (vrais) réels et l'arithmétique flottante est une des causes d'importantes pertes de précisions. Il faut donc garder à l'esprit que le simple fait de modifier l'ordre des opérations n'est pas sans conséquence. Mais le développeur n'est pas le seul à vouloir changer l'ordre des opérations. Le compilateur, dès qu'on lui demande d'optimiser le code (avec les options -Ox pour gcc par exemple), s'autorise à réordonner certains calculs. Bien que mathématiquement équivalents, ces changements peuvent avoir (ont) des conséquences sur la précision de calcul. Dès lors, un compromis doit être trouvé entre précision et rapidité d'exécution.
5.2 Impact de l'ordre des opérations
Pour illustrer l'impact de l'ordre des opérations lors d'un calcul sur ordinateur, prenons l'exemple de la somme des inverses d'entiers calculés de deux façons :
1. Somme de 1 à N :
2. Somme de N à 1 :
L'exécution en simple précision de ce programme (somme_des_inverses.cpp) donne les résultats suivants :
#include <stdio.h>
#include <iomanip>
#include <iostream>
float somme(int N){
float res = 0.0;
for (int i=1;i<=N;i++){
res += (1.0/i);
}
std::cout<<"somme de 1 à "<<N<<" : "<<std::setprecision(7)<<res<<std::endl;
res = 0.0;
for (int i=N;i>=1;i--){
res += (1.0/i);
}
std::cout<<"somme de "<<N<<" à 1 :"<<std::setprecision(7)<<res<<std::endl<<std::endl;
}
int main(){
somme(100000);
somme(1000000);
somme(10000000);
somme(100000000);
return 0;
}
$ ./somme_des_inverses
somme de 1 à 100000 : 12.09085
somme de 100000 à 1 :12.09015
somme de 1 à 1000000 : 14.35736
somme de 1000000 à 1 :14.39265
somme de 1 à 10000000 : 15.40368
somme de 10000000 à 1 :16.68603
somme de 1 à 100000000 : 15.40368
somme de 100000000 à 1 :18.80792
console
Reportés dans le tableau suivant, les résultats obtenus (avec en gras, les chiffres exacts) montrent qu'en effectuant le calcul de N à 1, le calcul est beaucoup plus juste (moins inexact) qu'en l'effectuant de 1 à N. Ceci s'explique par le fait que dans le premier cas, pour N grand, on finira par additionner des réels d’ordres de grandeur très différents, conduisant à de nombreuses absorptions qui provoquent des pertes de précisions. Dans le deuxième cas, ce phénomène arrive moins souvent et la précision est meilleure.
|
N |
105 |
106 |
107 |
108 |
|
Calcul de 1 à N |
12,09085 |
14,35736 |
15,40368 |
15,40368 |
|
Calcul de N à 1 |
12,09015 |
14,39265 |
16,68603 |
18,80792 |
|
Valeur exacte |
12,09015 |
14,39273 |
16,69531 |
18,99790 |
6. La norme IEEE-754
Dans les années 1980 (et même avant), les constructeurs et les compilateurs étaient déjà confrontés à ces questions : comment stocker les réels, comment calculer ? Mais sans concertation, les réponses de ces acteurs ont été, bien logiquement, différentes. Les calculs menés dans des contextes différents (architecture, compilateur) n'avaient alors aucune chance d'aboutir au même résultat. Un travail de normalisation a alors été engagé et a abouti à l'adoption de la norme IEEE-754 en 1985, révisée en 2008. Cette norme définit un cadre pour, par exemple, le format simple et double précision pour les réels (sur 32 et 64 bits). Il impose également l'arrondi correct pour cinq opérations (+, -, *, / et
).
Sans entrer dans les détails, l'objectif de l'arrondi correct est d'éviter la propagation des erreurs d’arrondis à chaque opération. Lorsque l'arrondi correct est respecté, le résultat est le même que si on effectuait le calcul en précision infinie (sur de vrais réels) puis on arrondissait ce résultat. Cette norme a, en revanche, laissé une certaine liberté pour toutes les autres opérations ; l'arrondi correct étant simplement recommandé. Ce choix, motivé par des considérations de performances, est à l'origine d'implémentations souvent différentes. Les résultats de calcul (à partir d'un code identique) sont donc encore aujourd'hui dépendants de l'architecture, du compilateur (et de ses options)...
Conclusion
Vous avez désormais les connaissances nécessaires pour comprendre d'où viennent les pertes de précision lors des calculs sur ordinateur. Rappelons tout d'abord que les nombres stockés ne sont qu'un sous-ensemble des nombres réels. Ainsi, chaque opération doit choisir un représentant dans l'ensemble des flottants, avec une perte de précision inévitable. De plus, certaines opérations ne sont pas tenues de choisir le meilleur représentant (le plus proche par exemple). Enfin, certaines optimisations du compilateur engendrent (en réordonnant les calculs) d'autres sources d'imprécision.
On comprend ainsi que certains calculs mènent à des résultats bien différents des vraies valeurs et que, dans tous les cas, il convient de s'interroger sur la qualité, la précision des résultats et leur reproductibilité.
Par ailleurs, il est possible d'améliorer la précision de calcul (en utilisant des bibliothèques de calcul ad hoc) ou d'estimer cette précision en utilisant d'autres arithmétiques. L'arithmétique stochastique permet d'estimer par exemple le nombre de chiffres significatifs d'un résultat alors que l'arithmétique par intervalle permet de donner un encadrement de ce résultat. Ces aspects feront peut-être l'objet d'un prochain article.
En attendant, j'espère que celui-ci a atteint un objectif : ne plus considérer le résultat d'un calcul sur ordinateur comme une valeur exacte ! Garder un regard critique...
Pour aller plus loin
Les sources d'inspiration de cet article sont multiples et complémentaires :
- La page personnelle de l'auteur (https://lmb.univ-fcomte.fr/Florent-Langrognet) contient quelques exposés et cours sur ce sujet.
- L'article de F. Langrognet (et contributeurs), « JDEV 2013 - Développer pour calculer : des outils pour calculer avec précision & Comment calculer avec des intervalles » (HPC Magazine, novembre 2013, pp,-51-65) revient sur le traitement de cette thématique lors des JDEV (Journées du DÉVeloppement logiciel) 2013, organisées par le réseau métier de l'enseignement supérieur et de la recherche DevLOG (Développement LOGiciel).
- L'école thématique CNRS « Précision et reproductibilité en calcul numérique » (http://calcul.math.cnrs.fr/spip.php?rubrique98) organisée par le réseau métier de l'enseignement supérieur et de la recherche Calcul en 2013.
- Le livre « Handbook of Floating-Point Arithmetic » de J.M. Muller, N. Brisebarre, F. de Dinechin, C.-P. Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D. Stehlé, et S. Torres (Birkhauser, 2010) est un livre de référence pour comprendre en profondeur l'arithmétique flottante.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture