La gestion d’informations spatialisées devient accessible au grand public avec la prolifération des récepteurs GPS dans les téléphones portables et les appareils photographiques numériques. Dans cette présentation, nous nous proposons d’exploiter quantitativement les photographies numériques prises en vue oblique en les projetant en vue azimutale par déformation géométrique s’appuyant sur des points de contrôle géo-référencés et de draper un modèle numérique d’élévation pour ajouter une troisième dimension aux analyses. Bien que recourant à des outils au travers d’une interface graphique, nous nous efforçons de conserver la possibilité d’appliquer les opérations en ligne de commande afin de pouvoir scripter les traitements sur un grand nombre d’images et ainsi traiter des séries temporelles telles que fournies par une webcam observant un glacier alpin pour en évaluer la couverture neigeuse.
1. Introduction
La gestion spatiale de l’information est accessible à tous depuis la prolifération des récepteurs GPS permettant de géolocaliser à peu près toute activité (par exemple, application OSMTracker1 pour Android).
De plus, de nombreuses opportunités se présentent avec des images de paysages prises en vue oblique [1], par exemple des photographies numériques acquises depuis des points élevés ou d’avion. Nous désirons fusionner ces deux sources de données que sont les évènements géolocalisés, les informations cartographiques et ce, complétées par des photographies prises en vue oblique par un observateur au sol afin de palier à la rareté et à la difficulté d’obtentions d’images aériennes. Notons cependant que les méthodes de traitement du signal proposées ici sont adéquates pour l’exploitation d’images prises depuis des drones personnels tels que la pléthore d’hélicoptères ou quadricoptères qui pullulent actuellement, munis d’instruments de prises de vues (webcams, appareils photographiques numériques).
La déformation géométrique entre le premier plan et l’arrière plan rend l’analyse quantitative [2] des informations complexes, en particulier en présence d’un terrain qui n’est pas plat. Ce problème classique dans le cas des prises de vues aériennes et satellitaires en orientation quasi-azimutale (angle par rapport à la normale du sol faible) est résolu par une approche rigoureuse de projection des images sur un modèle numérique de terrain ne nécessitant que les caractéristiques de l’instrument de prise de vue, sa position et son orientation au moment de la capture d’image [3]. Cette méthode se révèle cependant inexploitable dans le cas de prises de vues par appareils photographiques numériques ou webcams depuis le sol du fait de l’angle trop important par rapport à la normale au sol. Par ailleurs, les caractéristiques optiques de l’instrument de prise de vue sont souvent insuffisamment précises pour les exploiter directement, bien que certains auteurs aient sélectionné cette approche, par exemple nécessaire pour l’analyse stéréographique [4].
Une approche alternative consiste donc à se reposer sur un certain nombre de points de référence au sol - nommés Ground Control Points (GCP) – pour effectuer une bijection entre coordonnées sur une image et position sur le terrain. Cette approche ne repose sur aucune connaissance physique de l’instrument de prise de vue et se contente d’établir la relation locale entre des points dans l’espace et un pixel. Divers modèles d’interpolation sont proposés en fonction des connaissances de l’utilisateur sur l’environnement étudié. Finalement, le modèle numérique d’élévation (MNE) est utile pour projeter la photographie ainsi déformée pour un rendu aussi réaliste que possible et valider la cohérence avec la topographie.
Deux approches opposées pour l’analyse quantitative des informations contenues dans les photographies prises en vue oblique consistent donc soit à identifier la surface associée à chaque pixel en déformant une carte pour correspondre à la prise de vue2 ou, au contraire, à déformer l’image prise en vue oblique pour correspondre à la vue qui aurait été obtenue en projection azimutale [5]. Cette seconde méthode sera préférée car elle permet de fusionner des sources diverses dans un référentiel commun.
Il semble donc évident que plus le nombre de GCPs est important, plus la déformation géométrique de l’image épousera au mieux le modèle numérique d’élévation en tenant compte de variations locales de topographie. Cependant, la capture de GCPs – par exemple au moyen d’un récepteur GPS en se positionnant sur des points marquants de la photographie – est une activité fastidieuse et gourmande en temps, voir complexe si la cible remarquable a le mauvais goût d’être mobile. Nous proposerons donc l’alternative de se reposer sur Google Earth pour identifier les coordonnées GPS (latitude, longitude) de quelques pixels remarquables sur la photographie, puis de s’appuyer sur ces points pour déformer de façon appropriée l’image pour recouvrir un modèle numérique d’élévation.
Un certain nombre d’outils propriétaires existent pour effectuer ces opérations [6]. Notre objectif dans cette présentation tient en deux points : d’une part utiliser exclusivement du logiciel libre pour atteindre notre objectif et d’autre part être capable de scripter le traitement de séries de photographies, toutes prises du même site et selon la même orientation, afin d’automatiser la procédure de génération des images en projection azimutale. Le second soucis tient au désir d’utiliser des séquences de captures périodiques, par exemple grâce aux webcams diffusant continuellement des images sur le web, afin d’effectuer un traitement quantitatif d’analyse des images. Seule une approche exploitant la ligne de commande permet d’envisager un traitement en série d’une masse importante d’images. Dans tous les cas, une image aérienne ou satellitaire supportera l’identification des points remarquables entre la photographie analysée et le terrain, et fournira une référence sur laquelle se caler. Finalement, nous voudrons projeter en 3-dimensions le résultat du calcul pour en valider la pertinence.
2. QGis et accès à GRASS
Deux outils se démarquent dans la panoplie des logiciels libres disponibles pour le traitement d’informations géographiques compatibles avec une utilisation en ligne de commande pour le traitement séquentiel d’un grand nombre de fichiers de données : GRASS (Geographic Resources Analysis Support System, http://grass.osgeo.org/) et la bibliothèque GDAL (Geospatial Data Abstraction Library, http://www.gdal.org/). Ces deux outils, d’une prise en main un peu ardue, sont intégrés comme greffons (plugins) de l’interface graphique QGis. Nous proposons donc la séquence de développements suivante :
- exploitation de QGis pour les opérations les plus simples telles que charger des séries de points d’élévations (MNE – Digital Elevation Model ou DEM en anglais3) ou images,
- exploitation de QGis et de son greffon Georeferencer pour afficher une image prise en vue oblique et association de coordonnées GPS (points de contrôle – GCP) à des pixels remarquables de l’image. Ces opérations sont manuelles et donc difficiles à étendre à un jeu de données important,
- exploitation de GDAL dont la ligne de commande a été générée par QGis pour réaliser l’opération de correction géométrique depuis le shell,
- pour le moment, GRASS ne sert que depuis QGis pour quelques traitements de données additionnelles (affichage en 3D du MNE drapé, affichage des triangles de Delaunay) mais il est envisageable que les traitements effectués par GDAL y soient aussi accessibles, l’inspiration initiale de ce document provenant de http://grass.osgeo.org/wiki/Orthorectification_digital_camera. Cependant l’approche proposée consistant à connaître aussi bien que possible les conditions de prises de vues (position, ouverture angulaire, aberrations optiques) ne sont pas compatibles avec notre approche de déformation de l’image selon des points de contrôle, qui elle semble accessible par ailleurs (commande i.rectify).
La bonne pratique voudrait que nous partions d’images non géo-référencées, que nous allions obtenir manuellement la position spatiale de points de référence au sol (GCP) et que nous exploitions ces informations pour déformer les images en accord avec divers algorithmes d’étirement d’une feuille souple (rubber sheeting). En pratique, nous ne démontrerons qu’une fois l’acquisition manuelle de points GPS et exploiterons les coordonnées GPS en format WGS84 fournies par Google Earth dans la suite du document.
3. Sources de données
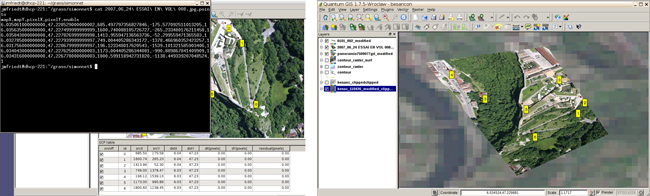
Nous avions présenté dans ces pages une exploitation de trames GPS dans divers environnements de traitement, dont GRASS [7]. Les outils ont passablement évolué depuis la rédaction de cette prose, avec l’apparition de la version stable (1.x) de Quantum GIS (nommé dans ce document QGis tel que indiqué à http://www.qgis.org/) autour de janvier 2009. Cet environnement graphique de gestion d’informations géographiques facilite la prise en main de divers outils au travers de greffons (plugins) qui complètent des fonctions de base aussi simples que le chargement d’informations matricielles (raster tel qu’un modèle numérique de terrain où chaque pixel se voit assigné une altitude) ou vectorielles (points GPS par exemple). Lorsque toutes ces informations sont géo-référencées dans un repère et un mode de projection commun, leur fusion se fait naturellement (Fig. 1). La compilation de l’ensemble des outils – graphiques et bibliothèques associées – est quelque peu fastidieuse et nous nous contentons d’exploiter les paquets pré-compilés pour plate-forme x86 distribués par QGis à http://www.qgis.org/en/site/forusers/alldownloads.html#debian. En particulier nous installons qgis, qgis-plugin-grass et, depuis les paquets Debian, gdal-bin ainsi que les dépendances associées.
Dans l’exemple qui va suivre, nous nous sommes contentés de demander à QGIS d’importer un fichier de données vectorielles contenant une trace GPS stockée au format KML (automatiquement reconnu) et un modèle numérique de terrain au format GeoTIF, à savoir un fichier bitmap contenant des méta-données sur la taille du pixel et la coordonnée géographique d’un coin.
Nous exploitons 3 sources de données librement disponibles :
- un modèle numérique de terrain parmi tous ceux actuellement disponibles depuis divers sites et notamment de la NASA (http://grass.osgeo.org/wiki/Global_datasets et http://asterweb.jpl.nasa.gov/gdem.asp). Nous avons pour notre part obtenu les images ASTER GDEM2 depuis http://earthexplorer.usgs.gov/ ou https://reverb.echo.nasa.gov. La résolution spatiale est de une seconde d’arc soit environ 30 m en latitude et 15 m en longitude pour la France. Il est cependant apparu à l’usage que GDEM2 est encore affecté d’un certain nombre d’incohérences ou de zones d’altitude indéfinie qui nécessitent une correction manuelle, faute de quoi le rendu des calculs n’est pas esthétiquement acceptable [8]. Nous nous sommes donc par la suite contentés du modèle numérique de terrain SRTM obtenu depuis la navette spatiale et qui couvre le monde avec une résolution de 100 m à l’équateur (3 secondes d’arc corrigé, disponible à http://srtm.csi.cgiar.org/ et en particulier http://srtm.csi.cgiar.org/SELECTION/inputCoord.asp),
- des images satellitaires telles que issues de la base de données Landsat ou, présentant une meilleure résolution spatiale et un meilleur suivi temporel, les previews des images haute résolution commercialisées par DigitalGlobe et accessibles gratuitement depuis https://browse.digitalglobe.com,
- des images en vue oblique soit obtenues manuellement par l’auteur, soit disponibles en licence CC sur internet (par exemple panoramio.com),
- le positionnement des points de référence au sol au moyen de Google Earth qui fournit la position GPS avec une précision inférieure à la taille du pixel des MNEs ou des images satellites qui nous concernent ici. Une source [9] annonce que les divers globes virtuels numériques sont cohérents entre eux à mieux que ±10 cm.
Le MNE est chargé sous forme de fichier GeoTiff, un fichier bitmap contenant un certain nombre de méta-données en complément de la matrice des altitudes, depuis le site http://earthexplorer.usgs.gov/ ou http://gdex.cr.usgs.gov/gdex/ (nécessite un enregistrement). Nous constatons par gdalinfo - outil lié à la bibliothèque GDAL - que
$ gdalinfo 20121028042508_188302717.tif
Driver: GTiff/GeoTIFF
Files: 20121028042508_188302717.tif
Size is 5260, 3342
Coordinate System is:
GEOGCS["WGS 84",
DATUM["WGS_1984",
SPHEROID["WGS 84",6378137,298.257223563,
AUTHORITY["EPSG","7030"]],
AUTHORITY["EPSG","6326"]],
PRIMEM["Greenwich",0],
UNIT["degree",0.0174532925199433],
AUTHORITY["EPSG","4326"]]
Origin = (5.454712000000000,47.672423999999999)
Pixel Size = (0.000277791254753,-0.000277780969479)
Metadata:
AREA_OR_POINT=Area
Image Structure Metadata:
INTERLEAVE=BAND
Corner Coordinates:
Upper Left ( 5.4547120, 47.6724240) ( 5d27'16.96"E, 47d40'20.73"N)
Lower Left ( 5.4547120, 46.7440800) ( 5d27'16.96"E, 46d44'38.69"N)
Upper Right ( 6.9158940, 47.6724240) ( 6d54'57.22"E, 47d40'20.73"N)
Lower Right ( 6.9158940, 46.7440800) ( 6d54'57.22"E, 46d44'38.69"N)
Center ( 6.1853030, 47.2082520) ( 6d11' 7.09"E, 47d12'29.71"N)
le système de coordonnées (WGS84) ainsi que les coordonnées des quatre coins sont renseignés dans divers champs du fichier TIF.
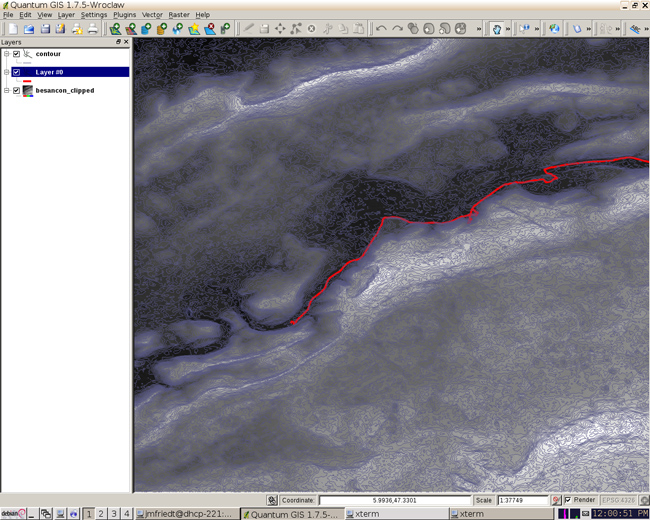
Figure 1 : Fusion de données matricielles (raster) de modèle numérique d’élévation (MNE) et de données vectorielles d’un trajet acquis par GPS au rythme de 1 point/s. Le MNE a été complété des lignes de niveau.
Ce fichier est chargé dans QGis au moyen de Layer > Add raster layer. Diverses analyses triviales sont possibles et notamment après ajout du greffon GDALTools, telles que la génération des courbes de niveau4 (Fig. 1) par Raster > Extraction > Contour qui fournit par ailleurs la commande GDAL suivante :
gdal_contour -i 10.0 /home/jmfriedt/grass/20121028042508_188302717.tif
De la même façon, QGis est capable de charger un fichier KML contenant les coordonnées GPS des points successifs d’un trajet, qui se superposent donc aux données précédentes sous réserve évidemment de se placer dans le même référentiel géographique (ici WGS84, référentiel par défaut du GPS).
4. Géoréférencement d’images
Il est difficile de se convaincre sur un MNE de la validité du positionnement. Nous allons donc nous efforcer d’ajouter à cette information matricielle d’altitude une image aérienne. Nous avons déjà décrit comment Google Maps est une source possible, à défaut d’être légale, d’obtenir des images géo-référencées avec une excellente résolution [10]. Nous nous contentons ici de reprendre une image de preview de DigitalGlobe5 [11]. Le module géo-référencé de QGis (Fig. 4) propose l’environnement nécessaire pour placer les points de contrôle au sol (GCP) et relier une position sur l’image à une information spatiale bidimensionnelle (indépendamment de toute information d’altitude qui n’est pas nécessaire lors de la déformation de l’image).
4.1 Ajout d’une image satellitaire
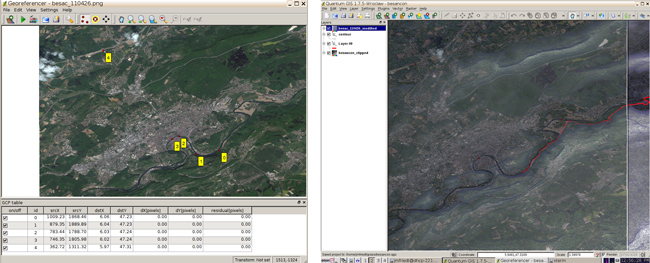
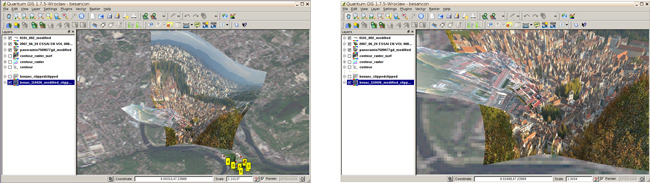
Nous avons choisi d’exploiter l’image satellite obtenue lors du passage au-dessus de Besançon acquise le 26 Avril 2011 et disponible en preview sur le site de DigitalGlobe. Compte tenu de la trajectoire des satellites en orbite basse (LEO), les images sont toujours orientées selon un axe nord-sud et les motifs y sont aisément repérables (Fig. 2).
Une fois le greffon georeferencer de QGis lancé, nous chargeons l’image obtenue sur DigitalGlobe et sélectionnons quelques points remarquables pour la positionner dans l’espace. Nous faisons l’hypothèse que DigitalGlobe a déjà effectué le travail de projection de l’image en vue azimutale et qu’il suffit d’une translation et d’une homothétie, voir éventuellement une rotation, pour placer tous les points de l’image dans l’espace. Une interpolation linéaire sur peu de points de contrôle dans les coins de la zone d’analyse qui nous concerne semble donc adéquate.
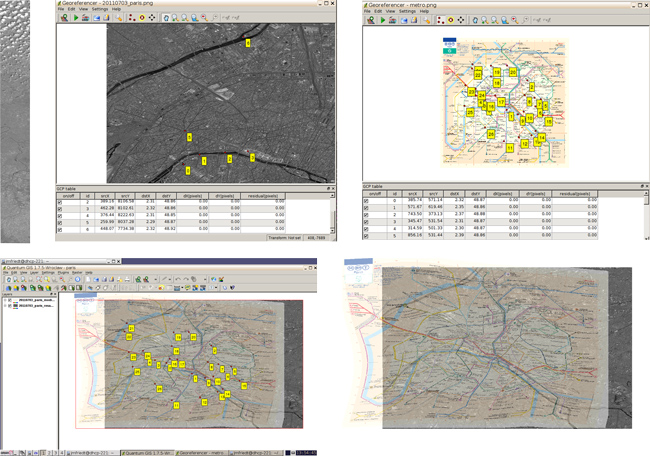
4.2 Positionnement d’une carte
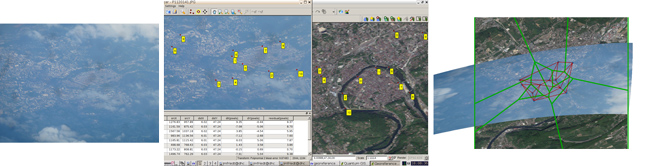
Avant de nous engager dans l’étape plus avancée de correction géométrique d’image en prise oblique, attelons nous à résoudre un cas simple, à savoir géo-référencer une image en prise de vue azimutale non-référencée (image issue des previews de DigitalGlobe sur la région parisienne – dans notre cas nous avons pris la version la mieux résolue de la bande acquise le 3 juillet 2011) et y superposer une carte non géo-référencée et sans vocation initiale à l’être, à savoir le plan du métro parisien. Cet exemple est sélectionné par la multitude de GCPs évidents à identifier sur Google Earth, sur l’image satellitaire (intersections de boulevards, parcs clairement visibles depuis l’espace) et sur la carte du métro.
Un résumé de la séquence d’analyse consiste donc en :
- charger l’image dans le greffon georeferencer et identifier la position GPS (latitude/ longitude) pour suffisamment de pixels (X,Y) pour permettre d’identifier le modèle numérique de terrain, soit en retrouvant les coordonnées dans Google Earth, soit en identifiant sur une image déjà géoréférencée avec suffisamment de précision,
- charger dans QGis au moyen de l’icone d’ajout de fichier matriciel (raster),
- charger dans GRASS à partir de QGis au moyen de r.in.gdal.qgis,
- ajouter dans GRASS au moyen de l’icône d’ajout d’un fichier raster,
- ajuster à la taille de la région d’intérêt de GRASS au moyen de r.resample,
- dans cet exemple, cette procédure est réitérée d’abord en repérant les coordonnées sur Google Earth pour l’image satellite, puis en repérant les coordonnées des stations de métro sur l’image ainsi positionnée.
Une fois les points de contrôle sélectionnés, le choix du mode de déformation et d’interpolation doit être sélectionné (symbole de la clé, ou Settings > Transformation settings) : nous sélectionnons en général Thin Plate Spline pour la transformation et les voisins les plus proches (Nearest neighbour) pour l’interpolation. Il est judicieux de ne pas activer l’option de définition de la résolution cible (Set Target Resolution) qui ne permet pas de trouver de solution. Un exemple de résultat de ce traitement est proposé en Fig. 3.
4.3 Cas de l’image en prise de vue oblique
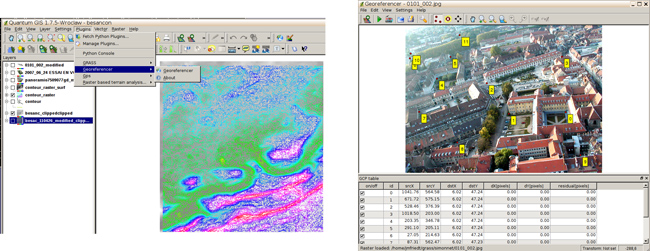
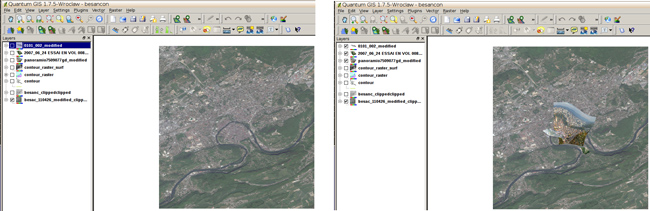
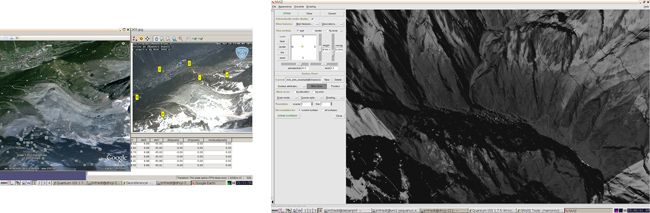
Nous nous proposons de réitérer la procédure de correction géométrique d’une photographie prise en vue oblique – ici depuis un ballon captif – pour la géoréférencer et ainsi compléter une image en vue azimutale (Fig. 4).
Le fichier de GCP est en ASCII (Fig. 5) avec une première ligne d’en-tête inutile : ce fichier est donc trivialement exploitable pour fabriquer la ligne de commande exploitant la bibliothèque GDAL afin d’incorporer ces points de référence dans le fichier GeoTIFF ou, par ailleurs, avec un peu de modification (élimination de la première ligne) chargement par GRASS. L’outil pour incorporer les GCP dans le fichier GeoTIFF est gdal_translate (traduction d’un format d’image vers un autre – ici de JPEG a GeoTIFF) : QGis nous propose par ailleurs de fabriquer cette ligne de commande pour nous. Une fois le fichier GeoTIFF convenablement renseigné, la commande gdalwarp effectue la correction géométrique elle-même selon une loi d’interpolation définie par l’utilisateur.
/usr/bin/gdal_translate -of GTiff \
-gcp 1041.76 564.581 6.02363 47.2353 \
-gcp 671.718 575.154 6.02292 47.235 \
-gcp 528.458 376.388 6.02153 47.2354 \
-gcp 1018.5 202.996 6.02219 47.2367 \
-gcp 203.348 346.784 6.01993 47.2351 \
-gcp 291.101 205.11 6.01816 47.236 \
-gcp 27.0485 214.626 6.01583 47.2355 \
-gcp 87.3128 562.467 6.02131 47.2344 \
-gcp 335.771 761.233 6.0228 47.2345 \
-gcp 1138.24 843.7 6.02419 47.2349 \
-gcp 32.0705 182.907 6.01508 47.2357 \
-gcp 350.837 63.4361 6.01447 47.238 \
"0101_002.jpg" "/tmp/0101_002.jpg"
/usr/bin/gdalwarp -r near -tps -co COMPRESS=NONE "/tmp/0101_002.jpg" "0101_002_jmfout.tif"
Seule la dernière étape du calcul mérite d'être scriptée pour un traitement automatique, l’identification des GCPs étant nécessairement une analyse manuelle fastidieuse mais qui ne peut être automatisée.
Nous avons constaté qu’une difficulté majeure de localisation de pixels d’images acquises en environnement urbain est la difficulté à visualiser la base des bâtiments ou, de façon générale, des points de référence au niveau du sol (Fig. 6). L’estimation de la qualité de la correction géométrique semble donc en l’état complexe, mais reste là encore un problème ouvert qu’il faudra résoudre pour généraliser la méthode de traitement (Figs. 7 et 9). Dans ce contexte, la photographie aérienne prise au dessus du terrain relativement dégagé de la citadelle de Besançon (Fig. 5, droite) semble un cas idéal malgré l’angle important des pentes autour de la forteresse qui induit des déformations significatives et donc la nécessité de sélectionner de nombreux points de contrôle.
5. De QGis à GRASS : visualisation 3D
Un point quelque-peu déroutant initialement est que bien que QGis fasse appel aux fonctions de GRASS au travers du greffon approprié, les ensembles de données gérées par les deux outils sont distincts. Ce n’est donc pas parce-que QGis connaît l’existence d’une couche qu’elle peut être traitée par GRASS. Il faut au préalable créer une carte GRASS et y incorporer les couches matricielles et vectorielles de QGis qui doivent y être traitées.
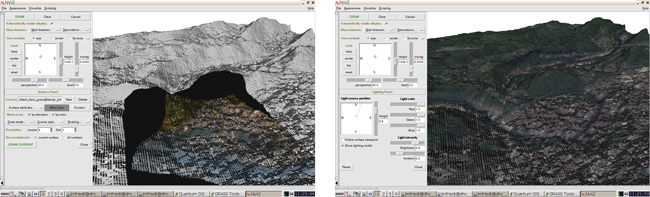
La principale motivation d’exploiter GRASS dans ce contexte tient en l’outil de visualisation 3D permettant de draper une image sur un modèle numérique de terrain et observer le résultat comme une surface en 3D. La procédure est décrite en détail à http://linfiniti.com/2010/12/3d-visualisation-and-dem-creation-in-qgis-with-the-grass-plugin/ mais le résultat est quelque-peu décevant (Fig. 8) en comparaison de l’outil professionnel de ArcGIS que sont 3D Analyst et ArcScene, en particulier lorsque le MNE GDEM2 est utilisé du fait d’un bruit excessif sur le jeu de données. Le résultat reste néanmoins exploitable pour valider la projection (Fig. 9). Le MNE (GDEM2) de ASTER est trop inhomogène pour permettre une projection propre. Nous avons constaté que malgré une résolution théorique annoncée inférieure, utiliser un raster de SRTM, plus homogène, fournit un résultat visuellement meilleur. L’alternative consistant à lisser GDEM2 par convolution donnera probablement la même résolution que SRTM et mieux vaut donc s’appuyer sur un jeu de données propre et validé.
Néanmoins, la disponibilité des outils classiques de traitement et d’analyse des informations spatiales semble justifier la compatibilité des méthodes de traitement avec GRASS, en se remémorant que le travail de correction géométrique et mosaïqué des images n’est que l’étape préliminaire au traitement quantitatif des informations contenues dans les vues azimutales (Fig. 10). Les triangles de Delaunay affichés sur cette figure représentent les surfaces formées par les plus proches voisins entre lesquels une interpolation sera faite lors de la correction géométrique des images – le choix de la triangulation vérifie qu’aucun autre GCP que les 3 sommets du triangle n’est inclus dans le cercle passant par les 3 sommets de chaque triangle. Les polygones de Voronoï6 (en vert sur Fig. 10) partitionnent l’espace en sphères d’influence : chaque polygone est centré sur un GCP (point connu) et s’étend jusqu’à ce que l’influence d’un autre point de référence devienne dominant. Les triangles de Delaunay et polygones de Voronoï sont une représentation duale du partitionnement de l’espace : les sommets des polygones de Voronoï sont les centres des cercles s’appuyant sur les sommets des triangles de Delaunay et chaque sommet d’un triangle de Delaunay est relié au polygone de Voronoï voisin. Il s’agit donc de distributions rationnelles de l’espace en régions d’influence de points connus permettant d’interpoler au mieux les grandeurs entre ces points de référence.
Maintenant qu’une image en prise de vue oblique est représentée en vue azimutale, avec chaque pixel couvrant une même surface sur l’image déformée, nous pouvons envisager d’analyser quantitativement les informations contenues dans les paysages ainsi observés.
6. Tout ça pour ça ... application au glacier des Pélerins
Le glacier des Pélerins [12, p.116] est un petit glacier au pied de l’Aiguille du Midi dans la vallée de Chamonix. Il s’avère être au premier plan de la vue de la webcam placée au sommet de l’Aiguille du Midi par la Compagnie du Mont Blanc7. En l’absence d’une présence physique sur place, ces images capturées automatiquement 6 fois par jours à intervalle de temps de 2 h par un crontab fournissent la base de données nécessaire à l’étude de la couverture neigeuse [13] de ce petit glacier de 1,2 km2 de superficie s’étendant jusqu`a une altitude de 2350 m [14, p.172].
Nous avons dans un premier temps obtenu la section du MNE SRTM pour la région contenant le massif du Mont Blanc, ainsi que l’image en tons de gris DigitalGlobe d’identifiant 1020010008CEF300 acquise le 24 juin 2009 (accessible depuis l’onglet Catalog de https://browse.digitalglobe.com). La figure 11 illustre le drapage sur le MNE de cette image satellitaire positionnée au moyen de quelques GCP sélectionnés autour du Mont Blanc, ainsi qu’un échantillon des photographies de webcam que nous allons exploiter au cours de corrections géométriques par l’identification, dans Google Earth, de points remarquables. Le village de Chamonix est visible au fond de la vallée et servira de référence lors de la recherche des images floues (mauvais temps et webcam dans les nuages). Une mise en contexte, résultat du traitement qui va être décrit ci-dessous, est proposé sur la Fig. 12 dans laquelle nous découvrons une nouvelle fonctionnalité de gdal_warp : la fusion de plusieurs images en tenant compte éventuellement d’un masque de transparence. La commande pour obtenir cette image composite est limpide, avec la série des images à fusionner suivie de la sortie : gdalwarp tt_composite_export.tif warp_130723_0905.tif gdal_merge.tif avec warp_130723_0905.tif générée depuis QGis au moyen du module r.out.tiff appliqué à la couche issue de la correction géométrique par georeferencer. Le fichier de localisation, d’extension .tfw, est généré simultanément.
Bien que automatisé, le traitement d’images n’a de sens que sur des images nettes et convenablement illuminées. Nous avions déjà présenté une méthode classique de recherche d’images floues au moyen de l’auto-corrélation [10]. Pour rappel, l’auto-corrélation est une transformation mathématique visant à rechercher le décalage d’un motif maximisant le taux de ressemblance avec un motif de référence. Il semble évident qu’un motif se ressemble fortement à lui même et une auto-corrélation présente toujours un maximum pour le décalage (translation dans le cas d’une image) nul. Le point qui nous intéresse n’est pas tant la position de ce maximum trivial à l’origine, que le comportement de la courbe à son voisinage. Une image nette ne se ressemble à elle même et nous n’avons aucune raison de retrouver les caractéristiques spatiales des pixels – sauf en présence d’un motif périodique qui n’est en général pas le cas – lors d’une translation spatiale de l’image. Ainsi, une image nette présente un pic d’inter-corrélation pour un déplacement nul et une décroissance rapide au voisinage de ce maximum. Au contraire, une image floue se ressemble à elle même si elle est légèrement translatée. Le cas classique que nous observons en pratique est un nuage qui englobe l’aiguille du Midi : dans ce cas l’image est uniformément grise et toute translation de l’image se ressemble à elle-même. Nous allons donc considérer la valeur de l’auto-corrélation bi-dimensionnelle en un point autre que la translation nulle et nous analyserons la valeur à une distance arbitrairement choisie de 10 pixels du centre. Cette procédure s’implémente sous GNU/Octave comme suit :
d=dir('13*1305.jpg'); % les images brutes de 13h05 en 2013
for k=1:length(d)
d(k).name
eval(['a=imread(''',d(k).name,''');']);
aa=rgb2gray(a);
aaa=aa(100:100+taille,100:100+taille);
xx=xcorr2(aaa-mean(mean(aaa)),'coeff');
s=size(xx);m=max(xx(:));
p=find(xx(:)==m);
[cx(k),cy(k)]=ind2sub(s,p);
mm(k)=xx(cx(k)+10,cy(k));
end
kb=find(mm>0.5); % les images ne sont pas bonnes
kg=find(mm<=0.5); % les images sont bonnes
Nous nous proposons de justifier de l’acquisition des connaissances présentées jusqu’ici pour exploiter quantitativement ces photographies de webcams. La procédure de traitement que nous proposons est sur la Fig. 13. Il est probable qu’un utilisateur expérimenté saura effectuer toutes les opérations qui vont suivre avec les outils cités ci-dessus, mais étant plus familier avec GNU/Octave (ou Matlab), nous allons quitter le monde de la gestion d’informations spatiales pour revenir à des outils plus classiques de traitement du signal.
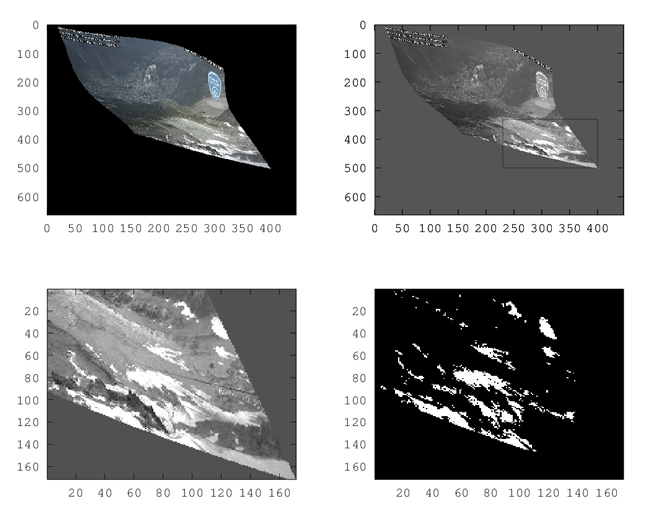
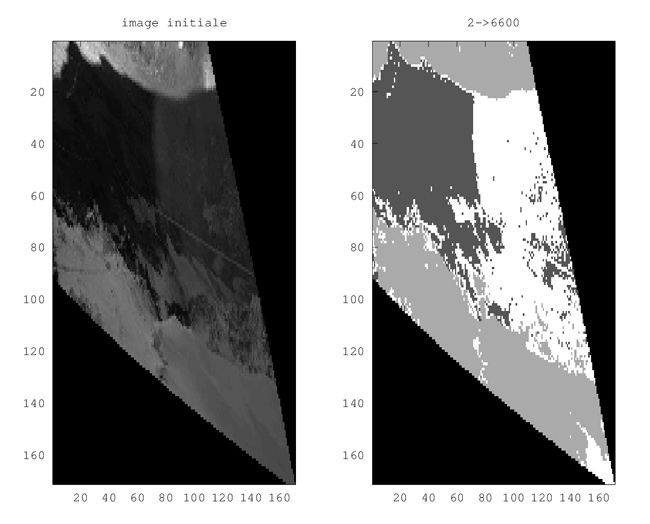
Ayant obtenu une image déformée géométriquement pour tenir compte de la topographie du terrain sur laquelle est projetée l’image (Fig. 13, en haut à gauche), nous sélectionnons une région comprenant majoritairement le glacier que nous étudions (Fig. 13, en haut à droite). Bien qu’il soit envisageable sous GRASS de définir un masque complexe, nous nous contentons ici d’une région rectangulaire. Cette image est convertie en tons de gris puisque la couleur ne permet pas d’améliorer la capacité de différenciation entre roche, neige et glace. Les méthodes classiques d’analyses multispectrales, en particulier lorsqu’une bande infrarouge est disponible pour différentier les réflecteurs du rayonnement solaire (index NDVI – Normalized Difference Vegetation Index – combinaison normalisée de la réflectance dans les bandes infrarouge et visible) ne sont pas accessibles ici, et un rapide test d’analyse en composantes principales ne semble pas savoir faire mieux qu’une simple analyse en intensité lumineuse sur chaque pixel. En conséquent, un seuillage est effectué sur chaque pixel de l’image en tons de gris (Fig. 13, en bas à droite) en assignant une pondération de 1 pour un pixel brillant (au dessus d’un seuil) et de 0 en dessous. Finalement, la somme des pixels est effectuée et, puisque chaque pixel comporte une surface connue suite à la correction géométrique, nous sommes en mesure d’estimer la surface du glacier couverte de neige (et donc protégée de la fonte). L’implémentation de ces concepts sous GNU/Octave s’obtient comme suit :
seuil_neige=250
d=dir('./wa*1305.tif'); % les images corrigees
l=1; % geometriquement
for k=1:length(d)
eval(['a=imread(''',d(k).name,''');']);
d(k).name
aa=rgb2gray (a);
aaa=aa(330:500,230:400);
seuil_neige=max(max(aaa));
if (seuil_neige>120) % en dessous de 120, ce n'est pas de la neige
seuil_neige=seuil_neige-20; else % on se laisse de la marge
seuil_neige=seuil_neige+1;
endif
k=find(aaa>seuil_neige); % seuillage
aaa(k)=0;k=find(aaa>0);aaa(k)=1;aaa=1-aaa; % 1 = neige, 0 sinon
% if (l<=16) % si on veut afficher les images seuillees
% subplot(4,4,l);colormap gray
% imagesc(aaa);colorbar;
% endif
somme(l)=sum(sum(aaa));
l=l+1;
end
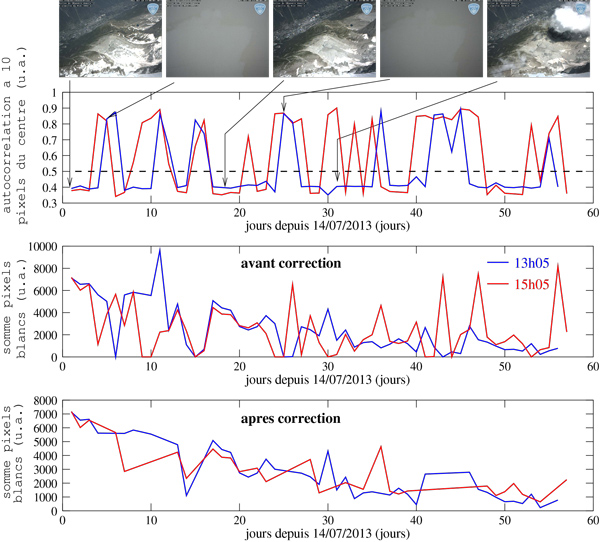
Le résultat de l’analyse d’images floutées ou non est présenté sur la Fig. 14, dans laquelle une série d’images identifiées comme floues est proposée à gauche et les images nettes à droite. L’analyse est uniquement effectuée sur la région de la photographie comportant le village de Chamonix (la cible présentant le plus de motifs et la plus lointaine de la caméra), le calcul d’inter-corrélation étant gourmand en ressources de calcul : une analyse sur une région restreinte suffit. Nous constatons que la classification est très efficace et ce, d’autant plus que nous avons choisi des horaires de prises de vue (13h05 et 15h05) maximisant le contraste des images. Un bref aperçu de Fig. 16, dont le graphique du haut donne la valeur normalisée de l’auto-corrélation à une distance de 10 pixels de la translation nulle, montre nettement la présence de deux classes, celles pour lesquelles l’auto-corrélation loin de l’origine est faible (image nette, valeur entre 0,4 et 0,5) et les images floues pour lesquelles cette valeur dépasse 0,5.
Ayant sélectionné les images dignes de traitement, nous découpons la région comportant le glacier (Fig. 15, gauche) et seuillons sur une valeur qui semble représentative de la présence de neige (Fig. 15, droite).
Finalement, les pixels blancs (valeur 1) et noirs (valeur 0) sont sommés pour estimer la couverture neigeuse : la conversion de pixel à surface s’obtient en analysant les méta-données d’une photographie corrigée géométriquement sous QGis. Nous y apprenons que chaque pixel occupe 1,81· 10−4 degrés/pixel, soit aux latitudes qui nous concernent, une surface de 14×20=281 m2 :
$ gdalinfo warp_130724_0905.tif
Driver: GTiff/GeoTIFF
Files: warp_130724_0905.tif
Size is 446, 664
Coordinate System is `'
Origin = (6.841708607073000,45.956579737414486)
Pixel Size = (0.000181024830052,-0.000181024830052)
Image Structure Metadata:
INTERLEAVE=PIXEL
Corner Coordinates:
Upper Left ( 6.8417086, 45.9565797)
Lower Left ( 6.8417086, 45.8363793)
Upper Right ( 6.9224457, 45.9565797)
Lower Right ( 6.9224457, 45.8363793)
Center ( 6.8820771, 45.8964795)
Band 1 Block=446x4 Type=Byte, ColorInterp=Red
Mask Flags: PER_DATASET ALPHA
Band 2 Block=446x4 Type=Byte, ColorInterp=Green
Mask Flags: PER_DATASET ALPHA
Band 3 Block=446x4 Type=Byte, ColorInterp=Blue
Mask Flags: PER_DATASET ALPHA
Band 4 Block=446x4 Type=Byte, ColorInterp=Alpha
Sur la Fig. 15, la courbe du haut indique quelle photographie est digne d’étude (en bleu pour une séquence prise tous les jours à 13h05 entre les 14 juillet et 9 septembre, rouge pour la séquence prise à 15h05) – seule une valeur au-dessous de 0,5 indique une image nette – la courbe du milieu, l’analyse de la surface enneigée pour toutes les images indépendamment de leur qualité – fournissant une courbe difficile à analyser – et finalement l’analyse (en bas) uniquement pour les images dignes d’intérêt. Nous y observons une décroissance monotone de la couverture neigeuse et une certaine cohérence entre les courbes obtenues avec les photographies acquises à 13h05 et 15h05. La valeur initiale de la courbe, 7000 pixels ou près de 2 km2, dépasse la surface du glacier et indique clairement que des zones neigeuses en dehors du glacier sont comptabilisées. La valeur finale, 1000 pixels ou 0,3 km2, est cohérente avec une fraction du glacier couverte de neige. Une validation sur le terrain serait évidemment nécessaire pour confirmer ces affirmations issues exclusivement de traitements d’images acquises par télémesure [15].
Cette analyse, effectuée selon une approche naïve de seuil fixe par rapport au pixel d’intensité (somme des composantes rouge, bleue et verte) la plus forte pour définir la neige, s’avère la plus robuste face à des approches plus complexes de segmentation. Une classification par l’algorithme kmeans() (disponible dans la boite à outils statistics de GNU/Octave) donne certes un résultat esthétiquement agréable, mais l’assignation de la multitude de classes (neige à l’ombre, neige au soleil, glace à l’ombre, glace au soleil, roche) s’avère excessivement complexe.
d=dir(['./wa*_1105.png']);
for kk=1:length(d) % application a toutes les images du repertoire
eval(['a=imread(''./',d(kk).name,''');']);
d(kk).name
a=a(:,:,(1:3)); % elimine la couche de transparence
aa=rgb2gray (a); % couleur -> tons de gris
aaa=aa(330:500,230:400); % se focalise uniquement sur le glacier
aaaa=double(reshape(aaa,171*171,1)); % matrice -> vecteur
k=find(aaaa>0); % on elimine le fond noir de la correction ...
b=aaaa(k); % ... geometrique par gdalwarp (sinon une classe de trop)
[idx, centers] = kmeans (b, 3); % segmentation sur 3 classes
aaaa(k)=idx; % assignation des classes sur l'image originale
bb=reshape(aaaa,171,171); % vecteur -> matrice
imagesc(bb); % affichage du resultat de la segmentation
end
À titre d’illustration, le traitement de la prise de vue de 13h05 du 8 octobre (Fig. 17) illustre clairement la discontinuité entre l’ombre projetée de l’aiguille du midi (en haut à gauche), le reflet sur la vitre de la webcam (en haut à droite) et la neige au premier plan (en bas), segmentation sans relation avec les motifs que nous recherchons.
7. Prévision des ombres projetées : une aide au traitement automatique des images
Un point critique pour classer de façon automatique les zones enneigées, englacées ou de roche tient en l’illumination. Il s’agit d’un problème bien connu en vision et traitement automatique des images : sans une bonne illumination homogène, le traitement numérique des images devient rapidement complexe. Dans notre cas, les ombres des nuages et autres artefacts météorologiques ne sont pas prévisibles mais nous pouvons au moins identifier les ombres projetées par le soleil, parfaitement déterministes. Connaissant les dates et horaires de prises de vues, nous connaissons la position du soleil et en déduisons, avec la topographie du site, le motif des ombres projetées (fonctions r.sunmask ou r.sun de GRASS). Ainsi, prédire la position des ombres et imposer la continuité des classes de part et d’autre des zones éclairées simplifie le problème d’identification de la couverture neigeuse des surfaces.
Nos essais sur un MNE en projection sphérique WGS84 se sont soldés par des échecs qui ont nécessité d’approfondir le problème jusqu’à trouver la solution que nous proposons ci-dessous, peut être pas optimale mais qui a le bon goût d’être fonctionnelle. Les cartes sont définies selon deux grandes classes de référentiels : non-projetées ou projetées. Dans le premier cas, un système de coordonnées sphérique définit la position de chaque point sur le globe – par exemple pour l’ellipsoïde utilisé par la majorité des récepteurs GPS – selon la convention WGS84 dans laquelle chaque point est défini par une longitude et une latitude en degrés. Cependant, ce mode de représentation des données (utilisé jusqu’ici) ne tient pas compte du fait qu’une carte ou un écran sont des objets plats, et qui par conséquent nécessitent une étape de projection d’une sphère vers un plan [17]. Le système de coordonnées projeté définit un certain nombre de régions – bandes selon les méridiens – pour lesquels la coordonnée sphérique est localement projetée sur un plan. Les diverses régions du globe ainsi définies tiennent compte des disparités locales entre l’elliposoï définissant WGS84 et la sphère idéale que pourrait représenter le monde si la Terre était homogène et n’était pas en rotation. Les conséquences évidentes de passer en référentiel projeté sont que :
- l’unité de distance n’est plus le degré mais le mètre. De cette façon, les distances sont plus faciles à estimer dans un référentiel projeté localement plan,
- la géométrie plane est plus facile à appréhender que la géométrie en coordonnées sphériques, ce qui aura une conséquence significative pour notre application.
Notre objectif est désormais de considérer la photographie acquise par la webcam de la Compagnie du Mont Blanc sur l’Aiguille du Midi le 22 Septembre 2013 à 13h05. Cette photographie présente une superbe ombre projetée qui interdit à peu près tout classement automatique de la couverture neigeuse sur le glacier. Si nous pouvons prédire la position de cette ombre projetée, nous pouvons ajouter un a priori additionnel sur l’algorithme de classification qu’est la continuité des classes de part et d’autre de l’ombre. Cependant, une application naïve de la fonction r.sunmask de GRASS qui prédit les ombres projetées par le soleil, sur un MNE en WGS84 échoue lamentablement. L’échec est illustré par l’indépendance du résultat du calcul avec l’élévation du soleil au-dessus de l’horizon, résultat évidemment aberrant puisqu’un soleil rasant doit induire de longues ombres projetées alors qu’un soleil au zénith n’induit aucune ombre. Diverses expérimentations nous ont permis de conclure qu’il est nécessaire de passer en coordonnées projetées (sur un plan local) au lieu de travailler en coordonnées sphériques. Pour l’Est de la France, la zone de projection se nomme WGS84/UTM31N. Nous devrons donc convertir l’ensemble des données en notre possession dans ce référentiel pour y appliquer les algorithmes de prévision des ombres projetées. Afin de rendre une longue histoire courte, notamment avec une description des expériences sur données simulées qui nous a amené à cette conclusion, le lecteur est renvoyé vers la page web http://jmfriedt.free.fr/proj_grass/projection.html.
Le résultat du calcul des ombres projetées, une fois toutes les données converties au format projeté WGS84/UTM31N, est présenté Fig. 18. Pour atteindre ce résultat, nous avons exploité la version 2.0.1 de QGis qui permet de passer d’un mode de projection à un autre simplement par l’application de la commande Save As .... Ainsi, nous avons défini une carte en référentiel projeté WGS84/UTM31 pour QGis, y avons chargé le MNE SRTM en indiquant que le format d’entrée est WGS84 (non-projeté) puis en sauvant ces données au nouveau format. Travaillant de même dans GRASS, une carte au format projeté WGS84/UTM31N est définie et le fichier que nous venons de sauvegarder y est inséré (r.in.gdal) en appliquant l’option d’ignorer le mode de projection (override projection). Ainsi, GRASS charge le MNE dans la projection appropriée et permet d’appliquer l’algorithme de traitement r.sunmask dans un référentiel approprié pour atteindre un résultat dépendant de l’élévation du soleil au-dessus de l’horizon. Finalement, la carte résultante, qui contient des valeurs arbitraires (NaN) pour les ombres projetées et des valeurs scalaires finies, est affichée en sélectionnant une transparence de l’ordre de 65% pour l’ensemble de la carte (mode Singleband pseudocolor) et une valeur de 100% pour les valeurs non-définies (penser à activer la bande spectrale 1 (Gray) comme sélection de la transparence, Fig. 19). La position du soleil, connaissant la position géographique de l’observateur et la date de prise de vue, est obtenue depuis le site de l’USNO8. Nous prendrons un soin particulier à réduire au strict minimum la surface analysée – au moyen de la définition de la zone d’analyse de GRASS auquel le MNE est ajusté par r.resample – car l’application de r.sunmask sur une large région avec une résolution égale à celle du MNE est excessivement gourmande en ressources de calcul.
L’application de l’algorithme de r.sunmask, gourmande en ressources calculatoires, ne semble pas savoir profiter de la disponibilité de plusieurs processeurs pour paralléliser ses opérations. Un calcul sur 1700×2300 points, pour une résolution spatiale de 10×10 m2, prend un peu moins de 72 heures. Il semble donc pertinent de s’interroger sur la résolution requise pour obtenir un résultat exploitable quant à l’ombre projetée. Le sommet de l’aiguille du Midi se trouve à une altitude de 3842 m tandis que le glacier des Pélerins présente un front à une altitude de l’ordre de 2400 m. La différence d’altitude entre la source de l’ombre projetée (supposée être l’aiguille du Midi) et la surface du glacier est donc 1442 m. Puisque l’angle du soleil autour du mois de Septembre est environ de 45°, l’ombre projetée est elle même longue de l’ordre de 1442 m. Détecter une variation de 1° de la position du soleil nécessite une résolution de 50 m puisque l’ombre projetée pour des angles de 44 et 46° est 1392 et 1493 m respectivement. Le calcul de la position du soleil au moyen du site de l’USNO pour quelques jours autour du 22 Septembre 2013, pour des prises de vues à heure fixe autour de 13h (heure local), indiquent que l’élévation du soleil varie de l’ordre de 0,4°/jour. Ainsi, une résolution spatiale de 30 m ne permettra que d’identifier à deux jours près la date de prise de vue, en supposant que le pixel de calcul soit significatif. Une identification de la date de prise d’une photo par la méthode de l’ombre projetée à la semaine près semble plus réaliste compte tenu de la résolution spatiale du MNE exploité ici (90 m annoncés à l’équateur pour SRTM).
Conclusion
S’étant familiarisé avec les outils de traitement spatial de l’information au moyen de QGis en faisant appel aux fonctions des bibliothèques GRASS et GDAL, nous nous sommes efforcés de nous affranchir de l’interface graphique en identifiant les lignes de commandes associées à chaque opération, obtenant ainsi une série de traitements parallélisables depuis un script sur un grand nombre d’images.
Nous nous sommes efforcés de démontrer l’utilité de ce concept pour le traitement quantitatif d’informations obtenus sur des images acquises sur des prises de vues obliques en exploitant les photographies acquises par une webcam dans le massif du Mont Blanc. La série de photographies ainsi corrigées géométriquement est utilisée pour estimer la couverture neigeuse sur un petit glacier alpin, après élimination des clichés inexploitables du fait de conditions météorologiques défavorables.
Au cours de ces analyses de séquences d’images, nous avons fait l’hypothèse que les points de contrôle identifiés sur une image de référence restent valables pour toute la séquence de prises de vues. Cette hypothèse devient erronée si la caméra est sujette à des petits déplacements, qu’il s’agisse de maintenance ou de l’effet du vent sur l’attache de la caméra sur son support qui la fait vibrer. L’observation de structures caractéristiques sur l’image doit permettre d’identifier ces mouvements et donc de les corriger, les conditions de prises de vues (grossissement de l’objectif, aberrations optiques) restant constantes. Ainsi, le point que nous n’avons pas abordé concerne l’identification préalable de la rotation et translation de photographies par rapport à une image de référence (registration) – peut être au moyen du module i.homography de GRASS [16]. Le classement à posteriori des diverses surfaces visibles sur la mosaïque des images (classification neige/glace) n’est ici que grossier avec un seuillage et une classification plus fine mériterait à être analysée en détail au moyen des outils dédiés proposés par GRASS (classification supervisée ou non9).
Remerciements
Les équipes de géographes des projets financés par l’Agence National de la Recherche (ANR) Hydro-Sensor-Flow et Cryo-Sensors m’ont introduit au problème du traitement de données géographiques et de l’exploitation des images en prises de vues obliques. A. Sauter (Univ. Paris I) m’a montré l’inadéquation du MNE GDEM2 et la nécessité d’utiliser SRTM pour un rendu visuel acceptable sous nviz. J.-P. Simonnet (labo. Chronoenvironnement, Besançon) m’a fourni une série d’images prises par ULM, dont une est utilisée sur la Fig. 5. Y. LeNir (EISTI, Pau) a mentionné l’efficacité de l’algorithme kmeans() pour segmenter une image. Le problème de la prévision des ombres projetées pour faciliter la classification des surfaces a aussi été formalisé au cours de cette discussion. Les références bibliographiques qui ne sont pas identifiables par une recherche sur le web ont été obtenues auprès de Library Genesis (gen.lib.rus.ec).
Références
[1] J.G. Corripio, Y. Durand, G. Guyomarc’h, L. Mérindol, D. Lecorps & P. Pugliése, Land-based remote sensing of snow for the validation of a snow transport model, Cold Regions Science and Technology 39 (2004), pp.94–104 (http://www.uibk.ac.at/geographie/personal/corripio/publications/corripioetal04_crst.pdf) ou http://www.meteoexploration.com/products/monitoring.html
[2] V. Lebourgeois, A. Bégué, S. Labbé, B. Mallavan, L. Prévot & B. Roux, Can Commercial Digital Cameras Be Used as Multispectral Sensors ? A Crop Monitoring Test, Sensors (8), 7300–7322 (2008), disponilbe à www.mdpi.com/1424-8220/8/11/7300
[3] i.ortho.photo est décrit à http://grasswiki.osgeo.org/wiki/Orthorectification_digital_camera
[4] E. Thibert, C. Vincent, A. Soruco, M. Harter, R. Blanc, R. Heno, Photogrammétrie numérique & risques naturels : Application à la dynamique des avalanches et aux chutes de séracs – Synthèse effectuée pour le Pôle Grenoblois Risques Naturelsdisponible à http://www.risknat.org/pages/programme_dep/docs/cemagref_etna/2009_Thibert-et-Vincent-jan11.pdf, ou C. Vincent, E. Thibert & M Harter, Etude du glacier de Taconnaz, disponible à http://www.glariskalp.eu/files/Action_2.A%20-%20Etude_du_glacier_de_Taconnaz.pdf
[5] J.G. Corripio, Snow albedo estimation using terrestrial photography, Int. J. Remote. Sensing, 25 (4), pp.5705-5729 (2004)
[6] D. Laffly, É. Bernard, M. Griselin, F. Tolle, J-M. Friedt, G. Martin & C. Marlin, High temporal resolution monitoring of snow cover using oblique view ground-based pictures, Polar Record 48 (1), pp 11-16 (Jan. 2012), disponible à http://jmfriedt.free.fr/S0032247411000519a.pdf
[7] J.-M Friedt, É. Carry, Acquisition et dissémination de trames GPS à des fins de cartographie libre, GNU/Linux Magazine France, Hors Série 27 (Octobre 2006)
[8] W.G. Rees, Assesment of ASTER Global Digital Elevation Model data for Arctic Research, Polar Record 48 (1) pp. 31-39 (Jan. 2012)
[9] V. Kaufmann, Measurement of surface flow velocity of active rock glaciers using orthophotos of virtual globes, Geographia Technica, Special Issue, pp. 68-81 (2010)
[10] J.-M Friedt, Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées, GNU/Linux Magazine France 139 (Juin 2011), disponible à http://jmfriedt.free.fr/xcorr.pdf
[11] P.T. Fretwell, M.A. LaRue, P. Morin, G.L. Kooyman, B. Wienecke, N. Ratcliffe, A.J. Fox, A.H. Fleming, C. Porter & P.N. Trathan, An emperor penguin population estimate: the first global, synoptic survey of a species from space, PloS one 7 (4), e33751 (2012), disponible à http://www.plosone.org/article/info%3Adoi%2F10.1371%2Fjournal.pone.0033751
[12] H.B. de Saussure, Voyages dans les Alpes: partie pittoresque des ouvrages (3ème édition), Ed J. Cherbuliez, (1855), disponible à http://doc.rero.ch/record/17091/files/CA_42.pdf
[13] D. Farinotti, J. Magnusson, M. Huss & A. Bauder, Snow accumulation distribution inferred from time-lapse photography and simple modelling, J. Geophys. Research (2010), p.F01014
[14] R. Vivian, Les glaciers du Mont-Blanc, Ed. La Fontaine de Siloé (2005)10
[15] R. Fallourd, Suivi des glaciers alpins par combinaison d’informations hétérogènes : images SAR Haute Résolution et mesures terrain, thèse de l’Université de (2012), disponible à http://tel.archives-ouvertes.fr/tel-00718596/
[16] i.homography est décrit à http://www.cp-idea.org/documentos/tecnologia/7_grassgisconference.pdf et disponible à http://grasswiki.osgeo.org/wiki/GRASS_AddOns#Imagery_add-ons.
[17] J. Lefort, L’aventure cartographique, Belin – Pour la Science (2005) ou J.-P. Snyder, Flattening the Earth - Two Thousand Years of Map Projections, The University of Chicago Press (1993)
1 http://code.google.com/p/osmtracker-android/
2 L’auteur a vu cette méthode mise en œuvre sur des clichés obtenus par photographie analogique, avant la prolifération du traitement numérique d’images, en plaquant un calque contenant des polygones de surface constante sur une image prise depuis le sol. Compter le nombre de polygones recouvrant une surface de couleur claire dans la photographie permettait d’estimer alors la couverture neigeuse sur un massif alpin.
3 http://eductice.ens-lyon.fr/EducTice/recherche/geomatique/veille/imagerie-3d/MNT
4 http://nathanw.net/2011/09/27/generating-contours-using-gdal-via-shell-or-qgis/
5 https://browse.digitalglobe.com
6 http://mathworld.wolfram.com/VoronoiDiagram.html
7 http://www.compagniedumontblanc.fr/fr/webcams et en particulier http://www.compagniedumontblanc.fr/webcam/Aiguille.jpg
8 http://aa.usno.navy.mil/data/docs/AltAz.php
9 http://www.portailsig.org/content/classification-d-images-superviseenon-supervisee-sous-grass
10 http://www.geologie-montblanc.fr/glaciers.html



 Ajouter à une liste de lecture
Ajouter à une liste de lecture