Il existe une multitude d'approches pour rétro-concevoir un produit. Après avoir présenté les différents contextes d'analyse nous évoquerons quelques techniques issues des domaines de la vérification et validation de logiciels.
1. Introduction
Il n'est pas compliqué de savoir ce qu'est la rétroconception, son étymologie est assez limpide : il s'agit de suivre le processus de conception à l'envers, partir du produit fini et déterminer comment il a été conçu pour comprendre sa fonction ou son fonctionnement interne.
Les techniques employées sont en général issues du monde de la conception et en particulier des phases d'analyse et de validation, c'est pourquoi nous parlerons plus souvent de technique d'analyse que de rétroconception.
Ces techniques peuvent être groupées en quatre classes, que nous verrons dans la prochaine section. Nous évoquerons ensuite quelques exemples dans chacune de ces classes en nous concentrant sur l'analyse de logiciels, une partie du vocabulaire et des remarques restant cependant valide dans le cas de la rétroconception de matériels.
Cet article n'a pas vocation à être exhaustif, en premier lieu parce que mes connaissances sont loin de l'être, mais il devrait vous donner le vocabulaire et quelques pointeurs vous permettant de développer vos connaissances sur des techniques existantes et encore aujourd'hui le sujet d'une recherche active.
2. Quatre contextes d'analyse
Les approches pour la rétroconception peuvent être classifiées suivant l'accès nécessaire au produit à analyser.
2.1 Accès aux mécanismes internes du produit
Une première distinction est l'accès aux mécanismes internes du produit.
Une analyse qui ne s'appuie que sur les entrées/sorties est une analyse en boîte noire (black box) ; si au contraire l'analyse intègre une observation des mécanismes internes, on parle d'analyse en boîte blanche (white box). L'analyse d'un fichier binaire exécutable, par exemple, est une analyse en boîte blanche dès qu'on s'intéresse ne serait-ce qu'aux bits qui le composent.
Une analyse en boîte blanche nécessite donc de pouvoir ouvrir le produit. Cela n'est pas toujours possible, dans le cadre de la rétroconception d'un logiciel s'exécutant sur une machine distante par exemple, et il est parfois préférable d'éviter si l'analyse concerne un matériel dont on ne dispose qu'un seul exemplaire qui risque d'être endommagé. On a alors recours à une analyse en boîte noire.
Néanmoins, les analyses en boîte noire peuvent aussi être utiles quand le produit est disponible : l'analyse d'un protocole implémenté par un logiciel sous forme binaire se fera d'abord en boîte noire, l'observation des entrées/sorties permet souvent d'obtenir une bonne approximation du protocole en question, approximation qui pourra éventuellement être précisée par une analyse en boîte blanche.
2.2 Accès au produit pendant son fonctionnement
La seconde distinction, qui permet de scinder ces deux classes d'analyse en quatre, est l'accès au produit pendant son fonctionnement. Si l'analyse repose sur des informations obtenues pendant le fonctionnement du produit, on parle d'analyse dynamique. Si au contraire l'analyse est indépendante de toute exécution, on parle d'analyse statique.
Un débogueur est donc un outil d'analyse dynamique. Un désassembleur, au contraire, est un outil d'analyse statique. Ce sont par ailleurs des outils d'analyse en boîte blanche.
Une analyse statique en boîte noire n'aurait pas vraiment de sens. En effet, une analyse en boîte noire implique l'observation d'une sortie qui n'a pu être générée que par une exécution du système. Les analyses statiques se font donc toujours en boîte blanche.
Ce qui permet de scinder la classe des analyses boîte noire en deux est le degré de contrôle sur le fonctionnement du produit. Si on observe des entrées/sorties sans interagir avec le produit, l'analyse est passive (ou hors ligne). Si au contraire on génère des données d'entrée qu'on soumet au produit, l'analyse est active (ou en ligne).
Encore une fois, la décision de se placer dans un contexte d'analyse ou un autre peutêtre un choix :
- Pour une analyse furtive d'un botnet, on peut choisir une analyse passive ;
- Dans le cadre de l'étude d'un malware, on peut préférer une analyse statique pour réduire le risque de compromettre son propre système ;
ou une nécessité :
- Si on ne dispose que d'une capture réseau pour un serveur distant qui n'est plus en ligne, on fera une analyse passive ;
- Si on ne parvient à intercepter aucun message sur les canaux de communication du produit, une analyse passive risque d'être peu informative ;
- Sur un code source incomplet, on fera une analyse statique.
L'analyse (et donc la rétroconception) d'un produit peut se faire dans l'un de ces quatre contextes : boîte noire passive ou active, boîte blanche dynamique ou statique. Un analyste ne va pas nécessairement se placer directement dans le contexte fournissant le plus d'informations, mais va plutôt naviguer d'un contexte à l'autre, éventuellement dans l'ordre dont on vient de les citer, pour obtenir le plus rapidement possible l'information qui l'intéresse à chaque étape de son étude.
Nous présentons maintenant de façon très superficielle quelques techniques utilisables dans chacun de ces contextes.
3. Analyse en boîte noire
Dans le cadre d'une analyse en boîte noire, on ne peut se reposer que sur les données d'entrée/sortie. Cela suppose de connaître et d'avoir accès aux canaux sur lesquels ces données circulent. Il faut donc parfois commencer par étudier l'environnement dans lequel la cible s'exécute pour les déterminer. Des moniteurs comme Process Explorer et Process Monitor de la suite Sysinternals peuvent aider à identifier les moyens de communication entre un service et une application cliente par exemple.
Avec un accès aux canaux de communication, l'analyse des données échangées peut commencer. Il y a principalement deux choses à identifier : le format des messages et le traitement effectué par la cible.
Il arrive que le format des données échangées ne soit pas entièrement propriétaire et que les données utiles soient échangées via un protocole de communication connu. Un outil connaissant ce protocole facilite grandement l'analyse. On peut évidemment citer ici Wireshark.
Il est également parfois possible d'identifier des éléments du produit en cours d'analyse par signature comportementale, c'est-à-dire en cherchant dans une base de données la réponse obtenue après l'envoi d'une séquence de messages particulière ; c'est ainsi que procède nmap pour deviner l'OS d'une machine distante par exemple.
Quand on finit par se retrouver face à un format de donnée et un traitement inconnus, il faut trouver un moyen de les décrire. Une table associant à chaque entrée observée ou générée la sortie correspondante n'est évidemment pas une solution satisfaisante. On cherche à comprendre le produit pour pouvoir le modifier ou interagir avec lui. L'idéal serait de les représenter par un code source bien documenté, cela peut être un peu trop ambitieux dans un premier temps.
Une solution élégante est de choisir une classe de modèles, par exemple les expressions régulières pour le format de donnée ou les machines de Mealy pour la relation entrée/sortie, et déterminer quel modèle dans cette classe correspond le plus à la cible : trouver une expression régulière simple permettant de reconnaître les sorties du système par exemple.
On peut essayer de faire ça à la main ou se tourner vers les méthodes d'apprentissage (machine learning) et d'inférence de modèle. Nous ne rentrerons pas plus dans le détail ici et nous allons maintenant nous intéresser à une méthode plus simple et plus brutale, dont l'ambition n'est pas de construire un modèle de la cible mais plutôt d'évaluer sa robustesse.
3.1 Fuzzing
L'appellation fuzzing (ou test en frelatage) prend son origine dans un projet soumis par Barton Miller à ses étudiants de l'université du Wisconsin à la fin des années 80. Le fuzzing est alors ce qu'on peut faire de plus simple en termes d'analyse boîte noire active :
- les entrées sont générées aléatoirement, vraiment aléatoirement, sans reposer sur un modèle des données d'entrée ;
- les sorties ne sont pas observées, on regarde juste si le programme termine en un temps donné. S'il termine, même avec un message d'erreur, l'entrée est considérée valide, sinon c'est qu'il a planté ou ne terminera probablement pas.
Les entrées provoquant un crash sont alors étudiées plus en détails pour en comprendre l'origine.
Lars Fredriksen et Bryan So, les étudiants de Miller, ont réussi à planter avec cette méthode entre 25% et 33% des utilitaires testés sur différents systèmes UNIX [1].
Heureusement, les logiciels ont gagné en robustesse, un flux aléatoire est en général rapidement rejeté comme une entrée invalide et un fuzzer naïf ne pourra pas pénétrer profondément dans un logiciel moderne. Le fuzzing a donc dû évoluer. Une première amélioration est la génération des entrées par modification aléatoire d'une entrée valide, similairement aux algorithmes génétiques (crossover, mutation). Certains fuzzers s'appuient plutôt sur un modèle des données, quelques-uns sont même spécifiques à un protocole ou un format de fichier particulier. D'autres quittent le monde de l'analyse en boîte noire et se basent sur l'observation du code binaire de l'application fuzzée.
4. Analyse dynamique en boîte blanche
Le fuzzing permet d'obtenir des entrées déclenchant un bug. L'étape suivante est d'étudier le comportement du programme sur ces entrées, par exemple avec un débogueur. On passe alors d'une analyse boîte noire à une analyse boîte blanche.
L'analyse boîte blanche sert également pendant ou avant le fuzzing. Un fuzzer naïf n'évalue que la surface de la cible. Pour un lecteur de fichier PNG par exemple, la première étape est de vérifier l'en-tête du fichier qui doit être :
89 50 4E 47 0D 0A 1A 0A
Un fuzzer purement aléatoire a une chance sur 264 de passer cette étape. Connaître le format d'entrée ou s'appuyer sur des variantes d'un ou plusieurs fichier(s) valide(s) est une amélioration notable. Malgré tout, évaluer la pertinence de l'analyse reste difficile, on ne peut pas dire si la totalité ou au moins la majorité du programme a été parcourue sans passer à une analyse en boîte blanche : une technique classique est d'instrumenter le code pour marquer chaque instruction exécutée au cours de la campagne de fuzzing. On parle de couverture (code coverage) de l'analyse.
Ainsi, quand le fuzzing est guidé par un corpus d'entrées valides, il est possible de privilégier celles parcourant une partie peu explorée du code. Malheureusement, ce n'est pas toujours suffisant et il faut parfois un corpus initial immense pour assurer une bonne couverture.
C'est pourquoi le fuzzing est encore l'objet aujourd'hui d'une recherche active pour améliorer ses performances. On se dirige vers des méthodes intelligentes, on parle de smart fuzzing, qui s'éloignent de plus en plus du fuzzing simpl(ist)e des origines, ce dernier permet pourtant encore à certains d'obtenir d'excellents résultats.
4.1 Fuzzing chez Google
La nécessité d'un corpus immense ne fait pas peur à Google. En 2011, ils ont réussi à trouver une centaine de bugs dans le lecteur Flash de Adobe [2][3] par fuzzing. Comme souvent chez Google, les données (ainsi que la puissance de calcul) ont été un élément déterminant.
Ils sont en effet partis d'un corpus de 20 téraoctets de fichier SWF... La première étape a été d'en extraire une liste de 20.000 fichiers offrant une bonne couverture du code binaire du lecteur Flash. Cela a nécessité une semaine de calcul sur 2.000 cœurs CPU.
Ces 20.000 fichiers ont servi à générer aléatoirement des entrées pour une campagne de fuzzing de trois semaines... encore sur 2.000 cœurs.
Cela leur a permis d'identifier 106 bugs après une première analyse par Adobe des différents crashs observés. Leur correction a nécessité 80 modifications dans le code du Flash player. Cette campagne de fuzzing a clairement été un succès. Cependant, le ticket d'entrée est très élevé : en caricaturant à peine, il faut posséder une copie du Web et pouvoir mobiliser un supercalculateur 24h/24 pendant un mois.
4.2 Exécution symbolique dynamique
Pour ceux qui trouvent ce ticket trop cher, il faut rendre le fuzzing plus intelligent. Outre la spécialisation à une cible particulière, certains fuzzers s'appuient sur des techniques développées dans d'autres contextes. C'est le cas de Fuzzgrind, qui s'appuie sur les exécutions symboliques dynamiques, aussi connues sous le nom d'exécutions concoliques (pour concrète symbolique) [4][5].
Cette technique, comme son nom l'indique, est la combinaison d'une exécution concrète avec une exécution symbolique. Le tableau suivant illustre ce concept sur un programme calculant :
max( abs(Arg), abs(Arg-10))
|
Instructions |
Trace concrète |
Trace symbolique |
|
1 : Var0 = Arg0; 2 : Var1 = Var0 - 10; 3 : if(Var0 < 0) 4 : Var0 = -Var0; 5 : if(Var1 < 0) 6 : Var1 = -Var1; 7 : if(Var0 < Var1){ 8 : return Var1; 9 : else { 10 : return Var0; 11 : } |
Var0 ← 3 Var1 ← -7 3 ≥ 0 ↓ -7 < 0 Var1 ← 7 3 < 7 return 7 |
Var0 ← x Var1 ← x-10 x ≥ 0 ↓ x-10 < 0 Var1 ← 10-x x < 10-x return 10-x |
La trace concrète ne nécessite pas d'explication, intéressons-nous donc d'abord à la trace symbolique.
Lors d'une exécution symbolique, les calculs ne sont pas effectués sur des valeurs mais sur des symboles. En arrivant sur une condition, il faut choisir quelle branche emprunter pour le reste de l'exécution. Sans trace concrète, on peut faire ce choix de façon arbitraire au risque d'emprunter un chemin impossible : par exemple, aucune exécution concrète ne peut passer par la ligne 8 sans passer par les lignes 4 ou 6. Une solution est de faire appel à un solveur pour éliminer les branches impossibles, mais cela peut être coûteux.
Lors d'une exécution symbolique dynamique, c'est la trace concrète qui choisit quelle branche emprunter, le problème est donc éliminé et on est assuré d'avoir une trace symbolique réalisable. La trace symbolique représente alors une classe d'équivalence dont la trace concrète est un représentant. En accumulant les conditions rencontrées, on obtient une formule P dont la solution est l'ensemble des entrées produisant le même chemin. Dans notre exemple :
P(x) = (x ≥ 0) & (x-10<0) & (x < 10-x)
Pour toute solution de ce système, l'exécution concrète empruntera le même chemin, la même séquence d'instructions :
1 → 2 → 6 → 8
Pour augmenter la couverture d'une analyse dynamique, on ne veut donc pas choisir une telle entrée pour la prochaine exécution. On peut faire mieux que prendre une solution de (not P) en remarquant qu'en conservant les conditions accumulées lors d'un préfixe de la trace, on obtiendra une trace passant par le même préfixe. Pour passer par le chemin 1 → 2 → 6 → 10, il suffit de résoudre l'équation :
(x ≥ 0) & (x-10<0) & !(x < 10-x)
Si une équation n'a pas de solution, c'est que le chemin n'est pas réalisable. En énumérant des équations de chemins, et grâce au progrès des solveurs SMT (Satisfiability Modulo Theories), il est donc possible d'énumérer tous les chemins pour obtenir une couverture maximale. Malheureusement « tous les chemins » cela peut faire beaucoup et même être infini, en particulier en présence de boucles. En effet, il n'y a pas de notion de boucle dans une trace, elles sont déroulées, et deux traces n'effectuant pas le même nombre de boucles correspondent donc à des chemins différents.
Considérons le programme suivant :
1 : index = 0;
2 : while( S[index] != 0 ){
3 : index++;
4 : }
5 : if( index < 1000 ){
6 : ...
7 : } else {
8 : ...
9 : }
En soumettant la chaîne « Pwd » à ce programme, on obtient la trace suivante :
|
Instructions |
Trace concrète |
Trace symbolique |
|
1 : index = 0; 2 : ( S[index] != 0 ) 3 : index++; 2 : ( S[index] != 0 ) 3 : index++; 2 : ( S[index] != 0 ) 3 : index++; 2 : ( S[index] != 0 ) 5 : ( index < 1000 ) 6 : ... |
index ← 0 'P' != 0 index ← 1 'w' != 0 index ← 2 'd' != 0 index ← 3 0 == 0 3 < 1000 ... |
index ← 0 S[0] != 0 index ← 1 S[1] != 0 index ← 2 S[2] != 0 index ← 3 S[3] == 0 3 < 1000 ... |
Contrairement à l'exemple précédent, on voit apparaître une constante dans la trace symbolique. En effet, index n'est modifié qu'aux lignes 1 et 3 et ne dépend jamais directement des entrées. Pour explorer la ligne 8, on voudrait inverser la condition rencontrée à la ligne 5, mais aucune entrée ne permet d'obtenir 3 ≥ 1000. Il faut donc chercher une solution de :
(S[0] != 0) & (S[1] != 0) & (S[2] != 0) & !(S[3] == 0)
et continuer le processus jusqu'à obtenir une trace passant par la ligne 8. Il est évident ici pour un humain qu'il faut prendre une chaîne de longueur au moins 1000, mais ce n'est pas si trivial pour une méthode automatique à cause de cette dépendance indirecte entre la chaîne de caractères et la valeur de index en sortie de boucle.
Ce problème se pose d'ailleurs également dans le cadre de l'analyse par teinte (data tainting), une technique similaire où les données sont associés à une teinte qui est juste propagée par chaque instruction et non transformée contrairement aux exécutions symboliques dynamiques. Cette teinte est utile dans le cadre de l'analyse de flux d'informations. Cela permet de savoir si le premier argument d'un printf est influencé par l'utilisateur, ou permet de retrouver des informations sur une donnée qui devrait rester secrète. On distingue au moins trois types de flux :
- les flux directs : par exemple une affectation ;
- les flux indirects explicites : entre S[0] (ou S[1], S[2]) et index dans notre exemple, puisque la valeur de S[0] a permis l'exécution de l'instruction index++ ;
- les flux indirects implicites : entre S[3] et index, car une autre valeur de S[3] aurait permis l'exécution de l'instruction index++.
Ce dernier type de flux est difficile à détecter dans un cadre purement dynamique, puisqu'il est influencé par des instructions qui ne sont pas exécutées dans la trace observée, mais qui pourraient l'être dans une autre trace.
5. Analyse statique
Il existe deux grandes familles d'analyses statiques :
- l'analyse syntaxique repose sur la forme du programme ;
- l'analyse sémantique s'intéresse à l'ensemble des comportements possibles du programme.
Dans tous les cas, on étudie le code sans l'exécuter. On n'a donc pas besoin d'avoir une trace passant par l'instruction 8 pour aller voir ce qui peut s'y passer. Le désavantage est qu'on peut être amené à étudier du code inaccessible, ou à considérer des comportements impossibles : par exemple, un outil statique pourrait indiquer un risque de division par zéro si une division par S[0] est insérée à la ligne 8. C'est ce qu'on appelle un faux positif, ou fausse alarme : le rapport d'un comportement qui n'est pourtant réalisé par aucune exécution concrète.
La plupart des techniques dynamiques ne produisent pas de faux positif, car elles reposent sur l'exécution du programme analysé. Quand un fuzzer exhibe une trace levant une exception, on est assuré que le programme peut lever cette exception. Des faux positifs peuvent se produire quand la propriété recherchée est plus difficile à distinguer qu'une exception. Dans l'exemple suivant, une analyse par teinte pourrait propager la teinte de edx à eax, bien que eax en sortie de bloc ne dépende pas de la valeur de edx.
add eax,edx
sub eax,edx
Malgré ce dernier point, les méthodes dynamiques présentent l'avantage de produire une trace d'exécution. Par contre, elles génèrent de nombreux faux négatifs : l'annonce de l'absence d'un comportement qui est pourtant réalisé par au moins une exécution concrète. En effet, ce n'est pas parce qu'un fuzzer ne rapporte pas de bug, que le logiciel fuzzé n'en a pas. Les analyses dynamiques ne considèrent qu'un ensemble fini de traces (ou de chemins).
Pour éviter les faux négatifs, il faut considérer tous les chemins possibles. Ce qui ne peut se faire en général qu'en analyse statique. Certaines analyses statiques ne produisent pas de faux négatifs, d'autres produisent faux négatifs et faux positifs. Le principal problème des faux positifs est qu'ils sont chronophages : étudier un bug qui n'en est pas un est une perte de temps, si on le corrige c'est encore pire. Les faux négatifs, quant à eux, occultent des comportements qui devraient être analysés.
Une méthode qui ne produit pas de faux négatifs est dite correcte (sound) ; si elle ne produit pas de faux positifs, elle est complète. Malheureusement, il ne peut pas y avoir de méthode entièrement automatique à la fois correcte et complète, la plupart des propriétés intéressantes sur les programmes étant indécidables. Certaines analyses statiques, en particulier les analyses syntaxiques, ne sont ni correctes, ni complètes, et peuvent produire faux positifs et faux négatifs.
Cependant, il arrive que des outils d'analyse statique corrects ne renvoient pas d'alarme (et donc, pas de fausses alarmes) sur certains programmes, l'analyse est alors complète. Cette propriété forte est particulièrement recherchée dans le domaine des systèmes critiques, où la moindre erreur peut avoir des conséquences humaines et financières considérables. L'outil Astrée, basé sur l'interprétation abstraite, a par exemple prouvé automatiquement l'absence de bogues à l'exécution dans le logiciel d'amarrage automatique de l'ATV (Automated Transfer Vehicle) Jules Verne utilisé par l'agence spatiale européenne pour ravitailler l'ISS [6].
5.1 Interprétation abstraite
L'interprétation abstraite [7] est une méthode d'analyse statique basée sur la sémantique des programmes qui formalise la notion d'approximation.
Une analyse sémantique, comme nous l'avons déjà vu plus haut, se fonde sur l'ensemble des traces d'exécution possibles d'un programme. Malheureusement, cet ensemble de traces est en général trop complexe pour être calculé ou analysé, on a donc recours à des approximations pour le simplifier.
L'objet concret étudié appartient au domaine concret, ici l'ensemble des ensembles de traces. Son approximation appartient au domaine abstrait. Les fonctions permettant de passer d'un domaine à l'autre sont nommées abstraction et concrétisation.
Reprenons l'exemple calculant max(|Arg|, |Arg-10|) et essayons de prouver que la valeur retournée est positive. Une première approximation est de ne pas considérer l'ensemble des traces possibles, mais l'ensemble des valeurs que les variables peuvent prendre à chaque instruction. Il s'agit bien d'une approximation, puisqu'on perd la relation entre la valeur que prend Var0 à l'instruction 1 et celle qu'elle prend à l'instruction 2 sur une trace, on sait juste que Var0 appartient au même ensemble, mais pas que la valeur est inchangée. Il s'agit en outre d'une sur-approximation, car on ajoute des comportements et on n'en oublie aucun.
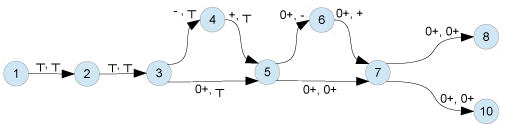
Par ailleurs, nous nous intéressons uniquement au signe de la sortie, nous allons donc approximer encore l'ensemble des comportements en ne conservant que les informations de signe. Ainsi, en arrivant à l'instruction 3, Var0 et Var1 peuvent avoir n'importe quel signe, on note leur valeur abstraite ┬ (top, ┬ est la notation usuelle pour l'élément maximal dans un treillis, un objet mathématique important dans la théorie de l'interprétation abstraite). L'instruction 3 sépare le flot d'exécution en deux branches. Une branche saute à l'instruction 5 avec Var0 positif ou nul et l'autre passe à l'instruction 4 avec Var0 négatif, qui mène à l'instruction 5 avec après avoir transformé Var0 en le rendant positif.
Fig.1 : Valeur abstraite de (Var0,Var1) sur le programme max(|Arg|, |Arg-10|)
On peut donc arriver à l'instruction 5 depuis l'instruction 3 avec Var0 positif ou nul, ou depuis l'instruction 4 avec Var0 positif. En faisant l'union de ces deux valeurs, on en déduit que Var0 est positif ou nul à l'instruction 5. En continuant ce raisonnement, on peut prouver que la valeur retournée est positive ou nulle.
Pour obtenir un résultat plus précis, il faut choisir un domaine abstrait (une approximation) plus précis. Un autre domaine abstrait classique est le domaine des intervalles, dans lequel chaque variable est bornée par deux valeurs. Dans notre exemple, ce domaine ne nous apporte pas plus d'informations, car la sortie dépend fortement de la relation entre Var0 et Var1 testée à la ligne 7. Il nous faut donc un domaine relationnel : les polyèdres par exemple. Un polyèdre est un ensemble convexe représenté par des contraintes. L'instruction 2, par exemple, introduit la contrainte (Var0 – Var1 == 10) qui peut être décomposée en :
(Var0 – Var1 ≥ 10) & (Var0 - Var1 ≤ 10)
Encore une fois, l'instruction 3 sépare le flot d'exécution en deux branches. Une branche saute à l'instruction 5 avec :
(Var0 ≥ 0) & (Var0 – Var1 ≥ 10) & (Var0 - Var1 ≤ 10)
et l'autre passe à l'instruction 4 avec :
(Var0 < 0) & (Var0 – Var1 ≥ 10) & (Var0 - Var1 ≤ 10)
qui transforme cet ensemble et mène à l'instruction 5 avec :
(Var0 > 0) & (-Var0 – Var1 ≥ 10) & (-Var0 - Var1 ≤ 10)
En faisant l'union convexe de ces deux ensembles, on en déduit qu'à l'instruction 5 :
(Var0 ≥ 0) & (Var0 – Var1 ≥ 10) & (Var0 + Var1 ≥ -10)
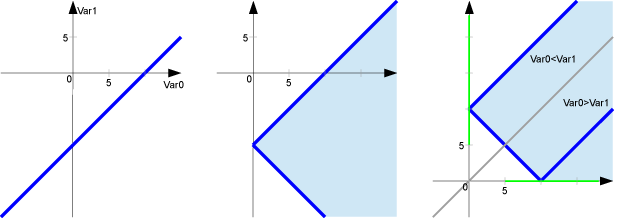
La figure 2 montre comment cet ensemble est transformé au cours du programme.
Fig.2 : Ensemble des couples (Var0,Var1) possibles aux lignes 3, 5, et 7. Les lignes bleues représentent l'ensemble exact, la zone bleue claire représente une approximation par un polyèdre convexe.
Finalement, on en déduit que la valeur retournée est supérieure ou égale à 5.
Encore une fois, le problème se complique avec les boucles. Reprenons notre analyse de signe sur l'exemple calculant la longueur d'une chaîne de caractères. En arrivant sur la boucle, la valeur de index est 0. Si le corps de la boucle est exécuté, on revient sur la condition avec index positif. Il faut considérer ce nouvel ensemble et analyser le corps de la boucle à nouveau. On arrive rapidement sur un point fixe, car notre domaine abstrait est fini. Si on refait cette analyse avec des intervalles, l'ensemble à considérer en entrée de boucle n'augmente que d'une valeur à la fois : [0;0], [0;1], [0;2]… L'analyse ne termine pas. Pour garantir la terminaison et accélérer la convergence vers un point fixe, l'interprétation abstraite utilise un opérateur effectuant une approximation (grossière) nommée élargissement (widening). En remarquant que seule la borne supérieure de l'intervalle est modifiée, on peut choisir [0; ∞[ et vérifier qu'on a bien atteint un point fixe.
L'invariant découvert par l'analyse est ici assez simple. Un domaine abstrait adapté aurait pu découvrir une propriété moins triviale :
∀i∈[0;index[, S[i] != 0
Nous avons ici considéré que les calculs se faisaient sur des entiers mathématiques et non des entiers machine pour simplifier les explications. Les outils d'analyse basés sur l'interprétation abstraite ne font pas cette approximation incorrecte. Ils sont également capables de manipuler correctement les flottants ou les vecteurs de bits.
L'interprétation abstraite permet donc d'inférer et de vérifier des propriétés non triviales sur des programmes de façon automatique. Elle rencontre un succès particulier dans le domaine des systèmes embarqués critiques et temps réel qui, en plus du besoin de garantie, présente un certain nombre de restrictions : ansi C, pas d'allocation dynamique, pas de récursion...
Sur des programmes plus généraux, les méthodes sémantiques évitant les faux négatifs comme l'interprétation abstraite ont la réputation de produire de nombreux faux positifs. Pourtant, les progrès constants de ces techniques et l'introduction de méthodes de tri des alarmes ou une interaction plus poussée avec l'analyste humain permettent de réduire considérablement leur nuisance. Par ailleurs, il s'agit également d'un problème de perception : lors d'une analyse syntaxique, on ne voit pas les faux négatifs, et il est souvent facile de « corriger », ou plutôt faire disparaître, toutes les alarmes levées par un analyseur syntaxique.
Conclusion
La rétroconception est une démarche opportuniste, il faut être capable de mettre en œuvre un certain nombre de techniques pour obtenir le plus rapidement possible des informations les plus pertinentes (pas forcément les plus précises), tout en respectant un certain nombre de contraintes liées à l'accès au produit analysé.
Les techniques spécifiques à la rétroconception restent peu nombreuses par rapport aux domaines voisins de l'analyse et de la vérification de programmes, qui connaissent une croissance importante due à l'intégration de logiciels de plus en plus complexes dans des systèmes de plus en plus nombreux.
Des outils automatiques puissants deviennent disponibles. Cependant, l'indécidabilité de la plupart des problèmes intéressants sur les programmes pourra toujours être exploitée par des techniques anti-rétroconception, et le rôle de l'expert reste, et restera encore un moment, prédominant.
Références
[1] « An empirical study of the reliability of UNIX utilities », Miller, Barton P. et Fredriksen, Louis and So, Bryan : http://doi.acm.org/10.1145/96267.96279
[2] « How Did You Get to that Number ? », Arkin, Brad : http://blogs.adobe.com/asset/2011/08/how-did-you-get-to-that-number.html
[3] « Fuzzing at scale », Evans, Chris et Moore, Matt et Ormandy, Tavis : http://googleonlinesecurity.blogspot.fr/2011/08/fuzzing-at-scale.html
[4] « DART : directed automated random testing », Patrice Godefroid et Nils Klarlund et Koushik Sen : http://doi.acm.org/10.1145/1065010.1065036
[5] « CUTE : a concolic unit testing engine for C », Koushik Sen et Darko Marinov et Gul Agha : http://doi.acm.org/10.1145/1081706.1081750
[6] « Int. Space System Engineering Conference, Data Systems in Aerospace DASIA'09 », « Space Software Validation using Abstract Interpretation », Bouissou, O. et Conquet, E. et Cousot, P. et Cousot, R. et Feret, J. et Ghorbal, K. et Goubault, E. et Lesens, D. et Mauborgne, L. et Mine, A. et Putot, S. et Rival, X.
[7] « Abstract Interpretation : A Unified Lattice Model for Static Analysis of Programs by Construction or Approximation of Fixpoints », Cousot, Patrick et Cousot, Radhia : http://doi.acm.org/10.1145/512950.512973



 Ajouter à une liste de lecture
Ajouter à une liste de lecture