Rendre vulnérable un code sûr, réaliser une porte dérobée indétectable, voici quelques possibilités des attaques par faute. Faites chauffer votre amplificateur RF, nous allons faire des étincelles !
On l’oublie souvent, mais un programme, même bas niveau, est un objet très abstrait. Que se passe-t-il si l’électronique déraille parce qu’une erreur y a été provoquée ? La frontière entre le matériel et le logiciel est source de nouvelles vulnérabilités. Voici une petite mise en bouche aux attaques par fautes matérielles, une technique puissante et peu connue.
1. Histoires de fautes
Une faute est l’effet obtenu, causé par un dysfonctionnement du système, souvent au niveau des signaux électriques. Les fautes sur les systèmes informatiques ont une histoire qui remonte aux premiers circuits intégrés. Dans les années 50, les tests nucléaires faisaient planter les appareils chargés de collecter des données. Puis la conquête spatiale a vu les premiers ordinateurs envoyés dans l’espace. Malheureusement, les rayons cosmiques généraient des erreurs. Plus tard, des éléments radioactifs présents dans les packages de puces électroniques perturbaient le fonctionnement de celles-ci.
Les environnements radiatifs ne font pas bon ménage avec l’électronique. Pour obtenir des puces plus fiables, il fallait être capable de simuler en laboratoire ces environnements. Les premières fautes par laser ont ainsi été obtenues dès les années 60.
En parallèle, la cryptographie moderne civile est née avec le DES (1975) et RSA (1977). Mais ce n’est que 20 ans plus tard (il y a 20 ans !) que les deux problématiques fusionnent. En 1997, deux papiers académiques indépendants montrent comment des fautes présentes durant l’exécution d’algorithmes cryptographiques (DES et [RSA] encore eux) permettent à l’attaquant de retrouver la clé secrète. Les attaques par faute étaient nées, devenant un enjeu de sécurité informatique.
2. Comment fait-on une faute ? À quoi cela sert ?
La beauté toute mathématique d’une attaque cryptanalytique ne doit pas nous cacher la réalité physique d’une attaque physique par faute : une faute est causée par des électrons en trop ou en moins au mauvais moment.
2.1. Moyens techniques
Les techniques pour créer ce mauvais comportement sont diverses, plus ou moins simples, plus ou moins coûteuses. En général, l’attaquant doit pouvoir accéder physiquement à la cible. Les attaques laser demandent un équipement coûteux et l’ouverture de la puce cible (retirer le package autour de la puce proprement dite). Mais leur précision est inégalée, il est possible dans certains cas de choisir le transistor à fauter. Beaucoup plus simple à mettre en œuvre, les perturbations d’horloge et d’alimentation. Dans le cas de la perturbation d’horloge, un cycle d’horloge unique est raccourci en dessous du temps nécessaire aux signaux pour se stabiliser. De même, si la tension d’alimentation est réduite pendant un temps suffisamment court, une erreur sera générée, mais la puce ne plantera pas. En effet, si la tension d’alimentation diminue, les signaux mettent plus de temps à traverser les transistors, à se propager, et donc peuvent ne pas être stabilisés à leur valeur correcte lors du front d’horloge suivant.
Ma technique préférée reste l’injection de faute électromagnétique. Placez la puce sous une antenne (en champ proche, la sonde doit être à quelques millimètres des lignes métalliques de la puce) et envoyez une pulsation de courant dans cette antenne, c’est-à-dire envoyez un gros courant durant un temps très court. Sous les bonnes conditions, une faute est générée. Pas de modification de la puce ou de la carte, on peut même cibler une partie précise de la puce. En effet, l’antenne est couplée avec les lignes métalliques à la surface de la puce, un peu à la manière des plaques à induction en cuisine. Ainsi un courant dans l’antenne sera transmis dans les lignes couplées : un bus de données, la ligne d’alimentation, etc.
Ces techniques permettent de créer physiquement des fautes et de cibler temporellement la perturbation de manière précise. Le prix des équipements nécessaires varie suivant les cibles, la précision et les techniques. Des cartes à « bas coût » [ChipWhisperer], ou un simple FPGA, permettent de s’essayer aux attaques physiques simplement. Un laser très précis peut vous coûter un demi-million d’euros. Entre les deux, l’injection électromagnétique reste abordable pour de petites structures ou un individu motivé (et c’est bien le problème du point de vue de la défense).
Il est possible de créer des fautes matérielles de manière purement logicielle. La plus connue de ces attaques est [RowHammer] qui permet de modifier des bits d’une mémoire « à l’usure ». Un autre exemple est [CLKSCREW], ici l’attaquant prend le contrôle du microcontrôleur qui gère l’énergie d’un téléphone (c’est-à-dire qui contrôle l’alimentation électrique et la vitesse de l’horloge). Ainsi, une plateforme d’injection de fautes matérielles est fournie gracieusement avec votre téléphone !
2.2. Un peu de cryptographie
Illustrons un peu la puissance d’une attaque par faute à travers un exemple sur l’algorithme de chiffrement symétrique AES (inspiré de [Giraud]).
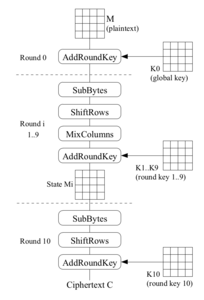
Figure 1
Sans entrer dans les détails, il suffit de savoir qu’un calcul d’AES est effectué sur un bloc de 16 octets (appelé le State) par l’application successive, par tours, de sous-fonctions (SubBytes, ShiftRows, MixColumns et AddRoundKey). Une clé de tour différente, dérivée de la clé maître de manière bijective, est utilisée pour chaque AddRoundKey.
À la fin de l’algorithme, un octet du chiffré (C) est calculé à partir d’un octet de la 10ème clé de tour (K10) et d’un octet du State à la fin du 9ème tour (M9) à l’aide de la formule suivante. SB est une s-box, une fonction élémentaire de SubBytes qui substitue un octet à un autre.
C = K10 xor SB(M9)
On simplifie ici en ne considérant qu’un seul octet, mais il faut évidemment appliquer ces opérations au State en entier.
Imaginons maintenant qu’un attaquant soit capable de générer une faute (toujours de valeur e = 0x01 par exemple) sur M9. Cette faute se propage donc jusqu’au chiffré (C*).
C* = K10 xor SB(M9 xor e)
L’attaquant ignore K10, c’est d’ailleurs ce qu’il cherche. Il peut utiliser une attaque différentielle pour gagner de l’information sur la clé.
C xor C* = SB(M9) xor SB(M9 xor e)
L’attaquant connaissant C, C*, e et la fonction SB, il n’y a en fait que deux M9 solutions de cette équation.
K10 = C xor SB(M9)
On a donc deux possibilités pour l’octet de clé K10, pas mal pour une seule faute. Il suffit de répéter l’opération avec un M9 (donc un texte) différent pour trouver K10 de manière unique. On peut paralléliser si tous les octets sont fautés pour retrouver la clé complète.
2.3. Modèles de faute
Le modèle de faute correspond à la modélisation de la faute au niveau d’abstraction considéré pour l’attaque. Au niveau physique, la faute est créée par des électrons en trop. Mais ces électrons supplémentaires circulent sur un bus, et inversent donc la valeur d’un bit lu (modèle bit-flip). Il s’agit d’un bit d’une instruction lors de sa lecture (prefetch), plus précisément la valeur chargée dans un registre a été modifiée d’un seul bit. Ainsi dans notre algorithme (AES), une valeur (M9) a vu un bit inversé (erreur mono-bit) donnant une faute e=0x01. Nous venons de voir comment cette faute pouvait permettre de retrouver une clé cryptographique.
Ainsi le modèle de faute est avant tout une vue à un niveau d’abstraction donné. La traversée des niveaux d’abstraction donne plusieurs interprétations à un même phénomène physique.
En pratique, obtenir un modèle de faute précis n’est pas toujours évident. La gigue (variance temporelle) empêche l’attaquant de cibler proprement un instant et le nombre de paramètres à gérer pour une injection réussie est très élevé. L’attaquant doit donc souvent se contenter d’un modèle de faute probabiliste : pour des paramètres donnés, dans x % des cas on obtient le modèle de faute 1, dans y % le modèle de faute 2, etc.
3. Fun with faults
Faisons une pause un moment pour imaginer un monde où l’attaquant a le pouvoir d’altérer une ou plusieurs instructions du programme exécuté selon sa volonté, de manière totalement indétectable pour la cible… Une goutte de sueur vient de couler le long de votre front ? Cela permet en effet de contrecarrer la plupart des techniques logicielles de protection. Le Secure Boot par exemple vérifie avant tout l’intégrité statique d’une image et ne peut souvent pas détecter l’altération dynamique d’une instruction de cette même image.
Au Laboratoire Haute Sécurité (LHS) de l’INRIA à Rennes, nous avons une plateforme d’injection de fautes électromagnétique performante à disposition. Nous essayons donc de créer des vulnérabilités dans notre application, au demeurant sûre d’un point de vue logiciel.
Figure 2
Notre cible ici est un petit microcontrôleur, un STM32F1 contenant un cœur Cortex-M3 à 24MHz sur une carte STM32VLDISCOVERY (disponible pour environ 10€). À l’aide d’un GPIO (un picot directement contrôlé par notre code), nous sortons un signal de synchronisation qui déclenche l’injection de faute. Ok, c’est de la triche, mais nous nous intéressons ici avant tout à ce que l’on peut faire avec des injections de faute. Les autres techniques de synchronisation sont principalement de déclencher sur des motifs d’entrées/sorties ou à l’aide de l’utilisation de canaux auxiliaires.
Nos équipements utilisés pour l’injection de faute sont : deux générateurs de signaux Keysight 33509B et 81160A, un amplificateur Milmega 80RF1000-175 et une antenne Langer RF B 0.3-3.
3.1. Détournement de flot de contrôle
Commençons par un cas simple :
if (correct == 1) {
status = 0xFFFFFFFF; }
else {
status = 0x55555555; }
Ce petit bout de code change une variable status selon une autre variable correct. Imaginez par exemple une vérification de code PIN. Selon ce programme, status et correct sont deux variables liées. Après ce fragment de code, il n’est normalement pas possible d’avoir :
status == 0x55555555 && correct == 1
Et pourtant, injectons une faute au cours de ce programme en fixant correct à 1, et observons la valeur de status. En fait, on va balayer temporellement une durée qui correspondra aux instants où l’on pense que le programme s’exécute. Ainsi par tâtonnement, on finit par trouver un instant d’injection dont le status lu vaut 0x55555555, et en utilisant un debuggeur on vérifie que correct vaut bien 1.
L’invariant n’est plus respecté, pourtant l’image n’a pas été modifiée statiquement. Si on vérifie le programme avant ou après l’exécution il est tout à fait correct. Les applications, nombreuses, du détournement dynamique du flot de contrôle sont laissées à l’imagination du lecteur…
Que s’est-il passé ? Sur cette puce, le modèle de faute supposé est le suivant : la valeur de l’instruction qui est en train d’être chargée (prefetch) est modifiée par le pulse électromagnétique. La nouvelle valeur est différente de quelques bits et c’est bien cette nouvelle instruction qui sera exécutée à la place de l’autre. Dans certains cas, cette instruction sera invalide et plantera la puce. Dans de nombreux cas, la nouvelle instruction n’a pas d’effet de bord et n’influe pas sur le reste du programme. Il s’agit alors d’un NOP (no-operation) virtuel. Enfin, dans certains rares cas, la nouvelle instruction ne plante pas la puce et a bien un effet sur le programme. On est alors en général surpris du résultat, par exemple avec un branchement aléatoire.
Dans notre exemple, un NOP sur l’instruction de comparaison peut expliquer le résultat observé.
3.2. Dépassement de tampon, le retour
Le dépassement de tampon (buffer overflow) est une technique d’attaque maintenant bien connue et dont on se prémunit relativement bien aujourd’hui. Dans ce nouveau cas d’usage, nous cherchons à rendre vulnérable le code suivant :
char big_text[256];
...
char text[128];
unsigned char key[16];
...
//copier au plus 128 octets de big_text dans text
strncpy(text, big_text, 128);
La variable big_text est remplie avec un motif (01 02 03…) facilement reconnaissable en mémoire.
Au-delà des faiblesses de ce code, il n’y a pas de vulnérabilité évidente. Même si la source de la copie est plus grande que la destination, la limite de 128 octets empêche le dépassement de tampon.
Sur notre microcontrôleur, l’appel à strncpy donne les instructions suivantes :
mov r2, r5 ; limite de copie (128) depuis r5
mov r0, r6 ; adresse de destination (text)
ldr r1, [pc, #24] ; adresse source (big_text)
bl 8004770 <strncpy>
Notre objectif est de supprimer la première instruction qui charge la limite de 128 octets. Ainsi, la limite est fixée par la valeur du registre r2 lors de l’appel, qui est complètement contingente ; cette valeur dépend du code exécuté précédemment. Nous nous remettons donc au hasard pour que r2 soit supérieur à 128.
Nous avons donc injecté une faute selon ce schéma. Et là… la puce plante. On lance le débogueur, on regarde la mémoire après une injection de faute réussie et on observe des zéros partout. Étrange… On regarde la valeur de r2 si la première instruction est supprimée, et on voit que r2 contient une adresse (0x2000xxxx). En regardant la documentation de strncpy, si la taille limite est plus grande que la taille de la source, le reste de la destination est remplie avec des zéros. Cela fait sens avec ce qu’on observe, mais du coup l’attaque ne fonctionne pas.
Seulement au cours de l’attaque, on balaye temporellement l’instant d’injection comme expliqué précédemment. Et un comportement étrange est détecté, autre que le plantage dû à l’effacement de la mémoire. La valeur de la clé est modifiée, mais la nouvelle valeur ne correspond pas au motif attendu (0x81 0x82 0x83 …) en cas de dépassement de tampon, mais au motif (0x71 0x72 0x73 …) qui vient quand même de big_text. En regardant la mémoire avec notre débogueur, nous nous apercevons que seuls 128 octets ont été copiés, mais l’adresse de destination a été décalée de 16 octets !
Ainsi, notre faute ne correspond pas ici à un NOP mais bien à la modification d’une valeur chargée dans un registre et donc de l’adresse de destination de la copie. Par chance, cette modification est ici une adresse décalée de 16 octets, notre clé est remplacée par une valeur prédéterminée.
Ce cas est une illustration de la puissance des attaques en faute, le dépassement de tampon est obtenu grâce à la modification de l’adresse de destination. Mais cela illustre aussi les difficultés expérimentales, on n’obtient pas toujours exactement l’effet voulu.
3.3. Porte dérobée activée par faute
Vous travaillez pour la Evil Corporation (ou la NSA...) ? Voici comment cacher une petite porte dérobée très difficilement détectable, adapté au cas particulier d’un programme ARMv7-M sur microcontrôleur.
Nous allons ici parler de la porte dérobée, c’est-à-dire le lanceur de la charge utile, pas de la charge utile elle-même que je vous laisse imaginer et cacher.
Sans plus attendre, voici notre porte dérobée qui sert à attendre un certain temps pour faire clignoter une DEL.
void blink_wait()
{
unsigned int wait_for = 3758874636;
unsigned int counter;
for(counter = 0; counter < wait_for; counter += 8000000);
}
Sans attaque par faute, votre puce ne montrera jamais de comportement compromis. Il faut une attaque pour déclencher cette porte dérobée, dans ce cas la valeur de wait_for est exécutée (la valeur étrange de cette variable est d’ailleurs le principal indice que quelque chose est louche).
Le principe est simple et se voit sur le code assembleur généré :
08000598 <blink_wait>:
push {r7, lr}
sub sp, #8
add r7, sp, #0
ldr r3, [pc, #44] ; (80005cc <blink_wait+0x34>)
...
adds r7, #8
mov sp, r7
pop {r7, pc} ; NOP après une injection de faute
.word 0xe00be00c ; @80005cc, 0xe00be00c = 3758874636
Nous utilisons une subtilité du compilateur gcc pour ARMv7-M (arm-none-eabi-gcc version 4.9.3 dans mon cas). Certaines constantes trop grandes dans une fonction (ici la valeur de wait_for) sont placées juste après le code de la fonction.
Ainsi, si on remplace l’instruction de retour de fonction (ici pop {r7, pc}) par un NOP à l’aide d’une injection de faute on va exécuter la mémoire juste après, donc la valeur de wait_for. Dans notre cas, cette valeur code deux instructions de branchements relatives renvoyant à l’adresse de notre charge utile.
Comme cette valeur est normalement une donnée, elle ne sera pas soupçonnée par de nombreux outils d’analyse statique. Sans la faute, la charge utile n’est normalement jamais exécutée. Il n’y pas de mécanisme simple avec une granularité suffisante pour empêcher d’exécuter ces données placées à la fin des fonctions.
4. Comment se protéger
Bon, nous avons vu l’efficacité des attaques par faute pour compromettre un code non nécessairement vulnérable à la base. On va donc chercher à se protéger de ces attaques. Comme souvent avec les attaques physiques, on ne cherche pas une protection absolue où l’attaque ne serait plus possible. Nous cherchons à augmenter le coût d’une attaque selon une ou plusieurs métriques prédéterminées : nombre de fautes à injecter, temps de l’attaque, coût de l’attaque…
4.1. Redondance, redondance
Expérimentalement, une attaque par faute n’est pas toujours facile. L’effet voulu est rarement obtenu dans 100 % des cas, parfois la carte plante… On peut rendre la vie de l’attaquant plus difficile encore, simplement en rajoutant de la redondance. Par exemple, répétez votre programme deux fois et vérifiez que les résultats sont identiques. Si l’attaquant à une probabilité p=0.1 de réussir une attaque, il a une probabilité p2 = 0.01 d’en réussir deux consécutivement.
La redondance peut ainsi être temporelle, mais elle peut aussi être spatiale si le même calcul est réalisé en même temps sur plusieurs cœurs. Les codes détecteurs voire correcteurs d’erreurs sont également une forme de redondance.
4.2. Détecteurs matériels d’injection
Il est possible de détecter matériellement certaines tentatives d’injection électromagnétique, les perturbations d’horloge et d’alimentation. Il faut pour cela vérifier la durée de la propagation d’un signal dans un circuit combinatoire par rapport à la durée du cycle d’horloge.
Il faut dont générer un signal gardien qui est au niveau haut uniquement quand le front d’horloge est autorisé, à un moment où le circuit combinatoire est stabilisé. Pour cela, on utilise généralement des générateurs de délais paramétrables dont la source est le front d’horloge précédant. En multipliant ces détecteurs sur la surface de la puce, il devient possible de prévenir les tentatives d’injections, même localisées.
4.3. Contrer un NOP
Une méthode formelle a été développée au cours de sa thèse par [Nicolas Moro] pour contrer le modèle de faute NOP où une seule instruction peut être remplacée par un NOP. Cela consiste à transformer le programme à protéger en un programme qui supporte la suppression d’une de ses instructions. Il divise pour cela les instructions en classes.
D’abord, les instructions idempotentes, elles peuvent être répétées sans autres effets sur le programme permettant ainsi la protection recherchée.
mov r1,r8
mov r1,r8
add r3,r1,r2
add r3,r1,r2
Les instructions séparables forment la seconde classe. L’instruction peut être remplacée par une séquence d’instructions permettant la protection du code.
add r1, r1, r3
L’instruction précédente n’est pas idempotente, mais elle peut être remplacée par la séquence suivante où rx est un registre disponible au point considéré.
mov rx, r1
mov rx, r1
add r1, rx, r3
add r1, rx, r3
La troisième classe est constituée par les instructions que l’on ne peut protéger. Cette classe est relativement réduite : elle contient par exemple l’utilisation de certains registres de configuration.
À l’aide de ces règles, nous pouvons protéger la majeure partie d’un programme contre un modèle de faute NOP, mais le surcoût est énorme ! Et cela ne protège pas si le modèle est différent d’un seul NOP.
4.4. Control Flow Integrity (CFI)
Les techniques de CFI visent à garantir le bon déroulement d’un programme, c’est-à-dire son flot de contrôle. Voici une version simplifiée tirée de [SOFIA] qui nécessite une modification matérielle du processeur exécutant les programmes protégés. Voici un programme abstrait constitué de 6 instructions adressées par leur indice : i0, i1, i2, i3, i4, i5.
Ce programme va être chiffré avec le schéma suivant pour chaque instruction :
i’ = Ek(PC_prec || PC) xor i
Ekest un algorithme de chiffrement avec une clé k, i est l’instruction à chiffrer, i’ l’instruction chiffrée, PC le Program Counter (le pointeur d’instruction) à l’exécution de i, ici l’adresse de l’instruction exécutée i, et PC_prec est la valeur précédente du Program Counter. Ce chiffrement nécessite bien sûr de déterminer les différentes valeurs de PC pour chaque instruction à l’avance.
Ainsi lors de l’exécution d’un programme, le processeur sauvegarde la valeur précédente PC_prev du Program Counter. Le programme en mémoire est i0’, i1’, i2’, i3’, i4’, i5’.
Pour exécuter i5, on déchiffre à la volée :
i5 = Ek(4 || 5) xor i5’
L’exécution est correctement déchiffrée si la succession des valeurs de PC est correcte. Si le flot de contrôle est modifié, par exemple par une attaque en faute, l’instruction ne pourra pas être déchiffrée correctement.
Ce schéma garantit la succession des valeurs de Program Counter, liées au flot de contrôle. Il y a bien sûr quelques inconvénients… Le plus important est que le schéma présenté ne permet que des flots de contrôle linéaires, pas de branchements. Le papier complet [SOFIA] propose un cas de figure où une instruction possède deux prédécesseurs hors du cadre simplifié présenté ici.
Conclusion
Nous avons vu la puissance des attaques par faute, mais aussi leur difficulté expérimentale. Il n’est pas toujours aisé d’obtenir exactement l’effet recherché. Tous les systèmes accessibles physiquement par l’attaquant sont exposés au risque, en particulier l’IoT. Ces attaques sont très peu prises en compte, à l’exception notable des cartes à puce efficacement protégées aujourd’hui. Le gros problème est que de plus en plus de fonctions critiques, comme le paiement, sont déplacées depuis des systèmes protégés (cartes à puce) vers des systèmes qui ne le sont pas suffisamment (téléphones).
Une attaque en faute ne compromettra directement qu’un seul objet, celui attaqué. Mais il est très difficile de se protéger contre un attaquant déterminé et bien financé. Notons que les technologies comme ARM TrustZone et Intel SGX ne protègent pas du tout des attaques physiques. Attention donc à ce qu’un objet compromis ne puisse en rendre d’autres vulnérables : les clés cryptographiques partagées sont à proscrire par exemple.
Remerciements
Merci à Sébanjila Kevin Bukasa, Jean-Louis Lanet, Hélène Le Bouder et Aurélien Palisse pour leurs aides et relectures.
Références
[RSA] Boneh et al., « On the importance of checking cryptographic protocols for faults », 1997
[ChipWhisperer] Site web officiel : https://newae.com/tools/chipwhisperer/
[RowHammer] Veen et al., « Drammer : Deterministic Rowhammer Attacks on Mobile Platforms », 2016
[CLKSCREW] Tang et al., « Exposing the perils of security-oblivious energy management », 2017
[Giraud] Giraud, « DFA on AES », 2004
[Nicolas Moro] Moro, « Sécurisation de programmes assembleur face aux attaques visant les processeurs embarqués », 2014
[SOFIA] De Clercq et al., « SOFIA : Software and control flow integrity architecture », 2016



 Ajouter à une liste de lecture
Ajouter à une liste de lecture