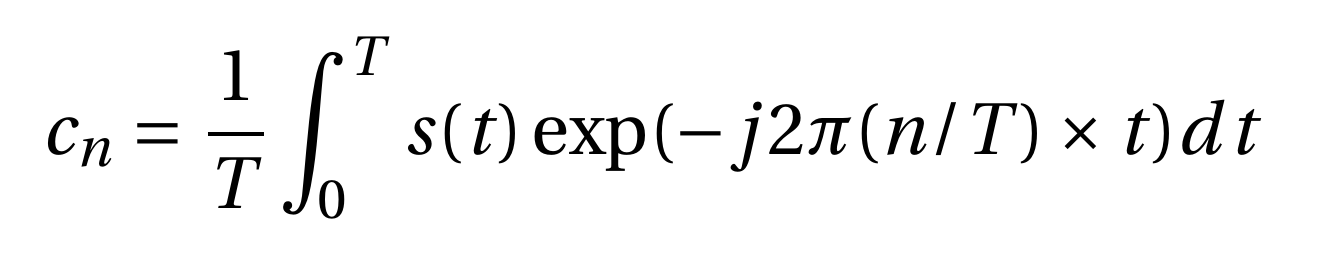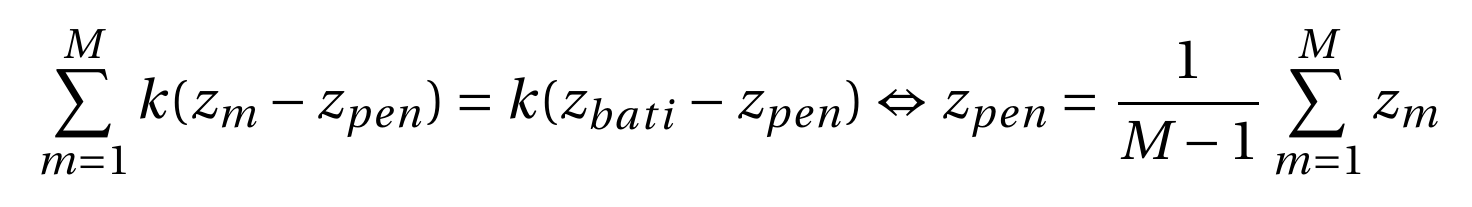L’évolution du traitement du signal est une histoire fascinante largement déroulée par David Mindell dans ses divers ouvrages [1] et citations [2]. Partant de l’ordinateur mécanique avec ses rouages, poulies, bielles et crémaillères, le passage à l’électrique au début du 20ème siècle, puis à l’électronique intégrée avec l’avènement du transistor et des circuits intégrés (VLSI) nous ont fait oublier les stades initiaux qui ont amené à notre statut actuel d’ordinateurs infiniment puissants, précis et compacts. Alors que cette histoire semble s’accompagner du passage de l’analogique au numérique – de la manipulation de grandeurs continues en grandeurs discrètes avec son gain en stabilité et reproductibilité – il n’en est en fait rien : un boulier fournit déjà les bases du calcul discrétisé mécanique, tandis que [3] introduit les concepts du calcul mécanique avec les traitements numériques avant de passer aux traitements analogiques.
De tels dispositifs ont été utilisés en pratique jusqu’à la Seconde Guerre mondiale, tel qu’en atteste [4] dans le contexte de l’étude des méthodes cryptographiques en mentionnant « The navy had asked the practical engineers at the Navy Yard under Don Seiler for help fighting code systems before the war began. By 1940 he built a fifty-wheel cam and gear device that was driven by hand cranks. It tested cipher and additives for divisibility by three. ».
Notre curiosité sur les ordinateurs mécaniques a été attisée par l’analyseur harmonique de Michelson (le même qui a monté l’interféromètre pour démontrer l’indépendance de la vitesse de la lumière avec la direction de déplacement de la Terre dans l’Espace). De façon générale, tout système linéaire peut s’exprimer dans le domaine spectral comme somme de composantes harmoniques par série de Fourier, fournissant une méthode de résolution en régime permanent bien plus efficace qu’une résolution dans le domaine temporel.
Pour rappel, l’analyse de Fourier s’appuie sur le fait que les combinaisons linéaires de fonctions périodiques conservent nécessairement les composantes spectrales du signal incident puisque A exp(jω1 t) + B exp(jω2 t) ne saurait contenir d’autres composantes spectrales que ω1 et ω2. L’invariance dans le temps des coefficients A et B garantit que la solution est stationnaire : il s’agit de la classe des systèmes linéaires invariants en temps, ou LTI (Linear Time Invariant).
Parmi les problèmes célèbres qui se résolvent selon cette approche, la position des astres dans le ciel ou la hauteur des marées ont eu un rôle social ou stratégique (date du débarquement concluant la Seconde Guerre mondiale en Europe [5]) déterminant.
Nous proposons une analyse restreinte du phénomène classique de Gibbs qui est la cause des sauts en début et fin des créneaux de signaux électriques rapides observés sur un oscilloscope lent (les termes « rapides » et « lents » prendront leur sens plus tard) au moyen de l’analyseur harmonique. S’agissant d’une mise en œuvre d’un ordinateur mécanique, il serait souhaitable d’aboutir à une réalisation concrète : nous compenserons notre incapacité à réaliser quoi que ce soit de fonctionnel en mécanique par une simulation dynamique sous FreeCAD.
1. L’analyseur harmonique
L’analyseur harmonique est un instrument mécanique conçu pour sommer des termes trigonométriques pondérés par la position d’un levier sur une tige mise en mouvement par une roue dentée. Une vidéo de son fonctionnement est disponible à [6] et l’ouvrage accompagnant la vidéo donne quelques informations techniques en s’étendant principalement sur les aspects esthétiques de la réalisation, sans entrer dans les détails du fonctionnement.
Pour résumer les grands principes que nous tirons de l’analyse de ces vidéos :
- un pignon fixé en bord de roue parcourt, lors de la rotation de la roue, les coordonnées cos(ω t),sin(ω t). Ainsi, un arbre suivant l’ordonnée du pignon présente une position sin(ω t) soit une fonction trigonométrique ;
- deux roues adjacentes de rayon R1 et R2 tournent aux vitesses angulaires ω1 et ω2 telles que R1ω1=R2ω2 (condition de non-glissement à l’interface), mais en sens opposé ;
- un ressort étiré de Δ z de sa position au repos induit une force F=kΔ z avec k la raideur du ressort (loi de Hooke) ;
- à l’équilibre, la somme vectorielle des forces agissant sur un solide s’annule, soit ∑F=0 si toutes les forces sont orientées dans la même direction.
Fort de ces rappels de mécanique du solide, la bijection entre le signal temporel s(t) supposé de période T et sa décomposition en série de Fourier (Fig. 1) affirme qu’il existe une série de coefficients cn tels que :
et ces coefficients s’identifient par :
Dans le cas particulier du créneau périodique égal à -1 de -T/2 à 0, puis égal à 1 de 0 à +T/2, cn s’identifie analytiquement en considérant que le créneau étant impair, les termes en cosinus (fonction paire) sont nécessairement tous nuls et seuls les termes en sinus (fonction impaire) subsistent. Ainsi, cn=1/T∫-T/2T/2sin(2π n/T x t)dt et comme la primitive de sin est -cos, cette intégrale est égale à :
Puisque cos(nπ)=1 si n est pair et cos(nπ)=-1 si n est impair, nous déduisons que cn=1−1=0 si n est pair et cn∝ 1/n si n est impair. Nous retrouvons le développement classique de la série de Fourier du créneau comme somme des termes impairs pondérés par l’inverse du numéro de l’ordre du coefficient.
2. Modélisation sous FreeCAD
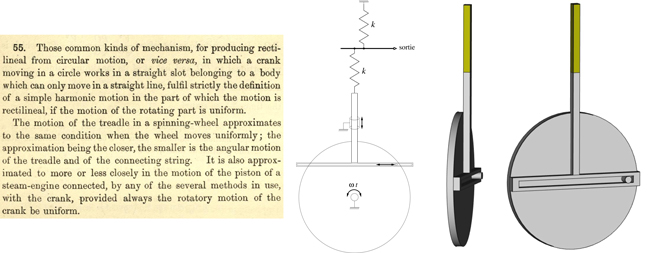
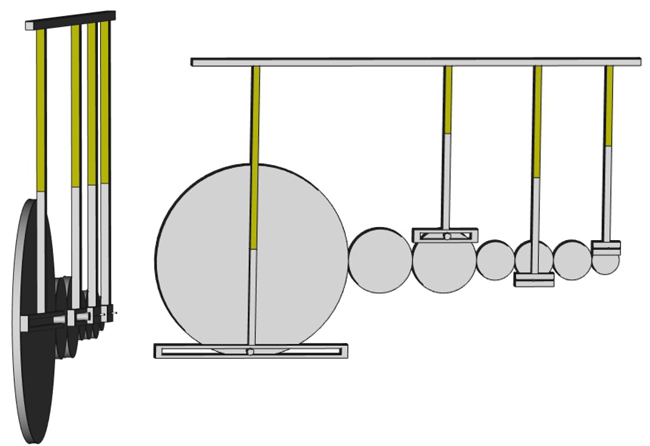
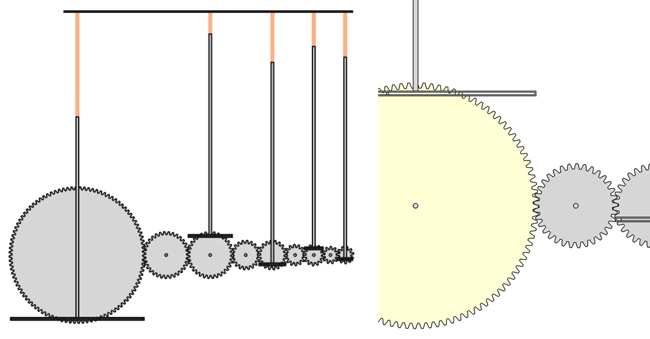
Nous commençons par dessiner la structure sous FreeCAD d’une série de roues dentées tangentes (afin de s’entraîner mutuellement), au bord de chacune desquelles nous plaçons un pignon pour entraîner une pièce en forme de T inversé, barre verticale guidée qui ne peut se déplacer que verticalement (glissière), entraînée par le pignon pouvant glisser le long de la gorge usinée dans la partie horizontale de la pièce. De ce fait, le déplacement vertical du T est le rayon de la roue multiplié par le sinus de l’angle de la roue au cours de sa révolution (Fig. 2) – ce mécanisme est nommé « manivelle-cadre » d’après Wikipédia qui en cite l’utilisation dans https://en.wikipedia.org/wiki/Tide-predicting_machine. Nous supposons que chaque roue est libre de tourner selon l’axe en son centre, que le pignon en bord de roue peut glisser dans la fente horizontale, et que la barre verticale est guidée dans un cylindre (non représenté) à l’aplomb du centre de la roue pour guider selon un mouvement de glissière et interdire tout mouvement horizontal de cette barre (Fig. 2, gauche). La partie brune en sommet de tige, de longueur qui sera variable, représente un ressort qui imposera donc une force proportionnelle à son élongation.
Par condition de contact des roues de rayon Ri les unes avec les autres, leur vitesse angulaire ωi respecte R1ω1=R2ω2=R3ω3 de façon à ce que ωi=R1/Riω1 : en choisissant judicieusement le rayon de la ième roue comme le rayon de la première roue divisé par (2i+1), nous avons bien des vitesses de rotation (donc des pulsations du mouvement vertical des pièces en forme de T inversé) qui croissent comme la séquence des harmoniques impairs (2i+1).
Tous les ressorts au sommet des pièces en T inversé sont reliés à une pièce commune guidée dans un mouvement vertical uniquement qui tient une mine en son extrémité : la position de cette mine peut tracer la séquence temporelle formée par la série de Fourier. Cette barre est par ailleurs retenue par un dernier ressort au bâti fixe de la machine pour lui éviter d’aller se coller contre le mécanisme des roues.
Les divers ressorts en parallèle agissent tous pour amener la mine d’ordonnée zm vers le mécanisme des roues selon une somme des forces qui doit balancer, à l’équilibre, la force de rappel du ressort lié au bâti d’ordonnée zb. Si chaque roue Ri place sa pièce en forme de T inversé en ordonnée zi, alors la somme des forces est ∑k (zi−zm) qui doit contrebalancer la force de rappel k(zm−zb) donc ∑(zi−zm)=zm−zb <-> (N+1)zm=zb+∑zi en considérant N harmoniques. Par ailleurs, les roues ayant été sélectionnées de rayon évoluant comme 1/(2i+1), l’élongation du ième ressort décroît comme i, vérifiant la pondération des coefficients de la décomposition en série de Fourier du créneau.
3. Scripter l’évolution dynamique du système en Python
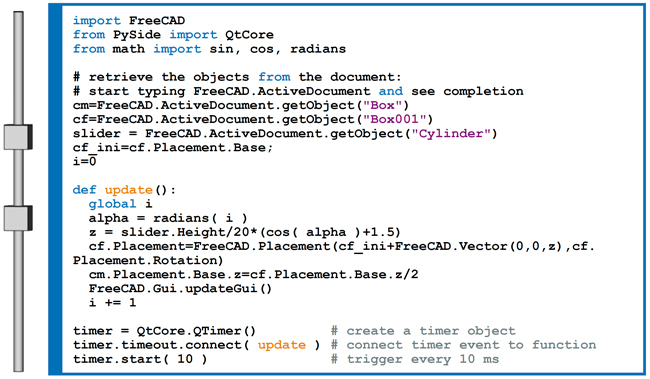
Ayant observé la vidéo de [9] et les scripts fournis en pièces jointes à la vidéo, nous nous sommes inspirés de http://linuxforanengineer.blogspot.com/2015/08/freecad-double-slider-mechanism.html pour animer le modèle d’analyseur harmonique. Le principe de base consiste à associer un timer se déclenchant périodiquement pour appeler une fonction mettant à jour les paramètres géométriques du modèle mécanique. Puisque FreeCAD permet de scripter en Python la position et la géométrie de chaque pièce, il reste à l’auteur d’implémenter les lois de composition des divers degrés de liberté pour évaluer l’évolution des pièces mobiles du système mécanique.
Plutôt que nous lancer dans le système complexe de la roue-pignon-T, considérons dans un premier temps le système simple de deux masses reliées par un ressort et guidées sur une glissière. Le premier ressort entre le bord de la glissière supposée fixe (d’ordonnée 0) et la première masse (d’ordonnée z1) est de même raideur et de même longueur que le second ressort qui relie cette première masse à la seconde masse dont la position z2 est supposée imposée par l’utilisateur. Ainsi, la force -k(z1) entre le point fixe et la première masse est égale à la force +k(z2−z1) entre la seconde masse et la première, et en régime statique où la somme des forces est nulle, il reste -kz1+k(z2-z1)=0 <-> z1=z2/2 (on aurait pu s’en douter intuitivement : il s’agit de l’équivalent mécanique du pont de résistances diviseur de tension). Le programme Python de modélisation du comportement de ce système va donc lire la position de la seconde masse mobile (cm) et en déduire la position de la première masse libre (cl) afin de la placer à la bonne ordonnée. Accessoirement, la masse mobile se voit imposer un mouvement périodique lent (pour vérifier l’hypothèse de conditions quasi statiques de somme des forces nulles).
Ces opérations s’automatisent dans la console Python de FreeCAD selon le programme ci-dessus. Nous commençons par charger les bibliothèques permettant d’accéder aux objets de FreeCAD, avant d’instancier les divers objets présents dans la scène que nous avons pris soin de charger. Notre approche pour connaître les noms des objets est, dans la console Python, de commencer à taper FreeCAD.ActiveDocument et d’observer les complétions proposées par l’éditeur. Nous constatons que les parallélépipèdes s’appellent Box, mais les cylindres restent bien Cylinder.
Notons qu’au lieu de directement inclure les commandes Python dans la console de FreeCAD, il est plus efficace d’utiliser son éditeur favori et appeler le script par :
Cette séquence charge le programme Python mon_programme.py situé dans /tmp et éventuellement le recharge (importlib.reload) lors de la phase de développement.
4. Généralisation à l’analyseur harmonique
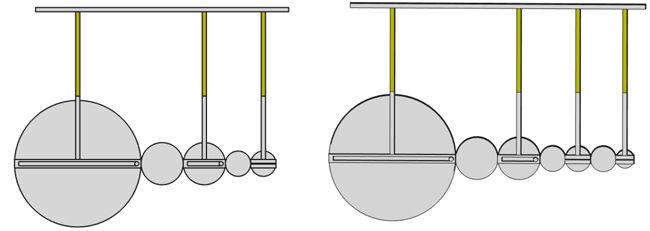
Cette rapide analyse se généralise à l’analyseur harmonique par les montages présentés en Fig. 3. Dans ce montage, 3 (gauche) ou 4 (droite) composantes spectrales sont analysées. Les ratios des roues sont de 15:5:3, c’est-à-dire que lorsque la première roue tourne à ω rad/s, la deuxième roue tourne à 3ω rad/s et la troisième roue à 5ω rad/s. Les roues intermédiaires ont pour vocation de changer le signe de la rotation sans changer la vitesse, étant de même diamètre que leur voisine. Finalement, le pignon de chaque roue est situé en bord de rayon, de façon à ce que la force exercée par chaque ressort décroisse comme le rayon, c’est-à-dire 1/(2N+1) pour la Nème roue dont le rayon a été ajusté pour que sa vitesse de rotation soit (2N+1)ω, ω étant la vitesse de rotation de la première roue qui entraîne les autres.
Un extrait du script Python pour contrôler cette séquence est :
Ce script Python fait tourner la roue (p1.Placement dont l’argument FreeCAD.Rotation prend en argument une rotation autour de l’axe de normale z) et déplace la hauteur de la barre horizontale du T pour suivre le mouvement de la roue (h1.Placement dont l’argument h1ini.Base est modifié de FreeCAD.Vector( 0,y1,0 ) avec y1 l’ordonnée du pignon sur la roue) pour finalement calculer la force appliquée à la barre horizontale reliant les divers ressorts et en déduire la position comme yvar=(y1+y2+y3+y4)/2. Cette relation est un cas particulier de la démonstration précédente qui indiquait que la barre qui porte une mine afin de tracer la courbe résultante du calcul et reliée par un ressort de même raideur k que tous les M autres ressorts au bâti statique de la machine vérifie :
en choisissant arbitrairement zbati=0. Nous trichons quelque peu, car nous avons résolu les équations et introduisons la solution en plaçant les éléments du modèle avec le bon angle ou la bonne position : il aurait été plus satisfaisant d’imposer des contraintes dans le modèle tel que décrit à https://www.freecadweb.org/wiki/Sketcher_Workbench et de ne faire évoluer que l’angle de la première roue pour voir, par conséquence des contraintes entre les pièces (entraînement, glissière...), les autres pièces se mettre en mouvement. Cette méthode nécessite de partir du plan 2D (sketch) et d’extruder les pièces contraintes entre elles au lieu, comme nous l’avons fait, d’assembler des éléments 3D.
Observer le mouvement du mécanisme décrit en Fig. 4 est hypnotisant, car malgré la trivialité de la démonstration, l’observation de la combinaison des forces introduites par les roues en mouvement se conclut par un mouvement selon une forme de créneau du stylo fixé en bout de barre fixe.
5. Résultats
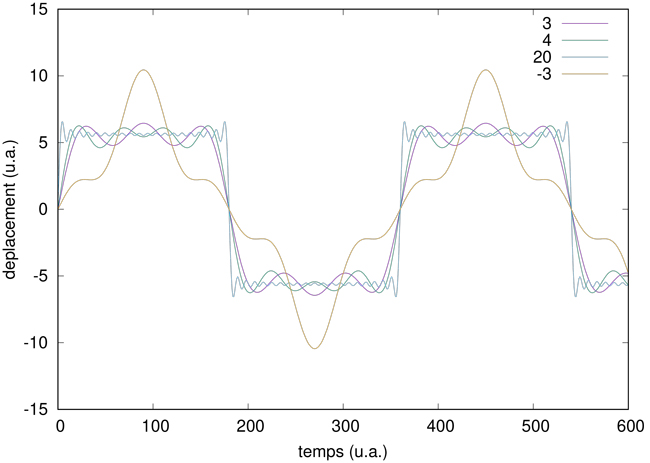
L’observation qualitative d’un mouvement s’apparentant à un mouvement en créneau est peu satisfaisante pour une analyse quantitative. Nous sauvons donc dans un fichier les positions successives de yvar. Nous constatons (Fig. 5) le parfait accord avec le modèle de somme des harmoniques impaires pondéré par l’inverse du numéro de l’harmonique. Nous avons aussi indiqué (orange) la conséquence d’oublier les roues intermédiaires : dans ce cas, l’harmonique 3 tourne dans la direction opposée des harmoniques 1 et 5 et la somme des forces résultantes ne ressemble pas à un créneau.
6. Automatisation de la synthèse du modèle
Atteindre l’objectif de l’analyseur harmonique de Michelson avec ses vingt composantes spectrales est passablement fastidieux, si chaque pièce est réalisée manuellement. Nous pouvons automatiser la création des pièces dans le script au lieu d’instancier des pièces dessinées à la main. FreeCAD a le bon goût de fournir dans la console Python les commandes correspondant à chaque opération manuelle, à la subtilité près que les positions sont sans unité alors que les longueurs sont données en mm, deux représentations incompatibles lors des opérations arithmétiques : les unités sont éliminées en considérant la propriété .Value d’une longueur.
À titre d’exemple de l’assemblage de la roue principale et de son pignon, le code ci-dessous illustre l’instanciation de deux cylindres, la définition de leurs paramètres (hauteur, rayon et position), puis de leur fusion.
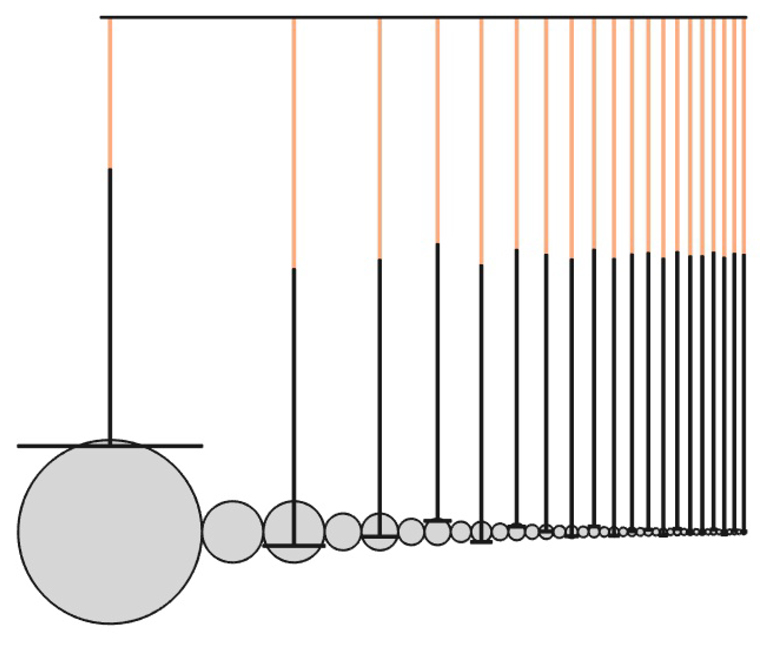
L’assemblage du dispositif complet avec ses 20 composantes spectrales est illustré en Fig. 6. Évidemment avec un tel nombre de pièces et en particulier le redimensionnement dynamique de la longueur des ressorts, le modèle devient plus lent à simuler, mais reste relativement fluide.
7. Modèle réalisable : remplacer les cylindres par des roues dentées
La découverte du greffon (workbench) FCGears pour la conception de roues dentées permet d’envisager de passer d’un modèle virtuel à un modèle réel. En effet, en remplaçant le rayon des cylindres par le nombre de dents dans la roue, nous obtenons un modèle réaliste d’entraînement, qui nécessite uniquement de transformer le rayon de valeur positive quelconque en nombre entier de dents, dont nous verrons les conséquences dans la prochaine section. Les attributs définissables de la roue dentée sont son épaisseur height et le nombre de dents teeth :
En passant l’attribut simple de la roue dentée de false à true, nous constatons qu’une roue dentée de M dents est équivalente à un cylindre de diamètre M mm. Par rapport à notre modèle précédent où les distances étaient paramétrées sur les rayons des cylindres, nous devons diviser toutes les dimensions par 2.
8. Sources d’incertitudes
Nous répétons à qui veut l’entendre la supériorité de l’électronique numérique sur les solutions analogiques, voire mécaniques. Que nous apprend ce modèle mécanique sur le sujet ?
- Remplacer les cylindres lisses par des roues dentées élimine le problème de glissement des surfaces les unes sur les autres, problème classiquement décrit dans les intégrateurs dans lesquels une roue glisse sur un disque en rotation [11]. Ce problème met d’ailleurs en évidence pratique le problème d’adaptation d’impédance couramment mis en œuvre en électronique analogique par le montage suiveur : comment garantir l’absence de couple sur le système entraîné (la roue intégratrice) pour éviter le glissement, compte tenu de la faible force de frottement avec le disque ? Ce problème est illustré dans [1] avec l’exemple de l’entraînement d’une tourelle de canon par un système de visée manipulé par un opérateur [11].
- Le pignon entraînant la pièce en T inversé chargée de convertir la rotation de la roue en mouvement de translation en sinus de l’angle ne peut se trouver sur la circonférence, induisant une pondération du mouvement qui n’est pas exactement en l’inverse de la pulsation.
- De façon générale, la pondération de la kième harmonique peut être autre que 1/k telle qu’illustré ici et en section 9 en plaçant le pignon d’entraînement de la pièce en T inversé ailleurs que sur la circonférence, avec l’incertitude d’usinage de cette position.
- La condition d’engrenage peut imposer une condition de phase entre roues adjacentes qui n’est pas exactement nulle comme le voudrait la théorie.
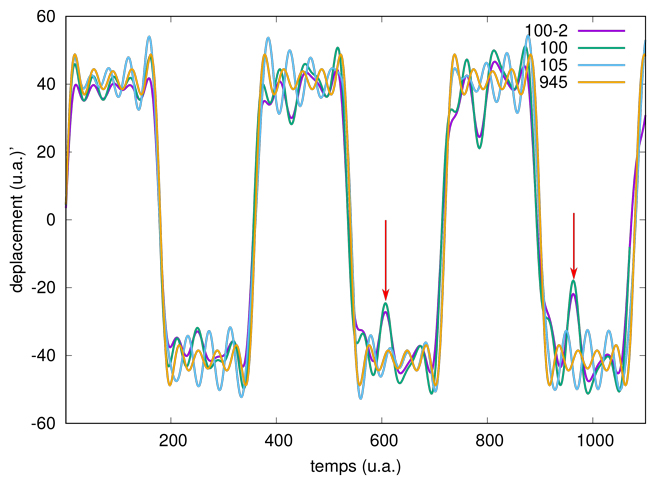
Tous ces défauts peuvent bien entendu être corrigés par une conception mécanique adéquate, mais visent à mettre en évidence les risques d’une conception analogique face à une solution numérique, a fortiori implémentée sur des entiers et ne souffrant donc pas des erreurs de calcul sur les nombres à virgule flottante. En figure 7, nous sommes passés d’un modèle avec un nombre arbitraire de dents (100) sur la roue la plus grande vers un nombre multiple des trois premières harmoniques (105=3 x 5 x 7) et des cinq premières harmoniques (945=3 x 5 x 7 x 9) pour finalement revenir au cas idéal. Comme les calculs des coefficients de Fourier sont des intégrales, ces erreurs s’accumulent pour donner un résultat dont l’erreur croît avec le temps.
9. Cas du triangle
Nous avions commencé cette étude par une erreur en plaçant les engrenages adjacents, oubliant de ce fait que les roues tournent en sens inverse et induisent donc un signe négatif dans l’argument de la fonction trigonométrie.
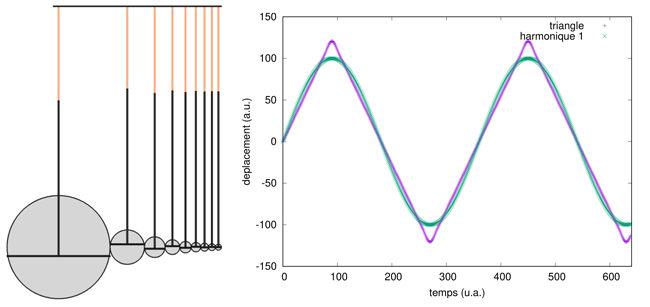
Nous retournons cette erreur à notre avantage en considérant les coefficients de la série de Fourier du triangle. La fonction triangle est une fonction linéaire croissante sur la première moitié de sa période et linéaire décroissante sur sa seconde moitié. Ainsi, les coefficients de la série de Fourier impliquent le calcul de la primitive de xsin(x) dont on se rappellera, lors de l’intégration par parties qui nous indique que ∫u’v=[uv]-∫v’u et en prenant u=x et v=−cos (donc u’=1 et v’=sin), que ces intégrales sont de la forme [sin(x)-xcos(x)] pour retrouver la solution classique que le coefficient de la nième harmonique, n impair, est (-1)(n-1)/2/n2. Le terme -1(n-1)/2 représente le changement de direction des roues adjacentes, tandis que la pondération en 1/n2 est respectée en plaçant le pignon dirigeant la pièce en T inversé non sur la circonférence de la roue, mais à 1/n de son rayon (qui lui-même décroît comme 1/n du rayon de la première roue). Une telle conception est illustrée en Fig. 8.
10. Réalisation
Les roues dentées sont réalisées en découpe laser sur plexiglas de 3 mm d’épaisseur (Fig. 9).
La contrainte sur la résolution des crans impose la dimension des roues. Partant d’un cran d’au moins 1 mm de longueur/largeur, la roue de 945 crans doit présenter une circonférence de 945 mm, soit un rayon de 150 mm. Ce diamètre de 300 mm va donc imposer l’extension du ressort tiré par la barre en T inversé fixée en périphérie. Or, un ressort ne peut être étiré excessivement sous peine de perdre sa propriété d’élasticité (relation linéaire entre force et extension au travers de la constante de raideur du ressort), mais atteindre un régime de déformation plastique irréversible. Ces contraintes déterminent les dimensions de l’instrument assemblé.
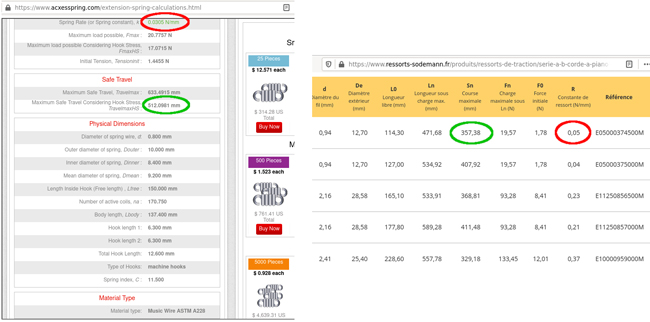
Par ailleurs, le couple raideur du ressort k et extension δ x vont déterminer la force F=k x δx appliquée sur la barre en T inversé ou les axes des roues et donc dimensionner ces éléments. Nous constatons en consultant les divers catalogues de fournisseurs de ressorts qu’il y a une relation entre le diamètre extérieur du ressort et le diamètre du fil : plus un ressort est de diamètre important, plus sa raideur est faible, mais aussi plus le diamètre du fil composant le ressort augmente, augmentant donc la raideur. Nous n’avons pu trouver de ressort de raideur inférieure à 0,05 N/mm, soit une force en pleine extension (30 cm) de 15 N ou l’équivalent exercé par une masse de 1,5 kg dans le champ de gravité terrestre (Fig. 10). Les pièces en T inversé aussi réalisées en plexiglas de 3 mm d’épaisseur sont incapables de résister à une telle force, et une conception plus robuste que la découpe laser de plastique est nécessaire pour ces pièces.
L’assemblage de l’instrument démontre les limites du prototypage rapide : le jeu excessif et la petite dimension des crans imposent une précision d’assemblage bien meilleure que le montage grossier abordé (Fig. 11). Néanmoins, avec bien des frottements et des passages grippés lorsque les vis guidant les barres en T doivent passer à côté des pignons de la roue dentée voisine, l’assemblage veut bien tourner et entraîner a bon rythme les diverses composantes de la série de Fourier. Cette expérience conduit à d’autant mieux respecter les montages incroyablement complexes des derniers ordinateurs mécaniques [4], avant le passage aux ordinateurs électromécaniques pour aboutir aux systèmes intégrés que nous connaissons actuellement.
Conclusion
L’intérêt de l’ordinateur mécanique, peu précis, encombrant et lent, peut paraître discutable à une époque de concentration quasi infinie de portes logiques dans un circuit intégré. Au-delà de son intérêt historique, l’ordinateur mécanique reste d’actualité dans les environnements hostiles dans lesquels la technologie de dopage de silicium ne saurait survivre [12], voire pour des traitements de signaux radiofréquences dont les vitesses ne sont pas (encore) accessibles aux traitements numériques en temps discret [13]. Ces principes s’abordent sans mettre en marche une fraiseuse en prototypant dans le monde virtuel de FreeCAD et ses scripts Python pour manipuler les positions et dimensions des pièces du modèle mécanique.
Le système de Michelson est passablement plus complexe par l’ajout de leviers intermédiaires qui permettent de dynamiquement pondérer la contribution de chaque roue (coefficient de la série de Fourier), sans s’imposer une contribution égale au rayon de la roue. Nous laissons le soin au lecteur de développer le modèle proposé ici pour atteindre la flexibilité de l’instrument de Michelson, voire de prédire par ce biais la prochaine marée.
Tous les scripts et vidéos des systèmes mis en œuvre dans ce document sont disponibles à https://github.com/jmfriedt/harmonic_analyzer_FreeCAD.
Références
[1] D.A. Mindell, Between Human and Machine – Feedback, Control and Computing Before Cybernetics Johns Hopkins University Press (2004) puis D.A. Mindell, Digital Apollo: Human and Machine in Spaceflight, MIT Press (2008)
[2] S. Bennett, A History of Control Engineering, 1930–1955, IET (1993)
[3] F.J. Murray, The theory of mathematical machines, revised edition, Kong’s Crown Press (1948)
[4] C.B. Burke, It Wasn’t All Magic: The Early Struggle to Automate Cryptanalysis, 1930s-1960s, Cryptologic History 6, National Security Agency (2002), p.153
[5] B. Parker, The tide predictions for D-Day, Physics Today 64 (9), 35–40 (2011) ou, plus complet, P. Kennedy, Engineers of Victory: The Problem Solvers who Turned the Tide in the Second World War, Penguin (2014)
[6] B. Hammack, An Old Mechanical Computer: The Harmonic Analyzer à https://www.youtube.com/watch?v=GyYflzRVu6M (YouTube, accédé Déc. 2019)
[7] W. Thomson Baron Kelvin, Mathematical and physical papers, vol. 6 Cambridge University Press, 277- (1911) disponible à https://ia802700.us.archive.org/1/items/mathematicalphys06kelvuoft/mathematicalphys06kelvuoft.pdf avec un exemple de coefficients de Fourier en p.295
[8] Lord Kelvin & P.G. Tait, Treatise on Natural Philosophy, vol.1, Cambridge University Press (1912), section 55, disponible à https://archive.org/details/treatisnatphil01kelvrich/page/n61
[9] J.G. Egas Ortuño, FreeCAD animation how to à https://www.youtube.com/watch?v=BHbnOlBvpLI (YouTube, accédé Déc. 2019)
[10] B. Hammack, P. Ryan & N. Ziech, Albert Michelson’s Harmonic Analyzer: A Visual Tour of a Nineteenth Century Machine That Performs Fourier Analysis, Articulate Noise Books (2014), disponible à http://www.engineerguy.com/fourier/pdfs/albert-michelsons-harmonic-analyzer.pdf
[11] A.B. Clymer, mechanical analog computers of Hannibal Ford and William Newell, IEEE Annals of the History of Computing 15 (2) pp.19–34 (1993)
[12] L’Automaton Rover for Extreme Environments (AREE) de la NASA, décrite à https://www.nasa.gov/feature/automaton-rover-for-extreme-environments-aree/, est un automate exclusivement mécanique conçu pour survivre aux températures extrêmes de Vénus où les sondes électroniques n’ont fonctionné que quelques dizaines de minutes à la surface de la planète.
[13] C. Ruppel & al., A review of optimization algorithms for the design of the SAW transducers, Proc. IEEE Ultrasonics Symposium pp.73–83 (1991) cite S. Fushimi & M. Morimoto, A design method of FIR filters suitable for SAW filters, Electronics and Communications in Japan (Part I: Communications) 71(2), pp.61–70 (1988). Plus formel, C. Campbell, Surface Acoustic Wave Devices and Their Signal Processing Applications section 8 « Using the Remez Algorithm for SAW filter design », Academic Press (1989)



 Ajouter à une liste de lecture
Ajouter à une liste de lecture