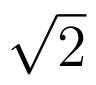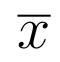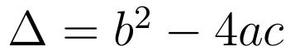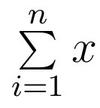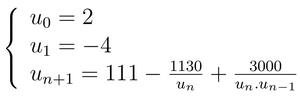Après avoir expliqué dans la première partie comment étaient stockés les réels flottants et, dans la deuxième partie, les mécanismes des opérations sur ces réels, nous savons maintenant pourquoi les calculs peuvent mener à des résultats inexacts. Nous terminerons cette trilogie par une note optimiste : il existe des solutions pour mesurer et améliorer la précision.
Nous passerons tout d'abord en revue les solutions pour améliorer la précision de calcul : augmenter le nombre de bits servant à représenter les flottantes et/ou généraliser l'arrondi correct. Puis, nous présenterons 2 arithmétiques (par intervalles et stochastique) qui peuvent être mises en œuvre afin d'estimer la précision.
Ayant lu attentivement les deux premières parties [1][2], vous connaissez les raisons pour lesquelles les résultats des calculs sur ordinateur ne sont pas (en général) exacts. Nous allons maintenant agir sur les leviers pour améliorer la précision ou l'estimer.
La première piste consiste à augmenter la précision de la représentation des flottants (le nombre de bits permettant de les stocker). La deuxième a pour ambition de combler l'un des principaux défauts de la norme IEEE-754, à savoir, la non-obligation de l'arrondi correct pour toutes les opérations. Il nous restera alors une méthode radicale : changer d'arithmétique. Ce faisant, nous aurons à notre disposition des outils très intéressants (indispensables ?) pour mesurer la précision. Car, à défaut de l'améliorer (ou avant de chercher à l'améliorer), il paraît indispensable de pouvoir l'estimer.
1. Augmenter la précision
1.1 Augmenter le nombre de bits servant à représenter les flottants
Les flottants n'étant qu'un sous-ensemble des (vrais) réels, il est tentant de vouloir densifier leur présence. Plus on aura de flottants à notre disposition, plus la représentation d'un réel par un flottant pourra être précise. La distance entre le réel et son représentant (le flottant) sera, en général, plus petite ; les erreurs d'arrondi seront alors réduites.
La norme IEEE-754 fixe le nombre de bits pour la représentation des réels simple et double précision (respectivement sur 32 et 64 bits), mais n'interdit pas de créer et d'utiliser d'autres réels (stockés sur un nombre plus grand de bits). Lorsque ce nombre peut être choisi, on parle alors de précisionarbitraire (ou multi-précision). C'est l'objectif de certaines bibliothèques (par exemple GMP - GNU Multi Precision) qui mettent ainsi à disposition de tels réels (et les opérations associées) et permettent d'améliorer globalement la précision.
Basées sur les mêmes principes de l'arithmétique flottante et la norme IEEE-754, ces bibliothèques héritent aussi de ses défauts : aucun problème de l'arithmétique flottante ne disparaît avec ces bibliothèques, elles repoussent simplement les problèmes, tentent de minimiser les défauts sans les faire disparaître.
Il est également important de noter qu'il n'est pas possible (sauf cas particuliers) d'établir une fonction liant la précision et le nombre de bits servant à représenter les flottants. On sait alors simplement que les résultats seront plus précis, mais sans savoir si cette précision sera suffisante ou si elle peut l'être avec moins de bits représentatifs.
Enfin, ce gain de précision a un prix non négligeable sur les temps de calcul qui sont directement impactés.
1.2 Généraliser l'arrondi correct
Comme nous l'avons vu dans la deuxième partie [2], la norme IEEE-754 n'impose l'arrondi correct que pour 5 opérations ( +, -, *, / et <peut_on_calculer_avec_un_ordinateur_partie_3_1.jpg>). En utilisant d'autres opérations (ce qui est assez courant), il n'est pas garanti que le résultat obtenu soit le meilleur représentant du vrai résultat. Cette caractéristique est a l'origine de pertes de précision et de non-reproductibilité des résultats d'un environnement à un autre.
Pour pallier ce défaut, des bibliothèques proposent des algorithmes garantissant l'arrondi correct pourtouteslesopérations sur les flottants simple et double précision. C'est le cas par exemple de CRlibm (Correctly Rounded mathematical library). Cette généralisation de l'arrondi correct a un coût (en terme de temps de calcul) qui est loin d'être négligeable. Par exemple, pour assurer l'arrondi correct du logarithme en double précision (c'est-à-dire garantir que le résultat de log(x) où x est un réel double précision soit l'arrondi du vrai résultat), il faut mener des calculs avec une mantisse de 118 bits. C'est à ce prix que l'on obtient la généralisation de l'arrondi correct permettant d'améliorer la précision des résultats.
Mais ce type d'approche ne règle pas tous les problèmes : les pertes de précision dues aux phénomènes d'absorption, de cancellation persistent.
1.3 Les deux mon général !
On vient de présenter deux solutions (indépendantes) pour améliorer la précision et certains se demandent si on ne peut pas agir simultanément sur ces deux leviers pour améliorer la précision . La réponse est positive ! La bibliothèque MPFR (multiple-precision floating-point computations) permet de disposer de flottants en multi-précision et de la garantie d'avoir des arrondis corrects pour toutes les opérations.
On dispose ainsi d'outils très intéressants pour améliorer la précision... au prix d'une augmentation du temps de calcul et de changements (non négligeables) dans nos programmes.
2. Recourir à d'autres arithmétiques pour estimer la précision
Avant de chercher à améliorer la précision, il faudrait sans doute savoir si elle doit l'être !
Nous avons vu que les calculs provoquaient des pertes de précision, mais est-ce toujours critique ? Une certaine imprécision n'est-elle pas acceptable dans certains cas ? En effet un résultat à 0,01 près peut être tout à fait acceptable dans certaines situations et pour certaines applications alors que pour d'autres cette précision n'est pas suffisante.
De même, vouloir augmenter la précision sans connaître ni celle d'origine, ni celle réellement obtenue peut ressembler à une fuite en avant dont le coût en terme de temps de calcul peut être considérable. Je vous propose donc dans la suite d'apporter des réponses à une nouvelle question : comment estimer, mesurer la précision ?
2.1 L'arithmétique par intervalles
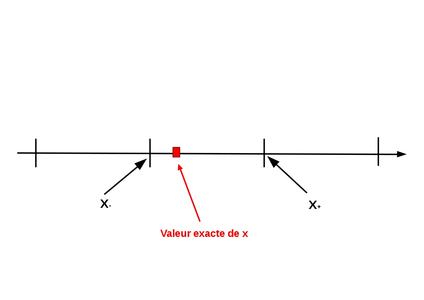
Revenons à la question fondamentale (voir figure 1) de l'arithmétique flottante : comment choisir le meilleur représentant d'un réel ? Finalement, tout ce que nous avons proposé depuis le début de cette série d'articles n'est qu'un ensemble de réponses, plus ou moins pertinentes, à cette question.
Fig. 1 : Quel est le meilleur représentant d'un réel ?
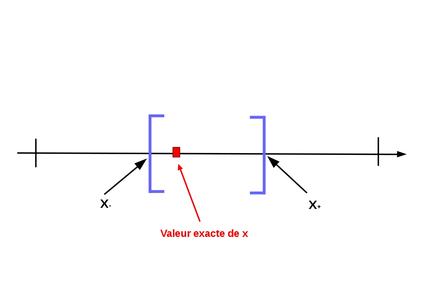
Plutôt que d'essayer de répondre à cette (délicate) question, nous allons repartir sur ce que l'on connaît avec certitude : la vraie valeur est comprise entre deux flottants. On se propose alors de choisir l'intervalle ainsi défini comme représentant de la vraie valeur (voir figure 2).
Fig. 2 : On choisit l'intervalle représentant le réel.
On passe donc d'une approche où l'on cherche une valeur « proche » de la vraie valeur (une approximation) à une approche où l'on sait (avec certitude) que la valeur recherchée est minorée et majorée par 2 flottants.
C'est d'ailleurs ce que nous faisons pour donner la valeur d'un réel (par exemple
,
) : nous pouvons soit donner une valeur approchée (avec une certaine précision, c'est-à-dire, un certain nombre de chiffres significatifs), soit donner un intervalle.
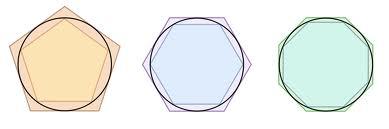
En réalité, cette idée n'est pas nouvelle, loin s'en faut. C'est ainsi qu'Archimède a procédé pour donner un encadrement de
. Pour estimer le périmètre d'un cercle, il encadre cette valeur par le périmètre d'un polygone régulier inscrit dans ce cercle, et par le périmètre d'un polygone régulier exinscrit (voir figure 3).
Fig. 3 : Estimation du périmètre d'un cercle par encadrement : le début de l'arithmétique par intervalle ?
On peut alors réaliser des opérations sur ces nombres (définis par des intervalles) : c'est l'arithmétiqueparintervalles.
La formule générale d'une opération entre deux intervalles X et Y s'écrit
: c'est l'ensemble des valeurs obtenues par l'opération entre les réels de chaque intervalle.
Par convention, on notera les intervalles avec des lettres majuscules (X, Y) et les réels avec des lettres minuscules (x,y).
On peut appliquer cette formule aux opérations de base. Ainsi pour l'addition, on obtient
(
représente le flottant inférieur à x et
le flottant supérieur),
pour la soustraction et
pour la multiplication.
Le principal atout de l'arithmétique par intervalles est qu'à chaque opération l'intervalle résultat contient le vrai résultat (inconnu). On obtient donc un encadrement de la vraie valeur. De plus, elle préserve l'associativité et la commutativité contrairement à l'arithmétique flottante (comme nous l'avons vu dans la deuxième partie).
Tout n'est pas parfait pour autant. Tout d'abord l'intervalle résultat peut être grand. On comprend bien l'intérêt d'avoir un encadrement du vrai résultat si l'intervalle est relativement petit, mais s'il est grand, l'information devient inutile. Quel est l'intérêt par exemple de pouvoir affirmer que le vrai résultat se situe dans l'intervalle
? Et malheureusement c'est une tendance naturelle de l'arithmétique par intervalles qui peut sur-estimer l'intervalle résultat lors de chaque opération et, in fine, donner un intervalle résultat très (/trop) grand. Pour limiter cette tendance, on doit conduire les calculs avec tact, quitte à les réordonner (ce qui est permis puisque l'arithmétique par intervalles l'autorise), ce qui nécessite des compétences avancées.
De plus, la mise en œuvre de l'arithmétique par intervalles oblige de changer très souvent le mode d'arrondi (pour déterminer
, on réalise une affectation avec le mode d'arrondi vers la gauche et pour
vers la droite) ce qui est très pénalisant en terme de temps d'exécution.
Je conseille à ceux qui souhaitent utiliser l'arithmétique par intervalles la bibliothèque MPFI (Multiple Precision Floating-point Interval library).
2.2 L'arithmétique stochastique
2.2.1 Impact du mode d'arrondi sur le résultat
Je reviens à la question fondamentale (voir figure 1) de l'arithmétique flottante : comment choisir le meilleur représentant d'un réel ? Et je pose la question qui arrive naturellement ensuite : quel est l'impact du choix du mode d'arrondi sur le résultat ?
Nous allons répondre à cette question au travers de deux exemples. Tout d'abord, rappelons qu'il existe quatre modes d'arrondi : RD (vers la gauche), RU (vers la droite), RZ (vers 0) et RN (au plus près) qui est le mode d'arrondi par défaut.
Exemple 1 : Résolution de l'équation du second degré
Pour cela nous allons calculer la valeur du discriminant
avec le programme equation.cpp ci-dessous :
#include <iostream>
#include <fenv.h>
using namespace std;
int main(){
fesetround(FE_TONEAREST);
float a, b, c;
cout<<"Valeur de a : "<<endl;
cin>>a;
cout<<"Valeur de b : "<<endl;
cin>>b;
cout<<"Valeur de c : "<<endl;
cin>>c;
float delta = b*b - 4*a*c;
cout<<endl<<"delta : "<<delta<<endl;
return 0;
}
La multiplication assurant l'arrondi correct, il est conseillé de multiplier x par lui-même plutôt que d'utiliser la fonction pow (qui ne garantit pas l'arrondi correct) pour élever x au carré.
Ainsi, avec le mode d'arrondi par défaut (au plus près), on obtient le résultat suivant :
Valeur de a :
0.3
Valeur de b :
2.1
Valeur de c :
3.675
delta : -9.53674e-07
La valeur du discriminant étant négative, la suite conduirait à calculer deux valeurs complexes comme racine de l'équation.
Si l'on mène ces calculs en changeant le mode d'arrondi (vers la droite) selon le programme equation_ru.cpp dans lequel seule la ligne fesetround(FE_UPWARD) est différente, on obtient 0 pour valeur du discriminant et donc une racine double (3.5) comme résultat de cette équation.
#include <iostream>
#include <fenv.h>
using namespace std;
int main(){
fesetround(FE_UPWARD);
float a, b, c;
cout<<"Valeur de a : "<<endl;
cin>>a;
cout<<"Valeur de b : "<<endl;
cin>>b;
cout<<"Valeur de c : "<<endl;
cin>>c;
float delta = b*b - 4*a*c;
cout<<endl<<"delta : "<<delta<<endl;
return 0;
}
Valeur de a :
0.3
Valeur de b :
2.1
Valeur de c :
3.675
delta : 0
Ainsi, un branchement conditionnel dépendant de la valeur d'un calcul (ici le discriminant) peut avoir des conséquences très importantes sur la suite. Une petite imprécision sur cette valeur peut mener à des résultats bien différents.
Il est intéressant de noter que le mode d'arrondi « vers la droite » permet de trouver la solution exacte de cette équation contrairement au mode d'arrondi au plus près.
Exemple 2 : Retour à la somme de n fois la valeur 0.1 :
Avec le mode d'arrondi par défaut (au plus près), on obtient (pour n =1000) : 99.99904633, soit une erreur de 0.001 alors qu'avec le mode d'arrondi « vers la droite », on obtient 100.0030442, soit une erreur de 0.003 (3 fois plus importante).
Conclusion : Ces deux exemples illustrent l'impact du mode d'arrondi sur la précision des calculs. De plus, ce n'est pas toujours avec le mode d'arrondi « au plus près » que l'on obtient les résultats les plus justes.
2.2.2 Et si l'on changeait le mode d'arrondi à chaque opération ?
À partir du constat précédent, on est en droit de se demander quel est l'impact d'un changement de mode d'arrondi à chaque opération. Nous allons reprendre le calcul de
en changeant de manière aléatoire le mode d'arrondi à chaque opération selon le programme somme_mode_arrondi_aleatoire.cpp ci-dessous :
#include <iomanip>
#include <iostream>
#include <fenv.h>
#include <stdlib.h>
using namespace std;
void changement_mode_arrondi(){
int v = rand()%4;
if (v == 0) fesetround(FE_DOWNWARD);
if (v == 1) fesetround(FE_UPWARD);
if (v == 2) fesetround(FE_TONEAREST);
if (v == 3) fesetround(FE_TOWARDZERO);
}
int main(){
//srand (time(NULL));
float x=0.1;
float res = 0.0;
for (int nbEssai=0; nbEssai<100; nbEssai++){
res = 0.0;
for (int i=0;i<1000;i++){
changement_mode_arrondi();
res+=x;
x=0.1;
}
cout<<setprecision(10)<<res<<endl;
}
return 0;
}
L'exécution de ce programme donne les résultats suivants (on ne donne ici que les 21 premiers) :
./somme_arrondi_aleatoire
99.99987793
99.99987793
99.99971008
99.99988555
99.99993133
99.99978637
99.99985504
99.99980163
99.99988555
99.99971771
99.99998474
99.99986267
99.99999237
99.99980926
99.99987792
99.99989318
99.99983978
99.99963378
99.99997711
100.0000457
99.99980164
En poursuivant, on obtient 100 valeurs comprises entre 99.9996 et 100.00002, soit une erreur toujours inférieure à 0.0004.
De plus si l'on change de graine dans la suite de nombres aléatoires (en décommentant la ligne //srand (time(NULL));), on obtient d'autres séries de valeurs dont parfois la bonne valeur (100) !
Cette expérimentation conduit à deux conclusions qui vont nous mener à l'arithmétique stochastique : les résultats sont globalement meilleurs et il arrive que l’on trouve le bon résultat.
2.2.3 Concepts de l'arithmétique stochastique
L'objectif de l'arithmétique stochastique n'est pas d'améliorer la précision des résultats (même si parfois on y arrive), mais de l'estimer.
À chaque opération, l'arithmétique flottante choisit un représentant du vrai résultat. Ce choix (conditionné par le mode d'arrondi et par les implémentations des opérations mathématiques) a un impact sur la suite des calculs. En changeant le mode d'arrondi aléatoirement, on propage ainsi différemment les erreurs d'arrondis dans les calculs. Au final, on obtient une valeur parmi un ensemble de valeurs possibles. Sans entrer dans les détails, en modélisant ainsi le processus de calcul, les résultats obtenus représentent un échantillon d'une variable aléatoire (le résultat calculé). En ajoutant quelques hypothèses (souvent vérifiées en pratique), on montre que la distribution de cette variable aléatoire est gaussienne. Ainsi, si l'on dispose de quelques résultats (des réalisations de cette variable aléatoire), on peut estimer la vraie valeur (la moyenne de cette variable) avec une certaine précision, ce que l'on peut faire avec un test de Student. On montre alors qu'en choisissant un intervalle de confiance de 95% et pour une taille d'échantillon de 3, on garantit un nombre de bits exacts avec une très grande probabilité.
Ainsi en menant les calculs trois fois (et en changeant le mode d'arrondi à chaque opération), on est capable d'estimer le nombre de chiffres exacts (les chiffres qui sont les mêmes pour ces trois résultats). Par exemple si les trois résultats sont 1.234 ; 1.25 et 1.26, on pourra alors affirmer que le vrai résultat est 1.2 avec une précision de 0.1 près.
2.2.4 Implémentation de l'arithmétique stochastique avec la bibliothèque Cadna
La bibliothèque Cadna implémente l'arithmétique stochastique décrite ci-dessus. Sans entrer dans les détails, on peut considérer qu'elle est composée de deux classes (float_st ou double_st) servant à représenter les réels stochastiques. Les données membres de ces classes sont trois réels (float ou double) décrivant trois valeurs possibles de ces réels stochastiques.
Toutes les opérations mathématiques ont été surchargées sur ces réels stochastiques. Ainsi une addition entre deux objets float_st sera traitée par la bibliothèque Cadna.
En pratique, il suffit donc de remplacer tous les réels (float et double) par des objets Cadna (float_st ou double_st) et d'ajouter quelques instructions (au minimum une ligne au début et une à la fin du programme).
Le programme somme_cadna.cpp permet de calculer
en arithmétique stochastique :
#include <stdio.h>
#include <iomanip>
#include <iostream>
using namespace std;
#include <cadna.h>
int main(){
cadna_init(-1);
float_st x;
cout<<"Entrez la valeur de x"<<endl;
cin>>x;
float_st res = 0.0;
for (int i=0;i<1000;i++){
res+=x;
}
cout<<"Somme des x (1000 fois) :"<<res<<endl;
cadna_end();
return 0;
}
L'exécution de ce programme donne les informations suivantes.
./somme_cadna
----------------------------------------------------------------
CADNA_C 1.1.9 software --- University P. et M. Curie --- LIP6
Self-validation detection: ON
Mathematical instabilities detection: ON
Branching instabilities detection: ON
Intrinsic instabilities detection: ON
Cancellation instabilities detection: ON
----------------------------------------------------------------
Entrez la valeur de x
0.1
Somme des x (1000 fois) : 0.100000E+003
----------------------------------------------------------------
CADNA_C 1.1.9 software --- University P. et M. Curie --- LIP6
No instability detected
----------------------------------------------------------------
Cadna est capable de détecter des instabilités dans le code (nous y reviendrons), mais l'information essentielle ici est l'affichage du résultat avec le nombre de chiffres exacts : 0.100000E+003 (soit 100.000). On peut donc affirmer que le résultat est 100 avec une précision de 0.001.
Prenons un autre exemple : la suite de Muller
. Nous avons vu dans la première partie [1] que cette suite convergeait vers 100 (en arithmétique flottante) alors qu'en réalité elle converge vers 6.
Le programme muller_cadna.cpp (ci-dessous) permet de calculer les valeurs cette suite en arithmétique stochastique :
#include <stdio.h>
#include <iomanip>
#include <iostream>
using namespace std;
#include <cadna.h>
int main(){
cadna_init(-1);
double_st u[30];
u[0] = 2;
u[1] = -4;
for(int i=2;i<30;i++){
u[i] = 111. - 1130./u[i-1] + 3000./(u[i-1]*u[i-2]);
cout<<"u["<<i<<"]"<<u[i]<<endl;
}
cadna_end();
return 0;
}
Il donne les résultats suivants :
./muller_cadna
----------------------------------------------------------------
CADNA_C 1.1.9 software --- University P. et M. Curie --- LIP6
Self-validation detection: ON
Mathematical instabilities detection: ON
Branching instabilities detection: ON
Intrinsic instabilities detection: ON
Cancellation instabilities detection: ON
----------------------------------------------------------------
u[2] 0.185000000000000E+002
u[3] 0.937837837837837E+001
u[4] 0.78011527377520E+001
u[5] 0.715441448097E+001
u[6] 0.68067847369E+001
u[7] 0.6592632768E+001
u[8] 0.644946593E+001
u[9] 0.63484520E+001
u[10] 0.6274437E+001
u[11] 0.62186E+001
u[12] 0.6175E+001
u[13] 0.613E+001
u[14] 0.60E+001
u[15] @.0
u[16] @.0
u[17] @.0
u[18] @.0
u[19] 0.99E+002
u[20] 0.999E+002
u[21] 0.9999E+002
u[22] 0.99999E+002
u[23] 0.999999E+002
u[24] 0.99999999E+002
u[25] 0.999999999E+002
u[26] 0.9999999999E+002
u[27] 0.99999999999E+002
u[28] 0.9999999999999E+002
u[29] 0.99999999999999E+002
----------------------------------------------------------------
CADNA_C 1.1.9 software --- University P. et M. Curie --- LIP6
CRITICAL WARNING: the self-validation detects major problem(s).
The results are NOT guaranteed.
There are 12 numerical instabilities
9 UNSTABLE DIVISION(S)
3 UNSTABLE MULTIPLICATION(S)
----------------------------------------------------------------
On peut ainsi constater que :
- Cadna détecte neuf divisions instables et trois multiplications instables lors du calcul des trente premières valeurs de la suite. Cette indication devrait déjà inciter à la plus grande vigilance quant à la précision des résultats.
- La précision des premières valeurs diminue à chaque itération : la treizième valeur (6.13) n'a déjà plus que deux chiffres significatifs après la virgule et à partir de la quinzième, il n'y a plus aucun signe significatif ! Le symbole @0 (appelé zéro informatique) signifie qu'il n'y a plus de chiffre significatif, le résultat obtenu est non différentiable de la valeur 0. Les valeurs qui suivent sont donc sans intérêt puisqu'elles sont calculées à partir de valeurs de précision nulle.
Il est important de noter que le changement quasi-systématique du mode d'arrondi pénalise fortement les performances : les calculs ne sont pas trois fois plus lents (comme on pourrait s'y attendre), mais plutôt de cinq à dix fois (mais ce facteur dépend fortement des calculs effectués). De plus, la mise en œuvre est relativement intrusive, car il faut changer tous les types réels dans le programme. Enfin, si l'on a recours à d'autres bibliothèques numériques, les calculs qui y sont effectués ne sont pas menés en arithmétique stochastique (sauf à modifier et recompiler ces bibliothèques).
Malgré ces quelques limites et défauts, l'arithmétique stochastique permet de recueillir une information essentielle : une estimation de la précision d'un résultat numérique. Cette information doit ensuite être utilisée à bon escient ; elle permet par exemple de savoir (en fonction du contexte) si cette précision est suffisante.
Un résultat numérique (obtenu avec un ordinateur) peut être considéré comme une mesure en physique : il n'a de sens que si on est capable de donner l'erreur de mesure.
Conclusion
Nous arrivons au terme de cette trilogie qui avait pour objectif de donner un coup de projecteur sur ces questions essentielles et trop souvent méconnues ou ignorées. Les calculs que nous effectuons sont (plus ou moins) faux ; mieux vaut le savoir et connaître les raisons afin d'agir pour estimer la précision et, si besoin, l'améliorer. Si vous portez désormais un regard critique sur les résultats de vos calculs (sans tomber dans la paranoïa), j'aurai atteint mon objectif...
Références
[1] LANGROGNET F., « Peut-on vraiment calculer avec un ordinateur ? », GNU/Linux Magazine n°193, mai 2016, p. 16 à 20.
[2] LANGROGNET F., « Peut-on vraiment calculer avec un ordinateur : les opérations », GNU/Linux Magazine n°193, mai 2016, p. 22 à 31.
Pour aller plus loin
Les sources d'inspiration de cet article sont multiples et complémentaires :
- La page personnelle de l'auteur (https://lmb.univ-fcomte.fr/Florent-Langrognet) contient quelques exposés et cours sur ce sujet.
- L'article de F. Langrognet (et contributeurs), « JDEV 2013 - Développer pour calculer : des outils pour calculer avec précision & Comment calculer avec des intervalles » (HPC Magazine, novembre 2013, pp,-51-65) revient sur le traitement de cette thématique lors des JDEV (Journées du DEVeloppement logiciel) 2013, organisées par le réseau métier de l'enseignement supérieur et de la recherche DevLOG (Développement LOGiciel).
- L'école thématique CNRS « Précision et reproductibilité en calcul numérique » (http://calcul.math.cnrs.fr/spip.php?rubrique98) organisée par le réseau métier de l'enseignement supérieur et de la recherche Calcul en 2013.
- Le livre « Handbook of Floating-Point Arithmetic » de J.M. Muller, N. Brisebarre, F. de Dinechin, C.-P. Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D. Stehlé, et S. Torres (Birkhauser, 2010) est un livre de référence pour comprendre en profondeur l'arithmétique flottante.
- Les pages personnelles de Fabienne Jézéquel, Jean-Michel Muller, Nathalie Revol (acteurs de ce domaine de recherche) sont des points d'entrée très intéressants.
- Références aux bibliothèques de calcul :
- gmplib : https://gmplib.org/
- crlibm : http ://lipforge.ens-lyon.fr/www/crlibm/
- mpfr : http://www.mpfr.org/
- mpfi : http://mpfi.gforge.inria.fr/
- Cadna : http://www-pequan.lip6.fr/cadna/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture