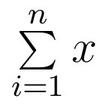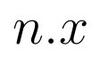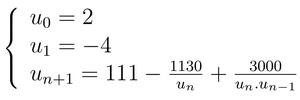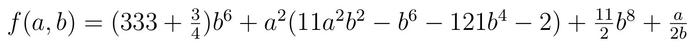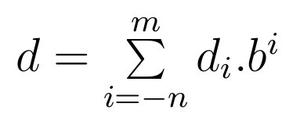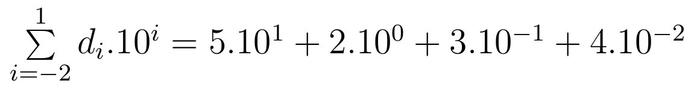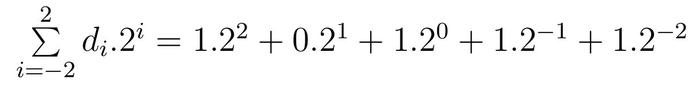Alors que le recours à l'ordinateur pour calculer toujours plus vite, modéliser toujours plus finement est inscrit dans une logique de progrès, il paraît indispensable de comprendre comment sont effectués ces calculs pour garder un regard critique sur la qualité des résultats qui ne sont qu'une approximation (plus ou moins bonne) des vraies valeurs. Comment sont stockés les réels, comment sont effectués les calculs, d'où viennent les erreurs de précision, peut-on les contenir ? Vous l'apprendrez en lisant cet article et sa suite.
Dans cette première partie, nous commencerons par donner quelques exemples afin de montrer que les erreurs de calcul arrivent très vite et peuvent, dans certains cas, donner des résultats totalement faux. Nous expliquerons ensuite comment sont stockés les réels dans les ordinateurs et montrerons ainsi que ces nombres réels (les flottants) ne représentent qu'un sous-ensemble des vrais réels.
Nous sommes tous (plus ou moins) conscients que les calculs réalisés sur ordinateur conduisent à des pertes de précision. Mais en connaissons-nous les raisons ? Avons-nous les moyens de les contenir ?
Avant de répondre à ces questions, je donnerai quelques exemples concrets pour illustrer le fait que nos ordinateurs commettent des erreurs, souvent minimes (mais avec des conséquences potentiellement graves), parfois très importantes. Puis, j'expliquerai comment sont stockés les réels sur ordinateur afin de détailler, dans un second article, les mécanismes mis en œuvre pour calculer et comprendre d'où viennent ces imprécisions.
1. Des erreurs dans les calculs
1.1 Somme de réels
Nous allons tout d'abord effectuer la somme de n fois la valeur (réelle) x sur un ordinateur selon la formule
Cet exemple est purement didactique car personne n'aurait l'idée de faire ce calcul ainsi alors que le résultat s'obtient directement (en une opération) avec
On trouve cependant de tels codes (ou très proches) ici ou là…
Pour cela, nous allons utiliser le programme somme.cpp écrit en C++ :
#include <iomanip>
#include <iostream>
int main(){
float x;
std::cout<<"Entrez la valeur de x"<<std::endl;
std::cin>>x;
float res = 0.0;
for (int i=0 ; i<1000 ; i++){
res += x;
}
std::cout<<"Somme de 1000 fois "<<x<<" = "<<std::setprecision(10)<<res<<std::endl;
return 0;
}
On utilise ici std::setprecision(10) pour afficher 10 chiffres (significatifs).
Lorsque l'on exécute ce programme, on obtient les résultats suivants
|
Valeur de x |
Résultat obtenu |
|
0,5 |
500 |
|
0,25 |
250 |
|
0,1 |
99,99904633 |
|
0,7 |
700,006958 |
On observe donc que pour certaines valeurs (0,5 ou 0,25), le résultat obtenu est exact alors que pour d'autres (0,1 ou 0,7), il est proche de la vraie valeur, parfois par excès, parfois par défaut.
La précision peut évidemment être augmentée en utilisant des réels « double précision ». Ainsi, en remplaçant les float par des double (voir somme_double.cpp ci-dessous), on obtient les résultats reportés dans le tableau suivant (avec 20 chiffres significatifs) :
#include <iomanip>
#include <iostream>
int main(){
double x;
std::cout<<"Entrez la valeur de x"<<std::endl;
std::cin>>x;
double res = 0.0;
for (int i=0;i<1000;i++){
res += x;
}
std::cout<<"Somme de 1000 fois "<<x<<" = "<<std::setprecision(20)<<res<<std::endl;
return 0;
}
|
Valeur de x |
Résultat obtenu |
|
0,5 |
500 |
|
0,25 |
250 |
|
0,1 |
99,999999999998593125 |
|
0,7 |
700,00000000000636646 |
Les résultats sont effectivement plus proches des vraies valeurs mais le constat est le même, on a simplement repoussé le problème : les vraies valeurs ne sont pas atteintes pour 0,1 ou 0,7.
Sommes-nous alors dans l'obligation de n'utiliser que certaines valeurs dans nos programmes pour que les résultats soient justes ?
1.2 Petites erreurs, grandes conséquences
On pourrait penser que ces petites imprécisions sont sans conséquence. C'est bien souvent le cas, fort heureusement ! Mais, ce type d'erreurs peut conduire à des drames, comme lors de la guerre du Golfe en 1991 en Irak. La coalition américaine disposait d'antimissiles Patriot capables d'intercepter en vol des missiles ennemis. Ce dispositif a parfaitement fonctionné jusqu'au jour où il a manqué sa cible causant la mort de 28 personnes. L'horloge interne de l'antimissile incrémentait le temps par intervalle de 0,1 seconde (avec une erreur de 0,0000000953 en étant codé sur 24 bits). Au bout de 100 heures, l'erreur cumulée était de 0,34s, suffisamment élevée pour que l'antimissile manque sa cible (le missile parcourt environ 500m en 0,34s).
Ce drame aurait donc pu être facilement évité en choisissant une autre valeur d'incrémentation ; ainsi avec un intervalle de temps de 0,25 par exemple, le calcul aurait été parfaitement juste, l'antimissile n'aurait pas manqué sa cible et la vie de 28 personnes aurait été épargnée.
1.3 Des erreurs parfois beaucoup plus importantes
1.3.1 La suite de Muller
La suite de Muller est définie par :
Le programme muller.cpp (ci-dessous) permet de calculer (en double précision) et d'afficher les 30 premières valeurs de cette suite :
#include <iomanip>
#include <iostream>
int main(){
double u[30];
u[0] = 2;
u[1] = -4;
for(int i=2 ; i<30 ; i++){
u[i] = 111. - 1130./u[i-1] + 3000./(u[i-1]*u[i-2]);
std::cout<<"u"<<i<<" = "<<u[i]<<std::endl;
}
return 0;
}
L'exécution de ce programme donne les résultats suivants :
$./muller
u2 = 18.5
u3 = 9.37838
u4 = 7.80115
u5 = 7.15441
u6 = 6.80678
u7 = 6.59263
u8 = 6.44947
u9 = 6.34845
u10 = 6.27444
u11 = 6.2187
u12 = 6.17585
u13 = 6.14263
u14 = 6.12025
u15 = 6.16609
u16 = 7.23502
u17 = 22.0621
u18 = 78.5756
u19 = 98.3495
u20 = 99.8986
u21 = 99.9939
u22 = 99.9996
u23 = 100
u24 = 100
u25 = 100
u26 = 100
u27 = 100
u28 = 100
u29 = 100
On s'aperçoit que cette suite semble converger vers la valeur 100 (comme sur tout système en précision finie) alors qu'en réalité elle converge (mathématiquement) vers la valeur 6.
Comment une telle erreur est-elle possible ?
1.3.2 La fonction de Rump
La fonction de Rump est définie par :
En prenant pour valeur a = 77617 et b = 33096, on obtient ≈-2,34.1029 (en simple précision) et ≈-1,1.1021 (en double précision). En codant cette fonction sous une autre forme (mathématiquement équivalente), on peut aussi obtenir les valeurs ≈+7,09.1029 ou encore ≈ +1, 17.
Mais quelle est la vraie valeur ? La réponse est consternante...voire inquiétante : aucune des valeurs précédentes. La vraie valeur est : −0,82739605994682136814116509547981629.
Ainsi, non seulement aucun système ne permet d'obtenir la vraie valeur mais en plus, les résultats sont en totale contradiction que ce soit sur l'ordre de grandeur ou le signe.
2. Représentation des réels en machine
Nous allons maintenant expliquer comment sont stockées les valeurs réelles dans les ordinateurs afin de commencer à comprendre d'où viennent ces erreurs de calcul.
2.1 Rappel sur les bases
Nous sommes évidemment familiers avec la base 10 mais ce que nous faisons quotidiennement avec cette base peut s'étendre à n'importe quelle autre. Ainsi, en base b tout nombre décimal d peut s'écrire avec m+n+1 chiffres (digits) de la façon suivante :
Les chiffres d'indice positif (ou nul) représentent les chiffres à gauche de la virgule et ceux d'indice négatif les chiffres à droite de la virgule. La valeur de d se calcule alors selon la formule :
Par convention, et quand cela est nécessaire, nous noterons la base en indice des nombres ainsi représentés. Par exemple 52,3410 est une représentation en base 10 alors que 101,112 utilise la base 2.
Si l'on revient en base 10, le nombre 52,3410 est bien égal à
soit
Il peut aussi se représenter sous une forme fractionnaire :
Nous allons nous intéresser plus particulièrement à la base 2, utilisée par les ordinateurs.
De la même façon, la valeur (en base 10) du nombre dont l'écriture en base 2 est 101,112 se calcule ainsi
soit
Sous sa forme fractionnaire il s'écrit
Conséquences :
Ayant formalisé les écritures des nombres en base b, on en déduit qu'on ne peut représenter exactement que les nombres fractionnaires de la forme
où X et k sont des entiers.
Ainsi, en base 10, on ne peut représenter que les nombres de la forme
et en base 2 que les nombres de la forme
Certains nombres peuvent être représentés dans une base mais pas dans une autre.
La représentation de
en base 10 n'est pas exacte, elle s'écrit : 0,[3]10 . De même pour celle de
qui, en base 2, s'écrit 0,000[1100]2.
Quel est le sens de l'écriture avec des [ ] ? La suite de chiffres entre crochets est répétée indéfiniment.
Ainsi 0,000[1100]2 désigne la suite (infinie) : 0,00011001100110011001100...
On commence à comprendre pourquoi la somme de 1000 fois 0,1 ne donne pas exactement 100 sur ordinateur. Mais ce n'est pas la seule raison ! Nous l'expliquerons plus en détail dans les prochaines pages.
2.2 Représentation des réels en virgule flottante
La représentation d'un réel en virgule flottante signifie que (contrairement à une représentation en virgule fixe), on peut placer la virgule où l'on souhaite, à un facteur bk près. Ainsi, 37,510 peut s’écrire : 37500.10 −3 ; 0,0375.103; 0,375.102; ...
Par convention, la représentation normalisée (unique) en virgule flottante d'un réel est définie par les caractéristiques suivantes :
- la partie entière (à gauche de la virgule) est systématiquement nulle ;
- tous les chiffres significatifs sont à droite de la virgule ;
- l’exposant est un entier (positif ou négatif).
Un nombre réel, en représentation normalisée, peut alors être stocké uniquement par sa mantisse (inférieure à 1) et son exposant.
37,510 , sous sa forme normalisée (0,375.102) , peut être stocké par sa mantisse (0,375) et son exposant (2).
Cette définition de la représentation normalisée est indépendante de la base. Ainsi, de la même manière, la représentation normalisée de 11011 (en base 2) est (0,11011).2101. Explication : on a décalé la virgule de cinq chiffres vers la gauche et on a donc besoin de multiplier par 25 qui s'écrit bien évidemment 2101 en base 2 !
Il est intéressant de noter (et on y reviendra dans quelques instants) que tous les chiffres significatifs étant à droite de la virgule, le premier chiffre après la virgule ne peut donc pas être un 0. En base 2, ce sera donc forcément un 1.
2.3 Représentation des réels sur ordinateur
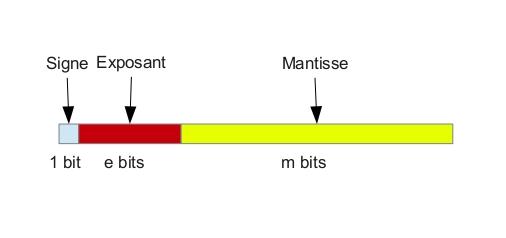
Un nombre réel est représenté sur ordinateur par un triplet (voir figure 1) :
- le signe (stocké sur 1 bit) : par convention, il sera négatif si ce bit vaut 1, positif sinon ;
- l’exposant (stocké sur p bits) . Pour des raisons pratiques, on ne stocke pas la vraie valeur de l'exposant mais l'exposant décalé c'est-à-dire un nombre entier compris entre 0 et 2e− 1 plutôt qu'un nombre compris entre −2e−1+1 et 2e−1. Le décalage (ou biais) est égal à 2e−1− 1.Pour une valeur de e=8, l'exposant décalé sera donc compris entre 0 et 255 plutôt qu'entre -127 et 128 et le décalage sera de 127.
- la mantisse (stockée sur m bits) représente un nombre réel compris entre 0 et 1. Comme nous l'avons vu plus haut, le premier bit de la mantisse étant toujours 1 (ceci est valable uniquement pour la base 2), nous pouvons omettre de le stocker pour gagner un bit supplémentaire de précision ; il sera appelé bit implicite. La conséquence est que la mantisse réelle sera égale à 1 + mantisse stockée. La valeur de l'exposant sera également adaptée (on retranche 1) pour représenter le même nombre.
Fig. 1 : Représentation d'un nombre réel sous sa forme signe – exposant - mantisse.
La norme IEEE-754 (sur laquelle nous reviendrons plus en détail) fixe la valeur de e et m pour les réels simple et double précision selon le tableau ci-dessous :
|
Type |
Signe (nombre de bits) |
Exposant (nombre de bits) |
Mantisse (nombre de bits) |
|
Simple précision |
1 |
8 |
23 |
|
Double précision |
1 |
11 |
52 |
De manière générale, la valeur d'un entier stocké sur 1+e+m bits en base 2 se calcule selon la formule
avec :
- s=-1 ou 1 ;
- e* : l'exposant réel (exposant décalé – décalage) ;
- m* : la mantisse réelle (1 + mantisse stockée).
La valeur de ce réel s'obtient donc (avec les valeurs stockées) selon la formule
La formule permettant de calculer la valeur d'un nombre à partir de sa représentation n'est pas valable pour tous les nombres réels. Il existe des exceptions pour représenter des réels de très petites valeurs absolues (y compris le 0) , de
de
et des NaN (Not a Number). Nous ne détaillerons pas ici la représentation de ces nombres stockés sous une forme dite dé-normalisée.
Je crois qu'il est temps de donner quelques exemples concrets pour s'assurer que tout le monde suit…
Exemple 1 : En simple précision, la valeur 0,5 est représentée par la suite des 32 bits suivants :
0 01111110 0000000000000000000000.
En effet :
- le bit de signe est 0 : le nombre est positif ;
- l'exposant réel est égal à la valeur de l'exposant stocké (01111110) – le décalage soit 26 + 25 + 24 + 23 + 22 + 21 − 127 = 126 − 127 = −1 ;
- la mantisse réelle est égale à 1 + la mantisse stockée (une suite de 0) soit 1 + 0 = 1.
Ainsi, on obtient 1.2−1 = 0,5.
Exemple 2 : Représentations de 0,1.
Comme nous l'avons vu, ce nombre ne peut pas être représenté en base 2, il existe donc une représentation de sa valeur par excès et une par défaut.
En simple précision, la suite 0 01111011 10011001100110011001101 donne la valeur de 0,1 par excès. En effet :
- le bit de signe est 0 : le nombre est positif ;
- l'exposant réel est égal à la valeur de l'exposant stocké (01111011) – le décalage soit 26 + 25 + 24 + 23 + 21 + 2 − 127 = 123 − 127 = −4 ;
- la mantisse réelle est égale à 1 + la mantisse stockée (10011001100110011001101) soit 1 + 2−1 + 2−4 + 2−5 + ... = 1,600000023841858.
Ainsi, on obtient 1,600000023841858.2−4 = 0,100000001490116.
La valeur de 0,1 par défaut est représentée par 0 01111011 10011001100110011001100. Il s'agit de la valeur juste inférieure à la valeur précédente. Pour l'obtenir, on a juste remplacé le dernier bit de la mantisse, celui de droite, appelé bit de poids faible (qui valait 1) par 0. Le calcul mène à 1,5999999046325684.2−4 soit 0,09999999403953552.
Conclusion
Vous savez désormais que les réels flottants (ceux de nos ordinateurs) ne représentent qu'un sous-ensemble des vrais réels. On comprend alors que les vraies valeurs ne peuvent pas, dans la grande majorité des cas, être obtenues par les ordinateurs qui ne travaillent que sur ce sous-ensemble.
Ayant défini la représentation des réels flottants, nous sommes maintenant prêts à comprendre les mécanismes mis en œuvre lors des calculs. C'est ce que nous ferons dans la deuxième partie de cet article (le mois prochain) en détaillant deux opérations (l'addition et la soustraction) et en expliquant ce qu'il se passe pour les autres opérations. Vous n'êtes pas au bout de vos surprises...
Pour aller plus loin
Les sources d'inspiration de cet article sont multiples et complémentaires :
- La page personnelle de l'auteur (https://lmb.univ-fcomte.fr/Florent-Langrognet) contient quelques exposés et cours sur ce sujet.
- L'article de F. Langrognet (et contributeurs), « JDEV 2013 - Développer pour calculer : des outils pour calculer avec précision & Comment calculer avec des intervalles » (HPC Magazine, Novembre 2013, p. 51 à 65) revient sur le traitement de cette thématique lors des JDEV (Journées du DEVeloppement logiciel) 2013, organisées par le réseau métier de l'enseignement supérieur et de la recherche DevLOG (Développement LOGiciel).
- L'école thématique CNRS « Précision et reproductibilité en calcul numérique » (http://calcul.math.cnrs.fr/spip.php?rubrique98) organisée par le réseau métier de l'enseignement supérieur et de la recherche Calcul en 2013.
- Le livre « Handbook of Floating-Point Arithmetic » de J.M. Muller, N. Brisebarre, F. de Dinechin, C.-P. Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D. Stehlé, et S. Torres (Birkhauser, 2010) est un livre de référence pour comprendre en profondeur l'arithmétique flottante.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture