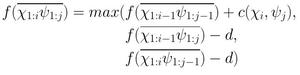Programmation dynamique et alignement de séquences

Depuis les années 70, les besoins en traitement automatique de génome n'ont cessé d'augmenter. Celui-ci étant constitué d'une suite de nucléotides, il a fallu trouver des moyens rapides pour pouvoir reconstituer le génome, et par la suite, comparer deux séquences. L'alignement de séquences est une tâche nécessaire à cet accomplissement.

Avant toute étude, nous définirons plus formellement ce que l'on va étudier : les séquences (partie I) et l'alignement (partie II). Une fois les concepts introduits, nous développerons la programmation dynamique en calculant une distance entre des séquences : la distance de Levenshtein (partie III). Viendront ensuite les méthodes d'alignement global et local. Tout au long de l'article, nous alignerons des séquences d'ADN, mais à la fin, nous aurons un exemple appliqué à la linguistique comparative. Tout notre code sera en Python 3.5.

1. Séquence

Posons les bases pour mieux se comprendre. Une séquence est une suite ordonnée d'éléments. Ce qui nous intéressera, ce sont des éléments provenant d'un ensemble fini. Par la suite, nous chercherons à aligner deux séquences χ (khi, à prononcer « qui ») et ψ (psi), de taille respectivement n et m. Le ième caractère de χ est noté χi . On notera aussi la sous-séquence de χ  entre le ième caractère et le jème caractère (inclus) comme χi:j. On aura ainsi χ = χ1:n et ψ = ψ1:m. Nos exemples proviendront de séquences de nucléotides. Le type utilisé sera str.

2. Alignement

On reprend nos séquences χ et ψ.

Pour apprécier de manière plus claire l'alignement, on va se doter d'une fonction dont les valeurs seront d'autant plus grandes que les alignements correspondront à nos attentes.

Lorsque deux caractères χi et ψj sont alignés, alors on parle de correspondance C (matching en anglais), si le caractère de la χi et un vide sont alignés, alors on parle d'insertion I (insertion) et, inversement, si un vide et  ψj sont alignés, on parle de suppression S (deletion). Ces mots sont choisis à partir du point de vue de la première séquence (donc c'est totalement arbitraire). Un vide est noté par un tiret -.

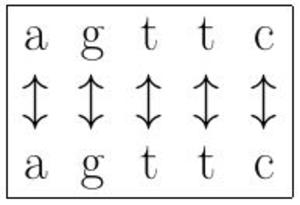
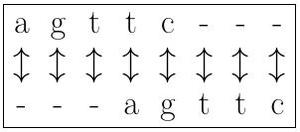
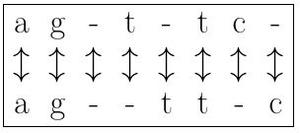
Par exemple, on peut choisir le nombre d'alignements parfaits de caractères comme présenté en figure 1. Cette méthode permet simplement de connaître la similitude entre deux séquences. Cela paraît encore bien insuffisant. Une solution plus proche de ce que l'on souhaite est de calculer le score comme le nombre d'alignements corrects pondérés moins le nombre d'alignements incorrects dus à une insertion ou une suppression (voir figure 2). La figure 3 présente un alignement plus correct, car contenant plus de correspondances.

3. Programmation dynamique et distance de Levenshtein

Formalisée par Richard Bellman, la programmation dynamique a permis l'essor de résolutions optimales pour des problèmes d'ordonnancement ou d'allocations (le terme de programmation est à comprendre au sens de programmation d'évènements et non au sens de codage). L'exemple typique donné dans le papier séminal [1] est celui de l'investissement. On commence avec une somme initiale : comment optimiser les investissements totaux au bout n étapes avec l'investissement d'une partie de la somme et l'épargne du restant ? Nous allons faire de même avec notre score d'alignement.

3.1 Mise en pratique de la programmation dynamique

La programmation dynamique [1] est  une méthode de résolution applicable à des problèmes qui ont une certaine forme. Cette forme est la suivante : la solution optimale d'un problème se déduit de la solution optimale de sous-problèmes du problème en question. Nous allons utiliser cette méthode de résolution pour l'alignement de séquences, mais commençons par un problème plus simple : calculer la distance de Levenshtein. Cette distance consiste à donner le nombre d'opérations (remplacement, insertion, suppression) minimal pour passer d'une séquence à une autre séquence. Mettons en pratique cette méthode : donnons les cas initiaux ainsi que les transitions.

Le cas initial est quand on n'a encore passé en revue aucune séquence, alors la distance est de zéro (ligne 4). Dans le cas un peu plus complexe où l'on souhaite passer d'une séquence de taille i à une séquence vide, il faut i opérations, d'où la distance i (lignes 5 et 6).

Passons aux transitions. On définit le score après avoir calculé la distance de Levenshtein entre la sous-séquence  χ1:i  et la sous-séquence ψ1:j comme étant s[i, j]. On choisit l'opération la moins coûteuse parmi la correspondance-modification, l'insertion et la suppression. Le coût par opération est de 1.

D'où :

• s[i+1, j+1] ← s[i, j] pour une correspondance ;
• s[i+1, j+1] ← s[i, j] + 1 pour une modification ;
• s[i+1, j+1] ← s[i, j+1 +1] pour une insertion ;
• s[i+1, j+1] ← s[i+1, j] pour une suppression.

Le score final est obtenu lorsque l'on a passé en revue tous les caractères des deux séquences :

3.2 Exemples

On commence avec un exemple simple. On considère le mot « langage » et le mot « langue ». On voit que les 4 premiers caractères sont communs aux deux séquences. En supprimant le deuxième « g » de « langage » et en modifiant son deuxième « a » en « u », on passe de « langage » à « langue ». On voit qu'il n'y a pas d'autres moyens plus simples. On peut conclure que la distance de Levenshtein entre ces deux séquences est de 2. Nous allons utiliser le programme écrit plus haut pour calculer la distance de Levenshtein sur des séquences un peu plus longues.

C'est déjà plus difficile à faire de tête. Pour utiliser notre fonction, il faut définir la matrice de coût :

Cette matrice de coût, nommée matrice_levenshtein, est un tableau à deux dimensions, une matrice, dont les éléments de la diagonale valent 0 et les autres éléments valent 1. Cela modélise le fait que toute modification d'un caractère coûte 1.

Le résultat donne 8. Mais comment faire pour savoir quelles modifications ont été faites ?

4. Alignement global

Nous rentrons enfin dans le vif du sujet. Nous allons voir ici un algorithme pour trouver une solution optimale à notre problème (voir [2] pour une explication plus complète).

4.1 L'alignement et l'algorithme de Needleman-Wunsch

L'algorithme de Needleman-Wunsch est le nom donné à l'algorithme de programmation dynamique appliquée à l'alignement global de deux séquences.

Il est une sophistication de l'algorithme de calcul de la distance de Levenshtein. L'alignement de deux séquences peut se décomposer en l'alignement de χi et ψj et l'alignement de χ1:i-1 et ψ1:j-1. C'est une sorte de résolution d'un problème par récurrence à deux indices, il suffit donc d'initialiser la résolution et de donner la transition de (i, j) vers (i+1, j+1), de (i, j+1) vers (i+1, j+1) et (i+1, j) vers (i+1, j+1) .

Nous utiliserons numpy (ligne 1) pour stocker simplement les valeurs dans un tableau, et pour les opérations possibles entre les tableaux (produit terme à terme ou encore retrouver l'indice dont l'élément correspondant est le plus grand, le fameux argmax). L'exemple de l'alignement de nucléotides est utilisé (ligne 2) pour son alphabet simple (seulement 4 éléments) :

Nous créons une fonction aligner_needleman_wunsch pour aligner nos séquences khi et psi. Nous utiliserons une matrice de remplacement, qui est le coût de changer un caractère en un autre et une pénalité penalite_is pour toute insertion et suppression.  matrice_remplacement est un ndarray de dimension 2.

Dans les lignes 6 à 9, on initialise le tableau qui accueille tous les scores d'alignement. Si on n'a encore rien aligné, alors le coût est zéro d'où mat_poids[0, 0] = 0. Si on a introduit seulement k caractères d'une séquence, alors on a k*penalite_is puisqu'on a fait k insertions ou k suppressions.

D'une manière similaire au calcul de la distance de Levenshtein, la figure 4 montre comment on calcule le score du meilleur alignement.

Nous rentrons enfin dans le vif de l'alignement par programmation dynamique. C'est ici que se passe la récursion. On choisit dans les lignes 13, 14 et 15 la transition qui apporte le meilleur score : soit la correspondance du caractère χi (chi[i-1] dans le code) avec ψj  (psi[i-1] dans le code), (on rappelle que les indices commencent à 0 en Python et à 1 dans notre formalisme mathématique), soit l'insertion du caractère χi, soit la suppression avec le caractère ψj . On utilise la variable mat_origine afin de conserver en mémoire le résultat que l'on a choisi afin de construire la solution. Sans ça, il faudrait rechercher le chemin utilisé pour construire la solution. C'est utile dans la partie rétrograde. Cette étape nous fournit déjà un résultat : le score optimal de l'alignement de chi et psi dans mat_poids[n, m].

La figure 5 montre comment se construit l'alignement en fonction du résultat de l'étape prograde.

Nous construisons enfin l'alignement ! Regardons maintenant pas à pas. Pour une itération donnée, on a i et j. On regarde d'où provient le score calculé en (i, j) dans mat_origine et on reconstruit l'alignement dans chi_alignement et psi_alignement. Il faut bien observer que ces deux séquences sont construites à l'envers (voir figure 5). La reconstruction se fait tant que l'on reste avec des indices admissibles.

4.2 Exemple

Les paramètres sont la matrice de remplacement (en anglais, on utilise plus souvent le terme de log-odds matrix) et la pénalité d'insertion-délétion. Le premier confère un fort avantage aux alignements de caractères identiques et pénalise plus légèrement les modifications de la même manière. Le second pénalise deux fois moins les insertions et délétions, ce qui signifie qu'il y aura plus tendance à rajouter des vides que d'aligner des mauvaises correspondances.

Résultat :

– – a a g t – a g c c a c t a g

g g a a g t a a g – – – c t – –

S S C C C C S C C I I I C C I I

Cet alignement est optimal selon les critères que l'on a donnés.

5. Alignement local

L'alignement global a tout pour nous plaire : on a deux séquences, et cela trouve le meilleur alignement en prenant en compte tous les caractères. En fait, cette manière de faire est salutaire quand on est sûr de traiter des séquences qui se ressemblent plus ou moins d'un bout à l'autre. Mais est-ce une situation courante ? En génétique, l'usage des alignements est de trouver des gènes qui se ressemblent, donc une suite de nucléotides similaires. Là où l’œil du biologiste est attiré, c'est quand il y a un haut score d'alignement à des endroits bien précis parce que ça signifie que deux gènes se ressemblent vraiment ou alors telle partie est très proche d'une autre. C'est pour cela, entre autres, que l'alignement local de séquences a fait son apparition : il vaut mieux un haut score pour une séquence groupée et un petit score global qu'un score global élevé et pas de haut score localement.

Changeons légèrement de représentation des états.

La classe Etats donne les états cachés que nous voulons retrouver. Si on les retrouve alors on a un alignement. La définition d'une classe héritant de IntEnum apporte un avantage supplémentaire par rapport à une simple classe avec des attributs de classe : ça montre que c'est un enum, mais c'est aussi un int, donc on sait le comportement que ça doit avoir.

L'initialisation n'est pas modifiée et l'étape prograde ne retient que les poids positifs en ajoutant   dans les propositions (ligne 11). En effet, max(0, x) est toujours positif ou nul, car si x > 0 alors max(0, x) > 0 et si x < 0 alors max(0, x) = 0. Cet ajout sert de commencement à un alignement local parce qu'un alignement local est jugé bon s'il dépasse   pour toutes ses sous-séquences.

Le meilleur alignement local se termine par le meilleur score possible. On cherche donc (ligne 18) le meilleur score dans mat_poids. Le début de l'alignement se trouve avec mat_poids[i_debut, j_debut] == 0 et mat_origine[i_debut, j_debut] == 3.

Prenons deux séquences de nucléotides (elles ont été conçues à la main et ne reflètent donc aucune réalité) :

Le résultat :

t g t – c a t

t g t a c – t

C C C S C I C

Seule la partie où il y a suffisamment de correspondances est retenue comme nous le souhaitions.

6. Cas pratique en génétique : l'algorithme BLAST

6.1 Les besoins en génétique

Dans les parties précédentes, nous avons vu de charmantes solutions qui font très bien le boulot, cependant elles sont loin d'être satisfaisantes. Et pour cause, l'usage fait en génétique pour rechercher des gènes proches d'un autre dans une base de données requiert des quantités de calculs inaccessibles avec nos algorithmes. Précisons le propos sur un exemple : l'algorithme de Smith-Waterman nécessite de construire un tableau avec m x n éléments (m et n sont les tailles des deux séquences) et d'y retourner pour construire la solution optimale. Rechercher dans une base contenant des milliards de séquences (https://blast.ncbi.nlm.nih.gov/Blast.cgi) est tout bonnement impossible. Il faudra faire des compromis.

6.2 Au cœur de BLAST

Les années 90 ont vu naître BLAST (Basic Local Alignment Search Tool), une famille d'outils encore aujourd'hui utilisée, car sans cesse améliorée [3][4]. Son succès est assuré par des heuristiques conçues pour accélérer la recherche de séquences similaires. Le problème auquel nous faisons face en génétique est de retrouver dans une base de séquences (qui est base_seqs) les séquences suffisamment similaires à une séquence donnée (qu'on nomme seq_ent).

La méthode de résolution repose sur trois idées :

1. seq_ent est découpé en n k-uplets, avec k défini à l'avance et n = len(seq_ent)- k + 1 . Chaque k-uplets se voit associer l'ensemble des k-uplets qui ont un score de similarité supérieur à un seuil avec seq_ent. Ce découpage entraînera une réduction de la taille des motifs dans les séquences de base_seqs. Ces calculs menés sur la seule séquence en entrée, il est plus avantageux de faire les calculs une bonne fois pour toutes que de les faire à chaque comparaison.
2. L'idée suivante consiste simplement à rechercher des correspondances exactes entre les k-uplets d'une famille homologue. Les alignements exacts sont plus faciles à calculer que de voir s'il y a eu des insertions et suppressions.
3. Enfin, comme on souhaite trouver les zones à fortes homologies, alors les alignements obtenus avec la seconde idée peuvent être étendus pour voir jusqu'où on peut trouver mieux. Cela se fait caractère par caractère : on ajoute le caractère (directement à droite ou directement à gauche) si le score de similarité  entre le k-uplet concerné de seq_ent et le k-uplet dans une séquence de la base, augmente. On fait ainsi jusqu'à ce que ce score diminue.

Finalement, on obtient des alignements entre seq_ent et les séquences de la base. L'explication donnée est valable dans un cas général, mais nous nous intéressons ici à des séquences de nucléotides et aussi aux séquences de protéines. Nous considèrerons les premières comme étant équivalentes. Aucun nucléotide n'a de raison d'être plus proche de l'un par rapport à un autre Ce constat n'est pas valable pour les protéines pour lesquelles un changement d'acide aminé n'influence en rien la fonction de la protéine ou, au contraire, peut bouleverser la structure d'une protéine.C'est pour cela qu'on utilisera ici une matrice de substitution (les matrices PAM et BLOSUM sont les plus utilisées). Une valeur positive indique qu'un acide aminé a tendance à muter en un autre, alors qu'une valeur négative désigne une confusion rare entre les acides aminés.

L'idée 1 est implémentée ici. Elle ne présente aucune difficulté :

La deuxième idée nécessite quelques éclaircissements : sous_seq est la liste de tous les k-uplets suffisamment proches de la séquence en entrée, quant à la base, elle est la liste des séquences qui nous sert de base de recherche. Pour chaque k-uplet lié à seq_int, on calcule l'ensemble des correspondances avec la base de séquences :

La troisième idée ne sera pas implémentée, car elle ne présente pas de défi particulier, outre prendre en compte toutes les conditions d'extension et d'arrêt. Si vous êtes intéressé par cette application, il existe la bibliothèque Biopython qui rend possible un usage clé en main de Blast et de bien d'autres algorithmes. Une présentation claire et précise est disponible [5].

7. Applications en linguistique comparative

La bibliothèque nltk [6] rassemble un ensemble de fonctionnalités nécessaires en TAL (traitement automatique du langage). On pourra y trouver des parseurs en lexème (tokenizer), des racinisateurs, ou, comme plus couramment dit, stemmers, des étiqueteurs morpho-syntaxique (Part of speech tagggers), etc. Tout pour permettre une analyse d'un texte écrit en langue naturelle (d'où le nom anglais du domaine NLP pour Natural Language Processing). Ce qui va nous intéresser ici, c'est la possibilité de charger un corpus qui contient un lexique de mots similaires de langues apparentées. Le corpus Swadesh contient un échantillon qui nous convient. Pour l'installation de nltk et le téléchargement du corpus Swadesh, je laisse la documentation vous aider.

On sélectionne l'anglais ("en" pour English), l'allemand ("de" pour Deutsch) et le néerlandais ("nl" pour Nederlands). Ces langues sont toutes les trois des langues dites germaniques occidentales. Une proximité géographique et une origine commune expliquent une proximité lexicale. Mais peut-on avoir une idée quantitative de cette proximité ?

Pour comparer des mots de langues différentes, il faut au moins une même base orthographique. C'est ce que l'on fait en normalisant chaque mot.

On cherche à récupérer, préparer et reformater les mots des langues souhaitées.

Le script suivant compare la distance de Levenshtein moyenne entre chacune des langues étudiées. La matrice des Levenshtein donne un coût 0 aux correspondances et un coût 1 aux non-correspondances.

Le résultat est [ 3.73429952 3.36231884 2.45410628]. On peut donc voir que le lexique anglais et celui du néerlandais sont significativement plus proches l'un de l'autre que le sont les autres entre eux. Ce n'est pas étonnant puisque ces deux langues-là sont dans un sous-groupe qui exclut l'allemand. Il est néanmoins important de noter que les résultats ne portent que sur l'orthographe des mots et non sur leur prononciation. De plus, le lexique utilisé n'est aucunement censé représenter les langues étudiées. On a au mieux un échantillon assez divers concernant la nature des mots (noms, verbes, pronoms, adjectifs, etc.). Pour mieux aborder la question, lire [7][8].

Conclusion

Nous avons étudié le formalisme de traitement de séquences, ainsi que celui de l'alignement. La programmation dynamique a été introduite afin de comprendre son mécanisme, et ce, à travers la distance de Levenshtein. Les alignements globaux et locaux ont dévoilé leurs secrets élémentaires. Finalement, deux exemples concrets ont été présentés avec leur lot de simplification d'un côté et de sophistication de l'autre.

Références

[1] BELLMAN R., « The theory of dynamic programming », RAND CORP SANTA MONICA CA, 1954.

[2] DURBIN R. « Biological sequence analysis, Probabilistic models of proteins and nucleic acids », Cambridge University Press, 1998

[3] ALTSCHUL S. F. et al., « Basic Local Alignment Search Tool », Journal of molecular biology, vol. 215, no 3, 1990, p. 403 à 410.

[4] ALTSCHUL S. F. et al., « Gapped BLAST and PSI-BLAST: a new generation of protein datanase search programs», Nucleic acids research, vol. 25, no 17, 1997, p. 3389 à 3402.

[5] DAMERON O. et FARRANT G., « La bioinformatique avec Biopython », GNU/Linux Magazine HS n°73, mai 2014, p. 84 à 97, https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMFHS-073/La-bioinformatique-avec-Biopython.

[6]  BIRD S., LOPER E. et KLEIN, « Natural Language Processing with Python » O’Reilly Media Inc, 2009 : http://www.nltk.org/api/nltk.html, installation de nltk : http://www.nltk.org/install.html, téléchargement de corpus : http://www.nltk.org/data.html.

[7] KONDRAK G., « A new algorithm for the alignment of phonetic sequences », Proceedings of the 1st North American chapter of the Association for Computational Linguistics conference, 2000, p. 288 à 295.

[8] NERBONNE J., HEERINGA W., VAN DEN HOUT E. et al., « Phonetic distance between Dutch dialects », CLIN VI: Proceedings of the sixth CLIN meeting, 1996, p. 185 à 202.

Pour aller plus loin

Les algorithmes présentés ici ne sont pas facilement adaptables aux données puisque les paramètres sont choisis à la main. C'est pour cela que des modèles probabilistes ont été introduits pour répondre à des besoins spécifiques. Les Pair Hidden Markov models en sont un bon exemple. Les alignements multiples sont aussi une extension utile avec les Profile Hidden Markov Model.

Une fois les séquences alignées, on peut se demander comment elles sont liées. La réponse est bien souvent que ces séquences ont évolué à partir d'une même séquence-ancêtre. La reconstruction des étapes de ces évolutions utilise le plus souvent des arbres.