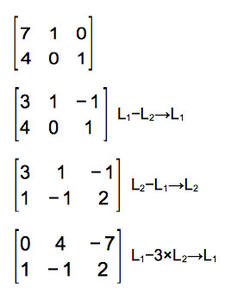Pour corriger un code QR avec erreur ou rature, on a besoin de savoir manipuler un corps fini précis, 𝔽256, encore faut-il savoir de quoi on parle.
En vue de corriger les codes QR décorés ou abîmés (voir articles précédents [1]), on a besoin de notions mathématiques plus poussées. Cet article va présenter la notion mathématique de corps fini, sur laquelle le code correcteur de Reed-Solomon est construit. On construira en Python le corps ℤ/pℤ où p est un nombre premier. Les codes sont disponibles sur GitHub [2].
Cet article parlera de mathématiques, contrairement aux autres. On présentera ce qu’est, de manière générale, un corps puis nous construirons un corps fini premier pour, dans l’article suivant, obtenir le corps dont nous avons besoin et les structures algébriques utiles à l’aide de briques orientées objet.
1. Un peu de mathématiques
Nous commençons par définir ce qu’est un corps avant de nous intéresser à une construction possible.
1.1. Qu’est-ce qu’un corps ?
En gros, un corps est un ensemble de « nombres » dans lequel on peut effectuer les quatre opérations sans se demander s’il n’y a pas un loup (dans Paris) ou une impossibilité (à part, bien sûr, diviser par 0).
Formellement, on se donne un ensemble K sur lequel on a deux opérations notées habituellement + et ×.
L’addition a les propriétés suivantes :
- Elle est commutative : a+b=b+a pour tous a et b de K ;
- Elle est associative : (a+b)+c=a+(b+c) quels que soient a, b, c∈K ce qui veut dire en pratique qu’on n’est pas tenu d’utiliser ni d’écrire des parenthèses ;
- La loi possède un élément neutre 0 pour lequel ∀a∈K, a+0=0+a=a ;
- Tout élément a a un « inverse » b qu’on appelle opposé, c’est-à-dire que a+b=b+a=0. On note b=−a et a−b=a+(−b).
Ceci veut dire que (K,+) est un groupe commutatif.
(K*,×) est aussi un groupe, non nécessairement commutatif (K* signifie K sans 0). L’inverse de a≠0 est noté 1/a ou a−1 puisque a−1×a=a×a−1=1.
Enfin, la multiplication est distributive par rapport à l’addition, ce qui veut dire que ∀a, b, c∈K, (a+b)×c=a×c+b×c et de même à gauche. Par convention, la multiplication est prioritaire sur l’addition, ce qui veut dire que a+b×c=a+(b×c).
On a tous déjà calculé dans des corps comme ℝ (l’ensemble des nombres réels) ou ℂ (les nombres complexes utilisés par exemple en électronique analogique). Ces deux derniers corps contiennent tous les deux le corps ℚ des fractions des entiers relatifs, c’est même le plus petit sous-corps qu’ils contiennent (on appelle ce sous-corps leur sous-corps premier). Ces trois corps sont infinis.
En revanche, l’ensemble ℤ des entiers relatifs n’est pas un corps car seuls 1 et −1 ont des inverses dans ℤ pour la multiplication (qui sont eux-mêmes), ℤ est cependant un anneau muni d’une division euclidienne.
Les flottants utilisés en informatique munis des opérations + et × ne forment pas un corps, même pas un anneau, rien en fait. Il faut le savoir quand on fait du calcul scientifique à cause de mantisses et d’exposants de taille limitée. Ainsi, 10100+10−100−10100=… eh bien ça vaut 0 pour une machine qui ne fait pas de calcul formel. C’est un pont aux ânes de prof de maths qui n’empêche pas de travailler avec en prenant quelques précautions. Par exemple, pour une calculette de poche couramment rencontrée en classe, 10n+10−n−10n vaut 0 dès que n⩾7. [3]
1.2 Premiers corps finis
Évidemment, un corps fini ne contient pas ℚ, ilest construit autrement.
On commence par choisir un nombre premier p, le reste de la division d’un nombre entier relatif par p est donc entre 0 et p−1. Voilà notre premier corps fini : {0,1,…,p−1} muni de l’addition et de la multiplication modulo p qu’on note ℤ/pℤ ou ℤp, parfois ℤ/p. Les corps finis ont tous pour sous-corps premier un corps fini du type ℤ/pℤ avec p premier (p est sa caractéristique).Pour distinguer les éléments de ℤ/pℤ des nombres entiers classiques, on les écrira surmontés d’une barre.
Ainsi, modulo 7 : ![]() car 11=1×7+4 et
car 11=1×7+4 et ![]() .
.
Attention, si n n’est pas un nombre premier, ℤ/nℤ n’est pas un corps. Par exemple, si n=4, ![]() n’a pas d’inverse puisque
n’a pas d’inverse puisque ![]() .
. ![]() est un diviseur de
est un diviseur de ![]() . Dans ce cas, les seuls nombres q qui ont un inverse sont ceux qui n’ont pas de facteur premier commun avec n, en d’autres mots, si PGCD(n,q)=1. On dit que ℤ/nℤ est un anneau (où à part l’absence éventuelle d’inverse pour la multiplication, la structure algébrique est la même, et en plus sans division euclidienne).
. Dans ce cas, les seuls nombres q qui ont un inverse sont ceux qui n’ont pas de facteur premier commun avec n, en d’autres mots, si PGCD(n,q)=1. On dit que ℤ/nℤ est un anneau (où à part l’absence éventuelle d’inverse pour la multiplication, la structure algébrique est la même, et en plus sans division euclidienne).
Qu’en est-il de la division, par exemple par ![]() ?
?
Si le corps est petit, on peut chercher l’inverse à la mainautrement dit par force brute : ![]() . Donc diviser par
. Donc diviser par ![]() revient à multiplier par son inverse qui est
revient à multiplier par son inverse qui est ![]() . L’algorithme efficace utilisé dans notre cas sera l’algorithme d’Euclide étendu qui donne les coefficients de Bezout u et v dans l’équation 4×u+7×v=1 (où u et v sont des entiers relatifs). En fait, seul u nous est utile, on l’obtient facilement à la main par la méthode de Blankinship (ou pivot de Gauß) [4] où on effectue des opérations élémentaires (combinaisons linéaires ou permutations) sur les lignes de la matrice suivante :
. L’algorithme efficace utilisé dans notre cas sera l’algorithme d’Euclide étendu qui donne les coefficients de Bezout u et v dans l’équation 4×u+7×v=1 (où u et v sont des entiers relatifs). En fait, seul u nous est utile, on l’obtient facilement à la main par la méthode de Blankinship (ou pivot de Gauß) [4] où on effectue des opérations élémentaires (combinaisons linéaires ou permutations) sur les lignes de la matrice suivante :
La première colonne contient un seul 1 et le reste est constitué de 0, on a terminé l’algorithme : u=2, v=−1 et 7×(−1)+2×4=1 donc l’inverse de ![]() est bien
est bien ![]() dans ℤ/7ℤ.
dans ℤ/7ℤ.
Cette méthode fonctionne aussi quand on veut calculer le PGCD de plusieurs nombres etleurs coefficients de Bezout.Ainsi, si la matrice à chaque étape est Mi,j, pour tout i∈{1;2}, Mi,1=7×Mi,2+4×Mi,3 pendant tout le déroulement de l’algorithme.
Voici la fonction qui retourne l’inverse de a modulo n, elle se trouve dans qrcodeoutils.py :
01: def bezout(n,a):
02: r,u,v,rr,uu,vv=a,1,0,n,0,1
03: while rr!=0:
04: q=r//rr
05: r,u,v,rr,uu,vv=rr,uu,vv,r-q*rr,u-q*uu,v-q*vv
06: return u%n,v%n
Il s’agit ici de l’algorithme classique qu’on peut alléger des variables v et vv qui n’ont aucune utilité dans la suite. On n’a pas vérifié si le PGCD était bien égal à 1, ce qui est immédiat dans un corps, on n’a pas non plus vérifié si a==0.
Le corps fini utilisé dans les codes QR n’a pas cette structure, trop simple, qu’on verra dans la partie suivante : un corps fini est un espace vectoriel de dimension finie sur un corps fini premier, tout comme ℂ est un espace vectoriel de dimension 2 sur ℝ (qui n’est cependant pas un corps premier). Voyons comment construire un corps ℤ/pℤ en créant une classe munie de toutes les méthodes adéquates.
2. Construction effective de ℤ/pℤ
On va construire pour commencer l’anneau ℤ/pℤ dans le cas où p est un nombre premier, c’est-à-dire le corps ℤ/pℤ, en Python.
2.1 Mémorisation
Mon second code, naïf, utilise une fonction qui retourne une classe Zn qui dépend du paramètre p (la classe est donc paramétrée). La construction fonctionne à peu près mais coince quand il faut commencer à vérifier les types dans les classes emboîtées. J’ai donc utilisé le code de Jeremy Kun [5] qui ressemble au mien [2], aux décorateurs prêts.
Un décorateur permet de modifier une fonction sans utiliser une batterie de tests (regardez mon deuxième code où je passe beaucoup de temps à vérifier finement les types). Le code de Jeremy [6] est certes puissant mais j’ai dû le modifier ponctuellement, notamment pour l’opération puissance ou la division euclidienne (sans intérêt dans un corps). Le voici en version francisée, dans qrcodeoutils.py :
def memorise(f):
cache=dict()
def fonctionmemorisee(*args):
if args not in cache:
cache[args]=f(*args)
return cache[args]
fonctionmemorisee.cache=cache
return fonctionmemorisee
if __name__=="__main__":
@memorise
def f(x):
print(x,x*x,"première passe")
return x*x
print(f(2))
print(f(3))
print(f(2))
print(f.cache)
print(f)
Voici la sortie de ce code :
> ./memorisation.py
2 4 première passe
4
3 9 première passe
9
4
{(2,): 4, (3,): 9}
<function memorise.<locals>.fonctionmemorisee at 0xb729c6ec>
On teste si la valeur est mémorisée. Sinon, on la stocke dans le cache qui est un simple dictionnaire. Évidemment, ce code stocke absolument tout sans contrôle. Dans un code qui tourne indéfiniment, il faudrait au minimum contrôler la taille du cache.
2.2 Construction de la classe modulo p
La fonction defzn définit une classe qui dépend du paramètre p qui est un nombre entier positif. Elle est mémorisée donc deux classes de mêmes paramètres p sont en fait identiques et non deux classes distinctes qui font néanmoins la même chose.
01: @memorise
02: def defzn(p):
03: class Zn():
04: def __init__(self,n):
05: self.n=n%p
06: self.corps=Zn
Le constructeur d’un élément de la classe le définit par ses propriétés : sa valeur et le corps auquel il appartient.
08: def __add__(self,m):
09: return Zn(self.n+m.n)
10: def __sub__(self,m):
11: return Zn(self.n-m.n)
12: def __mul__(self,m):
13: return Zn(self.n*m.n)
On définit l’addition, la soustraction et la multiplication dans ℤ/pℤ qui permettent d’utiliser les opérateurs binaires +, − et *.
14: def __truediv__(self,m):
15: return self*m._inverse()
La division (/ en Python 3 et non // qui est la division euclidienne que nous utiliserons plus tard mais pas dans un corps, et qui est définie par la méthode __floordiv__) nécessite l’inverse modulo p puisque diviser par un nombre est équivalent à multiplier par son inverse (comme on l’apprend au collège) soit ![]() , ∀a∈ℤ/pℤ, ∀b∈ℤ/pℤ*, la fonction _inverse est définie plus loin.
, ∀a∈ℤ/pℤ, ∀b∈ℤ/pℤ*, la fonction _inverse est définie plus loin.
16: def __neg__(self):
17: return Zn(-self.n)
18: def __eq__(self,m):
19: return isinstance(m,Zn) and self.n==m.n
La négation unaire (autrement dit l’opposé) est définie ainsi que le test d’égalité. Remarquez que les comparaisons < ou ⩾ n’ont aucun intérêt.
20: def __pow__(self,exp):
21: if exp>0:
22: prod=1
23: x=self.n
24: while exp>1:
25: if exp%2:
26: prod*=x
27: x*=x
28: x%=p
29: exp//=2
30: return Zn(prod*x)
31: elif exp==0:
32: return Zn(1)
33: else:
34: return self._inverse()**-exp
Il s’agit de l’opérateur de puissance ** y compris si l’exposant est négatif. Dans ce cas, on calcule la puissance positive de l’inverse. L’exponentiation rapide revient à décomposer l’exposant en base 2, c’est l’idée de la multiplication pratiquée en Égypte antique et encore aujourd’hui en Russie.
Par exemple si on doit calculer a45=a1a4a8a32, la suite des divisions de 45 par les puissances de 2 donne :
|
divisions |
45=2×22+1 |
22=11×2+0 |
11=5×2+1 |
5=2×2+1 |
2=2×1+0 |
1=1 |
|
reste |
1 |
0 |
1 |
1 |
0 |
1 |
|
prod |
a1 |
a1 |
a1a4=a5 |
a5a8=a13 |
a13 |
a13a32=a45 |
|
x |
a1 |
a2 |
a4 |
a8 |
a16 |
a32 |
35: def __str__(self):
36: return str(self.n)+"\u0305"
37: def __repr__(self):
38: return "%d [mod %d]"%(self.n,self.p)
La première fonction est utilisée par les fonctions internes str et print, la deuxième quand on affiche une liste d’éléments de la classe, voir ci-après.
39: def _inverse(self):
40: i,_=bezout(p,self.n)
41: return Zn(i)
Dans la fonction qui calcule l’inverse, on ne vérifie pas si l’élément est bien inversible, comme on travaille dans un corps fini, on suppose que tout va bien. Au cas où on diviserait quand même par 0, une exception sera levée dans la boucle dans la fonction bezout lors de la division euclidienne (ligne 04 du code source de bezout, voir plus haut).
42: Zn.p=p
43: Zn.__name__ ="ℤ/%dℤ"%p
44: return Zn
Enfin, on dote la classe elle-même des deux propriétés : son cardinal et son nom et on la retourne.
Jouons un peu avec notre classe :
if __name__=="__main__":
mod7=defzn(7)
print([mod7(i) for i in range(10)])
print(mod7(3)**-2)
print(mod7(2)*mod7(4)-mod7(5))
print(mod7(1).corps.__name__)
print(mod7.__name__)
z7=defzn(7)
print(z7==mod7)
On obtient ceci :
[0 [mod 7], 1 [mod 7], 2 [mod 7], 3 [mod 7], 4 [mod 7], 5 [mod 7], 6 [mod 7], 0 [mod 7], 1 [mod 7], 2 [mod 7]]
4̅
3̅
ℤ/7ℤ
ℤ/7ℤ
True
Conclusion
Voici ce qu’on peut faire en Python. Le problème est qu’il faut empiler beaucoup de briques par-dessus cette structure alors qu’en fait, on peut accélérer le processus. Ce qu'il ne faut pas faire pour corriger un code QR... et ce n'est pas fini !
Références
[1] PATROIS N., « Décoder un code QR », GNU/Linux Magazine n°194, p. 32 à 41.
[2] Le code et les exemples sont présents ici : https://github.com/GLMF/GLMF194.
[3] LANGROGNET F., « Peut-on vraiment calculer avec un ordinateur : les opérations », GNU/Linux Magazine n°194, p. 22 à 31.
[4] L’algorithme de Blankinship est présenté ici : http://www.les-mathematiques.net/phorum/read.php?5,516246.
[5] http://jeremykun.com/2014/03/13/programming-with-finite-fields/. J’ai francisé le code et je lui ai ajouté et supprimé ce qui me semble ou non pertinent mathématiquement (par exemple, la division euclidienne ou la valeur absolue n’ont aucun intérêt dans un corps fini).
[6] http://jeremykun.com/2012/03/22/caching-and-memoization/.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture