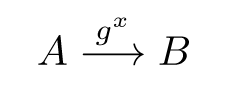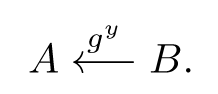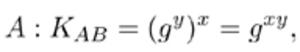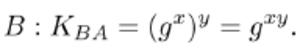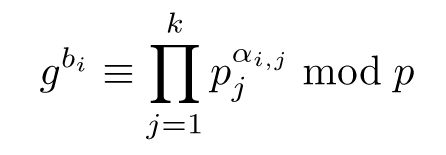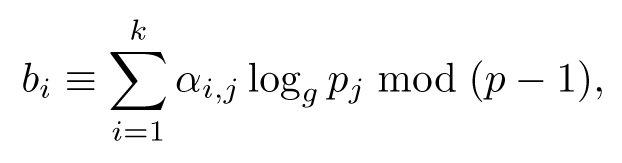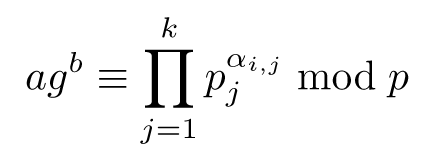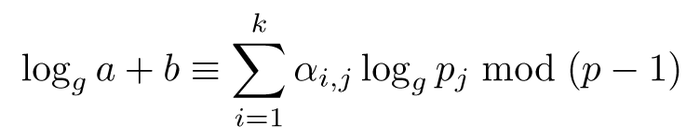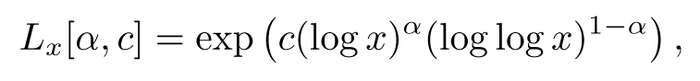Les tunnels sécurisés sont souvent basés sur des protocoles proches du protocole historique de Diffie et Hellman. La sécurité du tunnel repose sur la résistance de certains groupes finis aux algorithmes de calcul de logarithme discret. Nous faisons le point sur les méthodes de cassage connues.
1. Le logarithme discret : un problème peu médiatique
Contrairement au problème de la factorisation d’entiers qui attire beaucoup d’attention car il est lié de très près à la sécurité du cryptosystème RSA et du contenu de nos portefeuilles (cf. "Factorisation d'entiers : la voie royale du cassage de RSA" paru dans le hors-série n°5 de MISC), celui du logarithme a reçu moins de lumière, alors qu’il est tout aussi important, sinon plus.
Le protocole d’échanges de clés de Diffie et Hellman est rappelé ci-dessous. C’est en fait un méta-algorithme, au sens où il doit être instancié par un groupe fini G dans lequel le problème du logarithme discret doit être difficile à résoudre. On se contente généralement d’utiliser un groupe cyclique : si G est cyclique, alors tout élément de G peut s’écrire comme puissance d’un élément générateur g. Le problème du logarithme discret (LD) s’énonce ainsi : étant donné un élément a de G, comment trouver un entier x tel que a = gx? Un tel entier s’appelle le logarithme discret de a en base g.
L’exemple typique est celui des corps finis. Par exemple, dans (ℤ/11ℤ)* = {1, 2, …, 10} (le groupe des entiers inversibles modulo 11), on constate que tout élément est une puissance de 2 :
2 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 5, 25 = 10, 26 = 9, 27 = 7, 28 = 3, 29 = 6.
Nous allons passer en revue quelques algorithmes de résolution de ce problème, que ce soit des algorithmes génériques (qui marchent dans tous les groupes), ou des algorithmes utilisant des relations entre éléments du groupe (quand c’est possible).
2. Élimination des mauvais groupes
Le but du jeu est de trouver des groupes (finis) faciles (temps polynomial) à utiliser et dans lesquels le problème LD est difficile (au moins sous-exponentiel). L’un des groupes à éviter est simplement (ℤ/Nℤ, +), dans lequel le calcul du logarithme discret revient à effectuer un pgcd…
2.1. La réduction de Pohlig-Hellman
Il est utile d’étudier le problème LD dans un groupe abstrait où on ne saurait faire que la multiplication d’éléments. Soit donc G un groupe cyclique d’ordre n, engendré par a. Pohlig et Hellman ont montré que calculer le logarithme de a modulo n était équivalent à déterminer ce logarithme modulo chaque facteur de n, par application du théorème chinois. Ainsi, si n n’est composé que de petits facteurs premiers, résoudre LD est facile, puisqu’au pire on peut énumérer tous les logarithmes modulo chaque facteur premier.
À titre d’exemple, reprenons le cas de G = (ℤ/11ℤ)∗. Comme # G = 10, il suffit de calculer le logarithme discret modulo 2 et 5. Par le théorème de Fermat (Lagrange), on a a10 = 1, ce que l’on peut récrire (a2)5 = 1, donc tous les nombres a2 sont d’ordre divisant 5, ou encore des puissances de g2 = 22, qui est d’ordre 5. Ce qui veut dire que pour tout nombre a, on a a2 = (g2)i avec i∈ {0, 1, …, 4}. Il suffit de trouver ce i. Par exemple :
92 ≡ 81≡ 4 mod11 ≡ (22)1mod11,
ce qui conduit à log2 9 ≡ 1 mod5. De la même façon :
95 ≡ 1 mod11 ≡ (25) mod11
donc log2 9 ≡ 0 mod2. Et le seul entier k modulo 10 vérifiant k ≡ 1mod5 et k ≡ 0mod2 est k = 6.
2.2. L’algorithme de Shanks
Pour résoudre a = gx dans G avec 0 ⩽ x < n, on écrit x = cu + d, avec u un entier à déterminer, c et d les quotient et reste de x par u. On réécrit l’équation a = gx sous la forme :
a = (gu)c · gd
avec 0 ⩽ d < u et 0 ⩽ c < n/u. Si l’on note g−1 l’inverse de g dans G, on en déduit :
a (g−u)c = gd.
Nous avons ramené le problème à un problème à deux variables séparées. On commence par calculer tous les bd = gd pour tous les d possibles, de 1 en 1, appelés pas de bébé. Puis pour chaque valeur de c, on calcule de proche en proche la quantité a (g−u)c, ce sont les pas de géant. Si pour un c donné, on trouve une identité (g−u)c = bd, on a gagné.
Comment analyse-t-on cet algorithme ? Le nombre d’opérations de groupes est essentiellement u pas de bébé et au pire n/u pas de géant. Le nombre total est minimal pour u = √n, conduisant à un nombre 2 √n. L’espace mémoire de stockage pour les bd est également de √n éléments de G. D’un point de vue pratique, il est vital de stocker les bd avec une table de hachage, pour garantir des tests d’appartenance rapides aux pas de bébé.
Pour finir, il existe un autre algorithme de calcul de logarithmes discrets en temps O(√n), qui utilise peu de stockage, l’algorithme (probabiliste) de Pollard. Les deux algorithmes sont distribuables.
2.3. Conclusion provisoire
D’après ce que l’on vient de voir, un bon groupe ne doit pas avoir un cardinal composé de trop petits facteurs premiers. En outre, sa taille doit être suffisante pour que l’attaque en √n ne soit pas réaliste.
Le protocole de Diffie-Hellman
Dans cette version simple, Alice et Bob veulent établir une clé commune avec des valeurs qui transitent sur un réseau non protégé. Pour cela, ils choisissent un groupe G = ⟨g⟩ et effectuent le protocole suivant. Alice commence par choisir un nombre aléatoire x et envoyer gx à Bob :
Bob agit de façon symétrique :
À la fin des communications, Alice peut reconstituer la clé commune :
ce que Bob peut également faire :
Le problème de Diffie-Hellman est le suivant : étant donnés (g, gx, gy), calculer gxy. Le problème LD est : étant donnés (g, gx), trouver x.
Il est clair que si on sait résoudre LD, on sait résoudre DH. On sait que la réciproque est vraie dans de nombreux groupes G (travaux de Maurer et Wolf).
3. L’algorithme d’Adleman
Dès 1978, L. M. Adleman a proposé un algorithme de calcul sous-exponentiel de calcul de logarithme discret modulo p, qui est proche en esprit des algorithmes de factorisation (voir section suivante). Cet algorithme a été généralisé pour de nombreux groupes (corps finis généraux, certaines courbes algébriques), dès qu’une notion de nombres premiers peut être définie dans le groupe.
Cet algorithme n’est pas sans rappeler les algorithmes de factorisation utilisant des combinaisons de congruences. Il procède en deux phases : dans la phase de collection, on accumule les logarithmes discrets de nombres dans une base. Dans la seconde phase, on calcule des logarithmes individuels en s’aidant des résultats de la première phase.
Considérons le cas de (ℤ/101ℤ)*, engendré (lui aussi) par 2. L’idée est de trouver des relations qui nous donneront les logarithmes discrets des nombres {2, 3, 5, 7}, en partant de puissances aléatoires de g = 2 :
27 = 128 ≡ 33mod101, 29 = 7, 217 = 3· 52.
Comme log2 2 = 1, on en déduit que les logarithmes de ces nombres en base 2 vérifient :
7 = 3· log3 mod100, log7 = 9, log3 + 2log5 = 17,
soit log3 = 69, log5 = 24, log7 = 9.
D’un point de vue algorithmique, on crée un système linéaire entre les logarithmes des {pj}1 ⩽ j ⩽ k qui nous intéressent. Une relation
conduit par passage au logarithme
soit une relation linéaire entre les inconnues logg pj. Une fois que k relations ont été trouvées, on doit inverser ce système défini modulo p−1. Ce système est creux, mais contrairement à ce qui se passe pour la factorisation d’entiers, ce système n’est donc pas binaire, et donc plus difficile à résoudre.
Une fois cela fait, on cherche des b tels que :
et par passage au logarithme :
et il ne reste plus qu’à injecter les valeurs des logarithmes trouvés pour en déduire logg a.
Si l’on veut calculer le logarithme de 17, on trouve par exemple :
23· 17 ≡ 5· 7mod101
ce qui conduit à :
3 + log17 ≡ log5 + log7 ≡ 33,
d’où log17 = 30.
4. Complexité et records
L’analyse de cet algorithme fait intervenir la fonction
avec 0 ⩽ α ⩽ 1, introduite dans le précédent article. Comme pour la factorisation d’entiers, on peut utiliser des corps de nombres, ce qui conduit à la meilleure complexité connue : O(Lp[1/3, c]). Notons que la théorie nécessaire est plus complexe que dans le cas de la factorisation des entiers.
Le record actuel, dans (ℤ/pℤ)*, est pour p de 160 chiffres décimaux, obtenu par T. Kleinjung en 2007. Il lui avait fallu 3.3 années sur de PC 3.2 GHz Xeon64, terminant avec une matrice 2,177,226× 2,177,026 avec 289,976,350 coefficients non nuls, inversée en 14 ans de CPU. La partie inversion du système est très technique à faire marcher dans la vraie vie et reste un problème de recherche.
Conclusion
L’investissement théorique dans le logarithme discret a accompagné celui fait pour la factorisation d’entiers. En pratique, il existe moins d’équipes ayant cassé des logarithmes discrets, ce qui explique en partie les records plus petits.
La recherche de nouveaux groupes résistants aux algorithmes à la Adleman est un courant très fort en cryptographie. Les deux seuls candidats qui tiennent la route pour le moment sont ceux formés avec des courbes elliptiques et hyperelliptiques.
Pour les courbes elliptiques, les records de factorisation sont de taille modeste : 112 bits, avec 8.5× 1016 additions sur 200 PS3 pendant 3 mois et demi.