De l’espérance de vie d’un algorithme symétrique (ou l’AES dix ans après)

1. Introduction

Les progrès importants faits en cryptanalyse au cours des dernières années montrent que peu d’algorithmes symétriques résistent plus de quinze ans aux attaques. Les fonctions de hachage MD5 et SHA-1 ont été cassées respectivement treize et dix ans après leur publication. Parmi les huit chiffrements à flot recommandés en 2008 à l’issue du concours international eSTREAM, un a déjà été cryptanalysé et un deuxième présente des faiblesses importantes. Et l’exemple le plus frappant est naturellement celui de l’AES. L’AES vient en effet d’être victime pour la première fois d’une attaque qui semble légèrement moins coûteuse que la recherche exhaustive de la clé. Mais il a surtout motivé d’importants développements en cryptanalyse qui, s’ils ne mettent pas en danger la sécurité du chiffrement par bloc lui-même, se sont révélés plus graves lorsque l’AES était employé dans d’autres contextes (fonctions de hachage, scénarios à plusieurs clés, ...). Doit-on en conclure que tous les algorithmes symétriques récents, même conçus par des spécialistes reconnus, ont toutes les chances d’être cassés au cours de la décennie ?

Nous tenterons donc dans cet article de faire le point sur l’état des recherches concernant la cryptanalyse de l’AES. Nous décrirons dans une première partie cet algorithme. Et nous nous intéresserons ensuite à trois périodes de sa vie : les années d’incertitude (2001-2004), l’âge d’or (2005-2008), et finalement ce qu’on pourrait considérer comme les premières alertes (2009-2011).

2. Description de l’AES

2.1. Comment construire un chiffrement par bloc ?

Un chiffrement par bloc découpe un message en blocs de même taille, n bits (n doit être suffisamment grand pour éviter les attaques par dictionnaire, typiquement n=128 bits pour l’AES), et ensuite, chiffre chacun de ces blocs (nous n’aborderons pas ici le mode opératoire d’un tel système, c’est-à-dire la façon dont on l’utilise pour traiter les blocs de message successifs, mais celui-ci est extrêmement important). De façon générique, on décrit un algorithme de chiffrement par bloc E comme une application qui associe à un bloc de message de n bits, m, et à une clé de ℓ bits, K, un bloc chiffré de n bits, c : E_K(m)=c. Pour pouvoir déchiffrer, il faut naturellement que E_K soit une permutation pour toutes les clés possibles K. L’algorithme de déchiffrement correspondant, D_K, permet de déchiffrer c avec la même clé K : D_K(c)=m, autrement dit D_K est l’inverse de la fonction E_K pour toute clé K. La permutation de chiffrement E_K paramétrée par la clé K doit donc être facile à inverser. La clé K doit être également prise dans un espace suffisamment grand pour se prémunir contre la recherche exhaustive (essayer toutes les clés). Par exemple dans le cas de l’AES, K est de taille 128, 192 ou 256 bits, ce qui fait que la recherche exhaustive nécessite 2¹²⁸, 2¹⁹² ou 2²⁵⁶ essais, cette dernière borne étant très proche du nombre d’atomes présents dans l’univers estimé à 2²⁶⁵.

Les méthodes de construction de tels algorithmes restent très empiriques mais la plus usitée est l’utilisation d’algorithmes itératifs. Ces algorithmes sont composés de r étages et à chaque étage, ils font agir la même permutation interne f_Ki, appelée fonction de tour, paramétrée par une sous-clé K_i. Les sous-clés K₁,..., K_r sont différentes à chaque étage et générées à partir de la clé secrète K et d’un algorithme de génération de sous-clés (voir Figure 1).

Une méthode classique de construction de la permutation interne f est fondée sur ce qu’on appelle les réseaux de substitution-permutation (voir Figure 2). À chaque étage, on applique au bloc d’entrée X_i une substitution non linéaire puis une fonction généralement linéaire. Ces réseaux prennent au mot les deux concepts définis par Shannon : la confusion et la diffusion. La substitution, en général représentée par une série de boîtes S (des permutations non linéaires) appliquées en parallèle, garantit, si elle est bien choisie, une bonne confusion : elle fait disparaître les structures tant linéaires qu’algébriques du chiffrement. La permutation, elle, garantit une bonne diffusion de l’information : elle fait en sorte que chaque bit de sortie soit influencé par le plus grand nombre possible de bits d’entrée. Précisons également que l’usage des mots substitution et permutation est abusif. On peut effectivement parler de substitution en ce qui concerne les boîtes S même s’il peut y avoir confusion avec le terme de permutation, mais le terme de permutation est beaucoup trop approximatif pour désigner l’application linéaire qui suit. Cependant, l’emploi de ces termes reste classique en cryptographie, nous continuerons donc à les utiliser dans la suite de ce paragraphe.

Ce réseau doit également vérifier ce qu’on appelle l’effet avalanche : les modifications du texte clair doivent être de plus en plus importantes au fur et à mesure que les données se propagent dans la structure de l’algorithme. De ce fait, en perturbant un seul bit en entrée, on obtient idéalement une sortie totalement différente, d’où le nom de ce phénomène. En effet, si la diffusion des modifications des entrées sur les sorties n’est pas suffisamment grande, il sera possible d’établir des prédictions sur les entrées à partir de l’observation des sorties et donc d’obtenir un biais statistique.

2.2. Description de l’AES

L’AES est le standard actuel de chiffrement par bloc et utilise un réseau de substitution-permutation. Mais avant de décrire l’algorithme en lui-même, rappelons tout d’abord dans quel contexte Rijndael a été choisi pour devenir l’AES. En 1997, sachant déjà l’ancien standard de chiffrement par bloc, le DES, vulnérable, le NIST (National Institute for Standard and Technology) lançait un appel pour choisir un nouvel algorithme de chiffrement par bloc dont la longueur des clés de 128, 192 et 256 bits devait permettre de l’utiliser au cours du 21ème siècle. Ce nouvel algorithme porterait le nom d’AES (Advanced Encryption Standard). 15 propositions émanant des quatre coins du monde ont été soumises. En août 1999, après une première phase de sélection, 5 finalistes ont été retenus, il s’agissait de Mars, Serpent, Twofish, RC6 et Rijndael. C’est finalement Rijndael qui a été choisi comme AES le 2 octobre 2000. Il est aujourd’hui spécifié dans la norme FIPS-197 [13].

L’AES chiffre des blocs de 128 bits sous des clés de 128, 192 ou 256 bits. Le nombre d’étages est variable en fonction de la longueur de la clé : 10 tours si la clé maître fait 128 bits, 12 tours pour une clé de 192 bits et 14 tours pour une clé de 256 bits. Ces tours sont précédés d’une addition avec la sous-clé K  (un ou-exclusif bit à bit) tandis que le dernier tour ne contient pas l’opération MixColumns décrite plus loin. L’AES est un chiffrement orienté octet, c’est-à-dire que le bloc de 128 bits à chiffrer est représenté par 16 octets.

La fonction de tour de l’AES décrite à la figure 3 fait agir une même boîte S 16 fois en parallèle sur chacun des octets (cette étape s’appelle SubBytes dans la FIPS-197) puis une permutation linéaire (composée des opérations ShiftRows et MixColumns) suivie par un ou-exclusif bit à bit avec la sous-clé K_i du tour (appelé AddRoundKey).

La boîte S utilisée est composée elle-même de deux opérations : l’inversion dans le corps à 2⁸ éléments, suivie d’une transformation linéaire sur les mots de 8 bits. Cette boîte S n’a pas été choisie au hasard. En effet, elle offre une bonne résistance aux cryptanalyses linéaires et différentielles et suit le principe de confusion.

Quant à la partie linéaire, elle est composée des opérations ShiftRows et Mixcolumns qui agissent sur une matrice d’octets de taille 4 × 4. L’opération ShiftRows consiste à faire subir une permutation circulaire vers la gauche aux lignes de la matrice à chiffrer :

MixColumns est une fonction de diffusion optimale sur les mots de quatre octets qui porte sur chaque colonne de la matrice représentant le bloc d’entrée.

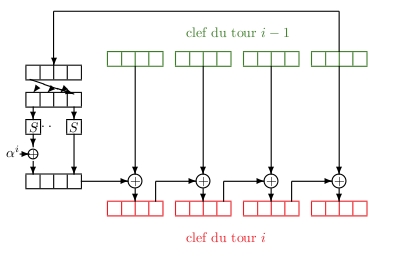
Le cadencement de clé qui permet de générer les sous-clés de chaque étage à partir de la clé maître K utilise les opérations déjà définies dans le chiffrement. Plus précisément, la clé maître K est représentée par Nk mots de 32 bits, Nk valant 4, 6 ou 8 en fonction de la longueur de la clé. Il s’agit donc d’étendre cette clé en Nb+1 clés K_i de 128 bits où Nb désigne le nombre de tours. Le schéma général du cadencement de clé est présenté à la figure 4 où F est la fonction qui décale de 1 octet vers la gauche les octets du mot de 32 bits et qui ensuite applique à ce mot de 32 bits 4 fois la boîte S de l’AES en parallèle et finalement ajoute une constante. Une fois ce tableau construit, les sous-clés sont prises dans l’ordre de leur utilisation : les 4 premiers mots de 32 bits vont donner la sous-clé K , les 4 suivants, la sous-clé K₁, et ainsi de suite.

3. 2001-2004 : doutes et certitudes

Entre 2001 et 2004 est apparue une nouvelle forme de cryptanalyse : la cryptanalyse algébrique. Il s’agissait de mettre en pratique l’attaque déjà proposée par Shannon dans son article fondateur de 1949 [22]. Cette attaque consiste à mettre en équation les relations liant un ensemble de messages clairs, l’ensemble correspondant de messages chiffrés en fonction des bits des sous-clés intervenant à chaque étage. Plus précisément et comme écrit dans [22] : étant donné un message clair de n bits, M = m₁, m₂, ⋯, m_n, une clé de ℓ bits, K=K₁, …, K_ℓ et le message chiffré correspondant C = c₁,c₂, ⋯ ,c_n, le cryptanalyste peut écrire les équations de chiffrement :

c₁ = f₁(m₁, m₂, ⋯, m_n, K₁, ⋯, K_ℓ) 

c₂ = f₂(m₁, m₂, ⋯, m_n, K₁, ⋯, K_ℓ) 

 ⋮  

c_n = f_s(m₁, m₂, ⋯, m_n, K₁, ⋯, K_ℓ)    

Dans ce système, tout est connu sauf les bits de clé K_i. Chacune de ces équations doit donc être complexe en les K_i et impliquer beaucoup d’entre eux. En particulier, elle doit avoir un degré élevé. Sinon, l’ennemi peut résoudre les équations les plus simples et ensuite les plus complexes par substitution.

3.1. L’attaque de Shannon sur l’AES

Si on applique cette idée au cas de l’AES, on génère les équations binaires suivantes :

- Pour le premier tour dont la sortie est le mot de 128 bits, x₁, l’équation impliquant les bits de x₁=(x₁¹, ⋯ , x₁¹²⁸), les bits du message m=(m¹, ⋯, m¹²⁸) et les bits de la sous-clé K =(K ¹, ⋯, K ¹²⁸) s’écrit :

(x₁¹ , ⋯ ,x₁¹²⁸) = F(m¹ + K ¹, ⋯ ,m¹²⁸ + K ¹²⁸)   avec  degF = 7.

- De même, si on écrit les relations liant les bits de la sous-clé K₁(K₁¹, ⋯, K₁¹²⁸) en fonction des bits de la clé maître, on obtient (la sous-clé K  étant en fait les 128 premiers bits de la clé maître K) pour une clé maître de 128 bits :

(K₁¹, ⋯ ,K₁³²) = G(K ¹, ⋯ ,K ¹²⁸)  avec  degG = 7  et  

(K₁³³, ⋯ ,K₁¹²⁸) = ℓ(K ¹, ⋯ ,K ¹²⁸ , K₁¹, ⋯ ,K₁³²)  avec  degℓ = 1.

- Pour le deuxième tour où la sortie est x₂, on obtient :

(x₂¹ , ⋯ ,x₂¹²⁸) = F(x₁¹ + K₁¹, ⋯ ,x₁¹²⁸ + K₁¹²⁸)  avec  degF = 7.

En poursuivant ainsi le raisonnement, on obtient un système d’équations dépendant des 128 variables de la clé maître (pour une clé de 128 bits), de 10 × 32 variables intermédiaires pour les sous-clés et de 9 × 128 variables intermédiaires pour l’état, soit un système de 1600 équations de degré 7 en 1600 variables.

3.2. Amélioration de Courtois et Pieprzyk [8]

On peut faire diminuer le degré algébrique du système précédent en utilisant l’idée développée par N. Courtois et J. Pieprzyk. Dans [8], les auteurs remarquent qu’il existe des relations de degré 2 entre les entrées et les sorties de la boîte S de l’AES. En effet, on a :

S(x) = x⁻¹  pour tout x ≠ 0, soit  xS(x) = 1, pour tout  x ≠ 0.

Ce que l’on peut réécrire en x²S(x) = x pour tout x.

Plus précisément, on peut obtenir ainsi 39 relations booléennes de degré 2 entre chaque octet en entrée et sortie d’un tour de chiffrement (ou de cadencement de clé). Dans le système précédent, on remplace 8 relations de degré 7 (les expressions dépendant de S) par 39 relations de degré 2. Ce qui revient à construire un système de 8000 équations de degré 2 en 1600 variables.

3.3. Comment résoudre ces systèmes ?

La question qui se pose alors est de trouver une méthode efficace pour résoudre un tel système polynomial. Il existe différentes techniques pour ce faire :

- La linéarisation qui consiste à remplacer toute variable de degré supérieur à 1 par une nouvelle variable puis à appliquer un pivot de Gauss sur le système linéaire qui en résulte.

- La résolution utilisant les bases de Gröbner dont le principe est d’utiliser une division euclidienne généralisée dans les idéaux de polynômes. On dispose d’un certain nombre d’algorithmes pour calculer les bases de Gröbner. Parmi les implémentations les plus efficaces de ces techniques développées à ce jour, on peut citer F4 et F5 développés par J.-C. Faugère [11] [12].

- Les SAT-solvers sont une classe d’algorithmes qui permettent de résoudre des instances particulières SAT. Rappelons que le problème de satisfaisabilité (SAT) est un problème de décision qui consiste à savoir s’il existe une solution à une série d’équations booléennes données.

- Évidemment, il existe des techniques ad-hoc qui permettent d’utiliser des méthodes particulières fonction du système lui-même (s’il est creux, sur-défini, sous-défini, etc.).

Mais il reste impossible de résoudre le système généré par un AES complet (comme précisé dans l’AES security report produit par le réseau d’excellence européen ECRYPT [19]). Pour mesurer à quel point ces attaques sont loin d’être effectives, on peut tenter de proposer un système réduit approprié que l’on peut casser, puis en déduire la complexité de résolution pour un AES complet. Parmi les principales tentatives, on peut citer le travail de C. Cid, S. Murphy et M. Robshaw qui, dans [7], ont créé une version réduite de l’AES sur F₂⁴ et ont pu attaquer jusqu’à 4 tours de cette version réduite montrant ainsi que l’AES complet était hors de portée d’une telle attaque. Mais il reste de nombreux problèmes ouverts sur le sujet, en particulier, il reste à déterminer l’influence du caractère creux du système sur sa résolution.

3.4. Prolongement des attaques algébriques

L’émergence des attaques algébriques a bien sûr eu des conséquences sur le monde de la cryptographie symétrique. D’une part, elles ont conduit à la définition des critères de résistance aux attaques algébriques afin de pouvoir choisir les meilleures composantes non linéaires pour les systèmes de chiffrement (dans le cas des algorithmes de chiffrement par bloc, il s’agit surtout des boîtes S). D’autre part, si les attaques algébriques semblent ne pas mettre en danger les chiffrements par bloc, elles se sont montrées efficaces contre de nombreux chiffrements à flot.

3.4.1. Critères de résistance aux attaques algébriques

Afin de résister aux attaques algébriques, l’immunité algébrique d’une fonction S opérant sur les mots de n bits est définie comme étant le degré minimal d d’une relation booléenne non nulle f telle que f(x,S(x)) = 0 pour tout x. On peut montrer qu’il existe une relation de degré inférieur ou égal à d dès que :

​

Cela implique que des relations de degré 2 existent si n ≤ 6 et que toute fonction avec 8 variables en entrée et en sortie a des relations de degré 3. Cependant, à l’heure actuelle, il n’existe pas de critère précis lié au nombre de relations de petit degré.

3.4.2. Attaques algébriques contre les chiffrements à flot

Même si les attaques algébriques semblent avoir une complexité trop élevée pour mettre en danger les chiffrements par bloc, elles se sont avérées un outil puissant quand il s’est agi d’attaquer les chiffrements à flot. Rappelons rapidement qu’un chiffrement à flot est un générateur pseudo-aléatoire qui produit une suite pseudo-aléatoire générée à partir d’une clé secrète partagée par les entités souhaitant communiquer. Jusqu’en 2003, la plupart des chiffrements à flot (comme E0, le chiffrement utilisé par Bluetooth) étaient composés d’un état interne dont le contenu était mis à jour via des relations linéaires et ensuite, le contenu de cet état était filtré par une fonction booléenne f choisie pour ses bonnes propriétés cryptographiques. C’est la sortie de cette fonction f qui constituait la suite pseudo-aléatoire binaire produite par le chiffrement.

Le principe général des attaques algébriques est d’exploiter la linéarité de la fonction de mise à jour du registre et ensuite d’utiliser des relations de bas degré induites par la fonction de filtrage f. Ainsi, il était possible de construire des relations de la forme : si f(x₁, ⋯ ,x_n)=1, alors g(x₁, ⋯ ,x_n) = 1 avec deg g < deg f. Cette technique a permis d’attaquer avec succès des algorithmes comme Toyocrypt, E0, Sober, LILI-128 ou Sfinks. Ainsi, en 2003, à la fin du projet NESSIE, processus de choix de primitives cryptographiques lancé par l’Europe, il ne restait aucun candidat (indemne d’attaques) dans la catégorie chiffrements à flot et générateurs de nombres pseudo-aléatoires : le portfolio NESSIE pour cette catégorie était vide !

C’est pour cette raison qu’en 2004, le réseau d’excellence européen ECRYPT a lancé le projet eSTREAM [10] d’appel à chiffrements à flot. En 2008, à la fin du processus de soumission et d’évaluation, ce sont finalement 8 (puis 7) algorithmes de chiffrement à flot qui ont été recommandés sur les 34 soumissions originelles. Tous ces finalistes utilisent une fonction non linéaire de mise à jour de l’état interne.

4. 2005-2008 : l’âge d’or

La certitude que l’AES résistait aux attaques algébriques l’a alors transformé en couteau suisse de la cryptographie. Cela a été rendu possible grâce à la démocratisation de l’AES, notamment à travers le nouvel ensemble de 7 instructions Intel^®, appelé Intel^® AES-NI, implémenté en dur dans les processeurs Intel^® Xeon et dans la deuxième génération des processeurs Intel^® Core^TM. Cet ensemble d’instructions a rendu l’AES encore plus rapide qu’il n’était et l’a introduit dans énormément de machines grand public.

L’actualité de l’AES a été cependant moins prégnante durant la période 2005-2008. En effet, c’étaient les fonctions de hachage qui étaient sous les feux de l’actualité. Tout d’abord parce que tous les standards choisis durant les années 90 étaient en train d’être attaqués avec beaucoup de succès. Déjà, MD4, standardisé en 1992 [20], avait été attaqué avec succès par H. Dobbertin en 1996 [9]. En ce qui concerne MD5 [21], il a fallu attendre 2004 et l’attaque de X. Wang [26] qui, après diverses améliorations, permet de trouver des collisions sur MD5 en quelques millisecondes. Dans le même temps, la famille SHA [16] [17] [18] ne sortait pas indemne de ces attaques [27] [25] : il est possible de trouver des collisions sur SHA-0 en 1 heure et sur SHA-1 en un temps calcul certes encore hors de portée, mais bien inférieur à ce que l’on attend pour une fonction bien conçue. De même, les autres fonctions de hachage existantes comme HAVAL [23] ou RIPEMD [24] ont été attaquées avec succès.

Ne survivait donc en 2005 comme standard pour les fonctions de hachage que SHA-2. C’est ce qui a poussé le NIST à lancer en 2007 une nouvelle compétition internationale pour choisir et standardiser une nouvelle fonction de hachage, SHA-3 (http://csrc.nist.gov/groups/ST/hash/sha-3/), qui devra être utilisée dans les années à venir. La date limite de soumission était octobre 2008. Le NIST a reçu 64 algorithmes des 4 coins du monde. Après une première phase de sélection en décembre 2008, 51 candidats ont été retenus pour le premier tour. Après le deuxième tour, 14 candidats ont été retenus, puis en décembre 2010, ce sont finalement 5 finalistes qui ont été choisis. La sélection du vainqueur devrait avoir lieu fin 2012.

Parmi les 14 finalistes du deuxième tour, 4 utilisaient des fonctions de l’AES ou s’inspiraient de sa structure et parmi les 5 finalistes restants, Grøstl [14] utilise une structure similaire à celle de l’AES.

Ainsi, l’âge d’or de l’AES a consisté en sa popularisation et en la diversification de l’utilisation des fonctions le composant.

5. 2009-2011 : premières alertes ?

Depuis 2008, au travers de la compétition SHA-3, le monde de la cryptographie symétrique s’est concentré sur la conception et les attaques de fonctions de hachage. Cela a permis des avancées notables en cryptanalyse, notamment sur la définition même de ce qu’est une attaque. Une partie de ces résultats a pu être appliquée à l’AES.

5.1. Attaque par rebond

Cette attaque a été introduite dans [15] et peut être vue comme une amélioration de la cryptanalyse différentielle.

5.1.1. Cryptanalyse différentielle

La cryptanalyse différentielle introduite par E. Biham et A. Shamir en 1991 [2] consiste à étudier l’évolution au cours du chiffrement d’une différence introduite dans un couple de messages m et m′ : m′= m + a. Le chemin différentiel à travers le chiffrement est probabiliste et dépend essentiellement du passage de la différence à travers les boîtes S. Pour calculer cette probabilité, on s’attache donc tout d’abord à calculer la probabilité de passage de la différence à travers chacune des boîtes S. On calcule donc la probabilité, évaluée sur toutes entrées X que la différence entre S(X+a) et S(X) soit égale à b, pour un couple donné (a,b) de différences en entrée et sortie.

Si on cherche à appliquer cette technique à 4 tours de l’AES, l’un des meilleurs chemins différentiels que l’on peut construire est celui représenté à la figure 5. Il s’agit de trouver un couple d’entrées qui diffèrent sur un octet et dont les sorties après 4 tours diffèrent également sur un octet.

5.1.2. Attaque par rebond

L’attaque par rebond est une amélioration de l’attaque différentielle classique : il ne s’agit plus de regarder un couple de différences d’entrée/sortie précis mais de s’intéresser à l’ensemble des couples de différences et de valeurs qui vont vérifier le passage à travers S₃ (voir Figure 6).

On choisit tout d’abord un couple de différences (δ₁, δ₂) sur 4 octets comportant des différences, comme indiqué à la figure 6. On traverse la partie linéaire pour, à partir de δ₁, obtenir une différence a sur 16 octets en entrée de S₃. De même, à partir de δ₂, on remonte jusqu’à la sortie de S₃ pour obtenir une différence b sur 16 octets en sortie de S₃. La probabilité qu’on puisse connecter les différences a et b en entrée/sortie de S₃ pour les 16 octets est 2⁻¹⁶ car pour une différence donnée en entrée/sortie (α, β) d’une boîte S, la probabilité que cette différence soit valide est 1/2. En d’autres termes : Pr[ ∃ X / S(X+α) + S(X) = β] = 1/2. Mais, à chaque fois qu’on trouve une paire (α, β) valide, cette différentielle est vérifiée par deux valeurs. Donc le nombre de valeurs qui vérifie la différence (a, b) est 2¹⁶ pour les 16 octets.

Il faut donc en moyenne essayer 2¹⁶ différences (δ₁, δ₂) pour obtenir un couple de différences valide (a, b) qui lui-même va donner 2¹⁶ valeurs qui vont vérifier cette différence. Le coût amorti pour obtenir un couple de valeurs vérifiant la différence (δ₁, δ₂) est donc de 1.

Afin de finir l’attaque, on remonte les tours restants au début et à la fin du chemin pour les valeurs trouvées et on teste si les valeurs obtenues sont correctes sur le reste du chemin.

Cette nouvelle technique a permis de montrer que 8 tours de l’AES ne se comportent pas comme une permutation aléatoire parfaite, autrement dit, pour 8 tours de l’AES, il existe des structures sous-jacentes qui permettent de le différencier d’une vraie permutation aléatoire. Cette attaque a également permis d’une part de cryptanalyser avec un succès raisonnable un certain nombre de soumissions SHA-3 comme LANE ou la version 2 de Grøstl, et d’autre part, de montrer le comportement imparfait de composants des fonctions de hachage Grøstl, ECHO ou Whirlpool. Cette technique d’attaque peut également être généralisée à d’autres types de structures comme celles des candidats SHA-3 JH ou Skein.

5.2. Attaques à clés liées

Le principe des attaques à clés liées a été introduit en 1993 par E. Biham [1], il est le suivant : l’attaquant dispose de couples clairs-chiffrés obtenus avec différentes clés liées par une relation de son choix. Cela peut paraître étonnant comme forme d’attaque et semble ne pas remettre en cause la sécurité d’un chiffrement par bloc lorsqu’on l’utilise de façon classique. Cependant, ces attaques deviennent pertinentes quand le chiffrement par bloc considéré est employé dans une fonction de hachage, par exemple avec la construction de Davies-Meyer pour laquelle le message joue le rôle de la clé. L’attaquant qui, dans le cas d’un chiffrement par bloc, n’avait aucun contrôle sur la clé, peut ici agir à sa guise sur le message.

De nombreux résultats récents utilisent ce modèle contre l’AES-256, c’est-à-dire l’AES utilisant une clé de 256 bits. En effet, la diffusion de différences dans l’algorithme de cadencement de clés de l’AES est plus lent pour des clés de taille 256 bits, comme le montre la figure 7.

Le premier résultat concernant les attaques à clés liées sur les 14 tours de l’AES-256 est dû à A. Birykov, D. Khovratovich et I. Nikolic dans [5]. Ils utilisent une différence sur les clés comme celle présentée à la figure 7 pour annuler les différences sur les états internes du chiffrement. Un exemple d’une telle annulation est présenté à la figure 8 pour les deux premiers tours de l’AES-256.

En continuant ainsi de façon probabiliste, le processus d’annulation des différences entre les sous-clés et les états internes du chiffrement, A. Birykov, D. Khovratovich et I. Nikolic arrivent à construire une attaque à clés liées sur l’AES-256 en entier nécessitant 2¹³¹ calculs, une place en mémoire de 2⁶⁵ en utilisant 2³⁵ clés différentes et permettant de retrouver la clé. La complexité de cette attaque est bien en-dessous de la recherche exhaustive de la clé qui nécessite 2²⁵⁶ chiffrements.

Dans [4], A. Birykov et D. Khovratovich ont amélioré ce résultat et leur nouvelle attaque à clés liées nécessite 2^99.5 calculs, une place en mémoire de 2⁷⁷ en utilisant 4 clés différentes et permet de retrouver la clé. Ils proposent également la première attaque contre une version complète de l’AES-192 avec une complexité de 2¹⁷⁶ calculs, une place en mémoire de 2¹⁵² en utilisant 4 clés différentes et 2¹²³ couples clairs-chiffrés. Finalement, dans [3], une attaque sur 9 des 14 tours de l’AES-256 permet de retrouver la clé avec une complexité de 2³⁹ calculs, une place en mémoire de 2³² en utilisant seulement 2 clés différentes. L’intérêt d’une telle attaque est qu’elle peut être réalisée en pratique.

5.3. Attaque par bicliques

Depuis 2009, est également apparue une nouvelle forme d’attaque appelée attaque par bicliques. Le but de cette attaque est de trouver des structures internes au chiffrement permettant d’améliorer la recherche exhaustive de la clé. Plus précisément, il s’agit de réussir à diviser le chiffrement en plusieurs sous-chiffrements et à utiliser des structures déjà calculées sur une partie pour simplifier la recherche exhaustive sur la suivante.

Dans le cas de l’AES et des résultats proposés dans [6], les structures utilisées pour améliorer la recherche exhaustive sont fondées sur des chemins différentiels à clés liées. Cela permet de construire les attaques résumées dans la table 1.

Il s’agit donc bien des premières attaques moins chères que la recherche exhaustive sur les trois versions complètes de l’AES. Elles ne mettent cependant pas en danger l’algorithme car leurs complexités sont extrêmement élevées. Elles révèlent cependant des faiblesses potentielles qui seront éventuellement mieux exploitées dans les années à venir.

Conclusion

Même si l’attention du monde cryptographique se concentre aujourd’hui sur la compétition SHA-3 et ses candidats, attaquer l’AES reste un défi permanent pour tout cryptanalyste et beaucoup d’efforts ont été faits pour tenter de l’attaquer. On peut cependant dire qu’actuellement, l’AES ne comporte pas de faiblesse notable et peut toujours être utilisé comme chiffrement par bloc même s’il semble que l’AES-256 n’offre pas une sécurité de 256 bits en raison des attaques à clés liées existant contre lui.

Comme nous venons de le voir, il est très risqué d’utiliser une primitive cryptographique pour une fonctionnalité pour laquelle elle n’a pas été conçue : il semble aujourd’hui dangereux d’utiliser l’AES comme fonction de hachage en mode Davis-Meyer par exemple. Il est également important de noter qu’à cause des attaques à clés liées, la clé maître doit être un secret tiré uniformément au hasard et que, par exemple, utiliser une clé, puis la modifier suivant une procédure déterministe au lieu d’en tirer une nouvelle, fait partie des méthodes à proscrire.

Les différentes expériences de standardisation de primitives de cryptographie symétrique ont montré que la durée de vie moyenne d’un algorithme est d’une quinzaine d’années, ce qui peut sembler peu mais ne semble pas si étonnant quand on sait qu’un standard concentre les tentatives d’attaques d’une grande partie de la communauté cryptographique. Est-ce alors qu’il faut déjà s’interroger sur la future durée de vie du finaliste de la compétition SHA-3 ?

Références

[1] Eli Biham, New types of cryptoanalytic attacks using related keys (extended abstract), in Advances in Cryptology - EUROCRYPT ’93, volume 765 of Lecture Notes in Computer Science, pages 398–409. Springer, 1993

[2] Eli Biham and Adi Shamir, Differential Cryptanalysis of DES-like Cryptosystems, J. Cryptology, 4(1):3–72, 1991

[3] Alex Biryukov, Orr Dunkelman, Nathan Keller, Dmitry Khovratovich, and Adi Shamir, Key recovery attacks of practical complexity on AES-256 variants with up to 10 rounds, in Advances in Cryptology - EUROCRYPT 2010, volume 6110 of Lecture Notes in Computer Science, pages 299–319. Springer, 2010

[4] Alex Biryukov and Dmitry Khovratovich, Related-key cryptanalysis of the full AES-192 and AES-256, in Advances in Cryptology - ASIACRYPT 2009, volume 5912 of Lecture Notes in Computer Science, pages 1–18. Springer, 2009

[5] Alex Biryukov, Dmitry Khovratovich, and Ivica Nikolic, Distinguisher and related-key attack on the full AES-256, in Advances in Cryptology - CRYPTO 2009, volume 5677 of Lecture Notes in Computer Science, pages 231–249. Springer, 2009

[6] Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger, Biclique cryptanalysis of the full AES. In Advances in Cryptology - ASIACRYPT 2011, volume 7073 of Lecture Notes in Computer Science, pages 344–371, Springer, 2011

[7] Carlos Cid, Sean Murphy, and Matthew J. B. Robshaw, Small scale variants of the AES, in Fast Software Encryption: 12th International Workshop, FSE 2005, volume 3557 of Lecture Notes in Computer Science, pages 145–162. Springer, 2005

[8] Nicolas Courtois and Josef Pieprzyk, Cryptanalysis of block ciphers with overdefined systems of equations, in Advances in Cryptology - ASIACRYPT 2002, volume 2501 of Lecture Notes in Computer Science, pages 267–287. Springer, 2002

[9] Hans Dobbertin, Cryptanalysis of MD4, in Fast Software Encryption, Third International Workshop - FSE 1996, volume 1039 of Lecture Notes in Computer Science, pages 53–69, Springer, 1996

[10] ECRYPT Stream Cipher Project eSTREAM, The current estream portfolio, eSTREAM, ECRYPT Stream Cipher Project, 2008, http://www.ecrypt.eu.org/stream

[11] J. Faugère, A new efficient algorithm for computing Gröbner basis (F4), Journal of Pure and Applied Algebra, 139(1-3):61–88, 6 1999

[12] Jean Charles Faugère, A new efficient algorithm for computing Gröbner bases without reduction to zero (F5), in Proceedings of the 2002 international symposium on Symbolic and algebraic computation, ISSAC ’02, pages 75–83, ACM, 2002.

[13] FIPS 197, Advanced Encryption Standard, Federal Information Processing Standards Publication 197, 2001, U.S. Department of Commerce/N.I.S.T.

[14] Praveen Gauravaram, Lars R. Knudsen, Krystian Matusiewicz, Florian Mendel, Christian Rechberger, Martin Schläffer, and Søren S. Thomsen, Grøstl – a SHA-3 candidate, Submission to NIST (Round 3), 2011

[15] Florian Mendel, Christian Rechberger, Martin Schläffer, and Søren S. Thomsen, The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Grøstl, in Fast Software Encryption - FSE 2009, volume 5665 of Lecture Notes in Computer Science, pages 260–276, Springer, 2009

[16] U.S. Department of Commerce, FIPS 180: Secure Hash Standard, Federal Information Processing Standards Publication, N.I.S.T., 1993

[17] U.S. Department of Commerce. FIPS 180-1: Secure Hash Standard (SHS), Federal Information Processing Standards Publication, N.I.S.T., 1995

[18] U.S. Department of Commerce, FIPS 180-2: Secure Hash Standard. Federal Information Processing Standards Publication, N.I.S.T., 2002

[19] European Network of Excellence ECRYPT, AES security report (ecrypt 2006), 2006, http://www.ecrypt.eu.org/ecrypt1/documents/D.STVL.2-1.0.pdf

[20] Ronald L. Rivest, The MD4 message-digest algorithm, Internet RFC 1320, 1992

[21] Ronald L. Rivest, The MD5 message-digest algorithm, Internet RFC 1321, 1992

[22] C. E. Shannon, Communication theory of secrecy systems, Bell System Technical Journal, 28:656–715, 1949

[23] Xiaoyun Wang, Dengguo Feng, and Xiuyuan Yu, An attack on hash function HAVAL-128, Science in China Series F: Information Sciences, 48(5):545–556, 2005

[24] Xiaoyun Wang, Xuejia Lai, Dengguo Feng, Hui Chen, and Xiuyuan Yu, Cryptanalysis of the hash functions MD4 and RIPEMD, in Advances in Cryptology - EUROCRYPT 2005, volume 3494 of Lecture Notes in Computer Science, pages 1–18, Springer, 2005

[25] Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu, Finding collisions in the full SHA-1, in Advances in Cryptology - CRYPTO 2005, volume 3621 of Lecture Notes in Computer Science, pages 17–36, Springer, 2005

[26] Xiaoyun Wang and Hongbo Yu, How to break MD5 and other hash functions, in Advances in Cryptology - EUROCRYPT 2005, volume 3494 of Lecture Notes in Computer Science, pages 19–35, Springer, 2005

[27] Xiaoyun Wang, Hongbo Yu, and Yiqun Lisa Yin, Efficient collision search attacks on SHA-0, in Advances in Cryptology - CRYPTO 2005, volume 3621 of Lecture Notes in Computer Science, pages 1–16, Springer, 2005