YAMS : encore un autre algorithme de tri !

Je pensais que tout avait déjà été inventé et que la question du tri était réglée depuis les années 60. C'est sans compter l'évolution des besoins, des architectures, et surtout des connaissances qui se croisent et s'émulent pour donner de nouvelles combinaisons inattendues. Revisitons donc ce vieux classique...

1. Théorie

Pourtant, il existe déjà tellement d'algorithmes de tri qu'en inventer un autre ne vaut pas la peine. Après tout, on connaît déjà tout de cette classe d'algorithmes et rien que la page Wikipédia sur le sujet [1] regorge de références toutes plus hétéroclites les unes que les autres. Je ne suis même pas sûr que Donald Knuth arrive un jour à en faire le tour. De plus, on sait pertinemment que l'algorithme de tri par racine (plus communément appelé radix sort) bat tous les autres à plate couture [2]. Ce ne sont au final que de banales permutations, n'est-ce pas, alors à quoi bon essayer de réinventer la roue ?

1.1 Motivations

Tout d'abord, le radix sort n'est pas le plus efficace pour les petites tailles (en raison de différents surcoûts), alors que je me retrouve parfois à trier des blocs de seulement 256 nombres. Aussi, dans sa version usuelle, il ne trie que des nombres. Ensuite, l'algorithme fourni par votre langage préféré n'offre peut-être pas les fonctionnalités que vous cherchez. Ou bien vous ne disposez pas d'une bibliothèque standard suffisamment élaborée pour fournir une fonction de tri, par exemple sur un microcontrôleur. Ou même, vous voulez contrôler finement l'allocation de la mémoire ou distribuer les opérations sur plusieurs processeurs, que sais-je...

Et les applications des algorithmes de tri sont innombrables, en particulier lorsque chaque donnée à trier (appelée clé, qui n'est pas forcément un nombre, mais une chaîne de caractères, par exemple) est associée à d'autres données annexes. Le tri effectue alors une permutation de ces éléments annexes en fonction de la clé, et ces permutations ont aussi énormément d'applications. Bref, les raisons ne manquent pas et ne se limitent pas au syndrome « Not Invented Here ».

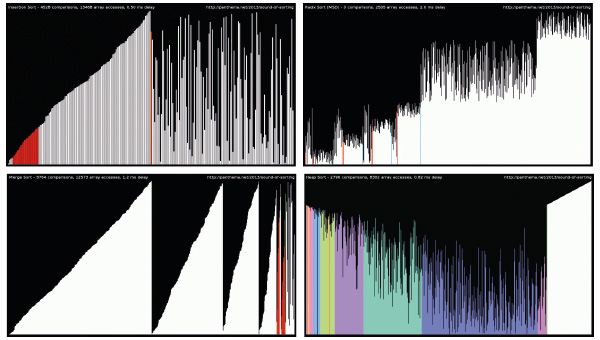
Mais un vrai hacker n'a pas besoin de raison pour bricoler des idées, et tel un con, il ose tout. La faute incombe ici à YouTube qui suggère des vidéos hypnotisantes de visualisation d'algorithmes de tri, mêlant couleurs, mouvements et fréquences sonores, qui stimulent simultanément des zones du cerveau qui n'ont pas l'habitude de ce combo.

Pour cela, je ne remercie pas Timo Bingmann [3] qui, en 2013, a créé quelques vidéos qui sont devenues virales et dont la figure 1 montre des captures d'écran. D'autres vidéos de ce type existaient depuis des lustres, mais en publiant le code source sous GPLv3, il a encouragé d'autres à explorer le sujet de la visualisation des algorithmes (et faire de l'audience au passage). C'est ainsi que YouTube s'est retrouvé envahi par ce type de vidéos.

S'en suit une impression de familiarité trompeuse, car voir un algorithme fonctionner donne une idée de l'intention et du principe, mais ne permet pas nécessairement d'en comprendre les subtilités, les choix, les compromis et surtout les astuces de codage. Pour les personnes qui « pensent visuellement », c'est un déclencheur irrépressible et les idées sortent de leur boîte de Pandore. Accrochez-vous.

1.2 Critères

Pour commencer, cela me chafouine de ne pas être sûr de suffisamment comprendre les concepts et toutes les subtilités de la moitié des algorithmes de tri existants. Je ne parle pas juste de l'idée générale qu'on résume en quelques phrases, mais des codes qui ont été optimisés, améliorés, prouvés et sont ainsi devenus des boîtes noires inflexibles, on entend même à l’avance le poncif péremptoire « cela ne sert à rien de regarder dedans puisque vous ne pourrez pas faire mieux ». On n’a même pas le droit d’essayer, juste pour voir ?

Même si ces algorithmes sont documentés et même enseignés aux programmeurs débutants, au final on ne peut pas tous les décortiquer facilement et surtout ils ne sont pas forcément évidents à adapter à nos propres besoins. On reste enchaînés à une boîte noire algorithmique, alors qu'il n'est même pas question de sécurité ou de cryptographie. L'accessibilité et la simplicité du concept de l'algorithme sont donc essentielles ici.

Pour cette raison, je me raccroche au « grand-père » des algorithmes de tri : le tri fusion [4] imaginé dès 1945 par von Neumann. J'ai toujours été attiré par son élégance et sa simplicité, il est assez efficace et ne requiert que quelques notions intuitives. Pour moi, c’est aussi simple qu’un jeu de cartes que l’on mélange en plaçant deux piles côte à côte, à la différence que chaque carte peut voir si sa voisine est plus élevée ou plus basse qu’elle-même afin de trier au lieu de mélanger. En plus, le tri fusion fonctionne avec des accès consécutifs à la mémoire, tels des flux de données, ce qui est apprécié autant par les lecteurs de bandes magnétiques d'antan que par les disques durs (pour lequel l’utilitaire sort(1) a été optimisé) ou les processeurs modernes (malgré l'augmentation de la taille des mémoires cache).

En effet, la plupart des algorithmes de tri ont été imaginés et créés à l'aube de l'ère informatique, à une époque où la mémoire à tores de ferrite était très limitée (c'était littéralement « cousu main ») et son accès était lent. Donc, le nombre d'accès à la mémoire ainsi que la quantité de données auxiliaires à allouer étaient des critères incontournables, bien que la vitesse d'exécution reste le plus important. Mais la structure des ordinateurs a évolué et s'est même emballée depuis deux décennies et nous devons revoir nos priorités. Peu d'algorithmes prenaient en compte l'importance de la mémoire cache, par exemple. Dans le cas du tri fusion, l'avantage d'effectuer des accès linéaires contigus permet au processeur d'optimiser ses transferts de données, par exemple en préchargeant la mémoire cache.

Reprenons l'argument de feu http://www.sorting-algorithms.com/ : il n'y a pas de meilleur algorithme, car cela dépend de nombreux facteurs dont les données à trier, les conditions initiales, les cas pathologiques à gérer ; mais surtout, l'algorithme idéal devrait avoir les propriétés suivantes, qui sont souvent contradictoires :

1. Stable : deux clés identiques gardent leur ordre, ce qui permet de chaîner le tri avec d'autres opérations.
2. Opère « sur place » en se contentant de l’espace des données initiales, avec une quantité limitée et constante de données annexes.
3. Effectue au pire O(n×log(n)) comparaisons de clés.
4. Effectue au pire O(n) échanges.
5. S'adapte aux cas où les données sont déjà triées ou s'il n’y a que quelques clés uniques.

Ce dernier point est un axe d'optimisation aisé, consistant à ajouter un algorithme pour soulager l'algorithme de tri principal, afin de traiter des données aux caractéristiques très simples. Cependant, nous ne pouvons pas nous reposer entièrement dessus non plus, car les données aléatoires, échappant à tout modèle, doivent aussi être traitées efficacement et sont très courantes.

Aujourd'hui, la capacité de la mémoire de nos ordinateurs est incommensurablement plus grande que dans les années 70 et le critère n°2 peut facilement passer à la trappe (à moins de devoir gérer des quantités énormes de données, ce qui reste rare à notre échelle). Mais si on doit ne manipuler que quelques millions d'entrées, utiliser deux ou trois fois plus de mémoire n'est plus un dilemme pour les programmeurs aguerris. C'est ainsi que le radix sort a pu se développer.

Les critères 3 et 4 sont des limites purement théoriques qui ne tiennent pas compte des autres contraintes. D'autant plus que si l'ordinateur peut fournir un autre espace tampon, nul besoin d'échanger des données une à une, on échange juste des pointeurs vers les espaces mémoire, entre des étapes majeures de l'algorithme, ce qui inverse le rôle d'un tampon de source à celui de destination et vice versa (c’est ce qu’on appelle la technique de double buffer). Sans oublier que le radix sort n'effectue pas de comparaison et que si les données sont déjà prétriées, il devrait y avoir seulement n comparaisons.

Quant au critère n°1, la stabilité n'est pas très importante, surtout si on sait que les clés sont toutes différentes. Sinon, on fait plus attention, tout simplement, par exemple en bricolant la clé pour contenir un hash des données annexes.

Pour revenir au n°2, avec le recul, on peut se dire que c'est un critère totalement arbitraire, pas uniquement sur le fond, mais aussi sur la forme. Il est bien sûr important que l'algorithme soit frugal en mémoire, mais la forme, la présentation, l'organisation de tous les algorithmes présentés dans les exemples disponibles ne change pas depuis des décennies : on commence par un tampon rempli de données, on opère le coup de baguette algorithmagique, et on retrouve ces mêmes données triées dans le tampon d’origine. C'est littéralement « un cas d'école », puisque justement c'est enseigné à l'école et cette organisation est reproduite partout. On pourrait même dire que c'est une forme canonique de tri qui a l'avantage de permettre la comparaison de différents algorithmes.

Mais en pratique, d'autres cas de figure peuvent exister, par exemple si on obtient les données au compte-gouttes, donc on voudrait pouvoir effectuer un tri partiel. On s'oriente alors logiquement vers le tri par insertion, mais sa performance laisse à désirer rapidement puisqu'il requiert O(n²) comparaisons. Pourtant, c'est ce qu'a choisi Tim Peters en 2002 pour concevoir Timsort [5], dans le but d'améliorer l'algorithme par défaut du langage Python, avant d'être repris ensuite par de nombreux autres langages et systèmes.

Pour résumer ma petite liste de courses, je cherchais un algorithme conceptuellement simple, assez efficace sans chercher la performance ultime, et je me suis retrouvé avec un cousin éloigné de Timsort, alors que je ne le connaissais pas encore.

1.3 Concept

Le concept central de YAMS peut se résumer ainsi : c'est un algorithme de tri fusion adaptatif dans un buffer circulaire bidirectionnel. Contrairement au tri fusion classique, et tel Timsort, YAMS traite récursivement des séquences de données triées qui ne sont pas de tailles fixes ou égales, mais dépendent de l'ordre des données en entrée. On peut donc considérer que c'est aussi un algorithme hybride, mais afin de rester simple, ce n’est pas un autre algorithme de tri qu’il utilise.

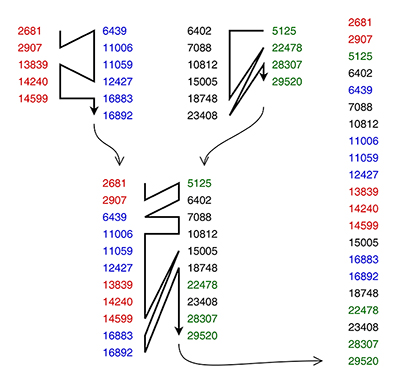
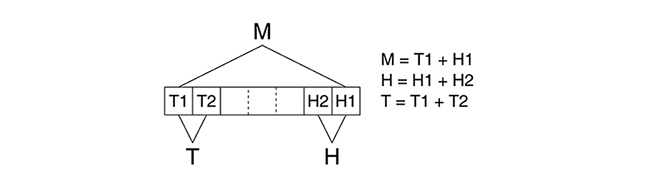
Reprenons les bases du tri fusion, illustré sur la figure 2 : il consiste à fusionner des paires de listes de nombres déjà triés, de façon récursive, pour au final obtenir une seule liste qui est le résultat attendu. Cette étape du tri est d'une grande simplicité : on compare les deux éléments en tête (ou en queue) de chaque liste, et on choisit le plus grand (ou le plus petit). Cet élément est retiré de sa liste et ajouté à la sortie, qui est usuellement une autre liste pour que le processus se répète.

Ce principe est simple, abordable aux novices, très flexible, et de nombreuses organisations des données sont possibles. C'est ainsi que YAMS diffère de Timsort dès qu'on regarde les structures mises en place.

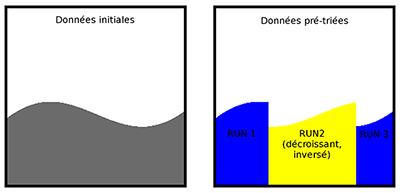
1.4 Prétri

Les listes ou séquences de nombres triés sont appelées des « runs » (figure 3) et commencent à être assemblées par YAMS par un filtre qui reçoit un nombre à la fois, séquentiellement. Cela permet donc d'alimenter YAMS par un autre algorithme, au fur et à mesure de la disponibilité de ses résultats. En d'autres termes, YAMS implémente une tranche du traitement des informations, il n'a pas besoin d'être atomique ou monolithique et certaines étapes peuvent être effectuées dans un ordre ou un autre. Par exemple, le prétri peut avoir lieu d'un coup, puis viennent les tris fusion, mais ces deux étapes peuvent aussi être entrelacées selon l'envie ou l'audace.

Le prétri remplit plus ou moins le rôle du tri par insertion qu'emploie Timsort, mais il essaie d'être plus efficace sans vouloir en faire autant. Timsort découpe les données en runs de deux types : croissants (avec une pente montante ou horizontale) ou bien strictement décroissants. C'est un autre détail divergent : YAMS essaie déjà de maximiser la longueur des runs, donc un run décroissant peut avoir une zone horizontale. L'algorithme en est un peu plus sophistiqué et n’est plus stable, mais l'idée est bien là.

Pour y arriver, le filtre de prétri définit un autre type de pente : indéterminé. Au début d'un run, on ne peut pas en déterminer la pente avec une seule valeur, donc l'état du filtre reste indéterminé tant qu'une valeur différente n'est pas entrée. C'est seulement à la fin, lorsque la pente change de sens, que le run est qualifié croissant ou décroissant pour de bon.

Une autre différence notable avec Timsort est que les runs n'ont pas de taille minimale, afin de garder l'algorithme aussi conceptuellement simple que possible. Cela limite la performance de YAMS, mais c'est un compromis acceptable. En pratique, un run a au moins deux éléments, sauf le cas particulier d'un début de run indéterminé avec un seul élément, lorsque le flux d'entrée se termine. En général, le tri fusion de runs très courts est moins efficace, car l'algorithme doit gérer plein de pointeurs et de compteurs. Timsort utilise le tri par insertion pour compenser, mais nous venons de dire que nous l'excluons, donc nous devons trouver d'autres approches.

Une astuce dans ce sens consiste à ne pas explicitement inverser l'ordre des données lorsqu'un run décroissant est détecté, alors que Timsort doit échanger les positions de chaque donnée. Selon le document expliquant sa conception [6] :

On pourrait dire à Tim : « ne te fatigue pas, marque le bloc comme décroissant et balaie-le dans l'autre sens au moment de la fusion », mais le reste de son algorithme serait trop complexe et nous allons bientôt voir une autre approche bien plus originale.

1.5 Espace annexe

Les caractéristiques de chaque run doivent bien être mémorisées quelque part. Comme Timsort, YAMS utilise une sorte de pile séparée pour se souvenir de la position et de la longueur de chaque run en cours de traitement. Si on s'accorde sur un maximum de 64 Ki nombres à trier, chaque run peut être représenté par un nombre de 16 + 16 = 32 bits (16 bits pour la taille et 16 bits pour l’index de début).

Cela occupe évidemment de la mémoire supplémentaire, mais c'est un surcoût acceptable. J'ai bien essayé d'intégrer cette pile dans l'espace de travail pour réduire l'empreinte, avec un succès mitigé : les types de données sont différents et il faut éviter une collision entre les données et la pile. Et puis l'allocation supplémentaire n'est pas si grande que ça.

En théorie, la profondeur maximale de la pile est la moitié de la taille du bloc de données à traiter, puisqu'un run contient au moins deux éléments (à l'exception du dernier élément, mais ce cas ne peut arriver que si un des runs a une longueur d'au moins 3 éléments, donc tout va bien au final). Donc pour trier 256 nombres, la pile doit avoir une profondeur de 128 runs. En pratique, nous pouvons limiter cette profondeur en décidant que si une pile plus petite est saturée, alors nous déclenchons la fusion d'un certain nombre de runs pour la vider un peu. Des heuristiques sont à déterminer pour prendre cette décision.

La structure de la pile doit suivre de près la structure des données représentées et nous allons voir que cet aspect important de YAMS le différencie encore plus de Timsort et des autres algorithmes connus.

1.6 L'espace de travail

C'est là que tout se joue : l'espace de travail stocke toutes les informations triées et à trier. Idéalement, on voudrait que sa taille coïncide avec celle des données traitées, mais voilà : YAMS utilise le tri fusion, donc nécessite au minimum un espace temporaire. Les algorithmes conventionnels basés sur la comparaison et l'échange sont adaptés aux espaces confinés, mais les motifs d'accès à la mémoire sont d'autant plus étriqués, avec des lectures et écritures parfois redondantes à des adresses imprévisibles et aléatoires, du point de vue d'un processeur moderne. Il existera toujours un compromis à trouver entre la quantité de mémoire allouée et l'effort de traitement.

Le choix du tri fusion implique l'utilisation de mémoire temporaire. Ce n'est plus un tabou depuis longtemps, puisque depuis 20 ans, Timsort utilise un tampon dans lequel il va recopier le run le plus court. Le radix sort quant à lui utilise deux espaces de travail, en plus d'un espace supplémentaire pour y collecter les statistiques cruciales à son efficacité.

La première caractéristique importante de l'espace de travail de YAMS est qu'il est unique, unifié, et sa taille est le double de celle des données. Cela simplifie beaucoup de choses, à commencer par la disparition de l'allocation de tampons temporaires.

Cet espace supplémentaire accélère encore le traitement global en éliminant aussi les copies de blocs, nécessaires lorsqu'on veut fusionner deux runs « à moitié sur place », en empiétant sur l'espace d'un des runs. Ce type de fusion reste bien sûr possible, mais la contrainte est levée lorsque l'espace de travail est garanti suffisamment large pour éviter une copie. Il ne faut pas oublier que les copies et déplacements ajoutent un surcoût non négligeable, car ce n'est pas juste la clé qu'il faut déplacer, mais aussi toutes les données annexes, qui peuvent être conséquentes selon les applications.

1.7 La pile à deux pôles

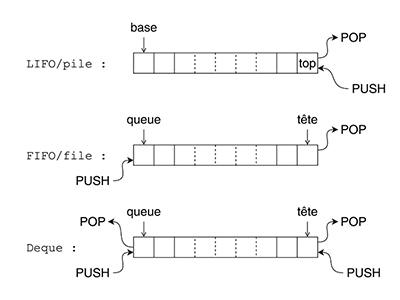
Nous en arrivons à la deuxième caractéristique de YAMS, qui le fait définitivement sortir du lot : l'espace de travail n'est pas un simple tableau, ni même une pile, mais une file d'attente à double extrémité [7], une hybridation de pile avec un buffer circulaire bidirectionnel. Il peut fonctionner en FIFO comme en LIFO dans les deux sens, ce qui permet d'ajouter ou d'enlever des données sur le pointeur de queue comme sur le pointeur de tête. L'adressage de l'espace de travail est circulaire, donc il n'y a pas vraiment de base, contrairement à une pile classique. Nous définissons un point de départ arbitraire et les pointeurs rebouclent automatiquement, sans se soucier des débordements, puisque par définition la taille allouée est suffisante pour éviter les collisions entre la tête et la queue.

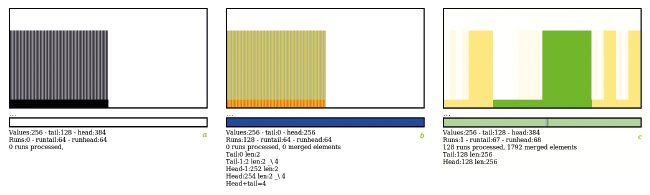
Les buffers circulaires [8] (figure 4) sont répandus (pour réaliser les FIFO et queues logicielles comme matérielles), mais cette structure plus générale, appelée aussi deque (abréviation de l'anglais double-ended queue) est peu courante. Comment en sommes-nous arrivés là ?

Revenons à l'étape du prétri, plus exactement lorsqu'un run décroissant est détecté. Les données venant d'une source extérieure sont comparées et placées au fur et à mesure dans l'espace de travail (figure 5a). Traditionnellement, les runs croissants sont placés « à gauche », basés sur l'index 0 et vont croître vers les adresses supérieures. Logiquement, l'inverse se produit pour les runs décroissants : les runs (qui doivent être croissants au final) sont reconstitués en accumulant les valeurs décroissantes dans l'ordre inverse, à commencer par l'index le plus haut du tableau (à droite donc) et en descendant.

Si on veut éviter de déplacer les données renversées, le système crée en fait deux piles différentes, une pour les runs croissants aux indices bas, et une autre pour les runs décroissants inversés, aux indices hauts (figure 5b). Cela fragmente aussi l'espace, mais a l'avantage de doubler les opportunités de combiner des runs, donc d'éviter des heuristiques foireuses (du style de celles qui ont failli coûter la vie à Timsort).

La solution consiste à unifier les structures évoquées à l'instant. La version actuelle de YAMS, illustrée par la figure 5c, utilise un adressage différent et considère que les deux suites de runs (chacune à une extrémité de l'espace de travail) ne font qu'une ! Les deux piles sont jointes, leurs bases sont alors communes et peuvent être placées n'importe où dans l'espace de travail si l'adressage est circulaire. C'est ainsi que la deque apparaît naturellement comme la structure la plus adaptée pour remplacer les deux piles. À partir de là, tout devient simple.

Nous en revenons à l'étape de prétri et au renversement évoqué plus tôt. Comment peut-on détecter la direction d'un run et éviter de recopier les données ? L'astuce est simplement une écriture spéculative des données entrantes aux deux « bouts » *, à la fois au niveau de la tête et de la queue, tant que la direction est indéterminée. L'écriture est moins pénalisante que la lecture, donc écrire deux fois simultanément est préférable à une écriture suivie d'une relecture et d'une réécriture. Ainsi, le renversement des runs est bien plus efficace qu'avec Timsort !

1.8 Heuristique de fusion

Les deux types de fusion (sur place ou non) sont possibles grâce à la marge confortable fournie par l'espace de travail, et ce degré de liberté supplémentaire permet ensuite de choisir la meilleure séquence de fusions. En effet, certaines séquences sont moins efficaces que d'autres, en particulier lorsque les longueurs des runs à fusionner sont très différentes. Il faut idéalement favoriser les fusions entre runs de tailles égales. Timsort utilise deux heuristiques pour maintenir un certain équilibre entre les trois runs du haut de la pile, alors que les degrés de liberté de YAMS permettent de choisir entre 4 mouvements et 4 candidats.

Le choix des prochains runs à fusionner est directement inspiré d'une version minimaliste de l'algorithme de construction des arbres de Huffmann [9]. Celui-ci consiste à toujours choisir les deux feuilles de plus faible poids pour les réunir. Ce point de vue peut être transposé à un algorithme de tri fusion, puisque ce dernier revient à créer un arbre binaire à mesure que des paires de runs sont fusionnées.

La contrainte ici est que les runs ne peuvent pas être appairés arbitrairement comme dans un algorithme de Huffman, car cela fragmenterait considérablement l'espace de travail. Et qui dit fragmentation dit efforts pour amalgamer les blocs consécutifs et beaucoup de déplacements. L'approche simplifiée, illustrée par la figure 6, considère simplement la longueur des runs au niveau de la tête et de la queue, et choisit la combinaison donnant le plus court résultat. Cela garantit que l'espace de travail reste contigu et il n'y aura pas de trou, donc pas de déplacement de blocs pour défragmenter l'espace.

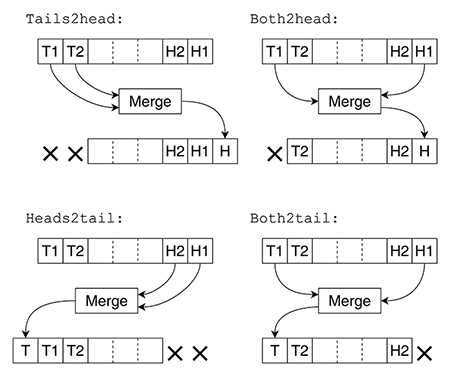
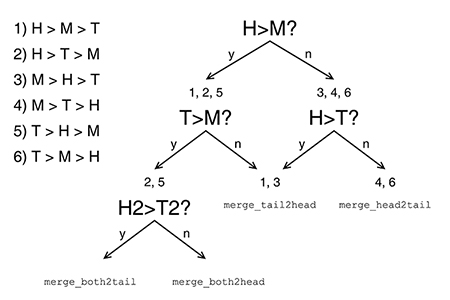
Quatre mouvements sont possibles et représentés sur la figure 7 :

1. Deux runs de queue fusionnés vers la tête, merge_tails2head().
2. Deux runs de tête fusionnés vers la queue, merge_heads2tail().
3. Un run de queue et un run de tête, fusionnés sur place vers la tête, merge_both2head().
4. Un run de queue et un run de tête, fusionnés sur place vers la queue, merge_both2tail().

Le choix des cas 1 et 2 est facile, car il est directement guidé par les données. Par contre, si le plus petit run est celui du milieu, alors il faut décider où la fusion aura lieu : cela dépendra des valeurs sous la queue et la tête afin de favoriser un arbre de Huffman plus équilibré lors de l'étape suivante.

Accessoirement, cette méthode crée des conditions où le run final trié peut se retrouver à cheval entre les deux extrémités de l'espace de travail. Le choix judicieux parmi les 4 mouvements possibles permet de corriger la position finale lors de la dernière étape, ce qui rend le bloc contigu du point de vue du programme. Par exemple, le bloc trié peut être écrit dans un fichier en une seule opération au lieu de gérer deux moitiés non contiguës, sans même recourir à un déplacement du bloc.

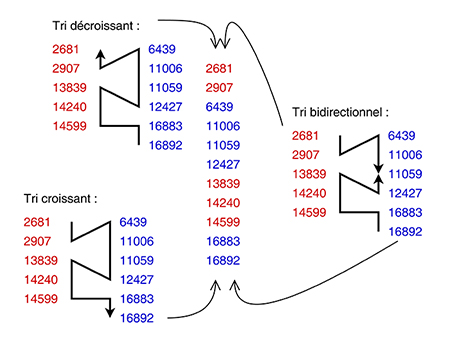
Cependant, pour les autres cas, une fusion d'apparence plus classique peut être préférable, car on peut l'accélérer, contrairement à une fusion sur place qui ne peut progresser que d'un bout à l'autre d'un run. Lorsque deux runs sont lus d'un côté de l'espace de travail pour être fusionnés de l'autre côté, l'opération peut progresser dans n'importe quel sens, des valeurs minimales à maximales, ou l'inverse, et même balayer dans les deux sens en même temps (figure 8) ! YAMS ne dépend pas directement de ce type d'algorithme, mais le permet, d'autant plus que les processeurs modernes peuvent gérer simultanément une centaine d'instructions en cours d'exécution en attendant des opérandes. Malgré sa simplicité, le tri fusion nécessite de nombreux sauts conditionnels difficiles à prévoir et un balayage simultané par les deux bouts permettrait de maintenir le pipeline occupé.

Une autre approche consiste à trier plus de deux runs simultanément, trois ou quatre par exemple. La procédure devient là aussi lourde à gérer et sa réalisation est donc repoussée à plus tard.

2. Développement

L'algorithme a été conçu en JavaScript et intégré à une page HTML dynamique (figure 9) pour maximiser les interactions dès le début, ce qui permet d'explorer plus vite les cas particuliers (grâce aux stimulus disponibles) et de collecter des informations pertinentes. De nombreux boutons permettent de tester certains aspects de l'algorithme et de voir directement le résultat, ce qui protège aussi contre les régressions.

2.1 Couches de base

Les deux premières couches logicielles à développer sont la gestion de la pile directionnelle des runs ainsi que l'espace de travail. Tous les deux sont des deques et partagent une structure commune, puisque leurs organisations respectives doivent parfaitement s'aligner. Les fonctions les plus connues sont HeadPush(), HeadPop(), TailPush() et TailPop(), on trouve aussi des fonctions qui lisent la valeur au niveau de la tête et de la queue : HeapTop() et TailTop() ainsi qu’au niveau en dessous. Ce sont des fonctions vraiment simples, mais les bugs s'y cachent facilement.

Les fonctions Push() de la pile de runs doivent aussi gérer automatiquement la fusion de runs consécutifs le permettant. Prenons par exemple un run ajouté au niveau de la tête : si la valeur minimale de ce run est supérieure à la valeur maximale du bloc précédent, ces deux runs peuvent être fusionnés directement au niveau de leur description respective. Les tests notch et hcton vérifient que le code gère correctement cette situation, qui est peu courante, mais requiert peu de complexité.

L'adressage circulaire implique que tous les calculs d'adresses doivent être modulaires, ou tronqués, ce qui alourdit un peu la lecture du code. Par exemple, au lieu d'écrire runtail++, on trouve runtail = RUNMASK & (runtail+1). La taille de la pile et de l'espace de travail sont ainsi contraints par le masque binaire à être une puissance de deux (ce qui est très courant en pratique). Au besoin, une version avec un saut conditionnel est possible :

Ce qui ajoute au moins trois instructions (comparaison, saut et assignation) alors que le masque binaire en ajoute une seule et ne met pas à genoux le prédicteur de branchements.

2.2 Prétri

Une fois les deux deques programmées, on s'occupe du préfiltre qui est ici réalisé sous forme d'une sorte de machine à états finis, définie par ces quelques variables :

Le code doit factoriser au maximum les opérations pour réduire sa taille. JavaScript ne permettant pas les goto (contrairement au C), les sauts en avant sont réalisés ici par des break dans des « named blocks » (ce que ne permettent pas tous les langages). La fonction YAMS_slope() est appelée en lui donnant comme argument dat, une nouvelle valeur à trier :

Lorsqu'un run est terminé, ou s'il n'y a plus d'autre donnée à entrer, la fonction process_extent() annule l’écriture spéculative inutile et enregistre le run sur l’extrémité correspondante de la deque.

2.3 Fusion progressive ?

C'est à la fin de cette fonction process_extent() que pourrait être appelé le code de fusion, si celle-ci doit s'effectuer progressivement. Des tests ont montré que cette approche séduisante se révèle en fait 10 % moins efficace qu'une fusion générale à la fin, puisque l'algorithme a alors moins de données parmi lesquelles choisir la meilleure action. Toutefois, le tri progressif reste possible, par exemple si la taille de la pile des runs devait être arbitrairement limitée.

Le déclenchement de la fusion ne doit pas être trop régulier afin d'éviter des accumulations de runs trop grands, qui bloqueraient la fusion des autres runs. Une méthode à faible complexité consiste à compter le nombre de LSB à 0 dans un compteur. En fusionnant deux runs chaque fois que le LSB est à zéro, cette méthode garantit un équilibrage de l'arbre binaire des fusions correspondant.

La séquence d’appels générée par le code ci-dessus est :

Cependant, on voudrait quand même garder quelques éléments libres pour plus tard afin d'avoir un peu plus de choix lors des prochaines fusions, donc elle n'est pas effectuée s’il reste 3 runs ou moins (ceci étant une valeur arbitraire). C'est moins flexible que la méthode de Timsort, mais elle limite notablement l'espace occupé par la pile, dont la taille dépend alors du logarithme du nombre d'éléments à trier.

Ce compromis sur la taille de la pile versus l'efficacité de l'algorithme s'explique aussi parce que l'algorithme binaire ci-dessus ne tient pas compte des données à fusionner. Sur ce point, la stratégie de Timsort est meilleure, bien qu'elle ne considère qu'une structure de pile classique. Il reste encore du travail sur ce côté de l'algorithme, mais l'approche recommandée est simplement de tout fusionner à la fin.

2.4 Fusion !

Lorsque tous les nombres ont été fournis à YAMS_slope(), il ne faut pas non plus oublier de terminer le processus avec le code suivant :

La fonction merge() entre enfin dans le vif du sujet, car elle décide de la stratégie de fusion, choisissant la source et la destination des runs à fusionner. Comme vous vous souvenez, nous avons typiquement 4 nombres à prendre en compte, ce qui fait 4!=24 combinaisons, alors qu'il n'y a que 4 mouvements possibles.

Pour simplifier, ce ne sont pas les tailles des 4 runs qui sont prises en compte, mais la taille des 3 runs qui en résulteraient. Il n'y a plus que 3!=6 combinaisons à tester, et l'arbre de décision binaire de la figure 10 montre que seulement quatre comparaisons suffisent, grâce à quelques cas congruents.

Le code suivant est la pure application du principe de la figure 10, avec en plus la gestion du cas particulier pour la dernière fusion ; celle-ci doit donner un bloc contigu dans l'espace de travail (comme évoqué au chapitre 1.8) :

Les quatre fonctions de fusion sont des intermédiaires pour deux fonctions symétriques, et servent surtout à calculer les indices de source et destination de chaque run. merge_tails2head() et merge_heads2tail() peuvent utiliser merge2low() et merge2high() indifféremment, car le résultat est écrit dans une zone totalement indépendante des sources (ce sont donc des candidats pour du tri bidirectionnel).

Par contre, merge_both2tail() et merge_both2head() vont surécrire un run source (car sinon cela crée un trou qui nécessitera plus tard une défragmentation) et le sens devient important pour empêcher la surécriture d'une valeur qui n'est pas encore lue. Donc, merge_both2tail() utilise merge2low() alors que merge_both2head() utilise merge2high(). Ci-dessous est un exemple de ces fonctions qui ne font que calculer les paramètres à passer à la fonction de fusion, et mettre à jour les pointeurs. C’est de l’arithmétique simple, mais qui n’est pas triviale, car chacun des quatre cas a ses propres subtilités et off-by-ones :

Pour la fonction de fusion elle-même, il n’y a pas de remarque particulière, à part encore une fois le soin pour la gestion des pointeurs. La version opérationnelle doit non seulement déplacer la clé, mais aussi les données annexes, qui ne sont pas prises en compte ici. Puisque seul le sens de balayage change, voici juste merge2low() qui fusionne en commençant par les éléments inférieurs :

2.5 Améliorations

YAMS n'est pas la panacée, mais pour certaines applications non critiques, il est « good enough » et surtout sa description tient dans un article de taille raisonnable, ce qui peut en faire un bon « cas d'école ».

La première amélioration à envisager pour accélérer le tri de données aléatoires (les plus courantes et les plus pénibles) consisterait à ajouter un autre algorithme de tri intermédiaire, entre la phase de prétri et la phase de fusion classique.

Timsort tire en partie sa performance particulière du tri par insertion préliminaire, mais ce n'est pas très rentable sur de gros blocs. Timsort utilise 64 éléments alors que j'envisagerais 8 au maximum. Un autre filtre de tri simplifié pourrait déjà fusionner des runs consécutifs de longueur 2 par exemple, très courants dans les données aléatoires, économisant ainsi de coûteuses décisions pour des blocs très courts. Le prix à payer serait une augmentation de la taille du code ainsi qu'une hyperspécialisation à certains types de données.

Une deuxième amélioration radicale serait la réalisation d'une fonction de tri bidirectionnelle, comme sur la figure 8, pour paralléliser le tri sur les processeurs modernes (du type Intel Core et équivalents). Cela n'aurait aucun intérêt pour les processeurs plus simples, mais rien n'oblige cette implémentation et YAMS est suffisamment flexible pour intégrer d'autres variations de l'algorithme, comme la fusion de 3 ou 4 runs simultanés, par exemple.

Une troisième possibilité consiste à modifier l'insertion des données en réutilisant l'espace de travail pour réaliser une version « sur place » de l'algorithme. Les données à trier peuvent être présentées en un seul bloc dans une moitié de l'espace de travail et le prétri s'effectue dans l'autre moitié, au lieu d'obtenir les données au compte-gouttes. Encore une fois, la décision revient à l'utilisateur.

J'ai aussi choisi, par simplicité, de ne pas faire de recherche dichotomique dans le run à fusionner, contrairement à Timsort. Le gain de performance est à quantifier, mais je ne pense pas qu'il justifie une complexité supplémentaire.

Enfin, le code source existant est parsemé de fonctions de traçage et de debug, mais surtout d'appels de fonctions qui sont parfois redondants et pourraient être « inlinés », et des calculs dupliqués ici et là. Quelques variables globales supplémentaires devraient factoriser ces opérations, au risque de rendre le code plus abscons. Ces optimisations « peep-hole » seront intégrées dans une version ultérieure, alors que la version actuelle doit s’assurer que l’algorithme fonctionne et qu’il fonctionne correctement.

Je suis sûr que vous aurez des remarques et objections, que je vous invite à partager, et surtout tester par vous-même ! Par exemple, des benchmarks sur différentes architectures et pour différents types de données seraient bienvenus pour comparer YAMS avec d’autres algorithmes.

3. Résultats

L’interface HTML n’est pas un exemple d’UI user-friendly puisqu’elle a été développée progressivement avec l’algorithme. Au moins, elle devrait fonctionner partout, et elle collecte et affiche des informations utiles pour déboguer l’algorithme, que ce soit avec l’affichage graphique (dans un <canvas> de 512×256 pixels) ou la console (accessible par la touche F11).

Le bouton « sort » lance le prétri, mais l’espace de travail doit auparavant être rempli de données, que vous pouvez dessiner avec la souris ou bien en cliquant sur l’un des 30 boutons de formes. L’option « autorun » active le prétri automatique si l’un de ces boutons est appuyé, et « progressive merge » active les fusions. Si cette dernière option n’est pas active, les cinq boutons sur le côté vont appliquer la stratégie correspondante de fusion, le bouton « auto » laissant l’algorithme choisir seul l’opération à effectuer.

Un compteur s’affiche en bas, appelé « merged elements », car il compte le nombre total de valeurs traitées (lues puis écrites) par l’algorithme de fusion. Plus ce nombre est bas, plus l’algorithme est efficace. Vous pourrez le constater en obtenant différentes valeurs finales, lorsque vous cliquez répétitivement sur un seul des quatre boutons de stratégie : le bouton auto donnera une valeur égale ou inférieure, car il adaptera l’algorithme aux données disponibles.

3.1 Steps

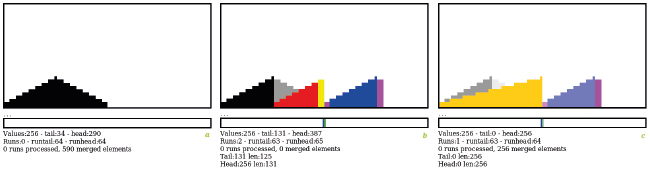
La figure 11 montre le détail des trois étapes du traitement de données en marches d’escalier, générées en appuyant sur le bouton « steps ». C’est un signal simple pour prendre en main l’interface.

D’abord, l’appui sur le bouton « steps » réinitialise l’écran et génère et affiche 256 nombres dans le canevas (figure 11a). La pile de runs est vide, les données brutes sont affichées en noir.

En appuyant sur « sort », ces données sont traitées par YAMS_slope() qui découpe les 256 nombres en 2 runs, le premier en bleu à droite, le deuxième en rouge à gauche (figure 11b). La deque est initialisée par défaut au milieu de l’espace de travail par commodité, mais cela pourrait être n’importe où. Les colonnes en jaune et magenta correspondent aux données écrites spéculativement : elles seront surécrites ou ignorées si elles sont inutiles.

La barre du bas montre l’occupation de la deque des runs : une barre verte correspond à un run ajouté à la tête, une barre bleue est un run ajouté à la queue.

La figure 11c montre le résultat de l’appui sur le bouton « auto » : puisque c’est la dernière paire de run, l’algorithme cherche à placer le résultat au milieu de l’espace de travail, avec la queue située entre 0 et 255 pour éviter la fragmentation du bloc de données et favoriser son utilisation ultérieure. Ici, le résultat apparaît en orange et surécrit une partie des données déjà présentes.

Vous remarquerez que les données précédentes ou surécrites sont atténuées et encore visibles (si elles sont supérieures) pour faciliter la compréhension des opérations, mais cela n’est qu’un artifice d’affichage et cela n’affecte en rien l’algorithme. De même, un run dépilé de la deque est éclairci pour montrer que la valeur n’est plus prise en compte.

Dans ce cas simple, le prétri fait le plus gros du travail et il n’y a qu’une seule opération de fusion. C’est un cas très improbable en pratique, mais il permet de tester le fonctionnement et l’efficacité du code.

3.2 LFSR

Ce premier cas était très simple, mais n’est pas du tout caractéristique d’une utilisation pratique. Plusieurs boutons fournissent des données aléatoires, mais malgré leur utilité, elles ne sont pas reproductibles. J’ai donc inclus un LFSR 8 bits qui a l’avantage non seulement d’être répétable, mais aussi d’être une permutation de tous les nombres de 0 à 255. Ainsi, le bloc trié doit être un triangle sans aspérité, sinon cela indiquerait que des données ont été altérées.

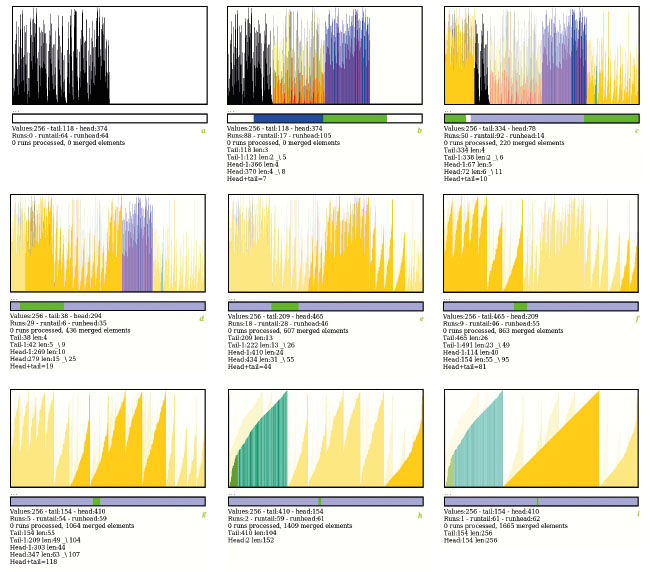
Il existe 16 polynômes générateurs dans GF(2)/8 et ils sont tous disponibles dans les boutons. Ils fournissent des données assez similaires, mais pas identiques, c’est une aide précieuse contre les régressions. Ici, nous cliquons sur « LFSR0 » et obtenons des données pseudoaléatoires pour tester l’efficacité du tri.

La figure 12a montre les données de départ générées par le LFSR (polynôme 0x8E pour les curieux).

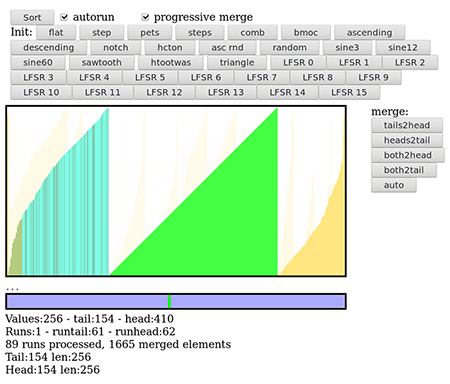
La figure 12b montre les résultats du prétri : les 256 valeurs ont été organisées en 88 runs, approximativement autant de runs croissants (barres bleues et magenta) que décroissants (barres jaunes et rouges). Les nombres du bas montrent les tailles des runs de tête et de queue : apparemment, les runs de queue sont plus courts (3 et 2) que les runs de tête (4 et 4), donc la première fusion s’effectuera de la queue vers la tête.

La première fusion est déterminante, car en mettant un run plus grand de l’autre côté, la fusion de ce côté-là sera moins probable que du côté d’origine. C’est un peu comme une prophétie autoréalisatrice, la prochaine fusion a de fortes chances d’être dans le même sens pour l’étape suivante, à moins qu’un run ait une taille très différente. C’est ce que nous voyons à la figure 12c où, après 38 étapes, la fusion s’est propagée vers la droite (après un petit retour en arrière visible en vert-cyan). Les blocs ont dépassé l’espace de travail qui reboucle sur la gauche automatiquement.

Les runs fusionnés sont toujours placés à droite, car leur taille est plus grande qu’à gauche (la queue) et les fusions continuent sur les figures 12d à 12i, les blocs deviennent de plus en plus gros, puisque les triangles sont de plus en plus faciles à distinguer. À la figure 12f, les fusions ont de nouveau dépassé la borne maximale de l’espace de travail et la fusion continue à gauche, sans s’en préoccuper. Il ne reste que 9 runs et les triangles sont tous distincts.

À la figure 12h, il ne reste plus que 2 runs, dont l’un (à gauche) a une couleur différente, indiquant une autre stratégie, ici de fusion « à moitié sur place ». Et la figure 12i montre le triangle final tant attendu, qui ne chevauche pas les limites de l’espace de travail, comme prévu.

Au total, l’algorithme de fusion a traité 1665 éléments, le maximal théorique est vérifié par le test « comb » (peigne) qui traite 1792 valeurs (figure 13c). Ce n’est pas un nombre pris au hasard : il y a 256 valeurs réparties dans 256/2=128 runs (la taille limite de la deque de runs), et 1792=256×log2(128). Dans cette configuration, un nombre plus élevé que 1792 indique que l’algorithme rencontre des difficultés, par exemple lorsque la fusion s’effectue au fur et à mesure de l’ajout de nouveaux runs, ou bien que la stratégie de fusion est mauvaise. En effectuant les fusions au dernier moment, le test avec les nombres aléatoires (« random ») oscille autour de 1700 à 1730 éléments.

Conclusion

Nous avons passé en revue quelques problématiques et astuces de programmation utiles aux algorithmes de tri et pouvant s’appliquer à d'autres types d'algorithmes. YAMS n’est pas révolutionnaire, car il reste un algorithme de classe O(n×log(n)), mais l'utilisation d'une deque joue ici un rôle déterminant et une fois qu'on y a goûté, on se demande pourquoi on se contentait de moins !

Le code source ainsi que les logs de développement sont disponibles sur la page du projet à Hackaday.io [10]. Téléchargez la dernière version, cliquez sur tous les boutons et qui sait si vous trouverez d'autres améliorations ?

Références

[1] Wikipédia : https://fr.wikipedia.org/wiki/Algorithme_de_tri

[2] Série de 3 vidéos en anglais expliquant méticuleusement le fonctionnement du tri racine par Creel :

• « Why is Radix Sort so Fast? Part 1 Why are Comparison Sorts so Slow? »,
  https://www.youtube.com/watch?v=_KhZ7F-jOlI
• « Why is Radix Sort so Fast? Part 2 Radix Sort »,
  https://www.youtube.com/watch?v=ujb2CIWE8zY
• « Why is Radix Sort so Fast? Part 3 Comparison and Code, Radix Sort vs QuickSort »,
  https://www.youtube.com/watch?v=TPpWvpnQq5s

[3] Bingmann, Time : « The Sound of Sorting - "Audibilization" and Visualization of Sorting Algorithms », mai 2013, https://panthema.net/2013/sound-of-sorting/

[4] Wikipédia : https://en.wikipedia.org/wiki/Merge_sorthttps://fr.wikipedia.org/wiki/Tri_fusion

[5] Wikipédia : https://en.wikipedia.org/wiki/Timsorthttps://fr.wikipedia.org/wiki/Timsort

[6] Peters, Tim : détails de la conception de Timsort, https://bugs.python.org/file4451/timsort.txt

[7] Wikipédia : « La deque », https://en.wikipedia.org/wiki/Double-ended_queuehttps://fr.wikipedia.org/wiki/File_d'attente_à_double_extrémité

[8] Wikipédia : « Buffer circulaire », https://en.wikipedia.org/wiki/Circular_bufferhttps://fr.wikipedia.org/wiki/Buffer_circulaire

[9] Wikipédia : « Le codage de Huffman », https://fr.wikipedia.org/wiki/Codage_de_Huffman

[10] Guidon, Yann : la page du projet YAMS sur Hackaday,
https://hackaday.io/project/186859-yams-yet-another-merge-sort