Un article en trois parties visant à appréhender l'ensemble d'une liaison numérique spatiale, de la réception du signal radiofréquence à la génération des images, en passant par le décodage des bits et la correction d'erreurs de transmission. Dans cette première partie, nous partirons de la couche matérielle jusqu'au code convolutif.
L'analyse du protocole de communication numérique d'images satellites est l'opportunité d'explorer toutes les couches d'un protocole de routage de signaux, de la couche physique avec le signal modulé en phase, en passant par les codes correcteurs d'erreur (convolutif avec décodage, selon l'algorithme de Viterbi et par bloc, avec Reed Solomon), pour finalement regrouper les blocs de données formant les vignettes d'images JPEG, qui seront finalement assemblées pour former une image complète. L'ensemble de la démonstration ne nécessite, d'un point de vue matériel, qu'une dizaine d'euros d'investissement, pour finalement avoir la satisfaction de maîtriser l'ensemble de la chaîne de communication exploitée dans les liaisons spatiales.
1. Introduction
La transition de l’analogique vers le numérique continue inexorablement (télévision analogique vers DVB-T, bande FM commerciale vers DAB, téléphonie), et les liaisons radiofréquences n’échappent pas à cette tendance, visant à optimiser l’occupation du spectre et la qualité des signaux transmis. Alors que le protocole analogique APT (Automatic Picture Transmission) des satellites météorologiques en orbite polaire basse de la NOAA est voué à disparaître avec la fin de cette constellation de satellites, la relève semble prise en charge par un protocole d’encombrement spectral sensiblement identique, mais numérique, permettant donc de transmettre des images de résolution accrue : LRPT (Low Rate Picture Transmission). Nous verrons que ce gain en performance se fait au détriment d’une complexité de traitement notablement accrue.
Il est probable qu’à peu près aucun lecteur ne s’intéresse à LRPT, ne serait-ce que du fait de la disponibilité d’outils de décodage libres fonctionnels. Pourquoi donc passer autant de temps à décoder les images transmises par le satellite russe Meteor-M2 [1], seule source de flux LRPT facilement (satellite en orbite basse) accessible actuellement (l’émetteur LRPT du Metop-A européen est cassé et Metop-C est en cours de mise en service, alors que ces lignes sont rédigées) ? D’une part, LRPT n’est qu’un exemple de la classe générale des protocoles numériques de communication actuellement exploités, avec des modulations de plus en plus complexes et des niveaux d’abstraction s’étendant sur toutes les couches OSI [2]. C’est donc non seulement l’opportunité d’explorer ces diverses couches et de comprendre concrètement leur sens pratique, mais également d'étudier des protocoles fortement inspirés de LRPT, qui sont utilisés pour les transmissions d’images haute résolution de satellites en orbite basse (même de Terra et Aqua de la constellation MODIS) ou géostationnaire [3]. Bien que nous devions quitter la chaîne de traitement proposée par cette dernière référence, le début de la chaîne d’acquisition et de traitement est identique au cas de LRPT. Par ailleurs, si on en croit les documents diffusés par les diverses agences spatiales depuis deux décennies, LRPT doit représenter l’avenir de la communication spatiale bas débit, même si les Russes sont les seuls à exploiter concrètement ce protocole dans la bande VHF (Very High Frequency – 30 à 300 MHz, donc incluant la bande autour de 137 MHz dédiée aux liaisons satellitaires) actuellement. Au-delà de ces aspects sciences appliquées, les techniques que nous mettrons en œuvre [4] sont exploitées dans une multitude d’interfaces numériques de notre quotidien, de la communication au stockage de données en passant par la télévision : [5] estimait en 2005 que 1015 bits/seconde étaient traités par des codes convolutifs pour la seule télévision.
Commençons par inspirer le lecteur en démontrant le résultat que nous cherchons à atteindre (voir figure 1). Meteor-M2 émet sur 137,9 MHz, donc les installations existantes pour la réception APT de NOAA [6] sont parfaitement fonctionnelles. Analyser la qualité de la réception est à peine plus complexe pour LRPT que pour APT : le mode numérique de communication ne se prête pas à une retranscription audiofréquence, comme c’est le cas pour APT avec sa douce mélodie à 2400 Hz, et seule une analyse de la constellation (voir section 1 de l’article du mois prochain) permet de savoir si son installation de récepteur et antenne est fonctionnelle. Il nous a fallu une dizaine de passages infructueux, avant d’obtenir une acquisition décodable. Le problème d’un satellite en orbite polaire, c’est qu’il passe souvent au-dessus des pôles, et seulement une fois par jour sur nos latitudes tempérées. Nous avons la chance de pouvoir recevoir le signal depuis le Spitsberg, par 79°N, à une latitude où les satellites en orbite polaire repassent toutes les 100 minutes. Si l’on n’y prend garde, on passe son temps à recevoir des émissions radiofréquences de satellites au lieu de travailler ! Le bonus est de recevoir une vue directe du Pôle Nord, sans aucun intérêt géographique autre que de dire qu’on peut le faire. L’illustration de la figure 2 a pour vocation de démontrer la simplicité du matériel nécessaire pour recevoir Meteor-M2 : comme pour les satellites de la NOAA, deux brins de fil rigide et un récepteur de télévision numérique terrestre (DVB-T) à base de R820T(2) et RTL2832U, utilisés comme source de radio logicielle suffisent. Ce matériel, léger et compact, s’il n’est pas disponible n’importe où, se bricole facilement avec les moyens du bord.
Fig. 1 : Image Meteor-M2 acquise depuis le Spitsberg. Le nord de la Scandinavie est visible en haut à droite de l’image, le Pôle Nord est vers le bas gauche de l’image.
Fig. 2 : Gauche : montage expérimental. Une antenne dipôle, un récepteur DVB-T et un ordinateur exécutant GNU Radio suffisent à acquérir les signaux de Meteor-M2 sur 137,9 MHz. Droite : résultat d’une acquisition d’un satellite NOAA (transmission analogique) depuis le Spitsberg. Depuis ce site d’observation, les satellites en orbite basse polaire réapparaissent toutes les 100 minutes, pour un passage d’une dizaine de minutes de visibilité environ.
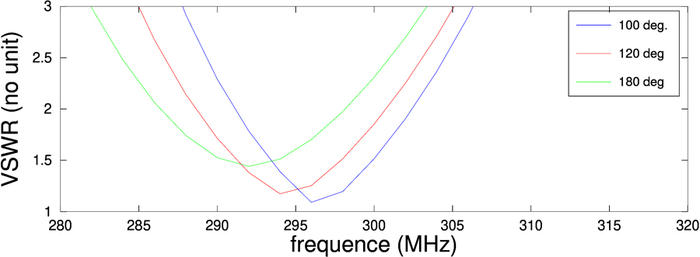
Le lecteur observateur aura remarqué (figure 2) que nous avons remplacé le simple dipôle par le dipôle à 120° préconisé par lna4all.blogspot.com/2017/02/diy-137-mhz-wx-sat-v-dipole-antenna.html. Pourquoi cet angle étrange ? Pour la même raison que les éléments d’une antenne discone présentent un angle par rapport au monopôle rayonnant et ne sont pas horizontaux : pour tenter d’adapter l’impédance. Pour nous en convaincre, une petite simulation NEC2 [7] nous permet d’estimer l’impédance à la résonance, en fonction de l’angle que font les brins du dipôle (ici deux brins de 25 cm, donc une longueur d’onde de 100 cm pour une fréquence théorique de 300 MHz) :
Et en effet, un angle de 120° nous rapproche des 50 Ω nominaux des connecteurs et câbles radiofréquences. En pratique, compte tenu de la proximité du sol et des éléments perturbateurs métalliques, dont la motoneige fait partie, les parasites capacitifs sont tels que l’antenne est nécessairement désaccordée. Respecter la théorie ne fait néanmoins pas de mal...
L’acquisition et le traitement se font en deux temps : GNU Radio se charge non seulement d’acquérir les données complexes en identité et quadrature (I, Q) issues du récepteur radiofréquence, mais effectue aussi un prétraitement pour compenser l’écart de fréquence entre le satellite en mouvement et notre récepteur au sol (section 5) et cale la détection des bits sur l’horloge cadençant la transition entre les états du flux numérique. Ce faisant, nous réduisons le débit de données et donc la taille des fichiers stockés sur le disque dur pour leur analyse ultérieure. L’image de la figure 1 a été décodée au moyen de meteor_decoder disponible sur github.com/artlav/meteor_decoder.git. Ce logiciel, écrit en Pascal (apt-get install fpc), se compile trivialement par ./build_medet.sh pour fournir l’exécutable medet qui s’exploite par ./medet fichier.s output -s avec fichier.s le fichier fourni par GNU Radio. Ce faisant, nous avons obtenu une très belle image, n’avons rien appris, et restons esclaves d’un développeur génial qui a fourni un outil parfaitement fonctionnel. Aucun intérêt donc.
Notre objectif, dans la suite de cette présentation, est de décortiquer medet, d’en comprendre le fonctionnement, et sans négliger le confort d’une application fonctionnelle, de profiter de l’opportunité de comprendre LRPT pour améliorer un peu notre connaissance des modes « modernes » de communication numériques.
2. Quand passera le satellite ?
La première question concernant la réception d’un signal radiofréquence d’un satellite en orbite polaire basse est de connaître son horaire de passage. En effet, en orbitant à environ 800 km de la surface de la Terre, le satellite en fait le tour toutes les 100 minutes, et n’est visible que d’un point donné de la surface de la planète pendant une douzaine de minutes. Pour des raisons historiques, notre outil préféré pour la prévision des passages de satellites est SatTrack, qui malgré son bug de l’an 2000 (http://pe1chl.nl.eu.org/SatTrack/) reste un excellent outil en ligne de commande parfaitement fonctionnel. Nous lui fournissons dans son fichier de configuration data/cities.dat un identifiant du site où se trouve le récepteur et ses coordonnées en latitude et longitude (négative vers l’est !), ainsi que les paramètres orbitaux des satellites dans tle/tlex.dat : le fichier issu de www.celestrak.com/NORAD/elements/weather.txt fournit de tels paramètres mis à jour régulièrement. En identifiant Meteor-M2 comme METEOR-M 2, nous obtenons la liste des passages sous la forme :
BTS SatTrack V3.1 Orbit Prediction
Satellite #40069 : METEOR-M 2
Data File : tlex.dat
Element Set Number: 999 (Orbit 21896)
Element Set Epoch : 27Sep18 21:20:50.463 UTC (2.3 days ago)
Orbit Geometry : 816.87 km x 823.72 km at 98.593 deg
Propagation Model : SGP4
Ground Station : NYA --- JQ58WW
Time Zone : UTC (+0.00 h)
Date (UTC) Time (UTC) of Duration Azimuth at Peak Vis Orbit
AOS MEL LOS of Pass AOS MEL LOS Elev
Sun 30Sep18 05:28:54 05:35:40 05:42:25 00:13:31 355 56 117 17.5 DDD 21930
07:10:16 07:17:34 07:25:00 00:14:44 10 81 153 28.4 DDD 21931
08:51:18 08:58:56 09:06:38 00:15:20 25 107 187 48.1* DDD 21932
10:31:55 10:39:41 10:47:31 00:15:37 41 131 220 77.6* DDD 21933
12:12:20 12:20:02 12:27:48 00:15:28 60 334 250 77.5* DDD 21934
13:52:24 14:00:07 14:07:53 00:15:28 83 1 276 68.9* DDD 21935
15:32:29 15:40:15 15:48:01 00:15:33 109 20 299 76.7* DDD 21936
17:12:46 17:20:32 17:28:22 00:15:37 139 226 318 79.1* DDD 21937
18:53:39 19:01:17 19:08:59 00:15:20 171 253 334 49.3* VVV 21938
20:35:17 20:42:35 20:50:01 00:14:44 206 277 349 29.2 VVV 21939
22:17:44 22:24:29 22:31:19 00:13:35 241 303 5 17.9 VVV 21940
Mon 01Oct18 00:00:55 00:07:00 00:13:09 00:12:14 277 330 23 11.9 VVV 21941
01:44:06 01:49:51 01:55:39 00:11:33 308 357 46 9.8 VVV 21942
03:26:49 03:32:46 03:38:46 00:11:58 333 24 76 11.1 VVV 21943
05:08:47 05:15:20 05:21:58 00:13:11 352 51 110 16.0 DDD 21944
06:50:13 06:57:23 07:04:41 00:14:28 7 76 146 25.7 DDD 21945
08:31:14 08:38:53 08:46:31 00:15:16 22 102 180 43.3* DDD 21946
10:12:00 10:19:42 10:27:32 00:15:33 38 124 213 71.4* DDD 21947
11:52:25 12:00:07 12:07:57 00:15:33 56 334 244 81.3* DDD 21948
13:32:33 13:40:15 13:48:02 00:15:28 78 355 271 69.3* DDD 21949
15:12:38 15:20:20 15:28:06 00:15:28 103 20 295 73.9* DDD 21950
16:52:51 17:00:37 17:08:27 00:15:37 133 228 314 84.9* DDD 21951
18:33:32 18:41:14 18:49:00 00:15:28 165 247 331 54.7* VVV 21952
20:15:02 20:22:28 20:29:54 00:14:52 199 273 346 32.3 VVV 21953
Nous ne considérons que les passages avec une élévation suffisante pour que le satellite soit clairement visible (typiquement une soixantaine de degrés, tels que fournis dans la colonne Peak Elev) et l’heure est ici fournie en temps universel (+1 ou +2 h pour la France).
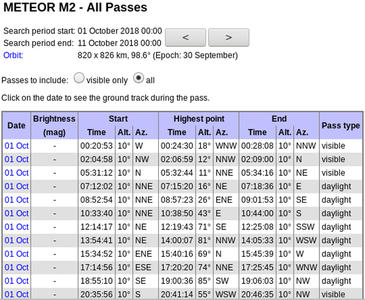
Nombre d’utilisateurs préfèrent cependant une interface graphique pour fournir ces résultats. Ceux possédant une connexion internet pourront simplement se contenter de demander à Heavens Above (www.heavens-above.com) de fournir les horaires de passage du satellite d’identifiant NORAD 40069 (figure 3) : les résultats sont cohérents avec ceux de SatTrack, si l’on considère que Heavens Above fournit les horaires en heure locale et non en temps universel (écart de 2 h au 1er octobre qui nous concerne ici), que Heavens Above ne mentionne pas le passage avec une élévation maximale inférieure à 10° et que les horaires d’acquisition (Acquisition Of Signal – ACQ ou AOS) et de perte (Loss Of Signal – LOS) de signal se font à 10° et non 0°, impliquant un décalage de 2 à 5 minutes entre les horaires.
Fig. 3 : Prévisions de passage par le site web Heavens Above.
En l’absence de connexion internet, le logiciel propriétaire maintenant abandonné WXtoImg (https://wxtoimgrestored.xyz/) – qui a longtemps fait le bonheur des récepteurs de satellites NOAA en orbite basse – peut être leurré pour prédire le passage de Meteor-M2. Cet exercice est surtout l’occasion d’étudier rapidement la structure des paramètres orbitaux fournis en 2 lignes (Two Line Elements – TLE). Les informations permettant de déduire la position d’un satellite autour de la Terre sont fournies par Celestrak sous la forme :
METEOR-M 2
1 40069U 14037A 18272.86150993 -.00000016 00000-0 12287-4 0 9997
2 40069 98.5921 321.1231 0004724 305.5966 54.4754 14.20654510219244
Le nom du satellite en texte libre est fourni en première ligne, suivi des paramètres orbitaux commençant par le numéro de la ligne et l’identifiant NORAD du satellite, suivi pour sa première occurrence du niveau de classification du satellite (Unclassified, Classified, Secret). Si nous voulons faire croire à WXtoImg que nous allons prédire le passage d’un satellite qu’il est conçu pour écouter – NOAA APT – nous devons forger un faux TLE avec les paramètres orbitaux de Meteor-M2 et un identifiant d’un satellite NOAA. Prenons par exemple NOAA 15, qui ne fonctionne plus très bien :
NOAA 15
1 25338U 98030A 18283.48448267 .00000100 00000-0 60924-4 0 9992
2 25338 98.7662 299.9712 0009347 251.7061 108.0475 14.25879899 61199
Ayant constaté que WxtoImg ne tient pas compte du nom de la première ligne, nous nous contentons de modifier l’identifiant dans la trame de Meteor-M2 par l’identifiant NORAD de NOAA 15, à savoir 25338. Cette simple modification se solde cependant par un échec : le dernier chiffre de chaque ligne est en effet une somme de contrôle (checksum) dans laquelle tous les chiffres sont sommés modulo 10, en considérant que le symbole - vaut 1 (les lettres et autres symboles ne sont pas pris en compte dans la somme). Sous GNU/Octave, ce calcul s’obtient par :
a="2 25338 98.7662 299.9712 0009347 251.7061 108.0475 14.25879899 6119"
a=strrep(a,'-','1');mod(sum(a(find((a<='9')&(a>'0')))-48),10)
Dans cet exemple, le calcul répond 9, qui est bien le dernier chiffre de la seconde ligne du TLE de NOAA 15. Ayant appris ces points, nous fabriquons la fausse trame :
METEOR-M 2
1 25338U 14037A 18272.86150993 -.00000016 00000-0 12287-4 0 9999
2 25338 98.5921 321.1231 0004724 305.5966 54.4754 14.20654510219246
Dans cette trame, nous avons discrètement remplacé l’identifiant NORAD de Meteor-M2 par celui de NOAA 15 et recalculé le checksum. Dans ces conditions, WxtoImg accepte d’effectuer le calcul, dont nous validons la cohérence avec Heavens Above et SatTrack. En effet, l’affichage de la figure 3 se compare favorablement avec la sortie de WxtoImg ci-dessous :
Satellite passes for ny-alesund, norway (78o55'N 11o54'E)
while above 0.1 degrees with a maximum elevation (MEL) over 40.0 degrees
from 2018-09-30 21:46:04 CEST (2018-09-30 19:46:04 UTC).
2018-10-01 UTC
Satellite Dir MEL Long Local Time UTC Time Duration Freq
NOAA 15 S 43E 40E 10-01 10:31:13 08:31:13 15:11 137.6200
NOAA 15 S 71E 20E 10-01 12:11:57 10:11:57 15:30 137.6200
NOAA 15 S 81W 9E 10-01 13:52:22 11:52:22 15:29 137.6200
NOAA 15 S 69W 10E 10-01 15:32:33 13:32:33 15:25 137.6200
NOAA 15 N 74E 16E 10-01 17:12:38 15:12:38 15:26 137.6200
NOAA 15 N 85W 10E 10-01 18:52:51 16:52:51 15:31 137.6200
NOAA 15 N 55W 7W 10-01 20:33:34 18:33:34 15:24 137.6200
Nous avons vu que la différence de 2 minutes entre SatTrack et les autres prévisions vient de ce que ce premier prédit l’horaire de passage au-dessus de l’horizon, alors que les deux autres prédisent le passage à une certaine élévation (par défaut 8°). On notera dans toutes ces prévisions les bienfaits de travailler à une latitude élevée (ici 79°N) où les passages se succèdent toutes les 100 minutes, permettant bien plus de tests que l’unique passage aux latitudes françaises.
Écoute des satellites depuis les régions polaires
Nous ne pouvions résister en regardant S. Prüfer présenter Space Ops 101 sur media.ccc.de/v/35c3-9923-space_ops_101#t=1265 à l’envie de reproduire les figures montrées entre 16 et 18 minutes, illustrant l’intérêt d’écouter les satellites depuis les régions polaires. Pour atteindre les résultats présentés ci-dessous au moyen de QGis (ici version 3.4) :
- installer un outil de prévision de position des satellites à partir des fichiers TLE et fournissant une sortie au format Shapefile : nous avons utilisé https://github.com/anoved/Ground-Track-Generator/ qui se compile trivialement ;
- générer la trace au sol du satellite qui nous intéresse. En fournissant la description TLE du Meteor-M2 obtenue autour du 1er octobre 2018 sur Celestrak tel que décrit dans le texte, nous exécutons gtg –input meteor.tle –output m2 –start epoch –end epoch+24h –interval 30s pour obtenir le fichier m2.shp qui contient les positions en coordonnées sphériques (WGS 72) du satellite vu du sol ;
- télécharger une base de données des frontières au format Shapefile. Dans notre cas nous avons utilisé l’archive disponible sur https://www.naturalearthdata.com/downloads/50m-cultural-vectors/50m-admin-0-countries-2/ ;
- nous devons toujours travailler en référentiel cartésien projeté pour effectuer des manipulations géométriques : il faut donc projeter les coordonnées sphériques en coordonnées cartésiennes dans les plans locaux tangents. Pour la France, WGS84/UTM31N donne de bons résultats (EPSG:32631) tandis que https://epsg.io/3576 nous enseigne que EPSG:3576 fournira une projection acceptable autour du Pôle Nord ;
- ayant découpé () la carte des frontières des pays autour des régions arctiques (jusqu’à une cinquantaine de degrés nord : pour cela créer un polygone par ), placer les sites de réception sur la carte, par exemple en chargeant un fichier ASCII contenant leur longitude et latitude ;
- tracer les cercles de circonférence connue sur les cartes. Pour ce faire, on sauvera les coordonnées des sites de réception dans un référentiel cartésien (souris bouton droit sur la couche contenant le symbole du site et en passant le CRS sur la projection appropriée), puis on tracera une zone d’exclusion par . Reste à identifier la circonférence de ces cercles. Le cas de l’angle par rapport au centre de la Terre pour lequel le satellite apparaît à l’horizon est trivial, car nous avons un triangle rectangle entre l’observateur, le centre de la Terre de rayon R et le satellite à une distance de R+r du centre de la Terre (r l’altitude de vol du satellite). Ainsi, l’angle formé entre l’observateur, le centre de la Terre et le satellite est V = arccos(R/(R+r)) et la longueur de l’arc de cercle visible depuis le satellite est R cos V = R•R/(R+r) = 3050 km. Il s’agit du rayon du cercle le plus large visible sur les figures ci-après. En pratique, il est illusoire de croire que nous recevrons un signal exploitable pour une élévation en dessous de V'=15°. Dans ce cas, l’identification du rayon du cercle déterminant la zone de visibilité nécessite de faire intervenir une trigonométrie à peine plus complexe, en remplaçant l’angle droit par un angle de (90+V'), mais la solution du problème reste unique avec un angle imposé (l’angle du satellite au moment de l’AOS), une distance centre Terre-observateur imposée (R) et une distance centre Terre-satellite imposée (R+r). La solution pour V'=15° est un rayon de la zone de visibilité de 1760 km. Finalement, nous ne nous fatiguerons pas à sortir affronter le froid arctique si le satellite ne passe pas au moins à V'=60° d’élévation maximale. Dans ce cas, le rayon de visibilité du satellite à une telle élévation maximale se réduit à 400 km autour du point d’observation. Ces deux cercles sont concentriques et centrés sur le site d’observation dans les figures ci-dessous.
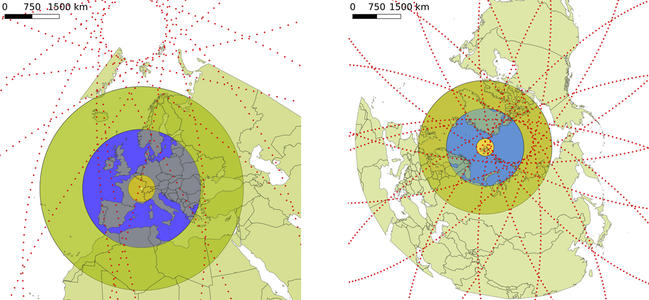
Nous déduisons de l’observation de ces figures qu’un seul passage par jour au-dessus de la France vérifie la condition d’élévation maximale d’au moins 60°, alors que 9 à 10 passages sur les 14 journaliers vérifient cette condition au Spitsberg.
Gauche : traces au sol (points rouges) du passage de Meteor-M2 vu depuis Besançon pendant 24 h. Droite : traces au sol du passage de Meteor-M2 vu depuis Ny Ålesund au Spitsberg. On notera qu’une seule orbite passe dans le cercle marquant une élévation maximale d’au moins 60° au-dessus de la France, alors qu’au moins 9 orbites vérifient cette condition au Spitsberg. La figure de gauche est en projection WGS84/UTM31N, celle de droite en WGS84/North Pole LAEA Russia. Le cercle le plus grand, centré sur le site d’observation, indique la visibilité du satellite à l’horizon (rayon de 3030 km), le cercle intermédiaire une visibilité à une élévation d’au moins 15° (rayon 1760 km) et le cercle le plus petit, une élévation d’au moins 60° (rayon 400 km).
3. Pourquoi un protocole aussi complexe ?
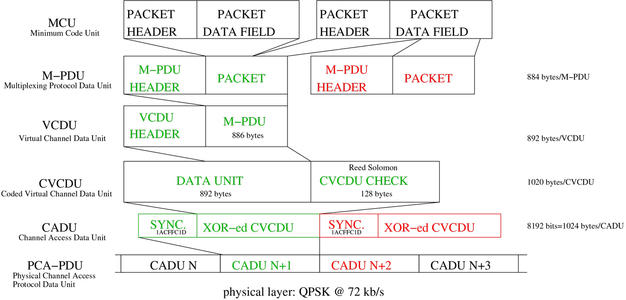
APT pour la communication analogique de signaux émis depuis les satellites NOAA est trivial [8] : une double modulation d’amplitude (intensité des pixels) et de fréquence (pour s’affranchir du décalage Doppler, alors que le satellite parcourt son orbite) transmet l’information décodée au sol par une succession de démodulateurs FM, puis AM. Pourquoi donc quitter ce mode de communication simple, au détriment d’une communication numérique encapsulant les paquets dans des couches successives de protocoles (figure 4), qui nous occuperont au cours de la lecture des pages qui vont suivre ?
Fig. 4 : Couches du protocole qu’il faudra parcourir pour passer du signal physique (en bas) à l’image (en haut) : la complexité du protocole tient en sa généralité et la virtualisation de multiples canaux d’informations numériques transmis par le satellite.
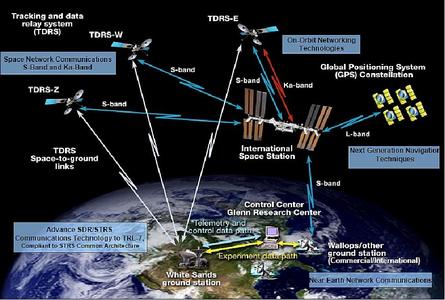
La quantité d’information transmise est limitée par la bande passante allouée, mais une bande passante donnée peut être utilisée plus ou moins efficacement pour transmettre une image de plus ou moins bonne qualité. Le spectre radiofréquence est une ressource rare et encombrée : Meteor-M2 promet une résolution accrue pour une occupation spectrale constante par rapport à APT, grâce à l’utilisation optimisée du spectre par la modulation numérique. Plus important, cette encapsulation des messages dans des couches successives – du même type que les couches OSI pour les réseaux au sol – s’inscrit dans une logique de partage des ressources de communications spatiales, tel que présenté en figure 5 (image NASA) suite à la présentation [9].
Fig. 5 : Illustration de la complexité des communications spatiales pour transmettre les informations acquises autour de l’orbite terrestre, en particulier des satellites en orbite basse (ex-navette spatiale et maintenant ISS à 400 km, Hubble à 550 km) qui ne sauraient être exploités efficacement en n’étant visibles que quelques minutes par jour depuis une station au sol. Seule l’utilisation d’un réseau de communication de satellites en orbite géostationnaire (TDRS aux États-Unis, futur EDRS en Europe pour les satellites Sentinel) garantit une liaison quasi permanente entre une agence spatiale et ses satellites. Illustration prise sur le site earth.esa.int/web/eoportal/satellite-missions/i/iss-scan.
Par exemple, un satellite en orbite basse telle que la station spatiale internationale (ISS, altitude 400 km) ou un satellite météorologique (altitude 800 km) passe d’horizon à horizon en 7 à 11 minutes, dans le meilleur des cas (passage au zénith). Avec une période de 90 minutes, cela signifierait que pour une liaison continue avec l’ISS, il faudrait 13 stations au sol le long de chaque orbite ou une station au sol tous les 3000 km, pas très pratique à mettre en œuvre, même si c’est ce qui a été fait au début de la course à l’espace. La solution est de communiquer au travers des satellites relais TDRS (Tracking and Data Relay Satellite), satellites en orbite géostationnaire qui servent de relais entre les satellites en orbite basse et moyenne et le sol. Cela signifie que non seulement, chaque plateforme volante possède une multitude d’instruments qui doivent se partager la bande passante et donc utiliser une méthode de partage du temps de communication plus subtile que la simple communication séquentielle que nous avons vue pour NOAA, mais qu’en plus un même satellite est susceptible de router les informations venant de plusieurs origines différentes et à terme, de plusieurs orbites différentes (p. ex. Lune ou Mars). De telles fonctionnalités sont par exemple fondamentales pour exploiter pleinement un satellite tel que le télescope spatial Hubble en orbite à environ 550 km de la surface de la Terre, dont on se rappellera qu’il ne s’agit ni plus ni moins que d’un satellite-espion regardant du mauvais côté. Tous ces éléments incitent donc à développer un protocole d’encapsulation et de routage des données qui puisse, par ailleurs, pallier à l’intermittence de la visibilité des satellites depuis une station au sol, avec éventuellement la nécessité de sauter d’une station à l’autre du fait de la rotation de la Terre (voir par exemple le Deep Space Network et ses stations distribuées sur tous les continents), sans que l’utilisateur final ne soit affecté par ces sources successives de données.
Ainsi, nous nous retrouvons avec la même difficulté que le routage des paquets IP puis l’encapsulation TCP ou UDP, mais sans les bibliothèques robustes et pratiques fournies par les diverses implémentations libres des couches réseau. Nous devrons donc dépiler nous-mêmes les couches du protocole pour en appréhender chaque subtilité. Heureusement, les informations sont disponibles, sous réserve de savoir où les chercher (on notera que l’auteur de la bibliothèque libfec que nous utiliserons ci-dessous, Phil Karn KA9Q, est aussi l’auteur de l’implémentation de TCP/IP pour MS-DOS que nous utilisions lors de nos premiers pas pour nous familiariser avec la connectivité internet aux balbutiements de Linux en 1994/1995, alors que les ordinateurs sous MS-DOS étaient encore le standard).
4. Comment attaquer le problème ?
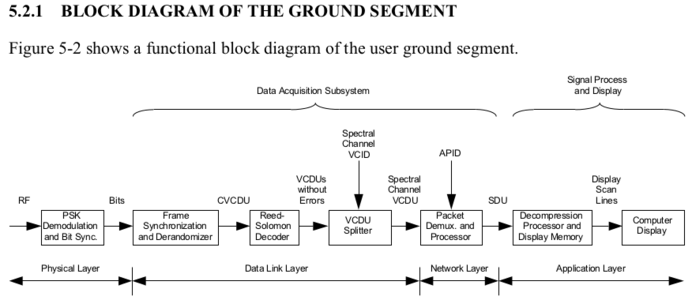
La transmission de signaux numériques, sur un canal de communication radiofréquence aussi variable qu’une liaison spatiale, nécessite un certain nombre de stratégies de protection des données contre les corruptions et pertes, voire de correction. Ces diverses couches protocolaires sont décrites dans les documents du CCSDS, le Consultative Committee for Space Data Systems, sur public.ccsds.org (voir figure 6).
Fig. 6 : Couches OSI et acronymes utilisés dans la littérature décrivant la transmission d’images par LRPT. Cette image est extraite de CCSDS 120.0-G-2 surpublic.ccsds.org/Pubs/120x0g2s.pdf.
La lecture des documents est pour le moins... ardue. Tentons de simplifier un peu la démarche en partant de la finalité (transmettre une image) pour arriver au signal que nous recevons (l’onde radiofréquence) :
- une image est découpée pour être transmise par le satellite sous forme de vignettes de 8x8 pixels ;
- chacune de ces vignettes est compressée (avec pertes) en JPEG : chaque image est donc de taille variable selon la quantité de détails restituée dans chaque vignette (très peu de coefficients pour une zone uniforme, nombreux coefficients pour les zones fortement structurées telles que les zones montagneuses). Ces étapes d’assemblage de l’image seront abordées en section 3 de l’article suivant du mois prochain ;
- une ligne d’images finale est constituée de 196 vignettes, pour une largeur de 1586 pixels ;
- la transmission d’images acquises à diverses longueurs d’onde (divers instruments) est alternée en envoyant des séquences de 196 vignettes d’une longueur d’onde, puis 196 vignettes d’une autre longueur d’onde. Entre les transmissions d’images, une trame de télémétrie est transmise (section 1.1 de l'article suivant) ;
- ces séquences de tailles variables sont regroupées dans des paquets de tailles fixes. Chacun de ces paquets contient la charge utile sous forme de 892 octets suivis de 128 octets pour la correction optionnelle par blocs d’erreurs de transmission, auquel nous ajouterons 4 octets d’en-tête pour la synchronisation (total : 1024 octets). Ce travail de regroupement des octets en phrases sera décrit en section 2 de l’article du mois prochain ;
- un code convolutif , que nous décrirons en détail, car formant le cœur de la difficulté théorique du travail, permet de corriger le bruit qui affecte aléatoirement la transmission. Chaque bit est doublé pour former par conséquent des trames de 2x8x1024=16384 bits (section 5.3) ;
- la couche matérielle consiste en une transmission en QPSK (4-PSK) [13] dans laquelle chaque paire de bits est codée sur un des quatre états possibles de phase {0, 90, 180, 270}°. Cette transmission s’effectue au rythme de 72 kb/s (section 5).
Ayant énuméré les grandes lignes de l’encodage qui suivent les grandes lignes des couches OSI (figure 6), nous devons dérouler le problème à l’envers pour passer des signaux radiofréquences reçus par récepteur de télévision numérique terrestre exploité comme source de flux de coefficients I/Q, pour le traitement logiciel de signaux radiofréquences.
5. Du signal radiofréquence aux bits
L’acquisition des signaux numériques, après transposition de fréquence pour nous ramener en bande de base, ne pose pas de problème : l’oscillateur local du récepteur DVB-T, utilisé comme source de données pour le traitement logiciel de signaux radiofréquence, est ajusté sur la fréquence centrale du message émis – 137,9 MHz dans le cas de Meteor-M2 – et la bande passante sélectionnée suffisamment large pour acquérir toutes les composantes spectrales contenant le signal imprimé sur la porteuse. Nous avons longuement discuté dans [14] comment la modulation de phase impose de régénérer au niveau du récepteur une copie de la porteuse émise avant modulation, et ce, en vue d’identifier la phase du signal par mélange et filtrage. Dans le cas des modulations binaires (BPSK – Binary Phase Shift Keying), nous avions vu que la porteuse non modulée s’obtient par traitement des coefficients (I, Q) par un estimateur insensible aux rotations de π (puisque l’encodage est imprimé sur la phase de la porteuse égale à 0 ou π), que ce soit par exploitation de la fonction arctan(Q/I) ou par mise au carré du signal qui fournit le double de la phase, soit 0 ou 2π, donc une porteuse ayant perdu sa modulation, mais au double de l’écart de fréquence entre le signal émis et la fréquence de l’oscillateur local du récepteur.
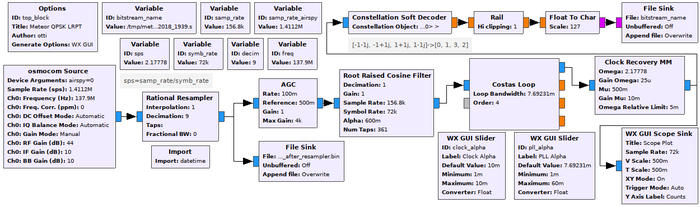
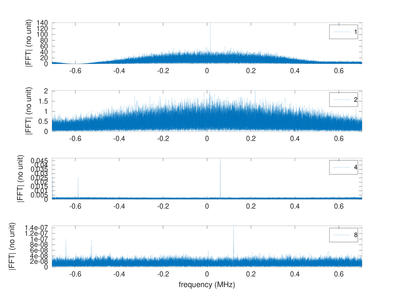
Le même principe se transpose exactement à la modulation en quadrature de phase, où l’information est imprimée sur la porteuse sous forme d’une phase égale à 0, π/2, π ou 3π/2 (figure 7, fortement inspirée de github.com/otti-soft/meteor-m2-lrpt/blob/master/airspy_m2_lrpt_rx.grc). Cependant, au lieu de simplement mettre au carré, l’élimination de la phase implique maintenant d’élever le signal à la puissance quatrième, fournissant un battement à quatre fois l’écart entre la fréquence émise et la fréquence de l’oscillateur local du récepteur (figure 8). Ce faisant, à bande passante d’acquisition donnée, nous ne pouvons nous permettre qu’un écart plus faible entre ces deux fréquences que dans le cas de BPSK.
Nous avons par ailleurs vu qu’une fois la porteuse reproduite (Costas), il se pose la question de la fréquence d’échantillonnage des bits, puisque l’horloge de l’émetteur et celle du récepteur ne sont pas synchrones et donc, la nécessité de détecter les transitions d’une valeur à l’autre de chaque bit pour asservir l’horloge d’échantillonnage de la phase. C’est le rôle des blocs de synchronisation d’horloge tels que Clock Recovery Mueller & Müller ou Polyphase Clock Sync, qui visent à ne fournir qu’un unique échantillon par symbole après asservissement de l’horloge d’échantillonnage sur les transitions du flux de données [13].
Ces deux tâches sont dévolues à GNU Radio non seulement parce qu’elles sont parfaitement fonctionnelles dans cet environnement, mais surtout en vue de réduire au maximum la taille des fichiers stockés pour leur traitement ultérieur. Plus nous décimons le flux de données avant stockage, moins grand sera le fichier : dans notre cas, nous nous efforçons d’obtenir le flux de bits en sortie de la chaîne de traitement, soit un octet par bit puisque les valeurs acquises n’ont pas encore été quantifiées en 1 ou 0, mais restent une probabilité d’être peut-être plutôt 1 ou plutôt 0. Nous verrons que conserver cette incertitude, compte tenu de l’encodage judicieux sélectionné lors de la transmission, maximisera nos chances de retrouver la valeur correcte de chaque bit. Ce format de stockage se nomme soft samples, au contraire des hard samples qui ont déjà été seuillés pour affecter la valeur de 0 ou 1 à chaque bit [16 p. 8].
Fig. 7 : Chaîne d’acquisition visant à minimiser la taille du fichier enregistré en traitant un maximum d’étapes dans GNU Radio, à savoir identification de la copie de la porteuse (boucle de Costas) et de l’horloge cadençant les données, en vue de retrouver la séquence de bits et ne sauver qu’un échantillon codé sur 8 bits pour chaque information (bit) transmise. Nous quantifierons (1 ou 0) ces échantillons lors du post-traitement pris en charge ultérieurement.
Fig. 8 : De haut en bas : spectre des coefficients complexes I+jQ présentant l’étalement du spectre ; mise au carré ; à la puissance 4 et la puissance 8. La mise au carré ne permet pas de comprimer l’étalement spectral pour retrouver la porteuse : ce n’est pas BPSK. La puissance 4 élimine la modulation et ne rend que la porteuse : c’est une modulation QPSK.
5.1 Format des données
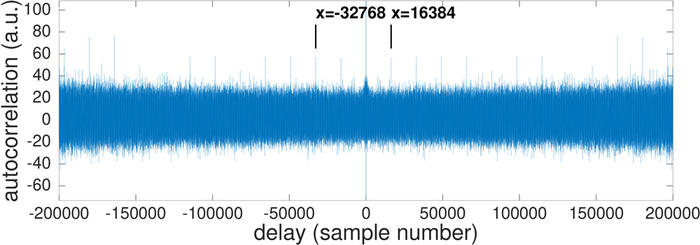
La première question que nous sommes en droit de nous poser est notre compréhension du format de données et si le fichier d’acquisition mérite d’être traité. Avant d’avoir la moindre idée sur le format d’encodage, nous pouvons simplement nous demander si un motif se répète. En effet, dans une encapsulation des messages sous forme de paquets, il est fort probable que la taille des paquets soit constante et que des motifs tels qu’un en-tête se répètent. Ainsi, l’autocorrélation du signal doit présenter des pics espacés de la période de répétition des messages (figure 9).
Fig. 9 : Autocorrélation de 400 kpoints représentant les soft bits en sortie du démodulateur GNU Radio, qui s’est chargé de retrouver la fréquence de la porteuse et l’horloge de la transmission QPSK. Des pics de corrélation se retrouvent tous les 16384 échantillons.
Nous observons des pics de corrélation séparés de 16384 échantillons (octets). Pour empiéter un peu sur la description qui va suivre, nous apprendrons que chaque paquet transmis par Meteor-M2 est composé de 1024 octets ou 8192 bits, que l’encodage proposé (code convolutif [17]) double le nombre de bits à 16384 et dans le format des soft bits, nous avons 1 octet pour représenter chaque bit du message transmis. La position des pics de corrélation observée dans la figure 9 est donc bien cohérente avec la forme du signal attendu : non seulement nous avons vérifié être capables de lire le fichier sauvé par GNU Radio et d’en interpréter correctement le contenu, mais nous savons que le signal acquis contient l’information transmise par le satellite et mérite donc d’être analysé.
5.2 Décodage des données
Nous avons donc obtenu une séquence d’octets dont la valeur sera plus probablement égale à 1 ou 0. Comme tout flux continu de données, il nous faut avoir un point de départ pour savoir quand traiter ces bits, les assembler en lettres (octets), puis en mots, phrases et paragraphes. L’approche classique pour identifier le début d’une transmission est de fournir une séquence prédéterminée dans le flux continu de bits, et de rechercher l’occurrence de cette séquence. L’estimateur de similitude entre les phases successives du signal et la séquence à trouver est l’intercorrélation. Qu’à cela ne tienne : la documentation technique de LRPT [18] nous informe que toutes les transmissions spatiales sont synchronisées avec le mot 0x1ACFFC1D. Facile donc : on va intercorréler le signal avec ce mot, et on trouvera la synchronisation par maximum d’intercorrélation.
Pas si vite. D’abord, les bits reçus depuis un satellite orbitant à plus de 800 km de la surface de la Terre sont bruités. On va donc chercher une certaine redondance pour maximiser nos chances de bien entendre le message transmis. Une méthode basique serait de simplement répéter le message, mais que faire si deux transmissions ne sont pas identiques ? Laquelle choisir ? Plus subtil, l’encodage convolutif prend un flux continu de bits, et fabrique une nouvelle séquence (plus longue) telle que chaque nouveau bit est une combinaison des bits d’entrée. Cette combinaison est conçue pour maximiser nos chances de retrouver le message initial : c’est l’encodage convolutif. Les bits ainsi encodés ne présentent plus le mot de synchronisation 0x1ACFFC1D, mais sa version encodée par convolution, que nous devons déterminer et rechercher dans la séquence de bits reçus.
5.3 Encodage convolutif du mot de synchronisation
Afin de maximiser nos chances de retrouver la valeur de chaque bit, un code convolutif qui étale l’information dans le temps est utilisé afin d’introduire de la redondance. Alors que l’encodage est excessivement simple à mettre en œuvre, le décodage de la séquence la plus probable, après corruption de certains bits lors de la transmission, est potentiellement très complexe. Une approche optimale du problème complémentaire qu’est le décodage est implémentée sous la forme de l’algorithme de Viterbi – du nom de son auteur, aussi cofondateur de la société Qualcomm – dont nous devons maîtriser les concepts pour obtenir des séquences de bits intelligibles.
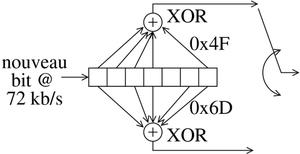
Fig. 10 : Codage convolutif : les bits dans le registre à décalage sont ponctionnés aux indices définis par les polynômes, additionnés en binaire (opération OU exclusif) et les deux bits résultants sont concaténés en sortie, induisant un débit de sortie double de celui d’entrée.
Les données d’entrée sont des soft bits, donc des séquences de valeurs codées sur 8 bits encodant chacune une valeur possible de bit. La convolution pour fabriquer les bits émis a pris chaque bit de la source, et en a fabriqué deux bits de sortie comme combinaison d’un certain nombre de bits d’entrée : l’algorithme de convolution est dit r=1/2, car il fournit deux fois plus de bits en sortie qu’en entrée et K=7, car le registre à décalage qui mémorise la séquence des bits d’entrée est de longueur 7 bits. Il existe une multitude de façons de voir la convolution : une approche représentative de l’implémentation matérielle ou en logique programmable (FPGA) de l’encodage convolutif, consiste en un registre à décalage servant de mémoire, alimenté par le nouveau bit de la séquence à encoder, et alimentant une ou plusieurs portes XOR pour fournir 1/r⩾1 bit en sortie pour chaque bit d’entrée (figure 10). Une façon d’exprimer les bits du registre à décalage alimentant la porte XOR est de fournir un polynôme, dont chaque puissance non nulle correspond à un point de connexion de la porte XOR (figure 10, en lisant de droite à gauche la représentation binaire de l’octet représentant chaque polynôme). À partir de cette expression polynomiale du code convolutif, nous pouvons exprimer la séquence d’opérations sous forme matricielle, tel que décrit sur http://www.invocom.et.put.poznan.pl/~invocom/C/P1-7/en/P1-7/p1-7_1_6.htm en considérant que le décalage à chaque pas de temps du contenu du registre à décalage revient à décaler les coefficients du polynôme sur la séquence (longue) de bits à encoder. Cette expression sous forme de matrice génératrice est naturelle dans le langage de Matlab, puisqu’il fournit une expression matricielle du produit de convolution et se traduit dans un cas simple sous GNU/Octave par :
d=[0 1 0 1 1 1]
G1=[1 1 1] % 0x7 r=1/2, K=3 (registre à décalage de 3 bits de long)
G2=[1 0 1] % 0x5
G=[G1(1) G2(1) G1(2) G2(2) G1(3) G2(3) 0 0 0 0 0 0;
0 0 G1(1) G2(1) G1(2) G2(2) G1(3) G2(3) 0 0 0 0;
0 0 0 0 G1(1) G2(1) G1(2) G2(2) G1(3) G2(3) 0 0;
0 0 0 0 0 0 G1(1) G2(1) G1(2) G2(2) G1(3) G2(3);
0 0 0 0 0 0 0 0 G1(1) G2(1) G1(2) G2(2);
0 0 0 0 0 0 0 0 0 0 G1(1) G2(1);
]
mod(d*G,2) % produit matriciel modulo 2 = XOR
Ici, nous avons alternance des coefficients des deux polynômes nommés G1 et G2, qui fournit bien un résultat cohérent avec celui annoncé sur home.netcom.com/~chip.f/viterbi/algrthms.html : 0 1 0 1 1 1 → 0 0 1 1 1 0 0 0 0 1 1 0.
Le déroulement de la matrice de convolution, proposée ici manuellement, se généralise au cas qui nous intéresse d’un code composé de deux polynômes appliqués à un registre à décalage de 7 bits, par :
% mot à encoder
d=[0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 0 1 ]; % 1A CF FC 1D
G1=[1 1 1 1 0 0 1 ] % 4F polynôme 1
G2=[1 0 1 1 0 1 1 ] % 6D polynôme 2
Gg=[];
for k=1:length(G1)
Gg=[Gg G1(k) G2(k)]; % fabrique la version interlacée des deux polynômes générateurs
end
G=[Gg zeros(1,2*length(d)-length(Gg))] % première ligne de la matrice de convolution
for k=1:length(d)-length(G1)
G=[G ; zeros(1,2*k) Gg zeros(1,2*length(d)-length(Gg)-2*k)] ;
end
for k=length(Gg)-2:-2:2
G=[G ; zeros(1,2*length(d)-(length(Gg(1:k)))) Gg(1:k)];
end i % dernières lignes de la matrice de convolution
res=1-mod(d*G,2); % mod(d*G,2)
dec2hex(res(1:4:end)*8+res(2:4:end)*4+res(3:4:end)*2+res(4:4:end))'
printf("\n v.s. 0x035d49c24ff2686b or 0xfca2b63db00d9794\n")
Nous constatons en exécutant ces quelques lignes, qui encodent le mot de synchronisation 1ACFFC1D00 par les deux polynômes 4F et 6D définissant les points de connexion des deux portes XOR sur le registre à décalage de 7 bits de long, que nous obtenons la séquence FCA2B63DB00D9794 qui est bien celle documentée sur [3]. Notez qu’il semble exister deux normes au sein de la NASA, dans lesquelles G1 et G2 semblent inversés. Ainsi, certains encodeurs et décodeurs disponibles sur le web, affirmant appliquer le bon code, ne donnent pas le bon résultat. Nous comprenons donc comment encoder le mot de synchronisation par la convolution.
5.4 Représentation de l’encodage par machine à état
Nous aurons besoin, lors de l’explication du décodage par l’algorithme de Viterbi, de comprendre les transitions d’état, c.-à-d. non pas seulement de comprendre le code convolutif en termes de produit matriciel, mais en termes de machine à état, avec une décision à prendre sur le cheminement le plus probable d’un état à l’autre. Comment donc exprimer ce problème, vu sous forme de produit matriciel, en termes de machine à état ?
Le code convolutif qui nous intéresse possède un registre à décalage de 6 bits, dans lequel nous insérons un 7e bit qui forme la nouvelle donnée d’entrée. L’encodeur a donc 26=64 états possibles. Nous ne les développerons pas tous ici, seulement ceux nécessaires à encoder le premier octet du mot de synchronisation.
Partons de l’état où tous les bits du registre à décalage sont à 0 (état que nous nommerons « a »). Deux cas sont possibles : la nouvelle donnée entrante est 0 ou 1, donc dans le code Octave précédent, nous avons deux cas d=[0 0 0 0 0 0 0] ou d=[1 0 0 0 0 0 0]. Dans le premier cas, les deux bits sortis par le code convolutif sont mod(d*G1’,2)=0 et mod(d*G2’,2)=0 ou 00, et dans le second cas mod(d*G1’,2)=1 et mod(d*G2’,2)=1 ou 11. Dans le premier cas, l’état de sortie est le même que l’état d’entrée donc a→a tandis que dans le second cas, la valeur « 1 » est entrée dans le registre à décalage, donc nous sommes passés en état interne [1 0 0 0 0 0] que nous nommons « b ». Cette séquence se poursuit pour donner le tableau suivant :
|
Bit d’entrée |
État d’entrée |
Nom |
Bits de sortie |
État de sortie |
Transition |
|---|---|---|---|---|---|
|
0 |
000000 |
a |
00 |
000000 |
a→a |
|
1 |
000000 |
a |
11 |
100000 |
a→b |
|
0 |
100000 |
b |
10 |
010000 |
b→c |
|
1 |
100000 |
b |
01 |
110000 |
b→d |
|
0 |
010000 |
c |
11 |
001000 |
c→... |
|
1 |
010000 |
c |
00 |
101000 |
c→... |
|
0 |
110000 |
d |
01 |
011000 |
d→e |
|
1 |
110000 |
d |
10 |
111000 |
d→... |
|
0 |
011000 |
e |
00 |
001100 |
e→... |
|
1 |
011000 |
e |
11 |
101100 |
e→f |
|
0 |
101100 |
f |
01 |
010110 |
f→... |
|
1 |
101100 |
f |
10 |
110110 |
f→... |
|
... |
... |
... |
... |
... |
... |
|
0 |
100001 |
u |
01 |
010000 |
u→c |
|
1 |
100001 |
u |
10 |
110000 |
u→d |
|
... |
... |
... |
... |
... |
... |
|
0 |
000001 |
z |
11 |
000000 |
z→a |
|
1 |
000001 |
z |
00 |
100000 |
z→b |
Dans ce tableau, les points de suspension dans le nom des états d’arrivée représentent des cas qui ne nous seront pas utiles dans l’encodage du premier octet du code de synchronisation (l’état « c » ne nous sera pas utile non plus, mais nous le présentons pour clarifier la démonstration). Les états « u » et « z » sont insérés pour illustrer les boucles qui se forment, lorsque nous suivrons la machine à état suffisamment longtemps. Nous encourageons le lecteur à ré-établir par lui-même ce résultat pour se convaincre de la pertinence de la démarche.
Nous exploitons cette table de transition d’états pour illustrer l’encodage de l’octet 0x1A (premier octet du mot de synchronisation). Les trois premiers bits à 0 du quartet de poids fort s’encodent par 00 et nous laissent dans l’état « a », et le dernier bit à 1 s’encode en 11 pour nous faire passer en « b ». Le bit de poids fort du quartet A est à 1 et nous sommes dans l’état « b », donc nous générons 01 et passons en « d ». Le bit suivant est à 0 (rappel : 0xA=0b1010) et avec un état « d », nous sortons 01 pour passer en « e ». L’état « e » prend en entrée un 1 pour sortir 11 et passer en « f » et finalement, « f » avec une entrée à 0 produit 01. Pour résumer, en encodant 0x1A nous avons produit 0b0000001101011101=0x035D qui est bien la valeur attendue (noter que 0x035D est l’opposé de 0xFCA2 que nous avions mentionné auparavant comme début de la solution d’encodage – à une rotation de 180 degrés près des bits, il s’agit de la même solution).
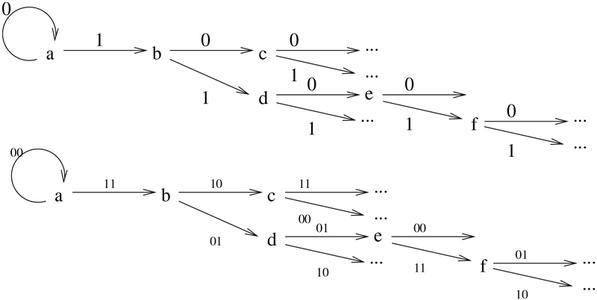
Une représentation en machine à état s’obtient donc telle que présentée sur la figure 11, avec en haut les états successifs de « a » à « f » en fonction de la valeur du bit d’entrée et en bas, les deux bits de sortie pour chacune de ces transitions.
Fig. 11 : Haut : états, nommés de « a » à « f » et transitions en fonction de la valeur du bit d’entrée. Bas : valeur des bits de sortie en fonction de ces transitions. En suivant le cheminement décrit dans le texte, l’entrée 0x1A=0b00011010 s’encode en 0b0000001101011101=0x035D.
5.5 Décodage d’un code convolutif : l’algorithme de Viterbi
Ayant établi la machine à état qui convertit un mot d’entrée en un mot de sortie de longueur double, nous désirons comprendre la séquence de décisions qui maximisera la probabilité d’inverser le processus, et ce, sachant que les données reçues ont pu être corrompues au cours de la transmission. Commençons par considérer le résultat avant d’aborder l’explication.
Nous verrons plus loin qu’une bibliothèque existe pour mettre en œuvre efficacement (en C) l’encodage et le décodage par convolution : nous utilisons libfec (github.com/quiet/libfec) décrit dans [3] et dont le code d’exemple vtest27.c a servi de point de départ pour implémenter le décodeur. Alternativement, www.spiral.net/software/viterbi.html fournit un générateur de code pour décoder par algorithme de Viterbi, respectant le code convolutif utilisé par LRPT. Nous appréhendons libfec avec le cas simple du décodage de la trame encodée FC A2 B6 3D B0 0D 97 94 – que nous avions vu résulter de l’encodage par convolution du mot de synchronisation – pour voir si nous sommes capables de retrouver le mot initial :
#include <stdio.h> // gcc -Wall -o t t.c -I./libfec ./libfec/libfec.a
#include <fec.h>
#define MAXBYTES (4) // le message final a 4 octets
#define VITPOLYA 0x4F // 0d79 : taps polynome 1
#define VITPOLYB 0x6D // 0d109 : taps polynome 2
int viterbiPolynomial[2] = {VITPOLYA, VITPOLYB};
unsigned char symbols[MAXBYTES*8*2]= // *8 pour octet->bit, et *2 Viterbi
{1,1,1,1,1,1,0,0, // fc
1,0,1,0,0,0,1,0, // a2
1,0,1,1,0,1,1,0, // b6
0,0,1,1,1,1,0,1, // 3d
1,0,1,1,0,0,0,0, // b0
0,0,0,0,1,1,0,1, // 0d
1,0,0,1,0,1,1,1, // 97
1,0,0,1,0,1,0,0};// 94
int main(int argc,char *argv[]){
int i,framebits;
unsigned char data[MAXBYTES]; // *8 for bytes->bits & *2 Viterbi
void *vp;
framebits = MAXBYTES*8;
for (i=0;i<framebits*2;i++) symbols[i]=1-symbols[i]; // flip bits
for (i=0;i<framebits*2;i++) symbols[i]=symbols[i]*255; // bit -> byte /!\
set_viterbi27_polynomial(viterbiPolynomial); // definition des taps
vp=create_viterbi27(framebits);
init_viterbi27(vp,0);
update_viterbi27_blk(vp,symbols,framebits+6);
chainback_viterbi27(vp,data,framebits,0);
for (i=0;i<MAXBYTES;i++) printf("%02hhX",data[i]);
printf("\n");
exit(0);
}
Avec la seule subtilité du code, qui prend en entrée les bits successifs (ici hard bits puisque déjà saturés à 0 ou 1) du mot à décoder, d’encoder chaque bit sur toute la plage représentant un octet (donc 0 ou 255 et non 0 ou 1), et d’éventuellement retourner les bits (0↔1) pour ne pas se retrouver avec le complément du mot recherché (rotation de phase de 180° de la modulation de phase initiale, par exemple). En exécutant ce code, nous recevons bien 1ACFFC1D qui est le mot recherché, nous comprenons donc comment utiliser libfec. Essayons maintenant d’appréhender l’algorithme sous-jacent.
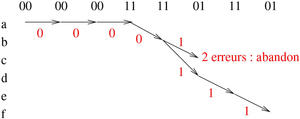
Le code convolutif implémenté lors de l’encodage a eu pour vocation d’introduire un effet de mémoire dans la séquence, afin de rendre la transmission robuste aux erreurs aléatoires qui pourraient ponctuellement s’introduire à cause d’un bruit uniformément distribué (en opposition d’un bruit ponctuel, qui corromprait une séquence contiguë de bits). Le problème du décodage consiste donc à parcourir la machine à état introduite dans la figure 11 à l’envers, en tentant de trouver le cheminement le plus probable compte tenu des bits reçus. Imaginons que nous recevions la séquence 0b0000001111011101 : quelle émission a permis de générer ce code transmis ? Le décodeur de Viterbi est initialisé avec tous ses bits à 0, donc dans l’état « a » en se référant à la figure 11. Nous recevons 00, donc nous restons en état « a » et savons que le bit émis était un 0. De même pour les deux séquences de 00 qui suivent, et la paire 11 nous indique que nous sommes passés en « b » après qu’un 1 ait été encodé. En recevant 11 quand sommes en état « b », il y a incohérence : « b » ne peut produire que 01 (si 1 était transmis) ou 10 (si 0 était transmis). Il y a donc un bit erroné qui a été reçu. Pour le moment, nous ne pouvons pas décider quelle voie poursuivre, donc nous continuons l’analyse selon les deux cas possibles, « c » et « d ». Les deux bits suivants sont 01 et là, nous constatons que la voie « c » est improbable, car l’état « c » ne peut produire que 00 ou 11, alors que « d » est bien capable de produire les 01 observés (bit émis correspondant 0) pour passer en « e ». Donc la voie « c » est abandonnée pour continuer en « d », puis « e ». Depuis « e », nous recevons 11 qui est une valeur possible (bit émis de 1) pour nous faire passer en « f » et finalement 01 est une valeur possible de « f » qui nous permet de déduire que le dernier bit transmis était un 0. Nous avons donc été capables de corriger le bit erroné et de déduire que la séquence la plus probable émise était 0b00011010=0x1A qui aurait dû donner lieu à 0b0000001101011101 où nous avons mis en évidence en couleur le bit erroné (voir figure 12).
Fig. 12 : En haut, la séquence de bits reçus groupés 2 par 2, car le code convolutif produit 2 bits de sortie pour chaque bit d’entrée encodé. En ordonnée, les états de la machine représentant l’encodeur. En rouge, le nombre d’erreurs cumulées sur chaque chemin du décodeur. En pratique, l’abandon d’une branche se ferait lorsque deux chemins rencontrent le même état : dans ce cas, la séquence cumulant le plus d’erreurs est abandonnée au profit de la séquence la plus probable, car présentant le moins d’erreurs cumulées.
Fort de ces connaissances, nous sommes en mesure de rechercher par corrélation dans la trame acquise l’occurrence du code de synchronisation après application de la convolution, qui serait la preuve de notre compréhension de l’encodage des messages, et de notre capacité à identifier le début des paquets transmis. Lorsque nous effectuons l’opération de corrélation entre le mot encodé FCA2B63DB00D9794 et la séquence de coefficients I/Q acquise et convertie en bits par la cartographie proposée en figure 13... le résultat est nul, pas le moindre pic de corrélation (figure 14, haut). Quelque chose nous échappe donc encore…
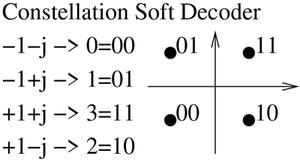
Fig. 13 : Constellation QPSK : chaque état possible de phase encode 2 bits. L’assignation de chaque symbole, de 0 à 3, vers les paires ici choisies arbitrairement, mais selon un code de Gray (1 seul changement entre deux paires adjacentes de bits) sera l’objet d’une partie du travail de décodage.
Fig. 14 : Corrélation pour les 4 cas possibles de rotation de la constellation QPSK avec le code connu de début de trame. Nous constatons que seul le quatrième cas – en bas – fournit des pics périodiques de corrélation représentatifs du début de trame. C’est donc cette attribution des 4 symboles de QPSK aux paires de bits correspondantes qui est correcte.
Conclusion
Dans cette première partie de la compréhension des couches du protocole LRPT documenté par le CCSDS pour recevoir les images issues de Meteor-M2, nous avons exploré les couches les plus basses correspondant dans la hiérarchie OSI aux couches physique et de trame. Nous pensons avoir obtenu, après décodage du code convolutif par l’algorithme de Viterbi, une séquence de bits corrigée des erreurs aléatoires de transmission, mais en recherchant l’occurrence du mot de synchronisation des trames, aucun pic de corrélation n’est apparu. Il nous manque donc encore un élément dans la compréhension de la séquence de transmission.
Au risque de briser le suspens du prochain épisode, nous verrons le mois prochain que l’erreur porte sur l’assignation de chaque symbole de la constellation QPSK vers une paire de bits : notre assignation arbitraire de -1-j→00, -1+j→01, +1+j→11 et +1-j→10 n’a aucune raison d’être valide. En corrigeant cette défaillance, nous serons capables d’aller jusqu’au décodage des imagettes JPEG que nous assemblerons pour former une image complète.
Remerciements
L. Teske et D. Estévez ont répondu à mes demandes de compléments d’information par courrier électronique. M. Addouche (Univ. de Franche-Comté à Besançon) m’a présenté le décodage du code convolutif par algorithme de Viterbi. Tous les ouvrages et références qui ne sont pas librement disponibles sur le web ont été obtenus auprès de Library Genesis sur gen.lib.rus.ec, une ressource d’une valeur inestimable pour nos recherches.
Références
[1] Meteor-M2 satellite : planet.iitp.ru/english/spacecraft/meteor-m-n2_eng.htm
[2] « Q.1400 : Architecture framework for the development of signalling and Operations, Administration and Management protocols using OSI concepts », ITU-T, 1993 : https://www.itu.int/rec/T-REC-Q.1400-199303-I/en
[3] L. TESKE, « GOES Satellite Hunt » : www.teske.net.br/lucas/satcom-projects/satellite-projects/
[4] J.-M FRIEDT, « Decoding Meteor-M2: QPSK, Viterbi, Reed Solomon and JPEG », FOSDEM 2019 : fosdem.org/2019/schedule/event/sdr_meteorm2n/
[5] G. D. FORNEY Jr, « The Viterbi Algorithm: A Personal History », 2005 : https://arxiv.org/abs/cs/0504020v2
[6] D. BODOR, « Réception de vos premières images satellite », Hackable n°25, juillet 2018 : https://connect.ed-diamond.com/Hackable/HK-025
[7] NEC : www.nec2.org
[8] J.-M FRIEDT, « Satellite image eavesdropping: a multidisciplinary science education project », European J. of Physics, 26, 969-984, 2005
[9] D. ISRAEL, « A Space Mobile Network », Conférence WiSEE, Déc. 2018, ou https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20170009966.pdf
[10] G. KRANZ, « Failure is not an option - Mission Control From Mercury to Apollo 13 and Beyond », Simon & Schuster, 2000
[11] A. MAKOVSKY, A. BARBIERI & R. TUNG, « Odyssey Telecommunications », DESCANSO Design and Performance Summary Series, 6, 2002 sur descanso.jpl.nasa.gov/DPSummary/odyssey_telecom.pdf : p.34 indique « The command format currently used for deep-space missions, including Odyssey, is defined in the CCSDS standard CCSDS 201.0-B-1. »
[12] J.-G. DUMAS, J.-L. ROCH, É. TANNIER, S. VARRETTE, « Théorie des codes - Compression, cryptage, correction », Dunod, 2007, chap. 4.6, ou R.H. MORELOS-ZARAGOZA, « The art of error correcting coding », 2de Ed., Wiley, 2006
[13] H. BOEGLEN, « Les bases des communications numériques avec GNU Radio », GNU/Linux Magazine n°225, 2019 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-225
[14] J.-M FRIEDT, « Radio Data System (RDS) - analyse du canal numérique transmis par les stations radio FM commerciales, introduction aux codes correcteurs d'erreur », GNU/Linux Magazine n°204, mai 2017 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-204/Radio-Data-System-RDS-analyse-du-canal-numerique-transmis-par-les-stations-radio-FM-commerciales-introduction-aux-codes-correcteurs-d-erreur
[15] J.-M FRIEDT, G. CABODEVILA, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », Open Silicium n°15, juillet-sept. 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-015/Decodage-des-signaux-de-satellites-GPS-recus-par-recepteur-de-television-numerique-terrestre-DVB-T
[16] S. LIN & D. J. COSTELLO, « Error Control Coding: Fundamentals and Applications », Prentice Hall, 1983
[17] A. VITERBI, « Error bounds for convolutional codes and an asymptotically optimum decoding algorithm », IEEE Trans. on Information Theory, 13 (2), pp.260-269, 1967
[18] E. NERI et al., « Single space segment - HRPT/LRPT Direct broadcast services specification », doc. MO-DS-ESA-SY-0048 rev. 8, ESA EUMETSAT EPS/METOP, 1 nov. 2000 : mdkenny.customer.netspace.net.au/METOP_HRPT_LRPT.pdf
[19] G.D. FORNEY, « The viterbi algorithm », Proc. IEEE 61 (3), pp.268-278, 1973
[20] R. SNIFFIN, « Telemetry Data Decoding », Deep Space Network 208, p.12, 2013) : https://deepspace.jpl.nasa.gov/dsndocs/810-005/208/208B.pdf, ou http://www.ka9q.net/amsat/ao40/2002paper/ illustrent les nombreuses déclinaisons possibles à partir de la même définition formelle du code.