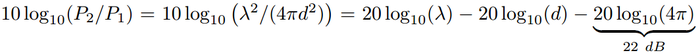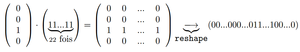La réception de signaux radiofréquences en vue de leur traitement logiciel ne nécessite pas forcément un matériel coûteux et dédié. Nous allons survoler les diverses interfaces d’acquisitions accessibles à l’amateur éclairé, pour insister sur l’exploitation d’interfaces probablement déjà disponibles autour de la majorité des lecteurs.
Le traitement numérique de signaux radiofréquences, au cœur de la radio logicielle (Software Defined Radio – SDR), nécessite un flux de données échantillonnées à intervalle de temps constant et connu. En effet, la connaissance et la maîtrise de la fréquence d’échantillonnage est fondamentale : nous acquérons périodiquement des signaux et ferons l’hypothèse que l’intervalle de temps entre deux mesures est connu tout au long du traitement logiciel du flux de données. Pour alimenter les chaînes logicielles de traitement du signal, diverses interfaces matérielles sont disponibles : nous allons passer ici en revue quelques-unes des interfaces les plus accessibles, en particulier par leur compatibilité avec l’environnement libre de traitement du signal qu’est GNU Radio, et poursuivrons sur le détournement de quelques sources facilement disponibles – carte son, oscilloscope, flux de données disponibles sur le Web – pour aborder le domaine de la radio logicielle. Nous verrons que de nombreuses options s’offrent pour aborder le sujet du traitement numérique de signaux radiofréquences, pour permettre une évolution progressive de la complexité des analyses effectuées sur les signaux observés. Nous survolerons les sources d’émission, en insistant dès à présent sur les dangers du brouillage, volontaire ou involontaire, lors de l’émission de signaux radiofréquences et des risques légaux associés : mieux vaut se contenter dans un premier temps de recevoir des signaux existant, avant de vouloir se lancer dans la génération de ses propres signaux, avec tous les risques que cela implique.
1. Caractéristiques des interfaces matérielles pour la SDR
Quelles sont les caractéristiques que nous attendons d’une source de signaux pour une application de radio logicielle :
- la gamme de fréquences de porteuse accessible. C’est souvent le premier paramètre analysé par les futurs acquéreurs de cartes d’acquisition, mais c’est finalement une donnée assez triviale puisqu’au pire, si une bande de fréquence n’est pas accessible à l’oscillateur local, il suffit d’ajouter un oscillateur externe et un mélangeur pour se ramener dans la bande accessible – c’est par exemple ce que font les upconverters du type http://www.nooelec.com/store/ham-it-up.html qui amènent le signal de la bande HF (0-30 MHz) vers une bande de fréquence accessible par les récepteurs faible coût qui ne commencent à fonctionner qu’à partir d’une vingtaine de MHz. La plage de fréquence de porteuse est donc certes intéressante, mais ne doit pas être prise comme le critère déterminant le choix de l’interface d’acquisition,
- la bande passante accessible. Cette grandeur est primordiale : Shannon nous informe de l’équivalence entre bande passante et contenu d’information, donc plus la bande passante est importante, plus riche est l’information qui pourra être extraite du signal échantillonné. Ainsi, une carte son avec ses 192 kHz ne permet que difficilement d’analyser un signal de la bande FM transposé en bande de base par un oscillateur radiofréquence externe (la largeur de bande d’une station FM est 250 kHz), alors qu’un récepteur de télévision numérique terrestre équipé d’un convertisseur analogique-numérique RTL2832 s’en acquitte sans problème avec ses 2,4 Méchantillons/s. La bande passante du récepteur est une chose, la capacité à transférer vers le processeur en est une autre. Il est courant d’effectuer un prétraitement au plus proche du convertisseur analogique-numérique – généralement sur le FPGA chargé de cadencer l’acquisition – et de ne transmettre vers le PC qu’un signal prétraité pour avoir été suffisamment décimé.
- le coût est de toute évidence un critère déterminant : on constatera que dans la plupart des cas, bande passante et coût évoluent de la même façon,
- la limite de détection, ou le plus petit signal détectable. Ici, nous avons choisi, un peu arbitrairement, d’indiquer la plus petite puissance d’une porteuse modulée en fréquence avec une excursion de 20 kHz et une fréquence de 2400 Hz permettant de démoduler l’information avec un rapport signal à bruit de 10 dB.
- certaines interfaces permettent non seulement de recevoir, mais aussi d’émettre. L’émission de signaux radiofréquences pose de nombreux problèmes légaux pour s’assurer de ne pas brouiller une émission existante, volontairement ou involontairement.
Attention !
Les critères permettant de qualifier un émetteur sont bien plus nombreux et complexes que ceux d’un récepteur, et pour commencer nous encourageons à uniquement recevoir, pour n’émettre qu’en étant parfaitement conscient des conséquences des risques de brouillage.
1.1 Réception
Diverses plateformes dédiées (voir figure 1) sont décrites ci-dessous, avant de proposer de détourner des interfaces matérielles souvent disponibles sans être nécessairement dédiées au traitement SDR, et finalement nous conclurons sur l’exploitation de signaux disponibles via Internet.
Fig. 1 : Les diverses plateformes testées dans cet article : de gauche à droite, l’Ettus Research B210, la PlutoSDR d’ADi, les récepteurs DVB-T, et la LimeSDR. La plateforme HackRF, présentée dans [1], n’était pas disponible pour ces tests.
Un résumé des principales caractéristiques de ces plateformes dédiées est proposé ci-après, incluant les paramètres que nous venons de citer. MIMO signifie que le récepteur propose plusieurs antennes, une fonction qui peut s’avérer intéressante pour des applications plus avancées de détection d’angle d’arrivée de signal, de détection synchrone ou RADAR, ou d’émission dans une direction déterminée. Par ailleurs, full-duplex signifie que nous pouvons émettre en même temps que nous recevons, en opposition à half duplex qui ne permet que soit l’émission, soit la réception. R820T2+RTL2832U réfère à la pléthore de récepteurs de télévision numérique terrestre détournés à des fins de SDR : nous utilisons pour notre part les options les moins chères comme support d’introduction au domaine présentant tous les défauts possibles de récepteurs faible-coût, pour un prix unitaire inférieur à 10 euros. Les autres plateformes sont des circuits dédiés de divers fabricants : nous avons exclu le haut de gamme Ettus Research qui, pour une bande passante de 200 MS/s, coûte la modique somme de 5270 euros auquel on ajoutera les cartes filles de transposition de fréquence ou de transmission des signaux bruts.
|
|
Bande passante |
Coût |
Gamme porteuse |
Résolution |
Flux continu |
Émission ? |
|
|
(MHz) |
|
(MHz) |
(bits) |
|
|
|
Carte son |
0,192 |
inclus |
≃DC–0.096 |
16 |
oui |
full-duplex |
|
Redpitaya |
125 |
200/260 euros |
DC–62,5 |
10/14 |
non/oui (voir section 2) |
full-duplex |
|
Oscilloscope |
|
|
|
≥8 |
non |
non |
|
R820T2+RTL2832U |
2,4 |
<10$ |
24–1700 |
8 |
oui |
non |
|
AirspyMini (R820T) |
3, 6, 10 |
99$ |
24–1700 |
12 |
oui |
non |
|
PlutoSDR |
20 (USB 2) |
149$ |
70–6000 |
12 |
oui |
full-duplex |
|
Lime SDR |
61,44 (USB 3) |
299$ |
0.1–3800 |
12 |
oui |
MIMO |
|
HackRF One |
2–20 (USB 2) |
300$ |
1–6000 |
8 |
oui |
half-duplex |
|
BladeRF 2.0 |
61,44 (USB 3) |
480$ |
47–6000 |
12 |
oui |
MIMO |
|
B210 |
61,44 (USB 3) |
1200$ |
70–6000 |
12 |
oui |
MIMO |
Ce tableau est en partie inspiré de www.crowdsupply.com/lime-micro/limesdr dont nous avons repris chaque information pour en valider la valeur.
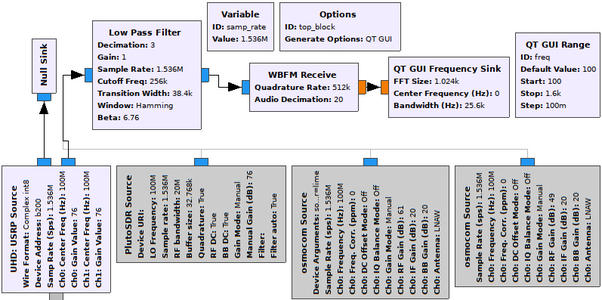
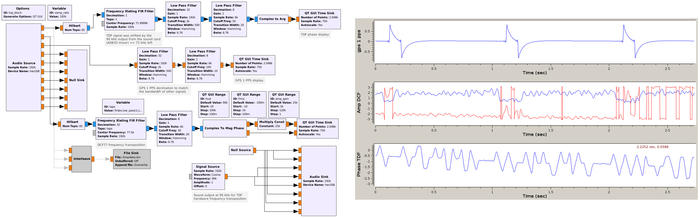
En plus de ces caractéristiques publicitaires, il est utile d’analyser les performances pratiques d’un récepteur. Une telle caractérisation est souvent dépendante des conditions d’application : nous nous sommes placés dans le contexte d’une modulation de fréquence telle que, par exemple, utilisée par les satellites NOAA, et pour une porteuse variant de 100 MHz (bande FM, aéronautique et spatiale), 434 MHz (bande Industrielle, Scientifique et Médicale), 1090 MHz (communications aéronautiques ADS-B) à 1600 MHz (satellites GPS et Iridium). Nous avons indiqué la puissance minimum de la porteuse, pour le gain maximum de chaque récepteur (valeur G à côté de chaque modèle) pour laquelle le signal modulé en FM à 2400 Hz avec une excursion de 20 kHz présente un rapport signal à bruit de 10 dB (par rapport au plancher de bruit) sur la démodulation. Les valeurs présentent une incertitude de l’ordre du dBm, et toutes les mesures sont faites en mode conduit avec comme source un synthétiseur Rohde & Schwarz SMC100A muni d’un atténuateur de 20 dB et capable de fournir un signal sur une porteuse de 9 kHz à 3,2 GHz. La chaîne de traitement en réception se contente d’un bloc GNU Radio WBFM qui décime avant d’alimenter un affichage du spectre du signal démodulé (voir figure 2).
|
|
Puissance minimale pour mesurer une modulation avec 10 dB de rapport signal à bruit |
|||
|
Fréquence porteuse |
100 MHz |
434 MHz |
1090 MHz |
1600 MHz |
|
R820T2 (G=49) |
-118 dBm |
-120 dBm |
-107 dBm |
-96 dBm |
|
Lime SDR (G=61) |
-106 dBm |
-120 dBm |
-122 dBm |
-115 dBm |
|
PlutoSDR (G=76) |
-111 dBm |
-113 dBm |
-111 dBm |
-112 dBm |
|
B210 (G=76) |
-116 dBm |
-118 dBm |
-117 dBm |
-117 dBm |
Fig. 2 : Chaîne de traitement GNU Radio pour caractériser la sensibilité des divers récepteurs sur une porteuse transportant une information modulée en FM (excursion de 20 kHz, fréquence de 2400 Hz). Ce graphique met en évidence la multitude de sources de signaux radiofréquences (bas) qui peuvent alimenter une même chaîne de traitement GNU Radio.
Nous constatons que tous les récepteurs présentent des planchers sensiblement identiques, un résultat qui ne devrait pas surprendre compte tenu du peu d’étages de réception radiofréquences disponibles. On peut en effet restreindre les front ends à quelques fabricants que sont Rafael Microelectronic avec son R820T(2), Lime avec son LMS{7,6}002M et évidemment Analog Devices qui fournit les solutions les plus souples et les plus performantes avec ses AD936x (x=1 sur l’Ettus Research B210, x=3 sur la PlutoSDR, x=4 sur l’Ettus Research B200) permettant d’atteindre des gammes de porteuse aussi vastes que 70 MHz à 6 GHz. Dans ces conditions, la différence entre les divers récepteurs tiendra aux divers composants passifs connectant l’antenne de réception au front-end : diodes de protection, transformateurs et autres éléments de filtrage peuvent être sélectionnés pour favoriser l’une ou l’autre gamme de fréquence : fournir des performances uniformes sur deux ordres de grandeur de fréquence présente des difficultés de conception difficiles à résoudre à coût réduit.
L’échelle logarithmique des décibels
Il est courant de discuter des puissances et tensions impliquées dans les signaux radiofréquences en décibels, une échelle logarithmique définie comme R = 10log10(P2/P1) (dB) le ratio entre deux puissances P2 et P1. Parler en décibels simplifie considérablement les calculs, car au lieu de manipuler des produits entre des valeurs très grandes et très petites, nous considérons des sommes sur des valeurs typiquement comprises entre quelques unités et quelques centaines. Prenons le cas d’un bilan de liaison : la puissance émise P1 s’étale sur une sphère de 4πd2 à la distance d donc la puissance reçue P2 est de l’ordre de P2/P1∝λ2/(4πd2) avec λ2 la surface typique de l’antenne qui intersecte la sphère qui distribue la puissance émise. En pratique, nous normalisons par l’angle solide de 4π steradians pour trouver l’équation de Friis de propagation en espace libre P2/P1= (λ/(4πd))2. Un signal Wi-Fi (λ=12,5 cm) est donc atténué de 10-8 à une distance de 100 m, ou en d’autres termes une puissance émise de 10 mW se retrouve à 10 pW à 100 m. Ces 8 ordres de grandeur ne sont pas simples à manipuler lors de tous ces produits, et il est bien plus simple de passer en échelle logarithmique pour dire que :
En se rappelant que log(a×b) = log(a)+log(b) et donc log(x2)=2log(x). Les auteurs préfèrent souvent parler en fréquence f plutôt que longueur d’onde et remplacent λ=c/f avec c=3×108 m/s et injectent 20log10(c)=169,54 dB dans le terme constant qui donne donc 169,54-22=147,54 dB, la constante classique à la fin de l’équation de Friis (au lieu de parler d’une multiplication par un facteur 4,2×10-8).
On notera que nous n’avons le droit de n’insérer dans un logarithme que des grandeurs sans unité. En effet, si nous écrivons log(d) avec d une distance, alors son unité est un log(m), qui n’a pas de sens physique. Cependant, si nous écrivons log(d/λ) = log(d)-log(λ), alors nous effectuons le calcul sur un ratio de longueurs (une distance en m divisée par une longueur d’onde en m) et nous avons bien un calcul sans unité. Il est classique en physique de vérifier l’homogénéité des unités des équations – à une constante près, cela garantit l’exactitude de l’ordre de grandeur du calcul. Lors du passage en décibels, cette normalisation est souvent implicite, et doit s’exprimer dans la nature de l’unité utilisée : lorsque nous normalisons une puissance par 1 mW, nous écrivons dBm, tandis que lorsque nous normalisons par 1 W nous écrivons dBW – ces deux grandeurs diffèrent d’un facteur 10log10(1000) = 30 dB. Lorsque nous normalisons une tension par 1 V, nous écrivons dBV. Ainsi, 0 dBm = log10(P/1 mW) donc P/1 mW = 1 ⇔ P = 1 mW.
Finalement, on notera que la puissance étant proportionnelle au carré de la tension (à une impédance près), les expressions concernant une puissance 10log10(P2/P1) deviennent en tension 10log10(V22/V12) (l’impédance se simplifie au numérateur et au dénominateur) qui devient classiquement 20log10(V2/V1). Ainsi, on passera souvent d’expressions en 10log10 quand nous manipulons des puissances en 20log10 lorsque nous manipulons des tensions ou des coefficients de diffraction (paramètres S).
Quel est l’intérêt d’une telle mesure de limite de détection ? Imaginons que nous désirions recevoir les émissions d’un satellite en orbite basse, par exemple un de la constellation NOAA à 800 km d’altitude et émettant 5 W. Supposons que le satellite et le récepteur au sol sont munis d’antennes isotropes, qui rayonnent indifféremment dans toutes les directions de l’espace (une antenne est symétrique, donc la condition est la même que nous soyons émetteur ou récepteur). Alors seule la conservation de l’énergie, qui distribue la puissance émise sur la sphère centrée sur l’émetteur, va déterminer la puissance qui atteint le récepteur : il s’agit des pertes de propagation en espace libre, ou Free Space Propagation Loss (FSPL) qui s’expriment en décibels comme FSPL = 20log10(d)+20log10(f)-147,55. Pour un satellite émettant à f = 137 MHz et distant de d = 800 km du récepteur, FSPL ≃ 133 dB. Émettre 5 W ou 5000 mW correspond à 10log10(5000) = 37 dBm (le « m » à la fin de dBm indique que nous exprimons toutes les grandeurs en mW). Nous constatons maintenant l’intérêt de travailler sur une échelle logarithmique où les produits en échelle linéaire deviennent des sommes : la puissance reçue au sol est 37-133 = -96 dBm qui est bien supérieure aux -118 dBm mesurés par exemple pour démoduler avec un rapport signal à bruit de 10 l’émission FM sur une porteuse proche de 100 MHz.
Au-delà des « simples » applications de réception de signaux radiofréquences, la SDR est parfaitement adaptée à de la caractérisation de composants ou réalisation d’instruments qui seraient hors de portée du budget de la majorité des amateurs. À titre d’illustration, une source de bruit (ici une diode Zener polarisée à 24 V et suivie d’une multitude d’amplificateurs – une quinzaine d’euros sur eBay si on ne veut pas assembler le circuit soi-même) alimente un filtre centré sur 140 MHz tandis que la PlutoSDR analyse le signal transmis. Sans prétention de mesure quantitative sur la rejection ou les pertes d’insertion du filtre, les mesures sont cohérentes avec une caractérisation par instrument dédié (figure 3), ici un analyseur de réseau Rohde & Schwarz ZNB8.
Fig. 3 : Caractérisation d’un filtre EPCOS centré sur 140 MHz alimenté par une source de bruit et dont le signal transmis est acquis par une PlutoSDR pour analyse par GNU Radio. Le résultat (droite) est en accord qualitatif (gauche) en termes de niveaux et quantitatif quant aux fréquences de coupure du filtre avec une caractérisation par instrument dédié (droite).
1.2 Émission
De même que nous nous contentons de quelques critères pour caractériser divers récepteurs répondant à notre besoin de recevoir des petits signaux, nous nous intéressons à une caractéristique bien précise des émetteurs qu’est le bruit de phase de la source, en passant sous silence les harmoniques ou niveaux de puissance accessibles. Le bruit de phase est une caractéristique fondamentale d’une source que nous développons ici pour sensibiliser le lecteur souvent peu familier avec ce concept.
Le bref survol pourra être approfondi en consultant rubiola.org/pdf-slides/2008T-jan-syrte-phase-noise.pdf ou E. Rubiola, « Phase noise and frequency stability in oscillators », Cambridge Univ. Press, 2008.
Bruit de phase
Un signal périodique s’exprime sous la forme Acos(ωt+φ(t)) : le bruit de phase décrit la fluctuation aléatoire φ(t). Le même concept est utilisé pour décrire les fluctuations d’un oscillateur, par rapport à un oscillateur idéal, ou les fluctuations introduites par un composant sur le parcours du signal issu de l’oscillateur.
Dans le domaine spectral, Sφ(f) = 〈(Δφ)2〉/B représente les fluctuations quadratiques moyennes (i.e., la variance) dans une bande B centrée sur la fréquence f (f est une fréquence de Fourier, écart par rapport à la porteuse), normalisées par la bande passante d’analyse B. La densité spectrale Sφ(f) est donnée en unité logarithmique dBrad2/Hz = 10log10(Sφ).
On notera que de nombreux instruments, incluant le Rohde & Schwarz FSWP, fournissent les mesures de bruit de phase en dBc/Hz. La relation formelle entre les grandeurs mesurées en dBc/Hz et dBrad2/Hz est un facteur 2, de sorte que dBrad2/Hz = dBc/Hz+3 dB puisque 10 log10(2) ≃ 3.
Ainsi, connaissant la densité spectrale de bruit de phase d’une source et la bande d’analyse, nous déduisons les fluctuations de phase induites par l’oscillateur local et donc la capacité à retrouver l’information qui a été imprimée sur la porteuse lors de la transmission, que ce soit sur la phase (modulation de phase PM) ou sur la fréquence (modulation de fréquence FM, la fréquence étant la dérivée de la phase). Nous verrons des bruits de phase variant de 20 dB : est-ce qu’une telle caractéristique a une quelconque importance ? Quand on voit l’émoi provoqué par une multiplication des prix des carburants de 1,2, ou 0,8 dB, imaginez l’état d’esprit du récepteur qui constate que son bruit de phase s’est multiplié d’un facteur 1020/10 = 100, soit des fluctuations de phase multipliées d’un facteur √100 = 10, à cause d’une mauvaise conception de son oscillateur local ! (on pourra se tourner vers le Venezuela pour se faire une idée : le taux d’inflation y était de 10 dB en 2017 et 40 dB en 2018).
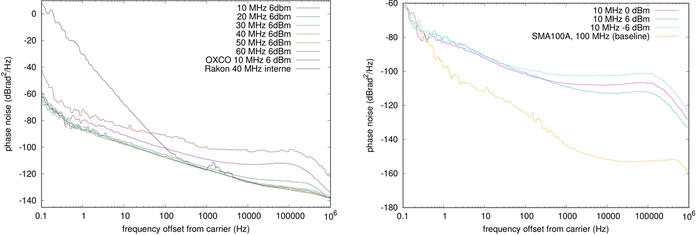
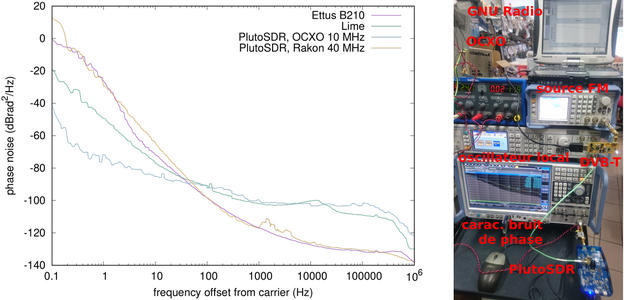
Nous proposons 3 mesures pour illustrer l’impact de l’oscillateur local sur les performances de la radio logicielle. Dans un premier temps, nous prenons l’AD9363 de la PlutoSDR et remplaçons son oscillateur de référence (Rakon RXO3225M) à 40 MHz par une source supposée idéale – un synthétiseur Rohde & Schwarz SMA100Aasservi sur un maser à hydrogène (voir encadré « Stabilité de diverses sources de fréquences ») – pour cadencer la carte à diverses fréquences comprises entre 10 et 60 MHz, toujours à la puissance nominale de 6 dBm=1,3 V sur une charge 50 Ω (contrairement aux expériences initiales de l’auteur, on évitera de dépasser cette puissance sous peine d’endommager de façon irréversible l’AD9363). Nous constatons (figure 4, gauche) que 40 MHz est bien la fréquence optimale, en dessous de laquelle le bruit de phase est dégradé de -131 dBrad2/Hz à -112 dBrad2/Hz, ou un facteur 100. Notre intérêt pour le bruit de phase sur une bande de 1 MHz porte par exemple sur le GPS qui commute sa phase à 1 MHz soit une bande passante de 2 MHz. Ainsi, un bruit de phase de -131 dBrad2/Hz se traduit par des fluctuations de phase de √(10-131/10×2⋅106) = 4⋅10-4 rad=0,05°. Dégrader de 20 dB ce bruit de phase se traduit donc par des fluctuations de phase qui deviennent 0,5° (en supposant le bruit constant sur toute la bande).
Fig. 4 : Gauche : bruit de phase en sortie de l’AD9363 équipant la PlutoSDR en fonction de la fréquence du signal cadençant le composant. Toutes les mesures sont faites avec un synthétiseur Rohde & Schwarz SMA100A asservi sur maser à hydrogène, à l’exception des mesures avec l’oscillateur d’origine (Rakon) et l’oscillateur contrôlé en température (OCXO). Droite : impact de l’amplitude du signal de référence sur le bruit de phase en sortie de l’AD9363, et plancher de bruit du SMA100A pour référence.
Stabilités de diverses sources de fréquence
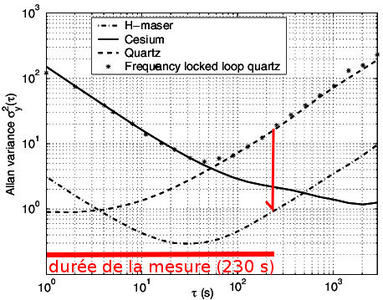
Tous les oscillateurs ne naissent pas égaux : la définition de la seconde se base sur la période d’une transition entre deux états d’un atome de cesium. L’horloge à cesium (Cs) est donc par définition l’horloge la plus stable possible à long terme. Cependant, une horloge à Cs exploite un oscillateur local, basé sur l’oscillation mécanique d’un bout de quartz, pour périodiquement sonder l’adéquation de sa fréquence avec la transition micro-onde de cet atome de Cs. Entre deux interrogations, qui prennent du temps, le quartz oscille librement en étant soumis aux aléas de son environnement (température, contrainte, accélération, irradiation, diffusion des électrodes pour le vieillissement long terme). Ainsi, à court terme la stabilité d’une horloge est donnée par son oscillateur de référence à quartz, et à long terme par l’interrogation d’atomes. Au lieu de sonder un jet d’atomes de Cs, un oscillateur à quartz peut sonder la fréquence de résonance d’une cavité remplie d’hydrogène : il s’agit du maser à hydrogène, présentant une stabilité optimale dans les durées d’intégration τ comprises entre quelques secondes et quelques milliers de secondes (voir figure 5, dans laquelle la variance d’Allan représente la variance des fluctuations relatives de fréquence intégrées sur une durée τ). Noter que les mesures de bruit de phase présentent un axe des abscisses gradué en fréquence de Fourier (Hz) alors que cette stabilité est graduée en temps (s) : plus nous nous rapprochons de la porteuse (fréquence de Fourier basse), plus longue est la mesure (τ grand). Ici avec 10 corrélations sur la décade 0,1–1 Hz, la durée de la mesure est d’environ 230 s. L’asservissement de l’oscillateur de référence sur le maser permet de gagner plus d’un ordre de grandeur en stabilité par rapport au quartz libre (flèche rouge verticale).
Fig. 5 : Stabilité de diverses sources de fréquence en fonction du temps d’intégration (reproduit de [2]).
Le second point que nous désirons aborder est l’impact de la puissance (ou amplitude du signal) fournie par l’oscillateur cadençant l’émetteur-récepteur (transceiver) radiofréquence. Cette fois, nous fixons la fréquence du signal alimentant l’AD9363 à 10 MHz, mais varions sa puissance de +6 dBm, 0 dBm ou -6 dBm (soit 1,3 Vpp, 0,6 Vpp et 0,3 Vpp dans une charge 50 Ω). Dans ce cas, le passage à zéro de la sinusoïde se fait avec une pente d’autant plus faible que l’amplitude du signal est faible. En effet, un signal d’amplitude A et de pulsation ω de la forme V(t) = Acos(ωt) présente une pente du passage à zéro de Aω V/s (maximum de la dérivée du signal Aωsin(ωt)). En effet, nous constatons bien (figure 4, droite) une dégradation du bruit de phase avec les amplitudes décroissantes.
Forts de ces considérations, nous pouvons maintenant comparer sereinement les diverses sources cadencées par leurs oscillateurs d’origine (figure 6) : la PlutoSDR et la B210 étant toutes deux munies de transceivers Analog Devices, un comportement sensiblement identique est attendu et effectivement observé. Le transceiver de Lime semble présenter un moins bon bruit de phase loin de la porteuse, mais une meilleure performance à long terme (proche de la porteuse). Finalement, nous pouvons nous interroger sur notre choix technologique proposé dans [3] de tenter de remplacer l’oscillateur 40 MHz compensé en température Rakon fourni avec la PlutoSDR par un oscillateur 10 MHz contrôlé en température Hewlett Packard HP10811. L’analyse de la figure 4 montre que la conclusion n’est pas triviale : au-dessus de 30 Hz (soit une constante de temps de 30 ms), l’oscillateur Rakon présente un bruit de phase plus faible et donc de meilleures performances. Cependant, notre objectif dans [3] est de leurrer le signal GPS, donc des signaux issus d’horloges atomiques embarquées dans des satellites, et nous ne pouvons pas nous permettre des fluctuations long terme de l’oscillateur local : le récepteur s’attend à un signal stable en fréquence sur de longues durées et risque de se rendre compte du subterfuge si la source dérive trop. En effet, sur des durées supérieures à 30 ms (fréquences de Fourier inférieures à 30 Hz), l’oscillateur contrôlé en température – qui compense activement les variations de son environnement, et en particulier thermiques – fournit une bien meilleure stabilité que l’oscillateur conçu pour minimiser l’impact des fluctuations de température, mais qui les subit néanmoins. Ainsi, nous rendons le décodage de la phase portant l’information du GPS plus difficile, mais nous garantissons une meilleure crédibilité du signal à long terme en remplaçant l’oscillateur Rakon par l’oscillateur HP : le choix n’était pas complètement stupide.
Fig. 6 : Gauche : caractérisation du bruit de phase des divers émetteurs compatibles avec les applications de radio logicielle. La PlutoSDR est caractérisée soit avec son oscillateur compensé en température (TCXO) d’origine (Rakon RXO3225M), soit avec un oscillateur contrôlé en température (OCXO). Droite : montage expérimental pour la caractérisation de la limite de détection (en haut, SMC100A utilisé comme source de porteuse modulée en fréquence) et le bruit de phase des sources (en bas, FSWP et synthétiseur SMA100A pour fournir le signal de référence à la PlutoSDR).
2. Détournement de sources existantes
Parmi les périphériques qui sont parfois déjà disponibles sans être utilisés pour les applications de SDR, nous regroupons les cartes son d’ordinateurs personnels et les oscilloscopes. Ces instruments ne sont en général pas considérés comme source de signaux SDR par manque de flexibilité, mais ils répondent à des besoins bien réels pour permettre au novice de découvrir le domaine avec du matériel déjà disponible. La carte son souffre d’une fréquence d’échantillonnage réduite – 192 kéchantillons pour les meilleures cartes son – mais bénéficie d’une multitude de canaux d’entrée synchrones et d’une excellente dynamique (16, voire 24 bits). Nous utilisons pour notre part une carte externe Scarlett 18i8 pour la réception de signaux VLF compris entre quelques dizaines de kHz et 96 kHz (figure 7, droite). En pratique, le repliement spectral permet de sereinement étudier le signal à 100 kHz de LORAN (LOng RAnge Navigation) – un signal de navigation pré-datant GPS et émis depuis le sol – mais les filtres anti-repliement interdisent l’analyse de TDF à 162 kHz. Un tel périphérique est aussi idéal pour analyser la propagation des signaux naturels dans l’atmosphère incluant les impacts de foudre [4]. Une carte son s’interface naturellement sous GNU Radio avec l’Audio Source qui présentera autant de signaux réels que de voies d’acquisitions (figure 7, gauche).
Fig. 7 : Une carte son Scarlett 18i8 permet d’acquérir 8 voies au rythme de 192 kS/s (gauche) – ici pour mesurer les signaux VLF de DCF77 (77,5 kHz – droite, milieu, en rouge la phase et en bleu l’amplitude), TDF (162 kHz – droite, bas pour la mesure de phase) et devrait acquérir LORAN (100 kHz) si nous pouvions recevoir son signal à Besançon, ainsi que l’impulsion périodique 1 PPS d’un récepteur GPS (droite, haut). TDF est trop haut en fréquence pour une acquisition directe : un signal à 90 kHz est généré par la carte son et alimente une des voies d’un mélangeur AD633 en vue de transposer le signal de 162 kHz à 72 kHz, apte à une acquisition par la carte son.
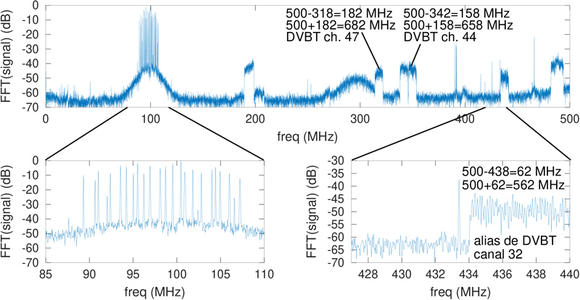
L’oscilloscope est un périphérique qui ne répond qu’à des besoins bien spécifiques, à savoir des signaux dont l’analyse ne nécessite pas la continuité des acquisitions. Un tel exemple concerne les RADARs, dont la portée maximale est limitée par la durée de l’acquisition (généralement exprimée comme la profondeur mémoire de l’oscilloscope), mais qui n’impose pas la continuité des acquisitions. Ce sujet fera l’objet d’une présentation détaillée ultérieurement. On pourra néanmoins déjà apprécier la capacité d’analyse de signaux radiofréquences acquis par oscilloscope numérique LeCroy WaveSurfer 454 en observant la figure 8.
Fig. 8 : Spectre du signal acquis par oscilloscope radiofréquence échantillonnant à 1 GHz. La bande FM autour de 100 MHz est clairement visible, ainsi que la bande de télévision numérique terrestre à 490 MHz qui nous intéressait au cours de cette expérience. Ce graphique illustre la nécessité de pré-filtrer les signaux avant échantillonnage : ici la bande FM tend à éblouir le récepteur qui tente de mesurer les signaux de télévision réfléchis par des cibles mobiles (application RADAR de la source non coopérative). Bas : zoom sur la bande FM (gauche) permettant de retrouver chaque station individuelle, et la bande ISM (droite) autour de 433,92±1 MHz. Il n’y a évidemment pas d’émission radiofréquence qui empiète sur la bande ISM : les indications dans la figure du haut et en bas à droite indiquent que les signaux à 438, 318 et 342 MHz sont en fait des signaux de télévision numérique terrestre (DVB-T) repliés dans la bande d’analyse en l’absence de filtre passe-bas à la fréquence de Nyquist de 500 MHz.
Un cas intermédiaire entre oscilloscope et source continue de données que sont les interfaces mentionnées dans le tableau en début d’article est la Redpitaya (figure 9). Cette plateforme de développement, disponible pour 200 à 270 euros chez Radiospares (en fonction de la résolution des convertisseurs analogique-numérique sélectionnés, 10 ou 14 bits respectivement), combine des convertisseurs analogique-numérique et numérique-analogique radiofréquences (125 MS/s en deux voies) et un processeur Zynq. Ce processeur allie une partie de logique programmable (FPGA nommé PL pour Programmable Logic) et un processeur généraliste (dual-core ARM nommé PS pour Processing System). Cette architecture permet de tirer le meilleur parti des deux mondes : FPGA pour des acquisitions et traitements simples avec des contraintes de temps réel dur et latences contrôlées au coup d’horloge près, et CPU exécutant GNU/Linux pour les communications de haut niveau (TCP/IP, NFS, stockage de données formatées) ou configuration du PL. Une architecture alliant PS et PL sur une même puce laisse présager d’excellents débits de communication et de palier, en partie les latences introduites par les communications numériques entre un oscilloscope et un PC muni d’interfaces telles qu’Ethernet ou USB. En pratique, les mesures sur Redpitaya exécutant GNU/Linux et configurée pour des transferts en DMA de 222≃ 4⋅106 octets (la plus grande taille actuellement accessible avec l’outil de synthèse Xilinx Vivado 2018.2) démontre que sans décimation (125 Méchantillons/s, deux voies et deux octets/échantillon), il faut 26 ms/acquisition (moyenne sur 100 mesures), tandis qu’en décimant par 2 il faut 34 ms, 43 ms en décimant par 3, 51 ms en décimant par 4 et 84 ms en décimant par 8. Sachant que sans décimation les 220≃ 106 échantillons nécessitent 8 ms pour être acquis, ou 16 ms avec une décimation de 2, 24 ms pour une décimation de 3, 32 ms pour une décimation de 4 et 64 ms avec une décimation d’un facteur 8, nous concluons que le temps de traitement des appels système (read et transfert de l’espace noyau vers l’espace utilisateur) nécessitent 19±1 ms. Ainsi, la bande passante maximale en flux discontinu est de 4⋅106/0,026 = 154 Moctets/s (discontinu, car le temps de transfert est supérieur au temps d’acquisition), et en flux continu (avec un temps d’acquisition supérieur au temps de transfert, donc permettant une stratégie de double buffer pour ne jamais perdre d’échantillon tel que vérifié lors de la décimation par 3) est de 4⋅106/0,024 = 166 Moctets/s pour une bande passante d’acquisition de 125/3 = 41,7 MHz. Cette bande passante peut être le résultat d’un prétraitement sur l’ensemble de la bande de mesure – 125 MHz – suivi d’une décimation dans le FPGA : ce partage des tâches est au cœur de divers environnements de développement distribuant les ressources entre logique programmable et système de traitement tels que celui fourni par Pavel Demin (pavel-demin.github.io/red-pitaya-notes), POD (github.com/Martoni/periphondemand), PyRPL (github.com/lneuhaus/pyrpl), Migen (https://github.com/m-labs/migen) et son cas particulier d’utilisation à l’instrumentation Artiq (https://m-labs.hk/artiq/) ou la solution que nous proposons, https://github.com/oscimp/oscimpDigital.
Fig. 9 : La Redpitaya, un processeur Zynq combinant FPGA et processeur généraliste, est équipée de deux voies radiofréquences de conversion analogique-numérique et deux voies radiofréquences de conversion numériques-analogiques [redpit].
3. Sources virtuelles
Le lecteur désireux de s’engager dans la radio logicielle sans investir dans du matériel avant de découvrir si le domaine répond à ses ambitions pourra profiter des WebSDR (http://websdr.ewi.utwente.nl:8901/) qui fournissent des sources large bande distribuées un peu partout dans le monde. Initié par Pieter-Tjerk de Boer en Hollande, ce projet vise à fournir une interface logicielle propice à l’acquisition et la dissémination de signaux obtenus de diverses interfaces matérielles. La majorité des applications, localisée un peu partout dans le monde, concerne des signaux dans la bande VLF (Very Low Frequency – en dessous du MHz), car plus faciles à acquérir et traiter en vue de leur dissémination. La liste des stations est disponible à http://www.websdr.org/. Bien que le récepteur radiofréquence couvre une large gamme de fréquence, il serait techniquement impossible d’envoyer en temps réel aux dizaines d’utilisateurs l’ensemble des échantillons acquis, la bande passante de communication n’étant pas suffisante. Ainsi, chaque utilisateur peut choisir la bande qui l’intéresse, éventuellement lui appliquer une des démodulations classiques (FM, AM) ou aucun (CW), et enregistrer le résultat dans un fichier de format compatible des fichiers audiofréquences habituels (.wav), avec une bande passante limitée à 14 kHz. Cette bande passante garantit d’une part le partage des ressources entre tous les utilisateurs, mais limite quelque peu la nature des signaux que nous sommes susceptibles d’analyser. Deux exemples vont nous permettre d’illustrer l’intérêt de la WebSDR : le signal DCF77 émis depuis Mainflingen en Allemagne (77500 Hz) utilisé pour synchroniser les horloges dites radio-contrôlées, et le signal LORAN émis depuis Anthorn en Angleterre. Le premier signal est aisé à recevoir de toute l’Europe, et n’importe quel bricoleur possesseur d’un ordinateur avec une carte son peut recevoir et appréhender le décodage de ce signal. LORAN est plus délicat : de fréquence plus élevée (100 kHz), malgré une puissance plus importante (50 kW pour DCF77 contre 200 kW pour Anthorn – www.loran.org/proceedings/Meeting2007/Session%204%20Developing%20eLoran/s4n4_text.pdf) et la distance plus importante entre l’Angleterre et Besançon rendent sa réception incertaine depuis l’Est de la France (bien qu’apparemment aisée depuis la Bretagne). La réception depuis Enschede en Hollande où se trouve l’université de Twente permet au moins de valider l’existence et la nature du signal, tel que nous l’illustrerons ci-après.
Les fichiers ne sont échantillonnés qu’à 14 kHz, donc ne sont utiles que pour des modes de communication très étroits, tels qu’utilisés en VLF. Par ailleurs, les acquisitions ne sont pas horodatées, interdisant la triangulation ou l’analyse cohérente des fichiers acquis par plusieurs stations. Un projet qui mériterait d’être poursuit serait de synchroniser les divers récepteurs WebSDR, par exemple en fournissant un signal stéréo (au lieu de mono) dont la seconde voie échantillonnerait le 1 PPS de récepteurs GPS situés à proximité de chaque récepteur. Ainsi des mesures de direction d’arrivée ou de temps de propagation seraient accessibles par analyse des signaux acquis par une multitude de stations spatialement distribuées.
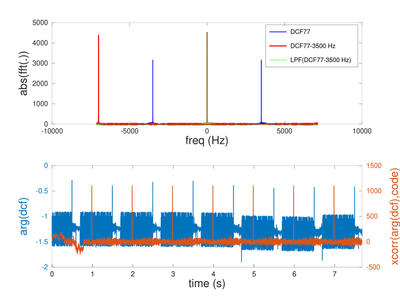
Fig. 10 : Gauche : waterfall de l’interface web de réception de signaux radiofréquence. Droite : signal temporel reçu par WebSDR en se calant à 77500 Hz. Un léger écart δf entre les fréquences de l’oscillateur local du récepteur et de l’émetteur se traduit par une oscillation lente du signal modulé en amplitude A reçu : Acos(2π⋅δf⋅t). En se décalant significativement – stratégie super-hétérodyne exploitant une fréquence intermédiaire – nous pouvons compenser cet écart en traitement numérique et retrouver toute l’information contenue dans le signal.
Fig. 11 : Analyse de la phase du signal acquis sur DCF77 et illustré en figure 10 : afin d’exploiter la phase, l’écart δf entre les fréquences des oscillateurs émetteur et récepteur doit être compensé. Ici, nous avons manuellement identifié cet écart comme égal à 0,08 Hz ou 1 ppm, clairement dans la plage d’incertitude d’un oscillateur à quartz faible coût. Ayant éliminé la dérive de la phase – argument de exp(j2πδft+φ), nous exploitons la modulation de phase φ en corrélant avec le code connu pour trouver finement la date des informations transmises par DCF77.
Les figures 10 et 11 présentent le traitement des signaux acquis par la WebSDR de l’université de Twente sur le signal DCF77, et illustrent les étapes de traitement classiques représentatif de ce que nous ferions en assemblant « à la main » un étage de réception grossier. En mode CW, la WebSDR se contente de mélanger le signal acquis avec un oscillateur local de fréquence LO. Nous avons longuement expliqué dans [5] que le problème de la réception de signaux radiofréquence est l’égalité de la fréquence des oscillateurs locaux de l’émetteur et du récepteur pour éliminer la porteuse. La figure 10 illustre la conséquence de cet écart : en rouge, le battement sur l’amplitude du signal est le résidu de cet écart de fréquence, qui n’est que de 0,08 Hz, ou 0,08/77500 ≃ 1 ppm (partie par million), une performance déjà excellente pour un oscillateur à quartz à faible coût. Afin de pallier cette déficience, nous choisissons de décaler volontairement l’oscillateur local de 3500 Hz (fréquence intermédiaire dans une architecture super-hétérodyne [5]), pour effectuer la seconde transposition de fréquence par logiciel, transposition qui permet de former les coefficients I et Q et donc d’exploiter la phase du signal en plus de son amplitude. En cherchant à annuler la pente de la phase après transposition (figure 11, bleu) en ajustant la fréquence de l’oscillateur local pour éliminer la dérive linéaire de phase, nous obtenons une estimation précise de la fréquence de l’oscillateur local du récepteur, dont un effet de bord inattendu est de permettre de remonter à la température des locaux du club radioamateur de l’université de Twente (en effet, la cause majoritaire de la variation de fréquence d’un oscillateur est sa température). Dans le cas particulier de DCF77, une modulation de phase est imprimée au signal en complément de la modulation d’amplitude, et la corrélation de la phase avec le motif connu (et décrit sur la page anglophone de Wikipédia de DCF77) permet d’obtenir des pics de corrélation pour la datation précise du signal, tel que décrit en détail dans [6]. Ici, la séquence de traitement a été :
pkg load signal % signal processing toolbox pour xcorr
fs=14238; % freq. d'échantillonnage (fournie par file fichier.wav)
load dcf.txt % motif de la modulation de phase (cf Wikipedia US/DCF77)
% ... de la forme 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 1 1 1 0 ...
fbits=77500/120; % la durée de chaque bit est de 120 périodes du signal DCF
N=floor(fs/fbits); % durée -> nombre d'echantillons
long=ones(N,1); % copie de chaque élément du motif du code pseudo-aleatoire
y=dcf*long'; % ... par multiplication matricielle et réorganisation
y=reshape(y',length(dcf)*N,1);y=y-mean(y);
flo=81000-77500-0.08 % 0.08/77500=1 ppm : transposition de fréquence
x=audioread('websdr_recording_start_2018-11-18T07_32_59Z_81.0kHz.wav');
freq=linspace(-fs/2,fs/2,length(x)); % ^ chargement du fichier WebSDR
temps=[0:length(x)-1]/fs;
lo=exp(j*2*pi*flo*temps); % transposition de fréquence et ...
signal=conv(ones(20,1)/20,(x.*lo'))(10:end-10); % ... filtre passe-bas
correlation=xcorr(y,angle(signal))(1:length(signal));
La petite astuce que nous utilisons pour rééchantillonner le code pseudo-aléatoire de la modulation de phase au même rythme que les données acquises consiste en une multiplication matricielle et une réorganisation des données résultantes. Imaginons que le code commence par [0 0 1 0] : nous savons ([7]) que chaque bit dure 120 périodes de la porteuse ou 120/77500 s. Nous échantillonnons le signal à fs=14238, donc chaque bit de phase dure 14238*120/77500 échantillons, qui a le bon goût d’être un nombre presque entier (N=22). Nous devons donc copier chaque bit N fois pour exprimer le code et les échantillons sur la même base de temps. Pour ce faire, nous avons :
Où chaque point de suspension représente une copie de N fois du motif qui le précède et le succède.
Conclusion
Les sources de signaux radiofréquences pour un traitement numérique (SDR) sont nombreuses, voire inattendues : chacun pourra sélectionner l’interface la plus appropriée à ses ambitions, ses objectifs et son budget. Pour notre part, nous avons fini par investir dans une Ettus Research B210 – pour son entrée multivoie et sa gamme de fréquences étendue – que 7 ans après avoir expérimenté sur les récepteurs DVB-T, dont nous n’avons toujours par prétention d’avoir atteint les limites. Ainsi, appréhender la SDR n’est probablement pas un problème budgétaire, mais plutôt de motivation avec un objectif concret qui fournira l’opportunité de mettre en pratique les concepts de traitement du signal échantillonné en temps discret. Pour conclure cette prose, une illustration d’un montage de caractérisation d’oscillateurs à base d’Ettus Research X310 proposant la capacité à être synchronisées en fréquence et en temps sur une source extérieure est proposée en figure 12. Pour donner un ordre de grandeur du volume de données généré par une telle interface, au rythme de 200 Méchantillons/s en I/Q et 16 bits/échantillons (soient 800 Moctets/seconde ou 6,4 Gb/s, justifiant l’interface 10 GbE), nous remplissons un disque d’1 TB en 20 minutes d’acquisitions !
Fig. 12 : Un assemblage d’USRPs X310 – le haut de gamme de la SDR à usage professionnel compte tenu du prix des récepteurs et des cartes filles – synchronisé en temps et en fréquence pour la caractérisation d’oscillateurs ultra stables.
Remerciement
C. Eustache (département d’optique, FEMTO-ST) a prêté sa LimeSDR pour sa caractérisation. Les divers équipements de l’Equipex OscillatorIMP du département temps-fréquence de l’Institut FEMTO-ST (Besançon) ont permis les mesures présentées dans cet article. Une infrastructure de prototypage et d’expérimentations par radios logicielles est disponible auprès de l’Equipex CortexLab de l’INSA Lyon.
Références
[1] D. BODOR, « Pour aller plus loin en radio logicielle : HackRF One », Hackable n°16, janvier2017 : https://connect.ed-diamond.com/Hackable/HK-016/Pour-aller-plus-loin-en-radio-logicielle-HackRF-One
[2] J. SAALAOUI, M. ADDOUCHE, F. LARDET-VIEUDRIN, F. VERNOTTE, « Frequency-Locked between a H-Maser and Cs Clock. », Proc. IEEE IFCS, 2004.
[3] G. GOAVEC-MEROU, J.-M FRIEDT, F. MEYER, « Leurrage du GPS par radio logicielle », MISC Hors-série n°19, février-mars 2019 : https://connect.ed-diamond.com/MISC/MISCHS-019/Leurrage-du-GPS-par-radio-logicielle
[4] R.L. DOWDEN, J.B. BRUNDELL, C.J. RODGER, « VLF lightning location by time of group arrival (TOGA) at multiple sites », J. of Atmospheric and Solar-Terrestrial Physics 64, 2002, pp.817–830.
[5] J.-M FRIEDT, « Quelques fondements théoriques pour aborder la radio logicielle », GNU/Linux Magazine n°224, mars 2019 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-224/Quelques-fondements-theoriques-pour-aborder-la-radio-logicielle
[6] J.-M. FRIEDT, C. EUSTACHE, É. CARRY, E. RUBIOLA, « Software-Defined Radio Decoding of DCF77: Time and Frequency Dissemination with a Sound Card », Radio Sciences 53, 2018.
[7] P. HETZEL, « Time dissemination via the LF transmitter DCF77 using a pseudo-random phase-shift keying of the carrier », 2nd EFTF (Neuchatel, 1988), pp.351–364 : Hetzel exprime la durée de chaque bit comme (77500:120) en p.355