L'interminable quête du parfait petit checksum : analyse comparée

Notre monde numérique fourmille de checksums. Ils sont partout ! Souvent enfouis sous des couches de protocoles matériels et/ou logiciels, ils permettent à notre civilisation de transmettre et de stocker des données de tous types, de façon si fiable qu'on n'y fait plus attention. Ce sont souvent les derniers gardiens invisibles de l'intégrité de nos données avant le plantage d'un programme. On les oublie donc facilement, mais le sujet revient forcément lors du développement d'un nouveau format de données, par exemple. Lequel choisir ? Pour y répondre, nous allons passer en revue des algorithmes existants en nous basant par moments sur des analyses publiées [1] [2] [3], et inclure l'expérience issue de la série d'articles commencée en 2005 [4], qui s'est terminée dans un cul-de-sac. Il était vraiment temps de s'en sortir.

1. Définition

Avant de nous (re)plonger dans cette interminable discussion, il convient de rappeler au lecteur, familier du sujet ou non, quelques détails importants sur les checksums, ou « sommes de contrôle » en français, pour nous assurer que nous parlons bien de la même chose.

D'abord, un checksum est une forme de signature non cryptographique, créée par la combinaison (logique ou arithmétique) de toutes les données d'un bloc que nous désirons « protéger », c'est-à-dire que nous voulons avoir une bonne chance de déterminer si ces données ont été altérées d'une façon ou d'une autre. Je parle de « chance » de détection, car la signature étant beaucoup plus petite que la donnée, le principe des tiroirs [5] implique que beaucoup de données différentes peuvent donner la même signature, ce qui va nous hanter tout au long de cet article.

On adjoint au bloc de données originales cette signature, souvent sous forme d'un champ appelé lui aussi checksum, qu'il ne faut pas confondre avec l'algorithme. L'ensemble bloc+checksum (le checksum étant souvent plus facile à mettre à la fin) est ensuite transmis (par exemple dans un paquet UDP, Ethernet ou USB) ou stocké (comme un firmware en mémoire flash), puis la signature est recalculée à la réception ou juste avant l'utilisation. Si la nouvelle signature ne correspond pas parfaitement, l'algorithme déclenche une erreur de protocole, retente une transmission ou essaie de reconstruire les données manquantes... Ou pas.

Par contre, lorsque le bloc est altéré, mais la signature reste valide, on parle alors d'une collision ou d'un faux négatif. Pour réduire la probabilité que cela arrive, on peut augmenter la taille de la signature, car idéalement, avec une signature de w bits de large et un algorithme parfait, la probabilité de collision est de 1/2^w. Un algorithme parfait n'existe pas, mais on tente de s'en approcher, car on désire garder la signature aussi petite que le taux de perturbation le permet. Mais contrairement aux signatures cryptographiques telles que MD5, SHA* ou DSA, un checksum doit être extrêmement pratique au détriment de la sécurité absolue.

Un checksum se distingue habituellement des autres types d’algorithmes par les choix ou compromis suivants :

• Complexité minimale : moins le checksum utilise d'opérations, plus il sera rapide à exécuter et économique à réaliser. On désire même que le calcul soit le plus rapide possible, donc l'algorithme doit être vraiment hyper simple.
• Grande facilité de réalisation : idéalement, un checksum est très facile à réaliser avec un petit programme comme avec un petit circuit électronique. On veut vraiment utiliser le minimum de ressources, que ce soient des unités de calcul ou de la mémoire, ce qui rejoint la contrainte de complexité minimale. Au passage, cela facilite aussi le portage sur un maximum de plateformes, ce qui est crucial pour qu'un nouveau format de données ait du succès.
• Signature de petite taille : le résultat du calcul tient souvent sur quelques octets au maximum pour éviter de gonfler la taille des données transmises ou stockées. Par exemple, l'entête des fichiers .EXE originaux (type MZ) contenait 2 octets, alors que les fichiers .ZIP ou .GZIP en utilisent 4. Par comparaison, une signature cryptographique faible utilise au moins 16 octets, alors que l'on recommande 32 à 64 octets aujourd'hui, ce qui est largement trop gros en pratique pour nos applications.
• Granularité de calcul : les ordinateurs 32 bits sont devenus majoritaires dans les années 80, et les ordinateurs 64 bits sont apparus dans le grand public autour de l'an 2000. Cependant, la plupart des checksums de base, créés dans les années 70 ou avant, utilisent des données sur 8 ou 16 bits (tel l'entête des paquets IPv4), typiques de la taille des registres des mini-ordinateurs de l'époque. Cette taille va aussi influencer la performance, car des mots de 64 bits traitent quatre fois plus de données à la fois que des mots de 16 bits. Un nouvel algorithme utiliserait donc des mots de 32 bits pour fonctionner sur les ordinateurs actuels ou les processeurs embarqués récents, mais chaque taille risque de pénaliser une plateforme et impose une limite de performance aux autres.
• Approcher la limite théorique de la fiabilité : la taille de la signature est directement liée à sa capacité de détecter une altération aléatoire. Ainsi, une signature sur 16 bits a une chance sur 65 536 de faux négatif, ce qui est souvent considéré comme raisonnable lorsque les données n'ont qu'une chance anecdotique d'être altérées, ou alors si l'utilisation des données corrompues ne crée pas de catastrophe en aval (par exemple, une image ou une vidéo, contrairement à un programme). Une signature sur 32 bits réduit le taux de collisions à une sur quatre milliards, ce qui est largement suffisant même lorsque les corruptions ont une probabilité modeste. Une signature sur 64 bits n'a donc pas lieu d'être, car dans de telles conditions de bruit, on utiliserait alors des codes autocorrecteurs tels que Hamming ou Reed-Solomon.
• Taille modeste des blocs de données : selon la fiabilité désirée et la probabilité d'altération du milieu, on protège des blocs de données plus ou moins longs. Si on n’en connaît pas la taille à l'avance, une signature fixe et large peut convenir. Par exemple, GZIP (RFC1952 [6]) utilise un CRC32, quelle que soit la taille des données, de quelques octets à plusieurs gigaoctets. Or, plus on a de données, plus elles sont susceptibles de subir une erreur et cela réduit mécaniquement la taille effective de la signature. Ainsi, à taux d'erreur égal, un bloc d'une taille T aura deux fois moins de chances d'être altéré qu'un bloc de taille 2×T. La taille de la signature de ce dernier devrait augmenter d'un bit afin de conserver un taux de détection équivalent au premier. En pratique, la granularité des blocs est aussi imposée par des contraintes matérielles ou logicielles, comme la taille des mémoires caches, des trames d'un réseau, des blocs d'un support de stockage ou des pages de mémoire virtuelle. Les blocs courts ou moyens sont donc privilégiés et 16 à 32 bits suffisent souvent pour des blocs de 1 Ki à 16 Ki octets.
• Sources d'altérations et modèle d'erreurs : les systèmes de communication d'antan étaient rustiques et sensibles aux bruits : une ligne téléphonique, un modem, une transmission radio, ou même un enregistrement sur bande magnétique altéraient souvent plusieurs bits consécutifs. Aujourd'hui, les couches de protocoles modernes ont ajouté des systèmes de correction d'erreurs très efficaces et on suppose aujourd'hui qu'une perturbation est parfaitement aléatoire, équiprobable, sans groupement. Actuellement, les checksums ont plus un rôle de dernier rempart contre des défauts ou erreurs matérielles occasionnelles, comme un neutron qui modifie un ou des bits en mémoire vive, un composant sur le point de rendre l'âme, un faux contact sur un connecteur ou même un bug logiciel ayant laissé derrière lui des données erronées. En aucun cas, le checksum ne peut protéger d'une altération maligne, puisque les algorithmes sont souvent connus, simples, ouverts et bien compris, comme le montre cet article, donc un attaquant n’a aucun mal à recalculer un nouveau checksum après avoir commis son méfait pour masquer ses traces (voir plus loin). Donc, les checksums actuels doivent surtout détecter des ajouts ou des suppressions de données, ou bien des mises à 0x00 ou 0xFF de tout un bloc. Les erreurs d'un ou de quelques bits sont toujours probables, mais assez faciles à détecter, alors que les erreurs plus complexes peuvent se recombiner pour empêcher la détection.
• Détection ou correction : les checksums ne contiennent pas assez d’information pour reconstituer les données originales après altération. Les codes correcteurs d'erreurs le permettent, au prix d’une plus grande quantité d’informations redondantes. L'utilisation d'un checksum implique souvent que le protocole mettra au rebut les données détectées comme altérées. Cela favorise les blocs courts si les données ont beaucoup d'importance, afin de ne jeter qu'un minimum d'informations utiles en cas d'erreur.
• Mixage et confusion : dans l'absolu, un checksum n'a pas la même contrainte de mélange des bits qu'un algorithme de hachage. Ce dernier doit idéalement modifier la moitié des bits du résultat si un bit en entrée est changé. Tout ce qui nous intéresse ici est de vérifier que les deux signatures (celle reçue et celle recalculée) sont strictement identiques, et si même un seul bit diffère, tout le bloc est rejeté. En pratique cependant, un meilleur mélange augmente la distance de Hamming (le nombre de bits qui diffèrent) et donc renforce le checksum, en particulier si c'est celui-ci qui est altéré.

En fait, on pourrait très bien se passer des checksums et le monde continue de tourner alors que beaucoup de fichiers n’en ont pas. Nous avons pourtant gardé cette bonne habitude, car il resterait toujours un doute parmi les plus suspicieux et surtout, il est toujours préférable de détecter une erreur le plus tôt possible, avant que ses effets ne se propagent au reste du système, détruisent d’autres données ou fassent planter l’ordinateur.

Donc, la simple question « est-ce que l'intégrité de ce bloc de données est garantie ? » implique de nombreuses réflexions philosophiques, techniques et mathématiques. Heureusement, contrairement au domaine de la cryptographie, la contrainte de simplicité nous fait commencer par le cas de figure le plus dégénéré possible.

2. XORsum

En parlant de cas dégénéré, la première approche est la pire, mais il est important de la mentionner pour au moins deux raisons :

• parce que cela va nous donner les bases techniques et les perspectives pour analyser les méthodes plus complexes ;
• et parce que malgré ses caractéristiques déplorables, on retrouve encore cet algorithme ici et là, pour des raisons qui m'échappent encore.

Le XORsum est simplement l'extension du principe de parité, sur tous les bits d'un rang donné, pour tous les mots d'un bloc. Par exemple, tous les bits de poids faible seront « XORés » entre eux pour donner le bit de poids faible du XORsum. Cela peut se résumer à deux lignes de code :

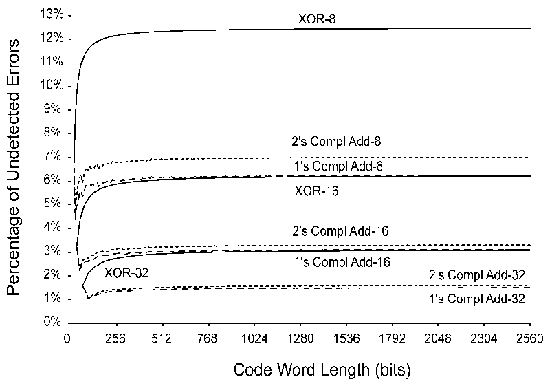
Et c’est tout. Une chose est sûre : ce code est minimal, simple et rapide, mais c'est bien le seul avantage. Pour le cas ci-dessus où on traite des octets, le résultat est sur 8 bits et on s'attend donc à une probabilité de collisions de 1/256=0,39 %. Le taux mesuré est ridicule : 12,5 %, soit seulement une chance sur huit ! Pourquoi ? Comment ?

Augmentons la taille des mots : pour 16 bits, le taux descend à 6,2 % et à 32 bits, 3,1 % seulement. La relation est linéaire et non exponentielle parce que toutes les parités sont indépendantes. Pour enfoncer le clou, XOR est commutatif et associatif, donc n'importe quelle permutation des données originales donnera le même résultat. Si on insère des zéros dans le bloc, même verdict. Le pire est que le XORsum ne peut pas détecter si un nombre pair de bits a été altéré à une même position, donc la moitié des altérations aléatoires seront ignorées.

On peut donc convenir que le XORsum est catastrophique et devrait être banni. Alors pourquoi est-il encore utilisé ?

3. Le checksum classique

Puisque l'opération XOR est trop simple, remplaçons-la par une opération un peu plus sophistiquée : l'addition. Nous obtenons alors une somme, ce qui est l'origine du terme « checksum ». Le code précédent est modifié sur un caractère seulement :

L'addition binaire ajoute de la complexité par rapport au simple XOR, puisque les bits des rangs supérieurs sont affectés par les retenues des rangs inférieurs, donc nous nous attendons à une meilleure détection des erreurs. En pratique cependant, nous obtenons ces taux de collisions :

• 8 bits : 7 %
• 16 bits : 3 %
• 32 bits : 1,5 %

C'est à peine deux fois mieux que XORsum et le résultat est toujours proportionnel à la taille de la signature, et non exponentiel !

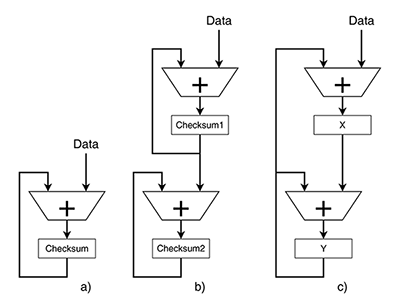
Depuis l'aube de l'informatique, ce type de checksum est employé faute de mieux pour les données peu sensibles, car à part un petit effet d'avalanche fourni par les retenues internes, il conserve la plupart des défauts de XORsum mentionnés plus haut. En effet, nous pouvons utiliser les mêmes méthodes d'altération pour créer artificiellement et facilement des signatures valides, puisque les lois de l'arithmétique disent qu'on peut toujours échanger des valeurs ou insérer autant de 0 qu'on veut, la somme sera inchangée. On voit aussi que la somme est tronquée, donc modulo 2^w, et l'arithmétique modulaire nous dit que la signature sera identique, si la somme des changements est égale à un multiple de 2^w. L'utilisation du XORsum est inexcusable, mais le checksum basique n'est pas recommandé non plus.

4. Checksum en complément à 1

Nous venons de voir que les additions du programme précédent « rebouclent » simplement à cause de la troncation. La retenue n'est pas prise en compte, on dit alors que l'addition est modulaire. Cela ne nous arrange pas, car c'est de l'information perdue, purement et simplement. Que faire ?

Il existe une forme de checksum où cette retenue est réutilisée, réinjectée dans le bit de poids faible de la somme, suivant un mécanisme appelé « addition en complément à 1 », qui fut utilisé du temps des premiers ordinosaures. La retenue en sortie est utilisée comme entrée de retenue dans l'addition suivante, on appelle aussi cette méthode « End Around Carry » (EAC) ou rebouclage de retenue. Cela permet aux avalanches de retenues de se propager circulairement sur tout le mot et évite que ce bit d'information soit perdu ou gâché.

Ce système gagne quelques pour cent sur le taux de collisions par rapport au checksum classique, comme si on ajoutait un bit à la largeur de la signature. C’est logique, puisque l’information peut enfin circuler du MSB vers le LSB. C'est peu, mais c'est presque gratuit sur les ordinateurs dont le bit de retenue est facilement accessible. Le checksum en complément à 1 a encore la plupart des défauts des deux autres systèmes, mais cela peut devenir une qualité dans certains cas, tel que le calcul du checksum de l'entête des trames IP, présenté dans la RFC1071 [7]. C'est justifié ici, car les routeurs doivent pouvoir facilement mettre à jour des champs (comme le TTL) sans devoir faire de calcul complexe ou recalculer tout l'entête. Moins il y a d’opérations, plus les paquets peuvent circuler vite !

Cependant, le complément à 1 a un défaut qu'il ne faut pas négliger. Si nous considérons une somme d'octets, au bout du premier rebouclage, la somme ne peut plus prendre la valeur zéro, ce qui réduit de 0,39 % l'espace de codage. Le protocole IP travaille sur 16 bits donc avec un handicap plus faible, mais le problème reste présent. D’un autre côté, un tel champ de checksum ayant la valeur 0 indiquerait une erreur.

Pour résumer la situation peu réjouissante jusqu'ici, rien ne vaut la figure 1 extraite de la thèse de Theresa C. Maxino en 2006 [1]. On y constate que la promesse d'une augmentation exponentielle de l'intégrité en fonction de la taille de la signature n'est pas tenue. Idéalement, il faudrait que chaque rang de bit puisse influencer tous les autres, et pas juste le rang supérieur. Pourtant, cette méthode reste très utilisée...

5. La version de Microsoft

Quand on parle de fausses bonnes idées, Microsoft n'est jamais loin. Les fichiers au format « Portable Executable » (PE) utilisés entre autres par les programmes (.EXE) et les librairies (.DLL) sont signés par une forme de checksum en complément à 1 sur 32 bits. On pourrait donc estimer la probabilité de collision à 1,4 % : ce n'est pas glorieux, mais ça devrait suffire.

En grattant un peu, tout s'effondre petit à petit. D'abord, l'algorithme n'est pas documenté officiellement, mais de nombreux hackers (aux intentions plus ou moins pures) l'ont examiné et reproduit. Les ressources disponibles sur Internet (en particulier [8]) pointent vers une adaptation de l'algorithme de la RFC n°1071 que nous venons d'examiner, dans une version qui calcule une signature avec des mots de 32 bits avant de la « replier » sur seulement 16 bits. Un autre octet est concocté par un algorithme secret et l'octet restant est souvent laissé à zéro.

En fait, l'algorithme secret ne serait que l'addition de la taille du fichier au checksum, ce qui explique l'octet de poids fort à zéro, puisque peu de fichiers occupent 16 Mio ou plus. On peut donc revoir largement à la baisse le taux de faux négatifs (*).

L'avantage de la RFC1071 est la vitesse pure : le code de Windows décompilé dévoile une séquence de 32 instructions identiques ADCL (addition de 32 bits avec retenue) consécutives. Avec 4 octets traités par cycle, on ne peut pas faire mieux en termes de vitesse, du moins avec un processeur 32 bits. Quant au choix scabreux de ne garder que 16 bits, on peut imaginer qu'il permettait de garder la compatibilité et le code existant pour gérer les antiques programmes DOS de type MZ, dont le checksum était sur 16 bits seulement.

À la base, l'algorithme est simple : on additionne entre eux tous les mots consécutifs de 32 bits, et la retenue sortante est réutilisée en retenue entrante à la prochaine instruction. Malheureusement, comme très peu de langages supportent l'accès au drapeau de retenue, les versions de haut niveau doivent utiliser un accumulateur deux fois plus grand pour accéder à la retenue. Un processeur 32 bits ne peut donc accumuler que 16 bits par cycle, comme le montre le code d'exemple de la RFC1071 :

L'astuce principale de ce code consiste à accumuler toutes les retenues dans la moitié haute du registre de 32 bits. Cela veut dire que le calcul sera valide tant que ce dernier n'aura pas débordé, et ce code de référence ne peut signer que 64 Ki mots (128 Ki octets) d’un coup.

Pour aller encore plus vite, sans accéder au bit de retenue, le code doit utiliser des mots de 64 bits, ce qui permet d'accumuler 4 milliards de nombres sur 32 bits avant que la retenue ne déborde, mais cela pénalise les processeurs 32 bits.

L'usage de code assembleur est donc privilégié pour ce type de checksum, qui permet d'obtenir une grande vitesse au détriment de la probabilité de collision, donc réduire la signature de 32 à 16 bits seulement est une aberration, surtout si le format du fichier a prévu un champ de la taille nécessaire. C'est donc une solution de type « good enough », l'algorithme fait ce qu'on lui demande dans la majorité des situations, ce qui ne signifie pas que cet exemple doit être suivi, car la RFC1071 reste un algorithme médiocre !

Pourquoi l’utiliser alors ? Peut-être que la réponse est « parce que le checksum des .EXE n’est pas important ». Les .EXE au format MZ permettaient de mettre une valeur indiquant que la signature n’était pas calculée, et j’ai vu récemment une estimation que 20 % des .EXE modernes ne l’étaient pas, tout comme 80 % des .EXE infectés par un virus ou un ver. La responsabilité ici repose donc entièrement sur Microsoft qui ne valide pas son propre mécanisme ! Quant aux signatures cryptographiques récemment introduites, c’est un tout autre débat.

6. Fletcher

Conscient des limites des checksums de base, John G. Fletcher [9] s'est dit qu'on pouvait au moins résoudre le problème de la commutativité en cascadant deux checksums tout en utilisant un modulo 255. Le complément à 1 que nous venons de voir est équivalent à un modulo 255, mais décalé d’une valeur, EAC couvre de 1 à 255 alors que mod255 couvre de 0 à 254. Par abus de langage, ces deux appellations sont parfois confondues, mais la subtilité reste.

L’algorithme de Fletcher, publié en 1982, est moins sensible aux transpositions ou décalages, car la position de chaque élément devrait affecter le résultat final. Ce mode de calcul à deux étages (un premier checksum, puis un deuxième qui « checksum » le premier) a été un peu utilisé à une époque sur Internet, comme le montre la RFC1146 [10], mais sans succès. La taille de la signature est doublée, mais il reste encore beaucoup de défauts.

Par exemple, des études [3] montrent que le placement de la signature (en tête ou à la fin d'un paquet) influence significativement le taux de détection d’erreurs :

« En pratique, placer le checksum en complément à 1 du paquet TCP à la fin du paquet détecte plus d’erreurs qu’un checksum de Fletcher placé en entête. »

De plus, puisque l'algorithme de Fletcher fonctionne modulo 255 (pour une signature sur 16 bits), deux valeurs très courantes (0 et 255) sont considérées comme égales, ce qui fait plus que réduire l'espace de codage des signatures :

« L’algorithme de Fletcher à complément à 1, cependant, a une faiblesse qui parfois contrebalance ses avantages probabilistes : puisque des octets contenant les valeurs 255 ou 0 sont considérés identiques par le checksum, certains cas communs pathologiques causent un échec total de Fletcher-255. »

Donc non, Fletcher n'est pas la panacée.

7. Adler

Mark Adler (à qui nous rendons grâce pour ses contributions à GZIP, zlib, PNG...) s'est dit que John Fletcher aurait dû choisir un modulo qui est un nombre premier. Car il est notoire (dans le domaine des générateurs de nombres pseudoaléatoires, du moins) que les nombres premiers permettent de mieux mélanger les bits entre eux et Mark, développant alors GZIP, cherchait lui aussi un checksum plus rapide que CRC32, sans ses inconvénients. Il dérive alors l'algorithme Adler32 [11], basé sur deux accumulateurs de 16 bits, mais avec comme modulo premier 65 521 (le nombre premier le plus proche de 65 535).

Cet algorithme est quasiment aussi simple et rapide que celui de Fletcher, rendant aussi possibles quelques optimisations intéressantes. En tant qu'ingrédient de la zlib, un format ouvert et utilisé par le tout Internet, il fait même l'objet d'une RFC [12] pour une utilisation dans les flux en temps réel. Cependant, des tests ont vite montré les faiblesses intrinsèques du choix du modulo : 65 521 est inférieur à 65 535 et 15 codes sont inutilisés (et pas juste un) donc paradoxalement, il est marginalement moins fiable que Fletcher32.

Mais surtout, dans le cas d'une utilisation sur un réseau avec des petits paquets qui se ressemblent beaucoup (ce qui est très courant, et très différent de l'utilisation prévue à l'origine), l'espace des valeurs prises par les signatures est pathologiquement réduit et les collisions sont beaucoup plus probables qu'anticipé. Une RFC [13] a été émise pour remplacer Adler32 par CRC32, plus lent, mais bien plus fiable.

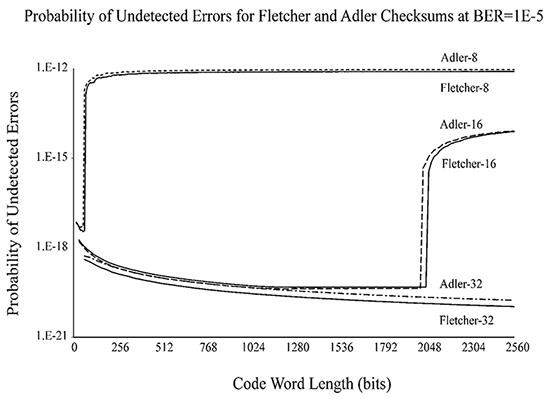
Pour conclure sur la question Fletcher vs Adler, je vous invite à lire le petit papier de Theresa Maxino [14] qui passe en revue ces deux algorithmes, revient sur leurs histoires respectives et surtout les met à l'épreuve. Cela confirme par des mesures que Fletcher est marginalement plus fiable que Adler, et nous apprend que le taux de collisions ne dépend pas linéairement de la taille des blocs signés. Par exemple, la figure 2 montre que Adler16 et Fletcher16 (tous les deux constitués d'une paire d'octets) perdent brutalement leur efficacité après avoir scanné 256 octets. La situation est moins catastrophique pour Fletcher32 et Adler32, reposant sur des accumulateurs 16 bits et avec une fiabilité raisonnable jusqu’à 128 Ki octets. Mais cela reste une solution « good enough », loin des performances d’un CRC bien conçu.

8. Les algorithmes cousins

Les algorithmes de hachage [15], tels qu'utilisés pour adresser des tables de hachage justement, partagent des caractéristiques et contraintes similaires, bien que les checksums se moquent des propriétés de diffusion, alors que c'est la raison d'être des algorithmes de hachage. Ces derniers devraient logiquement être plus lents, mais on peut tout à fait utiliser un algorithme de hachage pour remplir la fonction de checksum.

Ces dernières années, les travaux de Bob Jenkins [16], Paul Hsieh [17], D.J. Bernstein [18] et d'autres ont fourni des fonctions de hachage de plus en plus rapides et efficaces, aux propriétés éprouvées expérimentalement, mais aux fondements mathématiques encore incomplets. L'accélération vient de l'utilisation de plus de mots, de plus en plus larges, 32 puis 64 bits, augmentant d'autant plus les vitesses de calcul, mais aussi des combinaisons et des structures d'opérations simples, méticuleusement choisies et testées pour leurs propriétés statistiques. Les architectures superscalaires récentes accélèrent encore les calculs grâce à l'exécution parallèle des opérations indépendantes.

Ils sont bien plus efficaces que les anciens algorithmes de hachage tels que « Fowler/Noll/Vo » (ou FNV hash) [19] reposant presque uniquement sur la multiplication de longs nombres, ou d'autres utilisant une table de valeurs (tel l'algorithme de Pearson [20]). Pourtant, cette nouvelle vitesse provient de registres plus larges et plus nombreux qu'auparavant, donc ils demandent aussi plus de ressources que Fletcher32, par exemple.

Un compromis intéressant est l'algorithme Lookup3 [21] de Bob Jenkins, qui n'utilise que 3 variables de 32 bits et des opérations arithmétiques et booléennes simples, avec un parallélisme efficace et une structure régulière. La diffusion de l'information dans ces trois variables est très bonne, donc Lookup3 ferait un bon checksum. Cependant, certaines constantes internes ont été déterminées expérimentalement et aucune étude théorique ne vient valider leurs choix. De plus, la signature fournie est sur 96 bits, ce qui est bien trop grand pour un simple checksum (même si on peut ne garder qu’un ou deux mots).

Au moins, on sait qu'on peut faire quelque chose à la fois rapide et efficace sur les processeurs modernes, il manque juste un cadre mathématique solide.

9. Les CRC

Les Cyclic Redundancy Checks (abrégé en CRC), basés sur les LFSR (Linear Feedback Shift Registers), sont de facto les rois des checksums, de par leurs fondements mathématiques éprouvés, leurs caractéristiques reconnues, leur flexibilité à quasiment toutes les tailles imaginables... Leur efficacité à détecter la plupart des erreurs, très proches de la limite théorique, en a fait l'algorithme de prédilection depuis plus 40 ans, puisqu'on n'a encore rien trouvé de mieux. C'est pourquoi on retrouve les CRC presque partout.

J’ai exploré les LFSR et les CRC en long, en large et en travers dans 6 articles publiés dans GLMF #78, #81, #85, #93, #96 et #98 et d’autres auteurs ont présenté les corps de Galois pour des QR codes (Nicolas Patrois), ou expliqué le codage des informations des satellites GPS (J.M. Friedt), donc les détails théoriques ou de réalisation ne seront pas approfondis ici. Nous avons aussi vu plus haut que c'est l'algorithme de référence pour remplacer les checksums, même si Fletcher, Adler et bien d'autres cherchent une alternative depuis des lustres.

Car, en échange de leur grande fiabilité, les CRC sont lourds. Je ne parle même pas du choix du polynôme générateur, qui peut conduire à la collision de contraintes contradictoires. Par exemple, dès qu'il s'agit de faire tourner un CRC très vite, les limites sont vite atteintes, au point que les processeurs x86 proposent une instruction de CRC32 depuis l’extension SSE 4.2. On peut s'en réjouir, sauf si l'application considérée doit fonctionner sur une autre plateforme qu'un x86 récent (tel qu'un FPGA ou une autre famille de processeurs), ou bien si on désire utiliser une autre taille ou un autre polynôme que le 0x11EDC6F41 gravé dans la puce.

Les CRC forcent à faire de nombreux compromis dès que la performance est critique. Par exemple, un polynôme « dense » (avec la moitié des bits à 1) est plus efficace pour détecter les erreurs, mais sa réalisation matérielle s'alourdit à mesure qu'on veut calculer plus de bits en un seul cycle. Chaque bit ne nécessite qu'une couche de portes XOR, mais si on veut en calculer 8, 16 ou 32 à la fois, il faut aussi compter les délais de propagation de chaque résultat intermédiaire et il vaut peut-être mieux réaliser une table de constantes. C'est pour cette raison aussi que le CRC utilisé pour l'interface parallèle IDE utilisait 16 bits et un polynôme très épars (3 taps), ce qui permettait de réaliser facilement un circuit parallèle avec moins de portes logiques et donc de délais.

Mais les CRC sont intrinsèquement conçus pour protéger des flux de bits, tels qu'on pourrait les trouver sur un port série par exemple. Or, les ordinateurs fonctionnent par mots entiers et cela se sent dans les réalisations logicielles ! Calculer le CRC bit par bit est simple, mais lent. La plupart des logiciels utilisent une table de constantes pour paralléliser les calculs, mais sa taille augmente exponentiellement. Il suffit de 1024 octets pour calculer le CRC32 d'un octet, ce qui tient habituellement en mémoire cache, alors que 256 Ki octets sont nécessaires à calculer 16 bits d'un coup. Même en utilisant plusieurs tables, afin de calculer plusieurs octets simultanément à des positions différentes, cela limite la vitesse de calcul.

Pour rappel, voici une copie d'un algorithme très courant, issu de la RFC n°1952 [6], qui présente une version traitant un octet par itération :

Au-delà du défaut de l'initialisation à zéro (qui empêche de détecter si des zéros sont insérés au début), ce petit algorithme dépense beaucoup d'énergie pour chaque octet signé, d'une part pour le calcul de l'adresse de la table, d'autre part pour sa consultation, ce qui réduit l'efficacité sur les processeurs modernes. L'accès à la mémoire est lent par rapport aux calculs. Il est possible d'aller plus vite, mais comme de nombreux travaux le montrent (les miens ou d'autres comme [22]), la taille du code explose rapidement, à cause de la gestion du parallélisme des opérations et de l'alignement des données, car il faut traiter plus de mots à la fois. Un algorithme de base simple se transforme aujourd’hui en un enfer de développement.

Un autre grief à l'encontre des CRC à base de LFSR est qu'il est possible de les « planter ». On sait en effet qu'un LFSR doit être initialisé à une valeur non nulle, sans quoi son état n'évoluerait pas. Or, en injectant des données particulières dans un CRC, on peut contrôler son état interne, puis même le forcer à rester à l'état zéro aussi longtemps qu'on le désire.

C'est un défaut inhérent à ce type de circuits, qui à une époque permettait de planter un lien ATM avec une attaque DOS de seulement 127 paquets spéciaux [23]. Peter Fenwick rapporte un cas similaire sur les modems V.35 [2] dont le polynôme n'a que 20 bits : x^20 + x^3 + 1, soit une chance sur un million (donc tous les 128 Kio) de se retrouver bloqué par des données anodines. Il précise :

Donc pour s'en protéger, le CRC devrait aussi prévoir un circuit de détection de l'état bloqué. Cela augmente la complexité du système, sans pour autant résoudre le problème à la base. Pour contrer cela, les réalisations récentes ont considérablement augmenté la taille des LFSR, à 58 bits par exemple [23], alors qu'on sait que la vitesse d'un circuit diminue lorsque sa taille augmente. Les protocoles de transmission les plus récents comme USB3 ou PCI-E ont abordé les collisions par une approche statistique, au lieu de les empêcher par construction. Mais lorsqu'on a un marteau, tous les problèmes sont des clous, n'est-ce pas ?

10. Fibonacci

Un ami m'a rapporté le cas d'un morceau du code source de SQLite à https://github.com/endlesssoftware/sqlite3/blob/master/wal.c datant de 2010. Je ne sais pas s'il y a eu des versions antérieures utilisant cet algorithme de checksum. Il repose sur la séquence de Fibonacci au lieu d'un LFSR, ce qui est très astucieux et permet une très grande vitesse de calcul, avec 2 opérations pour 32 bits soit une demi-opération par octet, et seulement deux registres. Voici le commentaire qui explique le code :

La structure de Fibonacci est bien supérieure à celle de Fletcher/Adler, car elle referme la boucle, chaque accumulateur accumulant l'autre, et résout certains problèmes inhérents à la cascade de Fletcher. De plus, les propriétés mathématiques de la suite de Fibonacci sont bien connues et son taux de croissance φ est un nombre irrationnel entré dans la culture populaire. Cependant, les opérations sont ici modulo 2³², donc on se trouve dans le cas de la séquence de Pisano [24] et on sait d’avance que la période sera de 1,5×2³². Les bases mathématiques de cet algorithme prometteur ne sont pas parfaitement sûres et l'absence de gestion de la retenue me chafouine.

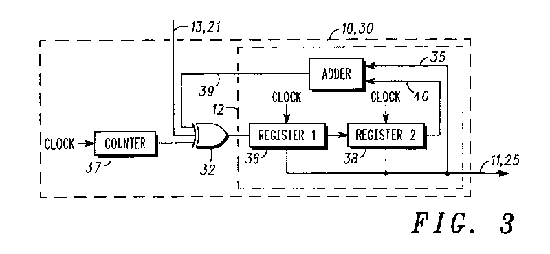
Toujours sur le thème de Fibonacci, je suis tombé sur le brevet GB2377142A [25] de Peter Miller (Motorola Solutions, Inc.) publié le 31/12/2002. La figure 3 montre que la structure de Fibonacci/Pisano est utilisée (parmi d'autres structures alternatives), mais il n'y a pas non plus de gestion de la retenue, ce qui rend le circuit sensible aux plantages. Pour l’éviter, l'inventeur a ajouté un compteur supplémentaire. Pourrait-on s'en passer ?

Enfin, Theresa Maxino mentionne dans sa thèse [1] un autre type de circuit :

La description est prometteuse, mais ni la structure ni les fondements mathématiques n’y sont abordés. Je n'arrive pas à me procurer le papier cité et le « future work » ne semble pas s’être concrétisé. J'ai trouvé le brevet US5526370, expiré en 2014, mais j'ai encore du mal à en faire le tour ou à comprendre son fonctionnement.

11. La solution

Au terme de cette rétrospective, nous constatons que le problème qui nous est posé n'est pas aussi simple qu'il paraît et les mathématiques viennent toujours détruire nos espoirs. La conception d'un checksum capable de rivaliser avec les CRC doit reposer sur des principes plus puissants, ce qui nous amène à chiner dans des domaines cousins, comme les algorithmes de hachage, les générateurs de nombres pseudoaléatoires ou même la cryptographie.

C'est là que nous retrouvons Bob Jenkins, auteur de Lookup3.c, mais aussi de nombreux autres algorithmes dans les domaines sus-cités. Il n'a pas créé de checksum, mais ses programmes reposent sur son « principe de l'entonnoir » [16] qui stipule qu'une opération doit être parfaitement réversible pour conserver les informations et donc empêcher des collisions. Par exemple, les opérations logiques AND et OR ne sont pas réversibles, mais XOR l'est, donc on retrouve cette dernière dans la plupart des algorithmes de chiffrement, par exemple.

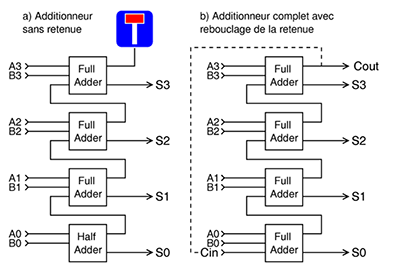
L'addition aussi est totalement réversible, mais uniquement avec des nombres de précision infinie ou bien dans un corps fini (le fameux corps de Galois utilisé par les LFSR et CRC). Cela explique que pour nous, l'addition en complément à 1 est (marginalement) meilleure que l'addition modulaire, proposée par les langages traditionnels qui bloquent l’accès au bit de retenue (**). Or, cette retenue contient de l'entropie, c'est-à-dire de l'information utile, et en l'ignorant, on augmente les chances de collisions. La figure 4 montre qu'en rebouclant la retenue, l'entropie du système est préservée, c'est-à-dire qu'on laisse à tous les bits une chance d'interagir avec d'autres données, et la chaîne de retenue interne ressemble presque à une sorte de LFSR verticalisé. On est sur le bon chemin, même si le complément à 1 a toujours des défauts.

Cette idée qu'il faut éviter une sorte de « voie sans issue » pour le flux de l'entropie est puissante et si on peut l'appliquer à l'intérieur d'une opération, on peut aussi l'appliquer entre les opérations. La faiblesse du checksum classique s'explique, sous cette nouvelle lumière, parce que l'information se retrouve bloquée dans une sorte de cul-de-sac, incapable d'influencer d'autres valeurs. L'algorithme de Fletcher propose de cascader les opérations, mais l'entropie finit tout de même dans un cul-de-sac de cul-de-sac.

L'algorithme de Fibonacci par contre continue de faire circuler l'information pour la mélanger encore et toujours, bloquée dans une boucle, mais pas un cul-de-sac. Sa complexité minimaliste de 2 additions par cycle reste équivalente à celle de Fletcher, sans la perte d'entropie, ce qui en fait un très bon candidat. On se demande bien pourquoi cette meilleure approche n’est pas encore recommandée aujourd’hui.

Il reste encore la question de la retenue, qui est ignorée par tous les exemples du chapitre précédent, ce qui rend ces algorithmes équivalents à un générateur de séquence de Pisano [24] lorsque des valeurs nulles sont scannées. La séquence de Pisano est étudiée depuis plus de deux siècles, donc on sait que ses caractéristiques sont décevantes. On ne peut pas non plus utiliser le complément à 1, car on sait qu'il considère deux valeurs (0 et tout à un) comme égales. Cependant, le principe du rebouclage de la retenue est très important et une légère modification du chemin de la retenue va tout résoudre : il faut considérer la retenue comme une variable à part entière.

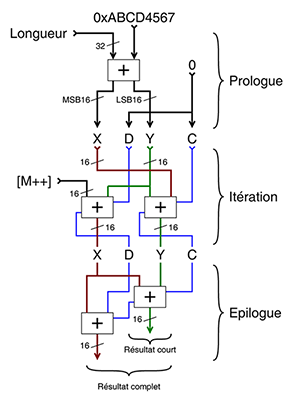
Le résultat est l'algorithme PEAC (la contraction de « Pisano + End Around Carry ») qui fonctionne très bien pour des largeurs W de 2, 3, 4, 10, 16 et 26 bits. La largeur W8 ne donne pas de résultat satisfaisant et la largeur de 32 bits est beaucoup trop longue à vérifier, je travaille encore dessus. Par contre, la largeur W16 fonctionne merveilleusement bien et donne l'itération de base suivante :

La question de l’alignement et de l’ordre des octets est laissée en exercice aux lecteurs les plus motivés, puisqu’en pratique, on préfère les éviter à cause de l’augmentation de la taille du code. Beaucoup d’autres choses peuvent être améliorées ou optimisées, par exemple la quatrième ligne (X=C avec transtypage) peut même être enlevée si la boucle est déroulée deux fois et les variables sont renommées. Avec 4 opérations par mot, soit 2 opérations par octet, ce n'est pas l'algorithme le plus rapide de tous, mais il reste compétitif, car certaines opérations peuvent s'exécuter en parallèle (si le processeur le permet).

À ma grande surprise, plusieurs défauts inhérents des autres checksums sont aussi résolus, en particulier :

• cet algorithme ne peut pas être « planté » par construction, car le seul moyen pour que X et Y soient à zéro implique que C soit à 1, ce qui relance automatiquement le système ;
• PEAC n’est pas commutatif, donc un échange ou un décalage des données en entrée doit modifier la signature ;
• contrairement à un CRC, PEAC travaille par mots et non par bits, donc chaque itération de base traite beaucoup plus de données par cycle ;
• PEAC utilise un rebouclage qui n'est pas en complément à 1, de par la façon dont sont séquencées les additions, donc X et Y peuvent tout à fait prendre la valeur 0 et exploiter la totalité de l'espace des valeurs de la signature. En fait, le système fonctionne en partie modulo 65 537, qui est un nombre premier !
• une signature finale large de 16 ou 32 bits est possible, sans modification du code, en utilisant au besoin X et/ou Y. Faire tourner l’itération à vide une ou deux fois à la fin suffit pour que l’entropie d’un registre se retrouve dans l’autre ;
• l'algorithme reste très facile à réaliser en logiciel comme avec des circuits électroniques ;
• si un bloc de données nulles est scanné, le système dégénère en un générateur de nombres pseudoaléatoires d'une période de 2 147 516 415 itérations. Chaque mot contenant 16 bits, l’état reboucle après plus de 4 Gio. La période correspond à 2³¹+2¹⁵-1, ce qui est proche de la limite théorique de 2³³ (les 33 bits correspondent à 2×16 bits plus la retenue). C’est équivalent au comportement d’un CRC, alors que ni Fletcher/Adler ni les autres checksums de base ne peuvent prétendre de telles périodes.

La figure 6 montre l'ensemble de l'algorithme de checksum sur 16 bits, avec son parallélisme au niveau des instructions (ILP) lui permettant de profiter simultanément de deux pipelines sur un processeur superscalaire. Le code qui l’utilise reste court, en voici un exemple minimaliste :

De nombreuses optimisations sont possibles, mais avant de terminer, vous vous demandez certainement pourquoi PEAC utilise une addition pour combiner la donnée à signer avec l'état des registres. En effet, l'opération XOR pourrait tout aussi bien fonctionner, elle utilise moins de circuits logiques et ne perturbe pas la retenue. Malheureusement, ce dernier point implique aussi que XOR travaille dans un autre espace mathématique que l'addition et des collisions se produisent lorsqu'on les mélange. Cela pourrait expliquer en partie certaines limitations des algorithmes tels que SipHash et Lookup3 qui sont de type add–rotate–xor (ARX).

Conclusion

Beaucoup, beaucoup de recherches ont été réalisées dans le domaine des checksums. L'intégrité des données est un domaine aussi vieux que l'informatique et tout le monde veut remplacer l'inébranlable CRC32, sans avoir réussi à s’en approcher. Le checksum idéal (rapide, minimal, fiable) existe-t-il vraiment ? J'ose le croire et je vous ai présenté un nouveau candidat basé sur des techniques connues depuis des décennies. Non seulement PEAC répond aux critères recherchés, mais il apporte aussi un nouveau cadre théorique, sur lequel d’autres algorithmes (autres que des checksums) pourront être construits.

PEAC est un sujet extrêmement riche que je n'ai pu qu'effleurer ici, sous un angle particulier. Certaines questions restent ouvertes (comme la validité de W32 ou W64) et l’extension aux modulos qui ne sont pas des puissances de 2 ouvre des perspectives dans le domaine des fonctions de hachage. Pour en savoir plus, le site web du projet [26] contient plus d'une centaine de logs qui explorent la structure, les propriétés, les applications et les variations de cet algorithme. Une vidéo [27] montre aussi son utilisation en tant que générateur minimaliste de nombres pseudoaléatoires. PEAC est déjà utilisé comme brouilleur dans un protocole de communication en radio numérique, que je voudrai vous présenter prochainement.

Références

[1] Maxino, Theresa C. « The Effectiveness of Checksums for Embedded Networks » mai 2006, thèse de l’Université Carnegie Mellon, http://users.ece.cmu.edu/~koopman/thesis/maxino_ms.pdf

[2] Fenwick, Peter M. « Checksums and error control », The University of Auckland, 2003
https://www.cs.auckland.ac.nz/compsci314s1t/resources/Checksums.pdf

[3] Stone, Jonathan ; Greenwald, Michael ; Partridge, Craig ; Hughes, « Performance of Checksums and CRCs over Real Data » nov. 1998 https://www.researchgate.net/publication/3334567_Performance_of_checksums_and_CRCs_over_real_data

[4] Guidon, Yann, « Réalisation du CRC pour le conteneur MDS » GLMF#78 décembre 2005, pp70-86.

[5] Wikipédia : « Le principe des tiroirs » https://fr.wikipedia.org/wiki/Principe_des_tiroirs ou « Pigeonhole principle » en anglais : https://en.wikipedia.org/wiki/Pigeonhole_principle

[6] Deutsch, P. : « GZIP file format specification version 4.3 » Request for Comments n°1952, 1996
https://datatracker.ietf.org/doc/html/rfc1952

[7] Braden, R ; Borman, D : « Computing the Internet Checksum », 1988
https://datatracker.ietf.org/doc/html/rfc1071

[8] Walton, Jeffrey ; « An Analysis of the Windows PE Checksum Algorithm » 2008 
https://www.codeproject.com/Articles/19326/An-Analysis-of-the-Windows-PE-Checksum-Algorithm

[9] Wikipédia anglais, « Fletcher’s checksum » https://en.wikipedia.org/wiki/Fletcher's_checksum « The Fletcher checksum is an algorithm for computing a position-dependent checksum devised by John G. Fletcher (1934–2012) at Lawrence Livermore Labs in the late 1970s. The objective of the Fletcher checksum was to provide error-detection properties approaching those of a cyclic redundancy check but with the lower computational effort associated with summation techniques. »

[10] Zweig, J. ; Partridge, C. : « TCP Alternate Checksum Options » RFC n° 1146, 1990 
https://datatracker.ietf.org/doc/html/rfc1146

[11] Wikipédia, « Adler-32 » https://fr.wikipedia.org/wiki/Adler-32 « Adler-32 est une fonction de hashage inventée par Mark Adler et dérivée de la fonction de Fletcher. »

[12] Deutsch, P. ; Gailly, J-L. : « ZLIB Compressed Data Format Specification version 3.3 » RFC n°1950, 1996
https://datatracker.ietf.org/doc/html/rfc1950

[13] Stone, J. ; R. Stewart, R. ; Otis, D. : « Stream Control Transmission Protocol (SCTP) Checksum Change » RFC n°3309, 2002 https://datatracker.ietf.org/doc/html/rfc3309

[14] Maxino, Theresa : « Revisiting Fletcher and Adler Checksums », 2006 
https://www.zlib.net/maxino06_fletcher-adler.pdf

[15] Wikipédia, « Liste de fonctions de hachage » 
https://en.wikipedia.org/wiki/List_of_hash_functions#Non-cryptographic_hash_functions

[16] Bob Jenkins, Bob : « A Hash Function for Hash Table Lookup » Dr Dobb's Journal, Sept. 1997 
http://www.burtleburtle.net/bob/hash/doobs.html

[17] Hsieh, Paul : « Hash functions » 2008 http://www.azillionmonkeys.com/qed/hash.html

[18] Wikipédia : « SipHash » https://en.wikipedia.org/wiki/SipHash « SipHash is an add–rotate–xor (ARX) based family of pseudorandom functions created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012, in response to a spate of "hash flooding" denial-of-service attacks (HashDoS) in late 2011. » Voir aussi https://github.com/veorq/SipHash/blob/master/siphash.c

[19] La fonction de hachage « Fowler–Noll–Vo » sur Internet : https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function et http://www.isthe.com/chongo/tech/comp/fnv/

[20] Wikipédia : La fonction de hachage de Pearson https://en.wikipedia.org/wiki/Pearson_hashing

[21] http://www.burtleburtle.net/bob/c/lookup3.c

[22] komrad36 « CRC: Fastest CRC32 for x86, Intel and AMD, + comprehensive derivation and discussion of various approaches » https://github.com/komrad36/CRC Cette page détaille 13 versions de l'algorithme CRC32, de la version la plus basique à la plus efficace, en utilisant du calcul explicite, puis des tables et enfin des instructions spécialisées.

[23] https://en.wikipedia.org/wiki/64b/66b_encoding#Run_length « The run length statistics may get worse if the data consists of specifically chosen patterns, instead of being random. An earlier scrambler used in Packet over SONET/SDH (RFC 1619 (1994)) had a short polynomial with only 7 bits of internal state which allowed a malicious attacker to create a Denial-of-service attack by transmitting patterns in all 2^7-1 states, one of which was guaranteed to de-synchronize the clock recovery circuits. This vulnerability was kept secret until the scrambler length was increased to 43 bits (RFC 2615 (1999)) making it impossible for a malicious attacker to jam the system with a short sequence. »

[24] La séquence de Pisano est la séquence de Fibonacci modulo un autre nombre entier, qui contrôle sa période : https://fr.wikipedia.org/wiki/P%C3%A9riode_de_Pisano

[25] Miller, Peter « Encoder for generating an error checkword » brevet, 2002 https://patents.google.com/patent/GB2377142A/en

[26] Guidon, Yann : la page du projet PEAC sur Hackaday https://hackaday.io/project/178998-peac-pisano-with-end-around-carry-algorithm/

[27] Guidon, Yann : « Générez des nombres aléatoires avec une seule addition grâce à Fibonacci » 2021 https://www.youtube.com/watch?v=7ujabF8Ofes