Cet article retrace les mésaventures d’un développeur qui devait ajouter un nouveau mode de chaînage dans une bibliothèque cryptographique écrite en Java. Entre les fautes de frappe dans les articles scientifiques, l’absence de vecteurs de tests, les brevets et l’inadéquation de Java, la tâche s’est avérée plus ardue qu’escompté.
Introduction
Afin de répondre aux besoins du marché, nos commerciaux nous ont demandé d’intégrer le chiffrement FPE (Format-Preserving Encryption) dans l’un de nos produits. Le cahier des charges qui nous a été confié se résumait à l’ajout d’un algorithme :
- standardisé, si possible par le NIST (plus rassurant d’un point de vue commercial) ;
- libre de droits pour que la solution puisse être utilisée sans contrainte pour nous ou nos clients.
Cette demande n’avait rien d’inhabituel. Nous y avions déjà répondu maintes fois par le passé. On se contentait alors de trouver la bonne bibliothèque « open source » et le tour était joué. Par « bonne bibliothèque », on entend :
- une communauté de développeurs active, garantissant la pérennité de la bibliothèque ;
- une large base d’utilisateurs témoignant de la robustesse de l’implémentation ;
- l’approbation d’experts indépendants pour l’assurance sécurité ;
- un modèle de licence compatible avec nos objectifs commerciaux (p. ex. licence MIT).
Cependant, avec FPE, la tâche s’est révélée beaucoup plus compliquée que prévu.
1. FPE
Le chiffrement préservant le format est devenu populaire il y a une dizaine d’années avec l’avènement de PCI DSS (Payment Card Industry Data Security Standard). PCI DSS certifie que votre numéro de carte de crédit restera confidentiel lorsque vous effectuez une opération financière en ligne. Quant au FPE, il facilite l’acquisition de ce label en chiffrant les données avec un minimum d’impact sur les applications qui les manipulent.
1.1 Concept
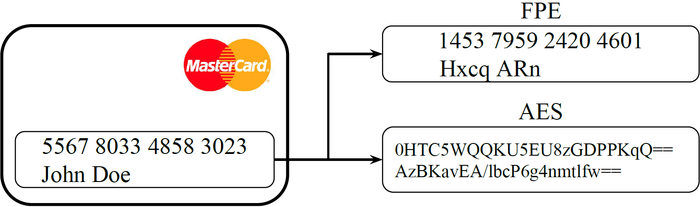
La figure 1 présente le concept. Le format des numéros de carte de crédit est une série de 16 chiffres. Si on les chiffre avec AES, on obtient une chaîne de bytes qui ne correspond plus au format initial. Le FPE génère une nouvelle série de 16 chiffres.
Figure 1 : Exemple de chiffrement d'une carte de crédit.
1.2 Utilisation
L’avantage pour la certification PCI DSS est évident. En utilisant FPE, il n’est pas nécessaire de modifier le format des structures de données d’une application existante pour rendre ses données inaccessibles aux équipes d'exploitation. Le résultat du chiffrement FPE tiendra dans le champ de la base de données prévu pour la donnée en clair.
Plus actuel, aujourd'hui, tout le monde a un œil sur Office 365, Salesforce ou une autre application « cloud ». Cependant, en Europe, on hésite à confier ses données à des pays tiers [24]. On voit donc apparaître des services qui chiffrent les données envoyées dans le cloud [25]. Problème, les applications ne marchent plus si on s’y prend n’importe comment. Typiquement, une application qui demande un numéro de carte de crédit rejettera probablement le chiffrement AES alors qu’elle pourrait être plus tolérante avec FPE.
FPE, c'est encore :
- échapper à la censure : une généralisation du concept appelée « Format-Transforming Encryption » (FTE) est utilisée par Tor pour contourner la censure sur Internet ;
- anonymiser des données de test : une alternative à la « tokenization » (voir par exemple le standard ANSI X9.119) pour générer des données anonymes à partir de données réelles.
Bref, chiffrer sans modifier le format est utile dès lors qu'on veut protéger la confidentialité d'une information sans perturber son traitement.
1.3 Implémentation
D'un point de vue théorique, il s'agit de définir le format à respecter puis de transformer la donnée en clair en une autre donnée respectant le même format. Si le format peut être défini comme un assemblage spécifique de caractères issus d'un alphabet particulier, le problème revient à permuter les caractères à l'intérieur de l'alphabet et à les réassembler correctement. Dans notre exemple du numéro de carte de crédit, l'alphabet est l'ensemble des chiffres 0, …, 9 et ces derniers sont assemblés en quatre groupes de quatre chiffres.
En pratique, on utilise souvent les éléments suivants pour permuter les caractères à l'intérieur de l'alphabet (d'autres constructions sont possibles) :
- un algorithme de chiffrement symétrique traitant des blocs de f bits comme AES ;
- un mode de chaînage permettant de travailler avec des entrées/sorties dont la taille n'est pas un multiple de f ;
- une fonction transformant une chaîne de caractères d'un alphabet particulier en une chaîne de bits pouvant être traitée par AES et son mode de chaînage.
2. Littérature et standards
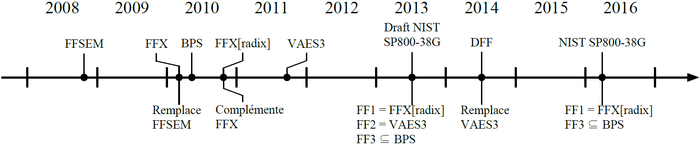
Notre histoire a débuté au cours de l’année 2015 par une recherche bibliographique qui a rapidement mis en évidence une première difficulté : l’absence d’un standard. Le NIST avait publié une première ébauche deux ans auparavant, mais aucune information concernant l'état du processus de standardisation ou une date d'aboutissement n’était donnée. Contrairement à AES et SHA-3 qui étaient des concours organisés par le NIST, la volonté de standardisation semblait venir de la compagnie Voltage. Les principaux jalons de la standardisation pouvaient se résumer ainsi (figure 2) :
- Voltage avait soumis l’algorithme FFSEM [3] au NIST en 2008. Deux ans plus tard, FFX [4] le remplaçait. Les deux algorithmes étaient protégés par des brevets.
- Un premier algorithme libre de droits était apparu en 2010. Comme FFX, BPS [12] utilisait un réseau de Feistel et une primitive interne standardisée, telle qu’AES. Il avait néanmoins certains avantages : compatibilité avec n'importe quelle longueur de données, pas de limite contraignante sur la taille de l’alphabet utilisé pour coder les données.
- Voltage avait rapidement réagi et proposé une extension de FFX, baptisée FFX[radix] [5], concurrençant BPS.
- Verifone avait enfin proposé VAES3 [8], un algorithme breveté en 2011. VAES ajoutait une étape de dérivation de clé à un algorithme existant (FE2 [21]) dans le but d’en améliorer la sécurité et augmenter la durée de vie de la clé.
- Dans une lettre datée du 2 avril 2013, Voltage annonçait que ses brevets protégeaient l’utilisation des réseaux Feistel pour le FPE [6, 7] et couvraient par conséquent BPS et VAES3.
- En 2013, le NIST publiait une première ébauche du standard [2] contenant FFX[radix], VAES3 et un sous-ensemble de BPS respectivement renommés FF1, FF2 et FF3. Le NIST refusait cependant de se prononcer sur les revendications de Voltage.
Figure 2 : Déroulement du standard.
Il n’existait donc pas de standard bien défini et les querelles juridiques nous laissaient dans l’expectative. Peut-on vraiment breveter l’utilisation d’une primitive cryptographique proposée en 1973 par IBM pour Lucifer, le prédécesseur d’un certain DES ? Cette situation n'est pas exceptionnelle, il y a beaucoup de brevets litigieux en cryptographie [26]. Une chose était claire : l’exigence de standard de notre cahier des charges ne serait pas triviale à satisfaire.
3. Logiciel libre et FPE
Aucune des bibliothèques cryptographiques que nous utilisions régulièrement n’offrait de FPE. Une étude de ce que proposait le monde du logiciel libre s’imposait. Peut-être y trouverions-nous la perle rare, ou au moins de quoi générer des données de test pour notre propre bibliothèque (le NIST ne fournissait de vecteurs de test pour aucun des candidats). Conformément à notre cahier des charges, nous n’avons retenu que les bibliothèques offrant au moins un des algorithmes figurant dans l’ébauche de standard du NIST. Nous avons par conséquent écarté d’emblée des bibliothèques telles que Botan ou le code open source de Cisco [14].
3.1 LibFFX
Distribuée sous licence GPL, la bibliothèque LibFFX [17] proposait une implémentation partielle en Python de FFX[radix]. Si LibFFX permettait bien de chiffrer des numéros de cartes de crédit, elle ne gérait cependant pas des alphabets de plus de 62 symboles (alors que la spécification parle de 216 symboles). Ce problème a été découvert par le développeur « lol500 » : une erreur se produisait lorsque la taille de l’alphabet, dénotée par « radix » dans le code ci-dessous, était supérieure à 36. La correction proposée par les développeurs de LibFFX nous a laissés dubitatifs :
if radix not in range(2, 37):
raise InvalidRadixException()
3.2 LibFTE
Une première version de la bibliothèque LibFTE [15] a été présentée lors de la conférence USENIX Security 2014. Elle proposait un concept légèrement différent en autorisant la transformation plutôt que la conservation du format (FTE). Néanmoins, lorsque les formats d’entrée et de sortie spécifiés sont identiques, LibFTE faisait du FPE. Nous avons toutefois rapidement écarté LibFTE :
- L’article indiquait que le chiffrement échouait avec une faible probabilité, même si les paramètres d'entrée étaient corrects.
- Les différents composants de la bibliothèque étaient écrits en C, C++ et Python. Le mélange de ces différents langages compliquait l’intégration dans notre application Java ainsi que la maintenance de la solution.
- Un premier fichier stocké dans le dossier racine du projet laissait penser que LibFTE était distribuée sous licence MIT. Nous avons cependant découvert que LibFTE utilisait la bibliothèque LibFFX soumise à la licence GPL. Il était donc difficile de savoir quelle licence s’appliquait à LibFTE.
LibFTE a de plus évolué de manière drastique après sa présentation à USENIX Security 2014 [16]. Elle était désormais dédiée au contour de la censure sur Internet et proposait une solution ad hoc pour transformer les en-têtes de protocole afin d’échapper au filtrage. Par conséquent, LibFTE ne permettait par exemple plus de chiffrer un numéro de carte de crédit tout en conservant son format.
3.3 MIRACL
M. Scott avait effectué une étude comparative des trois algorithmes proposés au NIST [22]. De son point de vue, BPS était le meilleur candidat. Il l’avait implanté dans MIRACL [18], sa bibliothèque cryptographique écrite en C et distribuée sous licence GPL (contraignante dans notre contexte). Il avait découvert et corrigé deux erreurs de frappe dans l’article décrivant BPS [12] et a également souligné que l’absence de vecteurs de tests compliquait sérieusement le développement.
Nous avons testé MIRACL et découvert que la bibliothèque était dans de très rares cas incapable de déchiffrer les données qu’elle avait elle-même chiffrées. L’explication résidait dans une autre erreur de frappe dans [12] (un « plus grand que » au lieu de « plus grand que ou égal à ») que nous avons signalée aux développeurs de MIRACL. Ces derniers ont rapidement proposé une nouvelle version de leur bibliothèque.
4. Java et FPE
Nous étions en janvier 2016. BPS était le candidat idéal. L’algorithme était, selon ses concepteurs, libre de droits [13]. Les revendications de Voltage demandaient toutefois une étude plus approfondie. MIRACL était la seule bibliothèque « open source » proposant une implémentation convaincante du FPE. Avions-nous découvert toutes les petites erreurs (aussi bien dans le code de MIRACL que dans [12]) ? Nous devions comprendre les moindres détails de BPS pour nous en convaincre. La meilleure approche était d’écrire notre propre bibliothèque et de la comparer à MIRACL.
Le risque que nous prenions était de travailler avec un algorithme en cours de standardisation. Les algorithmes pouvaient encore être modifiés pour améliorer leur sécurité à ce stade du processus. De plus, le NIST ne standardise pas nécessairement toutes les variantes d’un algorithme (AES n’est par exemple qu’un sous-ensemble de Rijndael ; dans la première ébauche du standard FF3 n'offrait pas toutes les fonctionnalités de BPS).
Nous devions encore choisir un langage pour le développement. Le produit dans lequel nous devions intégrer notre bibliothèque était écrit en Java. Pour faciliter le développement, le déploiement et la maintenance, nous avons donc décidé d’utiliser ce langage pour BPS. Notons que des bibliothèques écrites en C/C++ sont généralement plus performantes. Le choix de Java ne semblait toutefois pas pénalisant pour notre application qui demandait ses clés de chiffrement à un serveur distant : les délais de transmission et d’accès aux disques rendaient négligeables les quelques microsecondes nécessaires au chiffrement. Nous avons tout de même effectué un rapide test avec MIRACL (appel via la « Java Native Interface ») qui ne s’est avérée que deux fois plus rapide que notre code Java. La différence n’était pas assez significative pour changer de langage.
Les premiers tests semblaient concluants : nous obtenions les mêmes données chiffrées avec MIRACL et notre bibliothèque. Les problèmes sont apparus avec les nombres à virgule flottante : lorsque le texte chiffré était « Not a Number » (NaN), le déchiffrement ne fonctionnait pas toujours avec Java 7. Bizarrement, le résultat était correct en exécutant notre code avec Java 8.
Rappelons qu’un nombre flottant simple précision (32 bits) est constitué d’un bit de signe, d’un exposant de 8 bits et d’une mantisse de 23 bits (norme IEEE-754). Ce nombre est un « NaN » si son exposant est égal à 255 et sa mantisse différente de 0 (exemple : 0 11111111 00000000000100010000000).
Selon la norme IEEE-754, il existe de plus deux catégories de « NaN » :
- Les « QNaN » (« NaN » silencieux) n’interrompent généralement pas le traitement et se propagent d’une opération à l’autre. Le bit de poids fort de la mantisse d’un « QNaN » est égal à un.
- Les « SNaN » (« NaN » signalants) dénotent une opération invalide et génèrent une exception. Le bit de poids fort de la mantisse d’un « SNaN » est égal à zéro.
Afin de chiffrer des nombres à virgule flottante, notre bibliothèque les convertit en une chaîne de bits avec la fonction floatToIntBits. Une fois chiffré, le résultat est à nouveau converti à l’aide de intBitsToFloat afin d’être stocké. La documentation de cette fonction indiquait que le format d’un « NaN » pouvait être modifié (« Note that this method may not be able to return a float NaN with exactly same bit pattern as the int argument. »). Ce comportement était très problématique dans notre cas. Avec Java 7, le texte chiffré
était transformé en
par intBitsToFloat. Ce phénomène ne semblait pas se produire avec Java 8, mais nous ne comprenions pas pourquoi : la documentation de la méthode précisait également qu’un « NaN » pouvait être modifié. La documentation indiquait de plus que certains processeurs transforment un « SNaN » en « QNaN » lors d’une simple copie (« However, on some processors merely copying a signaling NaN also performs that conversion. »). Notre code générait des résultats différents en fonction de la version de Java et du processeur. Le slogan « write once, run everywhere » de Java ne s’appliquait pas au FPE.
Une solution envisageable serait d'utiliser une bibliothèque mathématique qui proposerait sa propre implémentation des nombres à virgule flottante avec un « NaN » unique (voir par exemple [27]). Cette approche est néanmoins trop contraignante, car elle obligerait les utilisateurs de notre bibliothèque à ne pas utiliser les float Java.
Une solution plus simple aurait été de ne convertir la représentation binaire du nombre flottant qu’au moment de l’affichage. L’objectif du FPE étant de conserver le format des données, cette approche n’était pas satisfaisante et nous avons décidé d’interdire les « NaN » : une donnée serait chiffrée itérativement tant que le résultat est un « NaN ».
|
|
Valeur flottante |
Représentation binaire fournie à BPS (floatToIntBits) |
Représentation binaire calculée avec BPS |
Conversion au format flottant pour le stockage (intBitsToFloat) |
Déchiffrement de la valeur stockée |
|
Java 7 |
0.06661743 |
Signe : 0 Exposant : 01111011 Mantisse : 0001000 01101110 10111000 |
Signe : 0 Exposant : 11111111 Mantisse : 10000000 00000000 00000001 (SNaN) |
QNaN |
-1.1849127E-30 |
|
Java 8 |
SNaN |
0.06661743 |
Tableau 1 : Exemple de chiffrement de nombres à virgule flottante.
Conclusion
Nous venions de terminer l’écriture de notre bibliothèque lorsque le NIST publia la version officielle du standard [1] accompagnée de vecteurs de test. Suite à une attaque suggérée par la NSA et effectuée par le NIST en 2015 [10], FF2 avait disparu (la faille venait du mécanisme de dérivation de clés ajouté à FE2 pour en améliorer la sécurité [21]). Les différences entre BPS et FF3 observées dans la première version du standard subsistaient :
- Le NIST imposait l'utilisation d’un réseau de Feistel de 8 étages et d’AES alors que la publication originale laissait le choix du nombre d'étages (8 étant la recommandation pour un bon compromis performance-sécurité) et de la primitive cryptographique.
- Plus ennuyeux dans notre contexte, le mécanisme permettant à BPS de chiffrer des données de taille arbitraire était définitivement écarté du standard. Notons toutefois que le FPE est essentiellement utilisé pour chiffrer des données de petite taille pour lesquelles ce mécanisme est inutile. Même si l’utilisation du standard nous est imposée, il sera donc souvent possible de travailler avec BPS.
Plusieurs nouvelles bibliothèques FPE en Java [19], Python, Go ainsi qu’un service de chiffrement dans le cloud [23] sont apparus suite à la publication du standard. Bouncy Castle a également annoncé l’ajout du FPE dans une prochaine version [11]. La question des brevets de Voltage (devenu HPE Security depuis son rachat par Hewlett Packard Entreprise en 2015) semblait le plus souvent ignorée. Les développeurs de [19] feignaient par exemple l’ignorance lorsqu’un utilisateur leur posait la question [20].
Une première attaque contre FF1 et FF3 était publiée au cours de l’été 2016 [9]. La publication décrit comment récupérer un message en clair lorsque l'ensemble des messages possibles est « petit », ainsi que des suggestions permettant d'éviter cette attaque. Contrairement aux concours AES et SHA-3, le NIST n’avait organisé aucune conférence consacrée à la sécurité et à l’implémentation des candidats au cours du processus de standardisation. Ceci pourrait d’ailleurs expliquer l’engouement tardif pour le FPE. La communauté attendait le standard avant de se mettre au travail. Nous suivrons peut-être la même stratégie si on nous demande à nouveau de travailler avec des algorithmes en cours de standardisation (en proposant toutefois une solution alternative en attendant le standard).
L’histoire racontée dans cet article confirme une fois de plus que l’écriture d’une bibliothèque cryptographique est une tâche compliquée où le moindre bug peut avoir des conséquences fâcheuses. Le chiffrement des NaN en Java est un excellent exemple : si nous n’avions pas découvert le problème et utilisé la première version de notre bibliothèque dans un cas concret, nos clients auraient peut-être été incapables de déchiffrer certaines de leurs données (tout comme pour le bug découvert dans MIRACL, il aurait toutefois été possible de réparer une base de données corrompue au prix du développement de logiciels spécifiques). Notons que des vecteurs de test ne permettent pas forcément de détecter de tels bugs et que nous aurions pu ne rien voir si nous n’avions travaillé qu’avec Java 8. Le logiciel cryptographique devrait par conséquent être libre afin qu’une large communauté d’experts et d’utilisateurs puisse l’évaluer. Même si cette approche ne garantit pas l’absence d’un bug (Heartbleed, Shellshock…), d’une faiblesse d’un algorithme ou d’une porte dérobée (notons que cette dernière peut également se cacher ailleurs que dans le code : dans le cas du générateur de nombres aléatoires Dual_EC_DRBG, la faille provient de l'algorithme et des paramètres par défaut proposés dans le standard), elle est essentielle pour obtenir du logiciel cryptographique de qualité. La taille de la communauté est cruciale ici (une bibliothèque développée par une seule personne et téléchargée quelques dizaines de fois inspire moins confiance qu’un logiciel activement maintenu par plusieurs développeurs et largement utilisé). Plusieurs de nos clients partagent déjà notre point de vue : ils se méfient du code propriétaire et nous demandent de travailler avec du logiciel libre. Notons que le logiciel libre impose des contraintes qui nous semblent trop souvent oubliées ou négligées : le suivi de l’évolution du code (forums de discussion, « commits » sur GitHub…) et l’éventuelle adaptation du logiciel à une nouvelle version du code open source.
La question qui nous taraude encore est de décider ce que nous allons faire de notre bibliothèque. Nous pensions proposer FF3 à nos clients désireux de travailler avec des algorithmes standardisés. Ce choix n’est peut-être pas définitif : ne serait-il pas plus judicieux de suivre les recommandations de [9] pour éviter certaines attaques ? De nouvelles attaques plus dévastatrices seront-elles publiées au cours des prochains mois ?
Références
[1] NIST SP800-38G : https://goo.gl/fw46dc
[2] NIST SP800-38G Draft : https://goo.gl/NBAz7j
[3] Terence Spies, « FFSEM » : https://goo.gl/dvxzHb
[4] M. Bellare et P. Rogaway et T. Spies, « The FFX Mode of Operation for FPE » : https://goo.gl/AlbMe5
[5] M. Bellare et P. Rogaway et T. Spies, Addendum to « The FFX Mode of Operation for FPE » : https://goo.gl/qPSFeR
[6] Voltage Security, Letter of assurance : https://goo.gl/DcvMq0
[7] Voltage Security, HPE FPE Patent Licensing : https://goo.gl/XVXxUZ
[8] J. Vance, « VAES3 scheme for FFX » : https://goo.gl/gZFdYM
[9] Message-recovery attacks on Feistel-based Format Preserving Encryption : http://eprint.iacr.org/2016/794
[10] M. Dworkin et R. Perlner, « Analysis of VAES3 » : https://goo.gl/D85SGu
[11] Java FIPS Road Map: https://goo.gl/7ErW4T
[12] E. Brier et T. Peyrin et J. Stern, « BPS: a FPE Proposal » : https://goo.gl/7pc8zt
[13] E. Brier et T. Peyrin et J. Stern, « BPS: Intellectual Property Statement » : https://goo.gl/fdfJ2w
[14] S. Dara, « Open Sourcing FNR an Experimental Block Cipher » : https://goo.gl/LTo0pl
[15] LibFTE : https://libfte.org/
[16] Second version of LibFTE : https://goo.gl/1Jbc1I
[17] LibFFX : https://goo.gl/twlmMg
[18] MIRACL Cryptographic SDK : https://goo.gl/jWhbGk
[19] Format-Preserving Encryption for Java : https://goo.gl/53j9vN
[20] Format-Preserving Encryption for Java Patents : https://goo.gl/Fa6LTc
[21] M. Bellare et T. Ristenpart et P. Rogaway et T. Stegers, « Format-Preserving Encryption » : https://goo.gl/9AXZBN
[22] A Note on the Implementation of Format Preserving Encryption Modes : https://goo.gl/qF4e3Y
[23] Gemalto ncryptify algorithms : https://goo.gl/53slNY
[24] Cloud Computing and the USA Patriot Act : https://goo.gl/rJ6A0s
[25] Cloud Access Security Brokers : https://ciphercloud.com/
[26] Irrelevant patents on elliptic-curve cryptography : http://cr.yp.to/ecdh/patents.html
[27] JScience Library : http://jscience.org/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture