BEAST, Lucky13, FREAK, LogJam, ou encore DROWN... Le point commun entre ces attaques sur le protocole TLS : l’exploitation de vulnérabilités connues depuis longtemps sur des algorithmes ou des constructions cryptographiques que l’on aurait dû abandonner depuis longtemps.
L’actualité de la SSI contient régulièrement des annonces concernant des vulnérabilités cryptographiques. Si certaines d'entre elles sont considérées comme théoriques, d'autres donnent directement lieu à une exploitation concrète. Cependant, même dans le premier cas, les faiblesses théoriques peuvent être converties en attaques réelles en quelques mois ou quelques années. C'est la raison pour laquelle les algorithmes ou constructions cryptographiques obsolètes, tels que SHA1, RC4 ou PKCS#1 v1.5, doivent être abandonnés dès que possible. Dans le cas contraire, développer une application de sécurité tient du funambulisme.
Les algorithmes cryptographiques sont omniprésents dans les systèmes d'information. Ils servent à sécuriser les communications, à stocker des mots de passe, ou encore à chiffrer les disques. Cependant, les spécifications qui définissent ces usages reposent souvent sur des algorithmes ou des constructions cryptographiques obsolètes, c'est-à-dire pour lesquels une faiblesse est connue. Bien que ces faiblesses soient parfois uniquement théoriques, ou apparemment inexploitables, force est de constater que les attaques ne peuvent que s'améliorer (Attacks always get better). Il est donc nécessaire de mettre en place des contre-mesures qui forcent les développeurs à faire des acrobaties dans le code cryptographique.
Cet article présente quelques exemples de primitives cryptographiques historiques dont l'implémentation est ainsi rendue délicate.
1. Ordre de l'application des primitives de chiffrement et d'intégrité
Dans de nombreux cas, la cryptographie sert à protéger des données en confidentialité et en intégrité. Pour cela, on utilise généralement d'une part une primitive de chiffrement symétrique, et d'autre part un MAC (Message Authentication Code), un algorithme permettant de calculer un motif d'intégrité. Ainsi, on pourra utiliser AES en mode CBC pour assurer la confidentialité et HMAC SHA256 pour l'intégrité.
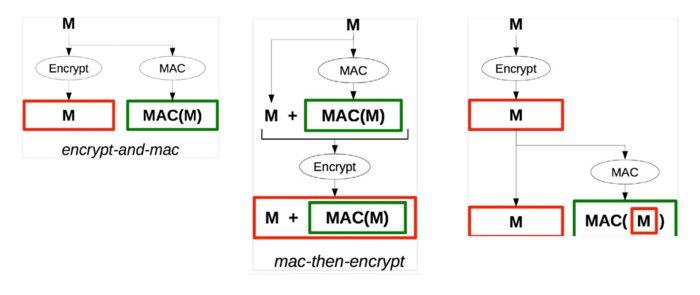
Dans un article publié en 2001, Krawczyk a étudié les manières génériques de combiner ces deux types de mécanismes [1]. Il a considéré trois constructions présentées à la figure 1 :
- encrypt-and-mac, où le message est d'une part chiffré, et d'autre part passé en entrée d'un MAC, pour produire le chiffré et le MAC côte à côte ;
- mac-then-encrypt, où on commence par calculer le motif d'intégrité sur le message, avant de chiffrer le tout (le message et le MAC) ;
- encrypt-then-mac, où le message est d'abord chiffré, puis un MAC est calculé sur le résultat du chiffrement.
Figure 1 : Illustration des trois grandes constructions pour combiner chiffrement et protection en intégrité.
En réalité, il existe également des constructions qui combinent nativement les protections en intégrité et en confidentialité. On parle de modes combinés. Comme ils sont relativement récents par rapport aux constructions obsolètes décrites dans cet article, ils sont présentés plus tard, dans les solutions.
Le problème de la première construction (encrypt-and-mac) est que l'attaquant a directement accès au MAC du message clair en clair. Si le MAC couvre uniquement le message, à l'exclusion de tout autre élément, le même message clair produira le même MAC, ce qui est en soi une information intéressante. Une variante de RDP (Remote Desktop Protocol) avait exactement ce problème, et permettait donc de repérer les frappes clavier répétées dans la saisie d'un mot de passe... La correction classique est de s'assurer que le MAC couvre également des données additionnelles, par exemple un compteur, pour diversifier les motifs produits.
Un problème commun aux deux premières méthodes est que l'attaquant peut facilement forger un chiffré que la victime ne pourra pas authentifier avant de l'avoir déchiffré. Cela ouvre donc le champ aux attaques à chiffré choisi, telles que les attaques reposant sur un oracle de padding, dont nous parlerons plus loin.
La construction encrypt-then-mac est celle qui garantit a priori les meilleures propriétés pour la confidentialité des données. En effet, avant même de songer à sortir sa clé pour déchiffrer le message, le destinataire du message est censé vérifier le motif d'intégrité, coupant de fait l'accès à un oracle de déchiffrement.
Il est cependant important de noter que même avec encrypt-then-mac, un développeur pourrait implémenter le déchiffrement d'une mauvaise manière, en déchiffrant dans tous les cas le message (et en ne vérifiant le MAC qu'après).
En pratique, encrypt-then-mac se retrouve dans IPsec et son mode ESP, alors que mac-then-encrypt était le seul mode utilisé dans TLS jusqu'à la version 1.2. Enfin, encrypt-and-mac se retrouve dans RDP et dans les premières spécifications de SSH.
Certains protocoles proposent également des modes de fonctionnement mettant uniquement en œuvre du chiffrement. Contrairement à une idée fausse, mais très répandue, de telles constructions n'apportent en général aucune garantie d'intégrité. Une illustration triviale est le chiffrement d'un message avec une primitive de chiffrement par flot tel que RC4 : toute inversion de bit sur le chiffré se traduira par l'inversion du bit de clair correspondant !
Que ce soit avec encrypt-and-mac, avec mac-then-encrypt, ou dans les modes sans intégrité, un attaquant peut forcer le destinataire à déchiffrer un message de son choix. On parle alors d'attaques à chiffré choisi.
2. Exemples d'attaques à chiffré choisi
2.1 Les oracles de padding dans le mode CBC
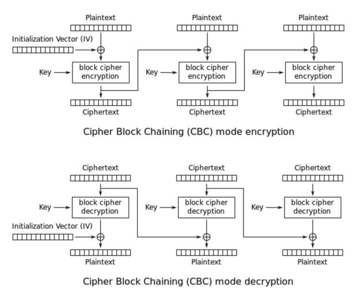
Considérons désormais un protocole dans lequel le mode CBC est utilisé avec la construction mac-then-encrypt. CBC (Cipher Block Chaining), décrit à la figure 2, est un mode opératoire utilisé avec les primitives de chiffrement par blocs (blockcipher). Avant d'appliquer le blockcipher de manière itérée, le message doit d'abord être complété pour atteindre une longueur multiple de la taille du bloc considéré. Cette étape est appelée padding (bourrage en français). Avec CBC, la méthode classique de bourrage consiste à ajouter n octets contenant la valeur n. S'il manque un octet à la fin du message, on ajoutera un octet à 01 ; s'il manque deux, on ajoutera 02 02, etc.
Figure 2 : Description du mode CBC. Source : Wikipédia.
Au déchiffrement, le destinataire commence par appliquer la primitive de déchiffrement de manière itérée pour obtenir une suite de blocs clairs. Il lui faut alors retirer le padding, c'est-à-dire lire le dernier octet. En notant x la valeur de cet octet, il faut ensuite s'assurer que les x derniers octets contiennent tous la valeur x. Si c'est le cas, le padding est jeté et le clair transmis pour vérification du MAC ; dans le cas contraire, c'est une erreur de padding.
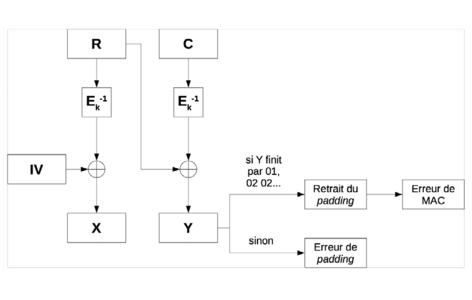
Si un attaquant peut distinguer entre ces deux cas, on parle d'oracle de padding. Il est alors possible d'exploiter la situation pour obtenir des informations sur un bloc chiffré de son choix C. En effet, l'attaquant peut simplement soumettre un chiffré de la forme R C, où R est un bloc arbitraire. Si la suite de blocs clairs obtenue par le destinataire se termine par 01, par 02 02, ou par 03 03 03... le padding est correct et on obtiendra une erreur de MAC. Sinon, ce sera une erreur de padding. La figure 3 présente le fonctionnement du déchiffrement et les deux erreurs possibles.
Figure 3 : Détails du déchiffrement d'un chiffré choisi par l'attaquant.
On suppose qu'un attaquant dispose d'un oracle de padding, c'est-à-dire qu'il est capable de distinguer une erreur de MAC d'une erreur de padding. Il peut alors soumettre en aveugle des messages de la forme R C en faisant varier R, jusqu'à obtenir une erreur de MAC. En reprenant les notations de la figure 3, l'attaquant sait que le bloc Y se termine par un padding correct, le plus vraisemblable étant 01. En notant pn-1 le dernier octet du clair recherché, et rn-1 le dernier octet de R, on a rn-1 xor pn-1 = 01.
Fort de cette information, l'attaquant peut alors continuer sa recherche de manière similaire sur l'avant-dernier octet, et ainsi de suite. Trouver la valeur de chaque octet parmi les 256 valeurs possibles requiert 128 essais en moyenne.
La première attaque contre CBC utilisant un oracle de padding a été décrite par Vaudenay [2]. En pratique, de tels oracles de paddingexistent. Par exemple, dans l'article [3], des chercheurs ont montré comment exploiter un service acceptant des messages XML chiffrés en entrée. Avec XML Encryption, l'attaquant peut généralement distinguer une erreur de padding (rejet rapide de la requête par la couche cryptographique) d'une erreur applicative (rejet d'un document corrompu par la couche applicative). Cela lui permet de soumettre de manière adaptative différents documents en entrée pour retrouver, petit à petit le clair.
2.2 Les oracles de format dans OpenPGP
Au-delà des oracles de padding, tout comportement du destinataire révélant une information sur la suite de blocs clairs obtenus peut en général être exploité par un attaquant. Par exemple, dans des travaux réalisés à l'ANSSI [4], nous avons étudié le format OpenPGP, qui utilise une construction proche de mac-then-encrypt.
À la réception, le destinataire déchiffre le message, dissèque (parse) le message obtenu pour extraire le motif d'intégrité, puis le vérifie. Le problème est ici que l'étape de parsing peut mener à des erreurs telles que l'absence d'un marqueur attendu à une position donnée. Si l'attaquant peut soumettre des chiffrés choisis et détecter cette erreur, il peut récupérer de l'information sur le clair. Il en résulte une attaque efficace.
Dans ce cas encore, si l'attaquant peut modifier le chiffré, le soumettre, et observer un changement dans le comportement du destinataire, une attaque est possible, car la vérification d'intégrité arrivera trop tard.
2.3 Contre-mesures
Contrairement à l'intuition qui inciterait un développeur à signaler chaque cas d'erreur avec un code particulier, il est souhaitable de ne pas donner d'information sur ces erreurs. Ainsi, de manière générale, les contre-mesures visent à empêcher un attaquant de distinguer des cas d'erreur différents. Pour cela, il faut tout d'abord uniformiser les messages d'erreurs renvoyés par le protocole ou l'application.
Cependant, cela n'est pas suffisant, car il existe d'autres manières pour l'attaquant de distinguer deux comportements différents chez son correspondant. Une de ces manières est de mesurer le temps de réponse. Une implémentation sécurisée devrait donc répondre en temps constant dans tous les cas d'erreurs, ce qui peut se révéler extrêmement difficile en pratique. En particulier, cela nécessite souvent de réimplémenter une partie du code cryptographique.
D'un autre côté, l'utilisation correcte du paradigme encrypt-then-mac facilite l'écriture d'une implémentation ne faisant pas fuir d'information : à la réception, le motif d'intégrité est calculé et comparé. Si le résultat est positif, le traitement continue correctement ; sinon, une unique erreur est retournée, sans que la clé de déchiffrement ou le message clair aient été manipulés. Une telle implémentation peut s'écrire simplement en réutilisant des briques existantes.
Pour être complet, il est possible d'écrire des versions de mac-then-encrypt qui soient sécurisées, mais il ne s'agit pas du mode CBC standard, ce qui ne permet pas une réutilisation de code existant.
3. Zoom sur le mode CBC dans TLS
Le mode CBC est utilisé dans le protocole de sécurité TLS, dans l'ordre mac-then-encrypt par défaut. Plusieurs attaques ont été décrites contre ce mode au cours des années, mais la personne qui le résume le mieux est Bodo Möller [5], qui décrivait dès 2001 les fondements théoriques de Lucky13, BEAST et POODLE.
3.1 Lucky13
Cette attaque, présentée en 2013 par Paterson et al. [6], mettait en pratique l'attaque théorique, décrite dans la section 2.1.
Longtemps, l'application à TLS a été considérée comme non pertinente, pour deux raisons :
- à la première erreur de déchiffrement (quelle qu'elle soit), la connexion est coupée et toute reconnexion subséquente mène à un changement des clés cryptographiques ;
- les messages envoyés sur le réseau en cas d'erreur de padding ou d'erreur de MAC sont chiffrés, et donc indistinguables pour l'attaquant.
Le premier argument peut être contourné assez facilement si l'on considère les éléments qui peuvent intéresser un attaquant : un mot de passe ou un cookie d'authentification. Comme ces éléments sont répétés à chaque nouvelle connexion, l'attaquant apprend à chaque fois un peu d'information sur le secret qu'il veut recouvrer. Ces informations partielles collectées dans les différentes connexions peuvent ensuite être agrégées.
Concernant le second argument, il est intéressant de se référer à la RFC 4346 (TLS 1.1) qui spécifie qu'une implémentation doit se protéger des attaques temporelles (timing attacks), en rendant le traitement des messages protégés essentiellement le même, que le padding soit correct ou non. Une proposition d'implémentation suit, indiquant que cette solution laisse cependant un petit canal auxiliaire concernant le temps d'exécution. C'est ce canal qui est exploité dans l'attaque Lucky 13.
À la suite de ces révélations, les développeurs des différentes piles TLS ont réécrit le code correspondant pour supprimer cette différence dans le temps d'exécution, menant en particulier à un patch sordide pour OpenSSL [7]. Pourtant, s2n, une implémentation récente de TLS, s'est révélé vulnérable à l'attaque, à cause d'une contre-mesure incomplète [8].
Face à ce problème, plusieurs approches sont possibles :
- documenter l'attaque dans une spécification en laissant le développeur traiter le problème ;
- réécrire la crypto à très bas niveau pour implémenter les contre-mesures nécessaires. OpenSSL contient une telle implémentation, au prix d'un patch illisible. Cependant, l'écriture de code cryptographique est un exercice délicat qu'il est préférable de laisser aux experts du domaine ;
- jeter le mode mac-then-encrypt, soit en implémentant encrypt-then-mac (défini pour TLS dans la RFC 7366), soit en utilisant un mode combiné tel que GCM. Ces solutions reposent respectivement sur une extension et sur une version particulière du protocole, ce qui nuit à la compatibilité.
3.2 BEAST (Browser Exploit Against SSL/TLS)
En 2011, Duong et Rizzo ont publié une attaque contre TLS, intitulée BEAST [9]. Cette attaque repose sur l'utilisation dans SSL et TLS 1.0 d'un IV implicite : en dehors du premier message, chaque message est chiffré en utilisant comme IV le dernier bloc chiffré du message précédent. Ainsi, l'IV qui va être utilisé pour le message à venir est connu d'un attaquant pouvant espionner le canal.
Or, dès 1995, Rogaway avait montré que cette connaissance pouvait permettre des attaques à clair choisi [10]. On suppose pour cela que l'attaquant, en plus de pouvoir observer les messages chiffrés, peut choisir une partie des messages clairs. Bien que cette description semble totalement irréaliste, les hypothèses sont remplies dans un navigateur...
Il est intéressant de remarquer que la contre-mesure avait été spécifiée dès 2006 dans la RFC 4346 (TLS 1.1), bien avant que la preuve de concept soit publiée. Cependant, l'attaque ayant été considérée comme théorique, presqu'aucune pile TLS n'avait mis en œuvre TLS 1.1 avant 2011.
3.3 POODLE (Padding Oracle On Downgraded Legacy Encryption)
Les attaques exploitant un oracle de paddingCBC peuvent être dévastatrices contre SSLv3, puisque le padding y est mal spécifié : seul le dernier octet du padding doit être vérifié par le destinataire. Cette observation a permis à des chercheurs travaillant chez Google de présenter en 2014 une preuve de concept exploitant un autre type d'oracle de padding : POODLE [11].
Par désespoir, certains ont même recommandé l'utilisation de RC4, pourtant victime d'attaques pratiques de plus en plus efficaces depuis 2013. Cependant, la seule solution est de bannir l'usage de SSLv3, un protocole vieux de plus de 20 ans.
Ce qui est intéressant, c'est qu'en écrivant des outils pour tester la vulnérabilité, des chercheurs se sont rendu compte qu'en fait, certaines piles TLS (et non SSLv3) implémentaient tout de même cette version faible du padding CBC pour les versions récentes ; on a alors parlé de POODLE-TLS.
Ainsi, le mode CBC tel qu'il est utilisé dans TLS a montré ses limites. La version actuelle du protocole, TLS 1.2, a introduit les modes combinés (et GCM en particulier) pour apporter un peu de modernité au protocole. Ces nouveaux modes seront les seuls spécifiés dans TLS 1.3, en cours de définition. Pour réellement profiter de cette avancée en termes de sécurité, il faut maintenant s'atteler à désactiver TLS 1.0 et TLS 1.1, en plus de SSLv2 et SSLv3 (ce qui devrait déjà être fait...).
4. PKCS#1 v1.5, Bleichenbacher et Million Message Attack
Les oracles de padding, décrits ci-dessus sur le mode CBC, existent également dans le monde de la cryptographie asymétrique. L'attaque la plus connue est due à Bleichenbacher [12], à l'encontre du mode de chiffrement de RSA décrit dans PKCS#1 v1.5. Cela concerne en particulier l'échange de clés par chiffrement RSA dans TLS. Une ressource utile sur le sujet est le site [13].
4.1 Description de l'attaque
L'objectif de notre attaquant est de déchiffrer C, qui correspond au chiffré de P avec la clé RSA (N, e). N est le module RSA, sur n octets, et e est l'exposant public.
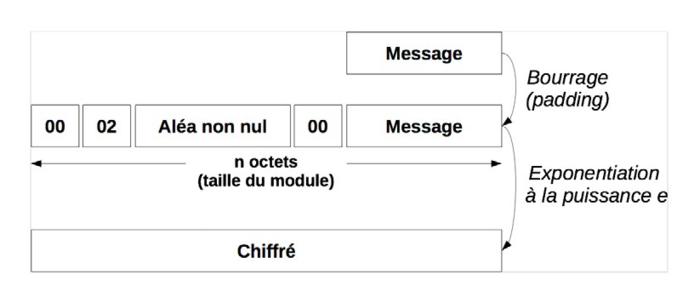
Avec PKCS#1 v1.5, chiffrer un message consiste d'abord à le compléter avec du bourrage pour obtenir la taille suffisante, c'est-à-dire n octets. Ce padding commence en particulier par les octets 00 02. Ensuite, le bloc est interprété comme un grand entier, et élevé à la puissance e (l'exposant public) modulo N. Ces étapes sont décrites dans la figure 4.
Figure 4 : Chiffrement PKCS#1 v1.5.
Lors du déchiffrement, le récepteur commence par élever le nombre obtenu à la puissance d (l'exposant privé) modulo N. Si le résultat obtenu ne commence pas par les octets 00 02, on a une erreur de padding.
Ainsi, si un attaquant sait distinguer une telle erreur d'un comportement normal, il pourra l'exploiter pour retrouver le clair P associé à un chiffré donné C. Pour cela, il envoie des chiffrés modifiés, de la forme C* = Xe * C [N] (où X est choisi par l'attaquant). Si l'erreur de paddingci-dessus n'est pas détectée, il sait que X * P [N] est compris entre 2A et 3A (en notant A = 28*(n-2)).
En émettant des demandes de déchiffrement successives, il pourra petit à petit trouver un encadrement de plus en plus précis de P, et le retrouver complètement à la fin.
L'attaque présentée initialement requerrait un million de requêtes pour retrouver un message chiffré avec une clé RSA 1024, d'où le nom de Million Message Attack. Bien que lourde à mettre en œuvre, cette attaque était très efficace avec SSL/TLS, puisque le standard spécifiait qu'un message particulier devait être retourné en cas d'erreur de padding ; de plus, étant donné que l'erreur survenait tôt dans l'échange, le message d'erreur était envoyé en clair et directement exploitable par un attaquant pour en faire un oracle de padding.
Afin de supprimer cet oracle de padding, une procédure a donc été décrite pour rendre les deux comportements indistinguables pour un attaquant :
1) dans un premier temps, le serveur génère une valeur aléatoire ;
2) ensuite, il tente de déchiffrer le message reçu et agit en conséquence :
2a) si le déchiffrement s'est correctement passé, il retourne le clair obtenu ;
2b) sinon, il retourne la valeur aléatoire préalablement tirée.
3) le reste de la négociation continue dans les deux cas.
La valeur retournée sert de secret partagé à partir duquel les clés sont dérivées. Ainsi, ces clés, utilisées à la fin de la négociation, seront fausses en cas d'erreur de padding. Cependant, l'attaquant ne pourra pas s'en apercevoir, puisqu'il ne connaît pas le clair attendu (c'est ce qu'il cherche).
4.2 Les vulnérabilités récentes
Tout d'abord, il est intéressant de voir qu'OpenSSL, l'implémentation la plus répandue de TLS, n'implémentait pas la procédure ci-dessus correctement [14]. En générant la valeur aléatoire après avoir constaté une erreur de padding, un attaquant pouvait mesurer une différence dans le temps d'exécution. Or nous avons vu précédemment que de telles différences, même faibles, deviennent tôt ou tard exploitables par un attaquant motivé.
Un autre cas d'oracle a été constaté dans une implémentation Java réutilisant une fonction standard pour déchiffrer PKCS#1 v1.5. Or, lorsque le padding était incorrect, une exception était levée. Bien que les développeurs avaient pris en compte la procédure ci-dessus, le temps passé à lever et rattraper l'exception était observable et pouvait mener à une attaque pratique [15].
Dans ce dernier cas, la bonne solution serait de modifier TLS pour utiliser PKCS#1 v2.1, spécifiée en 2002. En effet, cette version du standard rend les attaques par oracle de padding inopérantes. Cependant, la spécification de TLS, qui continue d'imposer PKCS#1 v1.5, force le développeur à choisir entre la modularité de son code (réutiliser une fonction existante, aux dépens d'une exposition à l'attaque de Bleichenbacher) et la sécurité (en redéveloppant lui-même la primitive cryptographique).
4.3 DROWN
L'actualité récente nous a prouvé que les bonnes attaques cryptographiques ont la vie dure. Le 1er mars 2016, une équipe de chercheurs a publié DROWN [16], une nouvelle attaque exploitant une variante de l'attaque de Bleichenbacher contre PKCS#1 v1.5.
Lorsque la contre-mesure contre l'attaque de Bleichenbacher est activée, l'attaquant ne peut normalement pas distinguer un message avec un padding correct (menant à une utilisation du message clair) d'un message invalide (menant à l'utilisation d'un aléa à la place du secret inclus dans le message). Cependant, comme l'ordre des messages est différent dans SSLv2, et que le mode EXPORT réduit la taille des secrets, un attaquant peut distinguer ces deux cas avec une recherche exhaustive sur 40 bits !
Les suites EXPORT sont une survivance du siècle dernier imposant aux équipements et logiciels cryptographiques d'utiliser des clés de taille réduite pour respecter diverses législations régissant l'export de produits cryptographiques. Pour rappel, elles ont également été mises en cause dans les attaques FREAK [17] et LogJam [18].
L'article présente donc une attaque permettant d'exploiter cette faiblesse pour déchiffrer un message échangé dans une connexion TLS robuste, à condition que l'attaquant puisse converser avec le même serveur (ou un serveur réutilisant la même clé RSA) en utilisant SSLv2 et une suite EXPORT.
De plus, les auteurs ont découvert deux vulnérabilités supplémentaires pour améliorer leur attaque. Le résultat, Special DROWN, consiste à déchiffrer un message en moins d'une minute sur un ordinateur standard, avec une probabilité de réussite de 1 %. L'attaquant n'a plus qu'à collecter une centaine de messages issus d'un même utilisateur pour obtenir ses secrets d'authentification, comme le cookie de session de son webmail.
5. Enseignements tirés/à tirer
5.1 Une évolution non linéaire des découvertes
En cryptographie comme ailleurs en sécurité, les attaques ne font que s'améliorer. Les exemples précédents l'ont montré, la technique de l'autruche n'est pas une bonne stratégie en sécurité à long ni même à moyen terme. Cependant, il est très difficile d'estimer quand une attaque considérée comme théorique sera exploitée sur un cas concret.
Au-delà des exemples précédents, on peut citer le cas de MD5, dont les premières collisions pratiques ont été démontrées en 2005. Cependant, comme les chercheurs ne savaient pas à l'époque choisir les messages menant à la collision, le problème a été considéré comme théorique... jusqu'en 2009 où la première attaque mettant en jeu une collision sur des certificats a été présentée [19]. Ce fut alors la course pour interdire MD5 dans les nouveaux certificats.
Le lecteur attentif remarquera que le même scénario est en train de se jouer avec SHA-1, dont la première collision pratique semble à portée de main. Bien que certaines mesures aient été prises, SHA-1 est encore très utilisé dans de nombreux contextes ; par exemple, le seul algorithme obligatoire dans DNSSEC est RSA/SHA-1, et le format OpenPGP repose exclusivement sur SHA-1 pour la protection en intégrité. Pour éviter un nouveau fiasco, devra-t-on attendre une attaque concrète sur SHA-1 pour voir disparaître cette fonction de hachage ?
Le plus dangereux, c'est que les chercheurs en cryptologie se désintéressent parfois de certains sujets, une fois qu'ils considèrent une primitive ou une construction comme cassée au niveau théorique. En 2013, lorsque deux équipes de recherche ont montré que l'utilisation de RC4 pouvait mener à des attaques sur TLS ou WPA, de nombreux chercheurs ont été surpris de voir que cet algorithme, pourtant cassé depuis une décennie, était encore très utilisé en pratique !
Il serait difficile de les blâmer, car la décennie a été employée à proposer de nouveaux algorithmes et constructions. À la manière d'un éditeur ne maintenant que la dernière version de son logiciel, la communauté cryptographique ne peut garantir des propriétés de sécurité que sur les primitives actuelles. Il semble donc utile de prêter l'oreille à cette communauté lorsqu'elle annonce qu'un algorithme est cassé.
5.2 Une redécouverte permanente
On peut attendre trois propriétés d'une application mettant en œuvre de la cryptographie :
- la sécurité vis-à-vis des attaques cryptographiques connues ;
- la compatibilité avec l'écosystème existant, parfois vieillissant ;
- la modularité, au sens réutilisabilité et maintenabilité, du code.
Certaines des attaques présentées précédemment ont été découvertes et corrigées, puis redécouvertes et recorrigées plusieurs fois, soit dans la même implémentation, soit dans une nouvelle implémentation. Dans de nombreux cas, la raison était que pour corriger un problème, il fallait remettre en cause une de ces trois propriétés. Avec un peu de recul, il semble qu'un développeur soit en pratique obligé d'en choisir deux parmi les trois :
- modularité et compatibilité reviennent à utiliser les primitives standards sans contre-mesure, au détriment de la sécurité ;
- sécurité et compatibilité consistent à réécrire des morceaux entiers du code cryptographique pour ajouter des contre-mesures complexes, au prix de la modularité (et donc de la maintenabilité et in fine de la sécurité en fait) ;
- sécurité et modularité s'obtiennent en faisant évoluer le standard, quitte à ne plus être compatible avec les vieux algorithmes et modes. C'est la seule solution viable dans la durée.
En conclusion, la cryptographie est importante en sécurité, et les non spécialistes du domaine considèrent généralement qu'il s'agit de la partie la plus sûre de l'édifice. Cette vision est généralement vraie, si on s'assure que les algorithmes et constructions obsolètes sont retirées au fur et à mesure. En particulier, le code vulnérable le moins dangereux est celui qu'on ne compile même pas : DROWN n'a pas affecté les installations à jour où SSLv2 avait été retiré purement et simplement. Cependant, il faut avoir conscience que ce retrait aura des conséquences en termes de compatibilité, qui devront être prises en compte dans le cycle de vie des produits et des services.
Remerciements
Je tiens à remercier Florian, Guillaume, Jean-Yves, Pascal, Benjamin et Jean-René pour leurs relectures constructives.
Références
[1] H. Krawczyk, The Order of Encryption and Authentication for Protecting Communications (or: How Secure Is SSL?), CRYPTO 2001
[2] Serge Vaudenay, Security Flaws Induced by CBC Padding - Applications to SSL, IPSEC, WTLS, Eurocrypt 2002
[3] T. Jager et J. Somorovsky, How to break XML Encryption, ACM CCS 2011
[4] F. Maury, J.-R. Reinhard, O. Levillain et H. Gilbert, Format Oracles on OpenPGP, CT-RSA 2015
[5] http://www.openssl.org/~bodo/tls-cbc.txt
[6] N. AlFardan et K. Paterson, Lucky 13: Breaking the TLS and DTLS Record Protocols, IEEE SSP 2013
[7] https://www.imperialviolet.org/2013/02/04/luckythirteen.html
[8] M. Albrecht et K. Paterson, Lucky Microseconds: A Timing Attack on Amazon's s2n Implementation of TLS, ePrint 2015
[9] T. Duong et J. Rizzo, Here Come The XOR Ninjas, Ekoparty 2011
[10] http://www.cs.ucdavis.edu/~rogaway/papers/draft-rogaway-ipsec-comments-00.txt
[11] https://www.openssl.org/~bodo/ssl-poodle.pdf
[12] D. Bleichenbacher, Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1, CRYPTO 1998
[14] https://twitter.com/OpenSSLFact/status/253060773218222081
[15] C. Meyer et al., Revisiting SSL/TLS Implementations: New Bleichenbacher Side Channels and Attacks, Usenix Security 2014
[18] https://weakdh.org
[19] Stevens et al., Short Chosen-Prefix Collisions for MD5 and the Creation of a Rogue CA Certificate, CRYPTO 2009