Dans un premier article [1], nous avons rappelé les problèmes de privacy inhérents à l'exécution de fonctions ou de modèles de Machine Learning (ML) sur des serveurs distants, et avons introduit la nouvelle technologie appelée chiffrement homomorphe (Fully Homomorphic Encryption, FHE, en anglais) permettant de résoudre ces problèmes. Dans ce second article, nous allons une étape plus loin, et expliquons comment chacun d’entre nous, développeur ou data scientist, peut utiliser Python pour concevoir ses propres fonctions ou modèles en FHE et les déployer.
1. Chiffrement homomorphe
Un algorithme de chiffrement homomorphe, Fully Homomorphic Encryption (FHE) en anglais, est un système capable d’effectuer des opérations sur des données chiffrées en produisant le même résultat que si les opérations étaient réalisées en clair. Par exemple, une addition en FHE de deux valeurs chiffrées, une fois déchiffrée, donne exactement le même résultat que l’addition en clair de ces deux valeurs d’entrée.
Les chiffrements FHE sont une version plus ambitieuse et souvent plus utile que les chiffrements dits partiellement homomorphes, qui ne peuvent réaliser qu'un seul type d'opération sur les chiffrés : par exemple, le RSA [2] est partiellement homomorphe pour la multiplication (quand on multiplie un chiffré c1 = m1e par un autre chiffré c2 = m2e, on obtient (m1xm2)e, qui est bien un chiffré de m1 x m2) modulaire, et le cryptosystème de Paillier [3] est partiellement homomorphe pour l’addition.
Les chiffrements partiellement homomorphes sont connus depuis les années 80. Cependant, trouver un schéma complètement homomorphe pouvant effectuer n'importe quelle opération a été un très long chemin. Pendant près de 40 ans, les meilleurs chercheurs en cryptographie se sont intéressés au problème, sans y parvenir.
Cependant, un jeune doctorant américain appelé Craig Gentry, étudiant du professeur Dan Boneh à Stanford, pensa que construire le premier schéma homomorphe [4] serait un excellent moyen de faire une belle thèse (cela va sans dire !). Il proposa en 2009 le premier schéma de chiffrement complètement homomorphe, prouvant de cette façon leur existence. Sa première construction était extrêmement lente, mais la voie était toute tracée pour l'arrivée ultérieure de nouvelles générations de schémas plus efficaces tels que BGV [5] en 2011, BFV [6a, 6b] en 2012, CKKS [7] et TFHE [8] en 2016.
2. Construire un écosystème pour le FHE
Pendant longtemps, le FHE resta l'apanage d’une minorité : développer une application en FHE était long, difficile, et un doctorat en cryptographie était plus ou moins indispensable pour s'y essayer ! C’est pour cette raison qu’un certain nombre de startups ou de projets de recherche sont apparus pour démocratiser l’usage de cette technologie et permettre à tout un chacun de développer des applications FHE, sans avoir à comprendre ce qui se passe sous le capot ou à développer sa propre technologie. Ce qui nous rappelle l’adage : « don't roll your own crypto » (« ne déployez jamais votre propre cryptographie »), utilisez plutôt une librairie conçue par des experts en cryptographie si vous n'en êtes pas un vous-même.
Zama fait partie de ces entreprises : fondée en 2020 par deux Français, son CTO n’est autre que Pascal Paillier, inventeur du schéma partiellement homomorphe du même nom. Zama développe des librairies open source [9] utilisant le FHE.
Dans notre premier article [1], nous avions mentionné la librairie TFHE-rs [10] ; ici, nous allons nous intéresser à une autre suite de produits, appelée Concrete [11]. Cette suite s'adresse aux développeurs Python (alors que TFHE-rs était fait pour les développeurs Rust et pour les cryptographes). Concrete comprend un compilateur qui transforme des programmes écrits en Python en leur équivalent FHE. Le framework contient également Concrete ML, qui se spécialise dans les tâches de Machine Learning et de Deep Learning.
3. Installation
Pour l’instant, les versions supportées par Concrete sont Python 3.8, 3.9, 3.10 et 3.11. Python 3.12 sera très bientôt disponible. L’installation se fait comme ci-dessous, directement dans le Terminal. Il est recommandé, comme dans toute utilisation de Python, de créer un environnement virtuel et de l’activer :
Pour installer uniquement Concrete :
Pour installer Concrete et Concrete ML :
Les sources, ainsi que les exemples d’illustration peuvent être trouvés sur notre repository https://github.com/zama-ai/concrete.
4. Premières prises en main
Pour commencer, vous pouvez très simplement reprendre l’exemple du README : ouvrez un fichier appelé tutorial_misc.py, et écrivez le code suivant ou copiez-le depuis le repository :
Vous pouvez alors lancer :
et le programme s'exécutera :
Expliquons maintenant ce qui s’est passé dans ce tutoriel :
- Nous avons importé Concrete dans notre script Python ligne 1.
- Nous avons défini la fonction que nous voulons exécuter en FHE, lignes 3 à 4. Ici la fonction est une simple addition, mais rapidement dans ce tutoriel, nous coderons des fonctions.
- Nous avons créé un objet fhe.Compiler ligne 6, en déclarant que les deux arguments de la fonction add seront chiffrés.
- Nous avons alors compilé la fonction lignes 8 à 11, c'est-à-dire que nous l’avons transformée en son équivalent FHE.
Cela a l’air très simple pour l’utilisateur (et tant mieux), mais ce qui se passe à ce moment-là sous le capot de la librairie Python est plutôt complexe. Encore une fois, le but est d’abstraire la complexité à l’utilisateur, pour que celui-ci utilise la technologie sans avoir à se soucier de l'implémentation de la cryptographie.
Arrêtons-nous sur la notion d’inputset : l’inputset est un ensemble de valeurs d'entrées (donc ici, de couples (x, y)) typiques qui sont utilisées avec la fonction add. Le but de l’inputset est de permettre à la compilation de calibrer les données durant le calcul, c'est-à-dire de connaître l’intervalle (min, max) utilisé par chacune des valeurs intermédiaires. Ces intervalles sont importants pour transformer la fonction en son équivalent FHE, opération qui nécessite de connaître la précision (taille en bits) des entrées et des valeurs intermédiaires. Si on utilise une valeur d’entrée hors de cet intervalle dans la fonction compilée, on est dans un cas classique d’overflow et le résultat de sortie sera aléatoire. À noter que Concrete vérifie les types d’entrées et empêchera cet overflow.
Une fois la fonction compilée, nous avons effectué la génération de clé lignes 13 et 14.
Cette fonction génère les éléments publics (qui seront envoyés sur le serveur et qui serviront pour l'exécution de la fonction en FHE directement sur les chiffrés) et les éléments privés (qui resteront sur le client, et qui serviront au chiffrement des entrées et au déchiffrement des sorties). Notamment, la clé privée reste toujours du côté du client, ainsi le serveur ne peut jamais déchiffrer les valeurs, maintenant ainsi la confidentialité.
Pour l'exécution, nous avons ici choisi une valeur de (x, y) au hasard (lignes 16 à 21), ici (2, 6). Nous avons chiffré (du côté du client) cette paire. Nous avons alors exécuté le circuit FHE sur les chiffrés (encrypted_x, encrypted_y) côté serveur. Enfin, nous avons déchiffré le résultat, côté client, et vérifié que le résultat était bien celui attendu.
La fonction précédente était une fonction très simple, dans un but didactique. Mais le FHE permet d'évaluer la version chiffrée de n'importe quelle fonction, il est donc possible de compiler des choses bien plus complexes. Par exemple, la librairie Concrete ML [12] contient des implémentations de réseaux de neurones entiers !
Partons maintenant sur l’exemple complet de cet article.
5. Private Information Retrieval
Dans notre repository [11], nous proposons un certain nombre de tutoriels et d'exemples : https://github.com/zama-ai/concrete/tree/main/frontends/concrete-python/examples. Notez que Concrete ML propose également des exemples orientés Machine Learning : https://github.com/zama-ai/concrete-ml/tree/main/use_case_examples pour les plus simples, et https://github.com/zama-ai/concrete-ml/tree/main/docs/advanced_examples pour les plus évolués.
Nous allons étudier un de ces use-cases : celui du « Private Information Retrieval » (ou récupération confidentielle d'informations), qui est abrégé par PIR. Le principe du PIR est d'effectuer une requête sur une base de données sans révéler au serveur ni la requête, ni ce qui est retourné. Une solution triviale serait d'envoyer au client une copie complète de la base de données, mais ce n'est souvent pas envisageable pour des raisons de confidentialité ou d'efficacité.
Dans la suite, nous présentons un exemple d'implémentation de système de PIR en utilisant la librairie Concrete. Le cas d'usage que nous proposons est celui d'une liste noire de numéros de téléphone « spams ». Lors d'un appel, le téléphone envoie une requête à la base de données, qui renvoie si oui ou non le numéro est connu pour des faits de spam ou de fraude. Cette base de données est stockée sur un serveur, et régulièrement mise à jour lors de chaque signalement des utilisateurs, ce qui explique qu’avoir une copie à jour en local sur chaque téléphone est impossible. Il est facile de comprendre l’enjeu de confidentialité : si tout ceci était fait en clair, le serveur connaîtrait tous les numéros appelants d’un utilisateur. Effectuer cette requête homomorphiquement permet la même opération, mais en préservant la vie privée des utilisateurs.
Concrètement, la base de données est représentée par une table, de taille N, contenant chaque numéro de téléphone possible et stockée en clair sur le serveur. Pour effectuer la recherche, nous représentons la requête i comme un one-hot-vector, c'est-à-dire un vecteur de taille N, contenant uniquement des 0 à l'exception du i-ème terme qui vaut 1.
Ci-dessous, nous donnons un exemple sur la plage des numéros commençant par 06 :
Index | 0 | 1 | 2 | ... | 99999998 | 99999999 |
Numéro | 06.00.00.00.00 | 06.00.00.00.01 | 06.00.00.00.02 |
| 06.99.99.99.98 | 06.99.99.99.99 |
Si on recherche le numéro 06.12.34.56.78, on construit un hot vector composé d’un seul 1 à l’index 12345678 comme suit :
Index | 0 | 1 | … | 12345678 | … | 99999999 |
One-Hot vector | 0 | 0 | 0 | 1 | 0 | 0 |
Ce vecteur est chiffré, et envoyé au serveur. Il suffit alors à ce dernier de calculer homomorphiquement le produit scalaire du vecteur chiffré avec la table. Le serveur renvoie ainsi un chiffré du i-ème élément sans avoir la moindre idée duquel il s'agit ! Une fois renvoyé au client et déchiffré par celui-ci, le téléphone peut savoir si le numéro est un spam, et le cas échéant ignorer l’appel.
Place au code ! Commençons par quelques imports :
Définissons la logique de one-hot-vector, un vecteur de size éléments, et de type entier de 8 bits :
À titre d'exemple, voici une simple implémentation en clair de la récupération d'un élément de la base de données en utilisant un one-hot-vector : il s'agit d'un simple produit scalaire.
Maintenant que la logique est claire, nous pouvons générer une mini base de données et compiler la version homomorphe :
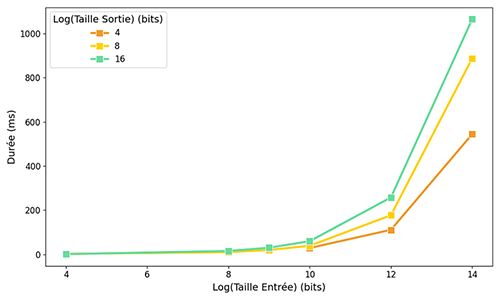
Intéressons-nous aux performances. Comme évoqué dans le premier article, la rapidité d'exécution de TFHE (le schéma homomorphe sur lequel Concrete repose) dépend de la taille des entrées de la table en bits, que nous notons log(N). De plus, le nombre d'éléments N dans la base de données a également son importance : une plus grande base nécessite un plus grand nombre d'opérations, donc le phénomène de croissance du bruit que nous avons introduit dans le précédent article est amplifié. Concrètement, cela signifie que nous avons besoin de paramètres cryptographiques plus grands pour continuer à produire des résultats corrects. Pour mieux visualiser ces phénomènes, nous avons fait tourner l'exemple pour différentes tailles d'entrées et de sortie et avons représenté les résultats sur la figure suivante. On peut voir que la requête devient de plus en plus lente lorsqu’on augmente ces deux tailles.
Afin d’améliorer les performances pour les grandes précisions, nous pouvons découper chaque entrée en k sous-tables, et manipuler k tables dont les sorties sont de taille p / k. Lorsqu'une requête est envoyée, le serveur calcule les k produits scalaires, renvoie les résultats au client, qui peut alors déchiffrer et concaténer les résultats en clair. Voilà comment le faire avec Concrete : dans ce cas, nous choisissons (arbitrairement) : N = 214, k = 4 et p = 32 bits ; cela génère donc des sous-tables de 32/4 = 8 bits. Pour référence, dans le code suivant les variables nommées database_length, number_of_subdatabase, database_output_bits correspondent respectivement à N, k et p.
La fonction de récupération est adaptée en conséquence. On calcule homomorphiquement les k produits scalaires (ils seront sommés plus tard côté client).
On génère une base de données aléatoires, de taille N, et on la décompose en k=4 sous-tables.
Il ne reste plus qu’à compiler en homomorphe.
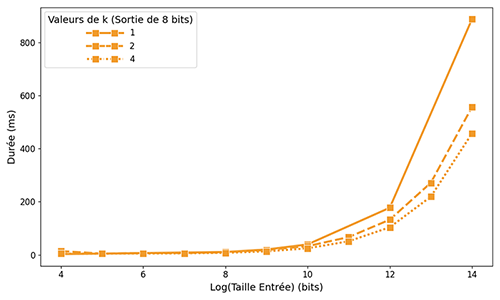
Nous mesurons la durée des requêtes pour différentes valeurs de k et compilons les résultats sur la figure suivante. Cela permet de mettre en évidence le gain de performances obtenu avec cette méthode pour une sortie de 8 bits et différentes valeurs de k : plus on utilise de sous-tables, plus la requête est rapide à taille d’entrée égale.
À présent, tout est prêt pour notre cas d'usage : la liste noire de numéros de téléphone ! Commençons par réfléchir au dimensionnement : la solution intuitive consiste à stocker, pour chacun des numéros de téléphone, un bit représentant si celui-ci est frauduleux ou non. En France, il y a 109 numéros possibles, ce qui correspond environ à 230 : comment utiliser notre algorithme pour savoir si un numéro est un spam ou non ?
La façon la plus simple serait d’avoir une table de taille N=230 contenant des éléments de 1 bit. Cette solution est un peu extrême, très lente, et il est possible d'être bien plus malin que ça.
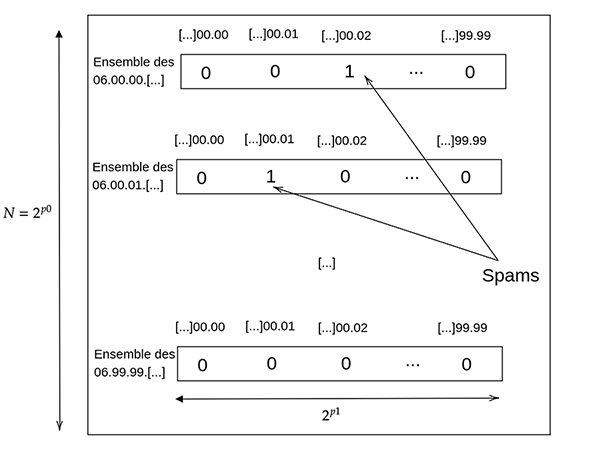
Au lieu d’avoir 230 entrées dans la table, essayons d’en avoir moins, et au lieu d’avoir seulement des sorties de 1 bit, essayons d’en avoir plus. Pour cela, représentons nos numéros de téléphone i comme i = i0 || i1, où || dénote la concaténation. Appelons p0 la taille en bit de i0 et p1 la taille en bit de i1. Nous devons alors avoir p0 + p1 = 30.
L'idée est d’utiliser une table de taille N = 2p0 entrées, et que chaque sortie de la table fasse 2p1 bits (un par numéro de téléphone). Ainsi, pour savoir si le numéro i est un spam, on effectue la requête qui retourne la i0-ième valeur de T (notée T[i0]) une valeur de 2p1 bits, et en prenant le i1-ième bit de cette valeur, nous saurons si le numéro est un spam. La figure 3 illustre cette construction.
Ce principe peut enfin se combiner avec l'idée des sous-tables : au lieu d’avoir une seule table qui retourne 2p1 bits, nous aurons k sous-tables qui retournent chacune 2p1 - log(k) bits.
Pour optimiser cela, nous pouvons alors chercher le triplet (p0, p1, k) qui est tel que :
- le temps d'exécution est minimal ;
- p0 + log2(k) * p1 >= 30.
Après une simple recherche exhaustive, nous pouvons récupérer la solution optimale : 1308 secondes en choisissant p0 = 28, p1 = 24 et k = 218, ce qui correspond à des entrées de 8 bits, avec 218 sous-tables dont les sorties ont 24 = 16 valeurs.
C'est encore un peu lent… Pour améliorer ça, nous pouvons imaginer laisser les 3 premiers chiffres du numéro de téléphone en clair, et chiffrer seulement les 6 derniers. Ainsi, seulement 20 bits deviennent nécessaires au lieu de 30 ! En relançant la fonction précédente, nous obtenons un optimum de seulement 2 secondes, ce qui est bien meilleur, surtout si nous voulons faire cette recherche en temps réel pour chaque appel.
6. Et si vous êtes curieux de savoir comment cela marche !
Notre exemple terminé, nous avons maintenant un programme capable de traiter des entrées chiffrées, mais nous avons utilisé la conversion en FHE en boîte noire. Intéressons-nous un peu plus à comment cette conversion s’est effectuée, sans entrer dans tous les détails.
La première étape de compilation est de transformer la fonction d’entrée en un graphe acyclique direct (ou DAG en anglais).
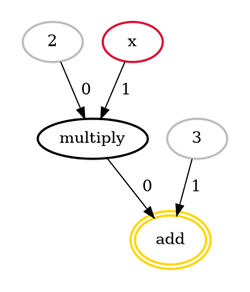
Prenons un exemple très simple :
Pour cette fonction, le compilateur générera le DAG présenté en Figure 4.
Cette représentation va nous aider à déduire le type des valeurs intermédiaires en fonction des valeurs d’entrées, passées via la variable inputset. Les opérations sont évaluées une à une pour chaque élément de l’inputset afin de trouver l’intervalle des valeurs intermédiaires et ainsi de déduire le type des variables.
Une fois cette opération terminée, la fonction est transformée dans une représentation intermédiaire (IR) qui nous servira d’entrée dans le processus de compilation proprement dit. Le compilateur Concrete étant basé sur LLVM [13], l’IR utilisé en entrée est MLIR [14], choisi pour sa facilité à manipuler des tenseurs et des opérations de haut niveau, ce qui correspond bien à nos cas d’usage (en particulier pour le Machine Learning).
Maintenant que nous avons une représentation intermédiaire uniforme, nous pouvons instrumenter la conversion en FHE. Une des premières étapes de cette transformation est de trouver les bons paramètres cryptographiques qui doivent être choisis selon trois critères :
- les tailles des variables manipulées (déterminées dans la première étape) ;
- la sécurité désirée (exprimée en bits et fixée au minimum à 128 bits) ;
- la probabilité d’erreur des calculs (cette notion liée au FHE est, dans le cas de Concrete, tellement faible que nous pouvons considérer les calculs comme toujours exacts).
Pour faire cette recherche de paramètres, Concrete s’appuie sur une librairie Rust, développée par Zama, nommée Concrete Optimizer. Elle optimise les paramètres cryptographiques en fonction des contraintes données plus haut pour produire les paramètres qui donneront les meilleures performances lors de l'exécution tout en garantissant la sécurité et l’exactitude.
La sécurité des paramètres est testée à l'intérieur de Concrete Optimizer grâce à un projet open source appelé lattice-estimator [15], qui tient compte de l’état de l’art des attaques sur « Learning with Errors » (LWE), la primitive de chiffrement utilisée dans le FHE.
Une fois les paramètres trouvés, en simplifiant, il ne reste plus qu’à traduire le DAG en une série d’opérations FHE paramétrées avec les sorties de Concrete Optimizer. Le binaire produit utilisera la librairie TFHE-rs pour les appels des opérateurs cryptographiques FHE.
À noter que pour avoir un aperçu du DAG et du MLIR généré par le compilateur, il est possible de les afficher en passant des options lors de la compilation.
Nous retrouvons au niveau du graphe le calcul des intervalles de valeurs des variables intermédiaires et leur typage, et dans la sortie MLIR, le code de l’ensemble de la fonction.
Nous avons ici grandement simplifié le processus de compilation : davantage d’explications sont données dans la documentation de Concrete. Et peut-être aborderons-nous cela dans un prochain article de MISC !
Conclusion
Dans cet article, nous avons expliqué l’usage de Concrete, pour que vous puissiez écrire vous-même vos programmes, directement en Python. Nous avons également détaillé un exemple complet, pour le « Private Information Retrieval ». Vous pouvez retrouver le code complet sur GitHub [16].
Il ne vous reste plus qu'à essayer vous-même de créer vos propres programmes !
Références
[1] « Introduction au chiffrement homomorphe », par Nicolas Bon, MISC n°132, mars 2024 :
https://connect.ed-diamond.com/misc/misc-132/introduction-au-chiffrement-homomorphe
[2] A Method for Obtaining Digital Signatures and Public-Key Cryptosystems, par Ronald L. Rivest, Adi Shamir et Leonard M. Adleman. Commun. ACM 21(2): 120-126 (1978)
[3] Public-Key Cryptosystems Based on Composite Degree Residuosity Classes, par Pascal Paillier. EUROCRYPT 1999
[4] Fully homomorphic encryption using ideal lattices, par Craig Gentry, STOC 2009
[5] (Leveled) fully homomorphic encryption without bootstrapping, par Zvika Brakerski, Craig Gentry, et Vinod Vaikuntanathan. ITCS 2012
[6a] Fully homomorphic encryption without modulus switching from classical GapSVP, par Zvika Brakerski.CRYPTO 2012
[6b] Somewhat practical fully homomorphic encryption, par Junfeng Fan et Frederik Vercauteren. Cryptology ePrint Archive, Report 2012/144
[7] Homomorphic encryption for arithmetic of approximate numbers, par Jung Hee Cheon, Andrey Kim, Miran Kim, et Yong Soo Song. ASIACRYPT 2017
[8] Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds, par Ilaria Chillotti, Nicolas Gama, Mariya Georgieva, et Malika Izabachene. ASIACRYPT 2016
[9] Zama GitHub repositories, https://github.com/zama-ai/
[10] TFHE-rs GitHub repository, https://github.com/zama-ai/tfhe-rs
[11] Concrete GitHub repository, https://github.com/zama-ai/concrete
[12] Concrete ML GitHub repository, https://github.com/zama-ai/concrete-ml
[13] The LLVM Compiler Infrastructure, https://llvm.org/
[14] Multi-Level IR Compiler Framework, https://mlir.llvm.org/
[15] Lattice estimator, https://github.com/malb/lattice-estimator
[16] Private information retrieval, notebook complet,
https://github.com/zama-ai/concrete/blob/main/frontends/concrete-python/examples/pir/PIR.ipynb



 Ajouter à une liste de lecture
Ajouter à une liste de lecture