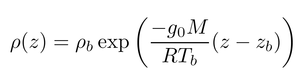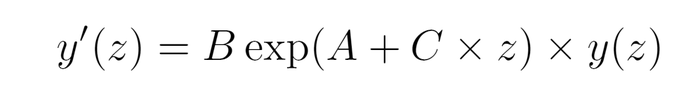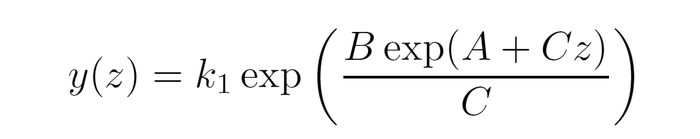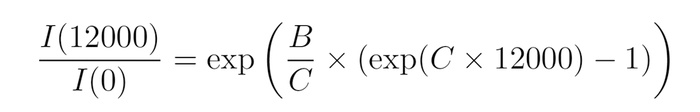Aspects expérimentaux et d’analyses de données.
1. Introduction
Les rayonnements ionisant – résultats de divers phénomènes grossièrement classés sous le nom de radioactivité – comprennent divers types de particules interagissant de diverses manières avec la matière et en particulier les corps biologiques. Depuis les rayonnements de nature électromagnétiques (ou photon dans leur dénomination corpusculaire) que sont les rayons gamma (issus de la désintégration d’un noyau atomique) ou X (issus de la relaxation d’un électron ou du rayonnement de freinage lorsqu’un électron voit sa trajectoire courbée), jusqu’aux particules chargées (protons, électrons ou noyaux atomiques, particules plus exotiques que sont les muons) ou neutres (neutrons), tous ces rayonnements contribuent à ioniser ou transformer la matière qu’ils rencontrent pour en affecter temporairement ou durablement les propriétés. La détection de ces divers rayonnements fait l’objet d’ouvrages complets [1] qui dépassent largement le cadre de cet exposé, et bien que la détection de neutrons reste encore une activité à la pointe de la recherche, la détection des rayonnements ionisants que sont les gammas et X est devenue, au travers du compteur Geiger-Mueller, une activité accessible à tout amateur désireux de s’intéresser à ce sujet.
Les sources radioactives sont relativement rares dans notre environnement, les poches de radon ou les minerais radioactifs restant des objets difficiles à identifier. Par ailleurs, notre planète est constamment bombardée de particules cosmiques, ainsi nommées car arrivant dans la haute atmosphère sans direction d’origine particulière autre que de venir de l’espace. Ces particules vont interagir avec l’atmosphère qui se comporte comme un écran en absorbant les composantes les moins énergétiques (qui fera l’objet du calcul d’absorption de la section 2.2), tandis que les particules les plus énergétiques se comportent comme source de gerbes de particules secondaires qui pourront pénétrer l’atmosphère. Nous allons voir que la loi d’absorption étant exponentiellement décroissante avec l’altitude, la quantité de rayonnements ionisants atteignant le sol est infime (sauf pour quelques expériences métrologiques qui nécessitent encore de se protéger des quelques rayonnements atteignant le sol en se cachant sous des montages [2] ou dans des mines souterraines [3]). Nous allons donc profiter de l’opportunité que sont les vols long-courrier, à une altitude de 11000 à 12000 m, pour étudier la distribution de ces rayonnements et en appréhender quelques caractéristiques.
Depuis quelques années, il est apparu qu’une classe professionnelle est particulièrement exposée aux rayonnements ionisants en altitude : le personnel naviguant des compagnies aériennes [4, 5]. Ce constat a induit un certain nombre d’études dont nous pourrons profiter pour analyser les données acquises par compteur Geiger au cours de voyages en avions. Par ailleurs, la dépendance de la mesure avec la latitude d’une part, mais surtout de l’altitude d’autre part, nécessite une mesure fine de ces deux grandeurs : un enregistreur de position GPS a déjà été décrit auparavant [6] et servira à positionner en trois dimensions chaque mesure d’un compteur Geiger. Nous compléterons cette étude expérimentale par quelques considérations bibliographiques, se supportant sur des informations librement disponibles sur internet, sur un phénomène associé bien que peu connu sous nos latitudes que sont les aurores boréales (et australes).
2. Rayonnements ionisants en altitude
La publication récente d’un ouvrage sur les débuts de l’exploration robotique de l’espace [7] nous rappelle que la mesure de rayonnements ionisants dans l’espace a été la première expérience scientifique résultant de la course à la conquête de l’espace. Les premières mesures par compteur Geiger ont permis d’identifier deux ceintures de fortes densités de particules ionisantes, plus tard baptisées par le nom de l’investigateur principal de ces expériences, Van Allen [8]. Soixante ans plus tard, les instruments mis en œuvre dans cet ouvrage ont atteint le grand public, qui n’exprime qu’un intérêt que très médiocre pour s’approprier les méthodes de mesures qui étaient appliquées aux débuts de la conquête spatiale. Heureusement, quelques esprits curieux s’efforcent de diffuser ces connaissances [9] : il a été démontré qu’il est possible de faire fructifier la perte de temps des transports en avion en profitant du vol pour mesurer l’absorption des rayonnements ionisants par l’atmosphère [10]. Nous nous inspirons de ces concepts pour développer quelques idées sur ces sujets dans les pages qui vont suivre.
2.1 Aspects expérimentaux
Un compteur Geiger est un instrument très simple [9] et donc robuste : une enceinte sous pression contrôlée, remplie majoritairement d’un gaz neutre, présente deux électrodes polarisées par une tension élevée. Une particule ionisante pénétrant cette enceinte induit une ionisation (perte d’un ou plusieurs électrons d’une molécule de gaz dans le compteur) et enclenche une réaction en chaîne dans laquelle des espèces chargées sont induites par accélération dans le champ électrique. Un choix judicieux de gaz tampons permet à la réaction de s’arrêter spontanément : l’utilisateur observe une impulsion de courant aux bornes des électrodes associée à cette circulation d’ions et d’électrons. Le compteur Geiger est l’aboutissement d’une idée de base fort simple [1, chap.5-6] consistant à considérer que les rayonnements ionisants produisent, en se propageant dans un gaz (par exemple l’air), des paires électrons-ions en éjectant par collision des électrons de la molécule ou atome qui les attirait. Si ce processus se produit dans un champ électrique, par exemple entre les plaques d’un condensateur, alors les ions et électrons sont attirés vers les pôles de polarité opposée et donnent naissance à un courant. Si la différence de potentiel entre les plaques du condensateur est faible, chaque famille de particule chemine vers l’électrode qui l’attire et le courant est proportionnel à la dose (chambre à ionisation). Si la différence de potentiel est augmentée, chaque paire ion-électron entraîne un nombre de particules proportionnel à son énergie initiale et un régime dit de “compteur proportionnel” est atteint dans lequel chaque impulsion de courant associée à la présence d’un quantum de rayonnement ionisant présente une amplitude liée à l’énergie de la particule incidente – ce mode de fonctionnement plus complexe dépasse le cadre de cette discussion. Finalement, en augmentant la différence de potentiel entre les plaques du condensateur, le régime d’avalanche est atteint dans lequel chaque particule ionisante donne naissance à une cascade de paires électrons-ions qui produisent un pic de courant facilement décelable mais dont l’amplitude n’a plus de lien avec l’énergie de la particule incidente : il s’agit du régime dans lequel fonctionne le compteur Geiger-Mueller. La seule conclusion notable de cette description est qu’un compteur Geiger ne permet pas de remonter à la nature du rayonnement ionisant (sauf à utiliser plusieurs compteurs encapsulés de façon à protéger certains capteurs de certains rayonnements) ni à l’énergie de la particule qui a induit une impulsion : un compteur Geiger fournit uniquement un décompte du nombre de particules ayant enclenché une gerbe de particules dans l’enceinte.
Un artéfact facilement observable en pratique lors de l’utilisation de compteurs Geiger et de détecteurs proportionnels, et qui a quelque peu perturbé les premières mesures spatiales [7], consiste en l’absence de recombinaison des ions du gaz du détecteur si le rayonnement incident devient trop intense. Dans ce cas, les impulsions de courant cessent pour être remplacées par un courant continu qui ne peut être détecté par le compteur habituellement utilisé après filtre passe-haut en sortie d’un tel instrument.
Figure 1 : Photographie du dispositif expérimental : un compteur Geiger-Mueller est alimenté par un port série, ici connecté à un adaptateur USB-série. Toute particule pénétrant le tube Geiger induit une gerbe de particules accélérées par une différence de potentiel suffisante pour atteindre le régime d’avalanche. Ce flux d’électrons est détecté comme une impulsion électrique qui génère une impulsion, comptée par l’ordinateur auquel est branché le compteur. Une fréquence trop élevée d’impulsions ne pourra être détectée et apparaîtra comme une absence de rayonnements, tel que observé dans les premières expériences de Van Allen. Noter l’évolution du débit de dose – d’un bruit de fond de 50 coups/minute à 1000 en présence de la montre aux aiguilles couvertes de radium – permettant de valider le bon fonctionnement du montage.
Pour une application visant à emporter un instrument de mesure dans un avion, l’apparence de l’objet est le point fondamental pour passer sereinement les contrôles de sécurité car il est préférable d’éviter d’avoir à ouvrir son sac à cause d’un montage suspect, à moins d’avoir une confiance extrême dans ses talents de pédagogue pour justifier l’intérêt de l’expérience et expliquer le fonctionnement dudit instrument au personnel de surveillance. Ainsi, nous abandonnerons l’idée de fabriquer nous même le compteur Geiger-Mueller mais opterons pour un dispositif réalisé par des développeurs expérimentés qui en particulier ont pris soin d’alimenter un instrument au moyen du port série uniquement, en optimisant la consommation électrique et en intégrant un élévateur de tension efficace et un circuit de mise en forme se contentant des ±12 V des signaux de contrôle du port série. Ainsi, un compteur Geiger est commercialement disponible pour environ 150 euros auprès de Aware Electronics1 sous la dénomination RM-60 (Fig. 1). La polarisation des électrodes est de nature capacitive, et bien que la différence de potentiel soit élevée, la consommation en courant est faible et grâce à l’excellente efficacité des convertisseurs DC-DC, une polarisation de plusieurs centaines de volts s’obtient depuis le port série (RS232) d’un PC en ne consommant que quelques milliampères. Dans l’expérience qui va nous concerner, nous alimentons le compteur Geiger au moyen du port USB d’un ordinateur personnel au cours du vol d’un avion de ligne afin de mesurer le débit de dose de rayonnement ionisant en fonction de l’altitude. L’inspiration de cette expérience vient du site web [10] qui reproduit, avec des moyens modernes, l’expérience historique de Hess (1912) qui a permis la découverte des rayonnements cosmiques lors d’un vol en ballon [11]. Par ailleurs, afin de mesurer l’altitude et la position (latitude/longitude) lors de l’acquisition des information du compteur Geiger, nous acquérerons simultanément la position GPS au moyen d’un enregistreur capable de mémoriser chaque seconde la position d’une antenne [6] placée devant le hublot de l’avion (les dimensions réduites des antennes patch fonctionnant au-dessus du GHz permettent de les cacher dans une manche sans se faire remarquer par le personnel naviguant). Avant de nous embarquer dans un vol en avion avec un compteur Geiger, nous vérifions au sol le bon fonctionnement du montage expérimental et du protocole de mesure : une montre de plongée Marc Nicol Skin Diver réalisée en 1967 avec des aiguilles fluorescentes excitées par une peinture chargée en radium permet de valider la mesure par le compteur Geiger. On notera la croissance du nombre de coups mesurés par minute – supposé représentatif du débit de dose – de l’ordre de 1000 cpm, ou à peu près le même ordre de grandeur que ce que nous observerons en vol. Cette mesure permet donc d’une part de valider le bon fonctionnement de l’installation, et d’intuiter le débit de dose ionisante subie en comparant avec un objet accessible dans la vie quotidienne.
2.2 Motivation historique – identification de la nature du rayonnement
Il est apparu en 1912 [12] au cours de mesures entre le sol et 8 km d’altitude que le débit de dose de rayonnements ionisants croît significativement avec l’altitude. Il a fallu plusieurs décennies additionnelles de recherches pour identifier la nature et l’énergie de ces particules, pour aujourd’hui conclure que des deux sources de rayonnements que sont le soleil et l’environnement galactique, la seconde source est prépondérante dans le cas qui nous intéressera [13]. Cependant, la contribution du flux de particules solaires et le champ magnétique associé sont déterminant dans nos observations car déterminent la quantité de particules galactiques susceptibles d’atteindre la Terre. Finalement, le couplage entre le champ magnétique terrestre – dipôle dont l’axe relie les pôles magnétiques en première approximation – et le champ magnétique solaire détermine la distribution en latitude du débit de doses de particules ionisantes.
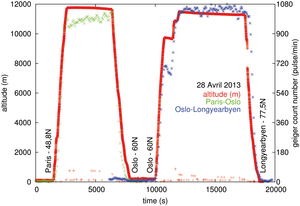
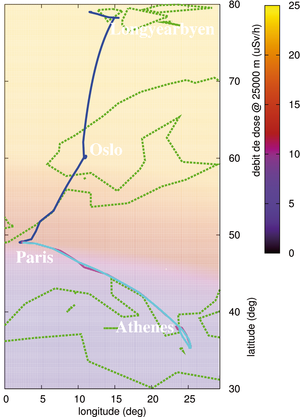
Figure 2: Mesure du nombre d’impulsions au cours d’un vol en avion entre Paris (48,8° N) et Oslo (60° N – vert) puis Longyearbyen (77,5° N – bleu), ainsi que l’altitude (rouge) enregistrée simultanément. Noter la décroissance lente de l’altitude (induisant une absorption croissante par l’atmosphère) alors que le débit de dose ne cesse de croître lorsque la latitude augmente, indiquant une augmentation du flux de particules cosmiques lorsque l’avion s’approche du pôle.
|
|
|
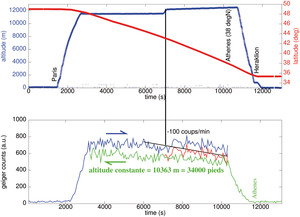
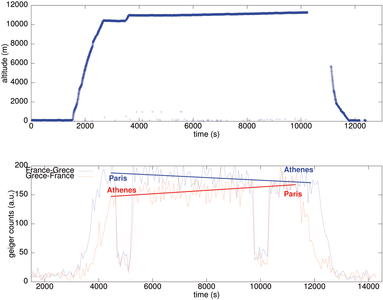
Figure 3: Mesure du nombre d’impulsions au cours d’un vol en avion entre Paris (48,8° N) et Heraklion (35.3° N – gauche, avec acquisition s’arrêtant au dessus de Athènes) puis un “saut de puce” entre Heraklion et Athènes (38° N – droite). En haut l’altitude du vol (bleu) aller – paramètre fondamental car déterminant la hauteur d’air absorbant les rayonnements – et la latitude (rouge) modulant l’intensité du rayonnement ionisant au travers du champ magnétique terrestre. En bas, la mesure par compteurs Geiger en coups/minute. En vert, la même mesure effectuée au cours du vol retour, i.e. en partant d’Athènes et à destination de Paris, vol à une altitude moindre et constante de 34000 pieds. Noter la variation d’altitude en cours de vol aller, que nous corrigeons sur la mesure du compteur Geiger par un décallage permettant de visuellement maintenir la tendance de la droite reliant comptage et latitude (bas, rouge). La droite noire sur la courbe du bas est un guide pour l’œil permettant de constater la continuité de la tendance, la droite vertical indique le changement d’altitude de l’avion. Droite : le vol en basse altitude (7000 m) démontre que le compteur Geiger ne détecte pas de variation notable de débit de dose de rayonnement ionisant sous 4000 m.
L’expérience dont les résultats sont présentés en Figs. 2 et 3 a consisté à embarquer, au cours de divers vols en avion, un compteur Geiger-Mueller et un récepteur GPS pour établir la dépendance du débit de dose de rayonnement ionisant en fonction de l’altitude et de la latitude. La dépendance avec l’altitude est évidente avec les courbes vertes et bleues (nombre de coups par minute du compteur Geiger) présentant une évolution proche de celle de l’altitude (courbe rouge) au cours du décollage et de l’atterrissage (Fig. 2), bien que le niveau de bruit du compteur Geiger empêche toute mesure à une altitude inférieure à environ 4000 m (Fig. 3, droite2). Cette relation entre nombre de coups et altitude est en accord avec la littérature puisque le débit de dose est connu pour croître au cours des 20000 premiers mètres au dessus du sol [14]. Plus subtile, la dépendance avec la latitude, observée au cours des paliers du vol à altitude constante, est clairement visible comme un croissance lente du débit de dose alors que nous nous éloignons de l’équateur, en accord avec un modèle que nous décrirons plus loin (section 2.4). La décroissance du débit de dose est particulièrement marquée lors du passage sous le parallèle de 45oN (Fig. 3, gauche), en accord avec les prévisions de ce modèle numérique.
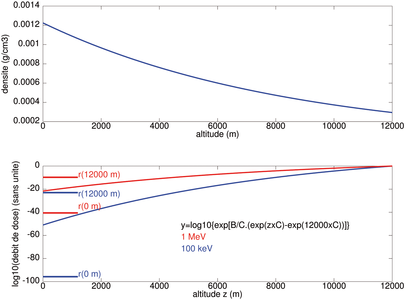
Figure 4: Évolution de la densité de l’air de l’atmosphère en fonction de l’altitude (excluant la contibution de la vapeur d’eau) et atténuation des rayonnements ionisants selon un modèle n’impliquant que l’absorption de photons. Les segments de droites horizontales sur le graphique du bas représentent le débit de dose observé au sol en supposant une densité r égale à celle au sol (droites du bas) ou à 12000 m (droites du haut) dans le cas de photons d’énergie 1 MeV (rouge) ou 100 keV (bleu).
L’atténuation de la dose de rayonnements ionisants est classiquement considérée comme étant déterminée par un taux d’absorption µ par unité de densité ρ du milieu dans lequel se propage le rayonnement, avec pour constat que µ ne dépend que de l’énergie de la particule. Cette considération est valable uniquement en l’absence de conversion de nature du rayonnement (désintégration ou gerbe de particules secondaires lors de l’interaction d’un particule incidente avec une particule de l’atmosphère). Nous considérons donc uniquement le rayonnement susceptible d’atteindre un avion en vol sans nous préoccuper de son origine (solaire ou galactique – nous verrons que seule la seconde source est compatible avec les énergie déduites du calcul – et primaire ou secondaire). L’intensité I du rayonnement varie par unité de longueur de propagation dL comme dI/I=−µ×ρ× dz. Cette équation classique, rappelant la loi de Beer-Lambert en optique, de l’absorption des rayons X ou γ se résout habituellement – pour une interaction locale – en considérant µ et ρ constants pour fournir une loi de décroissance exponentielle de l’intensité I en fonction de la distance parcourue z. La petite subtilité dans le cas de la propagation dans l’atmosphère tient en la variation de la densité de l’air avec l’altitude. Divers modèles d’atmosphère existent, et nous considérons ici une loi de la densité de l’air ρ(z) avec l’altitude z la plus simple en négligeant que la température évolue avec l’altitude :
nommée loi barométrique3 (Fig. 4, haut), où M=29 g/mol est la masse molaire de l’air, et g0=9,81 m.s−2 la constante de gravité au sol. Cette loi se déduit en supposant que l’atmosphère est formée par un gaz parfait fournissant une relation simple entre densité ρ, pression P et température T sous forme ρ=PM/RT avec R=8,314 J.mol−1.K−1 la constante des gaz parfaits et que le gradient de densité est dû à la pression de la colonne d’air, sans tenir compte ici du gradient altitudinal de température. L’atmosphère est segmentée en tranches pour adapter les paramètres libres que sont ρb la densité de l’air à la base de la tranche d’altitude zb de température Tb et ainsi analyser les divers cas de variation de température avec l’altitude. Nous n’allons pas dans ce calcul espérer établir la loi absolue d’absoption des rayonnements par l’ensemble de l’atmosphère mais simplement considérer le flux relatif entre le sol d’altitude zb=0 et l’altitude de vol d’un avion de l’ordre de 11000 à 12000 m (Fig. 2).
Dans ces conditions, nous obtenons une loi d’évolution de l’intensité des rayonnement ionisants de la forme
Sachant que la solution d’une équation de la forme
est de la forme
nous identifions la loi d’absorption en prenant C=−(g M)/(RTb), A=zb×g M/RTb=0 si zb=0 et B=−µ×ρb.
Le ratio de la dose entre le sol et l’altitude de vol est donné par la solution de cette équation différentielle considérée entre 0 et 12000 m. L’application numérique nécessite de connaître ρb(z=0)=101325 Pa, Tb(z=0)=288 K (ou 15 °C). Le terme B s’obtient directement depuis les valeurs tabulées par les laboratoires de métrologie, par exemple dans le cas des États-Unis selon les mesures effectuées par le NIST, http://physics.nist.gov/PhysRefData/XrayMassCoef/ComTab/air.html fournit les coefficients d’absorption des rayonnements ionisants électromagnétiques (gamma ou X) en fonction de l’énergie4. Le terme C ne dépend que de la couche basse de la tranche d’atmosphère considérée : C=−9,81× 29× 10−3/8,314/288=−1,19× 10−4 m−1 puisque les J qui apparaissent au dénominateur s’expriment en unité de base comme des kg.m2.s−2.
Le ratio entre la dose à 12000 m et le sol serait de l’ordre de
qui vaut 1051 (Fig. 4) en considèrant le coefficient d’aborption issu des valeurs tabulées B=0,15 cm2/g× 1,225× 10−3 g/cm3=1,84· 10−2 m−1 à 100 keV (courbes bleues en bas de la Fig. 4). Même à 1 MeV où µ=6,358· 10−2, I(12000)/I(0)≃ 1022 (courbes rouges en bas de la Fig. 4). Ces facteurs sont plusieurs ordres de grandeurs en désaccord avec les observations de la Fig. 2 : donc nous sommes à peu près certains qu’un modèle simpliste de Terre baignée dans un flux de photons ionisants (X ou gamma) n’est pas approprié pour décrire nos observations d’un ratio de l’ordre du % entre la dose observée à une altitude de 12000 m et le sol.
La littérature nous informe en effet de processus bien plus complexes avec une particule très énergétique incidente qui induit des gerbes de particules secondaires5 qui irradient l’avion en vol. En particulier, notre analyse grossière ne tient pas compte de toutes les autres particules mises en jeu dans les interactions (et en particulier les neutrons, complexes à détecter par leur absence de charge, qui font l’objet de recherches actuellement). Ces considérations vont nous amener à diverses réflexions quant à la contribution de l’activité solaire sur le flux de particules ionisantes arrivant aux altitudes de vol (section 2.4) et sur la variabilité avec la latitude de ce flux (le champ magnétique terrestre amène les particules chargées en direction des pôles et tend donc à augmenter la probabilité d’interaction avec l’atmosphère pour produire une gerbe de particules secondaires aux hautes latitudes).
On notera par ailleurs, dans le cadre d’une analyse quantitative des données acquises au moyen du compteur Geiger emporté en cabine, que l’intégrale sur le temps d’un vol du débit de dose (en coups/minute) devient une dose en tenant compte du facteur de calibrage proposé pour le compteur RM-60 qui nous concerne, à savoir coups/minute×1000/1050 devient des µR/h. Au cours d’un vol Paris-Oslo, nous constatons que la somme des mesures donne, pour les vols aller et retour respectivement, 74/60 à 80/60=1,2-1,3 mR=12-13 µSv. Cette valeur se compare avantageusement à celle prédite par un logiciel développé dans le cadre d’un projet européen visant à estimer la dose ionisante à laquelle le personnel naviguant est exposé au cours d’un vol – EPCARD dont le site web hébergé par l’université de Munich se trouve à http://www.helmholtz-muenchen.de/en/epcard-portal. EPCARD prédit qu’un vol à 11000 m d’altitude pendant 80 min encadré de 10 minutes d’ascencion et de descente engendre une dose de rayonnement ionisant de 17 µSv. Cet accord, avec une barre d’erreur de 50% certes, pour du matériel aussi simple et grossier et ne tenant compte que des interactions avec les photons, est surprenant mais satisfaisant. Cette analyse est issue de quelques conversions d’unités selon des modèles réducteurs mais nécessaires affirmant qu’un sievert est défini comme un dépôt d’énergie de 1 J/kg quelque soit la nature de la cible, que la conversion en gray (Gy) se fait à l’identique dans le cas particulier des photons (gamma et X), et que la relation entre Rötgen (R) et Gy suit 1 R=10 mGy.
L’absorption de rayonnements X et gamma par la matière selon une loi exponentiellement dépendante de la densité et de l’épaisseur de la couche absorbante est en pratique utilisée dans diverses applications. On notera par exemple le développement de mesures d’épaisseur et de densité de neige par EDF [15] (intéressé par le réservoir d’eau constitué par les précipitations neigeuses, le produit densité × épaisseur est la grandeur pertinente) et d’autres [16, 17], la caractérisation de couches minces déposées en applications microélectroniques [18] et de façon générale lors des processus de dépôt en salle blanche, voir même des applications aussi exotiques que la variation de densité de l’air [19], la présence de chambres dans les pyramides [20], ou la présence de magma sous un volcan [21].
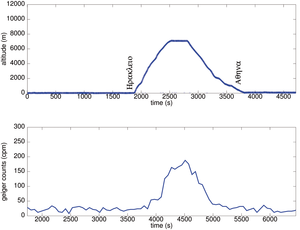
2.3 Tous les convertisseurs USB-RS232 ne sont pas égaux devant le compteur Geiger
Les ports série qui servent d’interface aux compteurs Geiger RM-60 n’équipent malheureusement plus les ordinateurs portables actuels, et un adaptateur USB-série est nécessaire. Nos première investigations de détection de rayonnements ionisants en vol se sont fait sur des trajets entre la France et la Grèce (Fig. 5) : la mesure qualitative était conforme à nos attentes, mais un artéfact observé sur diverses mesures ont suscité un doute quant à la qualité des informations collectées. En effet, alors qu’aucune activité ne modifiait le fonctionnement de l’ordinateur placé dans un sac en cabine pendant le vol, nous observons une chute du signal après un certain temps d’activité avant de reprendre un rythme de mesure normal. Il est par ailleurs apparu à l’analyse des données que le décompte des interruptions engendrées sur le port série est erroné et sous estime la dose reçue par le compteur. On prendra donc soin de tester divers convertisseurs USB-série avant d’espérer exploiter quantitativement les mesures selon un tel montage. Noter néanmoins sur la Fig. 5 la baisse de la dose en fin de trajet Paris-Athènes (bleu) alors que l’altitude ne cesse d’augmenter, en cohérence avec la baisse de latitude et donc un effet protecteur du champ magnétique terrestre accru. Afin d’appréhender la dose reçue au cours d’un tel trajet, on notera que le débit de dose en cours de vol (de l’ordre de 1000 coups/minute) est à peu près égal à la mesure obtenue sur une montre dont les aiguilles sont couvertes de radium et d’un matériau fluorescent pour être visible dans la nuit (Fig. 1).
Figure 5: Mesures de dose de rayonnement ionisant au cours de trajets Paris-Athènes : noter la chute systématique de signal 5000 et 10000 secondes après démarrage de l’expérience, sans qu’aucune manipulation sur l’ordinateur ne puisse en être la cause. Noter que la courbe bleue (bas) commence à Paris et finit à Athènes (débit de dose décroissant), tandis que la courbe rouge commence à Athènes et finit à Paris (débit de dose croissant).
2.4 Exploitation des modèles publiés sur le web
L’amateur ne peut que s’approprier des techniques de mesures et la physique associée à un phénomène aussi exotique que la présence de rayonnements ionisants en haute altitude lors d’expériences ponctuelles, et ne peut espérer contribuer significativement face aux projets nationaux ou européens qui traitent de ce sujet. Néanmoins, nous pouvons étendre notre connaissance en profitant des ressources proposées dans le cadre de vastes campagnes de recherche, telles que le projet EPCARD déjà mentionné auparavant. Au-delà de la publicité pour leur logiciel, nous trouvons sur leur site web un formulaire fort intéressant à http://www.helmholtz-muenchen.de/epcard/eng_geoinput.php pour calculer le débit de dose à un point donné au-dessus de la surface de la Terre, et http://www.helmholtz-muenchen.de/epcard/eng_fluginput.php pour calculer la dose reçue au cours d’un trajet en avion. Nous allons nous intéresser à cette dernière fonction pour étudier – au travers du modèle proposé – l’évolution dans le temps, et en particulier en fonction du cycle solaire – de la dose de rayonnement atteignant un avion effectuant un trajet donné. Deux cas nous intéressent : un vol aux environs de l’équateur, où le champ magnétique emportant les particules chargée vers les pôles est le plus stable; et aux environs des pôles qui sont les régions les plus sensibles aux variations de champ magnétique autour de la Terre. Le passage de requêtes manuelles vers le formulaire du site web est cependant long et fastidieux, ne permettant pas une étude exhaustive de ces paramètres. Nous nous efforçons donc d’automatiser la génération des requêtes. Une étude du flux de données entre le navigateur et le serveur web indique deux types de transactions : une requête de type POST et un échange de cookies. Bien que nous ayons initialement cru que l’échange de données se faisait au travers des cookies, il n’en est rien, et ce second aspect peut être négligé pour ne se concentrer que sur la génération des transactions POST6. L’outil curl permet d’émettre de telles requêtes au moyen de l’option --data, tandis que le greffon httpfox de firefox fournit la trame échangée. Celle-ci s’interprète trivialement une fois affichée, puisqu’elle est de la forme
anzahlprofile=1&einheit=meter&vonkurz=LFPG&nachkurz=LYR+&landetime=&zwpunkte=&\
adresse=&profil=profilangeben&day=15&month=06&year=2013&flightnumber=XX001&von=PARIS%\
2C+FRANCE+++++++++++++++++&uptime=00%3A30&obentime=04%3A00&flughoehe0=10000&downtime=00%\
3A30&nach=LONGYEARBYEN%2C+NORWAY++++++++++&send=Send+request
Nous y voyons évidemment apparaître les aéroports de départ et d’arrivée ainsi que l’altitude de vol, mais surtout les arguments month et year attribués de variables contenant année et mois du calcul. Ces deux variables sont donc bouclées dans un script bash de la forme
for annee in {1974..2013} do
for month in {1..12}
do
echo -n $annee $month
curl -s --cookie-jar test --data \
"anzahlprofile=1&einheit=meter&vonkurz=LFPG&nachkurz=LYR+&landetime=&zwpunkte=&\
adresse=&profil=profilangeben&day=15&month=$month&year=$annee&flightnumber=XX001&\
von=PARIS%2C+FRANCE+++++++++++++++++&uptime=00%3A30&obentime=04%3A00&flughoehe0=10000&\
downtime=00%3A30&nach=LONGYEARBYEN%2C+NORWAY++++++++++&send=Send+request" \
http://www.helmholtz-muenchen.de/epcard/eng_flugoutput.php | grep Sv
sleep 1 # ne pas affoler l'administrateur du serveur
done
done
Le résultat, qui ne conserve que la dose en Sievert (Sv), est un fichier de trois colonnes contenant l’année, la date et la dose après avoir éliminé les balises HTML au moyen de son éditeur de texte favori. Finalement, un tel fichier se traite au moyen de gnuplot pour interpréter les deux premières colonnes comme un date au moyen de
set timefmt "%Y %m"
set xdata time pl 'monthly' u 1:3 t 'rayonnement ionisant' repl
'MONTHLYshort.txt' u 1:3 axis x1y2 t 'taches solaires' set ytics
nomirror set y2tics set xlabel 'temps (mois/an)' set y2label
'nombre de taches solaires (sans unite)' set ylabel 'dose de
rayonnement ionisant (uSv)'
avec le fichier de nombre de taches solaires observées avec une résolution mensuelle obtenu à ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUNSPOT_NUMBERS/INTERNATIONAL. On comparera avantageusement ces résultats avec ceux présentés p.8 de http://www.npl.co.uk/upload/pdf/20061026_nuc_taylor_1.pdf (transparents de G. Taylor pour une présentation intitulée Solar Particle Effects in Aircrew Dosimetry).
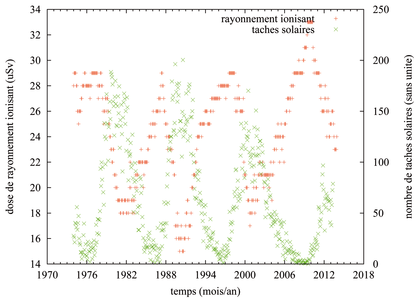
Le graphique résultant (Fig. 6) illustre superbement la relation entre activité solaire, indiquée par le nombre de taches solaires, et la dose de rayonnement ionisant atteignant un avion en vol. Étant donné que seules les particules du rayonnement cosmique galactique (et non solaire) contribuent aux gerbes de particules atteignant les avions, un regain d’activité solaire se traduit par un champ magnétique accru dans le système solaire et donc une capacité de déflection des particules incidentes accrues. Cette conclusion est parfaitement illustrée dans ce graphique, et confirme la faible contribution des rayonnements cosmiques d’origine solaire et donc trop peu énergétiques aux doses observées.
Figure 6: Évolution temporelle, avec une résolution mensuelle, de la dose de rayonnement ionisant reçue à une altitude de 10 km lors d’un trajet Paris-Longyearbyen.
De la même façon, nous pouvons afficher la distribution de dose atteignant un avion en fonction de sa position géographique (Fig. 7) en effectuant les requêtes au site http://www.helmholtz-muenchen.de/epcard/eng_geooutput.php en balayant les arguments de latitude et longitude :
for X in {0..179}
do
for Y in {0..89}
do
echo -n $X $Y
curl -s --data "day=23&month=6&year=2013&breitengrad=$Y&breitenmin=30&breite=NORD&\
laengengrad=$X&laengenmin=30&laenge=WEST&hoehe=10000&einheit=meter&adresse=" \
http://www.helmholtz-muenchen.de/epcard/eng_geooutput.php | grep Sv
sleep 1 # ne pas affoler l'administrateur du serveur
done
done
et cette procédure est réitérée avec les arguments OST à la place de WEST et SUED à la place de NORD pour couvrir tout le globe. Le fichier geo contenant trois colonnes avec longitude, latitude et dose, est épuré des commandes HTML puis nous allons cartographier son contenu sur un fond de carte représentant les continents. Ce script se modifie trivialement pour effectuer un balayage plus résolu que le degré d’angle en effectuant une boucle sur le dixième de degré et en passant par bc pour convertir avant la requête de l’url l’indice en fraction d’angle : for Xtmp in {0..450} ... X=`echo $Xtmp/10 | bc -l`... (Fig. 7, droite).
Dans le cas de la distribution géographique (world.dat fait partie des fichiers de démonstration fournis avec les distributions de gnuplot, 130517.txt étant un enregistrement des coordonnées GPS au cours d’un vol, épuré pour ne contenir que longitude et latitude en colonnes 1 et 2) :
splot "geo" using 1:2:3 with points pointtype 5 pointsize 1 palette linewidth 30, \
"world.dat" using 1:2:(0) with lines, '../130517.txt' u 1:2:0 w d
set key off
set view 0,0
repl
avec éventuellement l’option de modification d’aspect du graphique pour tenir compte des gammes différentes de latitude et longitude considérées par set size 1,2.5 pour une graphique 2,5 fois plus haut que large (Fig 7, droite).
|
|
|
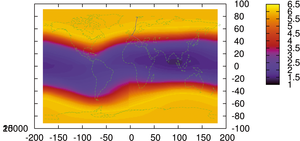
Figure 7: Distribution géographique du débit de dose de rayonnement ionisant à une altitude de 10 km (gauche) et zoom sur la région européenne sur laquelle nous avons expérimenté – ici débit de dose horaire calculé pour une altitude (choisie arbitrairement) de 25000 m. Graphique de gauche : en points bleus, le trajet suivi lors du vol Paris-Longyearbyen via Oslo dont la mesure est présentée en Fig. 2, et en magenta le vol Paris-Athènes présenté en Fig. 5.
3. Relation entre aurores boréales et activité solaire
Nous avons vu que le flux de particules atteignant la haute atmosphère est dépendant de l’activité solaire. Nous savons par ailleurs qu’un autre phénomène a été identifié comme généré par le flux de particules cosmiques – les aurores boréales. Le mécanisme selon lequel des particules entrant dans l’atmosphère après avoir été guidées par le champ magnétique terrestre forment les draperies lumineuses que sont les aurores boréales et australes dépassent les compétences de cet auteur. Par ailleurs, les aurores sont un phénomène particulièrement rares à nos latitudes qui méritent à peine de considérer de vouloir les observer tant elles sont peu fréquentes7. Cependant, le réseau global qu’est internet permet à des observateurs de partager les photographies de cet événement vers un lectorat moins chanceux que sont les observateurs européens. Nous allons profiter de ces bases de données en ligne que sont le partage de photographies numériques d’aurores pour inférer la relation avec le champ magnétique et le flux de particules solaires. Cette méthode de travail a été exposée pour divers domaines dans l’ouvrage [22].
L’origine des aurores est un problème bien plus complexe que l’image classique d’un flux de particules chargées venant de l’espace et dirigé vers les pôles par un champ magnétique modélisé par une structure dipolaire [23]. Pour la discussion qui nous concerne, nous nous contenterons d’accepter que la capacité du champ magnétique terrestre à orienter les trajectoires de particules chargées vers les pôles est le résultat d’une combinaison de propriétés intrinsèques du champ terrestre et son interaction avec le vent solaire et du flux de particules associé. Cette dépendance, en particulier lors de l’afflux important de particules lors d’évènements brefs que sont les éruptions solaires, permet de supposer une relation entre activité solaire et nombre d’aurores observables. Nous désirons analyser cette hypothèse en considérant la relation entre nombre de photographies numériques déposées sur les sites d’échanges de données et la densité de particules cosmiques détectées par les satellites météorologiques en orbite géostastionnaire de la NOAA. Ces données, avec une résolution temporelle horaire, sont disponibles sur http://www.swpc.noaa.gov/ftpdir/lists/ace2/.
|
|
|
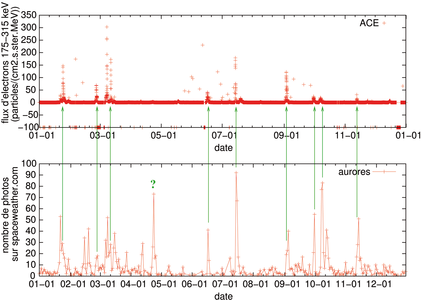
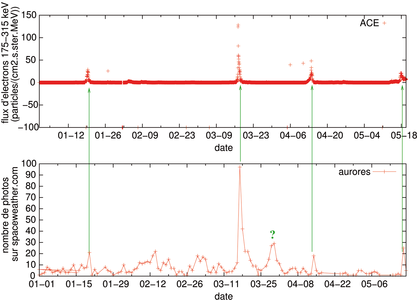
Figure 8: Comparaison du flux de particules observé par les instruments ACE à bord des satellites en orbite géostationnaires de la NOAA (haut) et du nombre de contributions de photographies d’aurores – principalement boréales – au site spaceweather.com. À gauche l’analyse pour l’année 2012 complète, à droite pour l’année 2013 en cours, avec dans ls deux cas les flèches vertes pour guider l’œil vers les évènements marquant, et les points d’interrogation pour les séries de prises de vues qui ne sont pas accompagnées d’un flux de particule significativement supérieur au niveau de base.
L’observation d’aurores est à peu près toujours impossible depuis nos latitudes, mais nous pouvons profiter de sites internet de partage de photographies de ce météore pour valider la corrélation entre la densité de particules dans l’espace entourant la Terre et l’occurence de ce phénomène. Sans prétention d’exactitude car entaché de divers artéfacts de mesure – période de l’année où la nuit, plus longue, favorise l’observation des aurore ou jour de la semaine propice aux sorties dans la nuit – la corrélation entre les deux mesures apparaît clairement (Fig. 8). Cette étude se contente d’analyser toutes les photographies soumises au site spaceweather.com, indépendamment de leur provenance géographique ou de la nature de la mesure, en fonction de la date et de compter le nombre d’occurences. Bien que les aurores apparaissent aussi de jour, le phénomène n’est pas visible à l’œil nu car moins intense et caché par l’illumination du Soleil [24]. Le script pour automatiser la récupération de la liste d’images soumises par les contributeurs à spaceweather.com et en extraire les dates de dépôt est simple : la commande se contente d’une requête (wget) des archives sur la thématique des aurores avec une liste commençant à partir d’un indice s (incrémenté par pas de 50 unités) que nous ferons croître pour couvrir l’intervalle de dates qui nous intéresse : spaceweather.com/gallery/index.php?&title=aurora&title2=lights&starting_point=$s Le résultat de ce décompte est ensuite traité
grep upload $s.dat | cut -d \> -f 7 | cut -d\ -f 1-2 | sed 's/\ /-/g' | grep "^[A-Z]" > $s.txt
pour fournir un nombre de photos par jour – sort resultat.txt | uniq -c, qui est la donnée que nous analysons en relation avec les mesures de ACE.
Le tracé pour près de deux années – 2012 et 2013 à la date de la rédaction de cette prose – illustre de façon visuelle la relation forte entre flux de particules cosmiques et occurence d’aurores boréales (les aurores australes étant peu présentes sur spaceweather.com). En particlier, des évènements intenses tels que mi-mars 2013 ou mi-juillet 2012 se retrouvent sur les deux graphiques, et toutes les séquences importantes de photographies (par exemple octobre 2012) sont associées à une augmentation du flux de particules. Le lecteur est encouragé à poursuivre cette étude sur une durée plus longue, par exemple allant jusqu’au dernier maximum d’activité solaire. Cette analyse est probablement extensible à d’autres bases de données de photographies numériques telles que Flickr, sous réserve que les auteurs aient convenablement identifié la nature de leurs prises de vues.
Conclusion
Les rayonnements ionisants sont un sujet peu connu du grand public et qui méritent d’être analysés expérimentalement pour en appréhender les effets de façon rationnelle. La capacité de reproduire, à un niveau amateur, des expériences qui ont donné lieu aux découvertes de ce phénomène il y a à peine 1 siècle est passionnante. Par ailleurs, la mise en commun d’une masse d’informations variées sur internet donne l’opportunité de tester des relations entre grandeurs dont la relation n’est pas évidente à priori, même en n’étant pas physiquement présent sur les sites d’observation. La seule limitation à cette activité de découverte tient donc en la curiosité du lecteur et le temps disponible pour traiter la masse d’informations disponibles.
Remerciements
Gregory Oestreicher (ass. Sequanux) a expliqué le principe des échanges de messages avec le site web EPCARD qui a permis d’automatiser l’obtention des résultats de calculs. Émile Carry (FEMTO-ST) et Simon Gascoin (CESBIO/CNES) ont amélioré une version préliminaire du manuscrit. Une présentation de V. Mares (Helmholtz Zentrum München) à Ny-Ålesund a inspiré le plan de cette présentation et nous a introduit à EPCARD. Les trajets entre la France et la Norvège ont été financés par le projet ANR CryoSensors, entre la France et la Grèce par le projet européen LoveFood.
Références
[1] G.F. Knoll, Radiation Detection and Measurement, Wiley (2010)
[2] C. Castagnoli, A. De Marco, A. Longhetto, P. Penengo, Measurements on the cosmic radiation intensity in the mont blanc tunnel, Il Nuovo Cimento Series 10, 35 (4), (1965), pp.969–976
[3] par exemple mines de Homestake au Dakota du Sud, de Sudbury au Canada, ou de Kamioka au Japon ; le laboratoire de San Grasso LNGS en Italie, ou plus proche l’ex-installation de missiles sur le plateur d’Albion (http://lsbb.oca.eu)
[4] B. J. Lewis, L. G. I. Bennett, A. R. Green, A. Butler, M. Desormeaux, F. Kitching, M. J. McCall, B. Ellaschuk & M. Pierre, Aircrew dosimetry using the Predictive Code for Aircrew Radiation Exposure (PCAIRE), Radiation Protection Dosimetry 116 (1-4), pp. 320-326, (2005)
[5] V. Mares; H. Yasuda, Aviation route doses calculated with EPCARD.Net and JISCARD EX, Radiation Measurements 45 (10), pp.1553–1556 (2010)
[6] J.-M Friedt, É. Carry, Acquisition et dissémination de trames GPS à des fins de cartographie libre, GNU/Linux Magazine France, Hors Série 27 (Octobre 2006)
[7] G.H. Ludwig, Opening Space Research: Dreams, Technology, and Scientific Discovery, American Geophysical Union (2011)
[8] J.A. Van Allen & C.E. McIlwain, Cosmic ray intensity at high altitudes (1956), disponible à www.dtic.mil/dtic/tr/fulltext/u2/091694.pdf
[9] D.Bodor, Construire un compteur Geiger-Müller soi-même c’est possible, Opensilicium 3 (2011). Diverses applications éducatives du compteur Geiger sont présentées à http://oldweb.ct.infn.it/~rivel/cosmic/Documents/Publications/List_Publications.html et en particulier F.Blanco, F.Fichera, P.La Rocca, F.Librizzi, O.Parasole & F.Riggi, Educational cosmic ray experiments with Geiger counters, Nuovo Cimento C29 (2006), pp.381-
[10] http://shaddack.twibright.com/projects/experiment_GeigerOnAPlane/
[11] J.R. Hörandel, Early Cosmic-Ray Work Published in German, Centenary Symposium: Discovery of Cosmic Rays (2012), à http://arxiv.org/abs/1212.0706
[12] P. Carlson, A century of cosmic rays, Physics Today 65 (2), Février 2012, p.30 disponible à http://www.physicstoday.org/resource/1/phtoad/v65/i2/p30_s1?bypassSSO=1
[13] P.K.F. Grieder, Cosmic Rays at Earth – Researcher’s Reference Manual and Data Book, Elsevier (2001)
[14] , G. Pfotzer, Dreifachkoinzidenzen der Ultrastrahlung aus vertikaler Richtung in der Stratosphäre – I, Messmethode und Ergebnisse, Physikalische Zeitschrschift 102 (23), pp.23–40 (1936)
[15] E. Paquet, M.-T. Laval, Experience feedback and future prospects for the use of EDF’s Cosmic-Ray Snow Gauges, Société Hydrologique Française (SHF), 2005, disponible à http://cr0.izmiran.ru/SLOW/DOC/SHF glacio-nivo 2005 _ENGLISH_.pdf et vulgarisé ‘a http://research.edf.com/research-and-the-scientific-community/research-activities/environment-and-renewable-energy/efficient-technology-44231.html
[16] R.M. Kogan, M.V. Niliforov & S.D. Fridman, V.P. Chirkov, A.F. Yakovlev, Determination of water equivalent of snow cover by the method of aerial gamma survey, Sov. Hydrol. Sel. Pap., (2), 183-187 (1965)
[17] M. Kodama, K. Nakai, S. Kawasaki, M. Wada, An application of cosmic-ray neutron measurements to the determination of the snow-water equivalent, Journal of Hydrology 41 (1-2), 1979
[18] A.M. Weinstein, C. D’Antonio, K. Mukherjee, Density of copper thin film measured by X-ray absorption, Nature 220, 777-778 (1968)
[19] R.N. Weltmann, S. Fairweather, D. Papke, Application of X-ray absorption to measurement of small air-density gradients, NACA (1951), disponible à www.dtic.mil/dtic/tr/fulltext/u2/a382390.pdf
[20] L.W. Alvarez, J.A. Anderson, F. El Bedwei, J. Burkhard, A. Fakhry, A. Girgis, A. Goneid, F. Hassan, D. Iverson, G. Lynch, Z. Miligy, A.H. Moussa, M.-Sharkawi, & L. Yazolino, Search for Hidden Chambers in the Pyramids, Science 167 (1970) pp.832–839
[21] C. Cârloganu , V. Niess, S. Béné, E. Busato, P. Dupieux, F. Fehr, P. Gay, D. Miallier, B. Vulpescu, P. Boivin, C. Combaret, P. Labazuy, I. Laktineh, J.-F. Lenat, L. Mirabito, & A. Portal, Towards a muon radiography of the Puy de Dome, Geosci. Instrum. Method. Data Syst. Discuss., 2, (2012), pp.76–780, disponible à www.geosci-instrum-method-data-syst-discuss.net/2/765/2012/, ou F. Fehr, Collaboration TOMUVOL, Density Imaging of Volcanos with Atmospheric Muons, 32nd International Cosmic Ray Conference (Beijing, 2011) à hal.archives-ouvertes.fr/docs/00/64/15/50/PDF/IcrcFehr.pdf, ou G. Saracino & C. Cârloganu, Looking at volcanoes with cosmic-ray muons, Physics Today p.60 (Dec. 2012)
[22] T. Segaran & J. Hammerbacher Ed., Beautiful Data, O’Reilly (2009)
[23] S.-I. Akasofu, The Northern Lights: Secrets of the Aurora Borealis, Alaska Northwest Books (2009)
[24] D.A. Lorentzen & A. Egeland, Dayside Aurora – the Fingerprint of the Polar Atmosphere, University Centre in Svalbard (UNIS) Publ.
2noter l’utilisation de la police Symbol du postscript en utilisant les caractères décrits à http://mathewpeet.org/lists/symbols/
3http://en.wikipedia.org/wiki/Barometric_formula
4Le LNE français effectue ces mesures au laboratoire Henri Becquerel LNE-LNHB du centre de Saclay du CEA – http://www.nucleide.org/ – mais ne semble pas diffuser ces informations sur le web ...
5Voir par exemple les informations proposées sur le site de l’observatoire Auger à www.auger.org/cosmic_rays/faq.html
6http://www.ietf.org/rfc/rfc1945.txt
7l’orientation du pôle magnétique au-dessus du nord Canada signifie que le cercle de parallèle 25-30° par rapport au pôle magnétique se situe dans des zones peu peuplées d’Europe du Nord – jusque vers 70-75°N géographique – alors que ce même parallèle magnétique descend en amérique du Nord jusqu’à environ 50-55°N pour atteindre des zones bien plus peuplées.