Nous complétons la mesure de distance des cibles RADAR par la mesure d’azimut rendue possible par la synthèse d’ouverture d’antenne, afin de localiser leur position et ainsi d’identifier précisément leur nature par superposition sur une photographie aérienne. La souplesse de la radio logicielle est illustrée par la montée en fréquence (2,4 GHz), sans modifier aucun élément matériel autre que les antennes.
Nous avons démontré notre capacité à réaliser un RADAR exploitant exclusivement des émetteurs et récepteurs de radio logicielle. Pour garantir la synchronisation du récepteur avec l’émetteur, nous acquérions sur une voie de référence du récepteur le signal émis, et sur la seconde voie (plateforme Ettus Research B210) le signal reçu par l’antenne réceptrice. Nous allons ici compléter la mesure de distance par une mesure d’azimut pour localiser la position de la cible. Ce faisant, nous allons aborder la synthèse d’ouverture d’antenne et le traitement du signal permettant de compléter la compression en distance par la compression en angle. Le résultat est une cartographie bidimensionnelle des cibles détectées qui sera superposée à une photographie aérienne du site, sans aucun degré d’ajustement pour faire correspondre les deux jeux de données. Nous explorerons par ailleurs l’utilisation, en complément de la source de bruit qu’est la PlutoSDR, d’un émetteur Wi-Fi comme source de signaux électromagnétiques illuminant la scène à observer. Des cibles à plus de 100 m sont ainsi détectées en émettant moins de 1 MW (0 dBm).
1. Introduction : l’antenne à synthèse d’ouverture
Nous avons établi que nous sommes capables de réaliser un RADAR présentant une résolution en distance de l’ordre du mètre en nous appuyant sur des plateformes de radio logicielle : Analog Devices PlutoSDR comme émetteur et Ettus Research B210 comme récepteur du signal de référence et du signal mesuré sur l’antenne réceptrice. Pour rappel, nous nous sommes proposés en cette période de confinement de réaliser un RADAR exclusivement avec le matériel à disposition, donc ces plateformes d’émission et de réception, antennes disponibles et divers passifs radiofréquences (coupleurs et atténuateurs).
Nous avons obtenu des informations sur la distance de réflecteurs et avons proposé une analyse, en nous appuyant sur une photographie aérienne de la région illuminée par l’émetteur radiofréquence. Nous avions, au cours de cette analyse, conclu que la fréquence de fonctionnement du RADAR n’a aucune importance, seule la bande passante du signal émis importe. En clair, si seule la distance R à la cible importe, alors seule la bande passante B du signal émis détermine la résolution en distance ΔR = c/(2B), sans que la fréquence centrale fc du signal n’intervienne. Technologiquement, il est plus facile d’augmenter B si fc est plus grande, et l’efficacité des antennes sera plus facile à maintenir surtout B si B ≪ fc, mais rien ne l’impose dans la physique du traitement du signal. Nous avions donc choisi une bande de 600 à 800 MHz, compromis entre la bande de fonctionnement des antennes de télévision numérique terrestre en notre possession, la bande de fonctionnement de la PlutoSDR et B210, et du coupleur que nous avions en notre possession.
Cependant, il serait intéressant de compléter la mesure de distance par une mesure d’azimut, c.-à-d. de direction d’arrivée du signal rétrodiffusé par un réflecteur. L’approche naïve pour atteindre ce résultat est de munir l’antenne réceptrice d’éléments directeurs, par exemple un réflecteur parabolique pour ne concentrer que les ondes arrivant dans l’axe de révolution du paraboloïde. Le problème de cette approche est son encombrement. En effet, l’ouverture angulaire (l’angle dans lequel la puissance rayonnée reste supérieure à la moitié de la puissance maximale) d’une antenne munie d’un réflecteur parabolique de diamètre D est ϑ3dB ∼(70λ)/D avec λ=300/fMHz la longueur d’onde du signal émis à fréquence f. Afin d’illustrer ce calcul, nombre de RADAR de technologie suffisamment ancienne pour ne pas avoir connu l’avènement de la synthèse électronique de faisceau d’antennes utilisaient une parabole pour diriger le faisceau électromagnétique vers la cible (p. ex. Crotale français, Hawk américain). Une rapide analyse d’une photographie d’un système Crotale équipant un véhicule finlandais (figure 1) documenté comme étant de 2,77 m de haut indique que la parabole fait environ 1 m de diamètre. Sachant (https://www.ausairpower.net/APA-PLA-IADS-Radars.html#mozTocId5336) que ce RADAR fonctionne entre 15 et 17 GHz, donc à une longueur d’onde de l’ordre de 1,8 cm, nous trouvons une ouverture angulaire de faisceau de 1,26°, proche des 1,2° annoncés sur https://www.army-technology.com/projects/crotale/. Cependant, le Crotale a été conçu dans les années 1950 et la source d’illumination (HPIR) du Hawk autour de la même époque : il ne s’agit donc plus de technologies à jour actuellement. Dans l’exemple des antennes UHF centrées sur 750 MHz (λ=40 cm) qui nous avait intéressées, une ouverture angulaire de 10° implique une parabole de 2,8 m de diamètre. Difficile à faire tenir sur un balcon, encore plus à orienter, et que se passera-t-il dès qu’il y aura un peu de vent ?
La solution évidente consiste donc à augmenter la fréquence centrale du signal émis fc pour réduire la longueur d’onde λ et donc le diamètre de l’antenne nécessaire. Dans la bande 2,45 GHz (où émettent Bluetooth, Wi-Fi et autres protocoles de communication numériques), la réduction de λ à 12,2 cm permet d’atteindre une taille de parabole raisonnable de 86 cm de diamètre à ouverture de faisceau constant, mais reste encore le problème de l’orienter pour balayer le secteur angulaire analysé. Cet argumentaire va justifier de quitter la bande 600–800 MHz pour nous intéresser à la bande Industrielle, Scientifique et Médicale (ISM) s’étendant de 2400 à 2480 MHz.
Par ailleurs, il est dommage de se contenter de 10° de résolution angulaire alors que le balcon sur lequel ces expériences sont menées fait 2,30 m de large et pourrait accommoder une antenne suffisamment grande pour atteindre une résolution angulaire meilleure que 4°.
Ainsi, au lieu d’utiliser une unique antenne de grand diamètre, une solution bien connue consiste à combiner une multitude de petites antennes. Chaque petite antenne présente une résolution angulaire médiocre, mais la combinaison des signaux, de par leur interférence constructive et destructive, peut accumuler l’énergie ne provenant que de la direction du réflecteur et ainsi améliorer la résolution angulaire pour atteindre celle d’une unique antenne du diamètre égal à la longueur de la base du réseau. Historiquement, cette combinaison de signaux se faisait avant la numérisation du signal, à grand renfort de déphaseurs analogiques entre émetteur et antenne ou antenne et récepteur. Alors que cette formation de faisceau s’effectuait par traitement analogique du signal, nous la mettrons en œuvre maintenant après numérisation du signal afin de garder le matériel au plus simple (et donc au plus souple).
Finalement, de même que nous avions établi que dans la relation entre la résolution en distance ΔR = c/(2B) et la bande passante de la mesure B, il n’était pas nécessaire de mesurer la totalité de la bande B d’un coup, mais que nous pouvions balayer les fréquences, il n’est pas nécessaire d’acquérir le signal de toutes les antennes en même temps. Nous pouvons nous contenter d’acquérir séquentiellement le signal pour chaque position d’antenne le long de l’ouverture équivalente. Une solution consiste à commuter les antennes au moyen d’un switch radiofréquence, mais qui se limite au nombre de voies des switchs : typiquement 8 voies (Hittite HMC321A avec lequel nous expérimentons, car alimenté en unipolaire TTL), avec au maximum 16 voies possibles à notre connaissance en version connectorisée. Une alternative consiste à déplacer l’antenne : il s’agit du principe du RADAR à synthèse d’ouverture, bien connu dans sa version aéroportée ou spatiale lorsque le vecteur de vol avance à vitesse constante et l’acquisition s’effectue périodiquement. Dans sa version au sol, nous déplacerons l’antenne réceptrice le long d’un rail : il s’agit du GB-SAR pour Ground-Based Synthetic Aperture RADAR [1].
La même analyse qu’auparavant, mais cette fois en remplaçant le diamètre de la parabole par le trajet parcouru par l’unique antenne avançant N fois par pas de d selon un chemin supposé rectiligne – aussi valable bien entendu pour un réseau de N antennes commutées équidistantes de d – indique que la résolution angulaire est ϑ3dB =(70λ)/(Nd) degrés (noter qu’on trouve dans diverses sources 0,89λ/(Nd) : dans ce cas, la résolution angulaire est exprimée en radians en prenant le cas théorique de 50° au lieu de 70° du cas du réflecteur idéal). Avec un balcon de 2,3 m de large et en travaillant à 2,45 GHz soit une longueur d’onde de 12,25 cm, nous pouvons espérer atteindre une ouverture angulaire de 3,6° ou une résolution azimutale de 3 m à une distance de 50 m, distance de la maison que nous cherchons à détecter.
Le SAR dans la fiction
Le RADAR à synthèse d’ouverture pour observer à travers les murs (Through-the-Wall RADAR –
TWR [2]) a été présenté récemment dans une série de télévision française. Alors que par ailleurs cette
même série s’était efforcée de sembler réaliste, la séquence du RADAR est affectée de nombreuses incohérences que nous pourrions passer sous silence si la scénographie en était améliorée. À une époque où la méconnaissance (ou la stupidité) de certains permet d’associer une émission radiofréquence (déploiement 5G) à une maladie propagée par virus, cette désinformation des séries semble plus nuisible que bénéfique.
Que nous montre l’épisode 5 de la saison 4 du Bureau des Légendes entre les dates 2160 s et 2230 s ? Un acteur balaie le long d’un mur une boîte qui ressemble à s’y méprendre à un TWR. Son mouvement le long du mur à vitesse constante est réaliste d’une mesure SAR. Malheureusement, une fois qu’il s’arrête de balayer en azimut la scène, les choses se gâtent. Alors que l’acteur a parcouru plusieurs mètres le long de l’azimut, sa boîte ne fait que quelques décimètres le long de l’élévation : même en contenant un réseau d’antennes verticales, la résolution doit être dégradée en ordonnée par rapport à l’abscisse. Une fois le balayage spatial arrêté, l’image continue à bouger. Ceci est erroné : seul un nouveau balayage permettrait de rafraîchir l’image (évidemment en terme cinématographique, voir un acteur faire des allers-retours le long d’un mur est moins attractif, mais c’est pourtant bien ce qui se passera dans la suite de ces pages). Enfin, la résolution des images n’est pas raisonnable. En supposant que les cibles sont à H = 2 m derrière le mur et que l’acteur a balayé L = 3 m, alors un doigt (tel que visible sur une image) supposé de R = 1 cm de large ferait un pixel si la longueur d’onde était λ ≤ R (L/H) = 1,5 cm soit une fréquence de fonctionnement de 20 GHz. Une telle fréquence est habituelle en RADAR, mais sera significativement absorbée par le diélectrique qu’est le mur, apparemment sans armature métallique d’après les images. Des fréquences de quelques GHz (dans notre cas 2,4 GHz pour rester dans la bande industrielle, scientifique et médicale) offrent un bon compromis entre pénétration et résolution décimétrique. La réalité des images acquises à travers un mur est en pratique moins explicite, telle que l’illustre par exemple l’image d’une pièce présentée en [3, Fig.5.9, p.166] extrait de [4].
Pour donner crédit à l’émission de fiction, pourquoi coller le RADAR au mur et ne pas rester à distance ? L’onde électromagnétique issue du RADAR rencontrerait dans ce cas une interface de plus – air-mur – à l’aller comme au retour avec une rupture d’impédance et donc un coefficient de réflexion significatifs (typiquement 3 à 4 dB pour chaque trajet pour un mur de permittivité relative de 5) qu’on évite en plaquant les antennes – convenablement adaptées en fréquence en tenant compte de la présence du diélectrique – contre le mur.
2. Périodicité spatiale de la mesure
Nous avons établi que nous allons synthétiser une antenne en déplaçant par pas discrets une unique antenne le long d’un rail d’une longueur D afin de traiter les signaux acquis pour simuler une antenne de largeur D. Comme dans tout système échantillonné par pas discrets, se pose la question du pas d’échantillonnage. Dans le domaine temporel, le problème est classique : Nyquist (puis Shannon) nous explique qu’il faut au moins deux points de mesure par la composante spectrale la plus élevée du signal, ou une fréquence d’échantillonnage au moins double de la fréquence la plus élevée dans le signal observé. Nous allons démontrer que la condition est la même spatialement, en remplaçant période par longueur d’onde.
Lors de la propagation d’une onde électromagnétique se(t) émise de fréquence centrale fc, deux termes déterminent la phase du signal reçu sr(t) :
![]()
Le premier terme jωt est la rotation de phase lorsque le signal de pulsation ω = 2πfc évolue au cours du temps t (en d’autres termes, la phase tourne de 2π chaque fois que le temps s’incrémente de 1/fc). Le second terme est la propagation du signal de vecteur d’onde k = 2π/λ qui est le pendant spatial du premier terme : chaque fois que le signal avance (r) de λ, la phase tourne de 2π. Le premier terme disparaît lors du mélange au niveau du récepteur qui ramène le signal de la bande radiofréquence centrée sur fc en bande de base centrée sur 0 Hz : en supposant que l’oscillateur de référence a tourné au même rythme ω pendant tout le temps de vol (c’est le problème du bruit de phase de l’oscillateur local qui détermine la fluctuation de ω au cours du temps), ωt est le même pour l’onde qui s’est propagée et l’oscillateur local et seul e(jkr) subsiste.
Supposons maintenant que l’antenne réceptrice se déplace de xp alors que l’émetteur reste en position fixe. Supposons que la cible se trouve en coordonnées cartésiennes en (x0, y0) tandis que l’antenne synthétique est obtenue en déplaçant un élément rayonnant unique par pas de xp selon l’abscisse à une ordonnée choisie arbitrairement comme nulle (référence). Dans ce formalisme, r = √(x02 + y02) avant déplacement de l’antenne, pour devenir après déplacement r = √((x02 - y02)2 + y02). Si la normale de la direction selon laquelle l’élément de l’antenne à ouverture synthétique présente un angle ϑ0 par rapport à la direction à la cible, alors le passage en coordonnées polaires qui indique que x0 = R0 sin ϑ0 et y0 = R0 cos ϑ0 nous permet d’établir que la variation de distance parcourue par le signal (aller-retour) lors du déplacement de l’antenne est :
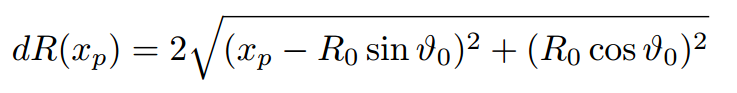
En supposant le déplacement de l’antenne xp petit devant la scène illuminée, nous pouvons transformer l’expression de dR par son développement en série de Taylor dR(xp) ≃ dR(0)+dR'(O)⋅xp autour de xp ≃ 0. La dérivée de la racine carrée n’est pas très sympathique, mais Wolfram Alpha nous rappelle que :
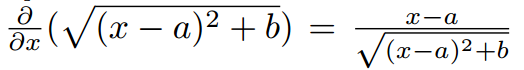
De sorte que :
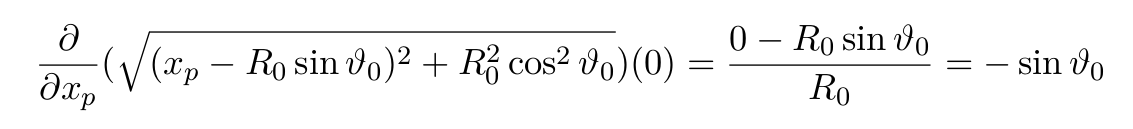
Puisqu’ici a2 + b2 = R02, et finalement dR(xp) ≃ 2(R0-xp sin ϑ0).
Le terme en R0, qui ne dépend pas de xp, est un biais de phase (terme constant) qui ne nous intéresse pas ici, et seul l’impact de l’incrément de xp nous intéresse : 2 x xp sin ϑ0 < λ et donc xp < λ/2 puisque |sin ϑ0 < λ| ≤ 1.
Nous avons donc retrouvé la condition d’échantillonnage de Nyquist-Shannon dans le cas spatial : il faut que le pas de déplacement de l’antenne soit inférieur à la demi-longueur d’onde centrale du signal émis. Noter que le même raisonnement en déplaçant le récepteur et l’émetteur (par exemple cas du RADAR monostatique) qui induit le double incrément du trajet (à l’aller et au retour) se serait conclu par xp < λ/4.
Afin de maximiser le rapport signal à bruit de la mesure, c’est ce dernier paramètre d’acquisition que nous utiliserons au cours de nos mesures.
3. Validation de la mesure en distance
Bien que nous ayons déjà démontré notre capacité à étaler le spectre en vue de maximiser B – dans la limite du débit de transmission d’USB – dans la bande UHD, notre décision de monter la fréquence de porteuse dicte de vérifier la cohérence de retard des échos avec les mesures antérieures. Par ailleurs, alors que nous avions choisi une approche de RADAR à bruit qui nécessitait un générateur dédié, nous proposons ici de tenter de remplacer la PlutoSDR en émission par un émetteur Wi-Fi. Ce sera l’occasion d’analyser et de justifier le mode de modulation de ce protocole omniprésent dans notre quotidien, et d’ouvrir la possibilité de coupler mesure RADAR avec communication numérique. Dans les deux cas, nous allons dans les paragraphes qui vont suivre valider la mesure en distance des réflecteurs avant de démontrer la compression en azimut, fournissant ainsi une démarche rationnelle pour déverminer un RADAR au cours de sa conception.
3.1 RADAR à bruit
Pour rappel de l’épisode précédent [5], l’étalement de spectre de la porteuse à fréquence fc s’obtient par modulation de phase avec une séquence aléatoire au rythme de B échantillons/seconde, occupant donc une bande passante de -B/2 à B/2 autour de fc. Ayant enregistré sur une voie radiofréquence de la B210 le signal émis, le signal reçu est corrélé avec le signal de référence pour trouver les retards représentatifs de la double-distance aux cibles. Comme l’oscillateur local des deux voies de réception de la B210 sont les mêmes, sa contribution au mélange s’élimine et le signal radiofréquence des deux voies est ramené de la même façon en bande de base pour transformée de Fourier de chaque voie, produit d’une transformée de Fourier avec le complexe conjugué de la seconde pour obtenir la transformée de Fourier de la corrélation. Si l’oscillateur local est décalé de δω de la fréquence nominale du signal reçu, le produit par le complexe conjugué élimine ce biais en fréquence, puisque exp(jδωt) x exp*(jδωt) = exp(jδωt) x exp(-jδωt) = 1. Ce faisant, nous notons que la corrélation est affectée du produit du module du signal émis et réfléchi. Cela ne pose pas de problème dans le cas d’un spectre uniforme tel que généré par du bruit, mais nous reviendrons ci-dessous sur cette hypothèse.
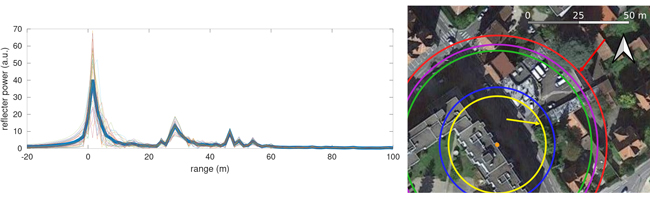
Nous ne reprenons pas ici tout l’argumentaire de [5] pour nous contenter de donner les résultats (figure 2) lors du balayage d’une bande de fréquences de 245050 MHz. Tracer les cercles de retard constant sur une photographie aérienne centrée sur l’emplacement du RADAR permet d’identifier l’écho à 50 m comme probablement réfléchi par la maison et en particulier son toit (flèche rouge) et l’écho à 25 m comme probablement associé aux parkings et les ruptures de pente dans le toit des box adjacents (flèche jaune). La mesure d’azimut doit permettre de lever ce doute.
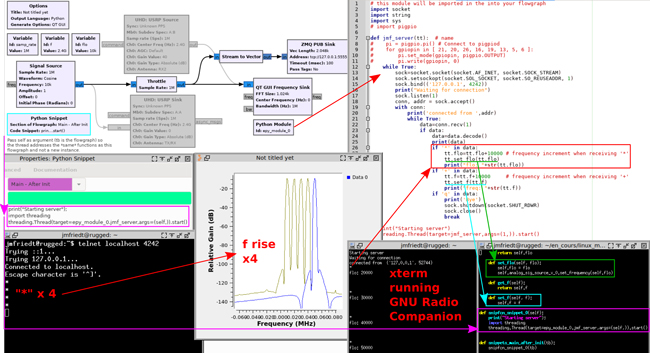
Nous avions insisté dans [5] sur l’intérêt de séparer les tâches et leur attribuer le langage le plus approprié : GNU Radio (Companion) pour l’acquisition de données en flux continu, Python pour commander les paramètres d’acquisition (fréquence de l’oscillateur local, ultérieurement position de l’antenne) et GNU/Octave – qui pourrait avantageusement être remplacé par numpy si les auteurs étaient aussi souples avec cette infrastructure qu’avec Matlab – pour le traitement du signal. Ce faisant, nous avions modifié le code Python généré par GNU Radio Companion, interdisant tout retour en arrière pour modifier graphiquement la chaîne de traitement : une fois le code Python modifié (pour l’ajout du serveur TCP notamment), nous ne pouvions plus ajouter autrement que manuellement des éléments à la chaîne de traitement. Cette approche est désormais révolue avec l’ajout de deux fonctionnalités dans GNU Radio Companion : les blocs Python Module et Python Snippet [6]. Le bloc Python Module permet de définir un code Python qui sera accessible depuis le bloc généré par GNU Radio Companion : de ce fait, intégrer le serveur TCP dans un tel bloc n’interdit pas d’ultérieurement modifier graphiquement la chaîne de traitement, le code Python étant toujours accessible. Cependant, le serveur TCP ainsi défini doit être instancié à un moment en lançant le thread qui attend la connexion sur la socket. C’est le rôle du Python Snippet qui insère un bout de code à l’emplacement voulu lors de l’initialisation de la chaîne de traitement – dans notre cas, juste après l’initialisation des structures de données et avant le lancement de l’ordonnanceur GNU Radio dans son Top Block. Fort de ces deux blocs, nous pouvons maintenant intégrer nos propres fonctionnalités programmées en ligne de commande dans un flux de traitement défini graphiquement. L’exemple que nous proposons ici consiste à changer la fréquence de l’oscillateur local, mais aussi si GNU Radio est exécuté sur Raspberry Pi, de faire appel aux GPIO pour par exemple commander un moteur qui déplace une antenne (figure 3).
Le seul point qui nous a posé problème dans ce développement est le passage des méthodes et variables locales de la classe appelante en vue de leur utilisation et modification dans le thread. Ce problème est résolu en passant comme argument à la création du thread la variable self. Cette variable est acceptée comme argument du serveur (ici, sous le nom de tt) et ainsi toutes les variables et méthodes de la classe appelante sont modifiables depuis le thread.
3.2 RADAR OFDM (Wi-Fi)
Wi-Fi, normalisé par le standard IEEE 802.11, est basé pour la bande 2,45 GHz qui nous intéresse sur une modulation exploitant une division du canal de communication en sous-porteuses orthogonales (OFDM pour Orthogonal Frequency-Division Multiplexing).
Le principe d’OFDM, qui divise une large bande spectrale en de petites sous-bandes, vient du constat que dans un milieu présentant des réflecteurs – typiquement un milieu urbain – certaines composantes spectrales sont annulées par interférence destructive entre le signal réfléchi et le signal direct entre l’émetteur et le récepteur [7, 8]. Plutôt que simplement perdre la liaison, OFDM partage le spectre en sous-bandes et étale l’information entre ces bandes. Compte tenu de la redondance et des codes correcteurs d’erreurs, la perte d’un canal de communication n’induit pas la perte de l’ensemble du message.
IEEE 802.11 a été implémenté dans GNU Radio par Bastian Bloessl sur https://github.com/bastibl/gr-ieee802-11. Le point le plus important pour nous dans son dépôt est le répertoire utils/packetspammer/ qui propose les outils pour passer un convertisseur USB-Wi-Fi en mode monitor qui accepte des commandes de bas niveau, comme émettre en continu des paquets sans respecter la norme d’échange d’informations de Wi-Fi. Tout comme dans la première approche, l’émission Wi-Fi est couplée (-10 dB) au travers de 20 dB d’atténuation vers la première voie, dite de référence, de la B210, tandis que la seconde voie acquiert le signal de l’antenne réceptrice. Le message transmis n’a aucune importance puisque seule la structure de la couche physique induit l’étalement spectral nécessaire. On prendra cependant soin à sélectionner un adaptateur USB-Wi-Fi supportant ce mode de fonctionnement : ce n’est pas le cas de tous les chipsets. Toutes les expériences ont été menées avec un adaptateur Wi-Fi Alfa AWUS036NEH capable d’émettre 20 dBm. Lorsque nous voulions émettre moins de puissance (pour éviter un signal de couplage direct excessif), nous avons inséré un atténuateur 20 dB en sortie d’émetteur Wi-Fi pour atteindre une puissance émise de 0 dBm.
L’utilisation de github.com/bastibl/gr-ieee802-11/tree/maint-3.8/utils/packetspammer est un compromis entre un taux de répétition le plus élevé possible avec des paquets les plus longs possibles, sans pour autant tenter d’envoyer une commande à l’interface Wi-Fi tant qu’elle est occupée. Nous avons utilisé packetspammer wlan0 -n 1000000 -r 400 -s 1350 sans avoir oublié au préalable de iwconfig wlan0 mode monitor, puis iwconfig wlan0 channel 3 pour sélectionner le canal sur lequel communiquer. C’est ainsi que depuis le script Octave, nous pourrons balayer les fréquences de porteuse en balayant les canaux par system(['/sbin/iwconfig wlan0 channel ',num2str(1+(frequence-1)*finc/5)]); qu’on adaptera évidemment au nom de son interface Wi-Fi. L’émission n’étant pas continue, on pourra ne conserver que les séquences pendant lesquelles la voie de référence a observé une émission de la carte Wi-Fi en testant le vecteur acquis depuis l’interface ZeroMQ et en bouclant, tant que le nombre requis de points pertinents n’a pas été obtenu :
Cette approche est aussi utilisée si la source non coopérative n’est pas contrôlée par l’utilisateur, mais profite d’émissions d’opportunité (cas du RADAR passif). Le principe consiste à définir un vecteur de valeurs consécutives en deçà desquelles nous considérons que l’émission a cessé (error_vector est une série de error_number valeurs à error_threshold fois le maximum de la séquence acquise), et à rechercher (findstr) cette condition dans le vecteur de données acquises sur la voie de référence tmpv2). Si aucun trou n’est observé, nous vérifions tout de même que l’émission n’a pas tout bonnement cessé (condition sur abs(tmpv2) supérieur à un seuil arbitraire de 0,05 en se rappelant que GNU Radio travaille entre -1 et +1, sinon affichage de « * » pour indiquer que l’émission Wi-Fi a cessé). En cas de coupure temporaire de l’émission, nous conservons tout de même la fraction pertinente, soit au début, soit à la fin, et concaténons ces mesures dans tmpmes jusqu’à atteindre le nombre de données nécessaires au calcul de corrélation qui suivra. À la fin, les matrices mes sont formées des séquences temporelles pour chaque canal fréquence.
Fort de cette analyse, l’émission est quasiment continue et particulièrement souhaitable pour une application RADAR, et en tous cas nous ne conservons que les points pendant lesquels l’émetteur a été actif. Il nous faut maintenant rechercher l’occurrence des réflexions des cibles dans le signal acquis sur la voie de mesure par corrélation avec le motif acquis sur la voie de référence. Cependant, Wi-Fi est une émission structurée pour transmettre une information numérique et non un bruit dont la corrélation est un unique pic de Dirac.
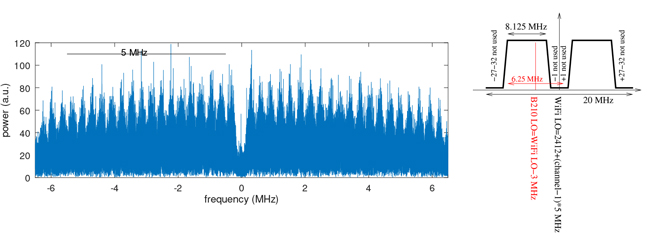
Cela nous amène à étudier la couche physique telle que nous l’a décrite H. Boeglen (Laboratoire XLIM, Poitiers). Chaque canal Wi-Fi se voit allouer 20 MHz. Les canaux sont séparés de 5 MHz : la bande de 80 MHz de large peut donc héberger 14 canaux, donc 11 sont en pratique accessibles avec l’émetteur Wi-Fi que nous utilisons en Europe. La fréquence centrale du canal N ≥ 0 est 2412+Nx5 MHz. Au sein de chaque canal, 64 sous-porteuses sont définies, avec un espacement de 20/64=0,3125 MHz. Quelques canaux sur les bords de chaque bande (-32 à -27 et 27 à 32) ne sont pas utilisés pour ne pas baver vers le canal adjacent, mais plus important pour nous, le canal 0 n’est pas utilisé pour ne pas amplifier de puissance autour de DC après transposition en bande de base. De ce fait, compte tenu de la bande passante réduite de l’USB recevant les signaux de la B210 qui, même avec USB3, est limitée à environ 6 à 6,5 Méchantillons/s sur les deux voies, nous avons choisi de n’acquérir qu’une fraction de chaque bande Wi-Fi avec une largeur inférieure à 10 MHz afin de rejeter le trou à la fréquence centrale (figure 4).
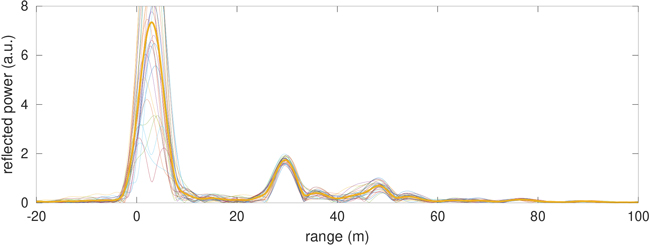
Lors des acquisitions, nous avons constaté des pics de corrélation périodiques cachant tout écho renvoyé par les cibles réfléchissant le signal émis. Il est apparu que la cause de cette structure périodique est la modulation OFDM qui module en puissance le spectre au sein de chaque canal émis. Lorsque nous concaténons les spectres acquis sur les canaux adjacents Wi-Fi, cette structure se maintient et se retrouve dans le domaine temporel, la transformée de Fourier d’un peigne étant un peigne. Il nous faut donc éliminer cette dépendance avec la fréquence de la puissance. Pour ce faire, nous remplacerons l’estimateur xcorr de corrélation de xcorr(ref, mes) = iFT(FT(ref)⋅FT*(mes)) avec FT la transformée de Fourier de la voie de ref de référence et de mes mesure, iFT la transformée de Fourier inverse, et * le complexe conjugué par l’estimateur xcorr(ref, mes) = iFT(FT(ref)/FT(mes)).
Du point de vue de la phase, le produit par le complexe conjugué ou le quotient reviennent au même, mais cette fois, nous faisons le quotient des modules au lieu de leur produit. Ce faisant, nous éliminons les fluctuations introduites par OFDM et nous retrouvons avec un spectre plat lors de la corrélation. Seuls les échos apparaissent comme des pics de corrélation lors de la transformée de Fourier inverse (figure 5).
4. Acquisition pour la mesure en azimut
Nous avons décidé de résoudre l’incertitude en azimut en synthétisant une antenne d’ouverture importante. Nous avons vu que pour respecter la transposition spatiale du théorème d’échantillonnage bien connu dans sa version temporelle, il faudra que l’espacement entre les antennes soit au plus de λ/2 pour lever toute ambiguïté sur la direction d’arrivée du signal. Cela signifie que pour couvrir le balcon de 2,3 m de large d’un réseau d’antennes fonctionnant à 2,45 GHz, il faudra 38 antennes. Cela va faire cher en B210 pour les récepteurs, ou nécessiter des commutateurs radiofréquences à plus de voies que nous ne pouvons en obtenir.
La solution de balayer l’antenne réceptrice en maintenant fixe l’antenne émettrice va nous permettre de respecter le cahier des charges de n’exploiter que du matériel disponible : deux antennes Wi-Fi Huber-Suhner de référence 1324.19.0007 (antenne patch à 2,4 GHz en polarisation circulaire gauche, 8,5 dBi nominaux de gain) sont en effet à notre disposition. Ainsi, nous remplaçons le réseau d’antennes par une unique antenne de réception que nous allons déplacer manuellement le long de la balustrade du balcon, et ce, en nous déplaçant de λ/4 ≃ 3,1±0,1 cm (figure 6).
5. Suppression du couplage direct
Nous avons rencontré au cours de nos développements une perte de sensibilité selon certaines géométries qui ont fini par être attribuées à une trop grande proximité de l’antenne émettrice de l’antenne réceptrice au cours de son balayage. Il est important de maintenir cette distance aussi grande que possible – dans notre cas, en plaçant l’émetteur sur le sol du balcon alors que le récepteur se déplace sur la rambarde 1 m plus haut, afin d’éviter de saturer l’étage d’amplification du récepteur. Sous cette condition, la fuite de puissance de l’émetteur vers le récepteur n’est pas spécialement handicapante si l’étalement de spectre est convenablement fait sans périodicité, qui se traduirait par des échos retardés dans le temps par le délai de répétition du motif. La fuite se traduira par un pic intense de corrélation proche des retards nuls, mais comme notre intérêt porte sur des cibles à plusieurs dizaines de mètres, nous omettrons simplement d’analyser les cibles les plus proches (< 3 m ou 2 pixels lors d’une mesure sur 100 MHz de bande passante) qui sont des artefacts de couplage.
6. Traitement des signaux
Nous avons établi que nous étions capables, par compression d’impulsion en distance (range compression), de corréler le signal émis avec le signal reçu pour accumuler de façon cohérente de l’énergie aux divers retards 𝞽 des impulsions réfléchies par une cible à distance d avec 𝞽 = 2d/c (c la vitesse de la lumière de 300 m/µs). Rappelons que la corrélation est une transformée de Fourier inverse d’un produit de transformées de Fourier (du signal de référence et du complexe conjugué du signal de mesure pour retourner le temps par rapport au théorème de convolution) – cette relation va nous être utile.
Une façon intuitive de voir pourquoi une transformée de Fourier sur la direction de balayage de l’antenne réceptrice induit une compression en azimut est d’analyser l’expression du déphasage induit par l’angle d’arrivée d’un signal d’orientation ϑ par rapport à la normale d’un réseau d’antennes linéaires uniformément distribuées (ULA – Uniform Linear Array) et séparées d’une distance d. La projection du vecteur d’onde k = 2π/λ sur la base du réseau d’antennes d indique que le déphasage est :
![]()
Pour la énième antenne, le déphasage ϕn = nkd sin(θ) qui est bien le produit de deux grandeurs duales, la position d’antenne nd avec le vecteur d’onde k = 2π/λ = 2πf /c. La série de mesures aux fréquences f induit la compression en distance (résolution inverse de la bande passante de mesure, donc de l’excursion de f) tandis que le balayage en position nd induit la compression en azimut :

Ceci est la transformée de Fourier de St dont la phase s’interprète comme la translation. Nous retrouvons les deux grandeurs duales permettant, par transformée de Fourier bidimensionnelle, de déduire la distance
R0 et l’azimut θ0 de la cible, donc sa position (R0 cos(θ0), R0 sin(θ0).
Supposons une cible en position (x0, y0) que nous exprimons en coordonnées polaires (R0 cos(θ0), R0 sin(θ0)) avec R0 la distance de la cible et θ0 son angle en azimut. Alors le signal reçu par l’antenne en position xp est de la forme :
Ceci en se rappelant que la phase induite est le produit du vecteur d’onde k = 2π/λ= 2πfq/c par la distance parcourue Rp = √((xp-r0 sin ϑ0)2 + (r0 cos ϑ0)2) où la cible est située à x0 = r0 sin ϑ0 et y0 = r0 cos ϑ0.
Nous avions déjà établi en section 2 que lorsque l’antenne réceptrice se déplace en abscisse de xp, son ordonnée étant supposée fixe en une origine arbitraire y=0, alors la distance parcourue entre le RADAR et la cible est de l’ordre (approximation au premier ordre du développement de Taylor du petit déplacement) de R0(xp) ≃ R0-xp sin θ0.
Grâce à cette approximation, le signal reçu est de la forme :
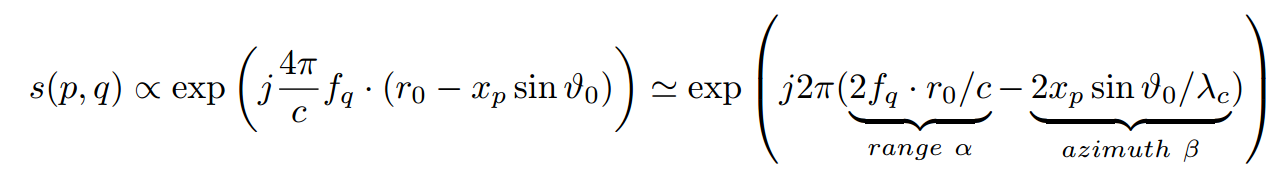
Ceci en supposant que fq/c = 1/λ ≃ 1/λc la longueur d’onde à la fréquence centrale de la bande émise si la bande passante est suffisamment réduite pour pouvoir approximer 1/x = Σn(-1)n⋅(x-1)n ≃ 1 autour de x ≃ 1 en ne conservant que le terme n = 0. Ainsi, l’expression exp(j4πfq(R0-xp sin θ0)/c) a bien permis de séparer R0 et θ0 et en notant R0 = α x c/(2fq) et sin θ0 = β/(2λc) en coordonnées polaires, ou x0 = r0 sin ϑ0 = αβ⋅c⋅λc/4 et y0 = r0 cos ϑ0 = cα/2cos(asin(λc β/2) en coordonnées cartésiennes, nous avons bien les grandeurs duales entre l’espace de Fourier et l’espace réel reliant (fq, xp) à (x0, y0 ) en utilisant la transformée de Fourier à deux dimensions.
Cette expression de α et β est importante, car elle établit la relation quantitative entre les paramètres de mesure (fq, xp) et la position de chaque cible (x0, y0 ) : il n’y aura aucun degré de liberté pour projeter les échos mesurés à distance R0 et selon l’azimut ϑ0 sur une carte pour identifier la nature des réflecteurs.
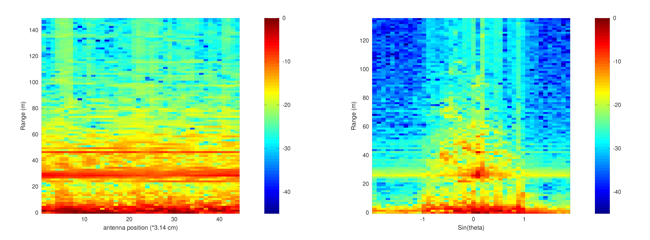
Cette compression d’azimut s’illustre en figure 8 qui fournit le graphique sous la forme distance à la cible en ordonnée et sinus de l’azimut en abscisse, incompatible avec une projection sur une carte.
Le passage de ces coordonnées polaires en coordonnées cartésiennes passe par la cartographie proposée avec le code :
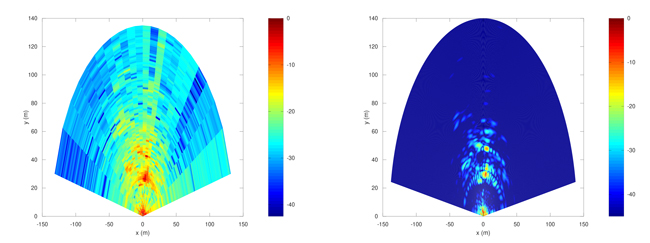
Le tout pour se conclure par la figure 9.
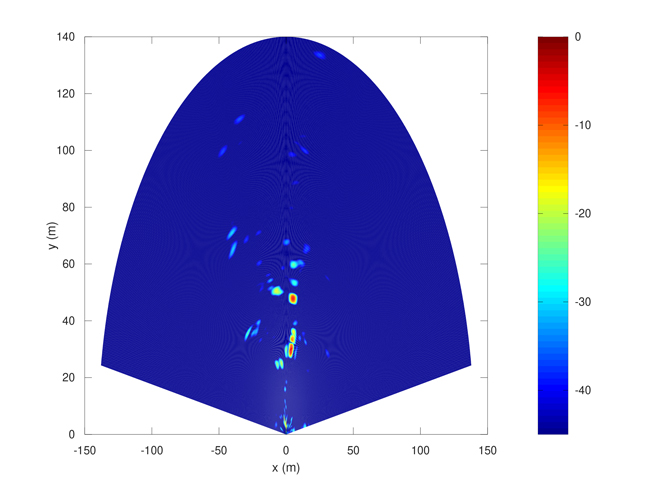
L’illustration de la figure 9 souffre clairement de fuite d’énergie le long de l’azimut, artefact de la transformée de Fourier inverse : pour rappel, la transformée de Fourier d’un rectangle (cible ponctuelle) est un sinus cardinal avec ses lobes latéraux qui réduit la résolution après transformée. Un traitement plus complexe de backprojection fournit le résultat de la figure 10 dans lequel les cibles sont convenablement focalisées, sans fuite d’énergie le long des axes radiaux ou azimuts.
7. Analyse des résultats
Nous avons vu que la conversion entre les paramètres de mesure (α, β) et les distances physiques (R0, ϑ0) en coordonnées polaires ou (x0, y0) est bijective : aucun degré de liberté ne permet d’ajuster par homothétie la position des échos. Seules l’orientation et la position de l’origine sont positionnées manuellement dans QGis. La figure 11 illustre le résultat pour un même jeu de données affiché à plusieurs échelles.
La figure 12 compare le résultat à plus grande échelle, donc avec un seuil de puissance plus bas saturé à l’affichage, entre une mesure par RADAR à bruit et RADAR réalisé par émetteur Wi-Fi. Ici encore, la comparaison est tout à fait convaincante.
8. Interférométrie
Au cours de toute cette étude, nous nous sommes contentés d’analyser le module du signal réfléchi par les cibles. Cependant, la corrélation en bande de base est une grandeur complexe qui est aussi caractérisée par une phase φ. Cette phase est liée au temps de propagation de l’onde 𝝉 par φ = 4πf𝝉 et toute variation de position de la cible dr se traduisant par une variation de temps de vol d𝝉 = dr/c entre deux mesures successives s’observe par une variation de phase dφ = 4πfδr/c en supposant que les images sont toujours prises du même endroit. Pour les RADAR aéroportés, il faut compenser des chemins différents, mais la situation est plus simple pour les mesures depuis le sol : il s’agit du domaine des GB-SAR (Ground-Based Synthetic Aperture RADAR) que nous aborderons dans le prochain article de cette série, et en particulier leur capacité à détecter finement des déplacements de la cible par analyse de la phase en complément du module, tel que nous l’avons fait ici.
Conclusion
Nous avons abordé les diverses étapes d’acquisition de signaux RADAR par radio logicielle et de traitement pour arriver à une image résolue en distance et en azimut. Nous avons vu pourquoi la fréquence centrale de porteuse avait dû être augmentée pour réduire l’espacement entre deux acquisitions alors que l’antenne réceptrice se déplace en ligne droite par pas constants, facilitant la compression en azimut qui s’apparente en première approximation à une transformée de Fourier inverse. Le résultat est une détection de cibles à plusieurs dizaines de mètres pour une puissance émise inférieure au milliwatt, grâce à l’excellent rapport signal à bruit amené par la corrélation lors de la compression en distance. La carte des cibles est en accord avec les photographies aériennes, sans qu’aucun degré de liberté ne permette d’ajuster les distances qui sont contraintes par les paramètres d’acquisition.
Nous nous sommes pour le moment contentés de traiter le module du signal acquis, alors que le flux de données I+jQ est un complexe comportant une phase. Nous verrons au prochain épisode comment exploiter cette phase pour détecter des mouvements sub-longueur d’onde, avec des applications aussi excitantes que les mesures géophysiques de glissement de terrain ou en génie civil, sur le mouvement des tabliers de ponts chargés par des véhicules.
Remerciements
Toutes les références qui ne sont pas librement disponibles sur le Web ont été téléchargées sur Library Genesis à gen.lib.rus.ec, une ressource indispensable à nos recherches et développements.
Références
[1] O. MONSERRAT, M. CROSETTO, et G. LUZI, « A review of ground-based SAR interferometry for deformation measurement », ISPRS Journal of Photogrammetry and Remote Sensing 93, pp.40–48, 2014 : https://www.sciencedirect.com/science/article/pii/S0924271614000884. Ce n’est pas complètement par hasard qu’un article de RADAR apparaît dans un journal de photogrammétrie : les deux techniques sont complémentaires, avec le RADAR actif insensible aux perturbations météorologiques (nous y reviendrons au prochain article de la série), mais moins résolu que les méthodes optiques.
[2] N. SCMCYKIN, A. DUDNIK, V. MONAHOV, « Low frequency through-wall radar-detector », Proc. 15th International Conference on Ground Penetrating Radar, 2014.
[3] F. AHMAD et R.M. NARAYANAN, « Conventional and Emerging Waveforms for Detection and Imaging of Targets behind Walls », M. Amin, Through-the-Wall radar imaging CRC press, 2017.
[4] R.M. NARAYANAN, X. XU, et J.A. HENNING, « Radar penetration imaging using ultra-wideband (UWB) random noise waveforms », IEE Proceedings-Radar, Sonar and Navigation 151(3), pp. 143-148, 2004.
[5] J.-M FRIEDT, W. FENG, « Analyse et réalisation d’un RADAR à bruit par radio logicielle », GNU/Linux Magazine France no240, septembre 2020 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-240/Analyse-et-realisation-d-un-RADAR-a-bruit-par-radio-logicielle
[6] M. MÜLLER : https://lists.gnu.org/archive/html/discuss-gnuradio/2020-06/msg00125.html
[7] C. ALEXANDRE, « Orthogonal Frequency Division Multiplexing(OFDM) », CNAM : http://easytp.cnam.fr/alexandre/index_fichiers/support/ele207_presentation_ofdm.pdf
[8] M. BRAUN, « OFDM Radar Algorithms in Mobile Communication Networks », 2015 : publikationen.bibliothek.kit.edu/1000038892/2987095
[9] H. FORSTÉN, « Synthetic-aperture radar imaging » : https://hforsten.com/synthetic-aperture-radar-imaging.html (rédigé 13/08/2019, accédé mai 2020).