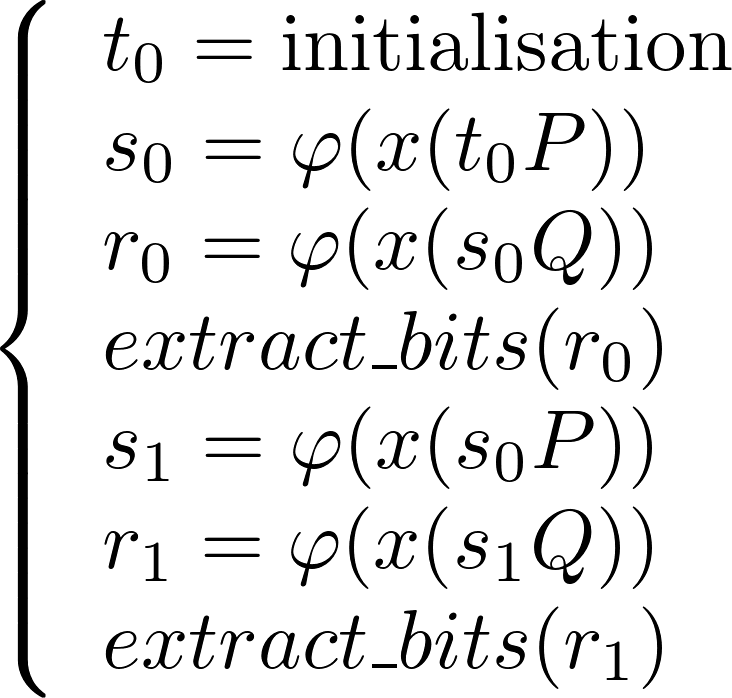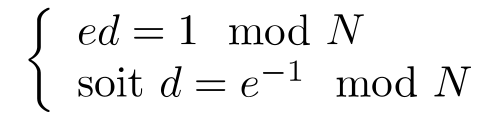Les cas concrets où un organisme (la NSA peut-être ?) a influencé l'élaboration d'un standard cryptographique dans le but d'y ajouter une faille de sécurité sont extrêmement rares. Le cas de Dual_EC_DBRG, Dual Elliptic Curve Deterministic Random Bit Generator, un générateur pseudo-aléatoire, est un des plus parlants, nourri de détails soulevant nombre d'hypothèses sur la manière dont ce dernier a été normalisé, diffusé et, peut-être, dont la faille a été exploitée.
Introduction
Ces dernières années auront vu naître plusieurs articles, documentations et projets répertoriant des programmes que la NSA mène à des fins de surveillance de masse. Mais qu'en est-il des cas pratiques où l'on a effectivement trace de son intervention ? Depuis l'élaboration de DES à la fin des années 1970, où la NSA avait choisi délibérément l'agencement des S-Box afin de rendre l'algorithme plus résistant à la cryptanalyse différentielle alors inconnue du monde universitaire, on ne peut plus nier le rôle proactif que joue l'agence de renseignement dans le milieu de la standardisation des primitives cryptographiques et, de manière plus générale, dans le monde des mathématiques appliquées à la cryptographie. En témoignent d'ailleurs sa présence ou sa proximité dans nombre d'organismes de normalisation et standardisation de moyens cryptographiques : NIST, FIPS, ISO, ANSI, IETF/IRTF. En 2013, des informations concernant notamment le projet SIGINT de la NSA (visant notamment à affaiblir les standards cryptographiques) mettent définitivement fin à toute zone d'ombre : la NSA a effectivement élaboré un générateur pseudo-aléatoire avec une porte dérobée, Dual_EC_DRBG. Mais ces informations ne racontent pas tout, car il ne suffit pas de proposer une norme. Encore faut-il qu'elle passe à travers les différentes étapes d'audit par plusieurs d'experts du domaine, qu'elle soit acceptée, qu'elle soit implémentée, utilisée et que la porte dérobée soit effectivement exploitable. Cet article va tâcher de présenter l'ensemble des éléments actuellement disponibles de l'histoire du standard Dual_EC_DBRG. À savoir, une partie du déroulement de sa normalisation, le fonctionnement du générateur et de sa porte dérobée et, enfin, l'exploitabilité de cette dernière dans un cas pratique avec TLS et la backdoor de Juniper/ScreenOS. Cet article repose essentiellement sur le travail d'analyse effectué par des chercheurs en cryptographie, Daniel J. Bernstein, Tanja Lange et Matthew Green entre autres, ainsi que sur des documents obtenus notamment par l'Electronic Frontier Fondation auprès de l'administration états-unienne dans le cadre d'une requête « FOIA » (Freedom Of Information Act) afin d'obtenir le plus d'informations possibles sur la manière dont est intervenue la NSA dans le déroulement de la normalisation. On s'attachera alors à présenter des faits vérifiés par ces travaux (tous disponibles en ligne), et à appuyer ainsi certaines hypothèses. Cependant, même s'il apparaît clairement que la NSA a effectivement produit l'algorithme avec une porte dérobée, rien ne permet de dire avec exactitude quelle était leur véritable stratégie, ni même parfois comment ils sont intervenus durant la normalisation et, ultime doute difficilement vérifiable, s'ils ont effectivement exploité la porte dérobée. Enfin, concernant le caractère mathématique du sujet traité, cet article présentera avant tout les détails concernant la porte dérobée plutôt que ceux liés aux choix de la structure de Dual_EC_DRBG en termes de qualité de générateur pseudo-aléatoire. Aussi, que les esprits mathématiques rigoureux pardonnent par avance les abus de langage du présent document. La première partie traitera essentiellement des problèmes non techniques soulevés par le processus de normalisation de Dual_EC_DBRG pour continuer avec une description du fonctionnement de la porte dérobée et l'exploitabilité de cette dernière.
1. Normalisation de Dual_EC_DRBG
Il serait difficile de réécrire l'histoire de la normalisation de Dual_EC_DRBG dans un ordre chronologique, tant celle-ci est à la fois une reconstruction après découverte de la backdoor qu'une analyse encore en cours. Tout d'abord, en juillet 2004, un workshop du NIST (organisme de normalisation US) se tenait en présence de la NSA. Il concernait la génération des nombres pseudo-aléatoires ; Dual_EC_DRBG y était présenté pour la première fois par un employé de Entrust dans une intervention intitulée « Number Theoretic DRBGs » [0]. Introduit alors comme une alternative intéressante en termes de robustesse du fait des problèmes de théorie des nombres sur lesquels l'algorithme repose, son avantage serait de pouvoir produire une preuve de sa sécurité. Il souffre cependant de gros problèmes de performances : cent fois moins rapide qu'un générateur basé sur un mécanisme de hachage par exemple. Il suscite par ailleurs de vives critiques de la part de plusieurs analystes l'année suivant sa publication dans sa phase de révision. Plusieurs faiblesses sont identifiées : aucune preuve de sécurité n'est apportée et un biais est présent lors de la génération ; deux publications au moins mettront en exergue ce dernier problème [1][2]. Aucune de ces remarques ne sera prise en compte par le NIST, la date limite de dépôt des commentaires étant dépassée. Pourtant, le document décrivant la norme (SP 800-90) sera modifié à plusieurs reprises jusqu'à mai 2006, comme le relève « Dual EC : A Standardized Back Door » [3]. L'année suivante, en 2007, durant la « rump session » de la célèbre conférence Crypto, Dan Shumow et Niels Ferguson (chercheurs en cryptographie à Microsoft) émettent l'hypothèse de la présence d'une porte dérobée dans le générateur Dual_EC_DRBG [4]. L'algorithme ne reposant que sur une seule instance du problème du logarithme discret et utilisant deux constantes pour ces calculs, si les constantes sont bien choisies (l'ensemble du fonctionnement est décrit dans la partie suivante), alors il est possible de prédire les futurs bits générés par le DRBG en ayant connaissance de quelques bits passés. Bien entendu, le NIST recommande d'utiliser les constantes spécifiées dans le document décrivant le standard (SP 800-90 Appendix A). Bien entendu, il est nécessaire d'utiliser spécifiquement ces constantes pour pouvoir être certifié FIPS (laboratoire qui teste l'implémentation afin de vérifier sa conformité), quand bien même il est possible d'en utiliser d'autres (également en Appendix A). Mais alors, comment ces constantes ont-elles été choisies ? C'est ce qui a été révélé en 2014 par la diffusion d'un échange d'e-mails entre John Kelsey (l'un des auteurs du document produit par le NIST) et Don Johnson (Cygnacom, qui aidait à l'élaboration du standard) datant d'octobre 2004 [5] :
Figure 1 : Extrait de l'échange d'e-mails mettant en évidence le choix des constantes P et Q dans Dual_EC_DRBG.
Dès à présent, il est certain que la NSA a généré les constantes, et potentiellement de façon à exploiter la porte dérobée. C'est là l'ultime doute à l'heure actuelle : savoir de manière certaine si ces constantes ont effectivement été générées ainsi que le décrivait l'attaque de Shumow-Ferguson. La réponse de la NSA [6] fut : « generated (P,Q) in a secure, classified way ». John Kelsey indique également en mai 2014 [6] que l'ensemble de l'algorithme a été soumis par la NSA. Fait étayé par certains documents [7] diffusés après un FOIA, où John Kelsey fait lui-même appel à l'agence pour le conseiller :
Figure 2 : Extrait de « 9.12 Choosing a DRBG Algorithm ».
Elain Barker (l'autre auteur du document SP 800-90) indiquera même dans un e-mail que John Kelsey n'est pas la bonne personne avec qui parler de Dual_EC_DRBG, mais qu'il faut plutôt contacter Debby Wallner et Bob Karkoska de la NSA. Soulignons l'importance de ce processus de normalisation, car il permettra de produire un algorithme qui sera inclus notamment dans les standards FIPS et ainsi présent dans nombre d'implémentations certifiées (pour n'en citer qu'une, OpenSSL-FIPS). Mais cela ne s'arrête pas là : selon Reuters [8] la NSA aurait payé 10 millions de dollars afin que l'entreprise RSA security utilise par défaut Dual_EC_DRBG dans leur bibliothèque cryptographique BSAFE. Quand bien même l'ensemble de ces éléments mettent en évidence la volonté de la NSA de produire un mécanisme ayant une porte dérobée, d'autres hypothèses existent s'appuyant notamment sur l'aveuglement des experts en cryptographie par rapport aux recherches sur les PRNG utilisant des mécanismes asymétriques, la longue explication de Jon Callas sur la liste de diffusion cryptography en est un parfait exemple [9]. D'autres éléments d'importance n'ont pas été détaillés dans cette brève description afin de ne pas trop générer de confusion : les brevets déposés [10] par Certicom dès 2005 concernant le mécanisme de la porte dérobée (Certicom connaissant donc déjà l'attaque en 2005 et l'avait également rapporté au NIST) ; l'alignement de l'ISO, organisme international, sur le projet de normalisation du NIST concernant les générateurs pseudo-aléatoires (avec Dual_EC_DRBG et les mêmes constantes !) suite à un rejet en bloc du programme de l'ISO par le gouvernement US ainsi que les différentes réponses données par la NSA.
2. Description de la backdoor
2.1 Fonctionnement du générateur pseudo-aléatoire
2.1.1 Les générateurs pseudo-aléatoires
Le générateur pseudo-aléatoire est la pierre angulaire des systèmes cryptographiques modernes (génération de clefs, salage). Il sert à produire des bits (on parlera de DRBG) ou plus communément une série de bits ou un nombre (il est nommé alors PRNG pour « pseudo-random number generator ») en prenant en entrée une donnée provenant d'un générateur de nombres aléatoires (tel que /dev/random sous GNU/Linux).
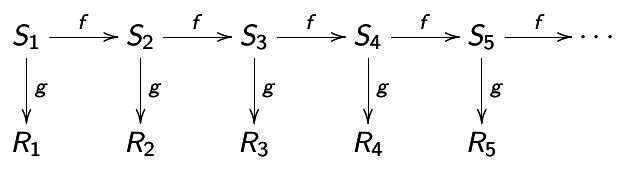
Figure 3 : Schéma d'un générateur de nombres pseudo-aléatoires à états (source : https://projectbullrun.org/).
Un premier état est généré à partir d'un RNG pour ensuite être dérivé deux fois :
À chaque fois que le PRNG est appelé pour obtenir un nombre, il met alors à jour son état interne en appliquant la fonction f (cf. formule ci-dessus) et dérive ensuite celui-ci avec une fonction g pour produire une certaine quantité de bits. On notera que, dans ce schéma, chaque mise à jour se fait sans l'ajout extérieur de données (provenant d'un RNG par exemple) et que la découverte d'un état interne permet de dériver l'intégralité des états suivants. La fonction g se doit donc d'être très difficile à inverser, autrement dit d'être une fonction à sens unique. Il existe à l'heure actuelle deux grandes façons d'élaborer ce genre de PRNG : en utilisant des primitives cryptographiques reposant sur des mécanismes symétriques (chiffrement par blocs) ou asymétriques (utilisant des problèmes mathématiques considérés comme difficiles à résoudre dans un temps raisonnable). Dual_EC_DRBG fait partie de la deuxième catégorie, très peu déployée du fait de ses faibles performances, mais proposée, car elle permet d'établir une preuve de sécurité (i.e. casser le mécanisme revient minimalement à résoudre une instance du problème mathématique sur lequel il repose).
2.1.2 Cryptographie à base de courbes elliptiques
Le problème essentiel sur lequel repose Dual_EC_DRBG fait appel aux bases de la cryptographie utilisant les courbes elliptiques. Quelques rudiments de mathématiques vont donc être introduits afin d'esquisser ce qu'est le problème de la résolution du logarithme discret sur une courbe elliptique. Une courbe elliptique E, telle qu'utilisée par Dual_EC_DRBG a la forme suivante (équation de Weierstrass) :
Elle est définie sur un corps fini ![]() avec p un nombre premier. On peut définir mathématiquement une opération d'addition sur la courbe, la somme de deux points de la courbe donne un troisième point sur la courbe. Un exemple d'addition :
avec p un nombre premier. On peut définir mathématiquement une opération d'addition sur la courbe, la somme de deux points de la courbe donne un troisième point sur la courbe. Un exemple d'addition :
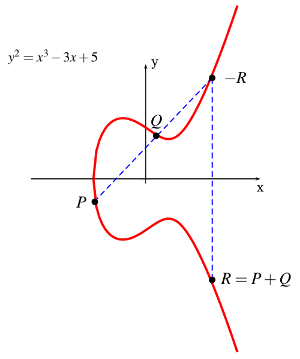
Figure 4 : Addition dans le corps associé à une courbe elliptique.
Si l'on prend un point P et qu'on l'additionne k fois avec lui-même, on obtient simplement la multiplication de P par le scalaire k : kP. Le calcul de kP est extrêmement rapide, mais il est en revanche très difficile de trouver k pour kP donné. La complexité ici est de l'ordre d'un calcul en temps exponentiel (uniquement pour certaines courbes, telles que celles du NIST utilisées par Dual_EC_DRBG). Ce problème se nomme problème du logarithme discret (sur une courbe elliptique) et fait l'objet d'intenses recherches mathématiques.
2.1.3 Dual_EC_DRBG
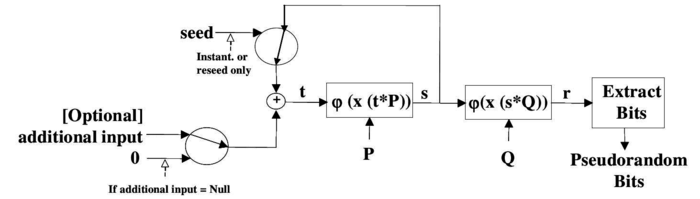
Voici le schéma de fonctionnement de Dual_EC_DRBG tel que défini dans le document du NIST (SP 800-90, il en existe plusieurs versions, qui seront brièvement commentées par la suite).
Figure 5 : Fonctionnement de Dual_EC_DRBG (source : NIST SP 800-90).
L'état interne du PRNG est un entier de 256 bits noté s (des variantes existent avec des tailles de 384 et 521 bits). Le résultat du PRNG (avant extraction des bits) est noté r. Une fonction de mise à jour et deux points P et Q sont définis sur une courbe NIST P-256 (ou P-384 et P-521). La fonction x effectue le calcul de l'abscisse du point fourni et la transformation d'un élément de ![]() en un entier est notée
en un entier est notée ![]() . Le générateur est composé de deux parties : une première consistant à générer de manière pseudo-aléatoire des points sur la courbe (via
. Le générateur est composé de deux parties : une première consistant à générer de manière pseudo-aléatoire des points sur la courbe (via ![]() , P et Q et l'état interne s) et une partie visant à extraire des bits de r. Voici un exemple simple du déroulement de l'algorithme (dans le cas où il n'y a ni « reseed » ni « additional input » et où la taille du nombre demandé fait deux fois la taille des bits extraits en deux tours de l'algorithme) :
, P et Q et l'état interne s) et une partie visant à extraire des bits de r. Voici un exemple simple du déroulement de l'algorithme (dans le cas où il n'y a ni « reseed » ni « additional input » et où la taille du nombre demandé fait deux fois la taille des bits extraits en deux tours de l'algorithme) :
Si l'étape « additional input » est utilisée, il suffit alors d'ajouter une étape de mise à jour de l'état interne en effectuant simplement :
La fonction d'extraction des bits supprime les 16 bits les plus significatifs et peut retourner au maximum 30 octets dans le cas de NIST P-256 (dans l'exemple ci-dessus, 60 octets sont demandés au total).
2.2 Fonctionnement de la backdoor
2.2.1 Version basique
Comme introduit plus tôt dans l'article, les points P et Q pourraient être générés de façon à ce que ![]() pour d connu de l'attaquant. Rappelons que le but de l'attaquant est d'obtenir l'état interne du PRNG afin de pouvoir prédire les futures sorties de celui-ci. Prenons la première séquence de bits en sortie du PRNG : on a 30 octets, il manque 16 bits, soit grosso modo
pour d connu de l'attaquant. Rappelons que le but de l'attaquant est d'obtenir l'état interne du PRNG afin de pouvoir prédire les futures sorties de celui-ci. Prenons la première séquence de bits en sortie du PRNG : on a 30 octets, il manque 16 bits, soit grosso modo ![]() candidats pour retrouver
candidats pour retrouver ![]() . En exploitant la relation entre P et Q (
. En exploitant la relation entre P et Q (![]() ), on met en évidence que pour un candidat donné R, on a
), on met en évidence que pour un candidat donné R, on a ![]() qui mène directement à la sortie potentielle suivante (on récupère l'état interne qui servira à produire une nouvelle séquence du PRNG
qui mène directement à la sortie potentielle suivante (on récupère l'état interne qui servira à produire une nouvelle séquence du PRNG ![]() . Il suffit alors de comparer ce dernier résultat à la prochaine séquence générée par le PRNG. Exemple :
. Il suffit alors de comparer ce dernier résultat à la prochaine séquence générée par le PRNG. Exemple :
On connaît deux sorties consécutives du PRNG :
On calcule une base de candidat pour ![]() en générant de manière exhaustive les points sur la base des 16 bits manquants de
en générant de manière exhaustive les points sur la base des 16 bits manquants de ![]() . Pour chaque candidat R, on effectue le test suivant (
. Pour chaque candidat R, on effectue le test suivant ( ![]() indique simplement une valeur test calculée à partir d’un candidat) :
indique simplement une valeur test calculée à partir d’un candidat) :

Si le résultat du test est positif, alors il y a une très grande chance pour que le candidat sélectionné soit bien ![]() on a ainsi la capacité de prévoir l'ensemble des sorties du PRNG. On connaît l'état interne
on a ainsi la capacité de prévoir l'ensemble des sorties du PRNG. On connaît l'état interne ![]() .On peut donc calculer l'ensemble des états suivants.
.On peut donc calculer l'ensemble des états suivants.
2.2.2 Correction pour exploiter la backdoor
Dans le fonctionnement tel que décrit ci-dessus, si l'option d'ajout de données externes est utilisée (« additionnal_input ») alors l'attaque présentée précédemment n'est tout simplement pas applicable. Dans une mise à jour du document de référence du NIST (SP 800-90) datant de 2007, une étape de mise à jour de l'état interne du générateur a été rajoutée [11]. Cette modification va notamment permettre de reproduire l'attaque présentée précédemment (et de retrouver l'état interne du générateur). Cependant, même si l'état du générateur venait à être découvert, il faudra pour l'attaquant deviner les données utilisées par l'« addionnal_input » afin de prédire effectivement les futures sorties du générateur. La porte dérobée a donc été partiellement réparée si l'ajout de donnée externe est utilisé. L'exploitabilité de cette dernière repose alors sur la qualité de la source d'entropie utilisée pour produire la donnée ajoutée à chaque appel du générateur.
2.2.3 Preuve de concept de la backdoor
Afin de pouvoir utiliser la backdoor il faut au préalable générer les constantes qui seront nécessaires à son exploitation. En pratique, il suffit seulement de modifier Q (la valeur P étant le générateur du groupe de la courbe NIST-P256) de la manière suivante :
Avec e une valeur aléatoire et d la clef secrète qui permettra donc l'exploitation de la porte dérobée. Il suffit alors de générer la clef secrète d tel que :
Avec N l'ordre du point P. La preuve de concept écrite en golang [20] pour l'occasion se base sur Dual_EC_DRBG sans l'utilisation de l'option « additionnal_input » et en utilisant la courbe NIST-P256. L'attaque implémentée est donc sensiblement la même que celle présentée précédemment, et utilise deux sorties du générateur pour retrouver son état interne.
% ./dual_ec_poc
[*] Candidates generation (based on one round of the DRBG)
[*] Testing candidates (based on one more round of the DRBG)
[*] Success! Future output:
-> next output 1: b7446786f160ad81b9e4d92695624d53a68309a87eb9cbdf71adb04d02aa
-> next output 2: a7691b4fe1b78df0866954685ef436937ce7e5db815e7dbd0007e2bf3eb6
[*] Dual_EC output 1: b7446786f160ad81b9e4d92695624d53a68309a87eb9cbdf71adb04d02aa
[*] Dual_EC output 2: a7691b4fe1b78df0866954685ef436937ce7e5db815e7dbd0007e2bf3eb6
La première implémentation publiée utilisant une attaque similaire est aussi disponible en ligne où l'ensemble des calculs est détaillé [19].
3. Cas pratique : déchiffrement d'un flux TLS
3.1 Introduction
Une des questions centrales qui s'est posée peu après la découverte de la faille dans la structure de Dual_EC_DRBG était sa possible exploitabilité dans un environnement réel. En 2014, un groupe de chercheurs a réalisé un travail conséquent [12] afin de mettre en œuvre une application pratique du générateur avec le protocole TLS. Pour ce faire, les grandes implémentations existantes de Dual_EC ont en partie été reversées : RSA BSAFE, Microsoft SChannel et OpenSSL. L'objectif de l'attaque est de déchiffrer un flux TLS enregistré (découverte des clefs de chiffrement). Des constantes utilisées pour l'occasion ont été générées telles que décrites dans l'attaque de base ![]() et ont donc été introduites dans les bibliothèques citées précédemment. La lecture de la publication [12] relève plusieurs éléments d'importance quant à l'implémentation même de Dual_EC_DRBG. L'un des plus marquants est qu'OpenSSL-FIPS (la version certifiée FIPS de l'une des bibliothèques les plus utilisées pour TLS) ne fonctionnait tout simplement pas du fait d'un bug dans le code qui empêchait toute utilisation du générateur Dual_EC [13]. Bienveillance caractérisée ? Quoi qu'il en soit, pour les autres bibliothèques, l'implémentation n'est pas toujours conforme au standard (pour SChannel) et les options disponibles (« additional input ») sont rarement intégrées malgré qu'elles pourraient réduire considérablement la possibilité d'une attaque efficace.
et ont donc été introduites dans les bibliothèques citées précédemment. La lecture de la publication [12] relève plusieurs éléments d'importance quant à l'implémentation même de Dual_EC_DRBG. L'un des plus marquants est qu'OpenSSL-FIPS (la version certifiée FIPS de l'une des bibliothèques les plus utilisées pour TLS) ne fonctionnait tout simplement pas du fait d'un bug dans le code qui empêchait toute utilisation du générateur Dual_EC [13]. Bienveillance caractérisée ? Quoi qu'il en soit, pour les autres bibliothèques, l'implémentation n'est pas toujours conforme au standard (pour SChannel) et les options disponibles (« additional input ») sont rarement intégrées malgré qu'elles pourraient réduire considérablement la possibilité d'une attaque efficace.
3.2 Quelques éléments pour l'attaque
Afin de rester concis et de ne pas reproduire l'excellente publication « On the Practical Exploitability of Dual EC in TLS implementations », l'attaque sera présentée uniquement dans ses grandes lignes. De nombreux protocoles cryptographiques (TLS, SSH) reposent sur l'utilisation de paramètres temporaires, générés aléatoirement à chaque nouvelle session. Pour TLS, les « nounces », les « session ID », certains paramètres Diffie-Hellman, sont autant d'exemples qui sont générés aléatoirement (en utilisant un PRNG) avant d'être envoyés au moment de la poignée de main TLS. Si le PRNG se trouve être Dual_EC_DRBG, il sera alors possible d'initier l'attaque pour autant que la quantité de bits récupérés soit suffisante. Or dans le standard TLS 1.2, les « nounces » font une taille de 32 octets (28 octets aléatoires, et 4 octets de « timestamp ») ; la génération du « session ID » est laissée libre dans le standard, et ne dépendra alors que de l'implémentation. Ensuite, selon les primitives cryptographiques utilisées pour le chiffrement du flux, l'attaque visera à déterminer les paramètres secrets de ces primitives, pour pouvoir ainsi déchiffrer le flux. Dans le cas d'ECDHE par exemple, l'état du PRNG du serveur est calculé sur la base des différents éléments aléatoires présents dans la poignée de main. Est ensuite calculé le secret partagé puis le « master secret » depuis lequel toutes les clefs de session sont dérivées. Notons que cette attaque est passive (et peut se faire a posteriori sur un trafic capturé) et est bien entendu effective contre les primitives permettant la confidentialité persistante (« Perferct Forward Secrecy ») telles que ECDHE, car elle permet de recalculer les clefs temporaires utilisées, c'est là tout l'avantage de compromettre le générateur pseudo-aléatoire. Les résultats obtenus par l'équipe vont, dans la pire situation, de moins d'une seconde pour BSAFE-C à trois heures pour SChannel afin de retrouver l'état interne du générateur et les clefs en utilisant un cluster d'AMD Opteron [12]. On pourrait également imaginer, en fonction des capacités de calcul disponibles, une attaque active permettant de compromettre l'authentification du serveur.
3.3 Réduction du coût de l'attaque : tentative de compromission d'un RFC ?
Le coût de l'attaque contre le protocole TLS est étroitement lié à la quantité de bits utilisés du générateur. Souvent, seulement 28 octets sont obtenus lors de la poignée de main TLS. Quatre propositions de RFC (« Internet-Draft », pouvant être proposé par quiconque) ont été soumises à l'IETF afin d'augmenter la quantité de données aléatoires utilisée par le générateur [14]. Trois d'entre eux ont été cosignés sans aucune ambiguïté par un membre de la NSA. Même si aucune de ces propositions n'a été acceptée, certaines librairies les ont implémentées (BSAFE notamment pour Extended Random [15]). Quelles que soient les différentes solutions proposées, le coût de l'attaque en est largement allégé. Par exemple, pour « Extended Random » la taille proposée pour les valeurs aléatoires échangées durant la poignet de main TLS est de deux fois le niveau de sécurité, ce qui permettra, même en utilisant les courbes P-384 ou P-521, d'appliquer directement l'attaque.
4. Cas réel : Juniper/ScreenOS
4.1 La porte dérobée, dérobée
En décembre 2015, une annonce de Juniper a secoué le monde de la sécurité informatique : deux portes dérobées ont été découvertes dans le code de ScreenOS (système d'exploitation notamment présent sur leur système de VPN). L'une est un accès administrateur avec un mot de passe écrit en dur dans le code [21] et l'autre, au moment de l'annonce, laissait supposer qu'un attaquant ayant la capacité d'enregistrer le trafic VPN d'un système Juniper pourrait tout simplement le déchiffrer. Autant dire que l'idée d'une attaque passive permettant le déchiffrement complet du trafic de certaines versions du VPN Juniper n'a pas laissé la communauté sans réaction. En effet, dès les jours qui ont suivi, l'hypothèse selon laquelle la porte dérobée reposerait sur Dual_EC_DRBG était étayée. Dans une comparaison de différentes versions de firmwares [22], on remarque que la valeur qui est modifiée se situe juste après l'ensemble des constantes utilisées par la courbe NIST-P256. Ralf-Philipp Weinmann confirme après avoir reversé une partie du code qu'il s'agit alors d'une constante (la coordonnée en x de la constante Q) utilisée par le PRNG. D'ailleurs, Juniper nous informe poliment sur son site que ScreenOS utilise effectivement Dual_EC_DRBG, mais avec des constantes maisons. Constantes qui donc, ont été modifiées par un attaquant aux alentours de septembre 2012. La potentielle porte dérobée (si Juniper a généré les constantes de façon à l'exploiter) a donc été… dérobée, et cette fois très certainement, de façon à pouvoir être exploitée.
4.2 Détails sur le PRNG
Le PRNG utilisé par ScreenOS ne repose théoriquement pas uniquement sur Dual_EC_DRBG, mais également sur ANSI X.9.31 (un PRNG basé sur 3DES). La sortie du premier générateur (Dual_EC) est utilisé comme seed par le second. Cependant, grâce aux différents travaux de rétro-ingénierie effectués, un bug a été mis en évidence par Willem Pinckaers démontrant que le second PRNG était tout simplement contourné. Voici les extraits de code mettant en évidence le bug présenté lors de l'édition 2016 de « Real World Cryptography » [23]. Le code suivant sert à produire 32 octets à partir de Dual_EC_DRBG et à le fournir en entrée du second PRNG (X9.31).
void prng_do_reseed(void)
{
...
if ( dual_ec_bytes(prng_output_buf, 32) != 32 )
{ /* log error */ }
// set X9.31 seed and X9.31 DES subkeys using prng_output_buf:
memcpy(&ansi_x9_31_seed, prng_output_buf, 8);
memcpy(&ansi_x9_31_3des_key, prng_output_buf+8, 24);
prng_output_idx = 32;
...
}
Ce second morceau de code sert à produire 32 octets dans « prng_output_buf ». Seul problème, « prng_output_idx » est fixé à 32 lors de l'appel (systématique) à la fonction « prng_do_reseed », la boucle for ne s'exécute donc jamais et aucune donnée provenant du second générateur ne sera utilisée. On a donc 32 octets provenant directement de Dual_EC_DRBG et pouvant ainsi être potentiellement exploitables. Ce bug daterait de la même période où Dual_EC_DRBG a été introduit dans ScreenOS, à savoir octobre 2008.
void prng_generate_block(void)
{
...
prng_output_idx = 0;
++blocks_generated_since_reseed;
if ( !prng_reseed_not_needed() ) // in default config, always returns 0
prng_do_reseed();
for ( ; (unsigned int)prng_output_idx <= 31; prng_output_idx += 8 )
{ /* obtain 8 bytes from X9.31, copy to offset in prng_output_buf */ }
}
4.3 Hypothèses sur le fonctionnement de l'attaque
Comme pour TLS, la base de l'attaque repose sur l'utilisation des « nounces » transmis lors des échanges IKE au moment de l'établissement du VPN. Contrairement à TLS, le choix de la taille de ces « nounces » est libre. Or, ScreenOS utilise une taille de 32 octets provenant directement de Dual_EC_DRBG comme nous avons pu le voir. Malgré tout, les « nounces » sont transmis après l'échange de clefs et devraient être générés également après (ce qui empêcherait que l'on puisse regénérer les clefs). Deux approches existent : prégénérer ou générer à la volée. Dans le cas de la version de ScreenOS utilisant Dual_EC, c'est une table prégénérée de « nounce » qui est utilisée, rendant ainsi plausible une attaque visant à déchiffrer le trafic VPN en regénérant les clefs échangées.
Conclusion
Après la suppression du standard dans les recommandations du NIST en 2014 ainsi que dans les différentes implémentations existantes (non sans bruit pour BSAFE), il y a des conclusions importantes à tirer de cette affaire. Premièrement, il ne fait aucun doute que des organismes tels que la NSA n'ont aucune place dans les processus de normalisation des moyens cryptographiques. Une requête avait d'ailleurs été déposée dans ce sens afin de faire sortir l'ancien directeur du groupe crypto de l'IRTF qui était employé par la NSA [16] (groupe qui, par exemple, doit recommander le groupe de travail sur TLS sur le choix des courbes elliptiques à utiliser). Deuxièmement, il ne faut accepter dans les standards aucune forme de constantes précalculées sans avoir accès à l'ensemble des tenants et aboutissants les ayant produites, et confirmer qu'ils reposent sur des calculs considérés comme objectifs ou aléatoires. Par exemple, à l'heure actuelle, l'ANSSI recommande des courbes elliptiques avec leurs constantes, le tout publié au Journal officiel [17], sans le moindre détail technique. Il existe notamment une initiative permettant d'établir des critères de sécurité dans la sélection des courbes elliptiques existantes [18]. Bien entendu, ces deux points ne solutionnent qu'une infime partie des problèmes liés à la standardisation des moyens cryptographiques. Ces derniers mois auront d'ailleurs vu beaucoup de discussions concernant la normalisation des courbes elliptiques (à l'IETF et pour la W3C Crypto API notamment) qui est un enjeu crucial à l'heure actuelle, car il détermine quelles solutions seront massivement déployées dans quelques années. Enfin, la tension entre des solutions de qualités non normalisées et des recommandations biaisées ne saurait que grandir si les organismes de normalisation et de recommandations ne réagissent pas afin d'augmenter leur indépendance et leur transparence.
Remerciements
Bien évidemment, cet article est essentiellement basé sur les différents travaux de recherche référencés dans les notes et j'en remercie sincèrement leurs auteurs. Merci également à Aurélien pour ses nombreuses relectures ainsi qu'à Évariste pour ses conseils avisés.
Références
[0] http://csrc.nist.gov/groups/ST/toolkit/documents/rng/NumberTheoreticDRBG.pdf
[1] http://www.math.ntnu.no/~kristiag/drafts/dual-ec-drbg-comments.pdf
[2] https://eprint.iacr.org/2006/190
[3] http://eprint.iacr.org/2015/767
[4] http://rump2007.cr.yp.to/15-shumow.pdf
[6] http://csrc.nist.gov/groups/ST/crypto-review/documents/dualec_in_X982_and_sp800-90.pdf
[8] http://www.reuters.com/article/2013/12/21/us-usa-security-rsa-idUSBRE9BJ1C220131221
[9] https://cryptome.org/2014/01/dual-ec-drbg-backdoor.htm
[10] https://projectbullrun.org/dual-ec/patent.html
[11] https://projectbullrun.org/dual-ec/standard-change.html
[12] http://dualec.org/
[13] https://marc.info/?l=openssl-%20announce&m=138747119822324&w=2
[14] http://sockpuppet.org/blog/2015/08/04/is-extended-random-malicious/
[15] https://tools.ietf.org/html/draft-rescorla-tls-extended-random-00
[16] https://www.ietf.org/mail-archive/web/cfrg/current/msg03554.html
[18] http://safecurves.cr.yp.to/
[19] https://blog.0xbadc0de.be/archives/155
[20] https://residus.eu.org/code/dual_ec_poc.go
[22] https://gist.github.com/pzb/4bdc09c577b1dff66770
[23] http://www.realworldcrypto.com/rwc2016/program/rwc16-shacham.pdf