Le système de navigation GPS est avant tout un système de dissémination de temps utilisé comme référence dans une multitude d’applications nécessitant une synchronisation de sites géographiquement distants. Nous démontrons ici comment une implémentation en radio logicielle des trames émises par les satellites permet de leurrer un récepteur en position et en temps (sortie 1 PPS).
Introduction
Navstar, devenu aujourd’hui GPS, est un système de géolocalisation basé sur la trilatération de signaux émis par une constellation de satellites. Conçu à des fins militaires, le segment civil n’est aucunement protégé contre les attaques. Cependant, ces attaques nécessitaient jusqu’à récemment un équipement peu accessible au commun des mortels. La situation change rapidement avec la disponibilité d’émetteurs programmables par radio logicielle.
Depuis la désactivation de son mode de résolution dégradée SA (Selective Availability) en mai 2000 [1][2], GPS s’est peu à peu insinué dans nombre d’activités quotidiennes, pour devenir omniprésent, ne serait-ce que par notre obsession à consulter les informations géoréférencées de notre téléphone mobile. Une étude anglaise estime [3] à 5 milliards de livres les pertes associées au brouillage de GPS pendant 5 jours, une tâche triviale et sans intérêt technique, mais qui met en évidence l’omniprésence des systèmes de navigation par satellite dans les infrastructures critiques d’un pays (penser navigation aérienne, synchronisation d’horloges et de transports ferroviaires, livraisons de colis...). Bien plus grave, nous nous proposons d’exposer ici le leurrage (spoofing) de GPS [4][5] : alors que brouiller nécessite un bête émetteur un peu puissant et se détecte immédiatement par une perte de service, le leurrage est plus subtil, car il introduit une information erronée pour un utilisateur qui croit avoir une information valable, et donc ne se rend pas compte de l’attaque [6][7].
Notre objectif est dans un premier temps de résumer les grandes lignes du fonctionnement de GPS [8] : nous insisterons sur le fait que le positionnement nécessite avant tout un transfert précis de temps pour permettre une trilatération. Nous démontrerons ensuite l’attaque sur divers récepteurs allant des téléphones mobiles aux récepteurs GPS grand public tels que U-Blox (qui équipent par exemple les drones DJI – nous laissons le lecteur imaginer la portée de l’attaque). Quelques contre-mesures triviales limitent la portée de l’attaque, mais ne l’interdisent pas, et nous verrons que même les GPS intégrés dans des véhicules sont leurrés sous réserve de prendre un peu soin à la qualité du signal émis. Nous conclurons avec quelques stratégies de contre-mesure envisagées.
1. Principe de GPS
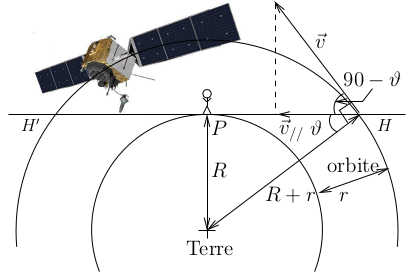
Fig. 1 : Schéma de l’orbite d’un satellite et notations utilisées dans le texte.
GPS, comme les autres systèmes de navigation par satellite (GLONASS russe, Galileo européen – de façon générale GNSS pour Global Navigation Satellite Systems), est formé d’une constellation de satellites en orbite à une vingtaine de milliers de kilomètres au-dessus de la surface de la Terre. La mécanique céleste – les lois de Kepler – impose un certain nombre de conditions sur les propriétés orbitales qui seront au cœur de notre capacité à contrer les attaques de leurrage si nous nous en donnons les moyens. En particulier, un premier paramètre que nous introduisons dès le début de cette discussion est le décalage Doppler introduit par le mouvement des satellites. En nous inspirant des notations de la fig. 1, nous constatons que lorsque le satellite apparaît au-dessus de l’horizon HH’, l’angle ϑ est donné par sin(ϑ) = R / (R+r) avec R = 6400 km le rayon de la Terre et r = 20000 km l’altitude du satellite sur son orbite. De ce fait, la projection du vecteur tangentiel de la vitesse v est v∥= |v→|sin(ϑ) = vR / (R+r). Compte tenu de la troisième loi de Kepler qui nous dit que le ratio du carré de la période au cube du rayon de l’orbite est constant, et sachant que les satellites en orbite géostationnaire, donc de période de 24 h, sont à une altitude de 36000 km, nous déduisons la période d’un satellite GPS de T = 12 h. Compte tenu de cette période et de la distance parcourue le long de l’orbite, nous déduisons une vitesse tangentielle de 2π(R+r) / T ≃ 13800 km/h = 3840 m/s. Nous en déduisons la vitesse radiale maximale lorsque le satellite est en H ou H’ de |v⃗| = 3840 x 6400 / 26400 = 930 m/s et donc un décalage Doppler δf maximal de δf=f .v/c avec f = 1575,42 MHz la fréquence de la porteuse et c = 3.108 m/s la célérité de la lumière : |δf| < 4.9 kHz. Cette limite sur le décalage Doppler est imposée par la physique céleste et ne peut en aucun cas être enfreinte : nous verrons qu’elle nous amène une première protection contre le leurrage des signaux GPS.
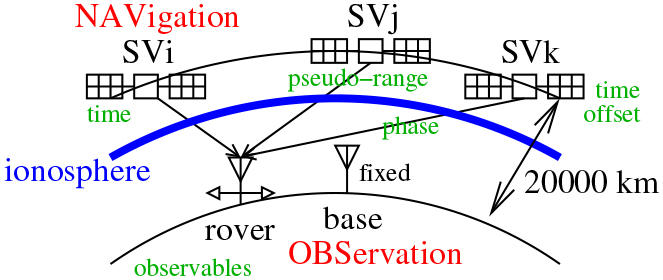
Fig. 2 : Segment spatial de GPS avec les éphémérides des véhicules spatiaux (SV), distingués par leur code pseudo-aléatoire, décrites par les fichiers de navigation, et segment au sol décrit par les fichiers d’observation RINEX.
Le signal de la porteuse porte une information doublement codée : d’une part un message rapide (1 Mb/s) encode le numéro de satellite émettant l’information, et d’autre part le message de navigation transmis par chaque satellite à bas débit (50 bits/s) est superposé sur ce code. Nous avons détaillé ces divers encodages dans [8], dans lequel nous nous étions arrêté à l’obtention des bits du message de navigation, sans en étudier le contenu. Toute la difficulté de leurrer GPS est de minutieusement reconstruire chaque trame en respectant les paramètres physiques de la transmission pour faire croire aux récepteurs les plus pointilleux que le signal est émis de l’espace. Les diverses trames du message de navigation sont décrites en détail dans [9] : ces quelques pages n’ont évidemment pas la prétention de reprendre les plus de 600 pages de ces deux ouvrages dont la compréhension est fondamentale. En particulier, ces documents expliquent comment passer des paramètres orbitaux des satellites (transmis dans les messages de navigation) et de la date des transmissions vers les pseudo-ranges tenant compte de la position du récepteur au sol. Le pseudo-range est l’élément clé du positionnement de l’utilisateur sur Terre, et l’information brute traitée par le récepteur au sol pour le positionner par trilatération. Ces pseudo-ranges sont en particulier transmis comme donnée brute dans les fichiers RINEX (Receiver Independant EXchange Format), format standardisé [10]pour échanger les informations entre récepteurs GNSS (fig. 2).
[10] définit un pseudo-range comme « The pseudo-range (PR) is the distance from the receiver antenna to the satellite antenna including receiver and satellite clock offsets (and other biases, such as atmospheric delays): PR=distance+c*(receiver clock offset–satellite clock offset + other biases) ». Il s’agit donc d’une estimation brute de la distance récepteur-véhicule spatial, indépendamment de toute correction de délai de propagation de l’onde dans les diverses couches atmosphériques.
Un exemple de mesure, extrait d’un fichier RINEX généré à partir d’un récepteur U-Blox monofréquence (L1) avec mesure de phase, est :
> 2017 12 22 5 57 46.0010000 0 12
G12 22028410.605 115760077.968 3307.683 46.000
G18 21024975.970 110486988.127 1088.977 45.000
G24 20360955.102 106997530.988 -437.104 49.000
J 1 37731461.503 198280150.949 713.158 45.000
J 2 37863385.498 198973438.883 -372.958 45.000
G15 21655567.700 113800790.795 -1526.538 48.000
G20 22301572.946 117195549.217 -2991.357 44.000
R16 21729491.824 116075061.937 3857.002 41.000
R15 19336042.668 103325965.774 -387.583 43.000
R 4 20461570.837 109570805.433 -1945.881 44.000
R14 21528858.057 114761049.343 -3182.688 38.000
R 5 19671117.697 105153436.303 1676.938 38.000
La première lettre indique la constellation, avec G pour GPS, R pour le GLONASS russe, et J pour les satellites QZSS japonais en orbite géosynchrone, entre 32000 et 38000 km.
Un rapide survol de la deuxième colonne de ces mesures nous conforte sur leur validité : la constellation des satellites GPS (véhicules spatiaux dont le nom commence par « G ») orbite à 20000 km au-dessus de la Terre. Les pseudo-ranges sont donc compris entre une vingtaine de milliers de km, et cette altitude ajoutée au diamètre terrestre de 2 x 6400 km (évidemment, un satellite GPS aux antipodes de l’observateur n’est pas visible, mais c’est un pire cas). Ici, les distances aux satellites sont comprises entre 20000 km et 22000 km pour GPS, un peu moins pour GLONASS, en accord avec nos attentes. Les Japonais (ces mesures ont été acquises depuis Sendai, au Japon) proposent un système de localisation basé sur des orbites géosynchrones avec des satellites à des altitudes plus élevées : ici encore les mesures sont en accord avec nos attentes, puisque nous observons 37800 km. Aucun satellite européen Galileo (nom commençant par « E ») n’est visible dans cette acquisition. Dans la 4ème colonne, les décalages Doppler sont eux aussi dans la gamme des valeurs décrites dans le texte. La 5ème colonne indique la puissance du signal, et la 3ème colonne une information de phase de la porteuse plus compliquée à analyser.
La conversion des pseudo-ranges décrits dans un fichier RINEX vers une information de datation ou de position est prise en charge par l’excellente bibliothèque d’outils libres rtklib (http://www.rtklib.com/), dont l’utilisation dépasse le cadre de cet article.
Il est important de maîtriser ce concept de fichier RINEX, car c’est grâce à ces fichiers de référence qu’un utilisateur peut améliorer, en post-traitement, l’estimation de la position de son récepteur en intégrant un certain nombre de corrections telles que le délai ionosphérique – retard de l’onde électromagnétique introduit par la densité variable d’électrons dans l’ionosphère. Pour cette raison, les utilisateurs de récepteurs d’un peu plus haut de gamme que les récepteurs grand public qui ne fournissent que les informations traitées au format NMEA (trop tard pour retraiter les données et en améliorer la résolution) peuvent télécharger les éphémérides de précision améliorée des satellites (observation des paramètres orbitaux au lieu de leur prévision) ainsi que diverses corrections, et ce grâce aux services de l’IGS (International GNSS Service) qui collecte les mesures précises de stations de référence distribuées à la surface de la Terre. Les deux types de fichiers RINEX sont les observations (extension finissant par o) issues du récepteur au sol qui permettent de corriger les observations faites par un utilisateur sur le terrain – ces fichiers ne nous intéressent pas ici – et les fichiers de navigation (finissant par n) qui donnent les paramètres orbitaux des satellites, indépendamment de toute notion de localisation au sol (fig. 2). Ce second jeu de données, décrivant les paramètres orbitaux des satellites de la constellation et ici acquis en traitant les messages de navigation transmis par les satellites, sera aussi disponible en version améliorée en précision sur divers sites chargés de disséminer les produits de l’IGS et répertoriés à https://kb.igs.org/hc/en-us/articles/202054393-IGS-FTP-Sites – par exemple ftp://cddis.gsfc.nasa.gov/gnss/products/ – pour fournir les informations d’entrée pour générer les signaux de leurrage du GPS.
Un second paramètre imposé par la physique de la constellation spatiale d’émetteurs radiofréquences est la puissance reçue au sol, déterminée par le bilan de liaison et en particulier les pertes de propagation imposées par la conservation de l’énergie – encore une fois un principe physique que nous ne saurions contourner lors de nos tentatives de leurrage. La norme décrivant GPS n’explicite pas la puissance émise depuis l’espace, mais la puissance reçue au sol : [11, p.14]nous informe que GPS doit fournir au sol une puissance du signal de -160 dBW=-130 dBm sur la porteuse L1 à 1575,42 MHz. Alors que nous avions décrit dans [8] comment ce signal se trouve sous le bruit thermique et ne peut donc être visible sur un analyseur de spectre en l’absence d’une antenne de fort gain telle qu’un radiotélescope, ce signal est remonté de 30 dB lors de la compression d’impulsion réalisée par la corrélation du signal acquis avec le code (connu) de chaque satellite. Le premier point important de cette analyse est que le niveau de signal reste excessivement faible au niveau du récepteur et tout émetteur au sol pourra très facilement dépasser cette puissance pour éblouir le récepteur. Au contraire, nous verrons que certains récepteurs vérifient le niveau des signaux reçus pour rejeter ceux présentant une puissance excessive et qui ne sauraient donc venir de l’espace.
GPS exploite un signal de 2 MHz de bande passante, donc toute attaque de leurrage nécessitera une source d’une telle bande passante. Nous utilisons la PlutoSDR de Analog Devices, disponible pour 85 euros chez Mouser (depuis qu’elle est épuisée chez Farnell). Ce circuit est capable d’émettre jusqu’à 0 dBm (1 mW) et d’atténuer sa sortie pour abaisser cette puissance.
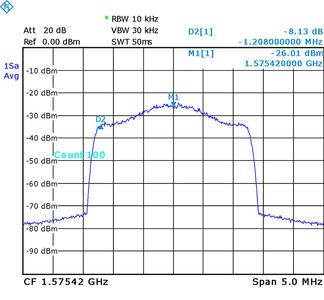
Fig. 3 : Spectre du signal émis par la PlutoSDR réglée sur un gain de 0 dB : la porteuse à 1575,42 MHz est étalée spectralement sur ± 1MHz par modulation en phase selon la séquence pseudo-aléatoire caractéristique de chaque satellite, induisant un niveau de -30 dBm environ dans la bande.
Ainsi, à titre de comparaison, notre émetteur servant à l’attaque peut émettre jusqu’à 1 mW (nous vérifions que l’atténuation 0 dB signifie une puissance émise de 0 dBm en mesurant le niveau de signal d’une porteuse émise continûment), que nous observons atteindre une puissance de -30 dBm après étalement du spectre par modulation de phase (fig. 3). Cette observation est en accord avec l’étalement de spectre sur 1023 bits qui abaisse la puissance crête de 10 log10 (1023) = 30 dB. Ceci est valable pour les divers satellites de la constellation, dont les signaux se somment après propagation. Les pertes de propagation en espace libre (Free Space Propagation Loss – FSPL) sont de FSPL = 20 log10 (d) + 20 log10 (f) – 147,55, avec la constante à la fin de cette équation donnée par 20log10 (c/4/π) avec c=3.108 m/s la célérité de l’onde électromagnétique dans le vide. À f=1575,42 MHz, ces pertes s’élèvent à 20 log10 (d) + 36 dB. Si nous émettons 0 dBm, alors les pertes nécessaires à atteindre les -130 dBm de la norme sont FSPL = 130 = 20log10 (d) + 36 dB, qui seraient atteintes pour une distance d = 10(130-36)/20=50 km. En pratique, nous émettons 20 dB de moins (option -A -20 du logiciel de synthèse des trames GPS que nous décrirons ci-dessous), soit une portée de l’attaque de l’ordre de 5 km. En ne prenant pas la norme, mais le bilan de liaison en espace libre entre le satellite qui émet 25 W (http://gpsinformation.net/main/gpspower.htm) avec un gain d’antenne de 13 dBi et les 182 dB de pertes de propagation le long des 20000 km qui séparent le satellite de la surface de la Terre, la puissance au sol est -125 dBm. Si nous désirons avoir au moins 3 dB de puissance de plus que le « vrai » signal, alors les 8 dB de différence avec le calcul précédent réduisent la portée de notre attaque à 5 km x 10(-8/20)=2 km, garantissant le peu d’impact sur l’environnement de travail de nos tests : nous avons vérifié que, probablement compte tenu de la médiocrité de l’antenne dipôle attaquée en sortie de la PlutoSDR sans balun [A], le signal GPS dépassait notre émission à une cinquantaine de mètres de l’émetteur.
2. Logiciel pour déployer l’attaque de leurrage
Ayant sélectionné la plateforme matérielle respectant les contraintes de fréquence de porteuse (1575,42 MHz), de bande passante (2 MHz) et de puissance émise, il nous reste à rédiger le logiciel de synthèse des signaux. Le travail n’est pas complexe, mais nécessite un soin particulier pour implémenter toutes les étapes : nous nous appuyons sur github.com/Mictronics/pluto-gps-sim pour démontrer l’attaque. Ce logiciel est impressionnant de concision puisqu’il implémente toute la séquence, de la lecture du fichier de paramètres orbitaux RINEX à la génération des messages de navigation en passant par toutes les transformations de coordonnées imposées par la mécanique céleste, dans un millier de lignes de code parfaitement lisibles (et donc modifiables pour injecter nos propres paramètres dans les messages transmis).
L’objectif de l’attaque par leurrage est de générer des signaux représentatifs de ceux émis par la constellation de satellites. Étant donné que tous les satellites communiquent sur la même fréquence de porteuse de 1575,42 MHz, le seul travail est de générer le flux de données complexes I/Q, somme des contributions des divers satellites, avec la modulation en phase du code de chaque satellite décalé en fréquence par l’effet Doppler associé à la position du satellite dans le ciel, et les messages de navigation permettant de positionner le récepteur sur Terre avec un retard introduit par la propagation du signal du satellite au sol tel que représenté par chaque pseudo-range. Afin de ne pas être perturbés par les vrais satellites de la constellation qui émettent en continu, nous devons absolument générer un signal de leurrage correspondant aux satellites visibles en un instant et lieu donné : faute de respecter cette contrainte, le récepteur recevra un mélange de « vrais » signaux et de « faux » signaux et ses chances de se fixer sur la position erronée sont réduites. Nous avons vu qu’à 20000 km d’altitude, les satellites mettent 12 h pour effectuer une orbite, donc exploiter la configuration valable quelques heures avant l’attaque reste pertinent. Le lieu introduit lors de l’attaque ne doit par ailleurs pas trop différer du site physique du récepteur pour que ce dernier voie une constellation similaire à celle des messages émis. La liste des satellites et leurs paramètres orbitaux tels qu’émis dans les messages de navigation des divers satellites sont publiés à https://cddis.nasa.gov/Data_and_Derived_Products/GNSS/hourly_30second_data.html avec une résolution horaire : ce service est utile en pratique pour la correction en post-traitement de signaux GPS acquis avec un récepteur unique (correction du délai ionosphérique notamment en l’absence de base de référence sur site), tel que nous l’avons décrit auparavant en mentionnant IGS.
Le jour courant de la date GPS s’obtient à sopac.ucsd.edu/convertDate.shtml : par exemple, le 30 juillet 2018 est le jour 211 de l’année, donc les éphémérides s’obtiennent à ftp://cddis.gsfc.nasa.gov/gnss/data/hourly/2018/211/. Le choix de l’heure tiendra évidemment compte du décalage entre heure locale et temps universel, soit 1 ou 2 h en France. cddis.nasa.gov/Data_and_Derived_Products/GNSS/broadcast_ephemeris_data.html#GPShourly nous informe que ce sont les fichiers finissant par n qui nous intéressent (broadcast ephemeris) pour connaître les paramètres orbitaux des véhicules spatiaux (SV) de la constellation : nous sélectionnons donc le fichier nommé hour2110.18n.Z (format hourDDD0.YYn.Z avec le jour DDD et l’année YY) :
./pluto-gps-sim -e hour2110.18n -A -20.0 -t 2018/07/30,10:00:00 -l 48.3621221,-4.8223307,100
Using static location mode.
Gain: -20.0dB
RINEX date = 30-JUL-18 23:30
Start time = 2018/07/30,10:00:00 (2012:122400)
PRN Az El Range Iono
04 110.0 80.4 20159594.4 1.7
05 33.5 8.9 24730267.9 4.4
09 320.7 5.1 25212521.1 4.5
16 302.7 51.7 21108967.6 2.0
20 144.1 7.2 25065494.6 6.2
21 133.7 64.8 21075459.6 1.9
23 292.6 5.3 25170257.9 4.5
25 120.9 6.6 25194957.8 6.4
26 292.6 82.7 20252112.2 1.7
27 256.8 22.9 23261110.3 3.3
29 64.7 31.3 22678543.7 3.1
31 193.6 33.0 22775272.7 3.0
L’outil original, gps-sdr-sim dont pluto-gps-sim est issu, propose en plus du mode statique un mode dynamique, qui nécessite cependant de sauver un fichier volumineux de coefficients I/Q (2,5 MS/s) précalculés avant exécution, limitant la durée de l’attaque à quelques minutes tout au plus. Ce fichier est généré à partir d’un trajet défini au format NMEA.
3. Démonstration : téléphone mobile et récepteur U-Blox
La première démonstration de l’efficacité de l’attaque porte sur les téléphones mobiles, outil de géolocalisation le plus couramment utilisé par le grand public actuellement. La figure 4 démontre le résultat de l’attaque sur 3 téléphones : un des téléphones a conservé les coordonnées du site acquises en exploitant les signaux de la constellation GPS (Besançon à 47°N, 6°E), les deux autres se sont fait leurrer par une position erronée choisie arbitrairement au sud de la France à 42.5°N, 2.3°E. Précisons que pour obtenir ce résultat, nous avons désactivé toute assistance de localisation telle que GSM ou WiFi : cette contrainte n’est pas limitante, car le brouillage est excessivement simple à mettre en œuvre par rapport à la complexité du leurrage, et éliminer ces assistances à la localisation ne pose pas de problème technique.
Fig. 4 : Trois téléphones mobiles sont soumis au signal de leurrage émis par la PlutoSDR : un téléphone Samsung (milieu) et un téléphone Sony (droite) se croient dans le sud de la France, tandis que le Samsung de gauche est resté à Besançon.
La même attaque est effectuée sur des récepteurs U-Blox de modèles Neo7M ou NeoM8T avec succès. Ces récepteurs sont intéressants, car en plus d’être utilisés sur de nombreux drones dont ceux commercialisés par DJI, ils fournissent les informations brutes (pseudo-ranges) permettant une analyse détaillée des signaux acquis, avant traitement pour extraire la localisation du récepteur. De ce fait, l’outil d’analyse des trames U-Blox Center fournit de nombreuses informations sur la nature des signaux reçus, dont des caractéristiques d’anti-spoofing et anti-jamming. Un premier critère de puissance rejette les signaux excessivement puissants qui ne pourraient venir d’un satellite [12].
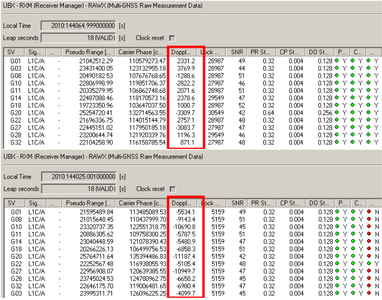
Fig. 5 : Impact de l’oscillateur local du synthétiseur de signaux sur le décalage Doppler observé par le récepteur U-Blox. Ici, un synthétiseur de fréquence asservi sur un maser à hydrogène cadence la PlutoSDR à la fréquence nominale de 40 MHz (haut) ou à 40 Mhz-200 Hz, soit un décalage de 5 ppm. Nous constatons que dans le premier cas les décalages Doppler sont bien dans l’intervalle autorisé par la mécanique céleste (±5 kHz), alors que dans le second cas les décalages de fréquence sont aberrants.
La figure 5 démontre l’impact d’une variation contrôlée de la fréquence d’horloge cadençant l’émetteur sur le récepteur. Alors que nous décalons l’horloge de l’émetteur de 5 ppm (200 Hz par rapport à la valeur nominale de 40 MHz), le récepteur continue à fournir des informations malgré la détection de dysfonctionnements tel qu’indiqué dans les colonnes de droite nommées PR (Pseudo-Range), CP (Carrier Phase) et DO (Doppler Measurement) : le récepteur U-Blox a bien détecté des valeurs incohérentes du décalage Doppler (DO rouge), mais cela ne l’empêche pas, dans sa configuration par défaut, de transmettre une position erronée.
Une tentative de leurrage similaire à celle démontrée sur téléphone mobile échoue sur le GPS de voitures. Nous attribuons notre échec à leurrer un véhicule à l’utilisation de tels indicateurs d’incohérence du signal reçu, à savoir puissance excessive et irréaliste pour des satellites en orbite, et décalage Doppler incohérent. Le premier point sera résolu par un ajustement de la puissance émise, le second par l’utilisation d’une source de fréquence plus stable que celle fournie d’origine avec la PlutoSDR.
4. Démonstration : GPS de voiture
Cette première expérience de leurrage échoue avec certains modèles de téléphone mobile, mais surtout échoue avec les GPS des voitures. Nous attribuons cet échec à l’écart de l’oscillateur local à la PlutoSDR à sa valeur nominale : même si le Rakon RXO3225M présente d’excellentes performances pour un oscillateur basé sur un résonateur compensé en température, il reste un écart de ±25 ppm à la valeur nominale qu’une « vraie » source GPS ne saurait jamais souffrir. Une horloge rubidium telle que celle équipant les véhicules spatiaux présente au moins une stabilité de quelques ppb au pire, soit au moins mille fois meilleures que cet oscillateur à quartz.
Notre première solution à l’incertitude sur la fréquence de l’oscillateur local consiste à exploiter un synthétiseur générant un signal à 40 MHz asservi sur un maser à hydrogène (voir l'article « Matériel pour la radio logicielle », publié dans GNU/Linux Magazine n°224) connu pour être exact. Nous penserons, au cours de cette expérience, à retirer le coefficient d’étalonnage introduit par Analog Devices dans le logiciel contrôlant la PlutoSDR. Ceci peut se faire en se logguant sur la carte avec un émulateur de terminal ou en ssh (login root, mot de passe analog), puis en exécutant :
echo 40000000 > /sys/bus/iio/devices/iio:device1/xo_correction
pour annoncer que la fréquence cadençant le circuit est exactement à 40 MHz. Cependant, cette nouvelle définition de la fréquence de l’oscillateur local n’est mémorisée que jusqu’au prochain redémarrage de la carte. Une solution pérenne consiste à définir une nouvelle variable d’environnement de U-Boot non-volatile.
fw_setenv xo_correction 40000000
Une fois cette modification matérielle effectuée, et en suivant la procédure de la section précédente, les véhicules sont eux aussi rapidement leurrés, pour amener des voitures garées à Besançon sur le parking de l’École Nationale Supérieure de Mécanique et Microtechniques (ENSMM) à croire qu’ils ont les roues dans l’eau au large de Brest (fig. 6). Notre hypothèse est donc la bonne, l’exactitude de l’horloge de la source est la cause du dysfonctionnement de l’attaque sur les GPS de véhicules.
Fig. 6 : Haut, droite : montage dans lequel l’oscillateur cadençant la PlutoSDR est remplacé soit par la sortie d’un synthétiseur de fréquence référencé sur un maser à hydrogène (ici inutilisé), soit par un quartz contrôlé en température (OCXO). Bas : deux véhicules – Renault (gauche) et Mercedes (bas, droite) – situés sur le parking de l’ENSMM se croient les roues dans l’eau au large de Brest.
Chaque Pluto est cadencée par un oscillateur à 40 MHz dont la fréquence exacte est calibrée et renseignée dans une zone mémoire non accessible trivialement par l’utilisateur. Dans notre cas, nous désirons expliquer à la PlutoSDR qu’elle sera désormais cadencée par un quartz stable à 10 MHz. Avant de lancer le noyau Linux, U-Boot modifie la valeur par défaut de l’horloge dans le devicetree chargé en mémoire pour appliquer la valeur de calibration. Pour ce faire, U-Boot fait appel au script adi_loadvals qui exécute :
fdt set /clocks/clock@0 clock-frequency ${ad936x_ext_refclk}
Le contenu de la variable ad936x_ext_refclk est obtenu par la lecture de la zone dédiée à la calibration et sa valeur est donc écrasée juste avant l’appel à adi_loadvals, rendant ainsi impossible à l’utilisateur de la surcharger pour la remplacer par sa propre valeur.
Pour contourner cette limitation et tel que présenté à ez.analog.com/university-program/f/q-a/77922/will-it-be-possible-to-feed-in-a-reference-clock-to-the-adalm-pluto/295481#295481, la solution consiste à modifier le script pour ajouter une nouvelle variable, qui, si elle est présente, sera utilisée à la place de ad936x_ext_refclk. Concrètement, le script original de
github.com/analogdevicesinc/u-boot-xlnx/blob/pluto/include/configs/zynq-common.h#L271 devient :
if test ! -n $"{ad936x_skip_ext_refclk}"; then if test -n $"{ad936x_custom_refclk}"; then fdt set /clocks/clock0 clock-frequency $"{ad936x_custom_refclk}"; elif test -n $"{ad936x_ext_refclk}"; then fdt set /clocks/clock0 clock-frequency $"{ad936x_ext_refclk}"; fi; fi;
Il devient ensuite possible de définir la variable ad936x_custom_refclk avec la valeur choisie :
fw_setenv ad936x_custom_refclk "<10000000>"
Rares sont cependant les lecteurs ayant accès à un maser à hydrogène, qui de toute façon ne peut être déplacé pour être amené sur le site de l’attaque. Nous pallions donc cette déficience en remplaçant le maser par un oscillateur à quartz de bonne qualité. Alors que les oscillateurs asservis sur des résonateurs compensés en température (Temperature Controlled Crystal Oscillator – TCXO) présentent des fluctuations de fréquences de quelques dizaines de ppm avec leur environnement, un oscillateur asservi en température (Oven Controlled Crystal Oscillator – OCXO) présente des fluctuations inférieures au ppm. Nous avons récupéré dans un compteur de fréquence (electronic counter) Hewlett Packard 5345A défectueux un excellent OCXO HP10811 [B]. Cet oscillateur présente une fluctuation relative de fréquence de 5.10-13 à la seconde pour monter à 5.10-12 à 100 secondes et dériver à long terme (fig. 7). Le quartz a été ajusté à mieux que 30 mHz de la fréquence nominale par comparaison avec le maser à hydrogène. Ici encore, en commandant un synthétiseur de fréquence avec cette source, l’attaque sur les véhicules se conclut sans problème, cette fois avec un montage ne nécessitant qu’une centaine de mA sous 24 V pour le chauffage et quelque mA sous 12 V pour l’oscillateur. La PlutoSDR n’a plus qu’à être configurée pour accepter une source à 10 MHz au lieu des 40 MHz nominaux pour s’affranchir du synthétiseur (voir encadré).
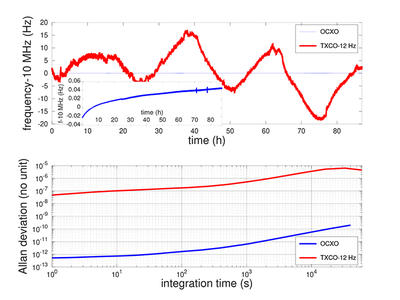
Fig. 7 : Haut : évolution au cours du temps de la fréquence du TCXO Rakon initialement fournie avec la PlutoSDR (rouge) et d’un OCXO HP10811. L’insert présente un zoom sur la mesure de l’OCXO sur sa propre échelle. Bas : variance d’Allan sur ce même jeu de données, illustrant le gain en stabilité de 5 ordres de grandeur par le passage du TCXO à l’OCXO. Toutes les mesures sont référencées à un maser à hydrogène : le TCXO est mesuré au moyen d’un compteur de fréquence Agilent 53132A, l’OCXO est caractérisé par un banc Symmetricom TSC5110A.
5. Décaler le temps
Une application classique de GPS pour le transfert de temps exploite le signal 1 PPS – 1 Pulse Par Seconde – qui représente un signal de synchronisation précis pour asservir des horloges sur la base de temps commune propagée par la constellation de satellites [13].
Fig. 8 : Distribution du délai entre deux signaux 1 PPS issus de deux liens White Rabbit (graphique de É. Meyer, Obs. Besançon).
Alors que le transfert de fréquence est un concept relativement abstrait pour le commun des mortels (penser réseau informatique et les Gb/s transmis – comment définir le /s de Gb/s pour deux ordinateurs séparés de plusieurs centaines de kilomètres ?), le transfert de temps est un concept bien concret (« je suis en retard, je ne vais pas arriver à l’heure à mon rendez-vous » – mais comment garantir que l’interlocuteur base la date du rendez-vous sur la même référence ?). Le transfert de temps et de fréquence sont deux activités duales qui ne respectent pas les mêmes contraintes. Une fréquence ou son intégrale la phase, décrit la caractéristique d’un signal périodique : par exemple, une sinusoïde à 10 MHz voit ses propriétés répétées toutes les 100 ns, et il est impossible de distinguer une période de sa voisine 100 ns plus tard. Si le passage à 0 du signal varie un peu dans le temps par rapport à une référence, l’oscillateur peut voir sa fréquence ajustée si nécessaire, mais aucune datation absolue n’est possible. Au contraire, le transfert de temps nécessite de transférer un évènement bref (« maintenant ») – donc intrinsèquement large bande, au contraire du transfert de fréquence qui est à bande étroite – et une datation absolue, et ne doit donc pas se répéter trop rapidement pour laisser le temps de fournir toutes les informations associées à l’impulsion (la date et l’horaire). Le signal 1 PPS (1 Pulse Par Seconde pour sa traduction française) [14, p.247]fournit une telle information : par définition, son front montant est supposé aligné avec l’information de date à transmettre (le début de la seconde), tandis que la durée et donc la position du front descendant ne sont pas normalisés. En parallèle de ce front montant, une information numérique est en général transmise pour informer de la date et l'heure associées à ce front. On se retrouve donc avec une configuration de l’horloge parlante : « au prochain top, il sera XX h ». Les récepteurs GPS ne sont pas les seuls à fournir 1 PPS : White Rabbit, implémentation de PTP (Precision Time Protocol) du CERN, fournit aussi son 1 PPS en parallèle du transfert de fréquence avec son oscillateur à 10 MHz. À titre d’illustration, la figure 8 de droite propose un exemple de mesure pendant un week-end du délai dt entre les 1 PPS issus de deux liens White Rabbit indépendants entre l’ENSMM et l’Observatoire de Besançon. Les fluctuations maximales sont de l’ordre de 200 ps, avec un écart type de l’ordre de 20 ps.
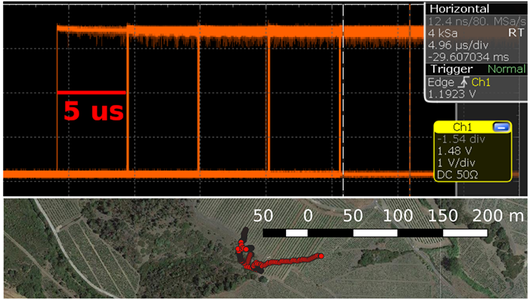
GPS est basé sur un transfert de temps, à partir duquel la position au sol est déduite par trilatération des pseudo-ranges. Les horloges embarquées dans les satellites ne sont pas exactes, mais dérivent. Plutôt que modifier le comportement des horloges pour les ramener à leur date nominale, il est judicieux de laisser les horloges dériver de façon déterministe et informer l’utilisateur de l’écart de temps entre l’horloge embarquée dans chaque satellite et le temps GPS. Cette information, remise périodiquement à jour, est transmise dans le message de navigation émis par chaque satellite [9, p.57]. Que se passe-t-il si nous décalons ce temps d’une valeur connue, par exemple par pas de 5µs dans l’application qui va suivre ?
Cette opération est simple dans une implémentation de radio logicielle : un paramètre du message de navigation à modifier de façon cohérente pour tous les satellites de la constellation, et le temps s’est virtuellement translaté. Comme les pseudo ranges sont calculés par pluto-gps-sim en tenant compte de ce décalage temporel pour une position au sol imposée, et puisque de toute façon toutes les horloges sont décalées de la même valeur (qui se compense lors de la trilatération), le récepteur ne verra pas sa position bouger. La figure 9 démontre ce concept en présentant d’une part l’impulsion 1 PPS qui représente le temps GPS sur un récepteur U-Blox Neo M8T, et d’autre part la position de ce même récepteur tel que fournie par ses trames NMEA. Nous constatons que le 1 PPS saute par pas de 5 µs que nous avons introduit volontairement toutes les 2 minutes (pour rappel, le 1 PPS d’un récepteur GPS monofréquence fluctue typiquement de ± 100 ns), mais que la position ne s’est de loin pas déplacée des quelques 7 km que laisserait présager un décalage du temps de 25 µs au bout de 10 minutes d’expérience. Quelques sauts de positions correspondent au temps de convergence des boucles d’asservissement du récepteur qui sont quelque peu surprises de ces sauts soudains de temps. Nous avons vérifié que le signal 1 PPS peut aussi être induit à dériver linéairement ou quadratiquement en jouant non pas sur l’offset de l’horloge de chaque satellite, mais sur sa dérivée première (paramètre AF1) ou seconde (AF2).
Fig. 9 : Haut : sortie 1 PPS d’un récepteur U-Blox Neo M8T indiquant le temps GPS sur lequel de nombreux oscillateurs (GPSDO) s’asservissent en faisant confiance au signal issu de la constellation de satellites, ici induite en erreur par pas de 5 µs. Bas : impact négligeable de la dérive de temps GPS induite par notre attaque sur l’estimation de la position du récepteur.
6. Palliatifs
Un numéro spécial récent de Proc. IEEE faisait l’état de l’art sur les attaques sur les systèmes de positionnement par satellite. Une première solution évidente consiste à fusionner multitude de données afin d’identifier une source d’incohérence : ajouter aux signaux issus de multiples constellations de satellites des informations émises au sol telles que WiFi ou téléphonie mobile (GSM, UMTS) réduit le risque, mais ne fait que repousser le problème, puisque ces sources additionnelles sont brouillables ou elles aussi leurrables (penser OpenBSC [15]).
Une faiblesse des constellations GNSS tient en leur très faible signal qui est aisément supplanté par des émetteurs au sol : une tendance tient à se positionner au sol par des signaux issus de constellations de satellites en orbite basse (e.g. Iridium NEXT), avec des signaux au sol considérablement plus puissants et cryptés. L’Europe a malheureusement décidé d’abandonner le déploiement d’un réseau très basse fréquence (VLF) d’émetteurs de localisation (eLORAN) qui pallierait aux attaques sur GPS : les États-Unis maintiennent ce réseau en l’étendant au Japon et à la Corée du Sud – tous deux susceptibles d’être brouillés par leur voisin qu’est la Corée du Nord – tandis que l’Arabie Saoudite, la Chine et la Russie (Chayka) maintiennent leur réseau de stations VLF pour conserver une autonomie vis-à-vis des constellations spatiales de positionnement. Leurrer un signal VLF puissant – 360 kW à 100 kHz pour eLORAN – nécessite une infrastructure autrement plus lourde qu’un émetteur de radio logicielle.
Finalement, après avoir mentionné les contraintes physiques d’une constellation de satellites (décalage Doppler respectant les lois de Kepler, distribution des sources dans l’espace imposées par la mécanique céleste), la solution ultime semble tenir dans l’utilisation d’un réseau d’antennes (ou alternativement d’une unique antenne en mouvement) pour identifier la direction d’arrivée des signaux et leur cohérence avec la géométrie de la constellation. Mener une attaque distribuée dans laquelle une multitude d’émetteurs synchronisés en temps et en fréquence pour reproduire la direction d’arrivée de chaque signal semble actuellement inaccessible, et cette solution semble celle favorisée par la majorité des articles de la revue mentionnée au début de cette section [16][17][18][19][20]. Cette approche s’accommode parfaitement d’une solution tout logiciel du récepteur (radio logicielle), tel qu’en atteste la participation des auteurs de GNSS-SDR [21].
Conclusion
Après avoir rappelé quelques principes de base de fonctionnement de GPS, de la couche physique à la couche logicielle, nous avons démontré l’aisance avec laquelle il est aujourd’hui possible de leurrer GPS, même dans des situations aussi critiques que les systèmes de navigation de voiture. L’objectif est de sensibiliser le lecteur aux dangers associés à une confiance aveugle dans les systèmes de positionnement par satellite, en particulier pour des infrastructures critiques : dans ce cas, des solutions de repli pour pallier un brouillage, voir une détection de leurrage par incohérence des signaux reçus (décalage Doppler en dehors de la gamme physiquement atteignable, puissance de signal excessive) sont nécessaires. Finalement, la solution multi-antennes avec mesure de direction d’arrivée des signaux de la constellation semble la solution la plus robuste pour se prémunir des attaques de leurrage.
Remerciements
Cette étude a été motivée par la création du laboratoire commun FASTLAB entre l’Institut FEMTO-ST, l’Observatoire de Besançon et la société Gorgy Timing. L’équipement acquis dans le cadre du Labex FIRST-TF et Equipex OscillateurIMP a fourni les signaux de référence pour qualifier les divers oscillateurs utilisés dans cette présentation, bien que nous insistions sur la capacité de tout amateur éclairé à reproduire ces expériences. Les références bibliographiques qui ne sont pas librement disponibles sur le web ont été obtenues auprès de Library Genesis à gen.lib.rus.ec, une ressource incontournable pour nos recherches.
Notes
[A] Un balun (balanced-unbalanced) est un transformateur chargé de convertir le signal non-balancé (distinguant masse et signal) vers un signal balancé pour attaquer les deux brins d’antenne qui sont symétriques.
[B] Cet oscillateur est disponible pour une centaine d’euros sur eBay. Alternativement, une horloge rubidium, disponible pour le même ordre de prix en seconde main telle que la Symmetricom X72, fera certainement l’affaire.
Références
[1] T.Humphreys, « How to fool a GPS », www.ted.com/talks/todd_humphreys_how_to_fool_a_gps (2012) puis news.utexas.edu/2013/07/29/ut-austin-researchers-successfully-spoof-an-80-million-yacht-at-sea
[2] J.F. Zumberge et G. Gendt, « The demise of selective availability and implications for the international GPS service », Physics and Chemistry of the Earth 26 (6–8), pp. 637–644 (2001), https://www.gps.gov/systems/gps/modernization/sa/
[3] « Satellite-derived Time and Position: A Study of Critical Dependencies », www.gov.uk/government/uploads/system/uploads/attachment_data/file/676675/satellite-derived-time-and-position-blackett-review.pdf
[4] R.T. Ioannides, T. Pany et G. Gibbons, « Known Vulnerabilities of Global Navigation Satellite Systems, Status, and Potential Mitigation Techniques », Proc. IEEE 104 (6) 1174--1194 (Juin 2016)
[5] K. Zeng & al., « All Your GPS Are Belong To Us: Towards Stealthy Manipulation of Road Navigation Systems », 27th USENIX Security Symposium (2018), disponible à people.cs.vt.edu/gangwang/sec18-gps.pdf
[6] L. Huang et Q. Yang, « Low cost GPS simulator: GPS spoofing by SDR », DEFCON 23 (2015), media.defcon.org/DEF%20CON%2023/DEF%20CON%2023%20presentations/DEFCON-23-Lin-Huang-Qing-Yang-GPS-Spoofing.pdf
[7] D. Robinson , « Using GPS Spoofing to control time », DEFCON 25 (2017), www.youtube.com/watch?v=isiuTNh5P34
[8] J.-M Friedt, G. Cabodevila, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », Open Silicium n°15 (2015)
[9] ESA, « GNSS data processing », gssc.esa.int/navipedia/GNSS_Book/ESA_GNSS-Book_TM-23_Vol_I.pdf et sa liste d’exercices gssc.esa.int/navipedia/GNSS_Book/ESA_GNSS-Book_TM-23_Vol_II.pdf
[10] « Norme RINEX - The Receiver Independent Exchange Format, Version 3.03 », https://kb.igs.org/hc/en-us/article_attachments/202583897/RINEX_303.pdf
[11] « Global Positioning System Standard Positioning Service Signal », www.gps.gov/technical/ps/1995-SPS-signal-specification.pdf (1995)
[12] A. Thiel et M. Ammann, « Anti-Jamming techniques in u-blox GPS receivers », www.u-blox.com/sites/default/files/products/documents/u-blox-AntiJamming_WhitePaper_%28GPS-X-09008%29.pdf (octobre 2009)
[13] W. Lewandowski & al., « Testing Motorola Oncore GPS Receiver and Temperature-Stabilized Antennas for Time Metrology », Proc. 28th Annual Precise Time and Time Interval Systems and Applications Meeting, https://tycho.usno.navy.mil/ptti/1996papers/Vol%2028_37.pdf (1996)
[14] C. Audoin et B. Guinot, « The measurement of time – Time, frequency and the atomic clock », Cambridge Univ. Press (2001)
[15] H. Welte, « OpenBSC network-side GSM stack », SSTIC 2010, www.sstic.org/media/SSTIC2010/SSTIC-actes/Projet_OpenBSC/SSTIC2010-Slides-Projet_OpenBSC-welte.pdf
[16] I.J. Gupta, I.M. Weiss, et A.W. Morrison,, « Desired Features of Adaptive Antenna Arrays for GNSS Receivers », Proc. IEEE 104 (6) 1195--1206 (juin 2016)
[17] J.L. Volakis, A.J. O'Brien, et C.-C. Chen, « Small and Adaptive Antennas and Arrays for GNSS Applications », Proc. IEEE 104 (6) 1221--1232 (juin 2016)
[18] A. Broumandan, A. Jafarnia-Jahromi, S. Daneshmand et G. Lachapelle, « Overview of Spatial Processing Approaches for GNSS Structural Interference Detection and Mitigation », Proc. IEEE 104 (6) 1246--1257 (juin 2016)
[19] M. Cuntz, A. Konovaltsev et M. Meurer, « Concepts, Development, and Validation of Multiantenna GNSS Receivers for Resilient Navigation », Proc. IEEE 104 (6) 1288--1301 (juin 2016)
[20] M.G. Amin, X. Wang, Y.D. Zhang, F. Ahmad, et E. Aboutanios, « Sparse Arrays and Sampling for Interference Mitigation and DOA Estimation in GNSS », Proc. IEEE 104 (6) 1302--1317 (juin 2016)
[21] C. Fernàndez-Prades, J. Arribas, et P. Closas, « Robust GNSS Receivers by Array Signal Processing: Theory and Implementation », Proc. IEEE 104 (6) 1207--1220 (juin 2016)