Lors du précédent article, nous avons parcouru les différents modes d'adressage du 6502, ce qui nous a permis d'élaborer quelques algorithmes simples, notamment pour réaliser des additions ou soustractions sur des nombres entiers de plus de 8 bits et même, des multiplications. Aujourd'hui, nous allons continuer dans cette voie en nous intéressant à la division et même aux nombres décimaux (à virgule), ce qui nous permettra de mettre un pied dans le monde effrayant de la trigonométrie !
L'assembleur, et en particulier l'assembleur 6502 avec toutes ses limitations, n'est certainement pas le meilleur langage pour les opérations mathématiques. Mais avec quelques astuces, on peut faire quelques miracles et cela nous permettra de découvrir comment représenter les nombres.
1. Clarification de la séquence CMP/BCC
Avant de rentrer dans le cœur du sujet, je voudrais clarifier un point qui me paraît important et dont on va avoir besoin par la suite. En effet, sur 6502, la suite d'opcode CMP/BCC est souvent source de confusion. Elle permet d'effectuer un saut uniquement si le registre A est inférieur à une valeur donnée alors que sur la majorité des autres processeurs, elle réalise l'inverse.
En français, on utilise le même mot pour les retenues dans les additions et dans les soustractions. En anglais, on dit « carry » pour les additions et « borrow » (emprunt) pour les soustractions. Sur le 6502, le drapeau C est utilisé dans plusieurs contextes. Pour les opérations de décalage, il s'agit du « bit qui dépasse ». Pour les additions, il est utilisé comme retenue. Mais pour les soustractions, c'est 1-C qui est utilisé comme retenue (borrow) contrairement à ce que l'on trouve ailleurs. Ce choix a été fait pour grandement simplifier l'électronique du 6502, mais cela a une conséquence pénible. En effet, les comparaisons (CMP, CPX et CPY) sont implémentées comme une soustraction dont on ne stockerait pas le résultat, mais qui modifie seulement les drapeaux N, Z, V et C.
Par exemple, si on a l'opération suivante : SBC #25, il y a une retenue seulement si le registre A vaut 24 ou moins. Et dans ce cas, le drapeau C est mis à 0 (puisque pour les soustractions, la retenue est 1-C).
Et de la même façon, la séquence CMP #25 / BCC suite branche au label suite: si A est inférieur à 25.
2. La multiplication par une variable
Les lecteurs fidèles et attentifs auront remarqué que l'on a déjà traité la multiplication entière entre deux variables lors du précédent article. Cependant, aujourd'hui nous allons aller un peu plus loin afin de stocker le résultat sur 16 bits, car nous allons en avoir besoin par la suite. En effet, si on multiplie deux nombres de 8 bits (entre 0 et 255), le résultat ne tient pas toujours (pas souvent en fait !) sur 8 bits. Par exemple, si on multiplie 100 par 100, le résultat ne tient pas entre 0 et 255, mais on a l'assurance qu'il sera entre 0 et 65535. 16 bits suffisent donc pour stocker le résultat, mais on va devoir modifier notre code afin de garder l'ensemble du résultat.
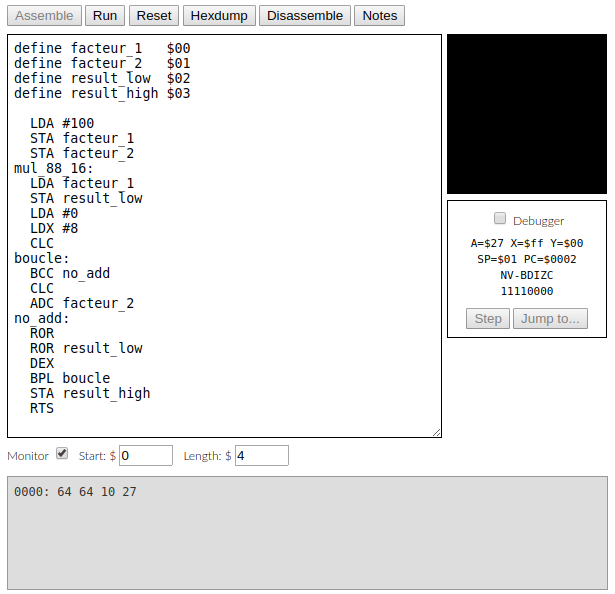
Voici une implémentation possible d'une multiplication 8 bits x 8 bits vers 16 bits. On multiplie chaque bit du premier facteur par le second facteur et on fait progresser le résultat de la droite vers la gauche. Cette méthode est quelques fois appelée « multiplication égyptienne » (voir [1]). Avant l'appel à cette routine, on mettra les facteurs dans facteur_1 et facteur_2. À la fin de l'exécution, les 8 bits de poids forts du résultat sont dans result_high et ceux de poids faibles dans result_low.
Dans cet exemple, on considère l'ensemble (A, result_low) comme une seule entité qui sera le résultat final. C'est pour cela que l'on décale les deux à la suite (ROR / ROR result_low).
En bas de la figure 1, vous pouvez voir les valeurs en hexadécimal de facteur_1, facteur_2, result_low et result_high : $64, $64, $10, $27, soit 100, 100, 16 et 39 en décimal. On a bien 39*256+16 = 9984+16 = 10000 = 100x100.
Je vous encourage à copier ce bout de code dans [2] et à l'exécuter, en changeant les valeurs de facteur_1 et facteur_2. Ce code est assez complexe et plein de subtilités. Si vous arrivez à le comprendre, la suite vous semblera plus facile, sinon c'est que vous êtes un être humain normal. Notez que vous pouvez exécuter ce programme pas à pas en cliquant dans la case « Debugger », ce qui permet de suivre l’évolution des registres A et X et des drapeaux (mais pas beaucoup plus, hélas).
3. Les divisions
Même si on l'utilise moins souvent que la multiplication, la division est une opération importante à avoir dans sa besace. Elle est cependant nettement plus complexe à mettre en œuvre.
3.1 Diviser par une puissance de 2
Comme pour les multiplications, les divisions par une puissance de 2 (2, 4, 8, 16, etc.) sont assez simples à réaliser, puisqu'il s'agit juste d'un décalage de bits vers la droite. Nous avons d'ailleurs utilisé cette idée pour la multiplication précédente, en considérant deux valeurs de 8 bits comme une seule de 16 bits.
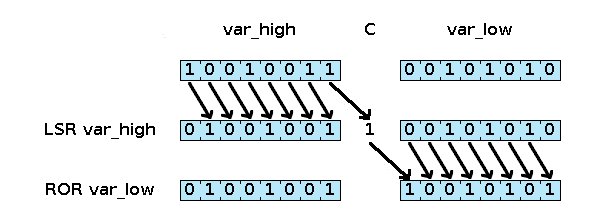
La figure 2 détaille le comportement d'un décalage sur 16 bits à l'aide des opcodes LSR et ROR. Notez les différents comportements de LSR et ROR. L'exemple suivant implémente par exemple une division par 4, en effectuant deux rotations sur 16 bits vers la droite.
3.2 La division par 3
Pour diviser par d'autres valeurs, le processus risque d'être beaucoup plus compliqué. On peut (et on va !) utiliser un algorithme général qui fonctionne pour toutes les valeurs, mais pour diviser par trois par exemple, on peut aller beaucoup plus vite.
Pour cela, on peut remarquer que 3 * 85 = 255, donc diviser par 3 revient à multiplier par 85/255. Or, on sait facilement multiplier par 85 et diviser par 256 qui est une puissance de 2. Vous allez me dire qu'on devrait diviser par 255 et non 256, ce qui est vrai, mais on effectue en fait une division entière (on se fiche pour l'instant de ce qu'il y a après la virgule), et il suffit de décaler un peu la valeur de départ pour ne pas avoir à se soucier de la différence.
Finalement, on arrive à l'idée que pour tout nombre N, N/3=((N+1)*85)/256.
Par exemple pour N=27, ((27+1)*85)/256 = (28*85)/256 = 2380/256=9.3, ce qui donne bien 9 en arrondissant à l'entier inférieur.
Pour N=42, on trouve 14.277 soit 14 en valeur entière, etc. (promis, ça fonctionne avec toutes les valeurs de N entre 0 et 255)
La valeur 85 est d'ailleurs particulièrement intéressante, puisqu'elle s'écrit %01010101 en binaire. Et donc multiplier un nombre par 85 consiste juste à additionner ce nombre tous les deux décalages (multiplication par 4). La partie compliquée du code suivant n'est donc que la gestion des additions sur 16 bits et des décalages sur 16 bits que nous venons de voir. On commence par mettre N+1 dans les variables f1 et f2, avant d'effectuer f2 = f2 + 4 * (f1 + 4 * (f1 + 4 * f1)). Après cela, le résultat de la division par 3 est dans f2_high.
Ce code (que je vous encourage à tester à l'aide de [2]) est je l'espère assez simple à suivre, mais il n'est pas très efficace. J'ai trouvé sur le forum NESDEV (voir [3]) plein d'algorithmes de division par toutes les valeurs entre 2 et 32. Notamment, pour la division par 3, on trouve ce bout de code, nettement plus court, qui ne garde pas inutilement les bits de poids faibles du résultat.
3.3 La division par 5
De la même façon, pour diviser par 5, on multipliera par 51 puisque 5 * 51 = 255.
On pourra donc utiliser l'algorithme précédent, en utilisant la formule N/5=((N+1)*51)/256.
Mais là encore, on peut se référer à [3] pour cette implémentation étonnamment courte :
En continuant de chercher les facteurs premiers de 255, on pourrait trouver des façons de diviser par 17 ou 51, mais l'occasion se présente plus rarement !
En revanche, on utilisera des divisions successives pour diviser par 6, par 10 ou 15, par exemple. Pour les autres valeurs, on utilisera soit [3] soit l'algorithme général présenté dans la partie suivante.
3.4 Les divisions par une valeur variable
L'algorithme général de division peut être un peu ardu à comprendre, c'est pourquoi je préfère à nouveau commencer par présenter une version 8 bits avant de passer à la nécessaire version 16 bits. L'implémentation que je propose dans le code suivant et la figure 3 est le même que celle étudiée en classe de CE2 (ou CM1, c'est vieux tout ça !) À chaque tour (un par chiffre, donc 8 ici), on regarde combien de fois on peut avoir notre diviseur dans le dividende/reste. L'avantage d'être en binaire est que la réponse est forcément 0 ou 1. On ajuste donc le résultat et on enlève éventuellement la valeur du diviseur au reste. Dans ce code, A contient le reste courant.
Quelques remarques sur cet algorithme :
- La même variable stocke le dividende et le quotient, ça permet d'avoir un code plus compact, mais demande plus d'attention pour tout comprendre.
- Le registre A contient en permanence le reste courant.
- Le cœur même de ce code est composé des lignes ROL quotient et ROL A, ce qui permet de passer au chiffre (binaire) suivant.
- À chaque tour, on a donc un décalage et une soustraction optionnelle.
- La division de 42 (101010 en binaire) par 5 (101 en binaire) telle qu'on la fait à l'école ressemble à ceci :
Il semble y avoir moins d'étapes parce qu'on n'écrit pas les zéros au début des nombres et que l'on commence par « abaisser » directement 101.
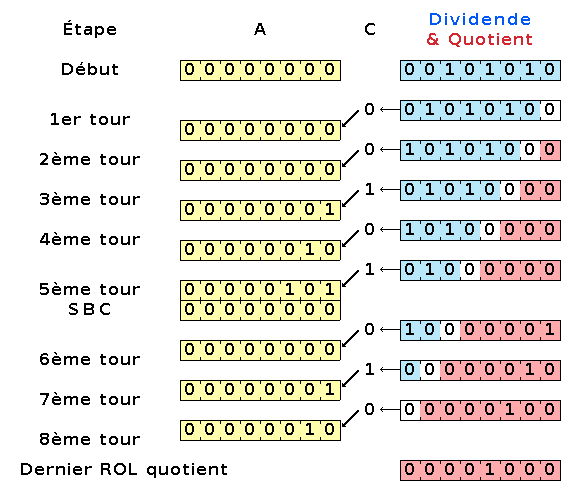
Sur la figure 3, on voit ce code en action pour diviser 42 par 5. Je n'ai représenté que le contenu de la variable quotient, du registre A et du drapeau C. À chaque tour, ces trois valeurs sont juste décalées, sauf au cinquième tour où le reste (A) n'est pas inférieur au diviseur, et où il y a une soustraction. Cela a pour effet d'introduire un 1 dans le quotient.
Une fois cette partie comprise, on peut passer à l'implémentation sur 16 bits, ce qui revient à remplacer les décalages et soustractions par leurs équivalents sur 16 bits et un tout petit peu d'astuces en plus que je vous laisse découvrir :
Comme précédemment, je vous invite à copier cette fonction dans [2] et à tester le tout. Avec les valeurs indiquées, on obtient bien 21 comme quotient et 167 comme reste, mais n'hésitez pas à tester avec différentes valeurs.
4. La virgule fixe
Nous voici donc en possession des quatre opérations de base, mais uniquement pour les nombres entiers. Si on veut aller plus loin avec des opérations plus complexes (racine carrée, logarithme, trigonométrie, etc.), il va nous falloir des nombres à virgule.
Il existe deux grandes façons de représenter de tels nombres dans nos machines qui ne savent manipuler que des entiers : la virgule fixe ou la virgule flottante.
Celle qui nous intéresse est la première. Elle consiste à avoir un nombre constant de chiffres (binaires) avant et après la virgule. Par exemple, avec nos registres de 8 bits, on pourrait décider d'avoir 3 bits avant et 5 bits après. Cela serait tout à fait possible, mais la précision ne serait pas très grande et accéder aux trois bits de la partie entière ne serait pas très aisé.
Maintenant que l'on sait manipuler des données sur 16 bits en utilisant deux emplacements de mémoire de 8 bits, il semble intéressant d'avoir 8 bits avant la virgule et 8 bits après. Un nombre en virgule fixe sera donc simplement deux octets et on pourra représenter des nombres entre 0 et 255, avec une précision de 1/256. Par exemple, 10 sera représenté par (10 et 0), 3.5 sera représenté par (3 et 128), car 3.5 = 3 + 128/256, et 1/3 sera représenté par (0 et 85). À chaque fois, on a un octet pour la partie entière (qu'on suffixera par _ent) et un octet pour la partie décimale (_dec).
Un petit mot sur la virgule flottante
Il existe une autre façon de représenter les nombres à virgule en informatique et c'est même la façon la plus répandue, mais elle est plus complexe à mettre en œuvre : la virgule flottante. C'est cette représentation qui a donné son nom au type de variable « float » que l'on rencontre dans de nombreux langages de programmation.
Dans ce mode, on choisit un nombre de bits, souvent 32 (mais cela peut aussi être 16, 64 ou même 80). Le nombre de bits après la virgule est toujours fixe (par exemple, 23 pour les « floats » les plus courants) et on suppose qu'il y a un 1 avant la virgule. On appelle ces chiffres la mantisse.
En plus de cette mantisse, on a un certain nombre de bits (8 pour les « floats ») représentant un exposant (signé) en base deux. Par exemple, avec une mantisse de 01010…0 (avec que des 0 dans les ...) et un exposant de +5, on a le nombre 1.0101 x 2^5, soit 101010 en binaire et 42 en décimal (je savais bien que c'était la bonne réponse !).
Comme vous le voyez, c'est nettement plus complexe que pour la virgule fixe, mais cela permet de représenter des nombres beaucoup plus grands ou beaucoup plus petits. Cependant, la mise en œuvre est tellement complexe que le document qui définit les nombres à virgules flottantes codés sur 32 bits est un PDF de 70 pages (Il s'agit de l'IEEE 754-2008, voir [4] ou [5]) !
4.1 Opérations simples en virgule fixe
Même si tout cela peut paraître assez compliqué, la bonne nouvelle est que réaliser une addition ou une soustraction en virgule fixe se fait exactement de la même manière qu'avec des entiers de 16 bits.
On a donc le code suivant :
Rien de surprenant, on a tout fait pour que cette partie soit simple. Et évidemment, les fonctions permettant de prendre la partie entière ou la partie décimale d'un nombre sont immédiates. En virgule flottante, c'est une autre paire de manches !
4.2 La multiplication en virgule fixe
Pour la multiplication, les choses sont un peu plus complexes si on ne veut pas perdre trop de précision. En effet, il ne suffira pas de multiplier les parties entières entre elles.
Si on a deux nombres à virgule fixe N (= N_ent + N_dec/256) et M (= M_ent + M_dec/256), leur produit est :
On se retrouve avec trois termes à additionner : A+B+C. A est une simple multiplication 8 bits x 8 bits vers 8 bits, et participera à la partie entière du résultat. Pour B en revanche, on va devoir effectuer deux multiplications 8 bits x 8 bits vers 16 bits et une addition 16 bits, c'est un peu plus complexe, mais cela n'utilise que des opérations que l'on sait déjà faire. Pour C, on effectuera aussi le même genre de multiplication, mais on ne gardera que les bits de poids forts (les bits de poids faibles sont perdus, faute de précisions).
Il suffit ensuite d'assembler le résultat en prenant des morceaux de A et de B pour la partie entière et des morceaux de B et de C pour la partie décimale.
Plutôt que de donner le code complet de la multiplication en virgule fixe dans ces colonnes, ce qui prendrait trop de place, voici une liste précise des étapes. Chaque étape consiste en l'appel d'une fonction que l'on a déjà détaillée, précédent de la préparation des paramètres et de la sauvegarde des résultats. J'appelle mul8 une multiplication 8 bits x 8 bits vers 8 bits et mul16 une multiplication 8 bits x 8 bits vers 16 bits.
On notera que A est une variable 8 bits alors que B, C et resultat sont des variables 16 bits. De plus, pour simplifier le tout, j'ai passé sous silence la gestion des nombres négatifs (comme c'est le cas tout au long de cet article).
4.3 La division en virgule fixe
On peut voir la multiplication précédente comme une multiplication 16 bits x 16 bits vers 32 bits dans laquelle on ne garderait que les 16 bits centraux.
Même s'il y a des méthodes (un peu) plus efficaces, on pourra procéder exactement de la même manière pour la division en virgule fixe, en réalisant une division sur 32 bits. Nous venons de voir en détail les divisions sur 8 bits et celles sur 16 bits, écrire la même chose sur 32 bits ne présente pas vraiment beaucoup d'intérêt, il faut juste jongler avec plus de variables 8 bits.
5. La trigonométrie
Les réfractaires aux maths (à qui je dis bravo d'être arrivés jusque là !) se demandent sûrement ce qui peut bien me donner envie de les torturer à grands coups de fonctions sinus ou co-sécante qui ont peuplé leurs pires cauchemars. La première raison est que je suis sadique, évidemment. Mais c'est aussi utile dans plein de domaines dont la 3D, la physique et que cela va me permettre de présenter un algorithme plutôt astucieux permettant de calculer à la fois le sinus et le cosinus d'un angle, en assez peu d'étapes.
5.1 Première méthode : une table précalculée
La première méthode qui vient à l'esprit pour implémenter une fonction compliquée en assembleur est l'utilisation d'une table de valeurs. Pour cela, on calcule à l'avance les valeurs des sinus et cosinus de tous les angles entre 0° et 360° et on les place dans un tableau en mémoire.
Cela peut fonctionner dans certains cas, mais ça prend une place folle en mémoire, sans parler du fait qu'il est compliqué d'adresser une zone mémoire plus grande que 256 octets avec un 6502.
On peut alors se limiter à une table plus petite, ne contenant les valeurs que pour les degrés de 10 en 10, cela nous fait une table de 72 octets (36 si on ne stocke que les parties décimales), mais on perd en précision, et pour les valeurs qui ne sont pas dans la table, il faut au moins faire une interpolation linéaire, ce qui implique des multiplications et des divisions en virgule fixe, bref, une horreur !
On gardera cette méthode que pour des cas très précis où l'on connaît à l'avance l'ensemble des valeurs en degré dont on va avoir besoin.
5.2 Deuxième méthode : développement limité
Une autre possibilité (pour les plus matheux) consiste à utiliser un développement limité des fonctions sinus et cosinus, c'est-à-dire utiliser une approximation polynomiale.
Par exemple, sin(x) = x-x^3/6+x^5/120-x^7/5040... Ça peut sembler une bonne idée, mais dès que x augmente un peu, il faut pas mal de termes, et c'est bourré de multiplications et de divisions. Ça a l'avantage de ne pas prendre beaucoup de place en mémoire (contrairement à la méthode précédente), mais c'est complexe à mettre en œuvre et très gourmand en temps d'exécution.
5.3 La méthode CORDIC
Il existe une méthode intermédiaire nommée CORDIC (pour COordinate Rotation DIgital Computer, voir [5]) qui ne nécessite qu'une toute petite table (un octet par bit de précision que l'on désire avoir, soit 8 dans notre cas), qui est facile à implémenter et très rapide puisqu'elle calcule à la fois le sinus et le cosinus d'un angle à peu près aussi rapidement qu'un seul calcul de division.
Dit comme ça, ça a l'air un peu miraculeux, et pourtant cela découle assez directement des formules trigonométriques suivantes :
Et oui ! C'est à ce moment de notre vie que ces formules ont enfin un sens ! Plus exactement, on va utiliser la forme où on met cos(b) en facteur pour faire apparaître une tangente (si vous ne connaissez pas ces formules, pas de panique, on peut évidemment les retrouver sur Internet et on a juste besoin de savoir qu'elles sont vraies) :
J'ai ajouté les formules pour cos(a-b) et sin(a-b) qui sont presque les mêmes, à un signe près.
Mine de rien, cela signifie que si l'on connaît sin(a) et cos(a), on peut calculer facilement cos(a+b) et sin(a+b) pour peu que cos(b) et tan(b) soient connus ou faciles à trouver et cela va nous permettre d’affiner les valeurs que l’on calcule (le sinus et le cosinus) à chaque étape.
Il nous faut une autre idée pour implémenter la méthode CORDIC, c'est celle du « juste prix ». Vous avez forcément joué à ce jeu idiot qui consiste à trouver un nombre choisi par quelqu'un d'autre qui vous répond « plus grand » ou « plus petit » à chaque essai. Une bonne méthode consiste à commencer au pif, puis à diviser l'intervalle restant par deux (ce qu’on appelle une recherche dichotomique). Par exemple, on pourrait avoir le dialogue suivant :
Et bien c'est exactement ceci que l'on va utiliser ici.
Pour calculer le sinus et le cosinus d'un angle alpha, on va partir d'un angle au hasard (mais dont on connaît le sinus et le cosinus) et le comparer à alpha. Si notre angle est trop petit, on ajoutera un angle moins grand en corrigeant les sinus et cosinus que l'on connaît avec les formules précédentes. Et s'il est trop grand, on fera pareil, en utilisant les formules pour cos(a-b) et sin(a-b). Il suffit ensuite de continuer avec des changements d'angle de moins en moins grands.
Il reste tout de même à choisir nos « b » intelligemment. En fait, on va plutôt choisir les valeurs de tan(b) pour qu'elles soient égales à 1/2, 1/4, 1/8, 1/16, etc. Comme cela, à l'étape n, on aura ce calcul à faire :
Et ceci nous simplifiera beaucoup la tâche, puisque diviser par une puissance de deux est très facile : il s'agit juste d'un décalage à droite ! Il reste le problème du cos(b), mais ce n'en est pas vraiment un, en fait. En effet la multiplication par cos(b) est faite à chaque étape, et par une valeur de b que l'on connaît à l'avance (cos(b) = cos(-b)). Donc au bout de 9 étapes, on aura en facteur cos(arctan(1/2))*cos(arctan(1/4)*...*cos(arctan(1/2^9)). On pourra donc multiplier tout à la fin (ou au début !) de l'algorithme nos sinus et cosinus par cette valeur qui ne dépend pas du tout de l'angle alpha.
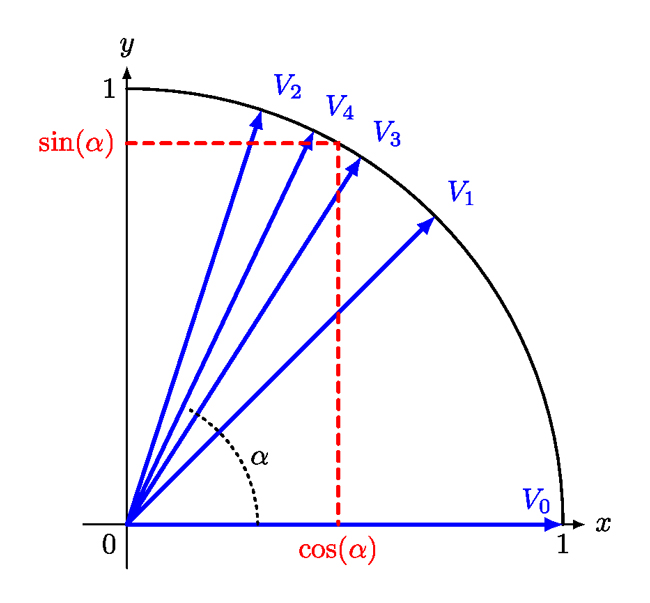
La figure 4 montre comment l'angle choisi « au hasard » à l’horizontale, V0 (0 est un nombre au hasard comme les autres !) converge vers l'angle voulu en passant par V1, V2, V3 puis V4.
5.4 Implémentation de la méthode CORDIC
L'implémentation de cette méthode, même si elle n'est pas très complexe, prend beaucoup de lignes en assembleur, aussi, je préfère vous donner une version qui mélange un peu de pseudo-code et d'assembleur (avec une syntaxe plus inspirée de « vrais » assembleurs que ce qui est disponible sur [2], ce qui préfigure de ce qu'on utilisera dans les prochains articles). Cela devrait être plus facile à suivre :
Note : on suppose que l'angle de départ est compris entre 0 et pi/2 afin de simplifier un peu, mais cela ne change pas fondamentalement l'algorithme.
La méthode CORDIC permet aussi de calculer plein d'autres fonctions normalement très complexes comme les logarithmes, les exponentielles, des racines carrées, etc.
6. La prochaine fois
On en a fini avec les calculs compliqués, au moins pour un bon moment. La prochaine fois, on s'intéressera à un autre composant de la NES (Nintendo Entertainment System) : le PPU (Pixel Processing Unit) ce qui nous permettra d'afficher quelque chose sur l'écran d'une vraie NES ou d'un émulateur. Rassurez-vous, on programmera toujours en langage d'assemblage 6502, mais on utilisera enfin un assembleur plus évolué que celui que je vous ai proposé jusque là.
Références
[1] https://fr.wikipedia.org/wiki/Technique_de_la_multiplication_dans_l%27%C3%89gypte_antique
[2] https://skilldrick.github.io/easy6502/
[3] http://forums.nesdev.com/viewtopic.php?f=2&t=11336
[4] http://irem.univ-reunion.fr/IMG/pdf/ieee-754-2008.pdf et https://fr.wikipedia.org/wiki/IEEE_754



 Ajouter à une liste de lecture
Ajouter à une liste de lecture