Nous nous proposons d’aborder un problème complexe de traitement d’image, à savoir la reconstruction de la structure tri-dimensionnelle d’un objet à partir d’une multitude de photographies de ce même objet prises depuis des points de vue différents. Parmi les outils libres pour atteindre ce but, la solution la plus sérieuse pour atteindre l’objectif d’un modèle quantitatif de l’objet (dimensions en unités réelles, en opposition aux nuages de points gradués en pixels) est un outil mis à disposition par l’Institut Géographique National (IGN) et orienté vers la production de modèles numériques de terrain et de façades : la suite de logiciels Apero et MicMac.
Dans ce contexte, notre présentation complète une étude antérieure qui s’appuyait sur le traitement d’informations spatialisées en s’appuyant sur les modèles numériques d’élévation [1] : ici, plutôt qu’utilisateur, nous serons producteurs de tels jeux de données (nous verrons qu’il y a encore du chemin avant que ce jeu de données que nous générerons nous-mêmes soit réellement exploitable et comparable aux jeux de données librement disponibles sur le web). Sans prétendre concurrencer la résolution d’outils professionnels que sont les LiDAR (version optique du RADAR qui mesure le temps de vol d’une impulsion électromagnétique dans les longueurs d’ondes visibles ou infrarouges) - outils extrêmement coûteux et complexes à mettre en œuvre - le traitement de photographies numériques offre une solution certes moins performante mais souple d’emploi, qui répond à de nombreux besoins dont nous exposerons quelques exemples ludiques ici.
La génération de modèles tridimensionnels d’objets à partir de séries de photographies numériques est un domaine en plein essor [2], probablement du fait de la démocratisation des ressources de calcul quasi-infinies et des capteurs optiques d’excellentes qualité et résolution à des prix dérisoires [3]. Le mot clé décrivant cette procédure de traitement d’images - qui inclut non seulement la partie traitement du signal mais aussi des règles d’acquisition des photographies numériques et, à terme, les outils de rendu et de traitement du nuage de points - est Structure from Motion, ou SfM suivant cet acronyme anglophone.
1. Principe de SfM
De nombreux outils permettent d’acquérir des images permettant une reconstruction tridimensionnelle de l’objet imagé. Celui qui a induit le plus de publicité auprès du grand public est probablement la Kinect de Microsoft, qui projette un nuage de points dans les longueurs d’ondes infrarouges (invisibles à l’œil nu) pour une reconstruction de la scène illuminée. Cette méthode ne s’applique qu’en intérieur et pour des portées réduites à quelques mètres, sans intérêt pour notre objectif de construire des modèles de terrain sur des extensions de plusieurs dizaines de mètres voire kilomètres. Les outils professionnels de cartographie par mesure de temps de vol d’impulsions laser (LiDAR) sont financièrement inaccessibles à l’amateur. Nous allons donc envisager d’utiliser les nombreux capteurs optiques qui nous entourent - smartphone, webcam, appareil photographique - pour générer des nuages de points tridimensionnels représentatifs de la scène observée sous différents points de vue.
Comme toujours en traitement d’images, le cœur de la méthode de reconstruction de la structure tridimensionnelle d’un objet photographié sous différents angles tient en la qualité des images initiales. Ne pas respecter les contraintes de prises de vues induit un échec presque certain du traitement qui va suivre (nous en rediscuterons plus tard, section 2). Une fois les images de l’objet acquises selon des principes exactement opposés à ceux du panorama - au lieu de prendre plein de photographies dans des directions différentes depuis un même site, on vise un unique objet selon des points de vue différents - l’objectif consiste à trouver les points identiques de l’objet sur diverses prises de vues. Nous avions déjà considéré dans ces pages le concept d’intercorrélation [4] pour retrouver des motifs identiques sur diverses images et en déduire le déplacement de l’objet considéré, mais ces algorithmes sont excessivement sensibles aux rotations et homothéties de vignettes d’images. Une combinaison efficace de traitement rendant le calcul insensible aux rotations et homothéties (analyse multi-échelles) a produit l’algorithme SIFT1 [5] qui comble ces lacunes de sensibilité de la simple intercorrélation. L’identification des points remarquables visibles sur diverses photographiques est un point clé de la chaîne de traitement, mais n’est que la première étape de la reconstruction du nuage de points qui nécessite d’identifier les propriétés optiques de l’objectif et les positions de prises de vues de la caméra, de retrouver la position de chaque point commun compte tenu de ces contraintes géométriques, et finalement visualiser le nuage de points résultant (typiquement quelques centaines de milliers de points)2 [6].
Il existe de multiples implémentations de ces concepts en vue de divers contextes et objectifs : nous avons en particulier constaté la disponibilité de Python Photogrammetry Toolbox (PPT), bundler3 et la solution que nous avons choisie d’approfondir, la série d’outils MicMac (Multi-Images Correspondances, Méthodes Automatiques de Corrélation4) de l’Institut Géographique National (IGN) (logiciels.ign.fr/?-Micmac,3-). En plus de la garantie de sérieux de l’utilisation par l’institut géographique et la perspective d’analyses quantitatives des nuages de points générés, un auteur qui commence sa documentation en expliquant qu’il a créé le logiciel parce qu’il « thought it would be fun to be able to make 3D models from my holidays pictures » [7] ne peut qu’avoir produit une excellente application qui réponde à nos ambitions. Nous verrons dans les pages qui suivent que nous ne serons pas déçus. Le documentaire d’Arte « Les derniers secrets de l’armée de terre cuite »5 propose que cette technologique révolutionne la capacité à archiver les informations tridimensionnelles : sans exagérer un tel enthousiasme, il nous semble en effet qu’il s’agisse d’une technologie accessible à tout lecteur motivé ne nécessitant aucun investissement financier autre que le temps d’apprendre à se servir des outils mis à disposition tel que décrit ci-dessous. L’accès à des capteurs optiques d’excellente qualité pour un coût dérisoire, d’une puissance de calcul quasi-infini dans chaque ordinateur, et la prolifération des vecteurs de vol que sont les drones, réunissent les conditions pour voir le domaine de la reconstruction tridimensionnelle de nuages de points à partir de scènes photographiées de divers points de vue se démocratiser et accéder à de multiples domaines d’utilisateurs [8, 9, 10] au-delà du cercle restreint de la vision par ordinateur.
La principale inspiration qui a initié cette prose a été la brève documentation fournie à http://combiencaporte.blogspot.fr/2013/10/micmac-tutoriel-de-photogrammetrie-sous.html, complétée évidemment par une lecture complète de la notice de mise en œuvre de MicMac fournie dans l’archive disponible en ligne. L’installation se fait en effet sans problème en rapatriant l’archive par mercurial6 et en suivant les consignes de LISEZMOI, que personne ne lit jamais et donc que nous reproduirons ici : en partant du répertoire contenant les sources $MICMAC
mkdir build && cd build && cmake ../ -DWITH_QT5=1 && make && make install
place dans $MICMAC/bin les exécutables (qu’on ajoutera à son $PATH) et dans $MICMAC/lib les bibliothèques, chemin qui mérite donc à être ajouté au début de son LD_LIBRARY_PATH. La documentation, contenue dans $MICMAC/Documentation/DocMicMac.tex, sera précieuse tout au long de cette présentation. Par ailleurs, chaque commande est associée à une aide en ligne complète “relativement” compréhensible : mm3d -help fournit la liste des outils MicMac, tandis que mm3d outil -help fournit les options de chaque outil.
2. Prise en main : conditions des prises de vues
Nous verrons ci-dessous que MicMac est capable de reconstituer tous les paramètres de prise de vue (position de la caméra, propriétés de l’objectif, focale) même en lui donnant des paramètres initiaux complètement erronés, mais atteindre un objectif aussi ambitieux nécessite de respecter une contrainte : toutes les photographies doivent être prises avec le même appareil photographique7, dans les mêmes conditions d’illumination (proscrire en particulier le flash qui induit des ombres portées variant avec le point de vue) et surtout avec la même focale (ou grossissement). La qualité du capteur optique n’a que peu d’importance : nous verrons ci-dessous des exemples pris avec un téléphone portable, une caméra digne d’une webcam, ou un appareil photographique numérique compact (tous bien loin du réflexe de compétition), mais en respectant la contrainte des 80% de recouvrement de la scène d’une image à l’autre, et focale fixe. Le lecteur plus rigoureux consultera http://www.tapenade.gamsau.archi.fr/TAPEnADe/PR_facades.html pour des considérations plus formelles sur les conditions de prises de vues, mais nous verrons plus bas que nous avons pu exploiter des séquences de prises de vues aériennes dans des documentaires télévisés donc le respect strict de ces règles n’est pas absolument nécessaire pour atteindre un résultat exploitable. Néanmoins, nous encourageons fortement le lecteur à consulter ce manuel de protocole de prises de vues qui, malgré son nom austère, fournit les règles de prises de vues (parfois difficiles à respecter) pour optimiser les qualités des photographies : en particulier, la page 9 (figure 11) indique comment photographier au mieux un bâtiment en prenant des photographies de divers angles, celles qui serviront à relier les diverses prises de vues de celles qui serviront à générer le nuage de points...
Avant d’engager la démarche de traitement, nous devons renseigner les propriétés optiques des instruments de prise de vue utilisés qui ne sont pas encore renseignés dans la base de données de MicMac. Cet ajout se fait dans le répertoire des sources à$MICMAC/include/XML_User/DicoCamera.xml en y incluant, pour le Panasonic TZ-10 et téléphone Samsung Galaxy S3, les informations contenues dans l’entête EXIF (nom de la caméra) et les dimensions (en millimètres) du capteur optique :
<?xml version="1.0" ?>
<MMCameraDataBase>
<!-- Pana TZ10 DSLR -->
<CameraEntry>
<Name> DMC-TZ10 </Name>
<SzCaptMm> 6.0 4.0 </SzCaptMm>
<ShortName> DMC-TZ10 </ShortName>
</CameraEntry>
<!-- Telephone Samsung S3 -->
<CameraEntry>
<Name> GT-I9300 </Name>
<SzCaptMm> 4.54 3.42 </SzCaptMm>
<ShortName> GT-I9300 </ShortName>
</CameraEntry>
</MMCameraDataBase>
L’information que nous fournissons dans SzCaptMm est la dimension du capteur optique en mm (souvent disponible sur le web), tandis que GT-I9300 rapporte le nom de l’appareil photographique tel que fourni dans l’entête EXIF (exiftool photo.jpg | grep Model).
Nous allons désormais décrire en détail la séquence de traitement proposée par Micmac qui va se décomposer en quatre étapes : identifier les structures remarquables sur des couples de photographies, calculer la position et les propriétés optiques de l’instrument de prise de vue à partir de ces points remarquables, visualiser ces informations pour valider la pertinence de ces étapes de traitement (une caméra placée dans une position aberrante résultera dans l’échec de la suite du traitement et indique que les paramètres de calcul des étapes précédentes ou les conditions de prises de vues sont incorrects), et finalement générer un nuage de points dense en plaçant dans l’espace tous les pixels des photographies représentant un même objet.
3. Premier essai ... au coin
Commençons par le résultat que nous allons atteindre : un nuage de points d’un coin parfaitement structuré par les fibres du bois ou par une carte fixée au mur (Fig. 1), une condition idéale de travail présentant un bon contraste et une bonne profondeur favorisant la recherche des points homologues entre les diverses photographies8. Nous verrons que l’obtention de ce résultat se résume par l’exécution séquentielle de 4 commandes : Tapioca, Tapas, Malt et Nuage2Ply. La majorité de ces applications sont capables de tirer parti des architectures d’ordinateur possédant plusieurs cœurs de calcul ou processeurs, réduisant significativement le temps de calcul en jonglant judicieusement sur la séquence d’exécution des processus.
Figure 1 : Haut : quatre photographies d’un coin reconstitué (bas) sous forme d’un nuage de 8,9 millions de points. La représentation du bas à droite inclut la position de la caméra au moment des prises de vues sous forme de triangle vert dont l’ouverture est représentative de la focale de l’appareil de prise de vue, et le sommet placé au niveau du plan focal. La zone “blanche” derrière l’équerre dans le coin supérieur gauche correspond à une région qui n’est pas visible sur l’image de référence (P1030124.JPG) et aucun point n’y a donc été associé dans le nuage.
Le plus important dans l’utilisation de MicMac est de comprendre la philosophie du logiciel : partant de photographies numériques ou numérisées dans le plan arbitraire du capteur optique de l’instrument de prise de vue, l’objectif sera de passer par diverses phases de réorientation des repères pour passer d’une description bi-dimensionnelle de la scène vers un nuage de points tridimensionnel. Chaque étape se traduit par la création d’un répertoire contenant les fichiers d’orientation, préfixé de Ori-. Ainsi, les divers calculs prendront en entrée le nom du répertoire contenant le résultat de l’étape précédente, et le nom du répertoire qui contiendra le résultat de la nouvelle étape. Omettre un nom de répertoire induira l’utilisation d’un nom par défaut, de nomenclature pas toujours évidente au départ. Ainsi, si nous commençons par calibrer les propriétés optiques de l’appareil photographique sur un jeu dédié de photographies, nous indiquerons que le résultat se trouvera dans un répertoire Ori-Calib par exemple en proposant comme argument de la commande appropriée Out=Calib. Lors de la séquence de traitement suivante qui vise à appliquer cet étalonnage à toutes les photographies, nous exploiterons le résultat précédent par InOri=Calib Out=Suivant pour stocker le résultat dans Ori-Suivant.
La séquence initiale de traitement que nous suivrons est directement inspirée de http://combiencaporte.blogspot.fr/2013/10/micmac-tutoriel-de-photogrammetrie-sous.html. Pour résumer cet excellent tutoriel :
1 - Le traitement commence par rechercher les points de correspondance (dit homologues) entre les diverses photographies au moyen de l’outil Tapioca. La documentation de MicMac [7, section 3.3.1] nous informe que le résultat de ce calcul est contenu dans le répertoire Homol, dont les fichiers sont simples à interpréter puisque contenant les coordonnées de début et de fin de déplacement de tous les motifs identifiés entre toutes les paires d’images (fichier au format ASCII si on a pris soin de conclure la commande Tapioca par l’option ExpTxt=1). À titre d’illustration, nous indiquons (Fig. 2) les vecteurs de déplacement des points homologues identifiés par SIFT pour une paire de photographies prises lors d’un vol au-dessus du Spitsberg (seul 1/10ème des points a été affiché pour ne pas surcharger les figures).
Figure 2 : Points homologues identifiés sur deux photographies successives (gauche et milieu), et superposition des deux photographies codées en couleur pour démontrer que les mêmes structures remarquables se retrouvent aux deux extrémités des vecteurs de déplacement, et ce malgré l’homothétie et la rotation entre les deux jeux de données. Les points homologues sont renseignés dans le répertoire Homol créé par Tapioca dans un format ASCII lisible par GNU/Octave si l’option ExpTxt=1est fournit.
Cet exemple nous permet de nous attendre à une mauvaise résolution de l’analyse sur les surfaces homogènes de neige et de glace qui risquent de manquer de points d’accroche.
En pratique, nous lançons :
mm3d Tapioca MulScale ".*jpg" 300 1000 ExpTxt=1
Bien que des expressions régulières POSIX (qui ne sont pas les mêmes que les regexp du shell !) puissent être utilisées pour définir la séquence de fichiers à traiter, nous avons pris l’habitude de nommer toutes les photographies brutes à traiter par l’extension .jpg, et les fichiers annexes (masques, homothéties des photographies de référence) par l’extension .JPG. Dans cette commande, la recherche des points remarquables visibles sur plusieurs photos s’effectue pour des résolutions dans le plus grand axe de la photographie allant de 300 à 1000 pixels afin d’accélérer le calcul : remplacer 1000 par -1 induirait une recherche jusqu’à la résolution maximale de la photographie, au détriment du temps nécessaire à faire aboutir cette étape. Il semble accepté que la plus haute résolution soit de l’ordre du tiers à la moitié de la résolution des photographies originales,
2 - Les points de correspondance entre photographies étant identifiés, les propriétés optiques des objectifs et du capteur sont calculées par Tapas. Dans un premier temps un sous-ensemble où toutes les photographies sont exploitées pour caractériser les propriétés optiques, modèle qui est ensuite appliqué à l’ensemble des données
mm3d Tapas RadialStd ".*jpg" Out=Cal1
mm3d Tapas AutoCal ".*jpg" InCal=Cal1 Out=Ori1
Les extensions Cal1 et Ori1 se traduisent par la création des répertoires Ori-Cal1 et Ori-Ori1 : il s’agit des répertoires contenant les résultats des calculs qui seront fournis comme argument pour l’étape suivante du traitement,
3 - La position et l’orientation déduites de la caméra au moment de la prise de vue sont observées sur un nuage de points grossier incluant des indicateurs de position de caméra sous forme de nuage de points, ici nommé PosCams.ply :
mm3d AperiCloud ".*jpg" Ori1 Out=PosCams.ply
4 - Ayant validé le positionnement de la caméra par rapport à la structure observée, le « vrai » calcul à proprement parler qui résultera dans le nuage de points précis se lance par
mm3d Malt GeomImage ".*jpg" Ori1 "Master=P1030158.jpg" "DirMEC=Resultats" UseTA=1
ZoomF=4 ZoomI=32 Purge=true
qui nécessite une image de référence pour identifier les pixels que l’on cherche à positionner dans l’espace. Cette image de référence fournit l’ensemble des points (en deux dimensions) pour lequel la position tridimensionnelle dans le nuage sera calculée. Afin de ne pas éterniser le calcul en cherchant la profondeur de chaque pixel dans une image très haute résolution, nous n’effectuons ce calcul que pour des zooms de 1/32 à 1/4 de l’image originale, en plaçant le résultat de calcul dans le répertoire du même nom,
5 - le résultat du calcul est converti en nuage de points par
mm3d Nuage2Ply "./Resultats/NuageImProf_STD-MALT_Etape_6.xml" Attr="P1030158Zoom4.JPG"
où l’homothétie de l’image originale d’un facteur 1/4 est obtenue par Imagemagick par la commande convert image.jpg -scale 25\% imageZoom4.JPG
Si le résultat atteint considère des photographies avec des zooms différents, on adaptera en cohérence ZoomF (1 pour la pleine résolution, qui prendra alors comme argument Attr de Nuage2Ply la même image que Master de Malt) et le numéro d’étape de NuageImProf_STD-MALT_Etape_6.xml (8 pour une image en pleine résolution). Alternativement, au lieu de créer une nouvelle photographie à l’échelle, il est possible de fournir en argument de Attr la photographie originale en pleine résolution et préciser le facteur d’homothétie par RatioAttrCarte=4.
L’application de cette chaîne de traitement la plus simple permet de valider chaque étape du traitement et, avec un peu d’habitude, identifier les palliatifs potentiels. Par exemple, Tapas présente une multitude de modèles de lentilles qui nécessitent un nombre croissant de paramètres. Le modèle le plus complexe est le plus souple - RadialExtended - ne converge pas toujours et un passage à un modèle simple - RadialBasic - maximise les chances de convergence en réduisant les dimensions de l’espace des paramètres. Il semble que RadialStd soit le modèle à tester dans la majorité des conditions. Cette étape d’identification des paramètres de l’objectif nous est apparue comme le point critique qui peut faire échouer toute la chaîne de traitement si les photographies ne respectent pas les consignes de prises de vues (focale constante, recouvrement de plus de 80% entre photographies, netteté).
Il est par ailleurs utile de comprendre quelques-unes des sorties de Tapas : au-delà des messages cryptiques d’erreur lorsqu’un paramètre manque (le plus souvent une information manquante dans l’entête EXIF des photographies à traiter), le seul message compréhensible que nous sachions analyser dans la chaîne de traitement est celui fourni par Tapas. Les valeurs fournies sous forme de
RES:[P1040263.JPG] ER2 0.559285 Nn 100 Of 179 Mul 115 Mul-NN 115 Time 0.00602202
RES:[P1040273.JPG] ER2 1.1225 Nn 96.5096 Of 573 Mul 311 Mul-NN 311 Time 0.0184491
se lisent comme une erreur résiduelle (quatrième colonne) entre divers paramètres du modèle tridimensionnel du nuage de points (qui doit idéalement devenir nul, et en pratique arriver autour du pixel, soit l’unité), la fraction des points considérés (sixième colonne) parmi les points homologues entre deux images (ici 100% et 96,5% respectivement), et le nombre de points homologues considérés (huitième colonne). Périodiquement, lorsque l’erreur résiduelle devient suffisamment petite, un des paramètres du modèle optique de l’instrument de prise de vue est libéré :
LIB DR1
et l’algorithme passe au paramètre suivant. Cette analyse de chaque étape du processus de traitement - vérifier la position des caméras, vérifier l’adéquation du modèle de lentille par la convergence des faisceaux épipolaires dans un volume inférieur au pixel, vérifier les cartes de corrélation Correl* - nous encouragent à ne pas automatiser l’appel aux outils successifs dans un Makefile mais au contraire d’activer chaque module manuellement et d’en valider visuellement le résultat avant de passer à l’étape suivante.
4. Outils de visualisation et de manipulation de nuages de points
Deux outils libres semblent particulièrement appropriés pour manipuler la masse énorme de points générés par le processus décrit ci-dessus : meshlab9 et CloudCompare10. Le premier est disponible en paquet binaire sous Debian GNU/Linux, le second se compile sans problème et mérite de s’y attarder par sa capacité à recaler deux nuages de points, estimer la différence entre deux nuages, et manipuler ces nuages pour n’en garder qu’un sous-ensemble. Afin d’illustrer ce dernier point, nous considérons une scène qui comporte de nombreux nuages que MICMAC traite comme situés à l’infini. En l’état, le résultat semble inexploitable, mais une recherche méticuleuse au point de convergence des lignes de fuite indique que le modèle 3D des alentours de la Gare de l’Est de Paris est bien présent, mais simplement noyé dans une foule de points inexploitables (nuages). Deux approches s’offrent à nous pour pallier à ce problème : définir un masque de traitement, ou couper les points inutiles. Nous commencerons par le second point pour finir par la première méthode.
Meshlab est souple d’emploi ... quand on a pris l’habitude de s’en servir. Parmi les raccourcis qui facilitent la vie, double cliquer sur un point définit cet emplacement comme nouveau centre de rotation/zoom, et Alt+molette permet de changer la taille des pixels affichés sur le nuage de points.
CloudCompare est un outil puissant de manipulation de nuages de points. Il permet notamment d’éliminer des zones inutiles, dans le cas qui va nous intéresser des nuages dans le ciel qui sont considérés par MicMac comme situés très loin de la scène qui nous concerne et donc rend la partie utile des données inexploitable. L’outil de manipulation ne devient actif qu’après avoir sélectionné un nuage de points dans le menu de gauche (nom du nuage surligné en bleu): il s’obtient dans qui permet de sélectionner les points du nuage que nous conservons dans ou en-dehors de la sélection. De cette façon, la scène considérée se cantonne aux points utiles et devient plus facilement visualisable au moyen de meshlab
Figure 3 : Haut : nuage de points de la place devant la gare de l’Est à Paris comprenant les points reconnus comme proches du site de prise de vue qui inclut un balcon au premier plan, et dans le ciel les nuages positionnés loin du site de prise de vue (une des images de la séquence de traitement est visible à gauche de la Fig. 4). Milieu : le nuage de point est sélectionné (surligné en bleu dans la colonne de gauche) et l’outil de découpe a permis de ne sélectionner que la zone utile. Bas : après avoir éliminé les points inutiles, le nouveau sous-ensemble du nuage pourra être visualisé dans meshlab convenablement centré pour une manipulation aisée.
L’alternative consiste à limiter l’analyse de corrélation dense de points similaires de Malt aux zones intéressantes. Cet outil permet en effet d’exploiter un masque définissant les zones d’intérêt (en blanc) et d’exclure les régions de l’image de référence que l’utilisateur sait ne pas contenir d’information utile. Ce masque est soit défini au moyen de Gimp tel que décrit dans http://combiencaporte.blogspot.fr/2013/10/micmac-tutoriel-de-photogrammetrie-sous.html (sauver le masque au format TIF, sans compression, en palette binaire blanc/noir au moyen de ) ou de l’outil fourni par MicMac sous le nom SaisieMasq (bouton de gauche pour définir le polygone à conserver qui sera marqué en vert, shift-bouton de gauche pour fermer le polygone, et finalement ctrl-bouton de droite et Exit pour sauver les fichier .tif du masque et .xml de description). Bien que plus rustique, ce second outil a le bon goût d’aussi générer le fichier XML de description du masque que nous devons remplir manuellement sinon. Au final, le masque permet de ne traiter que les zones en blanc (accélération) et de limiter le nuage de points aux zones d’intérêt (Fig. 4). Les masques sont pris en compte par défaut ou si l’option UseTA=1 de Malt est active. Par défaut l’extension de fichier est _Masq, qui peut être modifiée avec l’option MasqIm de Malt.
Figure 4 : Gauche : une des images originales exploitées pour créer le modèle de la place devant la gare de l’Est à Paris. Noter au premier plan le balcon et les nuages dans le ciel qui détériorent la qualité du nuage de points résultant. Milieu : masque éliminant (en noir) les régions sans intérêt. Droite : nuage de points résultant du calcul tenant compte de ce masque, et confinant donc le nuage de points aux zones d’intérêt.
5. Quelques cas pratiques
Nous proposons ici les cas qui nous ont motivés au cours de cette étude. Notre objectif n’a été aucunement de tenter d’atteindre la perfection du résultat, mais au contraire d’utiliser toutes les sources d’images disponibles, aussi dégradées soient-elles, pour estimer la robustesse des outils proposés par MicMac. Nous pouvons déjà affirmer que le résultat est impressionnant.
Le lecteur est par ailleurs encouragé, tant à titre pédagogique que pour se familiariser avec les résultats obtenus sur de « vrais » jeux de données acquis pour cette application, à tester les jeux de données mis à disposition par l’IGN à http://forum-micmac.forumprod.com/location-of-sample-data-sets-from-document-t640.html (noter que le serveur svn qui contient des données ne semble plus/pas actif, seul le serveur FTP a permis d’obtenir ces données dont l’utilisation est décrite au long de la documentation [7]).
5.1 Assemblage de photographies pour réaliser un objet en 3D
Une série d’outils rassemblés sous la nomenclature de Apero ne peut que servir à modéliser une canette.
Figure 5 : Gauche : une des photographies exploitées pour réaliser le nuage de points de la scène de la Fig. 6. Centre et droite : image de corrélation en cours de calcul, permettant de connaître l’état d’avancement de la fabrication du nuage dense de points parMalt. Droite : la carte des corrélations achevée, permettant d’identifier en blanc les zones de forte corrélation (calcul aisé du nuage de points) et en noir les zones où le calcul échouera.
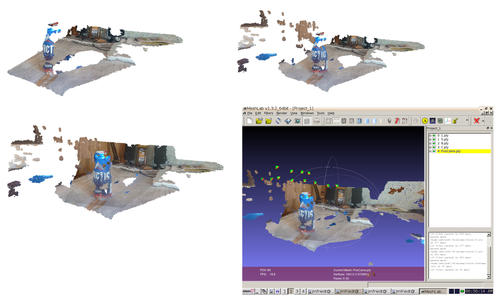
Cet exemple sera l’occasion de fusionner plusieurs nuages issus de plusieurs points de vue, et d’analyser les conditions de bon (et mauvais) fonctionnement de l’algorithme d’identification de points homologues. Avant de considérer la fusion des nuages de points, il est utile de mentionner les conditions de bon fonctionnement de l’algorithme de recherche des points homologues et analyser les fichiers de corrélation proposés par MicMac dans le répertoire de résultats de Malt (argument DirMEC=). D’une part les fichiers de corrélation Corr* indiquent l’avancement du calcul (utiliser un visualiseur d’images qui ne bloque pas le fichier en écriture, par exemple geeqie) puisque l’image est formée au cours du calcul, et d’autre part ce fichier indique en blanc les zones de forte corrélation (forte probabilité d’obtenir un nuage dense de points) et en noir les zones de faible corrélation (où le calcul du nuage sera impossible ou bruité). Le cas de la canette met en avant l’incapacité du logiciel à travailler sur des objets ne présentant pas de structure remarquable (dos d’ordinateur), réfléchissante (partie supérieure de la canette), ou évidemment transparente (Fig. 5).
Figure 6 : De gauche à droite et de haut en bas : somme de 1, 2 et 3 nuages de points couvrant des zones complémentaires de la scène. Chaque nuage de points est issu d’une nouvelle exécution de couple Malt et Nuage2Ply avec un argument Masterdifférent. Noter que la taille du trou dans le nuage de points derrière la canette est réduite avec l’ajout de chaque nouveau nuage de points, qui par ailleurs ne fait que compléter l’information déjà existante. En bas à droite : CloudCompare sert à fusionner ces nuages de points, ici incluant les positions de la caméra lors des prises de vues.
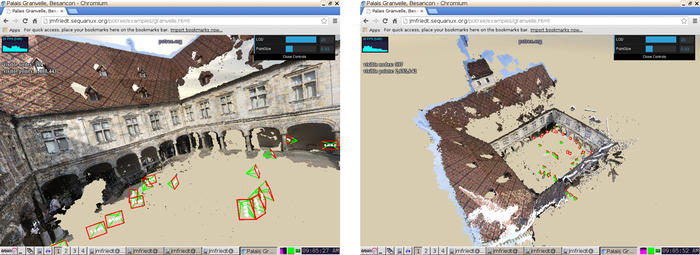
Bien que l’argument de Malt en recherche de nuage de points selon le modèle GeomImage nécessite une image maîtresse et donc ne concerne qu’un unique point de vue, nous pouvons itérer ce processus sur divers points de vue afin de multiplier les nuages de points concernant des zones complémentaires de l’objet analysé. Si les points homologues ont été identifiés sur toutes les images, alors tous les nuages de points sont générés dans un référentiel certes arbitraire, mais qui est toujours le même. Ainsi, tous ces nuages de points se superposent et peuvent être fusionnés dans un logiciel externe tel que CloudCompare. Cette séquence de travail est illustrée sur la Fig. 6 dans laquelle plusieurs nuages de points correspondant à divers points de vue sont séquentiellement ajoutés pour compléter le modèle tridimensionnel de la scène observée. Nous comprenons ainsi comment les auteurs de https://sites.google.com/site/geomicmac/cavites/tunnel-de-lave ont pu cartographier un tunnel de lave en assemblant une multitude d’images : même si tous les points de vue des images ne se superposent pas lors de la prise de vue, tant que tous les points homologues ont été identifiés lors de la même phase de traitement de Tapioca par recouvrements successifs d’une partie des photographies deux à deux, les divers nuages denses de points générés par Malt s’assembleront dans le même référentiel. Ce point est illustré par une modélisation par nuage de points de l’entrée du Fort des Trois Chalets près de Besançon (Fig. 7), somme de 3 nuages de points issus du traitement de 5 photographies numériques du tunnel. Ces résultats semblent indiquer que la photogrammétrie est particulièrement appropriée pour le relevé topographique sous-terrain, sous réserve que l’illumination des parois soit constante au cours des prises de vues.
Figure 7: Nuage de points de l’entrée du Fort des Trois Chalets près de Besançon : la configuration de tunnel est particulièrement appropriée pour la génération du nuage de points.
Compte tenu de notre objectif d’utiliser des instruments de prise de vue de qualité médiocre, la densité du nuage de points est augmentée (au détriment de la résolution) en abaissant le seuil de corrélation en dessous duquel l’analyse est rejetée : nous complèterons souvent les options de Malt par DefCor=0.001.
5.2 Photographies aériennes
Dans l’exemple précédent, nous avons sommé plusieurs nuages de points, chacun identifié par la photographie maîtresse qui a permis de sélectionner les pixels dont nous recherchons la profondeur lors du calcul du nuage dense de points (Malt). Dans le cas d’images aériennes, cette séquence est non seulement fastidieuse, mais elle signifie que le nuage de points généré ne sera colorisé que sur un petit segment. La notion d’objet tridimensionnel se prête mal aux modèles numériques d’élévation (MNE), qui s’apparentent plutôt à un plan sur lequel nous extrudons des élévations. Dans ces conditions, nous n’utiliserons par l’option GeomImage de Malt mais Ortho, qui ne nécessite pas d’image maîtresse mais uniquement la séquence complète des photographies aériennes. Par ailleurs, la mosaïque d’images orthorectifiées peut être assemblée (Tawny) afin de générer une grande image en couleur qui servira à draper le MNE. La séquence se résume donc à
mm3d Tapioca MulScale "0(0[5-9]|1[0-9]|2[0-7]{1}).jpg" 300 1000
mm3d Tapas RadialStd "0(0[5-9]|1[0-9]|2[0-7]{1}).jpg" Out=Cal1
mm3d Tapas AutoCal "0(0[5-9]|1[0-9]|2[0-7]{1}).jpg" InCal=Cal1 Out=Ori1
mm3d AperiCloud "0(0[5-9]|1[0-9]|2[0-7]{1}).jpg" Ori1 Out=PosCams.ply
mm3d Malt Ortho "0(0[5-9]|1[0-9]|2[0-7]{1}).jpg" Ori1 "DirMEC=Resultats3" UseTA=1 ZoomF=4 ZoomI=32 Purge=true
mm3d Tawny Ortho-Resultats3/
Nuage2Ply Resultats3/NuageImProf_STD-MALT_Etape_6.xml Attr="Ortho-Resultats3/Ortho-Eg-Test-Redr.tif"
Figure 8 : Gauche : le masque identifié par Malt lors de l’assemblage des photographies sur le plan moyen d’élévation. L’élévation ne sera calculée que sur les zones blanches. Droite : taux de corrélation lors de la recherche du nuage de points dense. Noter l’absence totale de corrélation au-dessus de la rivière.
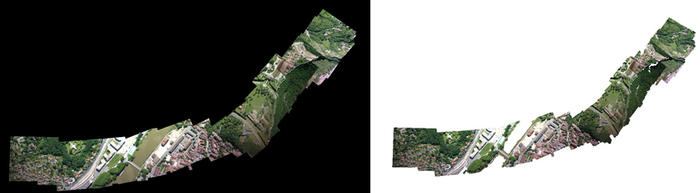
La séquence de photographies assemblées pour former le modèle numérique d’élévation le long d’une bande, qui passe au-dessus de la citadelle de Besançon et arrive au Doubs, a été acquise depuis un ULM équipé d’un appareil photographie réflexe en vision azimutale. Le masque (Fig. 8, gauche) présente dans le plan supportant le MNE les pixels (en blanc) pour lesquels l’altitude sera calculée à partir des photographies. Le taux de corrélation (Fig. 8, droite) est d’autant plus élevé que les structures au sol sont identifiables : le taux de succès sera favorable en milieu urbain, nul au-dessus du Doubs puisque l’eau ne présente aucune structure pour la corrélation de points d’accroches visibles depuis plusieurs prises de vues acquises séquentiellement dans le temps. Ces résultats se confirment en comparant la mosaïque des photographies corrigées des déformations de topographie et d’angle de prise de vue (Fig. 9, gauche) avec le nuage de points colorisés (Fig. 9, droite) : les zones de corrélation nulle ne présentent pas de point dans le nuage tridimensionnel. On se convaincra de la présence de la troisième dimension en se plaçant d’un point de vue oblique qui permet de vérifier la cohérence de l’élévation calculée (Fig. 10). Une alternative au mode de traitement Ortho est le mode UrbanMNE [7, p.63, sec. 3.12.1] qui a pour objectif de réduire la taille du masque de convolution qui tend à rendre le résultat flou (en passant d’un masque de 5×5 à 3×3 pixels), mais n’inclut pas par défaut la génération des images en vue azimutale. Ces dernières s’obtiennent en ajoutant les options LrOr=true HrOr=true à Malt UrbanMNE mais dans le cas présent, les traitements par Ortho ou UrbanMNE n’ont pas induit de différence significative entre les deux nuages de points.
Figure 9: Gauche : mosaïque des images orthorectifiées générée par Tawny pour draper le nuage de points (fichier Ortho-Eg-Test-Redr.tif dans le répertoire Ortho- fourni en argument de Tawny). Droite : le nuage de points drapé, en vue azimutale. Noter l’absence de drapage sur la rivière qui présentait un taux de corrélation quasi-nul et donc ne comporte pas de points.
Nous verrons plus tard (section 9) que ce traitement peut s’effectuer dans un référentiel absolu si la position des caméras au moment de la prise de vue est connue (par exemple en synchronisant la prise de vue avec un récepteur GPS). Dans ce cas, deux fichiers dans le répertoire Ortho- nous informent des paramètres de localisation de l’orthoimage présentée dans Fig. 9 : MTDOrtho.xml contient l’origine et l’extension de chaque pixel dans un format lisible par un humain, et MTDOrtho.tfw propose ces mêmes informations dans le format standardisé de géolocalisation des images au format TIF.
Figure 10: Vues obliques du même nuage de points qu’affiché sur la Fig. 9, mais cette fois en vue oblique, pour illustrer la présence de l’information d’altitude de chaque point.
5.3 Agencement des photographies
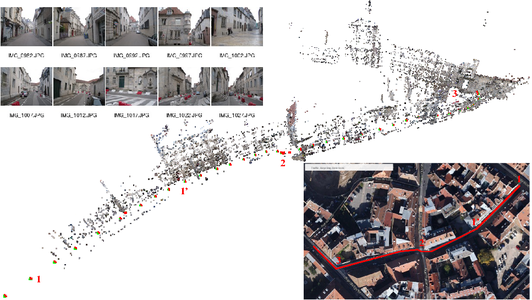
La recherche des points homologues entre photographies est le point clé de la capacité à identifier les paramètres optiques de l’appareil de prise de vue et la position de la caméra lors des acquisitions : cette opération est la première qui soit mise en jeu dans la séquence de traitement, par Tapioca. L’option d’appariement MulScale des photographies lors de la recherche des points représentant le même objet fonctionne dans la plupart des cas. Nous avons rencontré un cas particulier d’échec : le cas de prises de vues le long d’une rue que nous voulions cartographier, dans laquelle le logiciel confond plusieurs murs de bâtiments différents en leur associant des points considérés comme représentant la même structure (Fig. 11). La conséquence est de positionner des caméras en des emplacements totalement erronés, rendant le reste de la chaîne d’analyse voué à l’échec (d’où la nécessité de toujours valider le positionnement des caméras par AperiCloud). La solution a consisté à proposer à Tapioca d’utiliser la méthode Line qui se contente de rechercher les points homologues que sur les photographies d’indice +/-N dans la séquence de prises de vues, avec N fourni comme dernier argument. Non seulement nous accélérons ainsi la première phase de traitement, mais surtout nous évitons d’associer des points observés sur des bâtiments situés géographiquement en des points très lointains. Une situation similaire a été observée pour une chapelle dont les murs adjacents apparaissent similaires sur les photographies, ou les faces adjacentes d’une tour dans les fortifications de Vauban à Besançon (section 9.2).
Figure 11 : Prises de vues le long d’une rue : le positionnement correct des caméras n’est possible que par Tapioca Line 1500 3 significant que la recherche des points homologues ne se fait que sur les ± 3 photographies encadrant la prise de vue analysée. En insert : le tracé du parcours dans une vue aérienne de Google Maps, avec 4 points de repère le long du trajet. Micmac n’a pas pu interpréter le dernier angle droit après le repère 3 : les positions estimées des caméras après ce point sont aberrantes. Avec une marge de 5 photographies au lieu de 3 pour la recherche des points homologues, l’angle droit est détecté mais l’échelle est incorrecte dans cette nouvelle direction. Insert en haut à gauche : quelques-uns des 60 clichés acquis (appareil photographique compact Canon PowerShot A2200).
En désespoir de cause, si l’association automatique des photographies comportant des points représentant les mêmes structures échoue, la dernière solution consiste à fournir, au moyen de l’option File de Tapioca, la liste des couples de photographies à analyser au format XML de la forme
<?xml version="1.0" ?>
<SauvegardeNamedRel>
<Cple>img1.JPG img2.JPG</Cple>
<Cple>img1.JPG img3.JPG</Cple>
...
</SauvegardeNamedRel>
5.4 Récupération de séquences dans un film
La majorité des lecteurs n’a probablement pas la chance de pouvoir voler en ULM ou en hélicoptère pour acquérir ses propres séquences de clichés. Une source potentielle de données est d’extraire les séquences de vues aériennes de documentaires et de traiter ce jeu de données. Nous avons en particulier effectué ce traitement sur des vues des documentaires de Sylvain Augier (l’Europe vue du Ciel11, l’Île de France vue du ciel12) ou produits par Arte (Les Alpes vues du Ciel13. MicMac est tellement robuste que nous pouvons renseigner les informations associées à chaque image ainsi extraite avec à peu près n’importe quel paramètre que Tapas corrigera lors de l’identification des paramètres de prise de vue. Un zoom sur un monument au cours de la prise de vue est garanti d’échec du traitement, qui s’avère pourtant stable si le cameraman n’a pas touché au zoom pendant le film (Fig. 12).
L’extraction des images du film s’obtient par mplayer en utilisant comme sortie vidéo des fichiers jpeg de la meilleure qualité possible : mplayer -vo jpeg:quality=100 film.avi. Afin de commencer le film dans la séquence qui nous intéresse, on préfixe l’option -vo de -ss début avec début la date (en secondes) du début de la séquence intéressante. Évidemment, au rythme de 25 images/seconde, la quantité d’images résultantes est énorme et nous ne conservons qu’une image sur 10, soit une image toutes les 0,4 secondes. Il est inutile de vouloir traiter trop de prises de vues, on privilégiera plutôt des points de vue d’origine aussi séparés que possible du même site afin d’obtenir un nuage de points de bonne qualité. MicMac veut absolument un entête EXIF pour traiter les images14, même si le contenu est complètement erroné : nous nous contentons de copier l’entête EXIF d’une photographie numérique (JPEG) ref d’appareil photo sans nous soucier si la taille de l’image ou la focale sont en accord avec les prises de vues du film : exiftool -TagsFromFile ref *.jpg.
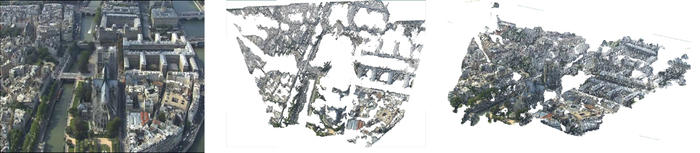
Figure 12 : Modèle de Notre Dame de Paris et de l’Île de la Cité par traitement d’images issues du documentaire Paris Vu du Ciel. Gauche : une des photographies extraites du DVD pour la reconstruction. Milieu : vue azimutale du nuage de points, sur laquelle l’Île de la Cité et les principaux bâtiments qui s’y trouvent sont clairement reconnaissables. Droite : vue oblique du même nuage de point, permettant de visualiser les deux tours de Notre-Dame de Paris qui dépassent du modèle.
Figure 13 : Haut, de gauche à droite : une des 58 images issues du documentaire “Paris Vu du Ciel” représentant l’Église Saint Eustache ; une carte de corrélation indiquant la capacité à traiter ces signaux malgré la résolution médiocre du film (768×576 pixels) ; et une des trois vues du nuage de points représentant l’église reconstituée. En bas : deux vues (depuis le parvis et en projection azimutale) du nuage de points représentant l’église, et à droite, la position de l’hélicoptère au-dessus de l’église au moment des prises de vues. Noter la forme allongée du cône vert, indicateur d’un téléobjectif, condition habituellement peu favorable au traitement photogrammétrique. Une analyse quantitative des altitudes permet d’affirmer que l’aéronef volait à une altitude égale à 6,7 fois la hauteur de l’église. Supposant une hauteur sous voute (fr.wikipedia.org.wiki/) de 33,46 m, alors l’altitude de vol est de l’ordre de 225 m, au-dessus des 200 m d’altitude légale imposée depuis 1998 afin de réduire les nuisances sonores, et en dessous des 350 m accessibles aux avions.
Les perspectives d’utilisation de documentaires disponibles sur internet sont ainsi quasi infinies (Fig. 13), mais le respect des contraintes de prises de vues n’est souvent pas satisfait par les documents d’amateurs disponibles par exemple sur YouTube (les possesseurs de caméra GoPro - de focale fixe donc appropriée pour ce traitement - ont une fâcheuse tendance à fixer l’appareil de prise de vue sur un casque qui change donc constamment de point de vue). Les séquences de prises de vues de sports extrêmes tels que le wingsuit sont particulièrement inappropriées pour une exploitation quantitative des images, tandis que les activités plus calmes que sont planeur ou ULM ont fourni une source de données pertinentes. Les documentaires professionnels semblent en général plus appropriés pour le traitement qui nous concerne, sous réserve de se cantonner aux séquences où le zoom est maintenu fixe pendant la prise de vue (Fig. 14).
Figure 14 : Modèle de Briançon en vue azimutale par traitement d’images en vues obliques issues du documentaire Les Alpes Vues du Ciel.
L’exemple de Briançon a nécessité un modèle de type GeomImage car l’avion volait en tournant autour de la ville lors de la prise de vue. Un autre exemple issu du second volume de La France vue du Ciel15 a extrait un modèle de Sète (Fig. 15) à partir d’une longe série de prises de vues assemblées par MicMac selon un modèle Ortho de Malt et redressées en tenant compte de la topographie, et ce malgré la résolution médiocre du DVD.
Figure 15 : Sète, vue oblique permettant de visualiser la topographie générée par les photographies du film, et vue azimutale. Droite : quelques-unes des photographies extraites du DVD pour assembler le nuage de points.
6. Second cas ... aérien
Un petit drone commercialisé comme jouet, le RC System Space Q4, est fourni avec une caméra embarquée pour un peu plus de 100 euros. Ce jouet, d’apparence anodine, va s’avérer un vecteur de prises de vues aériennes idéal malgré la médiocrité apparente de la caméra.
Figure 16: Drone en vol en intérieur muni de sa caméra
En particulier, la lentille fixe et l’absence de zoom garantit que les images extraites du film - toujours par mplayer -vo jpeg - enregistrées pendant le vol respectent les contraintes de traitement par MicMac (Fig. 16).
Ici aussi, les photographies issues du film ne possèdent pas d’entête EXIF, que nous renseignons de la même façon que dans la section précédente. Un aspect fascinant du traitement de ces images est la reconstruction de la trajectoire de vol du drone dans l’espace (Fig. 17). Nous voyons en particulier une application de ce concept à l’analyse des paramètres déterminant les lois de commande d’un drone lors de sa conception : alors qu’une centrale inertielle ne fournit que la dérivée seconde (accélération) de la position et la dérivée première de l’orientation (gyromètre), nous avons ici l’opportunité de remonter à une estimation directe de position et orientation (angles).
Figure 17 : Haut droite et bas : cartographie tridimensionnelle d’un couloir du laboratoire tapissé de posters grâce aux images acquises par un drone. La reconstruction de la trajectoire du drone est aussi impressionnante que la reconstruction de l’environnement dans lequel le drone a évolué. En haut à gauche : reconstruction de la trajectoire du drone dans une pièce vide carrelée. On notera la dextérité du pilote qui a évité de justesse le crash sur la partie gauche de la trajectoire !
7. Localisation du point de vue de prise de vue, comparaison avec GPS
Ayant vu que nous pouvons identifier la position de la caméra, il semble pertinent de s’interroger sur la cohérence de la position déduite par MicMac de la caméra par rapport à une mesure de référence, par exemple prise par GPS.
Figure 18 : De gauche à droite et de haut en bas : une des images prise depuis le train Besançon-Dijon avec un téléphone Samsung-S3 en vue d’une reconstruction 3D de la scène ; reconstruction 3D du bâtiment à partir d’une séquence de photographies numériques, incluant la position de la caméra au moment des prises de vues ; vue azimutale du nuage de points ; positionnement du nuage de points en vue azimutale sur Google Earth. Les flèches vertes et rouges sont un guide pour l’œil indiquant les éléments insérés depuis la vue azimutale et la position des caméras. Noter l’excellente corrélation entre la trajectoire de la caméra et le rail de droite du chemin de fer.
L’accord entre position prévue par MicMac par analyse des images et les sites de référence est impressionnante. Une première considération consiste à évaluer la position de la prise de vue sur un bâtiment photographié depuis le train Besançon-Dijon, à proximité de la gare d’arrivée, et positionner une projection en vue azimutale du modèle de bâtiment résultant du traitement d’image sur une carte issue de Google Earth. Le nuage de points du modèle de bâtiment intègre la position de la caméra qui est donc elle aussi positionnée sur Google Earth au cours du déplacement du train. La cohérence est excellente, avec un placement sur le rail de droite, en accord avec la position du photographe dans le wagon (Fig. 18). Un autre exemple d’accord excellent entre position de prises de vues extraite du calcul de MicMac et la position de la caméra enregistrée par GPS au moment des prises de vues est proposé dans [11].
Ces deux comparaisons s’obtiennent simplement dans Gimp en superposant une vue azimutale du nuage de points avec une photographie aérienne du site, ici extraite d’une capture d’écran de Google Maps. Une fois l’homothétie, la rotation et la translation convenablement effectuées (dans notre cas par tâtonnements successifs) pour que les bâtiments se superposent, il ne reste aucun degré de liberté pour placer les caméras sur les rails : l’accord tient au bon fonctionnement des algorithmes utilisés par MicMac (Tapas) pour identifier les propriétés optiques et les positions de la caméra en vue de constituer le nuage de points. Fort de ce constat, nous pouvons prendre le problème à l’envers et considérer que, connaissant des points de référence sur le terrain ou lors des prises de vues, nous allons être capable de convertir le référentiel arbitraire du nuage de points en un référentiel absolu avec un sens physique. Cette démarche sera suivie dans les deux sections qui suivent, d’abord en se positionnant par rapport à des points de contrôle au sol connus et visibles dans la scène, puis en exploitant les informations de position de la caméra au moment de la prise de vue.
8. Du qualitatif au quantitatif : les points de contrôle au sol
Une façon de générer un modèle quantitatif, avec des dimensions en unités connues (centimètres, mètres...) au lieu de pixels, consiste à fournir les coordonnées 3D de points de référence connus et visibles sur toutes (ou la majorité des) photographies. Tous les points n’ont pas besoin d’être visibles sur toutes les photographies mais un maximum de recouvrement garantit évidemment un meilleur résultat. Cette méthode ne fait donc aucune hypothèse sur les propriétés optiques ou de positions de l’instrument de prise de vue mais manipule uniquement des relations entre position de points de référence (GCP - Ground Control Points) sur la photographie (2D) et dans l’espace (3D). La qualité du résultat dépend de la précision de ces couples de points mais même sans être excessivement méticuleux, le résultat est impressionnant d’exactitude. Nos tests indiquent qu’en se contentant d’indiquer les positions sur le sol sur lequel se trouve un objet des distances de référence, la troisième dimension (la hauteur de l’objet au-dessus du sol) est identifiée avec la même résolution que la mesure qui est faite sur cet objet (de l’ordre de ±5 mm sur un objet de 12 cm de hauteur).
La qualité optique de l’outil de prise de vue n’est pas un frein au traitement des images. Un simple téléphone portable suffit, tel que le démontre la séquence de traitement qui suit basée sur des images prises par un téléphone portable Samsung S3. Ces images ne comportent pas dans l’entête EXIF l’information de focale équivalente sur film 35 mm : cette information est ajoutée, en prenant une valeur un peu au hasard (et inspirée des données glanées sur le web) par exiv2 -m set_exif.jmf *.jpg où le fichier de commande set_exif.jmf contient uniquement la ligne set Exif.Photo.FocalLengthIn35mmFilm 21, 21 mm semblant être une valeur couramment admise de focale lors du zoom le plus large sur ce téléphone. On notera que l’information arbitraire de focale que nous avons renseigné dans l’entête EXIF change quelque peu la position du nuage de points dans l’espace (en remplaçant grossièrement la focale de 21 mm par 40 mm) mais que l’exactitude de la hauteur de l’objet n’en est pas affectée.
La séquence de traitement, que nous fournissons complètement malgré la constance des premières étapes afin de bien identifier à quelle étape du calcul se fait le passage du référentiel arbitraire vers le référentiel des points de contrôle par GCPBascule :
mm3d Tapioca MulScale ".*jpg" 300 1500
mm3d Tapas RadialStd ".*jpg" Out=Init
mm3d AperiCloud ".*jpg" Init
mm3d GCPBascule ".*jpg" Init Ground Ground-Pts3D.xml GroundMeasure.xml
# compensation ponderee entre camera et GCP par Campari dans Final
mm3d Campari ".*jpg" Ground Final GCP=[Ground-Pts3D.xml,0.1,GroundMeasure.xml,0.5]
# on regarde ce que ca donne sans la ponderation ...
mm3d Malt GeomImage ".*jpg" Ground Master=20140518_110653.jpg DirMEC=Results ZoomF=4 ZoomI=32 Purge=true
mm3d Nuage2Ply Results/NuageImProf_STD-MALT_Etape_6.xml Attr=20140518_110653Zoom4.JPG
# ... et avec la ponderation ...
mm3d Malt GeomImage ".*jpg" Final Master=20140518_110653.jpg DirMEC=Campares ZoomF=4 ZoomI=32 Purge=true
mm3d Nuage2Ply Campares/NuageImProf_STD-MALT_Etape_6.xml Attr=20140518_110653Zoom4.JPG
L’opération clé est effectuée par GCPBascule qui prend en entrée le répertoire d’orientation issu du positionnement de la caméra (Ori-Init) et exploite les informations de position 3D (ici en centimètres, renseignées dans le fichier Ground-Pts3D.xml) des points de contrôle ainsi que la position (en pixels) sur chaque image de ces points de contrôle sur chaque photographie, tel que décrit dans GroundMeasure.xml. Le format de ces fichiers est simple, et inspiré des fichiers Dico-Appuis.xml (position 3D des GCP) et Mesure-Appuis.xml (position 2D des GCPs sur chaque photographie) contenus dans l’exemple des gravillons disponible à http://logiciels.ign.fr/?-Micmac,3- : chaque point de contrôle a un nom (balise NamePt) et une position (balise Pt) dans Ground-Pts3D.xml. Pour chacune des images (balise NameIm) renseignées dans GroundMeasure.xml, nous fournissons le nom du point de contrôle (balise OneMesureAF1I) et ses coordonnées en pixel sur la photographie (balise PtIm). Une fois le basculement de référentiel effectué, le calcul de la génération du nuage dense de points s’achève dans le nouveau référentiel et permettra, dans CloudCompare, de relever la position de divers points de la structure décrite par le nuage de points (l’icône en forme de cible permet de demander les propriétés d’un point, y compris ses coordonnées dans l’espace). Le résultat de ce traitement sur une peluche est proposé sur la Fig. 19, et a été développée dans un autre contexte dans [11].
Figure 19 : Gauche : coordonnées des GCP - en cm - sélectionnées sur les coins des lattes d’un plancher, visibles depuis la majorité des 6 photographies acquises par téléphone mobile de la peluche. Milieu : nuage de points généré et mesure dans CloudCompare de la hauteur d’une oreille de la peluche, sachant que tous les GCP étaient placés à l’altitude 0 et que la troisième dimension n’est donc extraite que du traitement photogrammétrique. Droite : mesure de cette même hauteur d’oreille. L’erreur est de l’ordre de 10% sur ce nuage de points non-compensé par Campari.
Nous avons complété cette étude avec l’ajout d’une fonctionnalité additionnelle qui pondère la position des GCP - nécessairement entachée d’erreurs - avec la position que prévoyait MicMac à partir des données photogrammétriques. Après avoir effectué le basculement du référentiel arbitraire (répertoire d’orientation Ori-Init) vers le référentiel des GCP (répertoire d’orientation Ori-Ground), nous pouvons demander à MicMac de tenter de corriger les incertitudes sur nos mesures de GCP compte tenu des ses propres informations sur la scène : cette opération est effectuée par Campari qui prend en argument le répertoire d’orientation des GCP, les fichiers XML des coordonnées en 3D et en 2D des GCP, et les pondérations relatives (entre GCP et position des caméras issues du traitement photogrammétrique). Nous pouvons choisir d’effectuer ou non une telle correction : la Fig. 20 illustre la différence entre les deux nuages de points résultants, tel que calculé par CloudCompare (fonctionnalité fournie par la 8ème icône en partant de la gauche en ayant pris soin de charger et sélectionner les deux nuages de points dans les répertoires Campares et Results).
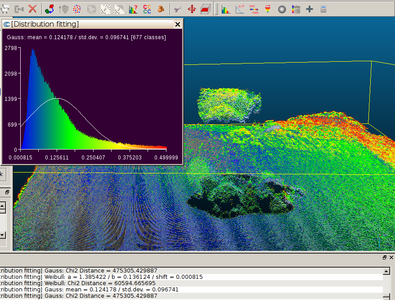
Figure 20 : Distance entre les deux nuages de points - avec ou sans application de la compensation par Campari - sur une échelle de 0 (bleu) à 0,5 cm (rouge). Un ajustement gaussien de qualité douteuse indique une valeur moyenne de l’écart de 0,12 cm, avec une erreur qui atteindrait les 3 mm au sommet de la tête de la peluche.
Cette méthode de travail est quelque peu fastidieuse car elle oblige à retrouver les GCP sur chaque photographie et de renseigner l’information. Des outils sont mis à disposition pour faciliter la tâche - SaisieAppuisInit et SaisieAppuisPredic - mais leur présentation dépasse le cadre de cet exposé.
9. Du qualitatif au quantitatif : exploitation de la position de la caméra au moment des prises de vues
Une alternative à l’identification de GCP sur chaque photographie est de renseigner la position de l’instrument de prise de vue et d’en déduire les grandeurs caractéristiques de la scène. Cette approche est particulièrement appropriée pour des scènes d’extension importante, pour lesquelles les GCP ne sont pas nécessairement connus avec précision mais un récepteur adossé à l’appareil photographique numérique fournit une précision suffisante [12]16.
9.1 De la sphère au plan
Le problème lié à l’utilisation du GPS concerne le passage des coordonnées sphériques - latitude et longitude en degrés - vers les coordonnées cartésiennes selon une transformation qui approxime localement la sphère par un plan. Comme le pirate qui a caché sa carte au trésor, le géographe préfère converser en pas (ou mètres dans la nomenclature moderne) vers le nord ou vers l’est plutôt qu’en degrés d’angle. Afin de géoréférencer la position de la caméra utilisée pour les prises de vues dans un référentiel gradué en mètres, nous devons traduire les positions GPS de l’appareil photo acquises selon le procédé décrit dans [12] en latitude/longitude vers des mètres en abscisse/ordonnée/altitude. Bien que MicMac s’associe à une bibliothèque dédiée à ce type de transformation (option ChSys de GCPConvert) - excessivement complexe si on tient compte des écarts de la forme de la Terre par rapport à la sphère idéale de nos cours de géographie élémentaire afin d’obtenir une résolution métrique - nous avons effectué la traduction de coordonnées sphériques (référentiel WGS84 utilisé par tous les récepteurs GPS) vers les coordonnées projetées (cartésiennes) au moyen de l’outil QGis (www.qgis.org).
La procédure est la suivante :
1 - Identifier, par correspondance des dates tenant compte des dérives des deux horloges (GPS et appareil photo), la position en référentiel sphérique WGS84 (latitude/longitude) de chaque photographie. Le GPS intégré dans les appareils photographiques numériques (en tous cas le Panasonic TZ10, à proscrire autant que faire se peut pour les applications autres que le gadget) fournissent un nombre insuffisant de décimales et un GPS externe est nécessaire,
2 - Sauver en format ASCII un fichier contenant une liste latitude/longitude/altitude correspondant à chaque photographie,
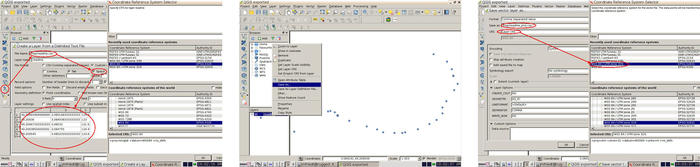
3 - Charger ce fichier dans QGis au moyen de l’icône de la forme d’une virgule (Fig. 21),
4 - Sauver ce même fichier en définissant le mode de projection, dépendant de la région géographique considérée. En effet, la Terre n’étant pas parfaitement sphérique, des modèles locaux de patatoïde permettent de tangenter au mieux un plan pour y projeter les points depuis des coordonnées sphériques vers des coordonnées cartésiennes [13, pp.228-241]. WGS84 est un référentiel en coordonnées sphériques (degrés) qui se projette en WGS84/UTM région (où région indique la longitude considérée) pour tangenter un plan local à chaque région - pour la France il s’agit de la région 31 pour les points qui nous concernent (donc UTM31N).
5 - Exploiter le fichier résultant dans MicMac en insérant la transformation de coordonnées implémentée dans OriConvert.
À l’issue de ce traitement, le fichier de coordonnées de la caméra au moment des prises de vues passe de
Y X Z
49.20993499999999 3.085168333333333 124.3
49.20936 3.084938333333333 123
49.20967333333333 3.08532 121.6
...
à
X,Y,Y,X,Z
506203.20328651543241,5450797.176053959876299,49.209935,3.08516833333333,124.3
506186.52307022450259,5450733.23488206975162,49.20936,3.08493833333333,123
506214.282665384875145,5450768.099197551608086,49.2096733333333,3.08532,121.6
...
Figure 21 : Séquence d’opérations sous QGis pour projeter les coordonnées GPS des sites de prises de vues.
En pratique, la séquence initiale de traitement est
mm3d OriConvert OriTxtInFile readme.gpsutm33Ncut Nav-RTL MTD1=1 NameCple=FileImagesNeighbour.xml
Tapioca File FileImagesNeighbour.xml -1
mm3d Tapas RadialStd ".*JPG" Out=Calib
mm3d Tapas AutoCal ".*JPG" InCal=Calib Out=All-Rel
mm3d AperiCloud ".*JPG" All-Rel Out=PosCams-Rel.ply
CenterBascule ".*JPG" All-Rel Nav-RTL Abs
mm3d AperiCloud ".*JPG" Abs Out=PosCams-Abs.ply
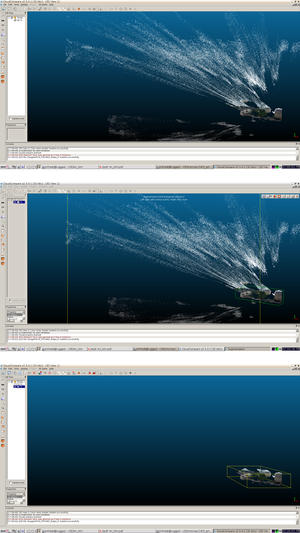
si l’on veut aider Tapioca à utiliser la position GPS des prises de vues pour rechercher les points homologues dans les images prises à proximité. Alternativement, on pourra effectuer toutes les recherches de points homologues et identification des positions de prises de vues dans le référentiel arbitraire de Tapioca et Tapas, avant de basculer vers le référentiel absolu du GPS par CenterBascule et finir, dans ce nouveau référentiel, de générer le nuage dense de points (Malt sur le répertoire d’orientation Abs). Les deux nuages de points visualisables dans CloudCompare que sont PosCams-Rel.ply et PosCams-Abs.ply permettent de valider, en demandant les caractéristiques de quelques points (icône en forme de cible), de vérifier le passage du référentiel arbitraire vers le référentiel absolu (GPS).
Figure 22 : Une tour au bord des remparts entourant Besançon, incluant les sites de prises de vues au moyen d’un téléphone portable muni d’un récepteur GPS.
La première (OriConvert) ligne transforme le fichier d’entrée (nommé readme.gpsutm33Ncut) de la forme
#F=N X Y Z
#
#image longitude latitude altitude
P1130740.JPG 506173.166790323157329 5450735.999143296852708 124.4
P1130733.JPG 506148.26461441826541 5450750.979183392599225 126.5
P1130730.JPG 506128.860635785094928 5450734.096877036616206 128.9
en un fichier exploitable par MicMac. La première ligne est analysée pour définir le format des données dans le fichier texte [7, section 12.3] : ici le premier caractère indique que le # en début de ligne sera considéré comme commentaire, puis que dans l’ordre nous trouverons le nom de la photographie, son abscisse, son ordonnée et son altitude. Un mot clé additionnel, S, pourrait indiquer la présence d’un champ inutile dans le fichier texte (qui ne sera pas analysé par GCPConvert ou OriConvert). En particulier, le fichier XML contient les couples d’images afin que Tapioca n’ait plus à rechercher les voisins par identification des points communs à diverses images mais qu’il puisse se baser sur la position de la caméra pour ordonner les photographies. La suite reste la même : identification des propriétés de l’optique de l’appareil de prise de vue et du nuage de points grossier. La nouveauté de ce traitement tient à CenterBascule qui transforme les coordonnées arbitraires du nuage de points en coordonnées absolues dans l’espace. Finalement, Malt complète le nuage de points dense en ne se basant plus sur les paramètres du répertoire d’orientation All-Rel mais du résultat du calcul de CenterBascule, à savoir Nav-RTL.
9.2 Insertion dans un outil de gestion d’informations spatialisées
Nous appliquons cette séquence à une tour de rempart sur les fortifications de Besançon. Le lecteur pourra se familiariser avec cet environnement en recherchant la coordonnée 47.2308N, 6.0186E dans Google Maps (barre de recherche).
Repartant de la séquence de photographies vue auparavant, nous avions pris soin de capturer ces photos au moyen d’un téléphone portable muni d’un récepteur GPS et exécutant OSMTracker17. Cette application a le bon goût de générer un fichier au format GPX, très simple à analyser, dans lequel les photographies prises depuis l’application sont marquées comme waypoints (balise wpt) associant une position (référentiel WGS84) à chaque photographie. Après extraction de ces informations, nous nous retrouvons avec un fichier de la forme :
N Y X Z
10.jpg 47.23082994114249 6.019135079959552 302.07939594541966
11.jpg 47.23082709250457 6.0189871931638095 300.11863592268435
12.jpg 47.230800730543464 6.018898687257535 298.2475180903055
...
que nous projetons sur WGS84/UTM31N dans QGis pour obtenir :
X,Y,N,Y,X,Z
728532.941096769180149,5235237.991666674613953,10.jpg,47.2308299411425,6.01913507995955,302.07939594542
728521.75988510530442,5235237.241747501306236,11.jpg,47.2308270925046,6.01898719316381,300.118635922684
728515.174332492286339,5235234.053077357821167,12.jpg,47.2308007305435,6.01889868725754,298.247518090306
728510.913302066153847,5235230.523033961653709,13.jpg,47.2307704923071,6.01884067241403,296.38010190175
...
Les deux premières colonnes sont en UTM, les deux secondes en coordonnées sphériques, et en dernier l’altitude. Si le traitement qui suit est effectué sur les données de position ainsi générées, la scène se retrouvera penchée à cause de l’incertitude sur l’altitude : alors que quelques mètres sont acceptables pour notre application en XY, l’erreur relative énorme sur l’altitude induit une erreur significative dans l’orientation de la scène finale. Sachant que nous étions sur un chemin de halage dont l’altitude ne varie pas significativement, nous avons remplacé toutes les valeurs de la dernière colonne (altitude) par une valeur constante pour toutes les lignes, choisie à 300 m (Fig. 23). Nous avons aussi translaté les axes X et Y pour éliminer les premiers chiffres qui induisent des erreurs d’arrondi de calcul (nous retranchons 728000 de X et 5235000 des Y, valeurs à mémoriser puisque nous devrons les ajouter aux coordonnées du nuage de points final que nous voudrons géoréférencer). Le document final prêt à être traité par MicMac contient donc les coordonnées de la caméra pour chaque prise de vue (fichier nommé position_UTM33_cut_Zcst.csv) :
#F=N X Y Z
10.jpg 532.941096769180149 237.991666674613953 300.
11.jpg 521.75988510530442 237.241747501306236 300.
12.jpg 515.174332492286339 234.053077357821167 300.
13.jpg 510.913302066153847 230.523033961653709 300.
...
Figure 23 : Illustration de l’effet de l’incertitude sur l’altitude des prises de vues sur le nuage de points. La tour penchée résulte du traitement des informations GPS brutes présentant une variation de l’ordre de ±5 m sur l’altitude de la caméra au moment de la prise de vue. La tour “verticale” résulte du même calcul mais sur une altitude fixée à la même valeur pour toutes les prises de vues.
La séquence de traitement est alors
mm3d Tapioca MulScale "(1[0-9]|2[0-4]).jpg" 300 1500
mm3d Tapas RadialStd "(1[0-9]|2[0-4]).jpg" Out=Init
mm3d Tapas AutoCal "(1[0-9]|2[0-4]).jpg" InCal=Init Out=Init1
mm3d AperiCloud "(1[0-9]|2[0-4]).jpg" Init1
mm3d OriConvert OriTxtInFile position_UTM33_cut_Zcst.csv jmfgps
mm3d CenterBascule "(1[0-9]|2[0-4]).jpg" Ori-Init1 Ori-jmfgps Abs0
mm3d Campari "(1[0-9]|2[0-4]).jpg" Abs0 Abs1 EmGPS=[jmfgps,0.1]]
mm3d Malt GeomImage "(1[5-9]).jpg" Abs1 Master=16.jpg DirMEC=Result1 ZoomF=4 ZoomI=32 Purge=true DefCor=0.001
mm3d Nuage2Ply Result1/NuageImProf_STD-MALT_Etape_6.xml Attr=16.jpg RatioAttrCarte=4
mm3d Malt GeomImage "(1[1-3]|2[0-2]).jpg" Abs1 Master=21.jpg DirMEC=Result2 UseTA=1 ZoomF=4 ZoomI=32 \
Purge=true DefCor=0.001
mm3d Nuage2Ply Result2/NuageImProf_STD-MALT_Etape_6.xml Attr=21.jpg RatioAttrCarte=4
mm3d Malt GeomImage "(10|2[3-4]).jpg" Abs1 Master=10.jpg DirMEC=Result4 UseTA=1 ZoomF=4 ZoomI=32 \
Purge=true DefCor=0.001
mm3d Nuage2Ply Result4/NuageImProf_STD-MALT_Etape_6.xml Attr=10.jpg RatioAttrCarte=4
Les trois premières lignes sont maintenant bien connues : recherche des points d’appui sur toutes les photographies pour travailler dans un référentiel commun (Tapioca), étalonnage de la caméra et recherche de leur position (Tapas). Le fichier en colonnes position_UTM33_cut_Zcst.csv n’est pas approprié pour une analyse par MicMac qui désire une série de fichiers au format XML : cette transformation est générée par OriConvert qui génère ici un nouveau répertoire contenant les orientations des caméras nommé Ori-jmfgps. Les photographies orientées dans un référentiel arbitraire (Init1, résultat du dernier Tapas) basculent dans le référentiel absolu des coordonnées GPS projetées (jmfgps) pour donner le nouveau répertoire d’orientations Abs0. Les positions GPS sont cependant entachées d’une erreur, et les positions des caméras calculées par MicMac (dans son référentiel arbitraire) ne s’ajustent pas parfaitement aux positions GPS (bruitées). Un ajustement des positions tenant compte des deux séries de données - photogrammétriques et mesures de position GPS - s’obtient par Campari qui ajuste le répertoire d’orientation absolu Abs0 pour générer le nouveau référentiel Abs1 qui sera utilisé pour générer le nuage de points fins par Malt. Nous avons été obligé de séparer le calcul du nuage fin en trois étapes distinctes exploitant chacun un sous-ensemble des photographies car sinon MicMac tend à confondre une façade avec une autre et effectuer des corrélations incorrectes entre points de façades opposées.
Les trois nuages de points sont insérés et fusionnés dans CloudCompare (fonction Merge), que nous avons sélectionné au lieu de Meshlab car ce dernier ne semble pas sauvegarder l’information de couleur lors de l’exportation du nuage de points en format ASCII (fichier d’extension XYZ). Un extrait de ce fichier est
508.69662476 255.29411316 316.57540894 253 254 255
508.73446655 255.26551819 316.57797241 252 254 254
508.70834351 255.15536499 316.51879883 232 237 241
508.74603271 255.12689209 316.52133179 192 202 212
qui ne semble pas stupide puisque les X et Y sont de l’ordre de 500 et 250 m respectivement, en accord avec la position des caméras que nous avions renseigné. Nous rajoutons à ces deux premières colonnes les valeurs 728000 et 5235000 respectivement pour nous ramener dans le référentiel absolu, chargeons ces valeurs dans QGis () au-dessus d’un fond d’image satellite (https://browse.digitalglobe.com, image couleur de GeoEye1 au-dessus de Besançon datée du 7 Août 2009 et rapidement géoréférencée au moyen de 3 points dont les coordonnées on été prises de Google Earth) et un modèle numérique de terrain (SRTM) pour valider le bon positionnement et orientation du nuage de points ainsi généré (Fig. 24). Bien que GeoEye1 soit annoncé avec une résolution de 1,84 m sur le produit final en couleur, la version dégradée des images disponibles en preview auprès de Digitalglobe présente, au niveau de Besançon, une taille de pixels estimée à 11 m*17 m - soit à peu près la même résolution que Landsat7 (http://landsat.gsfc.nasa.gov/?page_id=2376 et http://landsatlook.usgs.gov/ pour des liens vers les deux agences responsables de ce programme - NASA et USGS). Une vidéo résumant la séquence d’opérations pour charger le nuage de points dans QGis et associer une couleur à la hauteur de chaque point est mise à disposition à http://jmfriedt.free.fr/micmac_qgis.mp4 : l’attribut de hauteur encode la couleur en sélectionnant dans les propriétés de la couche vectorielle du nuage de points le symbole Graduated (au lieu de Single Symbol) et en lui attribuant la Column Z avec autant de classes que nécessaire. Si au contraire nous voulons garder les couleurs d’origine du nuage de points, nous restons en Single Symbol, et, après avoir cliqué sur Simple Marker, sélectionnons Data defined properties pour fabriquer l’expression qui définira la Fill Color par color_rgb(R, G, B).
Rappel pour le géopositionnement de photographies satellites
Nous avions décrit en détail [1] la procédure de recalage d’une image satellite se basant sur le géoréférencement de quelques points connus et déformation géométrique de l’image pour se caler sur ces points. Cette opération s’obtient au moyen du module georeferencerde QGis et en exploitant les points GPS acquis depuis Google Earth sur quelques points remarquables, ici les ponts qui traversent le Doubs autour de Besançon et une des “pointes” de la citadelle.
Figure 24 : Insertion du nuage de points de la tour dans QGis pour le replacer dans son contexte géographique - ici une image satellite GeoEye1 et un modèle numérique de terrain visible par transparence. La tour est convenablement localisée près du pont Charles de Gaulle (haut, milieu), tel que confirmé par la capture d’écran de Google Maps (bas, droite). QGis permet d’attribuer à chaque point une couleur associée aux champs RGB du fichier sauvegardé par CloudCompare, rendant ainsi sa couleur originale à chaque pixel du nuage de points (en bas, gauche).
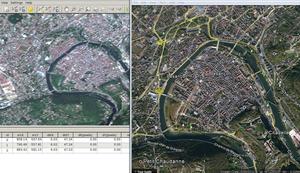
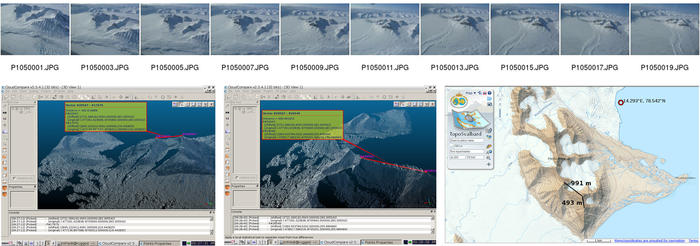
Ce même traitement appliqué à plus grande échelle au cours d’un vol en avion au-dessus du Spitsberg permet une analyse quantitative de l’exactitude du modèle ainsi généré (Fig. 25), excellente en abscisse et en ordonnée. Le résultat est cependant, sur cet exemple, très mauvais en altitude à cause d’un plan qui n’est pas d’altitude constante, lié au vol rectiligne de l’avion au cours de cette prise de vue. D’autres exemples dans lesquels l’avion fait le tour de la cible donnent de bien meilleurs résultats en élévation, malgré l’erreur en altitude du GPS. Nous n’avons pas cherché à retrancher ce plan moyen faute de points de contrôle au sol et un trait de côte mal défini sur ces photographies. Il est cependant utile d’être conscient de cette limitation avant de planifier un vol pour des prises de vues en avion ou en hélicoptère, opération coûteuse qu’il vaut mieux ne pas rater si les conditions d’acquisition des photos n’ont pas été bien maîtrisées.
Figure 25 : Haut : séquence de prises de vues pour calculer le nuage de points du modèle numérique d’élévation. Bas, gauche et milieu : mesure de la distance entre deux sommets après traitement tenant compte de la position GPS de l’appareil photo au cours du vol. Bas, droite, la mesure entre les mêmes deux sommets sur la carte de référence toposvalbard.npolar.no. Le point rouge indique une des positions de l’avion au cours des prises de vues.
9.3 Résolution
Nous sensibilisons le lecteur au problème de résolution du calcul si l’origine des coordonnées cartésiennes n’est pas amenée proche de 0. Dans le cas ci-dessous de photographies du bâtiment du CROUS à Besançon (Fig. 26) au bord du Doubs par le logiciel OSMTracker sur un téléphone Samsung S3, les photographies sont positionnées autour de (47.23°N, 6.02°E, 289 m) soit en UTM31N des coordonnées du type (728357 m, 5235782 m, 289 m). Nous avons effectué les opérations de bascule du référentiel et nuage dense de points dans ce référentiel et le résultat est catastrophique compte tenu de la résolution finie de la représentation des nombres en virgule flottante. Ramener les référentiels autour de 0 (en retranchant 728000 aux abscisses et 5235000 aux ordonnées) permet d’obtenir un résultat correct gradué en mètres. Nous pouvons ensuite replacer le nuage de points dans le référentiel absolu WGS84/UTM31N en rajoutant les coordonnées que nous avions soustraites pour effectuer un calcul correct : le format XYZ des nuages de points sauvegardés par CloudCompare contient aussi les 3 colonnes de couleur (RGB) et est directement lisible par GNU/Octave pour des opérations arithmétiques sur les deux premières colonnes.
Figure 26 : Haut : séquence de photos du bâtiment du CROUS à Besançon, et en dernier le masque qui a servi à contraindre le calcul dans la zone du bâtiment et exclure le ciel et la rivière en premier plan. Bas : à gauche le calcul en référentiel arbitraire où le résultat est excellent mais les dimensions ne sont pas exploitables. Milieu : référentiel absolu gradué en mètres mais résolution dégradée par la précision du calcul. Droite : référentiel absolu et résolution excellente en ramenant l’origine du repère près de 0. Dans tous les cas, la bulle contient les coordonnées d’un point dans la tour : noter le passage du référentiel arbitraire (abscisse/ordonnée inférieurs à 0) au référentiel absolu (altitude de l’ordre de 800 m, erronée par l’incertitude de calcul) et finalement le référentiel absolu ramené près de l’origine.
10. Dissémination des données
Les outils pour visualiser les nuages de points considérés jusqu’ici doivent être spécifiquement installés sur l’ordinateur de l’utilisateur, nécessitant donc une action volontaire de téléchargement du fichier de points et de chargement dans un outil dédié. Proposer la visualisation d’un tel nuage de points au travers d’une interface web permet de sensibiliser l’auditoire à la qualité du jeu de données avant de l’encourager à télécharger le fichier de points pour une exploitation locale. L’époque de VRML et de l’affichage de données vectorielles par une interface graphique de promenade sur le web semble révolue, pour avoir été remplacée par le protocole WebGL inclus dans HTML5. Mentionnons dès à présent que les considérations qui vont suivre présentent une chance non-négligeable de faire crasher le browser web : il est donc prudent de sauvegarder ses onglets avant d’accéder aux pages web citées ci-dessous.
Une première limitation de WebGL, qui semble liée à la volonté de sa compatibilité avec les plateformes mobiles que sont les téléphones portables et autre tablettes, tient au nombre maximum de points dans chaque nuage considéré : 64 Kpoints. Ainsi, comme pour les traces GPS incluses sur un fond de carte Google Earth au format KML, il faudra segmenter le jeu de données en une multitude de sous-ensembles respectant la contrainte de taille. Un environnement libre d’affichage de nuage de points qui nous est apparu le plus simple d’emploi est potree18. Cet ensemble de scripts JavaScript est exécuté par un serveur web pour afficher un nuage de points au travers d’une interface conviviale, sous réserve que le nuage de points ait été converti dans le format approprié, respectant les contraintes de WebGL : l’outil PotreeConverter19 est fourni à cet effet. Nos tests se sont limités à la conversion de nuages de points sauvegardés au format XYZRGB ASCII (fichier temporaire très volumineux) puisque tous les essais sur format de nuage de points au format PLY (binaire ou ASCII) se sont soldés par des corruptions de mémoire (segmentation fault). Après avoir exporté au format ASCII un nuage de points issu de la fusion dans Cloudcompare des divers résultats de calculs de Malt sur plusieurs images maîtresses, nous générons le répertoire de données requis par potree au moyen de PotreeConverter nuage.xyz -f xyzrgb -r 255 -s 0.1 -l 4 où -s est à adapter à l’extension du nuages de points (serait plutôt de l’ordre de l’unité pour un nuage géoréférencé par GPS, ici le nuage s’étend de +/-10 dans les 3 directions avec 8 décimales pour chaque coordonnée). Un fichier HTML contenant le code JavaScript d’appel aux bibliothèques de potree contient la position de la caméra (camera.position.x etc ...) et le chargement du nuage de points (pointcloudPath="../resources/pointclouds/granvelle2/cloud.js"; POCLoader.load(pointcloudPath);). Les plus de 4 millions de points comprenant ce nuage de points, qui représente le Palais Granvelle à Besançon (construit au 16ème siècle, abritant aujourd’hui le Musée du Temps), n’occupent que 50 MB sur le serveur web.
Figure 27 : Affichage d’un nuage de points de plus de 4 millions de pixels au travers des scripts potree exécutés par le serveur web de jmfriedt.sequanux.org/potree/examples/granvelle1.html, ici chargé par un client web chromium qui a le bon goût de ne pas crasher en chargeant un tel jeu de données.
Le dernier point qui manque dans cette prose par rapport à notre ambition initiale concerne le passage du virtuel au réel en passant du nuage de points à l’impression 3D, sujet actuellement à la mode chez les amateurs mais technique déjà largement utilisée par les professionnels (l’entrée de l’ENSG (École Nationale des Sciences Géographiques) présente un superbe modèle de la vallée de Chamonix) : ce point s’avère plus délicat qu'initialement escompté.
Conclusion
Nous avons décrit l’utilisation d’un outil libre fourni par l’IGN - MicMac/Apero - pour le traitement d’images numériques d’objets pris depuis divers points de vue pour obtenir un nuage de points tridimensionnel de la scène. Cet outil, initialement conçu pour l’observation de façades de bâtiments ou pour l’extraction de modèles numériques de terrains à partir de photographies aériennes ou en vue oblique, inclut la capacité à générer un modèle quantitatif - soit en incluant des points de contrôle au sol connus, soit en incluant l’information de position de la caméra au moment de la prise de vue.
Nous avons identifié un certain nombre de conditions sur les prises de vues et sur la trajectoire pour maximiser les chances de succès : comme dans tout traitement de signaux numériques, une source de données impropre sera incapable de fournir un résultat exploitable. Néanmoins, en vue de permettre à chacun de s’approprier cet outil, nous nous sommes efforcés de n’exploiter que des systèmes d’acquisitions d’images communément disponibles tels que téléphone portable, appareil photographique numérique compact, ou webcam embarquée sur un drone. Évidemment, les résultats sont bien meilleurs avec un appareil photographique réflexe muni d’un vrai objectif - en particulier la carte des corrélations sera uniformément blanche et présentera beaucoup moins de zones sombres que dans nos exemples.
Finalement, afin de dépasser le résultat purement qualitatif du traitement sans en perdre l’aspect ludique, nous avons inclus le nuage de points résultant dans un Système d’Informations Géographique (SIG) en ajoutant les données nouvellement générées dans le contexte de modèles numériques d’élévation et images satellites librement disponibles (avec une résolution nettement moindre que celle fournie par nos nuages de points acquis sur un bâtiment).
Les possibilités offertes par cet outil sont quasi infinies et dépassent largement le cadre de la géographie, pour être applicable à l’ingénierie ou à la reconstruction tri-dimensionnelle de pièces mécaniques (ou, dans notre cas, de jouets). L’extension à des modèles d’instrument d’acquisition d’images plus exotiques - par exemple le microscope électronique à balayage - qui ne respecte pas les hypothèses implémentées dans Tapas et Tapioca, nécessite une compréhension détaillée du code et de la théorie sous-jacente, qui dépasse les compétences de cet auteur. Cependant, la disponibilité des codes sources laisse ouverte la perspective d’étendre un jour les champs d’applications de MicMac : le lecteur est invité à s’en approprier les fondamentaux et adapter à ses propres besoins.
Remerciements
J.-M Friedt est ingénieur dans une société privée, hébergé par le département Temps-Fréquence de l’institut FEMTO-ST à Besançon, partenaire du projet de l’Agence National de la Recherche (ANR) CryoSensors, qui a financé la participation à l’excellente formation MicMac à l’ENSG ainsi que le trajet en Norvège pendant lequel les photographies des Figs. 2 et 23 ont été acquises. Cette prose a été rédigée avant la formation qui a fourni les bases théoriques et pratiques pour corriger un certain nombre de points qui restaient abordés superficiellement dans la version antérieure du manuscrit. Nous nous sommes cependant efforcés de ne pas inclure de concept nouvellement appris au cours de la formation qui n’avaient pas été abordés après consultation des documents librement disponibles sur le web.
Mes collègues géographes - D. Laffly (GEODE, Toulouse), F. Tolle & É. Bernard (ThéMA, Besançon) m’ont informé de l’existence de MicMac/Apero. S. Gascoin (CESBIO/CNES, Toulouse) m’a fourni une bonne partie des références bibliographiques. J.-P. Simonnet (Laboratoire de ChronoEnvironnement, Besançon) m’a fourni les photographies aériennes acquises en ULM pour générer les Figs. 8 à 10. Matthieu Deveau (IGN) a été à l’écoute de mes questions de novice auxquelles il a patiemment répondu. É. Carry (FEMTO-ST, Besançon, président de l’association Sequanux pour la promotion du logiciel libre) a installé les scripts JavaScript de potree sur le serveur web de sequanux.org.
Le site web gen.lib.rus.ec a fourni les documents inclus dans la bibliographie qui ne sont pas librement disponibles sur le web : toute recherche amateur (ou non) serait impossible sans cette ressource d’ouvrages scientifiques et techniques. Toutes les références bibliographiques de l’auteur sont disponibles à http://jmfriedt.free.fr.
Références
[1] J.-M Friedt, Correction géométrique d’images prises en vues obliques - projection sur modèle numérique d’élévation pour exploitation quantitative de photographies numériques, GNU/Linux Magazine France n.167, Janvier 2014, pp.42-57
[2] F. Remondino, S. del Pizzo, T. Kersten, S. Troisi, Low-cost and open-source solutions for automated image orientation - a critical overview. In: M. Ioannides & al (Eds.), Progress in Cultural Heritage Preservation, Lecture Notes in Computer Science,7616, Springer, Berlin Heidelberg, pp. 40-54 (2012)
[3] voir par exemple l’intitulé de la session “Cryospheric applications of modern digital photogrammetry from airplane, UAV, and ground-based instrument platforms” de l’American Geophysical Union à https://agu.confex.com/agu/fm14/webprogrampreliminary/Session3014.html, et plus généralement le blog de Matt Nolan à http://www.drmattnolan.org/photography/2014/
[4] J.-M Friedt, Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées, GNU/Linux Magazine France 139 (Juin 2011)
[5] D.G. Lowe, Distinctive Image Features from Scale-Invariant Keypoints, International Journal of Computer Vision, 60 (2) pp.91-110 (2004)
[6] Y. Egels & M. Kasser, Digital Photogrammetry, CRC Press (2001), et en particulier le chapitre 3 de cet ouvrage qui décrit les méthodes de réduction de l’espace des recherches de points homologues compte tenu des paramètres géométriques des caméras
[7] la documentation de MicMac se trouve dans le répertoire Documentation de l’archive mercurial (fichier DocMicMac.tex)
[8] W.W. Immerzeel, P.D.A. Kraaijenbrink, J.M. Shea, A.B. Shrestha, F. Pellicciotti, M.F.P. Bierkens, S.M. de Jong, High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles, Remote Sensing of Environment 150 (2014) 93-103
[9] M.J. Westoby, J. Brasington, N.F. Glasser, M.J. Hambrey, J.M. Reynolds, “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications, Geomorphology 179 (2012) 300-314
[10] I. Colomina, P. Molina, Unmanned aerial systems for photogrammetry and remote sensing: A review, ISPRS Journal of Photogrammetry and Remote Sensing 92 (2014) 79-97
[11] J.-M. Friedt, É. Bernard, F. Tolle, D. Laffly, Gestion d’Informations Spatialisées : outils libres pour l’exploitation de données géolocalisées - au-delà des aspects géographiques, séminaire CETSIS 2014 (Besançon, France), disponible à http://jmfriedt.free.fr/cetsis_sig.pdf
[12] J.-M. Friedt, Géolocalistion de photographies numériques, GNU/Linux Magazine France 96, Juillet/Août 2007 - noter la mise à jour du script de géolocalisation des photographies numériques suite au passage à la version 3 de l’API de Google Maps - bien que la méthode décrite dans l’article reste la même, l’implémentation est mise à jour dans http://jmfriedt.free.fr/photos_asc.txt. Par exemple, http://jmfriedt.sequanux.org/130929_kvad/photos_asc.php.
[13] J. Lefort, L’aventure cartographique, Belin-Pour la Science (2004)
1 http://en.wikipedia.org/wiki/Scale-invariant_feature_transform ou, plus complet, http://omiv2.u-strasbg.fr/imagemining/documents/IMAGEMINING-Stumpf.pdf
2 sans la présentation orale, le support de cours http://fad.ensg.eu/moodle/course/view.php?id=315 est un peu ardu à suivre mais fournit au moins une idée générale sur la démarche
3 www.cs.cornell.edu/~snavely/bundler/
4 http://www.tapenade.gamsau.archi.fr/TAPEnADe/Tools.html
5 http://www.arte.tv/guide/fr/050492-000/les-derniers-secrets-de-l-armee-de-terre-cuite
6 hg clone https://culture3d:culture3d@geoportail.forge.ign.fr/hg/culture3d : toutes les analyses proposées dans ce texte sont effectuées sur la version 3642 datée du 20 juin 2014
7 Il est possible de traiter plusieurs séquences de prises de vues prises avec des objectifs différents - par exemple gros plans pour la résolution et plans lointains pour l’assemblage - mais chaque ensemble de photographies sera traité individuellement dans un premier temps, en particulier pour identifier les propriétés optiques de chaque objectif.
8 Toutes les planches contact ont été générées par ImageMagick au moyen de montage -geometry 120x120+1+1 -tile 10x1 -label %f *.JPG contact.jpg
11 http://www.editionsmontparnasse.fr/p1001/L-Europe-vue-du-ciel-filmee-par-Sylvain-Augier-DVD
13 http://www.arte.tv/guide/fr/044681-002/les-alpes-vues-du-ciel ou http://www.arte.tv/guide/fr/044681-004/les-alpes-vues-du-ciel
14 nous n’abordons pas ici la possibilité de renseigner les informations manquantes dans les entêtes EXIF dans le fichier MicMac-LocalChantierDescripteur.xml
15 http://www.editionsmontparnasse.fr/p882/La-France-vue-du-ciel-filmee-par-Sylvain-Augier-DVD
16 Noter qu’un laboratoire de l’IGN a développé son enregistreur GPS, loemi.recherche.ign.fr/pdf/brochureGeocube1.pdf, qui fournit quant à lui la résolution centimétrique en mesure statique !
17 https://code.google.com/p/osmtracker-android/
18 https://github.com/potree/potree
19 https://github.com/potree/PotreeConverter