Banques en ligne : à la découverte d'EMV-CAP

1. Le standard EMV

1.1 Présentation

Le standard EMV voit le jour en 1994 et devient rapidement la référence de facto pour la communication entre la puce d'une carte bancaire (de débit ou de crédit) d'une part et les terminaux de vente ou distributeurs de billets d'autre part. Les initiales EMV proviennent du nom des 3 firmes l'ayant conçu et adopté initialement, à savoir Europay, MasterCard et Visa. Les spécifications de ce standard sont maintenues par EMVCo [1] et mises à disposition gratuitement sur leur site web.

D'après les derniers chiffres diffusés par EMVCo, plus d'un milliard de cartes de paiement incorporant la norme EMV sont en circulation. Au sein de l'Europe, un espace de paiement unifié a été mis en place (Single Euro Payments Area ou SEPA) et c'est la norme EMV qui a été choisie afin d'assurer l'interopérabilité entre les cartes et les terminaux de paiement.

Outre cet aspect d'interopérabilité, un autre argument mis en avant pour convaincre les organismes qui en étaient toujours à l'usage de la seule piste magnétique est la diminution du nombre de fraudes, notamment celles liées au simple clonage de ladite piste. Ainsi, les statistiques publiées l'année passée par l'association anglaise UK Cards attestent d'une réduction de moitié des pertes du secteur financier, liées à la contrefaçon des cartes bancaires entre 2008 et 2009 [2]. Cela est rendu possible grâce à une authentification des transactions financières par des moyens cryptographiques mis en œuvre par une puce intégrée à la carte. Enfin, disposer au sein de la puce de plusieurs applications distinctes ouvre la voie à de nouveaux développements et à des évolutions, même durant la vie d'une carte. Moneo, Maestro et Visa Electron sont déjà des applications rencontrées actuellement.

Une extension propriétaire de ce standard a été développée afin de bénéficier de la sécurité offerte par EMV dans des situations où la carte n'est pas directement disponible dans un environnement contrôlé tel qu'un distributeur de billets ou un terminal de paiement. Cette extension, appelée EMV-CAP, autorise l'usage d'une carte EMV sur Internet sans nécessité de changements logiciels sur les ordinateurs personnels des utilisateurs. Le but est de garder la même carte pour les opérations en ligne et pour payer ses achats ou pour retirer de l'argent dans un distributeur de billets.

1.2 Transaction EMV

Avant d'aborder le cœur du sujet, il nous semble indispensable de décrire sommairement une transaction EMV, car l'appareil d'authentification et de signature EMV-CAP (auquel nous ferons référence par la suite sous la simple dénomination calculette) réalise une transaction très proche d'une transaction EMV habituelle. Dans ce contexte, notre calculette est comparable à un terminal de paiement offline.

1.2.1 Aperçu

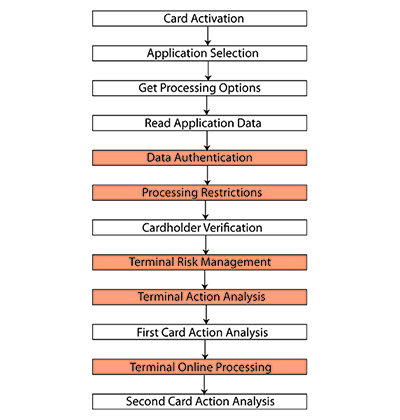
Les 4 volumes décrivant le protocole EMV (EMV Books, [1]) représentent une quantité énorme d'informations, et particulièrement indigestes par des renvois incessants d'un chapitre à l'autre. Une autre difficulté est également que le protocole EMV offre de nombreuses alternatives et c'est aux intégrateurs de faire les choix définitifs tout en gardant le coût des cartes le plus bas possible. C'est ainsi que la norme ne décrit pas moins de 5 possibilités d'authentifier le porteur de la carte (une d'elles est d'ailleurs de ne pas le faire !), elle différencie les transactions online et offline et propose 3 types d'authentification de la carte. La norme EMV n'est finalement qu'une grande boîte à outils... Néanmoins, une transaction se résume comme suit (voir figure 1) :

1.2.2 Sélection de l'application

Lors de l'introduction de la carte dans un terminal de paiement, les étapes initiales du dialogue, ainsi que l'envoi de l'ATR (Answer-To-Reset, réponse initiale) et la mise à niveau du protocole de communication se font classiquement selon la norme ISO7816-3 [3]. Le terminal tente ensuite de choisir l'application sur la carte en fonction d'une liste préétablie. En cas d'échec de la sélection d'une application, le terminal tente de sélectionner la suivante dans sa liste. Ce n'est qu'en cas d'épuisement complet de cette liste que la carte sera finalement refusée par le terminal. Il existe également une autre méthode optionnelle appelée Payment System Environment (PSE), par laquelle le terminal reçoit une liste d'applications en lisant le fichier 1PAY.SYS.DDF01 de la carte. La communication avec celle-ci se fait toujours dans le respect de la norme ISO7816-4 [4].

1.2.3 Initialisation de la transaction

Suite à la sélection de l'application et à l'envoi de la commande Get Processing Options qui sert à initier la transaction, la carte renvoie une première série d'informations, telles que l'AIP (Application Interchange Profile), qui indique au terminal les différentes opérations à faire pour mener à bien une transaction, et l'AFL (Application File Locator), qui indique la liste des données disponibles au niveau de l'application.

1.2.4 Lecture et authentification des données

Le terminal va lire ces données sur la carte, qui contiennent par exemple le numéro de la carte, la date d'expiration et la liste des données que la carte attend pour faire effectivement une transaction (Card Risk Management Data Object Lists, CDOL1 et CDOL2). Le terminal valide ensuite les données reçues par un des mécanismes suivants : SDA (Static Data Authentication), où les données de l'application sont signées par la banque lors de la création de la carte ; DDA (Dynamic Data Authentication), où en outre la carte contient elle-même une paire de clés RSA et est capable de signer un challenge provenant du terminal [5], et enfin, CDA (Combined DDA & application cryptogram generation) où le challenge est combiné à la transaction proprement dite.

1.2.5 Authentification du porteur

Vient ensuite l'authentification du porteur de la carte, selon l'une des méthodes listées et supportées par la carte. Par exemple, l'usage du PIN est supporté soit en clair, soit chiffré. Mais l'absence de vérification par un PIN est aussi reconnue comme une des méthodes disponibles (et utilisée par exemple aux péages autoroutiers). Le protocole EMV prévoit avant et après la vérification du porteur d'autres vérifications (pour les citer : Processing Restrictions, Terminal Risk Management, Terminal Action Analysis), mais sur lesquelles nous n'allons pas nous attarder car elles ne sont pas mises en œuvre par notre calculette.

1.2.6 Transaction proprement dite

Tout est en place pour que la carte génère un code d'authentification de message (MAC, Message Authentication Code) grâce au secret qu'elle contient (cette étape porte le nom de First Card Action Analysis). Pour ce faire, le terminal envoie les différentes données demandées par la carte (cf. CDOL1). En réponse, la carte génère un cryptogramme de 8 octets qui porte le nom d'ARQC (Authorization Request Cryptogram) dans les opérations en ligne.

Ce calcul se fait en deux temps. Tout d'abord, une clé éphémère de 128 bits est dérivée de la clé symétrique principale de la carte, elle aussi de 128 bits. La méthode de dérivation recommandée par EMVCo est d'utiliser triple-DES. Ensuite, la carte calcule un MAC reposant aussi sur un chiffrement triple-DES avec la clé éphémère sur non seulement les données présentées, mais également sur une série de données internes à la carte. Le chiffrement par blocs étant triple-DES, la longueur effective des clés est donc en réalité de 112 bits.

Ce cryptogramme est envoyé à la banque qui le valide en temps réel. Après validation, la banque envoie sa réponse à la carte par le terminal pour faire une Second Card Action Analysis. Ceci clôture l'échange et la carte sait que la transaction a été acceptée par la banque. La carte met à jour son historique s'il en existe un.

2. Et cet EMV-CAP ?

2.1 Contexte

Diverses méthodes existent pour authentifier un utilisateur qui désire faire des opérations bancaires par Internet. Les plus répandues sont les simples logins et mots de passe, ou les modules cryptographiques dont le fonctionnement consiste à répondre à un challenge affiché à l'écran, ou encore les dispositifs générant des OTP (one-time password). En France, certaines banques font usage de SMS pour demander confirmation d'un ordre de virement. La tendance actuelle est d'effectuer ces opérations hors de l'enceinte de l'ordinateur personnel pour être ainsi partiellement hors de portée des codes malveillants, keyloggers et autres joyeusetés et, cerise sur le gâteau, de fonctionner parfaitement quel que soit l'OS. Initialement, certaines banques proposaient des calculettes ne nécessitant pas de carte, telles que le Digipass, pour s'authentifier et signer des transactions financières. Aujourd'hui, les banques préfèrent distribuer des calculettes équipées d'un lecteur de carte à puce afin d'utiliser la carte bancaire pour cette nouvelle fonction (figure 2). La calculette est produite en masse et, contrairement aux Digipass et RSA SecureID, ne nécessite pas de personnalisation car elle ne contient aucune clé secrète, diminuant ainsi les coûts de fabrication et de gestion.

2.2 Spécifications

À l'initiative de MasterCard, le Chip Authentication Protocol (CAP) est développé avec l'idée de réutiliser en grande partie les éléments du protocole EMV. Visa a suivi en dénommant son produit Dynamic Passcode Authentication (DPA) [6]. Malheureusement, les spécifications de ce protocole ne sont pas publiées et il n'est pas aisé d'obtenir des informations précises sur son fonctionnement. En consultant le site d'un des fabricants de la calculette [7], nous découvrons qu'il existe plusieurs versions du protocole, mais sans obtenir des renseignements complémentaires.

2.3 Utilisation

2.3.1 Modes opératoires

Le fonctionnement de cette calculette se résume de la façon suivante. Lorsque l'utilisateur souhaite s'authentifier auprès du site web de sa banque ou effectuer une opération bancaire telle qu'un transfert, il est redirigé vers une page d'instructions à suivre. Après avoir inséré la carte dans le lecteur, l'utilisateur choisit parmi plusieurs modes. Nous en avons dénombré trois, mais tous ne se retrouvent pas nécessairement sur toutes les calculettes, car les banques n'en utilisent en général que deux (voir ci-dessous). L'utilisateur est ensuite invité à fournir son PIN ainsi que d'éventuelles données complémentaires apparaissant sur la page web de la banque et composées d'un ou de plusieurs nombres. La calculette fournit alors une réponse sous la forme d'un jeton, un one-time password (OTP) de 6 à 16 chiffres (8 sur les modèles observés), qui doit être introduit sur la page web. Le serveur de la banque valide alors cette réponse et accepte d'authentifier l'utilisateur ou d'effectuer l'opération bancaire demandée. Notons que certains sites marchands redirigent le client au moment du paiement vers le site de sa banque par une fenêtre pop-up. Il est ainsi invité à se servir de sa calculette et de sa carte pour finaliser la transaction.

2.3.2 Mode 1

Utilisé pour l'authentification. La page de la banque donne un challenge qui doit être saisi sur la calculette pour obtenir la réponse attendue. Ce mode est accessible par la touche [M1] des calculettes des banques qui l’utilisent.

2.3.3 Mode 2

Employé pour l'authentification par certaines banques n'utilisant pas le mode précédent. Aucun challenge n'est nécessaire et ceci correspond à la création d'un jeton d'authentification. Ce mode est accessible grâce à la touche [Identify] de cet autre type de calculette.

2.3.4 Mode 2 + TDS (Transaction Data Signing)

Afin de valider une transaction financière, la banque donne une ou des valeurs, telles que le montant ou le numéro de compte du bénéficiaire, qui doivent être fournies à la calculette pour obtenir la réponse attendue. Ce mode est accessible par pression de la touche [Sign] ou [M2] des calculettes. Habituellement, la banque se contente de deux valeurs, mais la calculette supporte jusqu'à 10 nombres de 10 chiffres, ce qui serait nettement plus laborieux pour l'utilisateur ! En outre, ce mode a été observé auprès de certaines banques pour valider une transaction avec un site marchand selon le protocole 3-D Secure [8].

2.3.5 Interopérabilité

Nous avons constaté qu'en Belgique, les calculettes ne sont pas spécifiques à une banque déterminée (bien que son nom y soit inscrit) et les opérations sont correctement validées lorsqu'on fait des essais avec des calculettes provenant d'autres banques. Un organisme certifie ces appareils [9], ce qui justifie probablement que le mode de fonctionnement soit identique malgré une dénomination des touches parfois différente. Ainsi, le Mode 1 est accessible sur les calculettes dépourvues de touche [M1], en pressant la touche [Menu] et en sélectionnant explicitement le Mode 1. Le Mode 2 est quant à lui accessible sur les calculettes M1/M2 en pressant [M2], mais sans introduire la moindre donnée, ou en pressant la touche [M1] et en introduisant un challenge composé d'un ou plusieurs zéros, ou même en utilisant la touche [M1] sans fournir de challenge (tout cela revenant au même, comme nous le verrons plus en détail).

3. Analyse d'EMV-CAP

3.1 Première tentative

En parcourant la littérature disponible sur la Toile, outre quelques brevets très instructifs [10], nous avons retenu deux documents qui proposent une analyse fouillée du protocole. D'abord un article émanant du groupe de Ross Anderson de Cambridge [11] qui, après avoir écouté des échanges entre une calculette et une carte, montre que celui-ci est très proche d'une transaction EMV, tout en ayant un certain nombre de différences qui ont été analysées et détaillées. Ainsi, bien qu'EMV et EMV-CAP puissent partager une même application au sein de la carte, elles existent généralement comme deux applications distinctes, partageant néanmoins un certain nombre de données dans un ou plusieurs fichiers communs. L'autre document est un travail de fin d'études réalisé à la Radboud Universiteit aux Pays-Bas [12], analysant les spécificités du système bancaire néerlandais. Malheureusement, la génération de certaines signatures (Mode 2 + TDS) n'est pas mentionnée dans l'article de Cambridge et, bien qu'utilisée par une banque néerlandaise, n'a pas pu être expliquée, ni reproduite dans le second document.

Partant de ces premiers éléments et tenant compte des spécificités des cartes bancaires belges (notamment les réponses reçues aux requêtes EMV), nous avons écrit un premier script censé jouer le rôle de la calculette. Nous avons bien pu obtenir une réponse de la carte bancaire interrogée, mais toute tentative de connexion au site bancaire échouait. Il était clair que nous ne disposions donc pas de suffisamment d'éléments pour reproduire une transaction EMV-CAP correcte.

3.2 Bus Pirate

L'écoute d'un échange entre une calculette EMV-CAP et une carte devenait dès lors incontournable. L'échange entre un lecteur et une carte, décrit dans la norme ISO7816, a les caractéristiques suivantes : la carte ne fait que répondre aux commandes reçues, en half-duplex selon un protocole série et de manière asynchrone malgré la présence d'un signal d'horloge. Il est facile d'intercepter physiquement les échanges à partir de montages rudimentaires (figures 3 et 4) !

Nous avons à disposition la ligne série, bidirectionnelle et d'un niveau électrique ne dépassant jamais la plage 0-5V. Ce signal n'est toutefois pas exploitable directement par un port série ordinaire, même avec une adaptation des niveaux électriques, car les vitesses de transfert ne correspondent généralement pas aux standards habituels. La solution viendra de Bus Pirate [13], une petite merveille de l'Open Hardware disponible pour quelques dizaines d'euros.

Dans [11] et [12], les équipes de Cambridge et de Radboud avaient programmé des cartes de développement FPGA, un poil plus cher et plus compliqué. Il est également possible de modifier les données à la volée si vous êtes prêt à bidouiller dans le firmware, ouvert, naturellement.

3.3 Mesure de la fréquence d'horloge

La vitesse de transmission de la ligne série dépend de la fréquence du signal d'horloge. La première chose à faire est donc de la mesurer. Pas besoin de fréquencemètre, le Bus Pirate l'intègre ! Nous connectons donc le signal Clock (signal d'horloge) à la sonde AUX, le signal Ground (masse) à la sonde GND. La mesure est réalisée après l'insertion de la carte-sonde dans la calculette et après avoir enfoncé la touche [M2] ou [Identify] pendant l'affichage du message PIN ? à l'écran.

3.4 Configuration de l'UART

Pour obtenir la vitesse du port série, le résultat obtenu doit être divisé par 372. Ce chiffre correspond au diviseur qui est utilisé dans la plupart des cartes et qui est aussi défini dans la norme ISO7816. Afin d'écouter un échange à une vitesse arbitraire, il faut calculer un coefficient Baud Rate Generator BRG=(4000000/baudrate)-1. La valeur obtenue est ensuite utilisée pour programmer l'UART du microcontrôleur du Bus Pirate, un PIC de Microchip. Voici les commandes pour écouter un échange lorsque l'horloge est cadencée à 1495552 Hz (BRG égal à 994), comme dans l'exemple repris ci-dessus. Nous connectons le signal IO à la sonde du Bus Pirate portant le label MISO/RX et correspondant à la broche RX d'un port série lorsque le mode UART est utilisé.

3.5 Écoute des données

Démarrer et arrêter l'écoute des données en transit sur l'IO se fait au moyen des commandes suivantes :

Les données apparaissent un octet à la fois. Il suffit d'un simple script pour les remettre en forme et rendre la lecture plus confortable. Il est aussi nécessaire de dissocier les données envoyées par la calculette de celles qui sont émises par la carte en se référant à la structure des APDU (blocs d'informations envoyées ou reçues par la carte [4]). Il faut également supprimer quelques octets présents dans la couche de communication sous l'APDU et dépendant du mode, T=0 ou T=1, décrits dans la norme ISO7816. Dans le cas d'un échange T=0 (mode orienté caractère), qui est celui auquel nous avons dû faire face, la carte répète l'octet de l'instruction (INS) avant que la calculette n'envoie ses données. Ainsi, lorsqu'elle envoie la C-APDU « 00 A4 04 00 07 A0 00 00 00 04 80 02 » (un SelectApp que nous expliquerons plus loin), nous observons la suite d'octets suivante : « 00 A4 04 00 A4 07 A0 00 00 00 04 80 02 ».

3.6 Exemple d'une transaction EMV-CAP en Mode 2

3.6.1 Trace

Voici un exemple d'échange entre une calculette et une carte de débit belge utilisée pour s'authentifier auprès du site web de la banque. L'opération demandée fut la plus simple opération EMV-CAP : un Mode 2 via la touche [Identify] (ou [M2] sans donnée). Pour une description complète des APDU échangés et de leur décomposition, nous invitons le lecteur à utiliser notre script [15] au moyen de la commande suivante : EMV-CAP.py --mode 2 --reader foo:cap_be --verbose --debug. Il fonctionnera avec une carte « virtuelle », en fait avec des traces préenregistrées et anonymisées. Si vous ne désirez pas installer le script, nous mettons également à disposition [15] la trace numérotée obtenue lors de l'exécution de cette commande et à laquelle nous nous référons en indiquant les lignes.

3.6.2 Sélection de l'application

Après un signal électrique sur la ligne Reset, la première réponse de la carte est l'ATR (Answer To Reset, ligne 1). Grâce à cette donnée, la calculette choisit les paramètres de communication avec la carte.

La calculette va tenter de se connecter à l'application A0000000038002 (VisaRemAuthen), qui est l'application de Visa implémentant DPA (Dynamic Passcode Authentication), leur version d'EMV-CAP (ligne 6). Celle-ci n'existe pas dans la carte testée et renvoie donc un message d'erreur (ligne 7). La calculette essaie ensuite l'application suivante (ligne 8). Il s'agit de A0000000048002 (SecureCode Aut), l'application EMV-CAP de MasterCard qui, elle, existe bien. La carte répond donc en une suite d'octets (ligne 9) qui sont des données sous la forme tag-longueur-valeur (TLV, selon l'encodage BER défini dans le standard ASN.1 [16]). Précisons qu'il ne s'agit pas pour autant d'une carte MasterCard, mais simplement d'une carte supportant EMV-CAP.

On y retrouve l'ID de l'application (AID, lignes 19-23), une structure Processing Options DOL (PDOL) définissant les options à fournir pour la commande suivante (lignes 30-42), spécifiées sous forme de couple tag-longueur (l'option à fournir est ici le type de terminal), les préférences de langue (lignes 43-49), ici juste « fr », mais il est possible d'en avoir plusieurs : « fren », la nationalité du détenteur de la carte (lignes 62-67), et enfin, d'autres données spécifiques à la banque (lignes 68-74).

3.6.3 Initialisation de la transaction

Pour pouvoir débuter la transaction EMV, la calculette transmet la commande GetProcessingOptions (lignes 134-143) avec 0x34 comme valeur de type de terminal (en fonction du PDOL décrit plus haut), ce qui signifie d'une part que le terminal (la calculette) est détenu par le porteur de la carte, et d'autre part, qu'il fonctionne en mode online puisqu'il y a un dialogue entre la banque et le terminal, même si ce sont nos petits doigts qui font le travail. La carte répond avec l'Application Interchange Profile (AIP, lignes 151-156) et l'Application File Locator (AFL, lignes 158-162). Ce dernier contient une liste de pointeurs codés sur quatre octets vers des fichiers. Les 5 premiers bits du premier octet contiennent le SFI (une forme de raccourci vers le fichier), les deuxième et troisième octets indiquent une fourchette de records à lire dans ce fichier et le quatrième indique s'ils sont signés. Ainsi 08040400 invite à lire le quatrième record du fichier SFI=1.

3.6.4 Lecture des données

La calculette lit alors les records mentionnés dans l'AFL (ligne 166). L'AFL de cette carte contient deux fichiers, dont le premier est commun avec l'application bancaire EMV classique et contient entre autres le numéro de la carte (lignes 174-179), les dates d'émission (lignes 187-192) et d'expiration (lignes 193-199), une copie de la piste magnétique numéro 2 (lignes 200-205), le pays d'émission (lignes 206-211), la monnaie (lignes 212-217) et sa représentation (lignes 218-224), ici l'euro et 2 chiffres pour les centimes. Le second fichier, propre à EMV-CAP, contient les données indispensables pour la suite des opérations : la liste des méthodes possibles d'authentification du porteur de la carte (lignes 242-247), un filtre appelé Issuer Proprietary Bitmap (IPB, lignes 236-241) dont le rôle sera détaillé dans les paragraphes suivants, et deux listes CDOL1 (lignes 248-314) et CDOL2 (lignes 315-394) qui définissent les données à fournir afin de demander à la carte de calculer un premier cryptogramme (selon CDOL1) et ensuite un second (selon CDOL2). Les données à fournir sont calquées sur EMV, mais la plupart d'entre elles (date, gestion du risque du terminal, etc.) sont simplement nulles car dépourvues de sens dans le contexte d'EMV-CAP. L'une d'elles est cependant importante pour certains modes : l'Unpredictable Number (UN). Nous y reviendrons. Rappelons qu'il n'y a pas d'authentification des données lues, contrairement à une vraie transaction EMV. C'est à cette étape que nous comprenons la différence avec [11] et [12] : les CDOL des cartes belges réclament des données supplémentaires dont nous ignorions les valeurs à fournir, notamment les Cardholder Verification Method Results.

3.6.5 Authentification du porteur

La calculette demande ensuite l'état du PIN (ligne 397). La réponse indique qu'il reste 3 essais possibles (lignes 398-406). Le PIN introduit sur le clavier est envoyé à la carte en utilisant un simple codage BCD (ligne 409). La réponse retournée par la carte indique que le PIN est correct (ligne 410).

3.6.6 Transaction proprement dite

Enfin, nous arrivons au cœur de la transaction : la calculette demande à la carte de générer un cryptogramme (GenerateAC) en présentant les données comme demandées dans le CDOL1 (lignes 411-422). Ces données sont fixes et l'Unpredictable Number (ligne 419) est nul, puisque dans le Mode 2 que nous sommes occupés à décortiquer, il n'y a pas de challenge. Le cryptogramme demandé est en fait un Authorization Request Cryptogram (ARQC) tel qu'on les retrouve dans les transactions EMV en ligne. En cas de véritable transaction, il aurait été envoyé à la banque, mais ici le protocole EMV-CAP détourne l'ARQC de son usage initial.

Selon les EMV Books, les cartes contiennent une gestion du risque intégrée laissée à la discrétion de l'organisme bancaire (par exemple pour évaluer le risque lié à des erreurs dans le protocole de transaction, à des montants anormalement élevés ou à de trop fréquentes transactions offline) et n'apprécieraient pas trop qu'on initie plusieurs transactions EMV sans jamais les finir. C'est pourquoi, pour conclure la session EMV-CAP, la calculette envoie une seconde requête pour un Application Authentication Cryptogram (AAC) signifiant à la carte que la transaction EMV est annulée (lignes 457-470).

Bref, pour la carte, rien ne s'est passé, mais nous avons soutiré une réponse signée de la carte qui va être transformée en un simple nombre à 8 chiffres, le jeton, et affichée sur l'écran de la calculette pour être transmise à la banque. La banque pourra ainsi authentifier le porteur. Nous verrons dans un instant comment se calcule le jeton à partir de la réponse de la carte.

3.7 Et les autres modes ?

Nous venons de détailler le Mode 2, mais qu'en est-il des deux autres modes décrits dans la section 2.3 ?

3.7.1 Mode 1

Dans le Mode 1, la calculette demande un challenge, qui est envoyé à la carte dans les deux commandes GenerateAC et plus précisément dans le champ Unpredictable Number (UN), codé en BCD. Cette localisation n'est en soi pas surprenante car la documentation d'EMV précise bien que ce tag est prévu pour donner de la variabilité au cryptogramme. Cela explique aussi pourquoi exécuter un Mode 1 sans donnée ou avec un challenge composé uniquement de zéros revient à exécuter un Mode 2 où l'UN est mis à zéro.

3.7.2 Mode 2 + TDS

Pour le Mode 2 + TDS dans lequel l'utilisateur est amené à introduire un certain nombre de données numériques supplémentaires par l'entremise du clavier, nous ne voyons assez curieusement aucune différence avec le Mode 2. Les données à signer ne sont pas fournies à la carte, tout simplement. Lors de l'écoute d'un échange avec Bus Pirate, nous remarquons que la calculette coupe le dialogue (le signal Clock est arrêté) avec la carte juste après la réponse du 2ème GenerateAC et ce, avant même que l'utilisateur n'ait commencé à taper les données au clavier ! Il est intéressant de noter que ceci diffère de la description faite du mode Sign pour les calculettes anglaises [11], qui est un Mode 1 étendu et pour lequel on retrouve le montant dans le champ Authorised Amount (un autre champ présent dans les CDOL) et le compte du bénéficiaire dans le champ Unpredictable Number. La calculette belge utilise donc les données fournies dans le Mode 2 + TDS uniquement pour faire varier la réponse affichée, tout comme la banque néerlandaise analysée dans [12]. Cela éveille quelques soupçons a priori, car la calculette ne semble pas dotée, jusqu'à preuve du contraire, d'une puissance de calcul impressionnante et, imaginons que nous arrivions à percer son mystère, nous pourrions signer des données à partir d'un jeton d'authentification ! Voire, si l'opération est réversible, partir de la signature de certaines données pour la transformer en signature sur d'autres données ! Tout cela ferait la joie des malwares et de leurs utilisateurs. La thèse néerlandaise [12] relève d'ailleurs en de nombreuses occasions les dangers potentiels de ce mode et de la sécurité par obscurité sans toutefois être en mesure de confirmer ou d'infirmer ces hypothèses. Mais l'histoire ne s'arrête pas là ;-)

3.8 Calcul du jeton pour les Mode 1 et Mode 2

La réponse au premier GenerateAC décrit dans l'échange commenté contient un peu plus que le cryptogramme de 8 octets (AC, lignes 442-447). Nous y retrouvons également le Cryptogram Information Data (CID, lignes 430-435) qui indique que la réponse est un ARQC, le compteur de transactions sur 2 octets (Application Transaction Counter, ATC, lignes 437-441) qui augmente d'une unité à chaque fois, et enfin, l'Issuer Application Data (IAD, lignes 448-453). Rappelez-vous du filtre qui avait été reçu dans le second record (IPB, lignes 236-241). Il sert à indiquer les bits qui doivent être pris en considération pour générer la réponse qui sera affichée par la calculette. Cette réponse s'obtient en alignant les valeurs des 4 tags et le filtre. La valeur du filtre indique à la façon d'un masque quels bits doivent ensuite être utilisés pour construire la réponse qui sera affichée sur la calculette, après une conversion en décimal [10].

Les valeurs envoyées dans la réponse de la carte étaient :

CID ATC  AC                              IAD

80  005A 513C1201B7DB02A0 06015603A400000700030000010002

Issuer Proprietary Bitmap (IPB) :

00  00FF 000000000003FFFF

Filtré :

         5A                        302A0

Soit en binaire 01011010 110000001010100000, et enfin, en décimal 23790240, qui était bien la valeur affichée par la calculette. La longueur maximale du jeton obtenu est donc directement fonction de la longueur effective du filtre, ici de 26 bits, donc de 8 chiffres.

On peut donc conclure qu'avec le filtre choisi ici, le CID et l'IAD n'interviennent pas dans le calcul de la réponse et seuls les 18 bits LSB de l'AC sont concaténés avec les 8 bits LSB du compteur de transactions. Grâce à ces 8 bits du compteur de transactions, la banque va se synchroniser avec la carte. Les 8 bits les plus significatifs du compteur de transactions doivent être gérés par la banque de manière implicite en tenant compte de l'historique des transactions. Remarquons que le choix du filtre peut différer d'une banque à l'autre, voire même d'une génération de cartes à l'autre au sein d'une même banque. En pratique, il semble que le filtre choisi soit commun à l'ensemble des banques belges analysées, sans doute sous l'égide de l'EPCI [9].

3.9 Calcul du jeton pour le Mode 2 + TDS

Nous avons vu que du point de vue de la carte, le Mode 2 + TDS ne se différencie en rien du Mode 2. La carte ne reçoit pas les données à signer, ni même un hash de celles-ci. C'est donc la calculette qui transforme les données introduites sur le clavier pour créer une nouvelle réponse tout en utilisant le cryptogramme et le compteur de transactions reçus en retour de la commande GenerateAC.

Nous avons tenté de trouver intuitivement une corrélation entre ces éléments, mais sans succès. Pour mieux cerner le problème, nous devons contrôler la réponse de la carte et voir en quoi elle influence la réponse affichée. Il n'est pas nécessaire pour autant de déployer une attaque MitM (Man-in-the-Middle) sur une vraie carte. En effet, il suffit de créer une applet [15] pour JavaCard qui répondra à la calculette ce que nous désirons. Le PIN peut même servir de moyen de contrôle de l'applet, par exemple pour programmer un cryptogramme précis sans devoir recharger une nouvelle applet dans la JavaCard. Nous avons testé notre applet avec des JavaCards utilisant le mode T=0. En faisant varier le cryptogramme lors d'essais successifs, nous nous apercevons qu'une inversion du premier bit de n'importe quel octet du cryptogramme n'influence pas la réponse affichée par la calculette. Ceci indique avec une forte probabilité que le cryptogramme est employé comme une clé DES. En effet, les clés DES sont de 56 bits, qui sont codées traditionnellement sur 64 bits. Et les bits supplémentaires servant en principe de bits de parité sont dans la plupart des cas purement ignorés.

Nous découvrons sur ces entrefaites la page de Wikipédia dédiée à EMV-CAP [17] (oui, oui, nous aurions pu commencer par là !) qui confirme l'idée de Message Authentication Code. Dans ce scénario, le résultat du Mode 2 sert de clé pour un CBC-MAC à base de DES. Le résultat du CBC-MAC est utilisé en lieu et place du cryptogramme et traité exactement comme dans l'exemple ci-dessus en préservant le compteur de transactions et en appliquant le filtre. Enfin, un document [18] décrivant une cardlet EMV-CAP précise que la réponse de la calculette serait conforme à la norme ISO 9797-1 Algorithm 1 (qui décrit le CBC-MAC) [19] en utilisant le cryptogramme AC comme clé.

En effet, après quelques tâtonnements, nous parvenons à convertir correctement avec OpenSSL le cryptogramme en un nouveau cryptogramme intégrant les données à signer. Ainsi, supposons que le nombre « 1234 » ait été saisi au clavier. Nous l'encodons en BCD et y ajoutons un bit-padding classique pour arriver à la taille d'un bloc DES (64 bits) :

Quelques essais supplémentaires permettent de découvrir d'autres détails. Si plusieurs nombres sont rentrés au clavier (maximum 10), ils seront concaténés avec le nibble 0xF utilisé comme séparateur. Si les données concaténées ne forment pas un nombre entier d'octets, un séparateur supplémentaire est ajouté avant de procéder au bit-padding. Si les données forment un nombre entier de blocs avant padding, alors un padding d'un bloc entier sera ajouté. Bien entendu, si plus d'un bloc est fourni au DES, seul le dernier bloc sera retenu.

Voici un autre exemple plus complet : introduisons les nombres 1234 et 3101234567 dans la calculette et nous obtenons comme réponse 11200903. En écoutant les échanges avec la carte, nous retrouvons le cryptogramme AC : 633FCCC4883A1C1F et l'ATC : 002A. Si nous appliquons les règles énoncées plus haut, la préparation des données en blocs destinés au DES donne 1234F3101234567F8000000000000000. Ces quelques lignes de bash nous donnent la même réponse que la calculette :

Ceci anéantit les craintes exprimées dans la thèse néerlandaise [12] ! Notre calculette a donc bien plus d'un tour dans son sac et est capable d'opérations cryptographiques dignes de ce nom. Il est en outre impossible de retrouver le cryptogramme AC complet qu'avait retourné la carte bancaire à partir des quelques chiffres affichés par la calculette (nous n'en connaissons que 18 des 64 bits avec le filtre mis en œuvre et le cryptogramme est différent à chaque utilisation). Il est donc impossible de transformer un jeton d'authentification (Mode 2) en une signature de transaction (Mode 2 + TDS) et a fortiori de transformer une signature en une autre.

Il importe de bien différencier à ce stade les opérations cryptographiques réalisées par la carte pour obtenir un cryptogramme et celle effectuée par la calculette. La carte prend en compte la valeur du compteur de transactions ainsi que son secret pour obtenir un cryptogramme au moyen d'une opération triple-DES, voire deux. Dans le Mode 2 + TDS, la calculette va se servir du cryptogramme fourni par la carte ainsi que les données introduites manuellement sur le clavier pour créer un jeton au moyen d'une opération simple-DES.

4. Les nouveautés

Il est déjà techniquement possible d'intégrer les fonctionnalités d'une calculette EMV-CAP directement dans la carte bancaire, tout en conservant les mêmes caractéristiques physiques de taille et de flexibilité (figure 5). Cela implique l'intégration d'un écran, d'un clavier et, oui, d'une batterie ! Nous avons eu l'occasion d'en tester quelques échantillons [20].

Il n'est pas facile de se servir de ce clavier et les fautes de saisie sont plus fréquentes. Cette solution reste toutefois très séduisante comme dépannage lorsqu'on doit réaliser une opération en ligne sans avoir sa calculette sous la main.

Il existe aussi des calculettes EMV-CAP qui lisent optiquement le challenge sur la page de la banque [21] s'il est présenté sous une forme graphique prévue à cet effet. Mais cela risque de poser des problèmes sur des équipements mobiles en raison de la taille et de la résolution de leur écran.

Mentionnons également l'existence d'une autre spécification de Mastercard plus récente : PLA (Perso Less Authentication) et sa déclinaison commerciale AA4C (Advanced Authentication for Chip) qui permet de rendre le protocole EMV-CAP possible avec des cartes EMV déjà déployées et dépourvues d'application EMV-CAP (et donc de filtre IPB).

5. Émulation logicielle d'EMV-CAP

Avec la compréhension du protocole EMV-CAP tel que mis en place par les banques belges, l'émulation de la calculette par logiciel est donc possible et a été réalisée. Cette application est disponible [15] à des fins didactiques. L'emploi de ce logiciel pour des opérations financières réelles présente un certain risque. En effet, l'intérêt de la calculette est d'isoler la carte bancaire des vilains malwares. Le mettre en œuvre sur un lecteur non sécurisé, c'est risquer qu'un keylogger intercepte votre PIN, qu'un malware accède aux informations de votre carte, voire qu'il intercepte votre transaction pour la modifier ou qu'il procède lui-même à ses propres transactions. Le papier de Cambridge [11] mentionnait justement dans son analyse des risques le fait qu'il est tentant pour les banques de fournir une solution logicielle plutôt que matérielle de la calculette, et le jour où votre site bancaire vous demandera de vous identifier en insérant votre carte bancaire dans un ordinateur et en tapant votre PIN au clavier, il sera sérieusement temps de vous inquiéter ! Pour toutes ces raisons, notre script est disponible uniquement sous une licence CC BY-ND [22] afin d'éviter que n'apparaissent des versions grand public qui passeraient sous silence nos mises en garde et viseraient à en généraliser l'usage.

Nous sommes en outre assez sceptiques lorsque certains annoncent [23] une émulation logicielle de la calculette et de la carte sur un iPhone, dont la clé secrète serait apparemment sécurisée uniquement par des méthodes logicielles.

6. Quid des autres vulnérabilités ?

Un certain nombre de problèmes potentiels de EMV et/ou EMV-CAP ont été soulevés ou rappelés notamment dans [11] et [12]. Nous venons de démontrer qu'il n'y a pas lieu de s'inquiéter de la façon dont le Mode 2 + TDS est implémenté et de balayer les craintes émises dans [12]. Nous allons passer rapidement en revue les principales autres sources d'inquiétude.

6.1 Se passer du PIN

Il y a un an, la publication d'une faille pouvant être exploitée dans certaines transactions EMV online [24] a créé un certain émoi. Cette faille rend possible une transaction en ne connaissant pas le PIN de la carte au moyen d'un appareillage contrôlant l'échange entre une carte EMV et un terminal. La faille repose sur le fait que la carte et la banque réalisent une transaction légitime sans PIN (nous avons vu au début de cet article que le PIN n'est qu'une méthode possible parmi d'autres) tandis que le terminal, qui, lui, veut un PIN, se fait abuser par une fausse réponse injectée : PIN Verify OK. Dans notre cas, ce n'est plus tant le terminal qu'il faudrait abuser, mais bien la banque et celle-ci refuserait bien évidemment une transaction EMV-CAP sans PIN car s'il est parfois optionnel dans EMV, il est bien obligatoire dans EMV-CAP ! La banque ne reçoit qu'un condensé de l'ATC et du cryptogramme. L'assurance qu'un PIN a bien été validé est fournie par la façon de générer le cryptogramme. En effet, outre les données fournies par le terminal dans sa commande GenerateAC, la carte utilise pour générer le cryptogramme des données internes telles que l'AIP, l'ATC et surtout le CVR (Card Verification Results). Cette dernière donnée contient un drapeau explicite indiquant qu'une vérification de PIN offline a été menée à bien [10]. Le CVR se retrouve également dans l'IAD fourni dans la réponse de la carte aux côtés du cryptogramme. Pour les Saint-Thomas qui nous lisent, mettre en commentaire la vérification de PIN dans notre script suffira pour montrer que la banque refusera alors les jetons fournis, C.Q.F.D. Quant aux cartes néerlandaises analysées [12], elles réagiraient en refusant de retourner un ARQC sans vérification préalable du PIN et retourneraient alors un AAC.

6.2 Confusion de modes

Un autre problème soulevé dans [11] est que le mode Sign employé en Angleterre peut amener à abuser les utilisateurs. En effet, en les invitant à effectuer une transaction de zéro (livres ou euros...), un attaquant a la possibilité de récupérer un jeton valide pour l'authentification puisque l'Unpredictable Number est mis à zéro. Heureusement que, comme nous l'avons expliqué, les calculettes belges ne proposent pas ce Mode 1 étendu pour signer des données, mais un Mode 2 + TDS, et la confusion n'est plus permise car le jeton sera différent.

6.3 Faiblesses du Mode 2

Lorsque le serveur de la banque n'envoie pas de challenge pour authentifier l'utilisateur (Mode 2), les jetons peuvent être extraits à l'avance et stockés. Ceci simplifierait certaines attaques de phishing car l'attaquant pourrait monter son attaque en deux phases : collecte de jetons par phishing puis utilisation plus tard plutôt que devoir agir en temps réel. Certaines banques utilisant ce mode réclament en outre un mot de passe, mais si un attaquant virtuel (malware) peut collecter le jeton, il n'aura pas grand mal à collecter le mot de passe également. Il nous semble donc plus adéquat de mettre en œuvre le Mode 1 pour l'authentification, au prix d'une manipulation supplémentaire de l'utilisateur.

6.4 Faiblesses du Mode 2 + TDS

Quant au Mode 2 + TDS, commun à toutes les banques belges observées, il souffre du même problème : des cryptogrammes peuvent être collectés à l'avance et employés plus tard pour signer n'importe quelle donnée, par exemple une transaction 3-D Secure. Ce sont en quelque sorte des chèques en blanc version numérique. L'auteur de [12], ne sachant pas quelle opération de mixage était effectuée en Mode 2 + TDS, pensait qu'il suffisait de collecter des jetons d'authentification pour les réutiliser dans ce mode. Mais nous avons découvert que le mixage se fait de manière robuste en utilisant le cryptogramme complet et non le jeton affiché. Collecter des cryptogrammes est certainement moins facile que de collecter les jetons via malware ou phishing. Mais cela reste possible, par exemple, sur un terminal marchand ou un distributeur qui aurait été trafiqué avec un shim, une petite pièce plate qui s'introduit entre les contacts de la carte et ceux du lecteur. Les anglophones parlent dans ce cas de shimming attack par opposition à la skimming attack que l'on connaît sur la piste magnétique. Une solution serait peut-être d'avoir un mode où la calculette effectuerait un hachage des données en amont et fournirait une partie du condensat sous la forme d'un Unpredictable Number à la carte.

6.5 Malwares et sémantique

À propos des malwares, un risque subsiste face à ceux qui interceptent ce que la banque vous envoie comme challenge pour signer un ordre de transfert et qui le substituent pour signer un autre ordre à votre insu. La solution se résume à : moins de sécurité pour plus de sécurité. En effet, dans leur première mouture, les challenges sont créés par une quelconque fonction de hachage cryptographique sur les données du transfert. Même si cela semble a priori une bonne solution, pour l'utilisateur, ce n'est qu'un grand nombre à l'allure aléatoire et il ne remarquera jamais une substitution par un autre challenge. C'est pour cela que, petit à petit, les banques abandonnent ce type de challenge pour privilégier des challenges sémantiques constitués, par exemple, du montant et d'une partie du numéro de compte du bénéficiaire. Le challenge est présenté de façon à ce que l'utilisateur comprenne comment il a été créé et ce qu'il représente. Ainsi, l'utilisateur a un rôle semi-actif dans la détection d'une éventuelle substitution frauduleuse (à condition qu'il se donne la peine de constater la corrélation mise en évidence). Une autre technique rencontrée consiste même à expliquer à l'utilisateur qu'il doit entrer une partie du compte du destinataire sans afficher ladite partie. Cela force l'utilisateur à être encore plus actif car au lieu de comparer de l'information, il doit fournir l'information par lui-même. Ce type de malware reste malgré tout un outil très dangereux en social engineering et il faut rester vigilant lorsque la page de la banque est différente et, par exemple, propose une étape de vérification supplémentaire « pour plus de sécurité contre ces fameux malwares », une attaque à l'instar de ces malwares déguisés en antivirus.

6.6 Aide au vol avec violence

Enfin, l'article de Cambridge [11] mentionne un risque d'un genre différent lié à la profusion de ce type de calculettes, car elles permettent facilement à un agresseur qui voudrait vous forcer à révéler votre code PIN de le vérifier instantanément à l'abri des regards. Bien sûr, créer un lecteur qui implémente un PIN Verify a toujours été possible, mais ici, l'équipement requis est mis à disposition du premier venu sous une forme anodine.

Conclusion

Nous vous avons invité à découvrir le fonctionnement des calculettes EMV-CAP distribuées par les banques belges. La calculette emploie une application résidente sur une carte bancaire pour faire une opération semblable à une transaction EMV en ligne qui aurait été avortée. Cela permet d'extraire une signature de la carte qui sert à la banque à authentifier son porteur ou à valider un ordre de transfert. La calculette ne contient pas de secret ou de personnalisation, ce qui en simplifie la gestion et le processus de distribution des calculettes.

Nous avons vu qu'il y a plus d'une façon d'implémenter EMV-CAP. D'ailleurs, les calculettes ne sont en général pas interopérables, sauf en Belgique où un organisme [9] est chargé de la certification nationale de ces appareils. Nous avons soulevé un coin du voile ensemble et nous avons expliqué la sécurité mise en place derrière l'obscurité de façade. Ceci nous a permis de modérer un certain nombre de craintes exprimées dans [11] et [12], notamment en ce qui concerne le Mode 2 + TDS et l'évitement du PIN. La sécurité des transactions bancaires sur Internet est certainement améliorée par rapport aux moyens d'authentification plus traditionnels et vulnérables aux keyloggers ou malwares. Néanmoins, au vu des diverses observations que nous avons énoncées, nous constatons qu'il y a des façons meilleures que d'autres d'implémenter EMV-CAP en pratique.

Aujourd'hui, EMV-CAP est utilisé par des banques, notamment en Belgique, en Angleterre, aux Pays-Bas, en Suisse, en Espagne, au Portugal, en Suède, en Slovénie, en Grèce, en Turquie, en Russie, au Mexique, au Viêt Nam, et cette liste n'est probablement pas exhaustive. En analysant quelques cartes bancaires françaises, nous avons vu que certaines d'entre elles contiennent l'application équivalente développée par Visa (DPA). Il est donc possible que certaines banques françaises proposeront une calculette à l'avenir. Vous pouvez utiliser le script [15] pour vérifier quelles sont les applications présentes sur votre propre carte, voire même lui faire générer un jeton !

Mais EMV-CAP dépasse le cadre bancaire. En témoigne l'exemple des autorités portugaises qui l'ont intégré dans leur nouvelle carte d'identité électronique [25] afin d'offrir au citoyen un moyen d'authentification via Internet ou même lors des contacts téléphoniques avec l'administration. Attendons-nous à voir le protocole EMV-CAP de plus en plus répandu dans un avenir proche et, qui sait, même en France ;-).

Enfin, il serait intéressant de voir s'il est possible de tirer profit de la profusion de ces calculettes interopérables pour développer une solution open source d'authentification, par exemple à base d'une JavaCard. Il n'est pas nécessaire de vouloir suivre une architecture EMV-CAP à la lettre, une utilisation des champs UN d'une part et IPB/AC d'autre part nous semble suffisante pour implémenter un protocole de challenge/réponse digital. Un brevet américain publié très récemment [26] explore d'ailleurs cette piste.

Remerciements

Nous remercions Gildas Avoine pour ses remarques toujours pertinentes, Michaël Peeters pour son aide dans l'écriture de l'applet pour JavaCard, Ludovic Rousseau pour son support dans l'utilisation de pyscard et les relecteurs pour leur aide lors de la rédaction de cet article.

Références

[1] http://www.emvco.com

[2] http://www.theukcardsassociation.org.uk/media_centre/press_releases_new/-/page/922/

[3] http://www.cardwerk.com/smartcards/smartcard_standard_ISO7816-3.aspx

[4] http://www.cardwerk.com/smartcards/smartcard_standard_ISO7816-4.aspx

[5] Eluard (M.), Lelievre (S), « YESCARD entre mythe et réalité ou un aperçu du système bancaire français » (section 3.3), MISC hors-série n°2 : 
https://connect.ed-diamond.com/MISC/mischs-002/yescard-entre-mythe-et-realite-ou-un-apercu-du-systeme-bancaire-francais

[6] http://www.visaeurope.com/aboutvisa/products/dynamicpasscode.jsp

[7] http://www.vasco.com/products/digipass/digipass_readers/digipass_800_range/digipass_810.aspx

[8] http://www.dictao.net/solutions/banque-assurance/paiement-en-ligne

[9] http://www.epci.be/unconnected_readers.htm

[10] WO03073389, EP1646976, US20110022521

[11] http://www.cl.cam.ac.uk/~sjm217/papers/fc09optimised.pdf

[12] http://www.ru.nl/publish/pages/578936/emv-cards_and_internet_banking_-_michael_schouwenaar.pdf

[13] http://dangerousprototypes.com/bus-pirate-manual/bus-pirate-feature-overview/

[14] Bodor (D.), « Parlez 1-Wire, I2C, SPI, MIDI et bien plus avec un seul outil : Bus Pirate v3 », Open Silicium n°2 : https://connect.ed-diamond.com/Open-Silicium/os-002/parlez-1-wire-i2c-spi-midi-et-bien-plus-avec-un-seul-outil-bus-pirate-v3

[15] http://sites.uclouvain.be/EMV-CAP/

[16] http://www.itu.int/ITU-T/studygroups/com17/languages/X.690-0207.pdf

[17] https://secure.wikimedia.org/wikipedia/en/wiki/Chip_Authentication_Program

[18] http://www.rb.ru/upload/users/files/3374/check-in-phone-technologie_security-english-_2010-08-12_20.05.11.pdf

[19] http://www.iso.org/iso/catalogue_detail.htm?csnumber=30656

[20] http://www.nidsecurity.com/microsite/mastercard/products/

[21] http://www.gemalto.com/products/ezio_optical_reader/

[22] http://creativecommons.org/licenses/by-nd/2.0/be/deed.fr

[23] http://www.arcot.com/resources/docs/ArcotOTP_for_CAP_DPA_Fact_Sheet.pdf

[24] http://www.cl.cam.ac.uk/~sjm217/papers/oakland10chipbroken.pdf

[25] http://www.cartaodecidadao.pt/images/stories/especificacoes%20-%20leitores%20base_v1.0.pdf
(page 5)

[26] US7882553