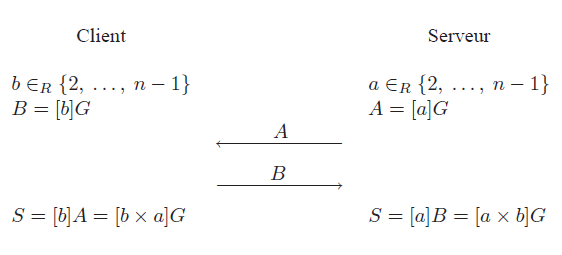La mise en œuvre pratique de mécanismes cryptographiques suppose tout d'abord de les concevoir, de les implémenter et de garantir une utilisation sûre. Au cours de chacune de ces étapes, des difficultés de natures diverses peuvent surgir avec un impact direct sur la sécurité du mécanisme considéré. Mais l'expérience des concepteurs ou le nombre des développeurs ne suffit pas toujours à éviter ces écueils. Illustration avec le protocole TLS et l'implémentation OpenSSL.
1. Description du protocole TLS
Le protocole TLS est constitué d'un ensemble de « sous-protocoles » parmi lesquels le protocole Record et Handshake.
Le protocole Handshake a pour tâches de négocier les algorithmes cryptographiques, d'échanger les valeurs pour la dérivation des clés de session et d'authentifier le serveur (et, optionnellement, le client).
Le rôle du protocole Record est d'assurer la confidentialité et l'intégrité des données applicatives notamment (le protocole est également sollicité au cours du protocole Handshake).
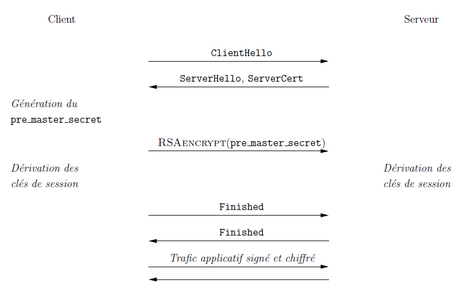
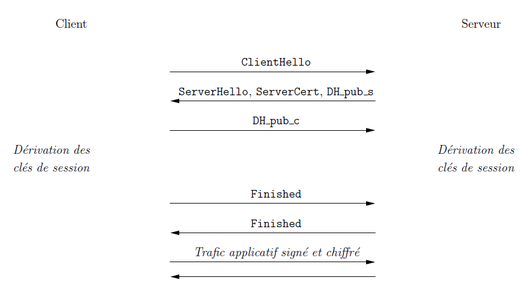
Le principal mode utilisé au cours du Handshake est sans doute le chiffrement RSA : le client génère pseudo-aléatoirement une valeur appelée pre_master_secret. Puis cette valeur est chiffrée avec la clé publique RSA du serveur (cf. Figure 1). Un autre mode d'échange consiste à utiliser le protocole Diffie-Hellman (DH). Dans ce cas, le secret DH négocié entre le client et le serveur fournit le pre_master_secret (cf. Figure 2).
Figure 1 : Description simplifiée du Handshake TLS avec RSA
Figure 2 : Description simplifiée du Handshake TLS avec DH
À partir du pre_master_secret et de deux valeurs publiques générées pseudo-aléatoirement, l'une par le client (client_random), l'autre par le serveur (server_random), des clés de session sont dérivées pour le chiffrement et la signature des données applicatives.
À l'issue de cette négociation de clé, le message Finished est transmis pour sanctionner le bon déroulement de l'échange. Ce message constitue une empreinte cryptographique de tous les messages de la négociation de clé échangés précédemment de part et d'autre. C'est le premier message de la session construit à partir du secret master_secretdérivé entre les deux correspondants.
Une description plus détaillée du protocole peut être trouvée dans [8, 9].
Le protocole a été implémenté sous la forme de plusieurs bibliothèques cryptographiques dont la populaire OpenSSL. TLS et OpenSSL sont des objets en évolution régulière. Ces modifications sont motivées par la prise en compte de nouveaux algorithmes correspondant à l'état de l'art (par exemple l'AES pour le chiffrement du trafic applicatif ou les opérations sur courbe elliptique pour la négociation des clés de session). Mais ces changements correspondent également à des correctifs destinés à contrecarrer des attaques de natures différentes.
2. Attaques par canaux auxiliaires
2.1 Gestion des erreurs dans le déchiffrement RSA
2.1.1 Description
Le mode le plus couramment utilisé dans TLS consiste à chiffrer le pre_master_secret avec la clé publique RSA du serveur. Le standard utilisé pour ce chiffrement correspond à PKCS #1 v1.5. Le chiffrement d'un message data selon ce standard se fait de la manière suivante. Soit k la taille en octet du module RSA et |data| la taille en octet de data. Un champ padding de k–3–|data| octets non nuls est généré et le bloc m décrit ci-dessous est construit :
m = 00 02 | padding | 00 | data
Puis ce bloc est chiffré avec RSA : c = me mod n.
Le padding a une taille dépendant de la taille de data, néanmoins padding a une taille minimale de 8 octets (par conséquent la taille de data ne doit pas dépasser k–11 octets). Ainsi, le format de m = P | ... | Pk–1 est le suivant :
- P = 0x00 ;
- P1 = 0x02 ;
- P2 à P9 : non nul ;
- au moins un octet entre P10 et Pk–1 est nul.
Que se passe-t-il si le message m' obtenu par le serveur après le déchiffrement ne correspond pas au format attendu ? Le serveur envoie au client une alerte spécifique decode_error pour signaler cette erreur de format.
Lors de la conférence Crypto 1998, Daniel Bleichenbacher a présenté une attaque exploitant ce bit d'information et permettant de retrouver le clair d'un message chiffré avec RSA PKCS #1 v1.5 (i.e. : le pre_master_secret dans le cas de TLS) [15].
Le principe de l'attaque est le suivant : l'attaquant choisit une valeur s et transmet la valeur cse mod n = (ms)e mod n à un oracle de déchiffrement (par exemple un serveur TLS). Si l'oracle retourne un message signalant une erreur de format lors du déchiffrement de cse, cela signifie que ms ne correspond pas au format d'un bloc clair PKCS #1. Dans le cas contraire, l'attaquant sait que ms respecte ce format.
La chaîne m = P | ... | Pk–1 a pour valeur P × 256k–1 + P1× 256k–2 + ... + Pk–1× 256 . Si m est au format PKCS #1, alors nécessairement P = 0 et P1 = 2. Les autres octets P2 à Pk–1 peuvent avoir (presque) toutes les valeurs entre 0 et 255. Par conséquent, on peut borner les valeurs possibles de m : un message m au format correct PKCS #1 est compris entre :
00 02 00 ... 00
et
00 02 FF ... FF
Autrement dit : 2 × 256k–2 ≤ m < 3 × 256k–2. Soit B = 256k–2, un message m au format correct vérifie donc 2B ≤ m < 3B.
Dans le cas où le déchiffrement RSA s'est correctement déroulé, la réponse de l'oracle (plus précisément : l'absence de message d'erreur relatif au format de ms) permet à l'attaquant de savoir que
2B ≤ ms mod n < 3B
Il en découle qu'il existe une valeur entière rtelle que
2B ≤ ms–rn ≤ 3B–1
d'où
(2B+rn) / s ≤ m ≤ (3B–1+rn) / s
Ainsi, l'intervalle des valeurs possibles pour m a été réduit : on passe d'un intervalle [2B, 3B–1] à un intervalle [a, b] où a = max(2B, 2B+rn) / s), b = min(3B–1, (3B–1+rn) / s).
En répétant ce procédé, on restreint graduellement l'intervalle jusqu'à trouver la valeur m. Le principe de l'attaque consiste donc à rechercher m de manière exhaustive. Néanmoins, la recherche ne porte pas de manière séquentielle sur chaque bit de m. L'information sur le format incorrect du déchiffré permet d'éliminer à chaque étape de l'attaque tout un ensemble de valeurs incorrectes.
2.1.2 Mise en œuvre
L'attaque de Bleichenbacher s'applique de manière générale à PKCS #1 indépendamment du protocole mettant en œuvre ce mécanisme de chiffrement. À titre d'exemple, l'attaque menée pour un module RSA 1024 bits aboutit après 220 appels à l'oracle de déchiffrement.
Vlastimil Klima, Ondrej Pokorny et Tomas Rosa [16] ont appliqué une variante de l'attaque de Bleichenbacher à TLS dans le cas d'un échange de clé par RSA. En exploitant la présence du numéro de version dans le pre_master_secret, ils parviennent à récupérer cette valeur secrète en moins de 55 heures de connexion avec le serveur TLS (pour RSA 1024). La connaissance du pre_master_secret permet à l'attaquant de calculer les clés de session et donc d'avoir accès au trafic applicatif transitant dans le tunnel TLS.
Lors de leurs expérimentations, 2/3 des serveurs TLS testés (choisis aléatoirement sur Internet) étaient potentiellement faillibles à cette attaque (i.e.: en cas d'erreur de déchiffrement du pre_master_secret, ces serveurs fournissent une réponse faisant d'eux un oracle utilisable pour mener l'attaque). Toutefois, comme le notent Klima et al., l'attaque est – en pratique – limitée par la capacité du serveur TLS à répondre pendant plus de 54 heures à des requêtes erronées (même si le client change son adresse IP régulièrement).
2.1.3 Contre-mesures
La contre-mesure préconisée contre l'attaque de Bleichenbacher consiste à ne pas renvoyer d'erreur explicite en cas de déchiffrement incorrect du pre_master_secret. Le serveur TLS doit générer une valeur pseudo-aléatoire de 48 octets et, en cas d'erreur lors du déchiffrement RSA, utiliser cette valeur comme pre_master_secret de remplacement (sans notifier d'erreur au client). Le serveur doit alors poursuivre la dérivation des clés de la même manière que si le déchiffrement avait été correctement effectué. La session TLS va s'interrompre d'elle-même lorsque le serveur va constater que le message Finished reçu du client à l'issue de la dérivation des clés est incorrect.
Une autre contre-mesure (préconisée par Bleichenbacher) consisterait à utiliser le chiffrement RSA OAEP (PKCS #1 v2.0). À l'heure actuelle (TLS 1.2), cette dernière contre-mesure n'a pas été implémentée pour des raisons de compatibilité avec les versions précédentes. Néanmoins, des recommandations d'implémentation liées au traitement du numéro de version lors du déchiffrement du pre_master_secret ont été ajoutées à la description du protocole TLS dans la version 1.2.
2.2 Timing attack par gestion des erreurs lors du déchiffrement d’un record
2.2.1 Description
Obtenir les clés de session TLS (en récupérant le pre_master_secret, par exemple) permet de déchiffrer toutes les données transitant dans le tunnel correspondant. Toutefois, l'accès aux clés peut être difficile. Par ailleurs, les données échangées peuvent être de valeur inégale aux yeux d'un attaquant. L'intérêt de celui-ci peut ne porter que sur une faible (mais précise) quantité de données, par exemple : un mot de passe. Ainsi, pouvoir déchiffrer une partie d'une communication sans nécessairement être capable d'obtenir les clés de chiffrement correspondantes reste intéressant.
Dans [17], Brice Canvel, Alain Hiltgen, Serge Vaudenay et Martin Vuagnoux présentent une technique permettant de récupérer des données transitant dans un tunnel TLS. La méthode est une extension améliorée d'une technique présentée par Serge Vaudenay.
Dans le protocole TLS, lorsque des données m sont chiffrées à l'aide d'un algorithme de chiffrement par bloc, le message effectivement chiffré consiste en un paquet de la forme
m| mac| pad | l
où :
- mac est le résultat du HMAC sur m notamment ;
- pad est un padding de l octets (chacun valant l) de sorte que m | mac | pad | l ait une taille multiple de la taille de bloc b de l'algorithme de chiffrement.
Après le déchiffrement du paquet, le padding est vérifié (les derniers octets du paquet clair doivent correspondre à l+1 octets valant chacun l). Puis le mac est vérifié. Supposons que, en cas d'erreur sur le padding ou le MAC, une erreur distincte soit émise : respectivement decryption_failed et bad_record_mac. La nature de cette erreur peut alors être exploitée par l'attaquant pour récupérer m.
Par simplification, considérons un bloc y = enc(x) obtenu par chiffrement de x (de taille b d'un bloc de chiffrement) avec un algorithme de chiffrement par bloc enc. y est récupéré par l'attaquant sur le canal de communication et l'objectif est de trouver x (un mot de passe par exemple).
L'attaquant procède octet par octet en commençant par rechercher les octets les plus à droite. Tout d'abord, il construit r = L| (u1⊕0x01) | (u ⊕0x01) où L est un bloc pseudo-aléatoire de taille b–2. L'attaquant envoie r | y au serveur qui procède au déchiffrement en mode CBC en calculant
r⊕enc–1(y) = (L| (u1⊕0x01) | (u ⊕0x01)) ⊕ (xb–1 ... x )
Les derniers octets de r⊕enc–1(y) sont censés correspondre au padding. Si la vérification du padding par le serveur renvoie « correct », cela signifie que (probablement)
u1⊕0x01⊕ x1 = 0x01
et
u ⊕0x01⊕x = 0x01
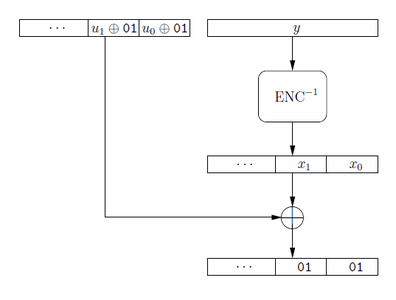
Autrement dit : x1 = u1et x = u . Si la vérification du padding est incorrecte, l'attaquant choisit de nouvelles valeurs u1, u (cf. Figure 3).
Figure 3 : Déchiffrement CBC de r | y. Ici, le choix u de l'attaquant est correct.
Une fois x1 et x trouvés, l'attaque se poursuit à l'aide d'un nouveau bloc r'= L' | u avec u = (c⊕0x02) | (x1⊕ 0x02) | (x ⊕ 0x02) où c est un octet. Le serveur procède au déchiffrement de r'| y. Il calcule r'⊕enc–1(y) = (L' | u) ⊕x dont les trois derniers octets valent (c⊕0x02⊕x2) | 0x02 | 0x02. Si la vérification du padding est correcte, cela signifie alors que c⊕0x02⊕x2 = 0x02 et donc que x2 = c. Et ainsi de suite pour les autres octets de x.
Ce qui précède correspond à la technique générale de Vaudenay. Toutefois, dans TLS, les messages d'erreur (tels que decryption_failed, bad_record_mac) ne sont pas envoyés en clair, au client mais chiffrés dans le tunnel. Par conséquent, l'attaquant n'a pas explicitement accès à ces messages. Par ailleurs, suite à la publication de l'article de Vaudenay, une erreur dans le padding est désormais traitée de la même manière qu'une erreur sur le MAC (au moins dans OpenSSL depuis la version 0.9.6c). De plus, ces deux erreurs entraînent la fin de la session TLS. Néanmoins, cette attaque peut toujours être mise en œuvre si l'attaquant parvient à distinguer les deux erreurs (padding et MAC). Pour ce faire, Canvel et al. utilisent un paquet de la forme f | r | y où f est une chaîne d'octets pseudo-aléatoires telle que le paquet f | r | y soit de taille maximale autorisée pour un record TLS. Avec un paquet de telle taille, on peut espérer distinguer les deux erreurs par la différence du temps de traitement du paquet. En effet, si le traitement du paquet est bien le suivant :
1. déchiffrement ;
2. vérification du padding ;
3. vérification du MAC ;
alors la session TLS prend fin plus rapidement en cas d'erreur sur le padding qu'en cas d'erreur dans le MAC (f est utilisé pour allonger artificiellement la durée de vérification du MAC).
Comme la session TLS prend fin à chaque choix incorrect de l'attaquant, celui-ci doit poursuivre l'attaque avec un nouveau bloc y' correspondant au chiffrement de x avec de nouvelles clés de session.
2.2.2 Mise en œuvre
Canvel et al. ont mis en œuvre leur attaque et ont ainsi pu récupérer le mot de passe utilisé dans l'authentification d'un client Outlook auprès d'un serveur de courrier IMAP. Notons toutefois que les tests réalisés l'ont été dans un réseau local, les perturbations sur le réseau étant donc notablement réduites. L'attaque suppose aussi que l'on puisse se placer en coupure entre le client et le serveur TLS pour injecter les paquets f | r | ydans le tunnel.
L'attaque tire également parti de l'utilisation d'outils statistiques pour filtrer les réponses reçues du serveur (le temps de réponse en cas d'erreur) et définir si le choix sur les octets de x est correct ou pas. Par ailleurs, la cible étant un mot de passe, usage a été fait d'un dictionnaire de mots de passe, ce qui a également contribué à réduire la complexité générale de l'attaque. À titre d'exemple, un mot de passe de 8 caractères est retrouvé au bout de 166 appels à l'oracle de déchiffrement avec une probabilité de succès de 1/2.
2.2.3 Contre-mesures
Les contre-mesures préconisées par les auteurs sont :
- Égaliser le temps de vérification du padding et du MAC en procédant à la vérification du MAC dans tous les cas.
- Vérifier le MAC avant le padding afin de rendre la vérification du padding négligeable par rapport à celle du MAC. Le paquet à chiffrer est alors de la forme m | pad | l| mac au lieu de m | mac | pad | l.
Un patch correspondant à la première proposition a été fourni pour la version OpenSSL 0.9.6e et antérieures. Par ailleurs, des recommandations d'implémentation liées au traitement du MAC ont été ajoutées dans la spécification de TLS à partir de la version 1.1.
3. Attaque par renégociation
3.1 Description
Le protocole TLS autorise à procéder à des renégociations alors qu'une session est en cours. La renégociation peut être motivée par le souhait de changer d'algorithme de chiffrement, de renouveler les clés de session, de procéder à une authentification d'un niveau plus élevé, par exemple. La renégociation se fait à l'initiative du client (par un message ClientHello) ou du serveur (par un message HelloRequest). Le nouvel échange de clé s'effectue au travers du tunnel TLS existant. À l'issue de la renégociation, les données applicatives sont protégées avec le nouveau contexte de sécurité.
Du point de vue applicatif, il n'y a pas de discontinuité entraînée par cette renégociation : les données applicatives transmises dans le précédent tunnel et dans le nouveau tunnel sont vues comme un tout. Considérons une session HTTPS [29]. Les données
GET /pizza?toppings=sausage;address=myaddress HTTP/1.1
transmises dans le précédent tunnel et les données
Cookie: mycookie
transmises dans le nouveau tunnel sont interprétées au niveau applicatif comme
GET /pizza?toppings=sausage;address=myaddress HTTP/1.1
Cookie: mycookie
Dans [1], Marsh Ray et Steve Dispensa expliquent comment cela peut être mis à profit par un attaquant pour tromper un serveur TLS et abuser d'un client légitime. L'idée générale consiste pour l'attaquant à établir avec le serveur une session TLS à la place du client puis à faire passer une session TLS du client légitime pour une renégociation auprès du serveur. Cela permet à l'attaquant de « préfixer » les données envoyées par le client légitime au serveur : le serveur va considérer que les données transmises dans le premier tunnel TLS (établi par l'attaquant) et celles transmises dans le deuxième tunnel (établi par le client légitime) proviennent toutes du client.
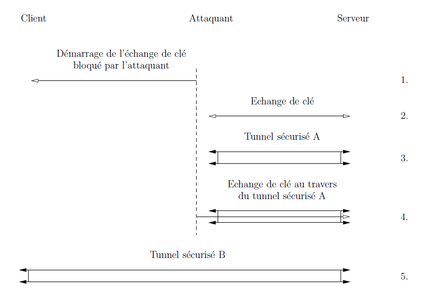
La figure 4 illustre une mise en œuvre de l'attaque par renégociation.
Figure 4 : Attaque par renégociation
Le déroulement de l'attaque est le suivant :
1. Un client débute une session HTTPS pour commander une pizza. L'attaquant, placé en coupure entre le client et le serveur, bloque le paquet ClientHello du client. L'attaquant établit alors une session TLS avec le serveur (en utilisant le même canal de communication que le client).
2. L'attaquant procède à un échange de clé avec le serveur.
3. Un tunnel sécurisé A est établi entre l'attaquant et le serveur. Au travers de ce tunnel, l'attaquant peut transmettre tout type de données au serveur. L'attaquant transmet au serveur la requête HTTP suivante :
GET /pizza?toppings=pepperoni;address=attackersaddress HTTP/1.1
X-Ignore:
sans retour chariot après X-Ignore:.
4. Puis l'attaquant transmet au serveur le ClientHello du client légitime bloqué à l'étape 1. Le serveur interprète ce paquet comme une demande de renégociation. Un échange de clé est donc effectué entre le client et le serveur au travers du tunnel établi par l'attaquant. L'attaquant, en coupure entre le client et le serveur, relaie les différents messages TLS entre le client et le serveur.
5. Un tunnel sécurisé B est maintenant établi entre le client et le serveur. L'attaquant n'a pas accès à ce tunnel. Le client peut transmettre au serveur tout type de données de manière sécurisée. Et le client procède à sa commande de pizza par la requête HTTP suivante :
GET /pizza?toppings=sausage;address=victimssaddress HTTP/1.1
Cookie: victimscookie
6. Le serveur reçoit successivement la requête de l'attaquant et celle du client légitime et les interprète comme :
GET /pizza?toppings=pepperoni;address=attackersaddress HTTP/1.1
X-Ignore: GET /pizza?toppings=sausage;address=victimssaddress HTTP/1.1
Cookie: victimscookie
Ainsi, l'attaquant commande la pizza... et le client légitime règle la facture.
Le serveur associe les données applicatives du premier tunnel (établi par l'attaquant) avec celles du deuxième tunnel (établi par le client légitime) car le deuxième tunnel est établi sous l'égide du premier. Pourtant, d'un point de vue cryptographique, il n'y a aucune corrélation entre la manière dont ces deux ensembles de données sont protégés (par exemple, les données des deux ensembles pourraient être signées par une même clé symétrique). Il y a donc une discontinuité dans l'authentification entre l'établissement du premier tunnel et l'établissement du deuxième. Et c'est de cette discontinuité que l'attaque tire profit. Par ailleurs, si le client légitime s'authentifie auprès du serveur, cela ne met pas en défaut l'attaque. Paradoxalement, le serveur pourrait considérer que cela correspond même à une authentification a posteriori de l'attaquant.
3.2 Mise en œuvre
Anil Kurmus a présenté un scénario possible de cette attaque avec le site Twitter. Tout utilisateur peut modifier ses paramètres de connexion à son compte (mot de passe). L'idée est de « préfixer » le message de l'utilisateur légitime :
Cookie: [...]
par une requête POST :
message=GET /HTTP/1.1 [...]
Le résultat ? Au lieu d'interpréter la requête comme un changement de mot de passe, le serveur web considère que les données correspondent à un message Twitter qu'il affiche donc sur le site de l'utilisateur offrant ainsi à tous le mot de passe (cf. Figure 5).
Twitter a rapidement corrigé son serveur, rendant maintenant ce scénario inapplicable.
Figure 5 : Mot de passe révélé sur Twitter (Crédit : Anil Kurmus)
3.3 Contre-mesures
L'impact de l'attaque par renégociation dépend de l'application protégée par TLS. Comme illustré plus haut, s'il s'agit de HTTP, l'attaquant peut détourner ou dérober l'accréditation du client légitime (présente dans la figure 4 sous la forme du cookie) à son profit et bénéficier d'un service qui sera crédité (et potentiellement facturé) au client légitime.
L'attaque par renégociation met en défaut les mécanismes d'intégrité de TLS puisque l'attaquant peut transmettre des données qui seront considérées par le serveur comme provenant du client légitime. Notons toutefois que, si l'on considère le scénario d'une transaction financière comme plus haut, l'attaque peut être découverte par le client si le serveur lui retourne un résumé de cette transaction (avant ou après validation de cette dernière). Dans ce cas, l'attaquant peut, au mieux, bloquer le message du serveur mais ne peut pas le modifier car il n'a pas accès au tunnel TLS établi entre le client et le serveur.
Si l'intégrité des données échangées entre le client et le serveur peut être mise en défaut, il n'en est pas de même de la confidentialité des données. À ce titre, l'attaque par renégociation ne remet pas en cause la robustesse cryptographique du protocole TLS en tant que tel.
Une manière (radicale) de contrer cette attaque est d'interdire les renégociations.
Cette correction a été apportée à la version 0.9.8l d'OpenSSL.
Comme TLS supporte les extensions, d'autres corrections sont toutefois possibles. La correction présentée dans [2] consiste à ajouter une extension appelée RenegociationInfo aux paquets ClientHello et ServerHello. Celle-ci indique aux correspondants s'il s'agit d'une première négociation et permet de détecter l'attaque.
Par défaut, un serveur TLS doit accepter un ClientHello contenant des extensions même s'il n'en comprend pas le sens. Néanmoins, anticipant des problèmes dus à la variété des implémentations, les auteurs de cette correction offrent une alternative à l'extension RenegociationInfo. Elle consiste à inscrire dans la liste des suites cryptographiques du ClientHello une valeur particulière (TLS_EMPTY_RENEGOTIATION_INFO_SCSV) signifiant qu'il s'agit d'un échange de clé initial.
La RFC 5746, décrivant cette correction, a été implémentée dans les versions 0.9.8m et 1.0.0a d'OpenSSL.
4. Mode d'opération : le cas de CBC
4.1 Description
Les algorithmes de chiffrement par bloc peuvent être utilisés selon différents modes. Le mode ECB consiste à chiffrer chaque bloc de données claires indépendamment. C'est le plus simple mais il comporte des inconvénients. Le mode CBC est donc employé dans le protocole TLS. Dans ce mode, le chaînage des blocs permet de masquer d'éventuelles récurrences dans les données claires. Néanmoins, ce mode peut être détourné par un attaquant pour récupérer des données transitant dans le tunnel TLS.
S'appuyant sur des travaux de Gregory Bard, Thai Duong et Juliano Rizzo ont mis en scène un tel scénario en 2011 [7] : l'attaque « Beast ». Le scénario est le suivant : un utilisateur légitime s'authentifie par mot de passe auprès d'un site internet. La transmission du mot de passe se fait par un tunnel TLS. Supposons que l'attaquant ait les capacités suivantes :
- Il peut observer le trafic chiffré échangé entre le client et le serveur TLS.
- Il peut injecter des données claires dans le tunnel TLS (sans toutefois pouvoir récupérer les données claires de l'utilisateur légitime).
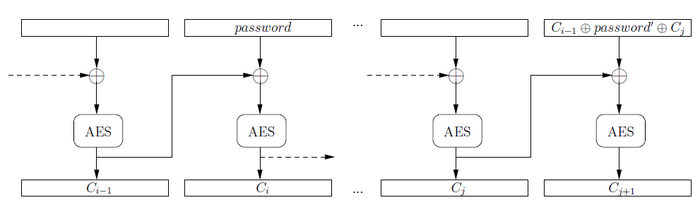
Pour découvrir le mot de passe password, transmis dans le tunnel TLS par l'utilisateur légitime, l'attaquant procède comme suit :
1. Il récupère le bloc chiffré Ci contenant password(par simplification, on supposera que password est de la taille d'un bloc de chiffrement, par exemple : 16 octets pour l'AES).
2. Il fait une hypothèse sur la valeur du mot de passe password' et injecte un bloc contenant password' dans le tunnel TLS.
3. Il récupère le bloc chiffré Cj correspondant à password'. Si Cj = Ci, alors l'attaquant en déduit que password = password'.
Autrement dit, l'attaquant se sert du tunnel TLS comme « distingueur » pour mener à bien sa recherche exhaustive sur la valeur du mot de passe.
Néanmoins, deux problèmes se posent :
- Si le client utilise un algorithme de chiffrement par bloc (comme l'AES), le mode CBC est utilisé. Dans ce cas, Ci ne correspond pas au chiffrement de password mais à aes(Ci–1 ⊕ password) où Ci–1 est le précédent bloc chiffré (cf. Figure 6).
- Si password a une taille de 16 octets, la recherche exhaustive correspond à un coût de 2128 « chiffrements TLS » (ce « chiffrement TLS » inclut notamment la construction de la trame claire, l'encodage des données, le calcul HMAC, le chiffrement AES). Et une recherche exhaustive sur 128 bits semble un tantinet délicate...
Figure 6 : Chiffrement CBC et recherche de password
Considérons la première difficulté. Elle peut être contournée dans TLS 1.0 car l'IV est prédictible. L'attaquant récupère le bloc chiffré Ci = aes(Ci–1⊕password). Il veut tester son hypothèse password'. Pour cela, il injecte dans le tunnel un bloc B = Ci–1⊕password'⊕Cj où Cj est le bloc chiffré qui aura précédé B. Ainsi, le chiffrement de Baboutit à :
Cj+1 = aes(B⊕Cj)
= aes(Ci–1⊕password'⊕Cj⊕Cj)
= aes(Ci–1⊕password')
Il suffit alors de comparer Cj+1 à Ci. S'il y a égalité, cela signifie que password = password'.
Considérons à présent la deuxième difficulté. L'astuce utilisée par Duong et Rizzo consiste à rechercher le mot de passe octet par octet. Soit password= p | p1 | ... | p15. La valeur de référence utilisée en pratique par l'attaquant va être Ci = aes(Ci–1⊕ (cste | p )) où cste est une valeur fixe de 15 octets (par exemple l'en-tête d'une requête HTTP). L'attaquant fait l'hypothèse que le premier octet du mot de passe est p 'et construit le bloc B = Ci–1⊕ (cste | p ') ⊕Cj qu'il injecte dans le tunnel TLS. Il récupère le bloc chiffré correspondant Ci+1 = aes(Ci–1⊕ (cste | p ')). Si Cj+1 = Ci, cela signifie que p = p '. Sinon, un autre bloc B est construit avec la même valeur cste et un autre choix pour p '. Il y a au plus 256 essais à faire pour trouver l'octet p .
Une fois p trouvé, la recherche porte sur p1 avec le bloc B = cste'| p | p1' où p1'est l'hypothèse de l'attaquant sur p1 et cste'est une constante de 14 octets (en pratique, cste' peut être obtenu à partir de cste en effectuant un décalage d'un octet à droite au fur et à mesure que les octets pk sont trouvés). L'attaquant effectue au plus 256 essais pour trouver p1 en utilisant comme nouvelle valeur de référence Ci = aes(Ci–1⊕ (cste'| p | p1)).
En procédant de cette manière, l'attaquant doit effectuer au maximum 256 essais pour chacun des 16 octets de password, soient 212 essais au plus, au lieu de 2128 essais. L'attaque implique également d'établir un nombre de connexions TLS égal au nombre d'octets de password (16 dans notre exemple) nécessaires pour récupérer les différentes valeurs de référence Ci.
Comme l'attaque porte sur les données claires, son coût dépend de la quantité de données que l'on cherche à récupérer. Autrement dit : l'attaque peut être relativement efficace s'il s'agit de retrouver un mot de passe chiffré par TLS mais nettement moins efficace s'il s'agit de déchiffrer des Mo de données.
4.2 Mise en œuvre
Considérons le cas d'une victime disposant d'un compte utilisateur auprès d'un site A (par exemple Paypal). Pour accéder à ce compte, la victime prouve son accréditation en transmettant un mot de passe au travers d'un tunnel TLS 1.0 établi avec A. Les conditions nécessaires à la réalisation de l'attaque sont les suivantes :
1. L'attaquant peut observer le trafic chiffré échangé entre le client et le serveur TLS.
2. L'attaquant peut forcer la victime à effectuer des connexions TLS vers un site (légitime) A (en HTTPS par exemple).
3. L'attaquant peut injecter des données claires dans le tunnel TLS établi avec le site A (sans toutefois pouvoir récupérer les données claires de l'utilisateur légitime).
La condition 3 permet à l'attaquant de tester ses hypothèses sur les différents octets du mot de passe, par injection du bloc B dans le tunnel TLS.
La condition 2 force la victime à établir (de manière répétée) un tunnel TLS au travers duquel elle transmet son mot de passe au site A. Cela permet à l'attaquant de récupérer les différentes valeurs de références Ci = aes(Ci–1⊕ (cste | p | ... | pk)) et les blocs chiffrés Cj+1 avec lesquels il vérifie son hypothèse sur les octets pk.
Selon Duong et Rizzo, les deux dernières conditions peuvent être réunies si la victime charge avec son navigateur une page contenant des liens pointant sur le site A d'une part. D'autre part, l'injection de données dans le tunnel TLS établi entre la victime et le site A peut se faire à l'aide d'un procédé de type cross-site request forgery qui permet à l'attaquant de berner le navigateur quant à l'origine des données reçues.
Duong et Rizzo ont présenté une illustration de leur attaque en récupérant le cookie de connexion d'un compte Paypal.
4.3 Contre-mesures
Cette attaque concerne TLS 1.0. Concernant les aspects cryptographiques, il « suffit » d'utiliser TLS 1.1 ou 1.2 puisque dans ces versions l'IV n'est pas prédictible (il est généré pseudo-aléatoirement pour chaque paquet TLS). Par conséquent, l'attaque ne fonctionne pas avec ces versions.
En effet, si l'attaquant ne connaît pas l'IV utilisé lors du chiffrement, il ne peut pas distinguer si son choix est correct ou pas lors de la recherche exhaustive des données claires. Attention : la machine ne doit pas seulement implémenter TLS 1.1 mais refuser de basculer en TLS 1.0 si le correspondant supporte uniquement TLS 1.0. Toutefois, l'utilisation de TLS 1.1 ou 1.2 à l'exclusion de la version 1.0 peut poser des problèmes de compatibilité étant donné que ces versions semblent encore peu supportées (dans les navigateurs notamment) à l'heure actuelle.
Une autre possibilité est de ne pas utiliser le mode CBC pour le chiffrement mais un algorithme de chiffrement par flot tel que RC4. Encore une fois, il s'agit ici d'interdire tout autre algorithme de chiffrement que RC4 (le navigateur ne doit pas opter pour un autre algorithme si le correspondant ne propose pas RC4 dans la suite cryptographique).
TLS propose soit des algorithmes de chiffrement par bloc en mode CBC, soit RC4.
Enfin, l'attaque ne peut fonctionner si les données sont compressées avant chiffrement.
Plusieurs années avant l'attaque Beast, une correction a été faite dans la bibliothèque OpenSSL (à partir de la version 0.9.6d, 09/05/2002) qui contrecarre de facto l'attaque de Duong et Rizzo. Cette contre-mesure consiste à placer un record vide comme premier élément à chiffrer dans le paquet TLS. À partir de ce record, un HMAC est calculé (incluant un sequence number implicite) et le tout est chiffré (après ajout d'un padding fixe). Comme les clés de session (chiffrement et signature) ne sont pas connues de l'attaquant, celui-ci ne peut pas connaître en avance la valeur du champ HMAC ni celle du bloc chiffré obtenu. Ceci permet donc d'obtenir un IV non prédictible qui sera utilisé pour le chiffrement du bloc suivant.
Toutefois, pour des raisons de compatibilité, cette contre-mesure peut être désactivée à partir d'OpenSSL 0.9.6e (30/07/2002). Et elle l'est par défaut...
5. Erreurs d'implémentation
Vous souvenez-vous du « bug » Debian ? Croyant corriger une fuite de mémoire provenant du code OpenSSL, des développeurs du projet Debian ont en réalité drastiquement réduit la source d'entropie utilisée pour générer des valeurs pseudo-aléatoires. La conséquence de ce bug : le nombre de clés RSA et (EC)DSA que le code OpenSSL « corrigé » pouvait générer s'est trouvé limité à un nombre si faible qu'il était possible de générer toutes ces clés. Les clés pouvant être énumérées, toutes les sessions TLS établies à partir de telles clés étaient donc compromises. Pire : les certificats correspondants sont restés potentiellement utilisables pour monter des attaques man in the middle, étant données les vérifications parfois partielles qui sont faites (notamment : absence de vérification des listes de révocation).
Néanmoins, d'autres types d'erreurs d'implémentation, plus subtiles, peuvent ruiner la sécurité d'un protocole.
5.1 Description
Imaginons un algorithme mal implémenté qui fournit un résultat correct en général, sauf dans certains cas particuliers lorsque certains paramètres sont utilisés. Cette erreur d'implémentation peut-elle être exploitée ? Oui si l'algorithme en question est sollicité à un moment crucial de la mise en œuvre d'un protocole de sécurité. C'est ce qu'ont montré Brumley, Barbosa, Page et Vercauteren [18] en s'appuyant sur des travaux de Biham, Carmeli et Shamir [19].
Biham et al. présentent un concept d'attaque tirant profit d'une erreur d'implémentation dans un logiciel ou un composant matériel. Le principe exposé est le suivant : l'opération implémentée retourne un résultat correct dans la grande majorité des cas (i.e. : pour la plupart des opérandes engagées dans le calcul) mais, pour certaines valeurs des opérandes, le résultat du calcul est faux. Illustrons ce concept avec l'exemple suivant correspondant à un produit scalaire [k]P selon la formule de Montgomery (algorithme 7).
Entrées : point P∈E, scalaire k = (kl-1...k1k0)2.
Sortie : point Q = [k]P∈E.
R0 = OR1 = P
for i = l–1 downto 0 step –1
if ki= 0 thenR1 = R0 + R1R0 = [2]R0
elseR0 = R0 + R1R1 = [2]R1
end
end
returnR0
Figure 7 : Produit scalaire selon la formule de Montgomery (version ladder)
Considérons une valeur P particulière telle que :
- le calcul [2]R est incorrect ;
- le calcul R + R1 est correct ;
- le calcul [2]R1 est correct ;
si le bit kivaut 0.
Si un attaquant souhaite recouvrer ki, il lui suffit de soumettre une telle valeur P à un oracle de calcul [k]P. Si le résultat final qui lui est retourné est correct, cela signifie que l'opération [2]R n'a pas été effectuée et l'attaquant en déduit que ki = 1. Si le résultat final est incorrect, cela signifie que l'algorithme est passé par l'étape [2]R et donc que ki = 0.
Il suffit donc à l'attaquant de construire ⌊log2(k)⌋+1 valeurs Pi telles qu'une erreur se produise à l'étape i (et uniquement à cette étape) du calcul [k]Pi. Le résultat des différents calculs [k]Pi révèle la valeur des bits ki.
Brumley et al. proposent une mise en œuvre concrète du concept ci-dessus. La version 0.9.8g d'OpenSSL présente en effet une erreur d'implémentation dans la multiplication modulaire x×y mod p où p = 2256– 2224+ 2192 + 296– 1 est l'un des paramètres de la courbe elliptique P-256 du NIST [20]. La formule utilisée pour effectuer ce calcul tire parti de la forme particulière de p.
L'attaque a pour but de trouver la valeur k utilisée dans le calcul [k]P. Le contexte dans lequel ce calcul est effectué est celui d'un échange de clé Diffie-Hellman statique (cf. Figure 8).
Figure 8 : Échange de clé Diffie-Hellman sur courbe elliptique (ECDH)
Dans le cas d'un échange ECDH statique, le serveur utilise une valeur a constante d'un échange à l'autre. Le fait que a (et donc A = [a]G) soit constant permet à l'attaquant d'effectuer de nombreux échanges de clé avec le serveur afin de recouvrer progressivement les digits de a.
La valeur [a]B = S correspond au secret négocié entre le client (l'attaquant) et le serveur. Ce secret commun fournit le pre_master_secret, élément principal de la dérivation des clés de session.
Si le calcul [a]B effectué par le serveur est correct, les clés de session seront correctement dérivées et le paquet Finished sera correctement construit. Inversement, si le calcul [a]B est incorrectement effectué, l'échange de clé échouera. Par conséquent, l'échange de clé est utilisé par l'attaquant comme distingueur pour savoir si la formule erronée a été mise en œuvre dans le calcul [a]B. L'attaquant utilise ce bit d'information pour savoir si son hypothèse sur la valeur de ai est correcte ou pas.
L'implémentation d'OpenSSL utilise une représentation NAF. Si on considère des digits de taille 4 bits, cela signifie que les composantes ai de a sont à valeur dans {–7, –5, –3, –1, 0, 1, 3, 5, 7}. De plus, par définition de la représentation NAF, un digit non nul est nécessairement suivi d'au moins 3 digits nuls. Ainsi, la découverte explicite d'un digit ai non nul implique la découverte implicite des 3 digits nuls suivants.
Cette attaque peut également être mise en œuvre dans le cas d'un échange Diffie-Hellman éphémère. Lors d'un échange DH éphémère, les valeurs secrètes a et b des deux correspondants doivent être renouvelées lors de chaque échange de clé. Toutefois, OpenSSL implémente une « optimisation » assez singulière. Lors d'un échange ECDHE, la valeur secrète a du serveur est effectivement différente d'un client à l'autre, mais cette valeur reste constante si des échanges de clé sont effectués avec le même client !
Cette optimisation est appliquée par défaut...
Cela viole le principe de forward secrecy et permet la réalisation de l'attaque.
5.2 Mise en œuvre
Dans le cas d'un échange ECDHE avec optimisation, la connaissance de a permet à l'attaquant de déchiffrer toutes les communications passées et futures établies entre le serveur et un client donné. En effet, à partir d'une valeur B = [b]G fraîchement générée par le client, l'attaquant est capable de calculer le secret partagé S = [a]B = [a×b]G.
Dans le cas d'un échange ECDH, la valeur a est persistante. Elle a été et sera utilisée par le serveur avec tous les clients. L'attaquant en possession de cette valeur peut donc accéder au clair des communications passées et futures établies entre le serveur et tous ces clients.
L'attaque est possible lorsque l'échange ECDH (ou ECDHE avec optimisation) est effectué avec les courbes elliptiques P-256 et P-384 (mais pas P-192, P-224 ni P-521 pour lesquelles des formules de calcul différentes sont utilisées). L'attaque permet de récupérer le secret a du serveur en 633 échanges de clé ECDH dans le cas P-256.
5.3 Contre-mesures
La formule de calcul erronée a été corrigée à partir de la version 0.9.8h d'OpenSSL. Plus généralement, une manière de prévenir une attaque reposant sur une erreur d'implémentation consiste à procéder à une vérification formelle du code source. Des contre-mesures algébriques peuvent également être déployées pour contrer l'attaque, telles que :
- le scalar blinding : [k]P est obtenu par la formule [k + r×n]P où r est une (petite) valeur choisie pseudo-aléatoirement et [n]P = O ;
- le point blinding : [k]P est obtenu par la formule [k](P + R) –T où R est choisi pseudo-aléatoirement et T = [k]R.
Comme une valeur pseudo-aléatoire intervient dans le calcul de [k]P, l'attaquant ne peut plus établir de corrélation entre le résultat du calcul et la valeur de k.
Conclusion
Un certain nombre de failles et d'attaques de TLS et OpenSSL a été présenté. La liste n'est sans doute pas exhaustive ni figée. Il est fort possible qu'elle s'étoffera à l'avenir.
Parmi les attaques décrites, certaines (notamment cryptographiques) étaient entièrement nouvelles alors et se sont révélées efficaces contre un protocole qui n'a pas été pensé (conceptuellement) pour y résister, entraînant une modification du protocole lui-même. D'autres attaques ont tiré profit des choix d'implémentation du protocole (par exemple les timing attacks). Parfois même, de discrètes erreurs d'implémentation nichées dans un coin obscur de la bibliothèque ont offert à l'attaquant le moyen suffisant pour ruiner la sécurité du protocole. Dans ces deux derniers cas, c'est l'implémentation qui est en cause.
Mais les attaques ne sont pas toutes nouvelles. Ainsi, l'attaque Beast (2011) s'appuie sur les travaux de Bard (2004, 2006) considérés comme essentiellement théoriques jusque-là. La mise en œuvre de Beast a été possible grâce aux développements d'un autre champ de la sécurité (réseau) dont les aboutissements ont servi de vecteur pour appliquer l'attaque de Bard.
D'autres attaques, sans être nouvelles dans leur concept, correspondent à la mise en œuvre (avec plus ou moins de succès) dans le monde réseau de techniques largement étudiées et qui ont fait leurs preuves dans d'autres domaines (par exemple : les attaques par canaux auxiliaires, telles que les timing attacks, sur des équipements électroniques comme la carte à puce).
Enfin, il ne faut pas négliger les failles les plus faciles à corriger mais toujours profitables à un attaquant : mauvaise configuration d'un serveur, support d'algorithmes « faibles », etc.
Si la publication d'une attaque ou la détection d'un bug constitue d'utiles piqûres de rappel, cela ne suffit pas forcément à renforcer la sécurité d'un réseau car il y a une latence plus ou moins importante (et un intérêt plus ou moins poussé) avant la prise en compte effective et le déploiement d'un correctif [21, 22].
Pour les administrateurs de serveurs TLS ou autres intéressés à la sécurité du protocole (et de leur réseau), plusieurs moyens sont offerts. Tout d'abord, des études sont régulièrement publiées concernant l'usage du protocole [23, 24, 25], des recommandations d'emploi [28, 30], ses performances [26] ou à l'occasion de la découverte de faille ou d'attaque [27]. Ces études permettent notamment d'observer l'évolution du déploiement et des usages du protocole (rapidité de prise en compte des correctifs, algorithmes les plus utilisés, etc.).
Enfin, plusieurs sites s'attachent à maintenir une veille sur la sécurité de TLS. Par exemple (mais ce ne sont sans doute pas les seuls) :
- SSL server survey de Netcraft : https://ssl.netcraft.com/ssl-sample-report/index ;
- SSL observatory de l'Electronic Frontier Foundation (EFF) : https://www.eff.org/observatory ;
- SSL Pulse de SSL Labs : https://www.trustworthyinternet.org/ssl-pulse/.
Références
[1] Renegotiating TLS, Marsh Ray, Steve Dispensa, 04/11/2009. Disponible à l'adresse http://extendedsubset.com/Renegotiating_TLS.pdf.
[2] Transport Layer Security (TLS) Renegotiation Indication Extension, Eric Rescorla, Marsh Ray, Steve Dispensa, Nasko Oskov, RFC 5746, février 2010. Disponible à l'adresse http://tools.ietf.org/html/rfc5746.
[3] Bug attacks, Eli Biham, Yaniv Carmeli, Adi Shamir, 2008. Disponible à l'adresse http://www.cs.technion.ac.il/~yanivca/BugAttacks.pdf.
[4] Practical realisation and elimination of an ECC-related software bug attack, B. B. Brumley, M. Barbosa, D. Page, F. Vercauteren, 24/11/2011. Disponible à l'adresse http://eprint.iacr.org/2011/633.
[5] BEAST, T. Duong, 25/09/2011. Disponible à l'adresse http://vnhacker.blogspot.com/2011/09/beast.html.
[6] Talking to Yourself for Fun and Profit, Lin-Shung Huang, Eric Y. Chen, Adam Barthy, Eric Rescorlaz, Collin Jackson, W2SP 2011. Disponible à l'adresse http://w2spconf.com/2011/papers/websocket.pdf.
[7] Here Come The ⊕ Ninjas, Thai Duong, Juliano Rizzo, 13/05/2011. Disponible à l'adresse https://docs.google.com/viewer?a=v&pid=explorer&chrome=true&srcid=0B2J69udptdboYzFmMTQxM2MtZGEwYi00YjA5LWEwM2QtMWNkZDVhZTJlY2Qy\&hl=en.
[8] SSL and TLS - Designing and Building Secure Systems, Eric Rescorla, Addison-Wesley, mars 2001,
[9] The Transport Layer Security (TLS) Protocol – Version 1.2, Tim Dierks, Eric Rescorla, RFC 5246, août 2008. Disponible à l'adresse http://tools.ietf.org/html/rfc5246.
[10] A Timing Attack against RSA with the Chinese Remainder Theorem, Werner Schindler, CHES 2000. Disponible à l'adresse http://www.springerlink.com/content/6rct1u31c2v17hf0/fulltext.pdf.
[11] Small Solutions to Polynomial Equations, and Low Exponent RSA Vulnerabilities, Don Coppersmith, Journal of Cryptology, volume 10, numéro 4, 1997.
[12] Timing-based attacks on RSA keys, OpenSSL Security Advisory, 17/03/2003. Disponible à l'adresse http://www.openssl.org/news/secadv_20030317.txt.
[13] Remote Timing Attacks are Still Practical, David Brumley, Nicola Tuveri, ESORICS 2011. Disponible à l'adresse http://eprint.iacr.org/2011/232.
[14] Lattice Attacks on Digital Signature Schemes, Nick A. Howgrave-Graham, Nigel P. Smart, 03/08/1999. Disponible à l'adresse http://www.hpl.hp.com/techreports/1999/HPL-1999-90.pdf.
[15] Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1, Daniel Bleichenbacher, Crypto 1998. Disponible à l'adresse http://www.bell-labs.com/user/bleichen/papers/pkcs.ps.
[16] Attacking RSA-based Sessions in SSL/TLS, Vlastimil Klima, Ondrej Pokorny, Tomas Rosa, CHES 2003. Disponible à l'adresse http://eprint.iacr.org/2003/052.
[17] Password interception in a SSL/TLS channel, Brice Canvel, Alain Hiltgen, Serge Vaudenay, Martin Vuagnoux, Crypto 2003. Disponible à l'adresse http://lasecwww.epfl.ch/memo/memo_ssl.shtml.
[18] Practical realisation and elimination of an ECC-related software bug attack, Billy Bob Brumley, Manuel Barbosa, Dan Page, Frederik Vercauteren, 24/11/2011. Disponible à l'adresse http://eprint.iacr.org/2011/633.
[19] Bug Attacks, Eli Biham, Yaniv Carmeli, Adi Shamir, 2008. Disponible à l'adresse http://www.cs.technion.ac.il/~yanivca/BugAttacks.pdf.
[20] Federal Information Processing Standards Publication – Digital Signature Standard (DSS), NIST, juin 2009. Disponible à l'adresse http://csrc.nist.gov/publications/fips/fips186-3/fips_186-3.pdf.
[21] Security holes... Who cares?, Eric Rescorla, USENIX Security Symposium, 2003. Disponible à l'adresse http://static.usenix.org/events/sec03/tech/full_papers/rescorla/rescorla.pdf.
[22] SSL and Browsers: The Pillars of Broken Security, Ivan Ristic, Wolfgang Kandek, RSA Conference 2012. Disponible à l'adresse https://community.qualys.com/blogs/securitylabs/2012/03/07/ssl-and-browsers-the-pillars-of-broken-security.
[23] SSL Server Security Survey, Eric Murray, 31/07/2000. Disponible à l'adresse http://web.archive.org/web/20031005013455/http://www.lne.com/ericm/papers/ssl_servers.html.
[24] Changes in deployment of cryptography, Eric Murray, USENIX Security Symposium, 2001. Disponible à l'adresse http://www.usenix.org/events/sec01/murray/index.htm.
[25] Cryptographic strength of SSL/TLS servers: Current and recent practices, Homin K. Lee, Tal Malkin, Erich Nahum, Internet Measurement Conference 2007. Disponible à l'adresse http://conferences.sigcomm.org/imc/2007/papers/imc130.pdf.
[26] Performance analysis of TLS Web servers, Cristian Coarfa, Peter Druschel, Dan S. Wallach, ACM Transactions on Computer Systems, février 2006. Disponible à l'adresse http://www.cs.rice.edu/~dwallach/pub/tls-tocs.pdf.
[27] When private keys are public: results from the 2008 debian OpenSSL vulnerability, Scott Yilek, Eric Rescorla, Hovav Shacham, Brandon Enright, Stefan Savage, Internet Measurement Conference 2009. Disponible à l'adresse http://cseweb.ucsd.edu/~savage/papers/IMC09.pdf.
[28] SSL/TLS : état des lieux et recommandations, Olivier Levillain, SSTIC 2006. Disponible à l'adresse https://www.sstic.org/media/SSTIC2012/SSTIC-actes/ssl_tls_soa_recos/SSTIC2012-Article-ssl_tls_soa_recos-levillain_2.pdf.
[29] Understanding the TLS Renegotiation Attack, Eric Rescorla, 05/11/2009. Disponible à l'adresse http://www.educatedguesswork.org/2009/11/understanding_the_tls_renegoti.html.
[30] TLS/SSL hardening and compatibility report 2011, Thierry Zoller, 2011. Disponible à l'adresse http://www.g-sec.lu/sslharden/TLS%20SSL%20hardening%20and%20compatibliy%20report%202011.zip.