Les techniques d'attaques en boîte grise sur du matériel peuvent être transposées avec succès à un domaine bien plus immatériel, la cryptographie en boîte blanche. Nous verrons ainsi comment adapter les attaques par DPA et par DFA aux implémentations logicielles en boîte blanche.
Les attaques présentées dans cet article visent des implémentations de chiffrement AES-128, mais elles sont applicables également au déchiffrement et aux versions AES-192 et AES-256. En outre, il existe des variantes pour la plupart des autres algorithmes de chiffrement par bloc (DES, 3DES, etc.).
1. Quelques nuances de gris
Qu'est-ce donc que ces histoires de couleurs désaturées ?
Il s'agit de références aux modèles d'attaque pris en considération. La conception d'algorithmes de chiffrement modernes se concentre classiquement sur le modèle de la boîte noire : le mécanisme physique chargé du chiffrement d'une donnée est considéré comme une boîte noire dont seules l'entrée et la sortie sont observables. Toutefois, l'algorithme est réputé connu si on respecte le fameux principe de Kerckhoffs qui énonce que la sécurité du système repose uniquement sur le secret de la clé employée.
Néanmoins, dans la réalité, la boîte n'est pas si noire et, outre les entrées et sorties, divers effets physiques du mécanisme de chiffrement sur son environnement sont observables : variations de consommation de courant, production d'émissions électromagnétiques, de chaleur, de son, de lumière, etc. Et certains de ces effets peuvent être influencés par les données intermédiaires traitées, donc indirectement par la clé de chiffrement. On parle alors de modèle d'attaques en boîte grise. Il est même possible d’agir sur l'environnement physique pour introduire sporadiquement des fautes de calcul.
Enfin, dans le cadre d'utilisations de la cryptographie en environnement particulièrement hostile, le modèle d'attaque a été étendu aux implémentations purement logicielles qui tournent sur du matériel sous contrôle de l'attaquant. Considérez par exemple les cas classiques de logiciels multimédias qui implémentent des gestions de contrôle des droits (DRM) pour protéger les films de... vous, le méchant utilisateur ! De même, les applications bancaires mobiles doivent protéger votre argent d'éventuels logiciels malveillants sur une plateforme régulièrement mise à mal par de nouvelles failles.
C’est le modèle d'attaques en boîte blanche et les capacités de l'attaquant sont quasi sans limites : analyses statique et dynamique de l'implémentation, observation et modification des instructions, des registres, de la mémoire, etc. Les seules véritables limites sont les capacités de calcul (en termes de puissance et de mémoire disponibles), le niveau d'expertise (en rétro-ingénierie et en cryptographie) et le temps disponible de l'attaquant.
2. Qu’est-ce qu’une boîte blanche ?
Par extension du modèle d'attaque, le terme boîte blanche (white-box en anglais) fait référence à l'implémentation logicielle d'un algorithme de chiffrement cryptographique censément robuste contre cette classe d’attaques. Le but est donc de rendre la clé indissociable de l'implémentation.
Notons qu'une implémentation doit également faire face en pratique à d'autres attaques que l'extraction de la clé, telles que l'extraction de la fonctionnalité de chiffrement et le calcul de son inverse : si l'attaquant a réussi à reconstruire des fonctions de chiffrement et de déchiffrement équivalentes, il n'a pas besoin de connaître la clé pour abuser le système.
La conception d’une boîte blanche repose généralement sur quelques grands principes. Les clés de ronde sont précalculées et diffusées le plus possible dans l’implémentation, typiquement sous forme de tables précalculées regroupant plusieurs opérations. Les entrées et sorties de ces tables subissent elles-mêmes plusieurs encodages. Enfin, il n’est pas rare d’appliquer quelques techniques d’obfuscation, voire de virtualisation, par-dessus le tout.
Jusqu’il y a peu, les seules attaques publiées sur les divers schémas de boîte blanche connus étaient des attaques algébriques sur les tables de ces schémas. Cela implique donc d’isoler la boîte blanche du reste du programme, d’en ôter les couches successives d’obfuscation, d’en comprendre le schéma et d’en extraire les tables afin d’être en mesure d’appliquer l’attaque algébrique idoine.
3. Attaque par canaux auxiliaires
Rien n'est ni tout noir, ni tout blanc, c'est le gris qui gagne. Philippe Claudel, Les Âmes grises
3.1 Principe de l’analyse différentielle de consommation
Comme expliqué dans l'introduction, certaines grandeurs physiques du mécanisme de chiffrement peuvent varier en fonction des données traitées et de la clé de chiffrement utilisée.
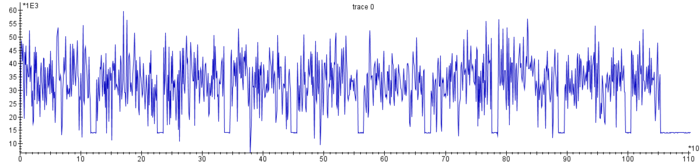
Paul Kocher et ses comparses présentent en 1999 l'analyse différentielle de consommation, la DPA (pour Differential Power Analysis) [DPA]. Le principe en est relativement simple. L'attaquant fournit une succession de blocs de données choisis aléatoirement à un mécanisme de chiffrement. Il en mesure, pour chaque bloc traité, la consommation électrique tout au long du processus, et récupère le résultat du chiffrement. Cette mesure est appelée trace. La figure 1 donne un exemple de trace de consommation d’un microcontrôleur calculant un AES-128. Les dix rondes de l’AES sont aisément repérables, la dernière étant plus petite, car dépourvue de certaines opérations.
Fig. 1 : Trace de consommation d’un AES-128.
Pour attaquer la clé de chiffrement, il faut viser des points de l'algorithme qui ne dépendent chacun que d'une fraction de la clé, si possible de manière non linéaire (sinon, des clés proches de la clé correcte donneraient facilement des faux positifs). Pour l'AES, l’observation des bits de la sortie des SBox de la première ronde est un choix intéressant, car ces bits ne dépendent que d’un seul octet de l’entrée et d’un seul octet de la clé à la fois et la Sbox apporte la non-linéarité souhaitée. Attaquons le premier octet de la première clé de ronde (qui est, dans le cas d’un AES-128, identique à la clé AES elle-même) et observons le premier bit de poids faible de la sortie de la SBox correspondante. Faisons une hypothèse sur la valeur du premier octet de la clé et, pour chaque bloc d'entrée, calculons le premier bit de poids faible de la sortie de la SBox. Selon sa valeur, zéro ou un, nous trions les traces de consommation en deux ensembles. Si la consommation observée diffère effectivement en un instant donné selon la valeur du bit observé de la sortie de la SBox et si notre hypothèse sur la valeur de l'octet de la clé est correcte, alors nous devrions voir une différence significative entre les deux ensembles de mesures. Pour cela, nous calculons la moyenne de chaque ensemble et enfin nous soustrayons l'une de l'autre. La moindre différence apparaîtra alors sous la forme d'un pic de corrélation. Si par contre la valeur choisie pour l'octet de la clé n'est pas correcte, le calcul de la sortie de la SBox conduira à un tri arbitraire des traces de consommation et il n'y aura statistiquement pas de différence significative entre les deux ensembles ainsi constitués. Le même raisonnement s'applique à tous les bits de sortie de toutes les SBox de la première ronde et la clé complète peut être reconstituée octet par octet. Une variante de l'attaque utilise non pas l’entrée, mais la sortie pour attaquer la dernière clé de ronde de l'AES.
Pour attaquer une puce physique, on utilisera plus volontiers des modèles de consommation étendus à tous les bits d'un octet de l'algorithme, car ces bits contribuent tous plus ou moins équitablement à la consommation électrique en un même instant et on considèrera typiquement leur poids de Hamming plutôt que les valeurs individuelles de chaque bit.
3.2 Application à des implémentations logicielles
Il va de soi qu'une implémentation résistante au modèle d'attaques en boîte blanche résiste également aux attaques en boîte grise. Alors, pourquoi perdre notre temps ? Parce que, selon l'état de l'art actuel, il n'existe aucune boîte blanche qui apporte une preuve mathématique de sa robustesse. De plus, l'approche des attaques en boîte grise est radicalement différente des attaques algébriques connues sur les boîtes blanches.
En effet, les attaques en boîte grise font très peu d'hypothèses sur le fonctionnement interne des implémentations attaquées, ce qui est heureux, car les détails d'implémentation des puces cryptographiques sont rarement disponibles. Bref, contrairement aux attaques algébriques, d'abord on tire, ensuite on réfléchit, éventuellement... si on a envie de comprendre pourquoi l'attaque a fonctionné.
Voyons comment concilier ces deux mondes : les implémentations en boîte blanche et les attaques physiques sur les mécanismes cryptographiques. Une approche naïve serait de mettre la boîte blanche dans une boîte grise et de l'attaquer : mesurer la consommation du CPU lorsqu'il exécute l'implémentation cryptographique. Cependant, ce serait se priver d'informations observables beaucoup plus précisément qu'une simple mesure de la consommation du circuit.
Pour observer le fonctionnement en détail d'un algorithme, il existe diverses techniques d'instrumentation qui produisent des traces d'exécution à partir d'un débogueur, d'un émulateur ou encore de cadriciels d'instrumentation tels que Intel PIN, Valgrind, DynamoRIO, QBDI, etc. En fin de compte, cela revient à procéder à une exécution pas-à-pas de l'algorithme où, à chaque instruction exécutée, les adresses et les valeurs de l'instruction, des données lues ou écrites en mémoire, voire des registres, sont soigneusement retranscrites.
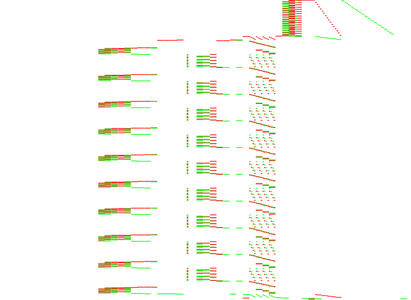
Une manière originale de traiter les données recueillies pour en avoir un aperçu global est de construire une représentation graphique. La figure 2 représente l'évolution de la pile lors de l'exécution d'une boîte blanche typique. L'abscisse représente l'adressage mémoire tandis que l'ordonnée est une ligne du temps qui s'écoule de haut en bas. Les données lues apparaissent en vert et celles écrites en rouge. Dix répétitions sur la gauche et neuf sur la droite, voici les dix rondes d'un AES-128 ! On distingue même la structure en carré de quatre par quatre de l'état interne de l'AES. Il est ainsi relativement aisé de repérer la position d'un AES en boîte blanche au sein d'un programme plus large.
Fig. 2 : Trace d’exécution de la pile d’une boîte blanche AES-128.
Mais comment passer des traces d'exécution obtenues à un équivalent des traces de consommation utilisées en DPA ? Une possibilité est de mettre bout à bout tous les bits des octets manipulés par le programme, par exemple ceux écrits sur la pile ou lus en mémoire ou même les adresses de ces octets, en se limitant si possible aux instructions de la première ronde observée visuellement afin d'éviter des calculs inutiles.
Ce déroulé des bits des octets observés est nécessaire, car, selon l'encodage interne propre à la boîte blanche attaquée, chaque bit a potentiellement une certaine corrélation avec les bits de la sortie de la SBox. Comme pour la DPA, de nombreuses traces d'exécution seront enregistrées avec des blocs d'entrée différents.
La trace obtenue, illustrée en figure 3, est fort différente visuellement des traces de consommation, car composée exclusivement de zéros et d'uns et son assemblage ne reflète plus vraiment une flèche du temps monotone. Pourtant, ce type de trace remplace à merveille la trace de consommation utilisée en DPA traditionnelle et, s'il y a effectivement une corrélation entre la sortie des SBox et les bits observés, la clé tombera.
Fig. 3 : Trace d’exécution mise en forme pour une DPA.
Les valeurs calculées par la boîte blanche ayant remplacé les valeurs de la consommation de la boîte grise, nous appelons cette attaque la DCA, la Differential Computation Analysis.
Les traces ainsi forgées ont la propriété remarquable d'être complètement dépourvues de bruit, contrairement aux mesures classiques de consommation. Cela permet d'appliquer des techniques de compression des traces telles que la suppression des valeurs qui restent constantes, quel que soit le bloc chiffré, ou des valeurs qui apparaissent de manière redondante, et d'accélérer d'autant la phase de calcul de la DCA.
3.3 Exemples concrets d’attaque par analyse différentielle des données internes
SideChannelMarvels est un ensemble de dépôts sur GitHub qui regroupe les outils pour mener à bien l'acquisition de traces d'exécution, la visualisation d'une trace, l'attaque de ces traces par analyse différentielle et enfin quelques exemples d'implémentations publiques de boîtes blanches, avec les scripts adéquats pour orchestrer les attaques. Les entrées, les sorties et les traces collectées sont passées à l'outil Daredevil qui tente de casser la première ou la dernière clé de ronde.
Voici le résumé de quelques résultats obtenus sur un PC standard, que vous pouvez reproduire par vous-même à partir du projet Deadpool :
- Hacklu2009 : il s'agit d'un exécutable Windows avec une interface graphique. Nos outils fonctionnant sous Linux, nous utilisons Valgrind pour instrumenter wine tandis qu'il gère l'exécutable et xdotool pour automatiser la saisie du bloc d'entrée. La sortie n'est pas observable, mais ce n'est pas grave, car elle n'est pas nécessaire pour une DCA sur le premier round. Par la lenteur de l'instrumentation choisie, il faut compter 80 s pour acquérir 20 traces. Puis 1,5 s pour retrouver la clé. Cette implémentation n'utilise pas d'encodage interne, ce qui explique le faible nombre de traces nécessaires.
- OpenwhiteboxChow : l'implémentation est écrite en Go, avec toute la phase d’initialisation que ce langage comporte. En se limitant aux instructions de l'AES proprement dit, l'acquisition de 200 traces prend 2 min. Comptez 6 min de plus pour l'attaque sans prétraitement de ces traces.
- CHES2016 : l'acquisition de 2 000 traces prend 15 min en se limitant au premier round et l'attaque 1 min.
Occasionnellement, pour certaines instances de ces exemples, certains octets ne sont pas cassés. Il faut alors soit casser la clé par énumération, soit appliquer une généralisation de la DCA en considérant, outre les bits des sorties des SBox de manière individuelle, leurs différentes combinaisons possibles.
4. Attaque par injection de faute
4.1 Principe de l’injection de faute sur une boîte blanche AES-128
Conjointement aux attaques par canaux auxiliaires, un autre type d'attaque très répandu dans les analyses physiques en boîte grise est l'injection de faute. La faute est induite dans le circuit par des parasites sur l'alimentation, sur le signal d'horloge, par des émissions électromagnétiques puissantes ou même par des émissions de lumière (par ex. laser) qui vont introduire localement un courant dans la puce par effet photoélectrique.
Une faute est injectée pendant l'exécution du calcul cryptographique, généralement dans les dernières rondes. Cette faute de calcul va se propager dans les opérations suivantes jusqu'à la sortie du composant cryptographique. L'effet de l'erreur est observé sur la sortie et, si on fait une hypothèse sur la nature de l'erreur injectée, l'erreur observée ne s’explique que pour certaines valeurs des octets de la dernière clé de ronde. S'il faut réduire davantage le nombre de clés candidates, d'autres fautes sont injectées, jusqu'à arriver à une seule clé ou un nombre suffisamment faible pour les essayer toutes et retrouver la bonne clé.
Le sujet a fort évolué ces dernières années, avec des techniques très complexes pour limiter le nombre de fautes nécessaires, car certains matériels ciblés, tels que les cartes bancaires, sont de mieux en mieux protégés et s'autodétruisent s'ils détectent une injection de faute, par exemple avec des capteurs de lumière.
Mais, dans le cas des exécutions en boîte blanche, nous n'avons pas ce genre de souci et autant utiliser la première attaque par faute sur l'AES révélée en 2002, la DFA (pour Differential Fault Analysis) [DFA]. En effet, cette attaque est relativement simple à comprendre, donc à implémenter, et a une propriété sympathique qui nous évite de devoir trouver de bons endroits pour injecter les fautes. Il suffira d'observer l'erreur sur la sortie pour déterminer si la faute a été injectée à un endroit utile ou non.
Rappelons dans les grandes lignes la structure du chiffrement AES-128. Le bloc d’entrée est disposé en un carré de quatre sur quatre pour former l’état qui sera transformé progressivement par des opérations élémentaires répétées en dix rondes et mélangé à onze clés de rondes dérivées de la clé AES principale. Parmi les opérations élémentaires, seul le MixColumns mélange plusieurs octets de l'état en appliquant une transformation linéaire sur chaque colonne. Les autres opérations n'affectent que les octets individuellement (SubBytes et AddRoundKey) ou ne font que les déplacer (ShiftRows).
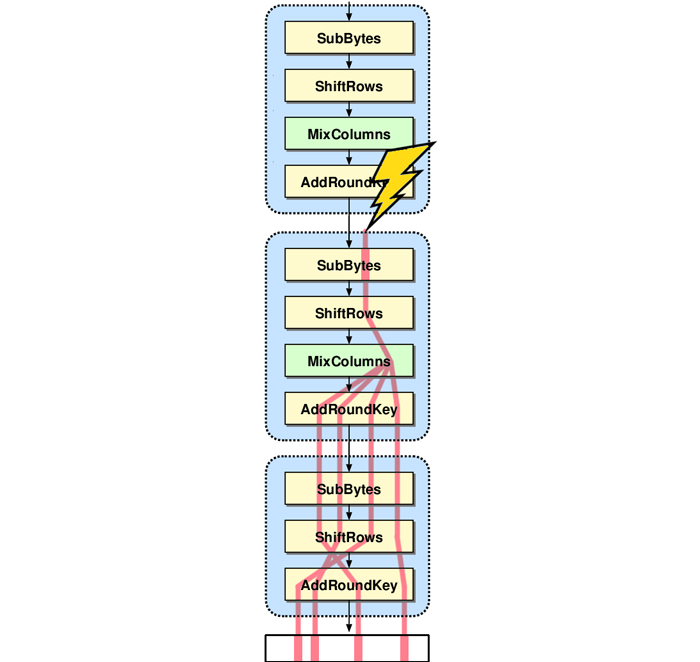
Voyons ce qui se passe lorsqu’un octet de l'état est corrompu quelque part entre les deux derniers MixColumns de l'AES. Aucune autre hypothèse n’est faite sur la nature de la faute injectée et on considère que cet octet peut avoir n'importe quelle valeur.
L'erreur se déplace dans l'état interne en cas de ShiftRows puis, lors de son passage dans le dernier MixColumns, elle se propage à toute une colonne, elle-même réarrangée par le dernier ShiftRows. Finalement, exactement quatre octets de la sortie sont corrompus par la faute injectée. Cette diffusion de l'erreur est illustrée en figure 4.
Selon la colonne affectée, il y a exactement quatre dispositions possibles de la diffusion de la faute sur quatre octets de la sortie. Les différences observées entre la sortie correcte et une sortie corrompue sur quatre octets ne peuvent s’expliquer que pour certaines valeurs des quatre octets correspondants de la dernière clé de ronde.
En pratique, il suffit d'injecter une faute à deux reprises dans une même colonne pour déterminer exactement ces quatre octets de clé de ronde et donc d'injecter a minima huit fautes pour déterminer la dernière clé de ronde dans son ensemble. Le keyscheduler de l'AES étant réversible, la clé de l'AES peut alors être calculée à partir de la dernière clé de ronde.
4.2 Application à des implémentations logicielles
Injecter une faute sur une implémentation logicielle peut se faire dynamiquement avec un cadriciel d'instrumentation, un débogueur ou un émulateur. Pour les implémentations n'ayant aucune contre-mesure spécifique à l'injection de faute, une simple corruption statique dans les données ou dans le code suffira.
En présence de contrôles d'intégrité, il est souvent plus facile d'ôter ces contrôles et d'injecter statiquement les fautes, car l'exécution ne sera pas ralentie, contrairement aux instrumentations dynamiques qui seront donc réservées aux cas les plus récalcitrants.
Pour injecter une faute statiquement, il suffit de faire une copie du programme ou de ses données et d'en changer un octet. Mais nous préférons éviter de devoir détricoter l'implémentation pour comprendre où injecter correctement la faute. Nous changerons donc chaque octet possible et observerons le résultat. S'il n'y a pas de table de données dans l'implémentation, il faudra corrompre chaque octet du code, ce qui implique pas mal de plantages. Dans ce cas, le plus simple est d'injecter des NOP pour limiter le nombre de plantages et éviter un ralentissement trop important de l’attaque.
À chaque exécution du programme corrompu, la sortie est comparée à la sortie attendue. Il va de soi que le même bloc d'entrée est utilisé pour toutes les exécutions. Plusieurs cas apparaissent alors :
- Le programme se plante ou prend plus de temps qu'attendu ou la sortie ne produit même pas les seize octets de données espérés. Visiblement, cette faute fut un peu trop violente... ;
- La sortie est intacte. La faute a affecté des données ou du code inutilisés. C'est assez courant en injection statique, car, pour un bloc d'entrée donné, une large part de l'implémentation AES n'est pas utilisée ;
- La sortie est complètement modifiée. La faute a probablement été injectée trop tôt (avant l'avant-dernier MixColumns) et les deux derniers MixColumns ont diffusé l'erreur à toute la sortie ;
- La sortie a un seul octet corrompu. La faute a probablement été injectée trop tard (après le dernier MixColumns) ;
- La sortie a exactement quatre octets corrompus. Les données sont probablement exploitables.
Dans ce dernier cas, pour déterminer la colonne dans laquelle la faute a été injectée, il suffit d’observer quels octets de la sortie sont affectés. Reste à savoir précisément dans quel octet de la colonne. Il faut donc considérer les quatre hypothèses possibles lorsqu'on énumère les candidats de clé possibles.
L'avantage du modèle en boîte blanche est qu'une fois qu’un endroit intéressant est repéré, il est aisé d’injecter d'autres fautes exactement au même endroit, ce qui est nettement moins évident lorsqu'on attaque une implémentation matérielle.
Néanmoins, les implémentations logicielles de cryptographie en boîte blanche ont une taille conséquente et corrompre chaque octet individuellement pourrait prendre un temps non négligeable. Cependant, pour une entrée donnée, seule une petite portion des données de l'implémentation sera utilisée. Il est donc plus efficace de modifier de larges portions d'un coup et de concentrer l'attaque aux endroits qui ont donné des résultats intéressants. L'interprétation des résultats est alors adaptée de la manière suivante :
- Si le programme se plante, prend plus de temps que prévu, ou si la sortie est corrompue sur plus de quatre octets : diviser la zone attaquée en deux et en corrompre chaque moitié tour à tour ;
- Si la sortie est intacte ou est affectée sur moins de quatre octets : la zone attaquée peut être complètement ignorée ;
- Si exactement quatre octets de la sortie sont affectés : si la zone attaquée est plus large qu'un octet, le risque subsiste d'avoir corrompu plus d'un octet de la colonne affectée et il vaut mieux également diviser la zone et recommencer.
Cette technique est très rapide sur les implémentations disposant de tables de données brutes, car de larges zones peuvent être modifiées sans plantage. Lorsque les tables contiennent des métadonnées, de larges fautes auront de grandes chances de casser leur structure et il faudra réduire en conséquence la taille des fautes injectées.
Enfin, si nécessaire, cette attaque peut se combiner avec l'analyse visuelle d'une trace telle que décrite plus haut, pour mieux cibler les zones à attaquer.
4.3 Exemples concrets d’attaque par injection de faute
Pareillement aux attaques DCA, parmi les dépôts des SideChannelMarvels, le projet Deadpool contient des exemples d'implémentations de boîte blanche avec les scripts adéquats pour les attaquer par injection de faute. Ils illustrent la stratégie présentée ci-dessus et font usage d'un volume de type tmpfs en RAM pour éviter de trop solliciter le disque dur par les multiples réécritures des implémentations altérées.
Les sorties corrompues collectées sont passées à l'outil JeanGrey qui tente de casser la dernière clé de ronde. En cas de succès, l'outil aes_keyschedule présent dans le projet Stark permet de calculer la clé AES-128 à partir de la dernière clé de ronde.
Voici le résumé de quelques résultats obtenus sur un PC standard, que vous pouvez reproduire à partir du projet Deadpool :
- NSC2013 Variant : une implémentation avec des tables brutes chargées depuis un fichier externe. L'application directe de la DFA sur l'ensemble du fichier externe retrouve la clé en 5,3 s et 420 exécutions.
- Karroumi : l'implémentation est en C++ et les tables sont sérialisées avec la bibliothèque Boost. Il faut donc limiter la taille des fautes à un seul octet à la fois. L’attaque sur l'ensemble des tables prend 162 s et 5 800 exécutions. Si on limite la plage mémoire à attaquer par l'observation d'une trace d'exécution, on arrive à 7 s et 200 exécutions.
- CHES2016 : les tables sont dans le binaire. Avec les paramètres standards, l'attaque échoue. Il y a bien des sorties avec quatre octets corrompus, mais aucune clé ne satisfait les équations de la DFA. Pour passer outre ces faux positifs, l'attaque doit se poursuivre pour acquérir plus de sorties. Par exemple, en cherchant jusqu'à 200 candidats de sortie par colonne, l'attaque réussit en 100 s et 20 000 exécutions.
- PlainCTF2013 : il s'agit d'un déchiffrement AES-128 qui, en outre, vérifie si la sortie semble correcte avant de la montrer. Il faut donc d'abord ôter ce test pour pouvoir observer la sortie. Il n'y a pas de section de données dans le binaire, uniquement du code. On injectera donc des NOP (0x90). La clé est retrouvée en 17 s et 1 000 exécutions, dont la moitié sont des plantages puisque cette approche naïve d'injection ne cherche même pas à remplacer proprement des opcodes complets.
5. Contre-mesures
Les contre-mesures matérielles classiques que sont le masquage par injection d'aléa ou la désynchronisation temporelle s'adaptent mal au modèle en boîte blanche : il n'y a aucune source d'aléas fiable disponible qui ne soit sous le contrôle de l'attaquant et l'observation du flot d'instructions permet de resynchroniser facilement les traces d'exécutions.
Il faut donc chercher la solution dans de nouvelles architectures de boîte blanche nativement immunes à la DCA et à la DFA. Néanmoins, les résultats d'une DCA réussie peuvent aider le concepteur à corriger son algorithme : nous savons sur quel premier échantillon de la trace d'exécution une corrélation est apparue, nous savons également comment nous avons construit cette trace et donc à quelle instruction cet échantillon est lié et, pour peu que le concepteur qui teste son implémentation l'ait compilée avec les informations de débogage, il sera en mesure de mettre le doigt sur la ligne exacte du code source à l’origine de la fuite, et donc de corriger ses contre-mesures.
Se prémunir naïvement des attaques par DFA est assez simple : il faut détecter la faute (par rejeu des derniers rounds, vérification de l'intégrité des tables,...) et éviter que l'attaquant n'ait accès à la sortie corrompue. Encore faut-il le faire de manière suffisamment subtile pour résister à une analyse du code...
Conclusions
Être résistant au modèle d'attaque en boîte blanche implique forcément d'être résistant au modèle en boîte grise. Néanmoins, personne n'a pu créer d'implémentation avec une résistance prouvée mathématiquement. L'avantage des attaques en boîte grise est leur applicabilité avec un minimum d'hypothèses sur l'implémentation attaquée et leur facilité de mise en œuvre, voire leur complète automatisation.
Pour résumer : essayons, on verra bien !
Certains affirment que les bonnes boîtes blanches sont immunes à ces attaques en boîte grise, car leur entrée et leur sortie sont encodées avec un encodage externe inconnu. L'encodage externe signifie simplement que les données n’apparaissent pas en clair au niveau de l’API mais, en général, il faut bien qu’elles le soient ailleurs dans l'application. Le seul encodage externe robuste serait un encodage traité par un serveur distant, à la fois des entrées et des sorties, ce qui est tout simplement impossible lorsque l'application doit suivre les standards cryptographiques utilisés en DRM ou dans le monde bancaire.
Quelques vendeurs de boîtes blanches ont compris la leçon et proposent aujourd'hui des contre-mesures spécifiques à la DCA et à la DFA. Ne vous étonnez donc pas si, bientôt, vous trouvez des implémentations labellisées plus blanches que blanches !
Aller plus loin
Pour celles et ceux qui souhaitent approfondir le sujet, je recommande les ressources suivantes, ainsi que leur bibliographie respective :
- Sur la DCA : J. W. Bos, Ch. Hubain, W. Michiels et Ph. Teuwen, « Design de cryptographie white-box : et à la fin, c’est Kerckhoffs qui gagne », SSTIC 2016, https://frama.link/dca_sstic ;
- Sur la DFA : Ph. Teuwen et Ch. Hubain, « Differential Fault Analysis on White-box AES Implementations », Quarkslab, 2017, https://frama.link/dfa_wbaes ;
- Le projet SideChannelMarvels (https://github.com/SideChannelMarvels) qui contient les outils ainsi qu'une quinzaine d'implémentations de diverses boîtes blanches et une bibliographie des travaux les plus récents dans le domaine (https://frama.link/dca_litterature).
Remerciements
Merci à Guillaume Heilles et Émilien Gaspar pour leur relecture attentive.
Références
[DPA] P. C. Kocher et al., « Differential power analysis », CRYPTO’99
[DFA] P. Dusart et al., « Differential Fault Analysis on A.E.S. », ACNS 2003