L’obfuscation binaire est utilisée pour protéger la propriété intellectuelle présente dans un programme. Plusieurs types d’obfuscations existent, mais grossièrement cela consiste en la modification de la structure du binaire tout en gardant la même sémantique d’origine. Le but étant de faire en sorte que les informations d’origine soient « noyées » dans un surplus d’informations inutiles qui rendra le reverse engineering plus long. Dans ce numéro, nous montrons comment il est possible d'analyser du code obfusqué avec le framework Triton à des fins de gagner du temps.
1. Introduction au framework Triton
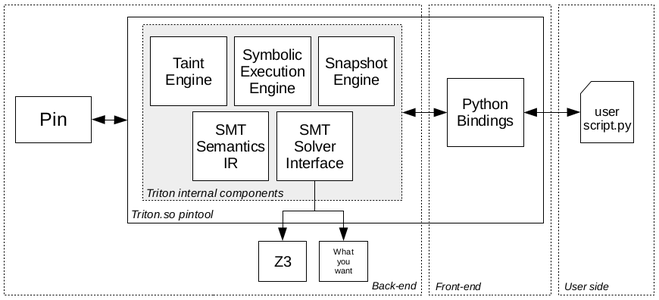
Triton [0] est un framework d'exécution symbolique dynamique (DSE, aussi appelé concolique) qui a été présenté au SSTIC 2015 [1] avec Florent Saudel. Il a été développé pour permettre d’analyser du code dynamiquement que cela soit pour de la recherche de vulnérabilités ou pour apporter une aide au reverse engineering sur du code obfusqué. Triton est constitué de trois grandes « catégories » qui sont :
- L’instrumentation binaire dynamique (DBI) à travers Pin. Son rôle est de récupérer le contexte concret associé à l’instruction courante puis de le transmettre aux engines.
- Les engines réalisent les analyses (analyse par teinte, exécution symbolique, gestion des instantanés et transformation des sémantiques en SMT2-Lib [2]).
- Ainsi qu’une partie bindings qui permet de pouvoir contrôler les engines à travers un langage de haut niveau comme Python.
Les engines sont le cœur de Triton et sont modélisés pour pouvoir communiquer entre eux ainsi qu’être contrôlés par l’utilisateur depuis les bindings Python. La figure 1 illustre le design de Triton dans son ensemble. Certains de ces engines seront décrits dans les prochains chapitres pour une meilleure compréhension du chapitre 2.
Figure 1
1.1. Moteur de teinte
Une analyse par teinte permet de garder une vision sur l’évolution d’une donnée précise durant l’exécution. Généralement, les entrées utilisateur sont marquées comme teintées et le rôle du moteur de teinte est de suivre l’évolution de ces entrées (quelles instructions interagissent avec les entrées, où ces entrées sont-elles stockées et répandues...). Au-delà de suivre l’évolution des données, cette analyse présente quatre intérêts au sein de Triton :
- Intérêt 1 : Son premier rôle est d’aider l’exécution symbolique à décider si la valeur d’une adresse mémoire doit être traitée symboliquement ou concrètement. Typiquement, si l’opérande source d’une instruction n’est pas teintée, la valeur concrète est suffisante. Dans le cas contraire, la valeur actuelle dépend des entrées spécifiées par l’utilisateur. Triton utilise donc la valeur symbolique de l’opérande source.
- Intérêt 2 : Le second rôle est un cas particulier. L'analyse par teinte et l’exécution symbolique travaillent toutes les deux sur les mêmes entrées. Pour la première, elles représentent les sources d’où se propage la teinte. Pour la seconde, ces cases mémoires teintées sont les variables symboliques sur lesquelles l’exécution va porter. L’exécution symbolique va se baser sur la teinte de la mémoire afin de construire les variables symboliques. Une case mémoire teintée, mais inconnue du moteur symbolique est le signe d’une nouvelle entrée, et donc une variable symbolique la représentant doit être créée.
- Intérêt 3 : La teinte peut aussi servir de filtre pour l’exécution symbolique. Au cours d’une trace, un grand nombre d’instructions n’agit pas sur les entrées spécifiées par l’utilisateur (aucune de leurs opérandes ne sont teintées). Ces instructions n’apparaîtront donc jamais dans les contraintes du Path Condition. Il n’est pas utile alors de les exécuter symboliquement. Cette optimisation de l’exécution symbolique grâce à l'analyse par teinte est utilisée au sein de MergePoint [3] et de FuzzWin [4].
- Intérêt 4 : Enfin, la teinte permet tout simplement de suivre visuellement la propagation d'une donnée à travers l'exécution.
Il est facile de pouvoir marquer une donnée comme un registre ou une case mémoire comme teintée depuis les bindings Python. L’API propose des fonctions comme taintReg() ou taintMem(). Ensuite, c’est le rôle du moteur de propager la teinte à travers les registres et la mémoire en se basant sur la sémantique des instructions. Le listing 1 est un exemple de code Triton qui marque tous les octets des arguments de la console lors de l’appel à la fonction main comme étant teintés.
Listing 1 : Teindre les entrées argv
def mainAnalysis(threadId)
rdi = getRegValue(IDREF.REG.RDI) # argc
rsi = getRegValue(IDREF.REG.RSI) # argv
while rdi != 0:
argv = getMemValue(rsi+((rdi-1)*8), 8)
offset = 0
while getMemValue(argv+offset, 1) != 0x00:
taintMem(argv+offset)
offset += 1
print '[+] %03d bytes tainted from the argv [%d] (%#x)' %(offset, rdi-1, argv)
rdi -= 1
return
1.2. Moteur symbolique
Dans le domaine de l’exécution symbolique, il existe deux grands axes qui sont l’exécution symbolique statique (SSE pour Static Symbolic Execution) et l’exécution symbolique dynamique (DSE pour Dynamic Symbolic Execution). Le choix entre le SSE et le DSE va se faire en fonction du type d’analyse que vous effectuez et des informations à disposition. Le SSE est principalement utilisé pour vérifier des propriétés sur un code donné alors que le DSE est utilisé pour la construction des contraintes correspondant au flux de contrôle d’une exécution ainsi que l'évolution d'une variable au sein de cette exécution.
Le rôle d’une exécution symbolique est de produire une formule logique correspondant au programme, à un chemin ou à l'évolution d'une donnée. De façon analogue au calcul formel, celle-ci se base sur des variables symboliques (ou symboles). Ici, le mot variable prend le sens mathématique. Elle représente une inconnue dans une formule. Autrement dit, c’est une variable « libre » et peut donc être substituée par n’importe quelle valeur.
Le rôle du moteur symbolique est de créer et de conserver toutes les expressions symboliques puis d’établir des liens entre les expressions et les registres/mémoire pour chaque point du programme. Chaque expression symbolique possède un ID unique (référence symbolique) qui lui est propre.
L'entrée symbolique est matérialisée par le couple <ID : Expr> qui est conservé dans un set d’expressions globales. Une expression peut contenir des références vers d’autres expressions, ceci nous permet de garder les expressions sous une forme SSA (Static Single Assignment) [5].
Le listing 2 illustre la représentation SMT2-Lib d'une expression pour une addition de deux registres. Les références #40 et #39 représentent les dernières expressions assignées aux registres RAX et RDX. La référence #41 représente la nouvelle expression du registre RAX après l'exécution de cette instruction.
Listing 2 : Expression SMT2-Lib de l'instruction ADD
Instruction: add rax, rdx
Expressions: #41 = (bvadd ((_ extract 63 0) #40) ((_ extract 63 0) #39))
1.3. Représentation des sémantiques en SMT2-Lib
Le langage SMT-Lib version 2 (que nous appelons SMT2-Lib) est la poursuite d’une initiative internationale visant à faciliter la recherche et le développement sur le problème de Satisfaisabilité Modulo Théorie (SMT). Cette nouvelle version est supportée par un bon nombre d’SMT solvers. De ce fait, traduire nos sémantiques et contraintes dans ce langage plutôt que d’utiliser l’interface C++ de Z3, permet par la suite de pouvoir utiliser n’importe quel SMT solver supportant cette norme.
1.4. Arbre syntaxique abstrait des expressions symboliques
Triton transforme chaque instruction assembleur en une liste d’une ou plusieurs expressions SMT2-Lib. Ce langage et son intérêt sont présentés dans le paragraphe précédent 1.3. Une formule SMT2-Lib est une S-expression, sa syntaxe ressemble fortement au langage Lisp ou Scheme. Toutes les opérations sont préfixées et une expression bien formée est comprise dans des parenthèses.
Chaque formule dispose d’un identifiant unique (ID) la représentant. Si une formule A dépend de la valeur d’une formule B, elle utilisera l’ID de B en lieu et place de l’autre formule. Ce principe de l’identifiant unique provient du SSA. Dans la suite de ce document, nous appellerons ces formules ainsi que cette représentation intermédiaire, « SSA-expression ».
Pour pouvoir manipuler ces expressions plus facilement, toutes les expressions sont manipulables par le biais d’un AST (Abstract Syntax Tree). Prenons comme exemple la portion de code assembleur du listing 3.
Listing 3 : Portion de code assembleur
1. mov al, 1
2. mov cl, 10
3. mov dl, 20
4. xor cl, dl
5. add al, cl
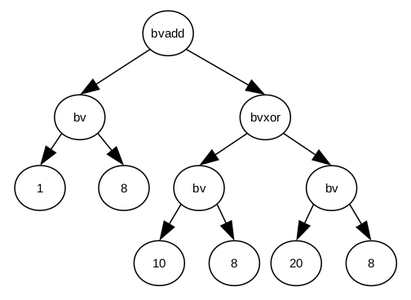
À la ligne 5, l’AST du registre AL est illustré par la figure 2. Cet AST représente la sémantique du registre AL en partant du point de programme 1 → 5.
Figure 2
Depuis l’API Python, il est possible de créer et de modifier des nœuds de l’AST. Le listing 4 illustre cette fonctionnalité.
Listing 4 :Manipulation de l'AST d’une expression
# Node information
[IN] node = bvadd(bv(1, 8), bvxor(bv(10, 8), bv(20, 8)))
[IN] print type(node)
[OUT] <type 'SmtAstNode'>
[IN] print node
[OUT] (bvadd (_ bv1 8) (bvxor (_ bv10 8) (_ bv20 8)))
[IN] subchild = node.getChilds()[1].getChilds()[0]
[IN] print subchild
[OUT] (_ bv10 8)
[IN] print subchild.getChilds()[0].getValue()
[OUT] 10
[IN] print subchild.getChilds()[1].getValue()
[OUT] 8
# Node modification
[IN] node = bvadd(bv(1, 8), bvxor(bv(10, 8), bv(20, 8)))
[IN] print node
[OUT] (bvadd (_ bv1 8) (bvxor (_ bv10 8) (_ bv20 8)))
[IN] node.setChild(0, bv(123, 8))
[IN] print node
[OUT] (bvadd (_ bv123 8) (bvxor (_ bv10 8) (_ bv20 8)))
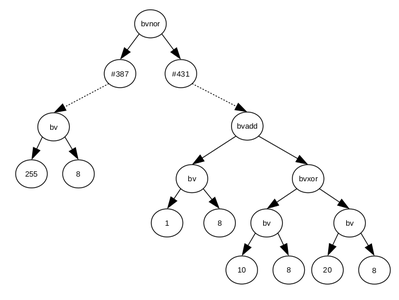
Il faut également noter que dans le cadre de Triton, la grammaire du SMT2-Lib pour l’AST a été légèrement modifiée. Les nœuds de type REFERENCE ont été rajoutés. Ceci nous permet de traiter les sous-graphes plus facilement et indépendamment des graphes parents en accord avec le SSA. Les nœuds de type REFERENCE sont des terminaisons, mais font référence à un sous-graphe. La figure 3 illustre ce procédé.
Figure 3
Étant donné qu’un nœud de type REFERENCE est une terminaison, l’API propose des fonctionnalités permettant de reconstruire le graphe complet d’une expression contenant des références. Pour cela, Triton parcourt l’expression initiale et remplace récursivement tous les nœuds de type REFERENCE par leurs graphes respectifs. Le listing 5 suivant illustre une reconstruction de graphe depuis l’API.
Listing 5 : Reconstruction d’un graphe contenant des nœuds de REFERENCE
[IN] zfId = getRegSymbolicID(IDREF.FLAG.ZF)
[IN] partialGraph = getSymExpr(zfId).ast
[IN] print partialGraph
[OUT] (ite (= #89 (_ bv0 32)) (_ bv1 1) (_ bv0 1))
[IN] fullGraph = getFullExpression(partialGraph)
[IN] print fullGraph
[OUT] (ite (= (bvsub ((_ extract 31 0) ((_ zero_extend 32) ((_ extract 31 0) ((_ zero_extend 3
0) ((_ zero_extend 32) (bvsub ((_ extract 31 0) ((_ zero_extend 32) ((_ sign_extend 24) ((_ ex
_ bv1 32)))) (_ bv85 32)))))) ((_ extract 31 0) ((_ zero_extend 32) ((_ sign_extend 24) ((_ ex
d 32) ((_ zero_extend 24) ((_ extract 7 0) (_ bv49 8))))))))) (_ bv0 32)) (_ bv1 1) (_ bv0 1))
2. O-LLVM
Dans ce chapitre, nous montrerons comment il est possible d’utiliser Triton pour pouvoir repérer et isoler les informations recherchées sans se préoccuper de l’obfuscation. L’obfuscation utilisée comme base d’exemple est la solution gratuite d'Obfuscator-LLVM [6]. O-LLVM travaille sur l'IR LLVM et propose trois types de passe :
- Une passe dite de Substitution qui remplace la forme normale d'une opération logique par une opération bit à bit [7].
- Une passe dite de Bogus Control Flow qui rajoute des basic blocks avant les basic blocks d'origine et met en place des prédicats opaques pour pointer vers les basic blocks d'origine [8].
- Une passe dite de Control Flow Flattening qui aplatit le graphe de flot de contrôle (CFG) [9, 10].
Pour illustrer au plus simple les fonctionnalités implémentées dans Triton à des fins d'aider un analyste lors d’un binaire obfusqué, nous avons compilé un simple binaire contenant toutes les options d’O-LLVM (-mllvm -sub -mllvm -fla -mllvm -bcf). Le binaire compilé attend un mot de passe valide et son CFG est illustré par la figure 4.
Figure 4
Notez que l'analyse des protections d'O-LLVM a déjà fait l'objet d'un article [19] par Francis Gabriel et Camille Mougey. Elle a été faite statiquement en utilisant le framework Miasm [20]. Nous proposons donc une autre approche basée sur l'analyse dynamique (les deux étant complémentaires).
2.1. Repérer le point d’entrée de ses données
Le reverse engineering est principalement axé sur de la recherche d’informations ainsi que la compréhension de comment sont traitées ces informations. L’obfuscation de code est justement là pour faire en sorte que ces deux principes soient les plus difficiles possible.
L’une des premières choses à faire est donc de repérer les données utilisateur. Ceci permet d’avoir un point d’entrée d’analyse sur ce qui est réellement intéressant. On sait que les données provenant de l’utilisateur sont, au premier contact, traitées en clair depuis la mémoire. De ce fait, nous avons développé un outil [11] Triton permettant de lister tous les accès mémoire et ainsi récupérer la première instruction qui va récupérer les données utilisateur - ce qui nous donne un point d’entrée d’analyse.
Le listing 6 illustre la sortie de l’outil. L’entrée A (0x41) est envoyée à la target et comme on peut le constater, l’instruction 0x4008c1 est la première instruction à traiter cette entrée. On peut désormais commencer notre analyse à partir de cette adresse. Par expérience, cette méthode de recherche est utile dans les binaires effectuant du trafic réseau ou du parsing.
Listing 6 : Trace mémoire avec Triton
$ ./triton ./memory_tracer.py ./target A
[...]
[W:4] 0x4007e4: mov dword ptr [rbp-0xb8], eax
W:0x7fff659e4a28: 00 00 00 00 (0x0)
[R:4] 0x4008b9: movsxd rdi, dword ptr [rbp-0x44]
R:0x7fff659e4a9c: 00 00 00 00 (0x0)
[R:8] 0x4008bd: mov r8, qword ptr [rbp-0x40]
R:0x7fff659e4aa0: 8d 50 9e 65 ff 7f 00 00 (0x7fff659e508d)
[R:1] 0x4008c1: movsx r9d, byte ptr [r8+rdi*1]
R:0x7fff659e508d: 41 (0x41)
[R:4] 0x400915: movsxd rdi, dword ptr [rbp-0x44]
R:0x7fff659e4a9c: 00 00 00 00 (0x0)
[R:8] 0x400919: mov r8, qword ptr [0x602040]
R:0x000000602040: 54 16 40 00 00 00 00 00 (0x401654)
[R:1] 0x400921: movsx esi, byte ptr [r8+rdi*1]
R:0x000000401654: 31 (0x31)
[...]
2.2. Isoler et suivre ses données avec une analyse par teinte
Repérer la première instruction qui traite l’entrée utilisateur est une chose, mais isoler toutes les instructions qui ont un lien avec l’entrée utilisateur en est une autre. Pour pouvoir suivre les données utilisateur à travers l’exécution, Triton met à disposition un moteur de teinte.
Une analyse par teinte permet justement de marquer une donnée à un instant T, puis, basé sur la sémantique de chaque instruction, le marqueur est répandu à travers l’exécution dans les registres et la mémoire. Dans le cadre d’un binaire obfusqué, cette méthode apporte un gain de temps d’analyse précieux.
Une analyse par teinte est bien souvent utile lors d’une passe d’analyse statique. Cela permet de cibler visuellement les instructions ayant une interaction avec l’entrée utilisateur. Pour pouvoir travailler sur une trace de façon offline, nous avons donc développé un outil [12] Triton permettant de sauvegarder tout le contexte d’exécution d’une trace dans une base de données. La structure de la base de données est illustrée par le listing 7.
Listing 7 :Base de données sur le contexte d’exécution d’une trace
> sqlite3 ./trace.db
sql> .schema
CREATE TABLE instructions(
addr INTEGER,
assembly TEXT,
exprs TEXT);
CREATE TABLE expressions(
id INTEGER PRIMARY KEY,
addr INTEGER,
expr TEXT,
tainted BOOL);
CREATE TABLE memoryAccess(
addr INTEGER,
accessType TEXT,
accessSize INTEGER,
accessAddr INTEGER,
contentAsString TEXT,
contentAsInteger INTEGER);
CREATE TABLE registersValue(
addr INTEGER,
id INTEGER,
name TEXT,
size INTEGER,
content INTEGER);
sql>
Après avoir teinté le point d’entrée utilisateur (chapitre 2.1), une base de données est créée contenant toutes les informations concernant la trace, y compris les expressions pouvant être contrôlées par l’utilisateur (listing 8).
Listing 8 : Expressions contrôlables par l'utilisateur
sql> select count(DISTINCT addr) from expressions where tainted=1;
15
sql> select * from expressions where tainted=1;
1902|4196550|((_ zero_extend 32) (bvsub ((_ extract 31 0) #1900) (_ bv735012004 32)))|1
1903|4196550|(ite (= (_ bv16 32) (bvand (_ bv16 32) (bvxor ((_ extract 31 0) #1902) (bvxor ((_ extract 31 0) #1900) (_ bv735012004 32))))) (_ bv1 1) (_ bv0 1))|1
[...]
sql>
Le fait d’avoir une base de données contenant les informations du contexte d’exécution permet d’apporter une aide au reverse engineering. Un plugin IDA a été développé permettant de coupler les informations dynamiques de Triton avec celles statiques d’IDA, comme afficher la teinte, la valeur des registres à chaque instruction, la couverture de code, etc.
Comme on peut le constater avec la figure 5, une analyse par teinte permet de rapidement isoler les instructions qui nous intéressent. On constate également que malgré l’obfuscation le data flow n’est pas répandu à travers tous les basic blocks, ce qui nous permet de cibler l’analyse symbolique plus facilement.
Figure 5
2.3. Résolution symbolique
Après avoir isolé la portion de code ayant une interaction avec l’entrée utilisateur (listing 9), une exécution symbolique peut être appliquée sur cette portion de code en partant du point d’entrée utilisateur comme variable symbolique jusqu’à la contrainte souhaitée.
Listing 9 : Portion de code issue de l'analyse par teinte
.text:00000000004008C1 movsx r9d, byte ptr [r8+rdi]
.text:00000000004008C6 sub r9d, 2BCF64A4h
.text:00000000004008CD sub r9d, 1
.text:00000000004008D4 add r9d, 2BCF64A4h
.text:00000000004008DB mov r10d, r9d
.text:00000000004008DE xor r10d, 0FFFFFFFFh
.text:00000000004008E5 and r10d, 0C764C206h
.text:00000000004008EC mov r11d, esi
.text:00000000004008EF xor r11d, 0C764C206h
.text:00000000004008F6 and r9d, r11d
.text:00000000004008F9 xor esi, 55h
.text:00000000004008FF and esi, 0C764C206h
.text:0000000000400905 and r11d, 55h
.text:000000000040090C or r10d, r9d
.text:000000000040090F or esi, r11d
.text:0000000000400912 xor r10d, esi
.text:0000000000400915 movsxd rdi, [rbp+index]
.text:0000000000400919 mov r8, serial
.text:0000000000400921 movsx esi, byte ptr [r8+rdi]
.text:0000000000400926 cmp r10d, esi
L’exécution symbolique nous permet de pouvoir résoudre une ou des contraintes (ici chaque caractère du mot de passe) sans devoir se préoccuper de comprendre la sémantique du programme - ce qui, dans un contexte d’obfuscation, est un gain de temps pour l’analyste.
Triton a justement été conçu pour pouvoir appliquer une analyse symbolique entre deux points. Pour cela, il faut dans un premier temps déclarer une variable symbolique en premier point (listing 10), puis créer une contrainte en deuxième point (listing 11) et enfin demander un modèle au solver satisfaisant la contrainte (listing 12).
Listing 10 : Création d'une variable symbolique sur le registre R9
if instruction.getAddress() == 0x4008C1:
convertRegToSymVar(IDREF.REG.R9, 64)
Listing 11 : Création d'une contrainte sur le flag ZF
if instruction.getAddress() == 0x400926:
zfId = getRegSymbolicID(IDREF.FLAG.ZF)
zfExpr = getFullExpression(getSymExpr(zfId).getAst())
# zf == 1
constraint = smt2lib.smtAssert(
smt2lib.equal(
zfExpr,
smt2lib.bvtrue()
)
)
Listing 12 : Récupération d'un modèle
model = getModel(constraint)['SymVar_0']
print ctypes.c_int32(model)
Le modèle obtenu correspond au premier caractère du mot de passe attendu. En répétant cette opération pour chacun des caractères ou de façon automatique en utilisant le moteur de rejeu [13], le mot de passe attendu est découvert en très peu de temps (moins d’une seconde). Cette opération peut également être appliquée sur des fonctions de hachage simples [14].
2.4. Analyse de la passe de Substitution
Bien souvent, sur du code obfusqué, résoudre des contraintes symboliques pour prendre des branches spécifiques, récupérer des clefs ou même générer des collisions n’est pas forcément le but recherché dans tous les cas. Dans certaines situations, il serait intéressant de récupérer les algorithmes d’origine et donc simplifier les expressions obfusquées.
Il existe plusieurs méthodes permettant de masquer une opération logique. La plus répandue est l’opération bit à bit (bitwise operation [15], voir également le listing 13), mais il existe aussi des opérations plus complexes comme les MBA (Mixed Boolean-Arithmetic) [16].
Dans le cadre d’O-LLVM, les opérations logiques sont transformées en opération bit à bit. Pour pouvoir simplifier les expressions, il faut dans un premier temps isoler les patterns atomiques représentant une opération bit à bit. Une fois le pattern isolé, le but est d’avoir une transformation qui prend en entrée l’arbre du pattern et qui renvoie un nouvel arbre simplifié. Pour chacune des transformations, il est nécessaire de prouver que le résultat de l’arbre de sortie est égal au résultat de l’arbre d’entrée pour tout x dans ℤ.
Listing 13 : Opérations bit à bit possibles pour un xor [17]
a ⊕ b = (a ∧ ¬b) ∨ (¬a ∧ b)
a ⊕ b = ((a ∧ ¬b) ∨ ¬a) ∧ ((a ∧ ¬b) ∨ b)
a ⊕ b = ((a ∨ ¬a) ∧ (¬b ∨ ¬a)) ∧ ((a ∨ b) ∧ (¬b ∨ b))
a ⊕ b = (¬a ∨ ¬b) ∧ (a ∨ b)
a ⊕ b = ¬(a ∧ b) ∧ (a ∨ b)
En reprenant le code du listing 9 et ayant extrait l’expression symbolique avec Triton, nous obtenons l’expression obfusquée suivante :
Listing 14 : Formule extraite du listing 9
e = (((((((SymVar_0 − 735012004) − 1) + 735012004) ⊕ 18446744073709551615) ∧ 18446744072759853574) ∨ ((((SymVar_0 − 735012004) − 1) + 735012004) ∧ (4294967295 ⊕ 18446744072759853574))) ⊕ (((4294967295 ⊕ 85) ∧ 18446744072759853574) ∨ ((4294967295 ⊕ 18446744072759853574) ∧ 85)))
Dans cette expression, plusieurs patterns peuvent être isolés. Le pattern le plus facile à isoler est (a − b) − 1) + b) et peut être transformé par l’opération (a − 1) (preuve 1).
Preuve 1 : (a − b) − 1) + b) = (a − 1)
>>> a,b,c = BitVecs('a b c', 64)
>>> e1 = (c == ((a-b)-1)+b)
>>> e2 = (c == (a-1))
>>> prove(e1 == e2)
proved
Ce qui, une fois remplacé, donne l’expression illustrée par la figure 6. Pour une meilleure visibilité, l’expression est découpée en deux parties. On sait également que les expressions de type a ⊕ UINT64_MAX peuvent être transformées par ¬a (preuve 2).
Figure 6
Preuve 2 : (a ⊕ UINT64_MAX) = ¬a
>>> a,b = BitVecs('a b', 64)
>>> e1 = (b == a^0xffffffffffffffff)
>>> e2 = (b == ~a)
>>> prove(e1 == e2)
proved
Une fois cette transformation effectuée, nous pouvons constater que dans chacune de ces deux parties, le pattern suivant : (¬a∧b)∨(a∧¬b) revient deux fois. Soit l’expression complète suivante : (¬a∧b)∨(a∧¬b)⊕(¬c∧b)∨(c∧¬b).
Le pattern de chaque partie est une opération bit à bit du ⊕ (cf. première opération du listing 13). Chaque partie peut donc être transformée par a ⊕ b (preuve 3).
Preuve 3 : (¬a ∧ b) ∨ (a ∧ ¬b) = (a ⊕ b)
>>> a,b,c = BitVecs('a b c', 64)
>>> e1 = (c == ((~a & b) | (a & ~b)))
>>> e2 = (c == (a ^ b))
>>> prove(e1 == e2)
proved
Une fois cette transformation appliquée, nous obtenons l’expression suivante : (a⊕b) ⊕ (c⊕b), qui peut se traduire par a ⊕ c (preuve 4).
Preuve 4 : (a ⊕ b) ⊕ (c ⊕ b) = (a ⊕ c)
>>> a,b,c,d = BitVecs('a b c d', 64)
>>> e1 = (d == ((a ^ b) ^ (c ^ b)))
>>> e2 = (d == a ^ c)
>>> prove(e1 == e2)
proved
Ce genre de transformation est bien connu des SMT solvers et peut donc être simplifié facilement sans avoir besoin d’effectuer du pattern matching (simplification 1).
Simplification 1 : (a ⊕ b) ⊕ (c ⊕ b) −→ (a ⊕ c)
>>> a,b,c,d = BitVecs('a b c d', 64)
>>> e1 = (d == ((a ^ b) ^ (c ^ b)))
>>> simplify(e1)
d == a ^ c
On peut donc conclure que l’expression obfusquée du listing 9 peut être simplifiée par l’expression ((SymVar0 − 1) ⊕ 85).
Dans le cadre d’O-LLVM, la forme normale des opérations bit à bit sont connues [18] et peuvent donc être facilement isolées, puis simplifiées via du pattern matching depuis un AST.
Le scénario le plus compliqué est celui où la forme normale de l’opération bit à bit n’est pas connue. C’est justement les recherches d’Adrien Guinet qui travaille sur le calcul symbolique bit à bit d’opérations arithmético-booléennes. En les simplifiant dans un espace particulier, il est possible d’identifier assez facilement des opérations booléennes pures. En ce qui concerne les opérations arithmétiques, grâce à certaines heuristiques, il est possible de retrouver des versions potentiellement plus « compréhensibles » que la version originale.
2.5. Analyse de la passe de Graph Flattening
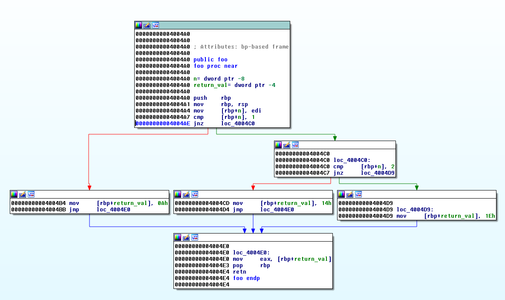
L'aplatissement de graphe (graph flattening) est une protection contre l'analyse statique couramment rencontrée. Elle consiste à « étaler » les basic blocks pour que leurs relations ne soient plus visibles. Pour mieux comprendre son fonctionnement, prenons le code du listing 15. Son CFG est illustré par la figure 7.
Figure 7
Listing 15 : Exemple de code
int foo(int n)
{
int val;
/* Basic block 0 */
if (n == 1)
/****************/
/* basic block 1 */
val = 10;
/****************/
/* basic block 2 */
if (n == 2)
/*****************/
/* basic block 3 */
val = 20;
/****************/
/* basic block 4 */
val = 30;
/****************/
/* basic block 5 */
return val;
/****************/
}
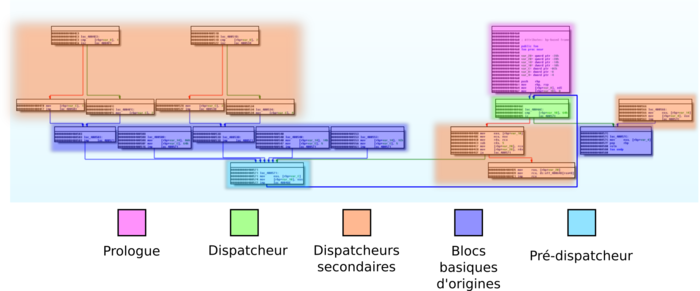
L’aplatissement de graphe va modifier le CFG de telle manière que les relations entre les différents basic blocks, ne soient plus explicites. Pour cela, le graphe va être transformé en ce qui s'apparente à une machine d'état. Le code du graphe transformé pourrait ressembler au listing 16 et dont le graphe est illustré par la figure 8 :
Listing 16 : Exemple de graph flattening du Listing 15
#define END_STATE 100
int foo(int n) {
int next_state, current_state;
int return_value;
current_state = 0;
while(current_state != END_STATE) {
switch(current_state){
case 0: //basic block 0
if (n == 1)
next_state = 1;
else
next_state = 2;
break;
case 1: //basic block 1
return_value = 10;
next_state = END_STATE;
break;
case 2: //basic block 2
if (n == 2)
next_state = 3;
else
next_state = 4;
break;
case 3: //basic block 3
return_value = 20;
next_state = 5;
break;
case 4: //basic block 4
return_value = 30;
next_state = 5;
break;
case 5: //basic block 5
return return_value;
next_state = END_STATE;
break;
}
current_state = next_state;
}
}
Figure 8
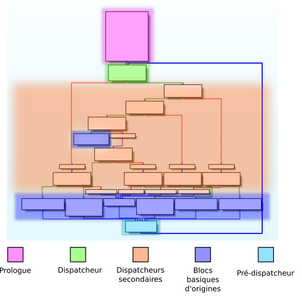
Généralement, le CFG ressemble à un grand switch dont les valeurs possibles sont les états et dont le contenu représente les basic blocks d'origines.
Dans le cas du graph flattening d'O-LLVM, la transition entre les états n'est pas aussi simple que l'exemple du listing 16, mais le principe reste le même. On le voit à travers son graphe (figure 8) qui a une même structure que le graphe de la figure 9, l'utilisation du moteur d’exécution symbolique et de teinte de Triton peut nous permettre de retrouver les relations entre les basic blocks de la manière suivante :
- Au début du programme, nous teintons ses entrées. Cela peut être des arguments, un fichier, un appel système, etc.
- Ensuite, nous continuons l’exécution du programme jusqu’à être dans un basic block du graphe d'origine - notez que nous partons du principe que nous avons identifié les basic block du programme d'origine (ou du moins une partie) et que nous recherchons uniquement leurs relations.
- Dans un basic block identifié, si une instruction fait appel à un contenu teinté (adresse mémoire ou registre) alors nous le convertissons en variable symbolique. Cela permet de ne pas faire d'exécution symbolique sur l'ensemble du programme, mais uniquement sur les parties intéressantes. De cette manière, la taille de l'expression symbolique est réduite et est plus simple à analyser.
- À la fin du basic block, nous demandons tous les états possibles en fonction des variables symboliques. Comme à un état correspond à un basic block, nous avons donc les relations recherchées. Les conditions étant les valeurs des variables symboliques, pour retrouver la correspondance entre un état et un basic block, on peut utiliser le moteur de snapshot de Triton. Ce qui nous permet d'injecter au début du programme l'état en question et nous regardons sur quel basic block nous arrivons.
Figure 9
2.6. Analyse de la passe de Bogus Control Flow
Le Bogus Control Flow est aussi une protection contre l'analyse de code statique. Elle consiste à ajouter des basic blocks qui ne seront jamais atteints au cours de l’exécution du programme. Mélangé avec les basic blocks du graphe original, il est difficile de distinguer ceux qui peuvent être exécutés de ceux qui ne le seront pas. Concrètement, O-LLVM insert un prédicat opaque qui sera utilisé pour faire un saut conditionnel. Comme ce prédicat a une valeur constante (vraie ou fausse) et indépendante des entrées du programme, l'adresse de l'instruction après l'exécution du saut sera toujours constante.
Ce prédicat est construit à l'aide de deux variables, X et Y. Comme dans le binaire il y a du graph flattening, il n'y aura pas de saut vers une adresse, mais un changement d'état. Regardons le cas du basic block à l'adresse 0x400816 (figure 10).
Figure 10
On voit que deux états sont utilisés, mais un des deux ne sera jamais placé dans la variable d'état. La condition se fait à travers l'instruction CMOVNZ qui place dans EAX, l'état 2 (0x7d094355) si R15B est différent de 1 sinon l'état 1 (0x621af252). R15B contient donc la formule du prédicat opaque et EAX l'état. On peut donc faire une exécution symbolique sur les registres EDI et R8D qui contiennent les variables X et Y puis regarder si une solution existe pour que EAX soit égale à l’état 1 ou 2. Puisqu'il s'agit d'un prédicat opaque, seul un des 2 états aura une solution.
Voici comment Triton peut nous aider à analyser ces blocks. Nous définissons l'adresse des deux variables X et Y (listing 17).
Listing 17 : Définition des adresses des variables X et Y
X_ADDR = 0x60204C
Y_ADDR = 0x602050
Puis nous définissons la liste des adresses des basic blocks à analyser (listing 18).
Listing 18 : Définition de la liste des basic blocks
BB_LIST = [
0x400C9B, 0x400B5D, 0x400B51, 0x4007FA,
0x4009C3, 0x4009F1, 0x4007F5, 0x4008A8,
0x4009DE, 0x400816, 0x400CAD, 0x400AAE,
0x400CB9, 0x400A12, 0x400BF9, 0x400CCC]
Enfin, nous spécifions l'adresse du pré-dispatcheur, car on est sûr que dans ce basic block l'état a été calculé (listing 19).
Listing 19 : Définition de l'adresse du pré-dispatcheur
END_BLOCK = 0x400CD3
enabled = False
enabled est une variable pour indiquer si nous sommes dans un basic block modifié par le Bogus Control Flow.
La première callback de type AFTER (appelée après une instruction) sert à convertir les registres utilisés pour contenir les variables X et Y en variables symboliques (listing 20).
Listing 20 : Conversion des registres en variables symboliques
def cafter(instruction):
global enabled
if len(instruction.getOperands()) == 2 and \
instruction.getOperands()[1].getType() == IDREF.OPERAND.MEM_R and \
(instruction.getOperands()[1].getMem().getAddress() == X_ADDR or instruction.getOperands()[1].getMem().getAddress() == Y_ADDR):
reg = instruction.getOperands()[0].getReg()
convertRegToSymVar(reg.getId(), 64)
enabled = True
return
La condition dans le if vérifie que l'instruction lit la mémoire à l'adresse d'une des deux variables. De plus, comme le basic block fait appel aux variables X et Y, nous sommes en présence du Bogus Control Flow et nous activons la variable enabled.
La seconde callback de type BEFORE (appelée avant une instruction) va nous servir à déterminer quel état ne sera jamais utilisé (listing 21).
Listing 21 : Détermination des 2 états possibles
def cbefore(instruction):
global enabled
if instruction.getAddress() in BB_LIST:
print "Dans le basic block", hex(instruction.getAddress())
if instruction.getAddress() == END_BLOCK and enabled:
EtatSymId = getRegSymbolicID(IDREF.REG.RAX)
node = getFullExpression(getSymExpr(EtatSymId).getAst())
state1, state2 = getStates(node)
EtatSymId contient l'identifiant de l'expression symbolique. GetFullExpression va nous retourner l'expression SMT complète et GetState va parser l'AST pour extraire les deux états possibles. On remarquera l'utilisation de l'expression symbolique contenue dans RAX et pas celle contenue dans la variable etat. Cela ne nuit pas à la généralité puisque dans tous les basic blocks, l'état est dans le registre EAX avant d'être mis en mémoire.
Ensuite, il faut déterminer quel état ne sera jamais utilisé. Pour cela, on essaye de résoudre l’équation pour les deux états possibles. S'il n'y a pas de solution, c'est que cet état est inaccessible (listing 22).
Listing 22 : Détermination de l'état inaccessible
expr = smt2lib.smtAssert(smt2lib.equal(node, smt2lib.bv(state1, 32)))
modelsState1 = getModel(expr)
expr = smt2lib.smtAssert(smt2lib.equal(node, smt2lib.bv(state2, 32)))
modelsState2 = getModel(expr)
if len(modelsState1) > 0 and len(modelsState2) == 0:
print "L'Etat 0x%x ne peut pas etre atteint"%(state2)
if len(modelsState1) == 0 and len(modelsState2) > 0:
print "L'Etat 0x%x ne peut pas etre atteint"%(state1)
En faisant appel à la correspondance entre état et basic block, on trouve ainsi les basic blocks inaccessibles.
Dernière chose, on concrétise tous les registres et toutes les adresses mémoires afin de ne pas avoir des expressions symboliques en cascade (listing 23).
Listing 23 : Concrétisation des registres et de la mémoire
concretizeAllMem()
concretizeAllReg()
enabled = False
L’exécution de ce script [21] sur le binaire donne le résultat illustré par le listing 24.
Listing 24 : Exemple d'exécution
$ ./triton ./ollvm/bcf.py ./samples/ollvm/crackme_xor_sub_fla_bcf e#####
Dans le basic block 0x4007fa
Dans le basic block 0x400816
L'Etat 0x621af252 ne peut pas etre atteint
Dans le basic block 0x4008a8
L'Etat 0x621af252 ne peut pas etre atteint
Dans le basic block 0x4009c3
Dans le basic block 0x4009f1
Dans le basic block 0x4007fa
Dans le basic block 0x400816
L'Etat 0x621af252 ne peut pas etre atteint
Dans le basic block 0x4008a8
L'Etat 0x621af252 ne peut pas etre atteint
Dans le basic block 0x4009c3
Dans le basic block 0x4009de
Dans le basic block 0x400b5d
L'Etat 0x97eecfa1 ne peut pas etre atteint
Dans le basic block 0x400bf9
L'Etat 0x97eecfa1 ne peut pas etre atteint
Dans le basic block 0x400c9b
loose
[+] Fin de l'analyse!
Le résultat précédent ne donne pas une liste exhaustive des états inaccessibles, mais seulement ceux qui ont été rencontrés lors de l'exécution. Une exécution avec d'autres entrées (dans notre cas d'autres arguments) peut donner davantage (ou moins) d’états inaccessibles.
Comme ces protections sont contre l'analyse statique, il est « normal » que l'analyse dynamique en vienne à bout. Néanmoins, contrairement à l'analyse statique, l'analyse dynamique ne permet pas d'être exhaustive puisque son analyse repose sur une trace d’exécution. Par contre, elle permet d'avoir accès au contexte et donc de cibler ainsi que d'analyser plus facilement certaines parties du programme.
Conclusion
Triton est un framework d'analyse binaire qui propose des composants supplémentaires au framework Pin permettant ainsi d'apporter une aide lors de reverse engineering. Dans ce numéro, nous avons essayé de montrer un cas d'utilisation de Triton pour analyser du code obfusqué, mais il est également possible d'utiliser Triton pour du debug ou de la recherche de vulnérabilités.
Notez que la protection analysée (O-LLVM) est une protection publique ce qui rend plus facile la déobfuscation. En effet, le réel challenge pour une protection est de rendre public son fonctionnement tout en gardant une difficulté d'analyse conséquente. Il faut également prendre conscience qu'une protection n'est pas là pour empêcher une analyse, mais seulement pour la ralentir. Si nous prenons l'exemple des jeux vidéo et que nous partons du principe que le plus grand bénéfice pour l'éditeur est pendant la première semaine de la sortie du jeu, il faut que la protection tienne au moins une semaine et que l'argent dépensé dans cette protection soit proportionnel aux bénéfices perçus.
Remerciements
High five à Aurélien Wailly pour son invitation à écrire dans ce numéro.
Références
[0] http://triton.quarkslab.com
[1] https://www.sstic.org/2015/presentation/triton_dynamic_symbolic_execution_and_runtime_analysis/
[3] Thanassis Avgerinos, Alexandre Rebert, Sang Kil Cha, and David Brumley. Enhancing symbolic execution with veritesting.
[4] https://github.com/piscou/FuzzWin/
[5] https://en.wikipedia.org/wiki/Static_single_assignment_form
[7] https://github.com/obfuscator-llvm/obfuscator/wiki/Instructions%20Substitution
[8] https://github.com/obfuscator-llvm/obfuscator/wiki/Bogus%20Control%20Flow
[9] https://github.com/obfuscator-llvm/obfuscator/wiki/Control%20Flow%20Flattening
[10] T László and Á Kiss, Obfuscating C++ programs via control flow flattening, Annales Univ. Sci. Budapest., Sect. Comp. 30 (2009) 3-19.
[11] http://triton.quarkslab.com/documentation/tools/#3
[12] http://triton.quarkslab.com/documentation/tools/#4
[13] http://triton.quarkslab.com/documentation/examples/#10
[14] http://triton.quarkslab.com/blog/first-approach-with-the-framework/#5.2
[15] http ://en.wikipedia.org/wiki/Bitwise_operation
[16] Yongxin Zhou, Alec Main, Yuan Xiang Gu, and Harold Johnson. Information hiding in software with mixed boolean-arithmetic transforms
[17] http://en.wikipedia.org/wiki/Exclusive_or
[19] http://blog.quarkslab.com/deobfuscation-recovering-an-ollvm-protected-program.html