Dès 2007, avec l'apparition des premiers clusters de PS3, les GPU se sont imposés comme les nouvelles plateformes reines du cassage de mot de passe grand public. Quatre ans plus tard, pourtant, les techniques de cassage GPU mises en œuvre publiquement restent rustiques et les subtilités déployées dans les outils de cassage sur CPU ne se retrouvent pas sur ces nouvelles plateformes. À travers l'exemple de l'outil crackNfast, dévoilé au SSTIC 2011, nous verrons dans cet article qu'une réelle marge de progression peut être franchie en combinant des techniques déjà connues avec la puissance des GPU.
1. De l'intérêt des Rainbow Tables
1.1. Concept macroscopique
L'utilisation de « Rainbow Tables », technique mise au point par Philippe Oechslin en 2003, est aujourd'hui bien connue de ceux qui ont, un jour ou l'autre, voulu casser un hash de mot de passe. D'un point de vue très macroscopique, cette technique s'opère en deux temps :
- On calcule d'abord les hashs d'une importante quantité de mots de passe potentiels. Les associations « mot de passe clair/mot de passe haché » que l'on calcule sont alors stockées à la volée dans une structure de donnée dédiée appelée « Rainbow Table ». Cette structure de données a cela de particulier qu'elle permet de virtuellement mémoriser plusieurs dizaines de milliers d'associations « mot de passe clair/mot de passe haché » en ne consommant que 128bits de mémoire.
- Lorsque le besoin de casser un hash se fait sentir, on recherche dans les Rainbow Tables dont on dispose si, par hasard, on n'aurait pas mémorisé une association « mot de passe clair/mot de passe haché » dont le haché correspond à ce que l'on cherche à casser.
Ce fonctionnement permet donc de stocker virtuellement énormément de puissance de calcul dans une Rainbow Table, puis d'utiliser cette puissance de calcul en quelques secondes/minutes lorsque l'on souhaite casser un mot de passe. Typiquement, il est possible de générer les Rainbow Tables sur une machine puissante hébergée en datacenter pendant plusieurs mois (étape 1 ci-dessus), puis d'utiliser les Rainbow Tables ainsi générées sur un simple ordinateur portable (étape 2 ci-dessus). Virtuellement, l'ordinateur portable dispose donc, pour un usage immédiat, de toute la puissance de calcul que la machine puissante a déployée pendant les mois de génération de la table.
L'exemple le plus marquant des conséquences de cette technique concerne certainement le hachage LM. Ce hachage, utilisé par les premières versions de Windows, complète les mots de passe par des octets nuls jusqu'à obtenir une suite de 14 caractères qu'il découpe alors en deux blocs de 7 caractères. Les lettres comprises dans ces deux blocs sont converties en majuscule puis les deux blocs sont hachés séparément. Casser un haché LM revient donc à casser deux mots de passe hachés ne contenant pas de lettres minuscules et ne dépassant pas 7 caractères de long. À raison de 50 millions d'opérations de hachage par seconde (ordre de grandeur atteint sur les corei5 récents), tester tous les mots de passe possibles demande environ 46h. En comparaison, le même cassage peut être réalisé en moins de 5mn grâce à une Rainbow Table de 48Go (qui aura pris quelques heures à être générée préalablement une bonne fois pour toutes). La technologie Rainbow Table a donc rendu le hachage LM, qui était déjà obsolète, complètement inutile puisqu'il se casse maintenant quasi-instantanément avec la puissance d'un ordinateur portable et les quelques Go de disques nécessaires au stockage des Rainbow Tables adéquates.
1.2. Limitations actuelles
La technologie Rainbow Table impose cependant plusieurs contraintes sur les mots de passe dont on veut pouvoir stocker les pré-calculs. Si on veut résumer la problématique : pour qu'un ensemble de mots soient éligibles à être utilisés en Rainbow Table, il faut que l'on puisse numéroter les mots le composant et que l'on dispose d'un algorithme permettant d'obtenir rapidement le Nème mot de cet ensemble, pour un entier N quelconque. Tout naturellement, les premières Rainbow Tables s'attaquaient donc à des ensembles simples constitués de toutes les combinaisons possibles, jusqu'à une certaine longueur, d'éléments d'un alphabet arbitraire. Ainsi, on trouve facilement des Rainbow Tables contenant les pré-calculs d'espaces du type : « toutes les combinaisons possibles de lettres minuscules ou majuscules jusqu'à X caractères de long » (X étant généralement inférieur ou égal à 8). Ce genre d'espace est particulièrement bien adapté à un usage en Rainbow Table, puisqu'à raison d'une poignée d'opérations mathématiques de type modulo, on obtient immédiatement le Nème mot de l'ensemble pour n'importe quelle valeur entière de N.
L'inconvénient principal de ces ensembles est son manque de pertinence, qui devient de plus en plus criant au fur et à mesure que l'on augmente la longueur maximale autorisée. En effet, ces ensembles contiennent, en grandissant, une proportion de plus en plus grande de suites de lettres dont l'usage en tant que mots de passe est hautement improbable. De ce constat sont nées plusieurs initiatives visant à améliorer la pertinence des espaces de mots utilisables en Rainbow Tables afin de pré-calculer moins de hash inutiles. La première de ces initiatives date de 2007 et permet l'utilisation de dictionnaires comme ensemble de mots à pré-hacher [https://sites.google.com/site/reusablesec2/drcrack]. La seconde initiative, qui a rencontré beaucoup plus de succès, date de 2008 et consiste à utiliser le produit cartésien d'ensembles classiques. En définissant des produits cartésiens, il devient ainsi possible de pré-calculer des ensembles largement plus pertinents. Par exemple, en considérant l'espace constitué de « toute combinaison de majuscule/minuscule de longueur 1 suivi de toute combinaison de minuscule de longueur jusqu'à 7 », on décrit un ensemble 128 fois plus petit que « toutes les combinaisons de majuscule/minuscule de longueur jusqu'à 8 » mais, en pratique, on ne perd quasiment aucun mot de passe. La pertinence de ce nouvel espace peut donc être considérée comme 128 fois plus importante que celle de l'espace « toute combinaison de majuscule/minuscule jusqu'à 8 caractères de long ». Ces ensembles, résultant de produits cartésiens d'ensembles élémentaires, ont donc actuellement le vent en poupe et permettent de largement tirer parti des habitudes consistant, par exemple, à débuter les mots de passe par une lettre majuscule et à les terminer par un chiffre ou un caractère spécial.
Cette course à la pertinence pourrait paraître inutile, et pourtant, elle seule permet d'augmenter encore drastiquement l'efficacité des attaques par Rainbow Tables. En effet, l'utilisation d'espaces classiques arrive aujourd'hui à ses limites et le pas à franchir pour passer des combinaisons de 8 caractères (alphabet ASCII imprimable complet) aux combinaisons de 9 ou 10 caractères est si colossal qu'il semble, aujourd'hui, hors de portée pour les années à venir (comptez plusieurs centaines de To pour stocker la Rainbow Table qui irait jusqu'à 9 caractères, par exemple). Les espaces combinés (résultats d'enchaînement d'espaces classiques) sont donc plébiscités, mais il est possible de faire encore mieux en utilisant des espaces à construction probabiliste.
2. Espaces probabilistes
2.1. Présentation
La problématique de décrire des espaces de mots de passe candidats pertinents n'est pas spécifique aux Rainbow Tables, elle a même largement précédé leur invention. Les logiciels d'attaque par force brute classiques offrent ainsi tous de nombreuses options permettant de sélectionner au mieux l'ensemble des mots que l'on souhaite tester. On retrouve, bien entendu, l'énumération exhaustive des combinaisons d'un certain alphabet jusqu'à une certaine longueur, mais on retrouve également les attaques sur dictionnaires (agrémentées de variantes permettant d'appliquer des règles de mutations aux mots du dictionnaire de base) et on retrouve surtout des approches statistiques. Ces approches statistiques visent à construire l'ensemble des mots candidats à partir de règles de probabilités extraites de vrais mots de passe. La plus connue de ces approches est certainement l'option --markov de John the Ripper, que nous allons voir plus en détail.
L'approche dite « de Markov » a été pensée par Arvind Narayanan et Vitaly Shmatikov en 2005 et publiée pour la première fois dans un papier intitulé « Fast Dictionary Attacks on Passwords Using Time-Space Tradeoff ». Il faudra cependant attendre 2007 pour qu'une implémentation grand public voit le jour en tant que patch pour John the Ripper, proposé par Simon Marechal [http://www.openwall.com/lists/john-users/2007/09/15/2]. Aujourd'hui, cette méthode de génération d'ensemble de mots candidats est largement reconnue dans le monde du cassage de mot de passe et l'échelle des complexités « de Markov » est régulièrement utilisée comme échelle de référence pour mesurer la qualité de mots de passe.
Le cœur de l'approche dite « de Markov » consiste à appliquer la théorie des chaînes de Markov, élaborée au XXème siècle par le mathématicien Andreï Andreïevitch Markov, à l'écriture de mots de passe. L'algorithme se base donc sur la modélisation de l'écriture d'un mot de passe en tant que « phénomène dont l'état à un instant donné ne dépend que de ses états précédents » (i.e. la prochaine lettre du mot de passe en cours d'écriture ne dépend que de celles qui ont déjà été écrites). Dans le cadre de la constitution d'un ensemble de mots de passe candidats à hacher, cela revient à générer des suites de lettres dont la probabilité d'être des mots de passe, mesurée d'après une approche en processus de Markov, est supérieure à un seuil arbitraire. Concrètement, la probabilité qu'a une suite de lettres quelconque d'être un mot de passe se calcule en réalisant le produit des probabilités d'apparition de chaque caractère qui le constitue en ne connaissant que le caractère qui le précède. Chacune des probabilités élémentaires (probabilité du passage du caractère X au caractère Y) s'obtenant au préalable par analyse d'un dictionnaire de mots de passe considérés comme représentatifs par l'attaquant. La probabilité du mot « passwd » d'être un mot de passe s'exprime donc ainsi :
P(« passwd ») = P(« p »).P(« a|p ») .P(« s|a ») .P(« s|s ») .P(« w|s ») .P(« d|w »)
Une fois que l'on est capable de mesurer la probabilité d'apparition d'une suite quelconque de caractères, dans notre référentiel issu de l'ensemble de mots de passe témoins ayant servi à calculer les probabilités, nous pouvons définir un ensemble de mots candidats pour une attaque par force brute. Pour définir l'ensemble des mots candidats, nous n'avons en effet qu'à choisir une probabilité d'apparition minimale arbitraire, et à générer toutes les combinaisons de caractères qui ont une probabilité d'apparition supérieure à ce seuil. La génération de cet ensemble de suites de caractères ayant une probabilité d'apparition supérieure à un seuil fixé est décrite dans le papier original de A.Narayanan et V.Shmatikov, et nous ne la détaillerons donc pas ici, sachez simplement que l'algorithme proposé permet d'obtenir rapidement la taille de l'ensemble en question ainsi que le Nème mot de l'espace pour un entier N quelconque.
2.2. Utilisation en force brute
Jusqu'en mai dernier, aucune implémentation publique n'utilisait ces espaces de Markov dans un contexte d'attaque par Rainbow Tables, alors qu'ils avaient justement été pensés initialement dans cette optique. La raison en est probablement la lenteur de l'algorithme permettant d'obtenir le Nème mot d'un ensemble. En effet, pour des fonctions de hachage rapides (NT, MD5, etc.), l'obtention du mot à hacher prend plus de temps que le hachage de ce mot, ce qui a tendance à décourager l'utilisation de ces espaces. Cependant, grâce à une astuce algorithmique, le patch de John the Ripper réussit à générer le Nème mot d'un ensemble de Markov extrêmement rapidement, pourvu que l'on connaisse le (N-1)ème. Cette pirouette est idéale dans un contexte d'attaque par force brute directe, mais malheureusement inutile dans un contexte de Rainbow Tables, d'où la probable vacuité d'implémentation publique de Rainbow Tables markoviennes jusqu'à il y a peu.
Depuis 2007 (date de la sortie du patch pour John the Ripper), une chose essentielle a cependant changé en cassage de mot de passe : les cartes graphiques sont devenues infiniment plus puissantes et les programmer est devenu infiniment plus simple (CUDA et OpenCL). Cet axe a tant évolué qu'aujourd'hui, les espaces de mots de Markov utilisables en Rainbow Tables (pourvu qu'elles soient générées sur carte graphique, ou sur plusieurs centaines de CPU en parallèle) sont les ensembles qui permettent de casser le plus de mots de passe. Cette inversion de leadership entre les espaces classiques et les espaces de Markov s'explique par la différence d'évolution de leur pertinence en fonction de leur taille. Là où la pertinence des espaces classiques stagne rapidement, celle des espaces de Markov continue à progresser. C'est cette différence d'évolution qui permet aujourd'hui aux espaces de Markov de dépasser la pertinence des plus gros espaces classiques, alors même qu'ils restent 20 à 50 fois plus petits.
Aujourd'hui, donc, les espaces probabilistes sont des acteurs majeurs du cassage de mot de passe en force brute « simple » ainsi qu'en force brute distribuée, et ils viennent de prendre pied dans le monde des attaques par force brute via Rainbow Tables. Étant donné les résultats qu'ils permettent d'obtenir, et que nous allons voir dans la suite de cet article, il y a fort à parier que leur variante Rainbow Table devienne elle aussi un classique.
3. Rainbow Tables probabilistes
3.1. Performances
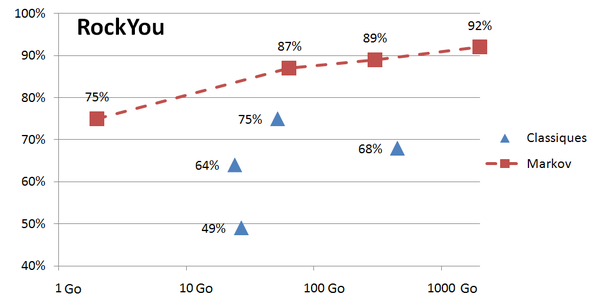
Pour mesurer la performance d'une technique de cassage de mot de passe, plusieurs métriques peuvent être utilisées. Dans cet article, nous allons considérer deux ensembles de mots de passe réels et, pour chaque technique de cassage de mot de passe, nous allons mesurer quel pourcentage de ces ensembles auraient été cassés par la technique en question. Les deux ensembles que nous considérerons sont, d'une part, l'ensemble des 32 millions de mots de passe du site web RockYou qui avaient été publiés en clair sur Internet en 2009 et, d'autre part, un ensemble de 500 000 mots de passe réels rencontrés lors de tests d'intrusions pour des entreprises majoritairement françaises.
Les résultats pour plusieurs Rainbow Tables (classiques et « de Markov ») sont relatés ci-dessous :
|
Rainbow Table |
Taille de la Rainbow |
Succès sur RockYou |
Succès sur les 500k |
|
MixAlphaNum 1-7 |
27 Go |
49 % |
13 % |
|
LowerAlphaNum 1-8 |
24 Go |
64 % |
49 % |
|
Markov 265 |
2 Go |
75 % |
50 % |
|
LowerAlphaNum 1-9 |
52 Go |
75 % |
52 % |
|
MixAlphaNum 1-8 |
453 Go |
68 % |
63 % |
|
Markov 300 |
64 Go |
87 % |
66 % |
|
Markov 315 |
300 Go |
89 % |
71 % |
|
Markov 335 |
2 To |
92 % |
78 % |
3.2. Do it yourself
Les Rainbow Tables de Markov sont donc clairement une solution viable pour le cassage de mot de passe puisqu'elles permettent d'obtenir des taux de réussite plus que convaincants en comparaison aux Rainbow Tables classiques. Lors de l'édition 2011 du SSTIC, un outil permettant de générer et d'utiliser ce type de Rainbow Tables a été présenté : crackNfast [https://www.sstic.org/2011/presentation/rainbow_tables_probabilistes/]. Dans cette dernière partie, nous allons voir comment générer nous-mêmes des Rainbow Tables de Markov avec cet outil, puis comment les utiliser.
Avant toute chose, il faut savoir qu'une carte graphique compatible CUDA est nécessaire à la génération de tables (donc basée sur chipset nvidia et relativement récente). Si vous n'en avez pas, il ne vous reste plus qu'à trouver un ami équipé d'une telle carte qui veuille bien vous générer des tables (à l'heure actuelle, nous n'avons pas connaissance de tables de Markov téléchargeables gratuitement sur Internet). Ensuite, il vous faudra, bien entendu, le code source de l'application crackNfast [http://www.lexsi.com/francais/cracknfast/] et le SDK CUDA. Enfin, il faut prévoir quelques heures de calculs.
La suite logicielle crackNfast est constituée de deux applications distinctes : cracknfast_gen, et cracknfast_search. La première de ces applications permet la génération de tables, la seconde permet l'utilisation de tables pour casser des hashs. En plus de ces deux outils, vous aurez besoin d'un programme tel que rtsort, qui permet de trier les Rainbow Tables (les Rainbow Tables « brutes » sorties de cracknfast_gen ne peuvent être utilisées par cracknfast_search qu'après cette étape de tri).
Les Rainbow Tables que vous allez générer sont caractérisées par trois propriétés : la complexité de Markov maximale que vous autorisez (i.e. la probabilité minimale autorisée pour être considérée comme un mot de passe selon la mesure en processus de Markov), la longueur des chaînes constitutives de votre table et le nombre de chaînes que vous voulez pré-calculer. Ceux d'entre vous qui sont les plus familiers avec les Rainbow Tables et/ou avec Markov pourront jouer en plus sur l'indice de table, le pourcentage de couverture et le fichier de statistiques à utiliser, mais je ne détaillerai pas l'influence de ces éléments ici.
Tout d'abord, il vous faudra décider de la « complexité de Markov » maximale que vous autorisez. C'est un indicateur qui se mesure en chiffres entiers et qui évolue inversement à la probabilité minimale (elle est proportionnelle au logarithme de la probabilité minimale). On utilise la complexité maximale plutôt que la probabilité minimale car le concept de « mot de passe complexe » est plus naturel que celui de « suite de lettres improbable ». À titre informatif, les valeurs de complexité de Markov que vous manierez usuellement varient entre 250 et 350. La complexité maximale va influer sur deux choses : la taille de l'espace (plus vous autorisez des mots complexes, plus l'espace grandit) et le taux de succès (plus l'espace de mots grandit, plus vous retrouverez de mots de passe). Le tableau présenté plus haut dans l'article vous donnera une idée des taux de succès, quant à l'ordre de grandeur de la taille de l'espace, vous pourrez l'avoir soit avec l'outil genmkvpwd (fourni avec le patch de Markov pour John the Ripper), soit avec cracknfast_gen.
Une fois la complexité choisie, il vous faudra décider de la longueur des chaînes constituant votre Rainbow Table. Une Rainbow Table est en effet exclusivement constituée de structures logiques appelées « chaînes », chaque chaîne occupant une taille fixe de 128 bits en mémoire. Ces chaînes, qui n'occupent que 128 bits, représentent virtuellement la mémoire de plusieurs milliers (voire dizaine de milliers) d'associations « mot de passe en clair/mot de passe haché ». La longueur des chaînes influera de deux façons sur vos tables : plus vous utiliserez des chaînes longues, plus vous stockerez d'associations « clair/haché » dans 128bits et donc plus vos Rainbow Tables seront petites sur disque. En revanche, plus vos chaînes seront longues, plus le temps de recherche dans les Rainbow Tables résultantes sera long (il peut varier de quelques secondes pour des chaînes de 2100 maillons à plusieurs minutes pour des chaînes de 18100 maillons, par exemple). Le choix de la longueur de chaîne relève donc du compromis temps/mémoire et reste à votre discrétion, tout en sachant que la taille de la table est proportionnelle à la longueur des chaînes alors que le temps de recherche, lui, est proportionnel au carré de la longueur de ces chaînes.
Une fois la complexité de Markov et la longueur des chaînes décidées, il ne vous reste qu'à déterminer le nombre de chaînes à calculer dans votre Rainbow Table. Nous avons déjà décidé du nombre d'associations « clair/haché » que stockera chaque chaîne (c'est sa longueur), nous connaissons la taille de l'espace de mot de passe que nous voulons pré-calculer, on pourrait donc croire qu'il suffit de diviser la taille de l'espace par la longueur de chaîne pour savoir combien de chaînes nous devons calculer pour couvrir tout l'espace. Malheureusement, la pratique est plus compliquée que cela. De par la nature des Rainbow Tables, on ne peut décider que du premier mot de passe de chaque chaîne, tous les suivants étant pris aléatoirement dans l'espace que nous avons défini. Ainsi, si on se contente de pré-calculer autant de combinaisons « clair/haché » qu'il y a de mots dans notre espace, nous pouvons être certains que quelques mots de l'espace de départ n'auront jamais été tirés au hasard alors que d'autres l'auront été plusieurs fois. Cette redondance d'information causée par le choix aléatoire d'un même mot plusieurs fois est hélas inévitable et rend les calculs nettement plus compliqués. L'étude probabiliste de ce phénomène a heureusement déjà était faite, mais étant donné qu'elle est relativement longue, nous nous contenterons donc de mémoriser quelques valeurs connues :
- Si on veut que notre Rainbow Table contienne les hachés d'environ 50 % des mots de notre espace, il faudra que l'on calcule en réalité un nombre d'associations clair/haché égal à 82 % de la taille de l'espace.
- Si on veut avoir les trois quarts des mots de passe dans une Rainbow Table, il faudra que celle-ci contienne deux fois plus d'associations « clair/haché » qu'il y a de mots dans l'espace de départ.
- Enfin, si on veut que notre Rainbow Table couvre relativement bien l'espace que nous avons défini, par exemple en contenant le haché de 90 % des mots, il faudra qu'elle contienne quatre fois et demi plus d'associations « clair/hachés » qu'il y a de mots dans l'espace !
Par exemple, si votre espace de Markov contient 100G mots (ce qui est le cas de l'espace dont la complexité de Markov maximale est fixée à 259), il vous faudra pré-calculer 82G hashs pour que la Rainbow Table générée ait une chance sur deux de casser un mot de passe ayant une complexité inférieure ou égale à « Markov 259 ». Il est à noter que la solution optimale pour obtenir des tables couvrant plus de 75 % de l'espace est en fait de générer plusieurs tables d'indice différent, ce que nous n'aborderons pas ici. Le lecteur intéressé pourra se référer aux mathématiques générales des Rainbow Tables pour trouver les paramètres idéaux à la génération de Rainbow Tables ayant 99,9 % de couverture.
3.3. Exemples
Imaginons à présent un cas pratique : nous souhaitons générer une petite table à titre d'exercice. Par exemple, nous allons décider d'une complexité maximale de Markov valant 265, car c'est la plus petite présentée dans cet article (donc la plus rapide à générer). Pour la longueur des chaînes, le paramètre de choix principal va être la vitesse de recherche : pour une table d'exercice, nous ne voulons pas qu'un cassage de hash prenne de trop longues minutes, nous choisissons donc des chaînes de longueur 2100. La table servant uniquement d'exercice, nous nous contenterons d'avoir 50 % de chance de casser un hash dont le mot de passe serait dans l'espace de Markov 265, nous devons donc calculer le nombre de chaîne tel que, multiplié par la longueur que nous avons choisie, nous obtenions 82 % de la taille de l'espace de Markov 265. L'espace de Markov 265 compte environ 183G mots, la longueur des chaînes étant de 2100 maillons, nous devons calculer environ 71 670 000 chaînes.
$ ./crackNfast_gen
Usage : ./crackNfast_gen TableIndex NbChains OutfileName [ChainLen = 10000] [MarkovComplexity = 327] [MarkovFileName = "stats"] [CUDA device's ID (starting with 0)]
$ ./crackNfast_gen 1 71670000 my_pretty_rainbow.rt 2100265
Le calcul de la table devrait prendre entre 1h et 4h environ, en fonction de la puissance de votre carte graphique. Une fois la table générée, il ne reste plus qu'à lui appliquer un traitement de tri (avec l'utilitaire rtsort, par exemple), puis à la renommer en suivant la convention attendue par cracknfast_search :
$ ./rtsort my_pretty_rainbow.rt
(...)
$ mv my_pretty_rainbow.rt NT_MKV265#stats_1_2100x87400000_test50PC.rt
La Rainbow de test est alors prête à être utilisée avec crackNfast_search pour casser des hashs au format NT. L'utilisation de crackNfast_search est beaucoup plus simple que celle de crackNfast_gen et ne nécessite aucune compréhension des mécanismes de Rainbow Tables. Vous n'avez en effet besoin que d'une Rainbow Table et d'un fichier texte contenant les hashs que vous voulez casser (la syntaxe correcte est d'un couple login/hash par ligne, le login et le hash étant séparé par un symbole « : »). Les arguments à spécifier à crackNfast_search sont donc le fichier Rainbow Table à utiliser, le fichier texte contenant les hashs à casser, et éventuellement le nombre de threads que vous voulez utiliser pour la recherche.
$ ./crackNfast_search NT_MKV265#stats_1_2100x87400000_test50PC.rt Hashs_a_casser.txt
Bien entendu, cette Rainbow Table de démonstration ne cassera pas grand chose (après tout, elle n'a même pas pris une journée à être générée), mais sachez qu'il est possible d'atteindre, avec des machines quasi-standards, des Rainbow Tables de complexité allant jusqu'à couvrir 99 % de l'espace de Markov 335. Un autre exemple de Rainbow Table plus utilisable (90 % de Markov 275) pourrait être généré comme suit sur quasiment n'importe quelle machine :
$ ./genmkvpwd stats 275 | tail -n 1
len=19 (10488 KB for nbparts) 539 G possible passwords (539967057392)
$ python -c "print 4.5*539967057392)/2100.0"
1157072265.84
$ ./crackNfast_gen 1 1157072266 my_pretty_rainbow_with_90pc.rt 2100 275
( ici on attend entre 20h et 40h, selon la carte graphique...)
$ mv my_pretty_rainbow_with_90pc.rt NT_MKV275#stats_1_2100x1039775582_testbis90PC.rt
$ ./rtsort NT_MKV275#stats_1_2100x1039775582_testbis90PC.rt
Conclusion
Les Rainbow Tables de complexité 335 permettant de casser environ 90 % des mots de passe utilisés en situations réelles, et ces tables existant pour les formats de hachages simples type NT et MD5, on peut considérer qu'il est impérieux d'abandonner ces formats trop simples lorsque cela est possible et d'en adopter d'autres qui utilisent un salage (aléatoire) afin de rendre improbable les attaques par Rainbow Tables.