Il y a quelques années, les musiques des années 70 et 80 sont revenues à la mode. Puis, cela a été le tour du rétrogaming. Et voici venu le temps du rétrocomputing. Créer de petits programmes ou même des jeux à l’ancienne, tout en assembleur sur de très vieilles machines 8 bits n’est pas si complexe que ça. C’est d’ailleurs le but de cette série, qui s’intéresse à la mise en œuvre d’un des tout premiers microprocesseurs.
Quand il était petit, un de mes amis a créé un super héros dans une B.D. Et comme il est super fan de rétrogaming, en mars dernier, il m'a dit que ça le ferait marrer de le voir dans un jeu NES (Nintendo Entertainment System, la première console Nintendo).
J'avoue que je n'avais jamais programmé pour cette console (que je n'ai d'ailleurs jamais possédée !), mais le défi me semblait amusant.
Cette console sortie en 1985 se programme essentiellement en assembleur et a une architecture assez différente de ce que l'on connaît de nos jours. Ce côté découverte me plaît beaucoup.
Le microprocesseur utilisé dans la NES est un 6502, un CPU ultra simple créé par MOS Technology en 1975. Cette puce est en effet composée de seulement 3510 transistors. Pour comparaison, l'Intel 4004 de 1971, qui est considéré comme le tout premier microprocesseur (4 bits) en avait 2300. Et un Core i7, toujours chez Intel, en possède de l'ordre du milliard (oui, vous avez bien lu !)
Figure 1 : le cœur du 6502, il est presque possible de compter les transistors !
1. Architecture de la NES
La NES n'est pas seulement un microprocesseur, elle comporte aussi quelques autres composants.
Tout d'abord, le processeur qu'elle utilise n'est pas vraiment un 6502, mais une version un peu restreinte, qui ne comporte pas la partie « Calcul BCD » (je reviendrai sur ce point plus tard), affublé d'un générateur de son nommé APU (pour Audio Processing Unit). Ces deux éléments sont en effet regroupés dans une puce nommée 2A03, pour la version NTSC et 2A07, pour la version PAL. Celle-ci a été créée spécifiquement par le constructeur japonais Ricoh, plus connu pour ses appareils photo. L'étude de la partie sonore de la NES fera peut-être l'objet d'un prochain article.
Pour la partie graphique, la NES utilise un PPU (Pixel Processing Unit) toujours produit par Ricoh et dont la désignation est RP2C02, pour la version NTSC ou RP2C07, pour la version PAL. Le PPU ne permet pas de disposer d'un framebuffer permettant d'accéder à chaque pixel, comme c'est le cas sur toutes les machines récentes. En revanche, il permet de disposer des tuiles de 8x8 pixels sur un canevas de 32x30 tuiles, afin de créer un fond d'écran pouvant défiler soit horizontalement, soit verticalement. La résolution de la NES est donc de 256 pixels par 240. À ceci s'ajoute la possibilité d'afficher 64 sprites, également de 8x8 pixels, indépendantes du fond. Il existe tout un tas de restrictions, tant au niveau des couleurs que du placement des sprites, mais cela ne sera pas traité dans cet article.
Voilà ce qu'il en est des composants principaux de la console NES. À ceci s'ajoutent une puce d'identification des cartouches, 2 ko de RAM, quelques composants logiques et la gestion de l'alimentation. Le reste de l'électronique se trouve en effet sur les cartouches de jeux elles-mêmes, et encore, il ne s'agit que de deux ROM, l'une de 16 ou 32 Ko pour la partie programme et données générales, et l'autre de 8 Ko, pour les données graphiques.
2. Le vénérable 6502
Tout ceci peut sembler bien exotique et c'est en partie vrai, pour tout ce qui est graphique et sonore sur cette console. En revanche, le microprocesseur 6502 est plutôt un grand classique et on le retrouve, lui ou l’un de ses dérivés, dans de nombreuses machines mythiques. Il est déjà présent dans l'Atari 2600, la console de 1977, mais aussi sur bon nombre d'ordinateurs personnels des années 1980 : l'Apple II, le Commodore 64, les Oric 1 et Atmos, pour ne citer que les plus connus.
Figure 2 : Une relique des années 1980 l’Oric 1, concurrent du ZX Spectrum, mais propulsé par un 6502.
2.1 Chaîne de compilation et émulateurs online
La programmation en assembleur peut faire peur, au premier abord. Cependant, il s'agit d'un langage très simple, surtout avec des processeurs aussi anciens que le 6502. La syntaxe de l'assembleur 6502 est en effet dépouillée et peut se résumer ainsi :
- Tout ce qui suit un ; sur une ligne est un commentaire.
- Chaque ligne contient quatre zones :
- Un label, optionnel, un nom unique qui permettra d'effectuer un saut à cet endroit-là dans le programme. Il commence dans la toute première colonne et se termine par un :.
- Un opcode, c'est ainsi que l'on nomme les instructions en assembleur. On les appelle aussi quelques fois mnemoniques. Sur le 6502, tous les opcodes sont de trois lettres, résumant ce que fait l'instruction. Par exemple INX pour « incrémenter X ».
- Une éventuel opérande (le paramètre de l'opcode, s'il en a un).
- Un éventuel commentaire, jamais nécessaire, toujours recommandé.
Une ligne de code assembleur peut donc ressembler à ça :
debut: STA $63,y ; sauvegarde A
Ici, debut: est un label, STA est l'opcode, $63,y représente l'opérande, et ; sauvegarde A est un commentaire.
- Les nombres présents dans la partie opérande, forcément entiers, peuvent être exprimés en décimal (normal) ou en hexadécimal, si on précède d'un $ ou encore en binaire, si on les précède d'un %. Les trois lignes suivantes sont donc strictement équivalentes :
STA 42
STA $2A ; 2 * 16 + 10 = 42
STA %00101010 ; 32 + 8 + 2 = 42
Si l'opérande commence par un #, le nombre suivant le # sera directement utilisé comme valeur. On appelle cela une valeur immédiate, car elle est donnée immédiatement dans l’instruction assembleur elle-même. Sinon, le nombre sera considéré comme une adresse en mémoire, à laquelle il faudra récupérer la valeur. Ces deux façons de faire (immédiate ou non) sont ce que l’on appelle « modes d’adressage ». Il en existe bien d’autres supportés par le 6502, comme nous le verrons dans le deuxième article de cette série.
Les nombres manipulés par le 6502 sont des entiers pouvant aller de 0 à 255. Rien d'autre. Il est toutefois possible d'interpréter aussi ces nombres comme allant de -128 à 127, en utilisant la représentation appelée « complément à 2 ». Cela ne change strictement rien à la façon dont le 6502 gère les nombres (il ne sait pas comment on va les interpréter), mais il nous permet de connaître le signe d'un nombre, si on désire l'interpréter comme signé.
On trouve facilement des programmes permettant de transformer du code écrit en assembleur 6502 pour en faire un exécutable, qu'on pourrait lancer via un émulateur par exemple, et ce, quel que soit votre OS favori. Les plus communs sont asm6, vasm ou ca65. Les modalités d'installation et d'utilisation de ces programmes, avec leurs spécificités, se trouvent sans problème sur Internet.
Cependant, pour apprendre et tester de petits bouts de code, il est bien plus pratique d'utiliser des assembleurs / émulateurs en ligne. Parmi ceux-ci, on peut citer :
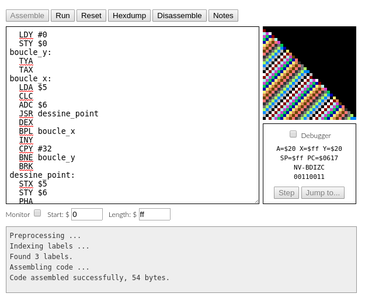
- http://skilldrick.github.io/easy6502/, que l'on que peut voir en action sur la figure 3. Je le conseille pour tester les exemples que je donne. Il inclut par ailleurs un didacticiel, mais que je trouve un peu abrupt.
- http://www.6502asm.com/ contient des exemples de code pour une machine imaginaire, utilisant un 6502 pour afficher des graphismes. Il est possible de modifier les exemples ou d'écrire un programme depuis zéro. Ne permet malheureusement pas d'inspecter les registres.
- http://www.visual6502.org/JSSim/ ne permet pas de proposer du code, mais uniquement du binaire. Cependant, il réussit la performance d'afficher tous les transistors du 6502 activés par chaque instruction. À voir, ne serait-ce que par curiosité.
Figure 3 : Le site « Easy6502 » en action, qui permet d’écrire du code assembleur directement, de le tester, de l’exécuter pas-à-pas, en examinant l’état des registres. Ici, il montre le résultat du programme exemple, présenté en fin d’article.
3. Présentation du jeu d'instructions du 6502
Le 6502 est un microprocesseur purement 8 bits et ne dispose que de registres 8 bits, à l'exception du pointeur d'instruction, alors que certains processeurs de la même époque, comme le Z80 par exemple, permettent d'associer des paires de registres, afin de manipuler directement des données de 16 bits. De plus, le jeu d'instructions est extrêmement limité, avec tout juste ce qu'il faut pour réaliser l'ensemble des opérations basiques.
3.1 Les registres
Les registres d'un microprocesseur permettent de stocker, modifier, tester des données de manière plus efficace qu'avec des données en mémoire. Le 6502 ne propose que 6 registres, et ils sont assez spécialisés.
3.1.1 Le registre PC
PC est Le compteur de programme. Il s'agit du seul registre 16 bits du 6502. Il contient l'adresse de l'instruction (opcode) en cours.
On ne peut évidemment pas utiliser ce registre pour stocker quoi que ce soit, on ne peut d'ailleurs pas directement connaître sa valeur. Il s'incrémente tout seul à chaque instruction exécutée, et ne peut être sinon modifié qu'avec des instructions de saut.
3.1.2 Le registre S
S est le pointeur de pile. Le 6502 a une toute petite pile, permettant de stocker les adresses de retour des fonctions ou d'autres données.
La valeur maximale de ce registre est 255 et il est décrémenté à chaque empilage de données (deux fois pour une adresse). On peut changer la valeur de ce registre, mais pas lire sa valeur.
3.1.3 Le registre P
P est le registre des flags (drapeaux). Ce registre contient l'état actuel du processeur (quelles options sont actives), ainsi que des bits précisant le résultat de certaines opérations.
Certains bits de ce registre peuvent être manipulés à la main : ceux qui concernent les options du processeur. Les autres sont positionnés automatiquement par des instructions de comparaison (mais pas uniquement). On utilise généralement le contenu de ce registre pour effectuer des sauts conditionnels (voir plus bas).
Les bits de ce registre sont les suivants :
- Le bit 0, C, est le bit de retenue, il est utilisé dès que le résultat d'une opération ne tient pas sur 8 bits, ce qui arrive assez souvent. On peut aussi changer la valeur de ce bit, en particulier à l'aide des instructions CLC et SEC. L'état de ce bit est souvent testé avec les opérations de branchement BCC et BCS.
- Le bit 1, Z, est le bit nommé « Zéro ». Il est modifié par beaucoup d'opérations. Il est mis à 1, si le résultat d'une opération est 0 et à 1, sinon. On notera l'humour des concepteurs du 6502 de choisir le bit numéro 1 de ce registre comme « Zéro », dont le but est justement d'être à 1 pour une opération qui renvoie 0 et vice-versa.
- Le bit 2, I est le bit d'interruption. Ce bit permet d'activer ou de désactiver les interruptions, à la main, il n'y a pas d'instruction qui le modifie directement, en dehors de CLI et SEI.
- Le bit 3, D est le bit « Decimal ». Lorsque ce bit est positionné, les additions et soustractions (les instructions ADC et SBC) considèrent que chaque octet est composé de deux quartets (4 bits), dont la valeur ne va que de 0 à 9. Dans ce mode, la valeur représentée par un octet va donc de 0 à 99, ce qui peut être pratique pour certains calculs. Ce n'est toutefois pas souvent utilisé. Ce bit n'existe pas sur la NES.
- Le bit 6, V est le bit « oVerflow » (dépassement). Ce bit n'est modifié que par ADC et SBC. Il est mis à 1 uniquement si le résultat d'une opération signée ne tient pas dans l'intervalle [-128, 127].
- Le bit 7, N est le bit négatif. Il est positionné à 1 si une opération amène à une valeur dont le bit 7 est à un (supérieure à 127).
- Les bits 4 et 5 ne sont pas utilisés.
3.1.4 Le registre A
L'accumulateur. Le premier registre enfin utile ! On peut écrire des données dans ce registre, les lire, faire des additions, des soustractions, des opérations bit à bit (ou, et, ou exclusif, décalages) et des comparaisons.
Il s'agit du registre que l'on utilisera le plus.
3.1.5 Les registres X et Y
Ce sont deux registres d'index qui ont presque le même rôle. On peut stocker et lire des données avec ces registres, mais les seules opérations arithmétiques que l'on peut leur appliquer sont l'incrémentation et la décrémentation.
De plus, on peut les utiliser dans des modes d'adressage spéciaux, pour lire ou écrire des données dans un tableau. Ils sont donc parfaits pour faire des parcours de tableaux, des copies, des recherches, etc.
Voilà pour les registres.
Ça ne fait pas beaucoup, les autres microprocesseurs en ont souvent beaucoup plus. Par exemple, le préhistorique 4004 en avait 16, le Z80 aussi ou presque. La famille du 6502 fait donc exception sur ce point.
Si on a besoin de stocker des valeurs, on utilisera donc souvent la mémoire RAM (un peu plus lente) ou la pile (encore plus lente).
3.2 Les instructions du 6502
Voyons maintenant de quelles opérations on dispose. Là aussi, le choix va être très limité.
3.2.1 Copie de données
Comme sur tous les microprocesseurs, l'opération que l'on fait le plus fréquemment sur un 6502 est la copie de données.
Il y a trois classes d'opérations de copie : soit d'un registre à l'autre, soit d'un registre vers la mémoire, soit de la mémoire vers un registre. Le 6502 différencie ces trois classes directement dans le nom de l'instruction, et propose pas moins de 12 instructions de copie (sur les 56 qu'il possède en tout !)
Les copies entre registres se feront avec les opcodes TAX, TAY, TSX, TXA, TXS et TYA. Le T signifie « transfert », même s'il ne s'agit que d'une copie. La lettre suivante désigne le registre d'où provient la valeur et la dernière lettre le registre qui recevra la valeur.
Par exemple, TAX copie le contenu du registre A dans le registre X. On notera l'absence de copie entre les registres X et Y et que seul X peut échanger sa valeur avec S.
Les copies depuis un registre vers la mémoire se font avec les opcodes STA, STX et STY, qui stockent évidemment les registres A, X et Y dans un emplacement mémoire donné en paramètre. Nous verrons la syntaxe des paramètres dans le prochain article sur les modes d’adressage.
Par exemple, STA $1138 stockera la valeur du registre A à l'emplacement mémoire 1138 (en hexadécimal).
Les copies vers un registre se font avec les opcodes LDA, LDX et LDY. Ces instructions prennent également un paramètre, qui peut être soit un emplacement mémoire soit directement une valeur.
Exemple :
LDA $2812 ; lit depuis l'adresse $2812
LDX #42 ; met la valeur 42 dans X
Note : les ; permettent de débuter un commentaire en langage assembleur.
Toutes les opérations de copies positionnent les bits N et Z du registre des drapeaux, en fonction de la valeur copiée.
3.2.2 Fun with flags (drapeaux)
Certains opcodes ont pour seul rôle de changer un bit du registre P (les drapeaux).
Ainsi, CLC, CLD, CLI et CLV permettent de mettre à zéro les bits de retenue, de calcul décimal, de masquage d'interruption et de dépassement, respectivement.
De la même façon, SEC, SED et SEI mettent les bits correspondants à 1.
Notez qu'il n'y a pas de SEV.
3.2.3 Opérations logiques (bit à bit)
Les microprocesseurs sont composés avant tout de portes logiques. Ce n'est donc pas étonnant de retrouver les opérations correspondantes dans le jeu d'instructions du 6502. Les opcodes AND, ORA et EOR réalisent respectivement un ET, un OU et un OU exclusif entre chacun des bits du registre A et l'opérande, et stocke le résultat dans A.
Pour rappel, voici les tables de vérité de ces opérations, pour un bit.
AND :
|
A |
opérande |
résultat |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
ORA :
|
A |
opérande |
résultat |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
EOR :
|
A |
opérande |
résultat |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Afin de bien comprendre ces instructions, voici un exemple qui réalise ces opérations sur les valeurs $F0 (soit %11110000 en binaire) et $55 (soit %01010101 en binaire) :
LDA #%11110000
AND #%01010101 ; A = %01010000 ($50)
...
LDA #%11110000
ORA #%01010101 ; A = %11110101 ($F5)
...
LDA #%11110000
EOR #%01010101 ; A = %10100101 ($A5)
...
L'opérande est ici une constante, on pourrait aussi utiliser une adresse mémoire (voire des choses plus complexes, comme on le verra dans le prochain article).
À noter qu'il n'y a pas d'instruction permettant d'inverser tous les bits de A.
On utilisera EOR #$ff pour ça.
N'hésitez pas à tester cela dans un des émulateurs en ligne que j'ai précédemment cités, afin de bien comprendre comment tout cela fonctionne. Les émulateurs donnent en outre l'état des drapeaux N et Z, ce qui est très pratique.
3.2.4 Opérations arithmétiques
Il n'y a que deux opérations arithmétiques disponibles sur le 6502 : l'addition et la soustraction. Et encore, il ne s'agit que d'un cas particulier de ces opérations.
L'addition se fait avec l'opcode ADC. L'un des deux nombres additionnés est forcément le registre A et l'autre est donné par l'opérande. Mais à cela s'ajoute le bit de retenue (C). L'opération réalisée est donc A = A + op + C et pas simplement A = A + op, comme on pourrait s'y attendre.
Ce n'est pas un hasard. Cela permet tout de même de faire l'opération attendue, si on pense à remettre C à zéro auparavant avec l'instruction CLC (sauf si on sait qu'il vaut déjà 0). Mais prendre en compte la retenue va permettre de faire des additions sur des nombres de 16 bits. Pas directement bien sûr, mais en faisant deux additions et en propageant la retenue.
Prenons l'exemple suivant : on veut additionner 500 et 300. Aucun de ces nombres ne tient sur 8 bits. On peut coder 500 comme étant 1 * 256 + 244, soit 1 et 244 en mémoire. De la même façon, 300 = 1 * 256 + 44, soit (1, 44). Pour additionner les deux, on peut additionner 244 et 44, ce qui fait 288 = 1 * 256 + 32, puis additionner 1 et 1, plus 1 de retenue, ce qui fait 3, le résultat est donc (3, 32), et 2 * 256 + 32 = 800, c'est bien la bonne somme, mais la retenue est importante !
Ce sera plus facile à suivre avec un exemple de code. On suppose que l'on a un nombre (par exemple 500) stocké sur les deux octets aux adresses $1000 et $1001, et un autre nombre (par exemple 300) stocké sur les deux octets aux adresses $1002 et $1003. On veut avoir le résultat de l'addition dans les deux octets aux adresses $1004 et $1004.
CLC ; on s'assure de ne pas avoir de retenue pour la première addition
LDA $1000 ; première partie du premier nombre (bits de poids faible)
ADC $1002 ; première partie du second nombre
STA $1004 ; on stocke le résultat (32) et la retenue est à 1
LDA $1001 ; deuxième partie du premier nombre
ADC $1003 ; deuxième partie du second nombre
STA $1005 ; on stocke les bits de poids fort du résultat
Et s'il n'y a pas de retenue, C vaut simplement 0 après la première addition et cela continue de fonctionner de la même manière
Ici aussi, tester ce code dans un émulateur avec tout un tas de cas différents peut mieux aider à comprendre comment ça marche. L'exemple a été donné pour des nombres de 16 bits (deux fois 8), mais on pourrait continuer de la même manière pour gérer des additions sur 24 bits, 32 bits ou même plus !
Pour cet exemple, j'ai supposé que le mode décimal (bit D) n'était pas positionné. Le raisonnement resterait le même, si ce n'est que la retenue serait alors positionnée dès qu'un résultat est supérieur à 99 (et non plus à 255).
L'opcode SBC fonctionne un peu de la même manière, c'est-à-dire qu'il prend en compte la retenue, mais il l'utilise à l'envers. Ainsi, l'opération réalisée par SBC valeur est en fait A = A - valeur - (1 – C). Et donc pour éviter d'avoir un résultat faux, on mettra cette fois-ci C à un par un appel à SEC avant la première soustraction.
Si l'on considère nos nombres comme signés (ce qui n'est qu'une convention, rappelons-le), en plus de la retenue, le drapeau de dépassement (V) pourra nous être utile. Il sera mis à un si le bit de signe de A est faux, suite à un dépassement de 127 ou de -128.
Ces deux instructions sont les plus complexes à comprendre dans l'apprentissage de la programmation du 6502.
3.2.5 Rotations de bits
Comme nous venons de le voir, les seules opérations arithmétiques du 6502 sont l'addition et la soustraction. Il n'y a pas de multiplication ni de division, sauf dans des cas particuliers.
Cela passera par le décalage de bits. Par exemple, l'opcode ASL qui porte soit sur A soit sur un emplacement en mémoire (mais pas sur les registres X ou Y) permet de décaler les bits de A vers la gauche, réalisant une multiplication par 2. Le bit de poids fort de A (qui « sort » du registre) est mis dans le bit de retenue (C). Et le nouveau bit de droite est un 0.
Exemple :
LDA #%00100111 ; A contient 39
ASL ; A vaut maintenant %01001110 (78) et C = 0
ASL ; A vaut maintenant %10011100 (156) et C = 0
ASL ; A vaut maintenant %00111000 (56) et C = 1
On a bien une multiplication par 2 à chaque étape (et d'ailleurs 56+256 = 312 = 156 * 2).
De la même façon, il est possible de réaliser une division par 2 à l'aide de l'opcode LSR, qui réalise un décalage vers la droite. Là encore, le bit sortant (à droite) se retrouve dans le registre C, et le bit entrant est un zéro.
Exemple d'utilisation de LSR :
LDA #%10101100 ; A contient 172
LSR ; A vaut maintenant %01010110 (86) et C = 0
LSR ; A vaut maintenant %00101011 (43) et C = 0
LSR ; A vaut maintenant %00010101 (21) et C = 1
Les opcodes ROL (ROtate Left) et ROR (ROtate Right) réalisent à peu près la même opération que ASL et LSR, si ce n'est que le bit entrant est celui qui était dans C avant l'instruction.
On peut voir ces deux opcodes comme des rotations des bits du registre A ou d'un emplacement mémoire.
Exemple avec ROL et ROR :
CLC ; on s'assure que C vaut 0
LDA #%10101100 ; A contient 172 et C = 0
ROL ; A contient %01011000 et C = 1
ROL ; A contient %10110001 et C = 0
ROR ; A contient %01011000 et C = 1
ROR ; A contient %10101100 et C = 0
À noter que ces rotations se font sur 9 bits (les 8 bits du registre + le bit de C).
Et encore une fois, cela a été fait intentionnellement, cela permettra de faire également des rotations sur 17, 25, 33, mais aussi 32, 24, 16 ou 8 bits assez facilement. Nous verrons ces astuces dans un prochain article.
3.2.6 Incrémentation / décrémentation
Les registres X et Y sont très souvent utilisés comme index de tableau. C'est pourquoi, même si on ne peut pas faire de soustraction ou d'addition avec eux, il est possible de les incrémenter ou les décrémenter à l'aide des opcodes INX, INY, DEX et DEY.
À noter qu'il est possible d'incrémenter / décrémenter une valeur dans un endroit en mémoire à l'aide de INC et DEC, mais que ces opérations ne sont pas disponibles sur le registre A. On utilisera donc par exemple CLC suivi de ADC #1 pour incrémenter A.
3.2.7 Comparaisons et branchements
Toutes les instructions que l'on a vues jusqu'à présent se déroulent les unes à la suite des autres. Mais un langage de programmation ne serait pas très intéressant, si l'on ne pouvait pas rendre des parties de code optionnelles (par des tests genre if) ou si l'on ne pouvait pas faire de boucle. L'assembleur 6502 permet donc plus ou moins de réaliser ces constructions. Il est en effet possible de « sauter » à une position du code (définie par un label) en fonction de l'état de certains bits du registre P (drapeaux).
Cela se fait en général en deux temps : on utilise d'abord une instruction permettant de positionner ces drapeaux, puis on fait appel à une instruction de saut conditionnel.
L'opcode CMP est très souvent utilisé pour la première partie. Il permet de comparer le contenu du registre A à une valeur donnée directement ou quelque part en mémoire. On peut voir cette instruction comme une soustraction entre A et la valeur. Par exemple, si on utilise CMP #42, le bit Z des drapeaux sera mis à 1 uniquement si A contient bien 42, le bit C (retenue) sera mis à 1 uniquement si A est supérieur à 42.
De la même façon, les opcodes CPX et CPY permettent d'effectuer une comparaison, mais avec le contenu des registres X et Y.
Une fois que les bits Z, N, C ou V sont positionnés comme on le souhaite, par une instruction de comparaison ou une autre (beaucoup d'opcodes modifient effectivement ces drapeaux, en fonction de leur résultat), on peut utiliser l'un des opcodes suivants afin de sauter à une autre partie du programme :
- BEQ label (Branch if EQual) saute au label si Z = 1 (si on a une égalité après une comparaison).
- BNE label (Branch if Not Equal) saute au label si Z = 0.
- BCS label (Branch on Carry Set) saute au label si C = 1.
- BCC label (Branch on Carry Clear) saute au label si C = 0.
- BMI label (Branch if Minus) saute au label si N = 1.
- BPL label (Branch if Plus) saute au label si N = 0.
- BVS label (Branch on oVerflow Set) saute au label si V = 1.
- BVC label (Branch on oVerflow Clear) saute au label si V = 0.
Exemple de test (de type if) :
... ; code qui modifie A
CMP #42 ; on compare A à 42
BCC plus_loin ; s'il est inférieur, on saute plus loin
... code que l'on ne veut exécuter que si A >= 42
plus_loin:
Exemple de boucle (exécutée 40 fois) :
LDX #0 ; on initialise X à 0
label: ; une boucle est un test avec saut en arrière
... ce que l'on veut exécuter 40 fois...
INX ; X = X + 1
CPX #40 ; On compare X à 40
BNE label ; Si X ne vaut pas 40, on boucle
Il arrive que l'on veuille aussi faire des sauts inconditionnels, par exemple pour créer des boucles infinies (sans condition de fin). On utilisera alors l'opcode JMP, qui réalise exactement cela et permet de faire des sauts n'importe où en mémoire, alors que les sauts conditionnels sont limités à 128 octets en avant ou en arrière.
Un dernier type de saut est l'appel de fonction, que l'on nomme sous-routine en assembleur. Cela se réalise avec l'opcode JSR (Jump to Sub-Routine) qui commence par mettre sur la pile l'adresse juste après la sienne, avant de réaliser un saut inconditionnel. Le bout de code appelé se termine en général par l'opcode RTS (ReTurn from Sub-routine), dont le rôle est de récupérer l'adresse de retour sur la pile, afin de pouvoir continuer l'exécution normalement par la suite.
Exemple :
...
JSR ma_fonction ; appel à ma fonction
... ; l'exécution se poursuivra ici
ma_fonction:
... ; le code de la fonction
RTS ; on retourne au code appelant
On notera qu'aucun mécanisme particulier n'est prévu pour passer des paramètres aux fonctions. On pourra les passer via les registres A, X ou Y, ou encore les placer sur la pile nous même (en se rappelant que sa taille est très très limitée). L’utilisation d’une pile d’appel permet toutefois à une sous-routine d'en appeler une autre sans soucis.
Il existe une variante à RTS nommée RTI (ReTurn from Interrupt). Cet opcode est utilisé à la fin d'une routine de traitement d'interruption. Au moment où une interruption survient, le processeur empile non seulement l'adresse de retour, mais aussi le registre des drapeaux, car une interruption peut survenir n'importe quand et donc possiblement entre un CMP et un BNE, par exemple. Dans ce cas, on doit pouvoir revenir exactement au point où on en était avant l'interruption. C'est pourquoi l'opcode RTI récupère à la fois l'adresse de retour et le contenu du registre des drapeaux sur la pile.
3.2.8 Empilage / dépilage
Comme nous venons de le voir, la pile est utilisée lors des appels aux sous-routines. Mais on peut l'utiliser directement pour y placer des données avec PHA (PusH A), qui place le contenu de A sur la pile et PLA (PulL A), qui fait l'inverse, en récupérant une valeur sur la pile et en la plaçant dans A. Plus rarement utilisé, les opcodes PHP (PusH P) et PLP (PulL P) permettent de faire de même avec le registre des drapeaux.
3.2.9 Instructions inclassables
Nous venons de voir 53 des 56 instructions du 6502. Les 3 restantes sont un peu particulières.
Commençons par BIT, qui prend forcément une adresse comme opérande. Les deux bits de poids fort de l'octet situé à cette adresse sont copiés dans N et V, et si le résultat d'un AND A aurait été de zéro, le bit Z est mis à 1. Cela me paraît hyper spécifique, et j'avoue ne pas avoir trouvé d'application directe de cet opcode, qui peut en revanche servir pour certaines astuces d'optimisation.
J'ai parlé précédemment d'interruption, sans vraiment définir ce dont il s'agissait. J'y reviendrai en détail dans un prochain article. En attendant, il suffit de savoir qu'une interruption peut être déclenchée (ce qui appelle automatiquement une sous-routine particulière) soit par le matériel, quand une patte particulière du 6502 change d'état, soit de manière logicielle. L'opcode BRK permet en effet de déclencher volontairement une interruption. Si l'utilité de cet opcode ne vous saute pas aux yeux, c'est assez normal, on ne l'utilise que dans des cas très particuliers.
Enfin, la dernière instruction supportée par le 6502 est simplement NOP. Cette instruction ne fait rien du tout ! Elle est généralement utilisée pour réaliser des boucles d'attentes.
4. Exemple d’application
Après ce parcours un peu indigeste de l’ensemble des instructions du 6502, vous avez bien mérité un exemple un peu amusant. Il s’agit de l’exemple, dont vous pouvez voir le résultat sur la figure 3.
Entrez ceci sur le site http://skilldrick.github.io/easy6502/, puis appuyez sur le bouton « Assemble ». Et si vous n’avez pas fait de faute de frappe, vous pourrez appuyer sur le bouton « run » et admirer le résultat.
Hormis la partie dessine_point (qui dessine un point aux coordonnées X et Y, avec la couleur A), vous êtes en mesure de comprendre comment ce petit programme fonctionne. Que ce soit le cas ou pas, n’hésitez pas à expérimenter en modifiant les valeurs, en changeant les instructions, etc. C’est en codant qu’on apprend !
LDY #0
STY $0
boucle_y:
TYA
TAX
boucle_x:
LDA $5
CLC
ADC $6
JSR dessine_point
DEX
BPL boucle_x
INY
CPY #32
BNE boucle_y
BRK
dessine_point:
STX $5
STY $6
PHA
TYA
LSR
LSR
LSR
AND #3
CLC
ADC #2
STA $1
TYA
ASL
ASL
ASL
ASL
ASL
ORA $5
TAY
PLA
STA ($00),y
LDY $6
RTS
5. La prochaine fois
Avec aussi peu de possibilités à notre disposition, on peut se demander comment on va pouvoir réaliser grand-chose. La réponse tient en deux idées fondamentales : les modes d'adressage, qui feront l'objet du prochain article, et qui montreront comment manipuler des structures de données complexes, et les astuces de programmation, qui vont nous permettre de faire des merveilles, en associant des opcodes qui semblent à première vue n'avoir rien à faire ensemble.
On n'a pour l'instant découvert que la face visible de ce formidable iceberg qu'est la programmation en assembleur.
Références
- http://www.obelisk.me.uk/6502/reference.html bonne documentation de référence, où chaque opcode est bien détaillé (en anglais malheureusement).
- http://nesdev.com/ le site de référence de la programmation sur NES en général et avec le 6502, en particulier.
- http://www.6502.org/ qui regorge d'informations, d'archives et d'astuces.