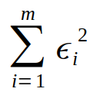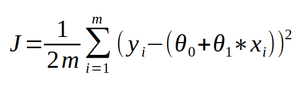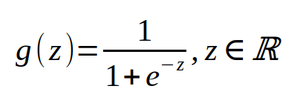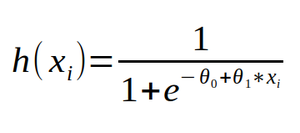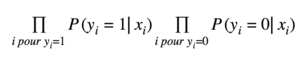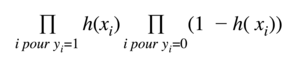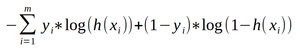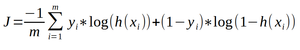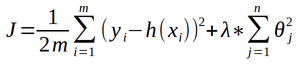Le Deep Learning est aujourd’hui de toutes les initiatives, de tous les discours. Aussi puissant qu'effrayant, il nous permet par exemple de rendre nos voitures autonomes, mais aussi de détecter automatiquement des visages dans une vidéo. Comme bien souvent, ça n’est pas la technologie elle-même qui est ou non morale, mais bien son application. Bien entendu, les questions d’éthiques inhérentes à ces sujets dépassent largement le cadre de cet article. Pour autant, une compréhension des mécanismes qui régissent ces solutions permettra au lecteur de se faire une idée plus précise et objective de la portée et de la validité de ces algorithmes. Précisons toutefois que ce travail se veut une introduction succincte s’appuyant davantage sur l’intuition que la rigueur purement mathématique. Ainsi, certains raccourcis scientifiques seront pris au profit de la fluidité et de la compréhension.
Le Deep Learning, c’est d’abord un genre d’algorithmes issus du Machine Learning, ou apprentissage automatique. Dans cet article, nous assimilerons l’apprentissage automatique à l’apprentissage supervisé : c’est-à-dire que nous avons accès à un ensemble de variables descriptives du problème, souvent notées X, et une variable que nous cherchons à prédire, notée y et appelée la cible. Nous voulons faire apprendre à la Machine un modèle qui permet de passer de X à y. Par exemple, si je cherche à prédire le prix d’achat d’un appartement (la cible), je peux utiliser des variables comme la surface, le nombre de pièces, la date de construction ou rénovation, mais aussi le cours des taux d’intérêt, le délai que le vendeur se donne, etc. Comment donc apprendre un modèle pour ce cas d’usage précis ?
Apprendre, une affaire de coûts
Bien que défrayant la chronique dernièrement, l’apprentissage automatique n’est pas une science nouvelle. La perspective d’enseigner à un automate, une machine à calculer, une tâche de manière automatique remonte même au prélude de l’informatique moderne.
Un questionnement historique
Le terme Machine Learning a été défini pour la première fois en 1959 par Arthur Samuel. Cette définition pourrait se traduire par « l’apprentissage automatique est le sujet d’étude qui fournit à un ordinateur la capacité d’apprendre sans être programmé de manière explicite ». Il est remarquable de constater que même si la notion d’ordinateur est nouvelle, les scientifiques s’interrogent déjà sur la possibilité de leur faire « apprendre » quelque chose.
Pour autant, cette définition n’est pas vraiment pratique. En effet, elle ne définit pas ce que signifie apprendre, ce qui rend ardue la possibilité de s’assurer que la machine arrive à le faire, d’autant plus si on ne doit pas la programmer explicitement. Cette première approche, plus métaphysique que scientifique, a toutefois permis de jeter les bases d’une réflexion qui aboutira bien plus tard.
Une définition plus pragmatique
C’est en 1998, soit près de quarante ans plus tard, que Tom Mitchell formalisera réellement une définition du Machine Learning, que nous utilisons encore à ce jour. Cette définition, la voici :
« On dit d’un programme informatique qu’il apprend d’une expérience E par rapport à une classe de tâche T et une mesure de performance P, si la performance de son exécution de la tâche T, mesurée par P, s’améliore avec l’expérience E »
En première remarque, nous ne parlons plus d’ordinateur, mais de programme informatique. Ensuite, cette définition introduit une notion fondamentale : la mesure de la performance.
Prenons l’exemple précédent comme illustration : la tâche T est de prédire le prix d’un appartement. Une expérience E est un exemple d’appartement pour lequel on a l’ensemble des valeurs des variables descriptives (surface, nombre de pièces, etc.) et la valeur de la variable cible (le prix d’achat). Il nous reste toutefois à choisir une mesure de la performance. Intuitivement, prenons comme mesure de la performance l’écart entre la valeur réelle du prix d’achat et la valeur que notre modèle prédit, et notons la P.
Si P tend vers zéro, alors notre modèle de prédiction est bon. Notre modèle, le programme informatique, apprend si en augmentant les expériences à sa disposition E, la prédiction du prix d’un appartement T s’approche de plus en plus vers la valeur réelle du prix de l’appartement, améliorant ainsi P.
Par conséquent, apprendre revient à améliorer une mesure de la performance de prédiction en ajoutant de l’information. Cet ajout, ce peut être davantage d’exemples d’apprentissage ou plus de variables descriptives. Cette hypothèse absolument fondamentale est ce qui va permettre de définir mathématiquement le Machine Learning.
Un modèle d’apprentissage que nous connaissons tous
Supposons que pour l’exemple d’apprentissage précédent, nous utilisons uniquement comme variable descriptive la surface du bien.
Un peu de formalisation
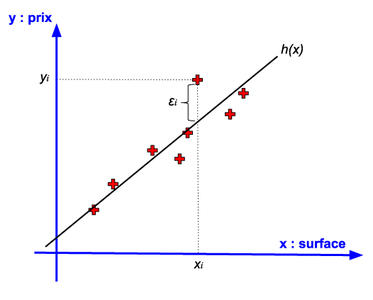
Nous disposons de quelques exemples d’apprentissages, notés (xi, yi), pour lesquels nous avons d’une part la surface du bien (xi), et d’autre part la valeur du prix d’achat (yi), que l’on représente sur la figure 1.
Fig. 1 : Un problème de prédiction d’une valeur continue : le prix d’un bien immobilier.
Les exemples d’apprentissage (les expériences) sont les points rouges. Au vu de la distribution des points, et compte tenu du fait que nous ne disposons que d’une variable (la surface) nous allons choisir un modèle affine pour la prédiction. En effet, il semble possible d’approximer le nuage de points par une droite ; nous allons donc définir le modèle, noté h comme hypothèse : h(xi)=ϴ +ϴ1*xi.
L’enjeu désormais est de déterminer le couple (^ϴ , ^ϴ1) qui permettra au modèle de prédire au mieux le prix des appartements en n’utilisant que la surface. Pour déterminer sa performance, nous allons définir l’erreur ϵi : ϵi=yi-h(xi).
Ainsi, si l’ensemble des ϵi tend vers zéro, les prédictions de notre modèle sont bonnes, et nous avons appris notre modèle à la machine.
Une mesure de la performance globale
Il est compliqué de considérer individuellement l’ensemble des erreurs pour mesurer la performance du modèle. Tout d’abord, avec cette définition, ϵipeut être positive si le modèle prédit une valeur inférieure à la valeur réelle, ou négative si le modèle prédit une valeur supérieure à la valeur réelle. Si on veut sommer les erreurs, nous allons avoir des effets de compensation qui ne reflèteront pas la performance réelle du modèle. Ainsi pour mesurer la performance globale du modèle, nous allons considérer la somme des erreurs au carré, soit :
Où m est le nombre de points considérés. Il s’agit d’une somme de termes positifs. Elle est nulle, donc minimale, lorsque l’ensemble des termes qui la composent sont eux-mêmes nuls. Par contre, cette somme croît avec le nombre d’expériences considérées. Ainsi, on préfèrera diviser la somme des erreurs par le nombre de points considérés, ce qui nous fournit la moyenne des erreurs au carré. On appelle cette fonction le coût, noté J, et défini dans sa forme développée comme :
Le problème d’apprentissage vient donc de se transformer en minimisation de la fonction coût. Si nous trouvons les paramètres (^ϴ , ^ϴ1) qui minimisent J, alors on pourra dire du modèle qu’il aura appris. Notons toutefois que cette forme de fonction coût est valable quel que soit mon modèle h.
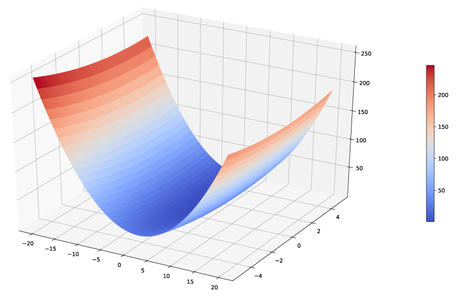
Comment trouver le minimum de cette fonction coût ? Mathématiquement, ce problème est relativement simple et nous pourrions en trouver une solution analytique. Cependant, il arrive que le modèle h soit bien plus complexe ; on ne pourrait pas trouver une solution par résolution d’équation. Une première stratégie consiste à en générer une surface représentative pour déterminer la solution. Une telle surface, dans le cas présent, ressemble à celle donnée en figure 2.
Fig. 2 : Surface représentative de la fonction coût J.
En ayant cet espace de points, on est capable de voir que le minimum de la fonction coût se trouve en un jeu de coordonnées de l’espace. Il y a cependant deux problèmes à cette approche.
Le premier, c’est que cette méthode est astreinte à, au plus, deux paramètres à déterminer. Au-delà, comme on ne dispose pas de méthode de visualisation à plus de trois dimensions, on serait incapable d’utiliser cette méthode essentiellement graphique.
La seconde et sûrement la plus importante, concerne la performance de cette recherche de minimum. En effet, pour déterminer un point optimal, on se retrouve, dans notre exemple, à calculer la fonction coût pour des centaines de milliers de couples. Le calcul d’un seul point prend un temps, certes court, mais non nul, ce qui n’est pas rentable d’un point de vue calcul. Sommes-nous en mesure de trouver une stratégie qui nous permette de déterminer le minimum de cette fonction coût en calculant un minimum de points ? En d’autres termes, que peut-on utiliser pour parcourir l’espace de la fonction coût de manière efficace pour en trouver le minimum ?
Une méthode vieille de près de quatre siècles
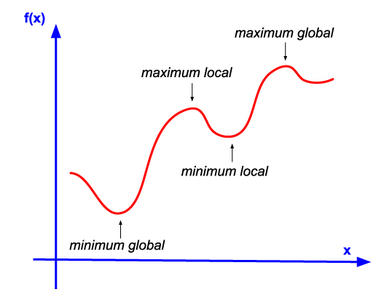
Si jamais le minimum de la fonction coût est unique, alors chercher localement le minimum nous amènera à trouver le minimum global. Dans notre exemple, de par sa convexité (la forme de bol), la fonction coût admet un minimum global.
Par ailleurs, supposons que je dispose d’un outil qui me permette, en un point donné de la fonction coût, de calculer la direction de plus forte croissance autour de ce point. En prenant l’opposé de cette direction, nous parcourons la fonction coût en direction d’un minimum local, et ce de manière optimale. Comme la fonction est convexe, cette stratégie nous amènera au minimum global.
Il se trouve qu’un tel outil existe, et qu’il est bien connu des mathématiciens ; il s’agit du gradient. En physique par exemple, le gradient de la température dans un volume est l’ensemble des vecteurs définis pour chaque point de l’espace par la direction des températures les plus froides vers les températures les plus chaudes.
La méthode de la descente de gradient se déroule ainsi pour notre exemple à deux variables :
- Je choisis au hasard un couple de départ (ϴ , ϴ1) pour lequel je calcule le coût J(ϴ , ϴ1) ;
- Je calcule le gradient du coût, noté grad(J(ϴ , ϴ1)). Il s’agit d’un vecteur qui, au couple (ϴ , ϴ1) donné, me donne la direction de plus forte croissance ;
- Je cherche un nouveau couple (ϴ , ϴ1) à partir du couple initial, tel que ce nouveau couple se trouve dans la direction exactement opposée au gradient, c’est-à-dire dans la direction de plus forte décroissance ;
- Je réitère jusqu’à convergence.
L’étape de convergence est la plus critique. Pour s’assurer d’une convergence régulière, une stratégie consiste à prendre la direction du gradient, mais d’en pondérer la norme : par exemple, on sait dans quelle direction chercher, mais on ne prendra que 10% de la norme du gradient. Cette approche conservative nécessitera plus d’itérations pour trouver le minimum, mais son évolution sera stable. Dans notre exemple, nous sommes sûrs de la convergence, du fait de la régularité de notre fonction coût.
En revanche, il existe des fonctions coûts non-convexes, qui admettent par exemple plusieurs minima locaux. Par exemple, la courbe représentative de la figure 3 nous montre une fonction avec plusieurs maxima locaux, un seul minimum global, et un minimum local.
Fig. 3 : Une fonction non-convexe.
Il a donc fallu trouver des méthodes qui permettent d’adapter le mécanisme de recherche à ces situations complexes. En réalité, le cœur de l’apprentissage d’un algorithme consiste à faire la recherche optimale de minimum ; ces méthodes d’optimisation sont le cœur de l’ingénierie du Machine Learning des 20 dernières années.
Nous avons réussi l’apprentissage de ce modèle, que le lecteur attentif aura reconnu comme étant la méthode des moindres carrés. Que peut-on dire de cette méthode pour des problèmes où la variable cible n’est pas continue ?
Régression, classification, mêmes outils
Lorsque la variable cible est continue, on parle de régression. En revanche, lorsque la variable cible est discrète, par exemple 0 ou 1, on parle de classification.
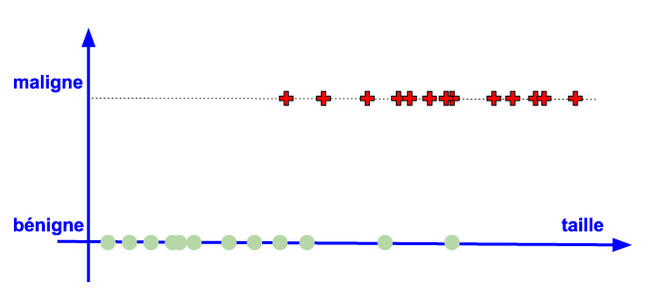
L’exemple historique pour les algorithmes de classification, certes peu joyeux, est la détection de tumeurs malignes. On cherche à prédire la probabilité qu’une tumeur soit maligne en fonction uniquement de sa taille. La répartition des points d’apprentissage est disponible sur la figure 4.
Une cible discrète
Pour le formalisme, on admettra ici que le critère bénigne correspond à 0 alors que le critère maligne correspond à 1.
Figure 4 : Un problème de classification.
Le modèle ici n’est plus une fonction continue, mais bien une probabilité. Ainsi, on définit h comme étant la mesure de probabilité qu’une tumeur soit maligne, en connaissant uniquement sa taille, soit h(xi)=P(yi=1|xi).
Comme h fournit une probabilité, il n’est pas question d’avoir une approche par régression affine. Pour cela, intéressons-nous à la fonction sigmoïde définie par :
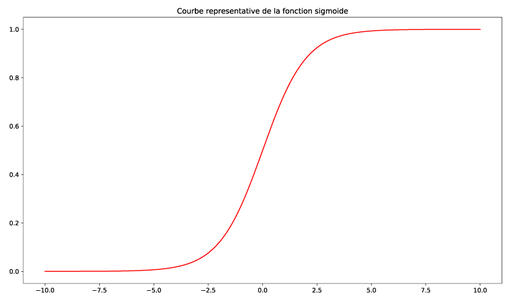
Sa courbe représentative est disponible en figure 5.
Figure 5 : La fonction sigmoïde.
On constate que la fonction sigmoïde projette l’espace des réels dans l’espace [0, 1], l’espace des probabilités, ce que nous cherchons précisément. Pour donner suffisamment de degrés de liberté au modèle h, nous n’allons pas utiliser la taille directement, mais une relation affine de la taille. Ainsi, la fonction sigmoïde se décalera le long de l’axe des abscisses au besoin grâce au coefficient ϴ . Le coefficient ϴ1, lui, permettra d’influencer la zone d’inflexion de la fonction sigmoïde. En d’autres termes, il permettra d’étaler ou de réduire la portion de courbe qui passe d’une valeur proche de 0 à une valeur proche de 1. En jouant sur ces deux paramètres, on cherchera à faire correspondre cette courbe à la distribution des données en apprentissage. Pour le modèle h, cela revient à dire que :
Il reste à déterminer (ϴ , ϴ1) tels que h colle au mieux à la distribution des données. On appelle ce modèle régression logistique, bien qu’il s’agisse d’un algorithme de classification.
Pour la régression, nous avons introduit à ce stade la fonction de coût égale à la valeur moyenne des erreurs au carré. On comprend facilement que cette fonction coût n’a aucun sens dans le cas où la variable à prédire est une classe. En effet, qu’est-ce que la différence entre la valeur réelle (0 ou 1) et la probabilité d’être un 1 ? Il va nous falloir déterminer une autre fonction de coût pour ce problème.
Le maximum de vraisemblance
Ce que notre modèle se doit de maximiser, c’est la probabilité correspondante à la valeur réelle. En d’autres termes, notre modèle est bon si :
- quand yi=1, h(xi) tend vers 1 ;
- quand yi=0, h(xi) tend vers 0.
Cela revient à maximiser la grandeur P(Y|X); cette grandeur, c’est la probabilité de réalisation de tous les yi en sachant tous les xi . La maximiser, c’est optimiser le maximum de vraisemblance. Essayons de dériver cette grandeur :
P(Y|X)
On considère que tous les yi sont indépendants. Cette probabilité est donc égale au produit des probabilités individuelles, donc maximiser ce terme revient à maximiser :
Or, les yi sont soit égaux à 0 soit égaux à 1 donc cela revient à maximiser :
Or, la probabilité d’être un 1 est le complémentaire de la probabilité d’être un 0 :
Or, on a construit h pour être la probabilité pour yi d’être un 1 sachant xi. On maximise donc :
La fonction qui transforme le produit en somme est le logarithme. Comme il est croissant sur son espace de définition, on maximise :
On va chercher à factoriser cette expression en utilisant le fait que yi est soit égal à 1 soit égal à 0, donc on maximise :
Ce qui revient à minimiser :
On tient presque notre fonction coût à minimiser ! On va juste appliquer un coefficient positif de moyenne, afin d’avoir une erreur moyenne par prédiction, donc on minimise :
Cette fonction coût J s’appelle la cross-entropy. On vient de démontrer que la minimiser revient à maximiser la vraisemblance. C’est la fonction coût qu’on utilise pour apprendre notre modèle.
Un formalisme qui passe à l’échelle
Nous admettrons que cette fonction coût est convexe. Il se trouve que la dépendance entre la variable et les poids à déterminer est linéaire ; c’est précisément le choix que l’on a fait pour la construire. Ce choix n’est pas anodin. En effet, on peut calculer le gradient de cette fonction coût, et chercher son minimum par descente de gradient, conformément à l’algorithme d’optimisation que l’on a décrit dans le cas de la régression. Ainsi, on détermine les paramètres ϴ et ϴ1 de la même manière qu’en régression pour l’apprentissage du modèle, de par sa linéarité.
Cette généralisation est d’ailleurs plus importante : même si j’ai un grand nombre de variables en entrée, tant que la dépendance est linéaire entre les paramètres du modèle et les variables en entrée, je serai capable de minimiser la fonction coût par descente de gradient et ainsi déterminer les poids optimaux pour apprendre mon modèle.
La définition de Tom Mitchell nous invite à augmenter l’information pour améliorer l’apprentissage du modèle. Pour ce faire, nous pouvons augmenter le nombre de variables du modèle, c’est-à-dire la dimension. Pour augmenter la dimension dans le cas où nous avons une seule variable descriptive, nous pouvons prendre des transformations de cette variable, et les plus élémentaires sont les élévations à la puissance. Par exemple, dans le cas de la régression, nous pouvons prendre le modèle :
Nous utilisons exactement la même fonction coût, et nous déterminons l’ensemble des poids par descente de gradient. Cette généralisation à dimension infinie est la puissance des méthodes linéaires, mais elle comporte une dérive importante ; elle empêche au modèle de généraliser.
Généralisation et performance, tout est affaire de compromis
Reprenons l’exemple de régression, mais seulement avec, par exemple, 5 points disponibles pour l’apprentissage. On cherche un modèle, qui prend en entrée la surface du bien, et qui prédit le prix de l’appartement. Nous venons de voir que nous pouvons prendre autant de puissances que l’on veut pour la variable en entrée de notre modèle.
Apprendre par cœur n’est pas comprendre
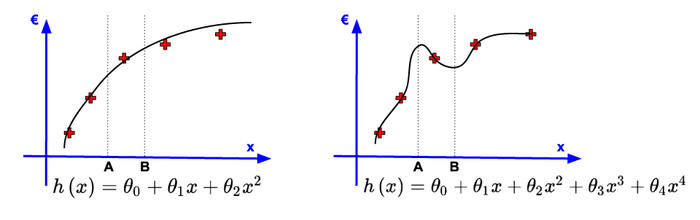
Selon cette logique, plus j’ai d’informations, plus j’ai de pouvoir pour prédire, donc je vais prendre le maximum de puissances possibles. Or, il existe un résultat fondamental en mathématique ; pour 5 points donnés, il existe un unique polynôme de degré au plus 4 qui passe par l’ensemble de ces points. Ce résultat se généralise, quel que soit le nombre de points : il s’agit des polynômes d’interpolation de Lagrange. Je peux donc minimiser la fonction coût au point de la rendre nulle, puisque la distance entre la valeur réelle et la valeur prédite est nulle. Une illustration d’un tel modèle est disponible en figure 6.
Fig. 6 : Comparaison de deux modèles de régression.
On compare le modèle de puissance 4 avec un modèle de puissance 2. On constate que le modèle de puissance 2 est plus éloigné des points d’apprentissage que le modèle de puissance 4, pourtant il semble plus naturel. En effet, si on doit utiliser ces deux modèles pour faire de nouvelles prédictions sur des points qui n’ont pas été en apprentissage, par exemple les points A et B, les prédictions du modèle de puissance 2 sont plus probables que les prédictions du modèle de puissance 4. Pour ce dernier, la surface de l’appartement B est plus grande que celle de l’appartement A, mais le prix de A est plus élevé que le prix de B, ce qui n’est pas physiquement cohérent. Ainsi, même si le modèle de puissance 4 a une fonction de coût nulle en apprentissage, il prédit moins bien que le modèle de puissance 2.
On dit du modèle de puissance 4 qu’il a sur-appris, c’est-à-dire qu’il a appris par cœur les données d’apprentissage, et qu’il ne généralise pas.
Comment s’affranchir de ce phénomène ? Déterminer a priori la bonne puissance ? Dans un cas multidimensionnel, cette intuition est très difficile à avoir. On va donc se munir d’un outil qui le fera automatiquement, et ce quelle que soit la dimension des données en entrée. Cet outil va agir directement sur la fonction de coût en apprentissage. En effet, il conviendra toujours de diminuer la fonction de coût, mais aussi d’ajouter un coefficient supplémentaire qui empêchera le sur-apprentissage. La nouvelle fonction coût s’exprime ainsi :
Le nouveau coefficient est la somme des poids au carré que multiplie un facteur λ. Cette somme est une somme de termes positifs. Elle est nulle lorsque tous les facteurs de la somme sont nuls, ce qui revient à dire que tous les poids sont nuls, sauf le poids ϴ .
Ainsi, si λ est infini, quelles que soient les valeurs des poids, la seule façon de minimiser la fonction coût est de choisir des poids nuls, et donc notre modèle se limitera à prédire une valeur constante ; on dit que le modèle a sous-appris. On peut voir ce terme comme un coût d’existence du poids ; si celui-ci a une valeur absolue qui n’est pas proche de 0, il doit significativement diminuer l’erreur de prédiction pour se justifier. À l’inverse, si son apport sur l’erreur de prédiction n’est pas significativement important, il sera nul, donc non considéré.
Par ailleurs, nous pouvons toujours calculer le gradient de la fonction coût, et ce sera cette nouvelle expression du gradient que nous utiliserons pour trouver le nouveau minimum de la fonction coût. Cette méthode s’appelle la régularisation, et grâce au formalisme que nous avons mis en place, elle s’applique également au cas de classification. Le facteur est une constante à déterminer, que nous prenons le plus souvent égale à 1, et que l’on optimise généralement en dernier.
Le compromis biais-variance
On comprend donc qu’un modèle est bon s’il est suffisamment complexe pour comprendre la distribution des données en entrée, ce que l’on appelle la variance, mais s’il est suffisamment régulier pour généraliser à de nouvelles données, ce que l’on appelle le biais. Parfois, la régularisation ne suffit pas pour s’affranchir du sur-apprentissage.
Tout l’enjeu est de trouver cet équilibre, idéalement de manière automatique. Pour ce faire, il nous faut deux ensembles de données. Le premier, que l’on va appeler le jeu d’entraînement, est celui sur lequel nous allons apprendre. Le second, que l’on va appeler jeu de test, est un ensemble de données pour lequel on a la valeur réelle de la cible, mais sur lequel on va mesurer la performance de notre modèle. Cette mesure nous renseignera sur la capacité du modèle à généraliser.
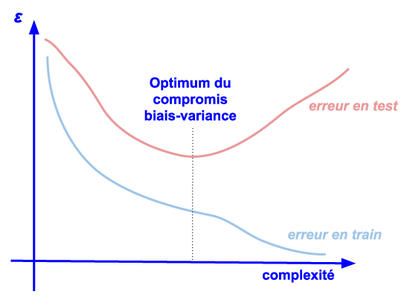
Dans notre cas linéaire, la complexité peut être le nombre de variables qu’on s’autorise pour l’entraînement. Suivre les courbes de performances en entraînement et en test en fonction de la complexité nous donne la figure 7.
Fig. 7 : Courbes d’apprentissage.
Lorsque mon modèle est trop peu complexe, l’erreur en entraînement et en test sont équivalentes, et diminue lorsque la complexité augmente ; le modèle sous-apprend. On peut augmenter cette complexité jusqu’à un point d’inflexion. Il s’agit du point à partir duquel l’erreur en entraînement continue de décroître, alors que l’erreur en test augmente. Au-delà de ce point, le modèle sur-apprend. Le compromis biais-variance correspond précisément à ce point d’inflexion : c’est l’optimum de complexité pour lequel notre modèle généralise au mieux, tout en ayant compris le plus finement la distribution des données en entrée.
Et le Deep Learning dans tout ça ?
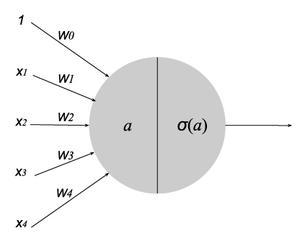
Le Deep Learning n’a pas révolutionné le domaine du Machine Learning par de nouvelles méthodes de calcul, des algorithmes complètement nouveaux, ou même des agents indépendants. Il permet un assemblage d’une complexité époustouflante des briques élémentaires que nous venons de voir, et particulièrement la régression logistique. Pour rappel, on peut représenter la régression logistique schématiquement, comme sur la figure 8
Fig. 8 : La régression logistique vue comme un neurone.
On parle d’une représentation sous forme de neurone. Ce neurone est composé de plusieurs caractères :
- des entrées : x1, x2, …, xn ;
- de poids associés à ces entrées : w0, w1, w2, …, wn. Par convention, on les appelle w et pas ϴ dans un réseau de neurones. Ils forment un produit scalaire avec les entrées, que l’on note a ;
- d’une fonction d’activation, ici notée σ, qui est la fonction sigmoïde. Notons qu’il en existe d’autres.
Il se comporte exactement comme la régression logistique que nous avons présentée précédemment. En revanche, cette représentation va nous permettre de créer un réseau de régressions logistiques.
Un réseau de neurones
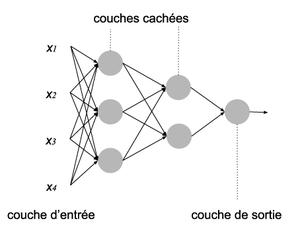
La véritable avancée du Deep Learning consiste à agréger ces neurones en des architectures complexes. On utilisera les mêmes fonctions coûts et la même méthode d’apprentissage, mais en passant à l’échelle. Une première idée d’architecture consiste à agencer ces réseaux par couches de plusieurs neurones, comme sur la figure 9.
Fig. 9 : Un réseau de neurones.
Cette architecture possède seulement deux couches cachées (si on ne compte pas l’entrée). On ne peut donc pas dire que c’est une architecture profonde. Il est important de noter qu’à chaque arête correspond un poids qui multipliera la sortie de la couche précédente pour nourrir l’entrée de la couche suivante. Notons que comme la brique élémentaire est une régression logistique, le problème est linéaire par rapport à ses variables d’entrée. On va donc sans surprise utiliser une descente de gradient pour entraîner ce modèle. Il y a cependant une petite particularité avec ce qu’on a vu pour la régression logistique.
Apprendre un modèle pas à pas
Le nombre de paramètres à déterminer a explosé avec l’architecture neuronale. Il s’agit en effet de l’ensemble des poids, chacun étant représenté par une arête, auquel on ajoute un poids supplémentaire par nœud, le biais, qui est en fait le w0. Par convention, nous ne le représentons pas sur le schéma. Le caractère profond du Deep Learning provient d’ailleurs du fait qu’en pratique, on a beaucoup plus de couches cachées. Apprendre l’ensemble de ces poids par descente de gradient sur une fonction coût est complexe. En effet, si je modifie le poids de la couche d’entrée, les valeurs d’entrée de la couche cachée changent, alors que je dois aussi changer les poids de la couche cachée. Ces interférences entre couches empêchent d’avoir une approche classique au niveau des itérations d’apprentissage. Il va nous falloir propager l’information de mise à jour dans toute la structure, pour que tous les poids s’actualisent en même temps. Cette propagation doit se faire dans les deux sens. Le premier consiste à passer de couche en couche l’information d’entrée, jusqu’à la couche de sortie. Ayant la valeur en sortie, on est capable de calculer la fonction coût. Puis dans un second temps, on propage le gradient de la fonction coût de couche en couche (dans le sens inverse de précédemment) pour pouvoir faire une mise à jour de tous les poids. Résumons l’apprentissage d’un tel réseau :
- On initialise tous les poids du réseau (arêtes et biais) ;
- On calcule la couche de sortie pour l’ensemble des points d’apprentissage : on appelle cette étape la forward propagation ;
- On calcule la fonction coût ;
- On calcule le gradient de cette fonction coût par rapport à chacun des poids du réseau : on appelle cette étape la back propagation ;
- On met à jour en même temps chacun des poids du réseau par descente des gradients calculés précédemment ;
- On itère à partir de l’étape 2 jusqu’à convergence.
On comprend donc le fort besoin de calcul d’un réseau de neurones pour l’entraînement ! On appelle cette approche l’apprentissage par batch : le gradient est égal à la valeur moyenne des gradients pour chacun des points d’apprentissage. C’est pour ces besoins de performances que nous nous sommes récemment orientés vers des calculs sur GPU, l’émergence de frameworks dédiés à ce type de calcul comme Tensorflow, voire l’apparition nouvelle de composants électroniques dédiés : TPU, FPGA...
Par ailleurs, les méthodes de régularisation que l’on a vues pour la régression logistique s’appliquent également ici. Elles sont prises en compte dans l’expression de la fonction coût.
Apprendre un modèle morceau par morceau
L’approche par batch est très stable : elle utilise l’ensemble des points pour faire une mise à jour. C’est parfois ce qui la contraint dans la recherche d’un optimum. De plus, pour cette méthode, l’étape d’entraînement est très gourmande en calcul. Il existe une autre méthode qui permet d’alléger la charge. En effet, le calcul de la fonction coût et donc de ses gradients consiste en une somme, somme qui comporte autant de facteurs que de points d’apprentissage. Une idée consiste à ne prendre qu’une partie des données disponibles, qu’on appellera un mini-batch, et de les utiliser pour l’apprentissage par forward/back propagation. On fera donc une mise à jour des poids par mini-batch, et on parcourra l’ensemble des données en itérant sur chacun des mini-batch. Lorsque tous les mini-batch ont été parcourus, on dit que l’on a réalisé une epoch. Dans cette configuration, l’ordre des mini-batch est important, puisque le premier mini-batch va influencer les poids du calcul pour le second mini-batch, etc. Cette approche, presque contre intuitive, va permettre au modèle d’apprendre plus rapidement, et surtout de manière moins contrainte, ce qui donnera des résultats potentiellement différents de l’approche par batch, mais bien souvent plus robustes et plus performants. La variante extrême de cette approche consiste à ne prendre qu’un seul point par mini-batch : c’est ce qu’on appelle de l’apprentissage stochastique.
Des architectures de plus en plus complexes
Ce procédé d’assemblage de briques élémentaires en des structures plus complexes, c’est ce qui permet de créer les architectures que l’on connaît et que l’on utilise aujourd’hui. En effet, si jamais l’information que je souhaite traiter s’agence géométriquement, comme dans une image, je vais faire en sorte que ma structure neuronale traite l’information localement dans l’image. Il s’agira de filtres, comme des patches que j’appliquerai à mon image pour en extraire l’information. La valeur de chacun des éléments de ces patchs se déterminera encore par descente de gradient. C’est précisément l’approche qu’utilisent les fameux réseaux de neurones convolutifs (Convolutionnal Neural Nets ou CNN).
En revanche, si mon information possède une structure séquentielle, comme dans le son, ou même le texte, je vais penser mon architecture neuronale pour qu’elle prenne en compte le point en cours (par exemple, le caractère de texte que je considère), mais aussi le ou les points précédents. Ces approches sont celles des réseaux de neurones récurrents (Recurent Neural Nets ou RNN). Une des formes les plus évoluées de ces réseaux sont les LSTM : Long Short Term Memory, que vous croiserez dans les prochaines pages. D’ailleurs, une architecture faisant l’objet d’un article est décrite figure 10. Elle possède deux cellules LSTM et une couche dense pour la prédiction, ce qui représente le nombre impressionnant de 850 000 paramètres à déterminer.
Fig. 10 : Prédire du texte ? Rien de plus simple.
Cependant, aussi élaborée soit la structure neuronale, qu’elle comporte plusieurs couches CNN ou RNN, que les neurones aient une fonction d’activation différente, retenez que ce sont de vastes modèles linéaires en entrée auquel on ajoute une non-linéarité par l’accumulation de couches et les fonctions d’activation. Cette propriété de linéarité, c’est ce qui va nous permettre d’apprendre nos inconnues, les poids de la structure neuronale, par descente de gradient.
Si vous ne deviez retenir qu’une chose (ou deux)
Le Machine Learning repose sur une hypothèse fondamentale : apprendre, c’est améliorer ma performance à l’exécution d’une tâche en ajoutant des exemples d’apprentissage. Cette approche très descriptive de la notion d’apprentissage conduit à un constat crucial. Tel que défini aujourd’hui, le Machine Learning repose uniquement sur la corrélation et non pas sur la causalité pour générer de nouvelles prédictions. C’est bien souvent suffisant, mais c’est précisément ce qui ne permet pas de construire des algorithmes vraiment intelligents.
Le Deep Learning, c’est d’abord une méthode de Machine Learning. On construit donc des modèles de Deep Learning avec un ensemble de données d’entrée pour lesquelles on dispose de la vraie valeur à prédire. Il convient ensuite de définir un ensemble de paramètres (le réseau) qui permettront de faire l’association entre les valeurs d’entrée et la valeur à prédire. Ces paramètres, nous les déterminerons comme étant ceux qui minimisent une fonction coût (la mesure de performance), et ce grâce à une méthode itérative et numérique inventée par Sir Isaac Newton : la descente de gradient. Notons que la plupart des architectures éprouvées sont des heuristiques qu’on utilise parce qu’elles marchent ; en Deep Learning plus qu’ailleurs, l’efficience fait preuve. L’aspect deep provient simplement du fait que le nombre de ces paramètres est absolument pharaonique, et qu’ils sont agencés dans des structures d’une complexité extrême. La contrepartie de devoir déterminer autant de paramètres est importante : il faut parfois passer par du matériel dédié pour que les temps de calcul soient admissibles, mais aussi, et surtout, il nous faut disposer d’une quantité impressionnante de données en apprentissage. L’avènement technologique du big data et l’invention de nouveaux hardwares ont permis relativement récemment d’obvier à ces contraintes, ce qui justifie l’essor actuel du Deep Learning.