Le « Radio Data System » est largement utilisé pour transmettre des informations numériques par voie hertzienne notamment pour le radioguidage (TMC). L’acquisition des blocs numériques reçus est décrite dans [1]. Une correction d’erreur de transmission est ensuite appliquée, en principe. On peut la simuler en restant très proche de l’implémentation matérielle par quelques lignes de code. Mais ce code est a priori mystérieux. On souhaite l’expliquer complètement de manière concise et faire quelques expériences pour tester les possibilités de correction. Les principes du RDS sont valables pour de nombreux autres codages.
1. Le codage RDS
1.1 Syndromes
À tout mot binaire m on associe le polynôme ayant m comme suite de coefficients (les degrés correspondent aux poids des bits). Le polynôme syndrome S(m)(x) est le reste de la division du polynôme m(x) par le polynôme générateur gen = x10 + x8 + x7 + x5 + x4 + x3 + 1. Les mots de code RDS sont des mots binaires m de 26 bits de syndrome S(m) nul.Les mots de code correspondent ainsi aux polynômes de degré au plus 25 divisibles par gen. Pour coder une information, par exemple en radioguidage l’avertissement « Gros animaux sur la route », on lit dans une table un mot de 16 bits, ici : [0100010000101011].
En fait, les 5 bits de gauche sont une information supplémentaire variable dont il est inutile de parler ici, la table donne les 11 autres bits.
On lui ajoute 10 bits nuls à droite pour obtenir 26 bits (qui ne forment pas encore un mot de code), m’ = [01000100001010110000000000], soit 0x110AE98, on divise le polynôme associé m’(x) = x24 + x20 + x15 + x13 + x11 + x10 par gen, obtenant S(m’)(x)=x⁹+x⁷+x⁴+x3, la somme des deux polynômes donne le mot de code m = [01000100001010111010011000]. Il s'agit de polynômes à coefficients entiers modulo 2, donc avec la règle 1 + 1 = 0, ce qui fait que l'opération m(x) + p(x) sur les polynômes correspond à l'opération xor, m ^ p sur les mots. Notons pour la suite l’additivité des restes : S(m ^ p) = S(m) ^ S(p). Comme m’ s’écrit 0x110AC00, on peut utiliser le code suivant comme dans [2] pour calculer son syndrome :
/* D'après https://github.com/bastibl/gr-rds */
#include<iostream>
#include<bitset>
using namespace std;
const unsigned long gen = 0x5B9;
//x^10+x^8+x^7+x^5+x^4+x^3+1;
const unsigned int gdeg = 10;
const unsigned int mlen = 26;
// ini vaudra 1
unsigned long int divise(unsigned long mot, unsigned long ini) {
unsigned long reg = 0;
unsigned int i;
for (i = mlen; i > 0; i--) {
//on traite les bits non nuls
if ((mot >> (i-1)) & 0x01) reg= (reg <<1) ^ ini ;
//multiplication par x
else reg = (reg << 1) ;
//syndrome
if (reg & (0x01 << gdeg)) reg = reg ^ gen;
}
return(reg);
}
int main(void) {
unsigned long message,sortie ;
cout << "Entrer le message, exemple 9726E0" << endl;
cin >> hex >> message ;
sortie=divise(message,1);
cout << "Le syndrome est "<< hex << sortie << endl;
bitset<10> binaire(sortie); cout << binaire << endl;
return 0;
}
Il faudra comprendre ce code un peu plus loin pour aborder la correction d’erreurs.
1.2 Détection d’erreurs
Quand le syndrome d’un mot reçu est non nul, il y a eu une erreur de transmission. Un unique bit d’erreur est forcément détecté parce qu’aucun monôme xa n’est multiple de gen, et de même une erreur de deux bits est détectée parce qu’aucun binôme xa + xb de degré au plus 25 n’est divisible par gen. Mais une erreur de trois bits aux poids 6, 16, 25 soit 0x2010040 n’est pas détectée. Il ne faut cependant pas se décourager, car il n’y a que 7 configurations de trois bits indétectables sur 2600 possibles. Une salve de longueur l (anglais : burst) estun mot dont tous les bits sont nuls en dehors de l places consécutives (l’erreur précédente est une salve de longueur 20). On constate que les erreurs de transmission radio forment le plus souvent des salves de longueur relativement petites. Une salve d’erreurs de longueur 10 sera toujours détectée parce qu’un polynôme xap(x)n’est pas divisible par gen quand p est de degré au plus 9. On peut vérifier que ce codage détecte 99,8 % des salves de longueur au plus 11 et 99,9 % de toutes les salves.
2. Correction d’erreurs
2.1 Principe de Kasami
Dans l’article [4], T. Kasami a montré que le choix du générateur gen et de la taille 26 permettait de corriger tout mot de code perturbé m ^ b par une salve b d'erreurs de longueur au plus 5. On appellera par la suite « petite salve » toute salve de longueur au plus 5. La propriété fondamentale vérifiée par Kasami est « il n'y aucun mot de code RDS formé par deux petites salves distinctes b ^ b’ ». Supposons que l’erreur b d’un mot de code perturbé par une petite salve d'erreurs, m ^ b, soit piégée (anglais : trapped) c'est-à-dire que le syndrome S(b)= S(m ^ b) ait tous ses bits nuls en dehors des 5 bits de poids de 5 à 9, (comme 0x1f). Alors S(b) est aussi une petite salve et S(b) ^ b est un mot de code RDS formé de deux petites salves, donc on a trouvé l’erreur, car d’après Kasami b = S(b). Pour se ramener à cette situation, il faudra utiliser la cyclicité.
En fait, le code de Kasami comporte 27bits, mais seuls 26 sont utilisés enRDS.
2.2 Code cyclique associé
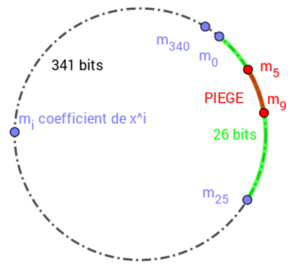
Fig. 1 : Code RDS.
Le code RDS est un code raccourci du code de longueur 341 définit par le même générateur gen (voir figure 1). On peut compléter à gauche les 26 bits d’un mot de code RDS par des 0 pour obtenir un mot du grand code. Le polynôme cycle(x) = x341 - 1 = x341 + 1 est divisible par gen(x) et cela explique le choix de 341 comme le plus petit entier convenable. Étant donné un mot m de longueur 341 et un polynôme P, on notera P*m le mot de même longueur correspondant au reste modulo cycle(x) de P(x)m(x). En particulier, x*m est le mot décalé à gauche d'une place, circulairement, le bit de poids 340 devenant de poids 0. Comme gen divise cycle, tout mot décalé d'un mot du code 341 reste dans le code : c'est un code cyclique. La propriété de Kasami s’adapte : « il n'y a pas de mot du code 341 formé de deux petites salves distinctes, et tel que les places des bits non nuls soient dans un arc d'amplitude 26 », un arc étant un intervalle modulo341 comme {23, 22, ..., 0, 340, 339}. On se ramènera à cette situation par décalages (x* )d pour piéger une petite salve d’erreurs. Une propriété très utile venant directement de la définition de la division est : S(P*m) = S(P*S(m)) = S(S(P)*m), pour tout polynôme P et mot m de longueur 341. Elle permet d’expliquer le codage de calcul du syndrome puis celui de la correction d’erreurs.
2.3 Calcul du syndrome
Pour calculer le reste par gen d'un monôme xa, on utilise récursivement la relation S(x*xa - 1) = S(x*S(xa - 1)). La multiplication par x se code comme décalage à gauche <<. Comme les syndromes sont de degrés au plus 9, après un décalage le calcul du reste ne comporte que deux cas de figure suivant que le quotient est 0 ou 1. Pour le monôme précédent, on devrait faire une boucle de durée a, mais on va faire une boucle de longueur fixe 26, qui tourne à vide (reg = 0) tant que l'initialisation reg = ini, (ini = 1) n'entre pas en jeu au bon temps où le monôme est détecté dans un mot donné. Le premier if fait cette initialisation. Les calculs des syndromes de tous les monômes d'un mot sont combinés dans la même boucle.
2.4 Correction d’erreurs
Avant de coder, on peut prévoir que, si l’on sait qu’il n’y a qu’un bit d’erreur, il peut être corrigé : xa et xb ont des syndromes différents, car xa + xb n’est pas dans le code (a < b < 26). On peut trouver ainsi la position a par une table de syndromes (voir [1]). Par contre, comme me l’a signalé J-.M. Friedt, on ne peut pas toujours distinguer, donc corriger deux bits d’erreurs par leur syndrome (voir le complément à son article dans l’encadré). Une erreur de deux bits de poids 25 et 13 soit 0x2002000 a, par exemple, le même syndrome que deux bits d’erreurs de poids 20 et 2, soit 0x100004.
Erratum
En page 29 de GNU/Linux Magazine 204 [1], nous avions remarqué que « (…) pourquoi [m2runiq,m,n]=unique(m2r,'rows'); renvoie moins de lignes dans m2runiq qu'il n'y en a dans m2r, alors que toutes les lignes sont uniques ? ». La réponse est simple : parce que nous avions fait une erreur dans l'analyse des lignes de la matrice contenant les syndromes permettant d'attribuer une double erreur à une paire de bits. En effet, nous avions mal utilisé la fonction uniq(), et la recherche des doublons dans la matrice de corrections d'erreurs aurait du être :
[m2runiq,m,n]=unique(m2r,'rows'); % length(m2runiq)~=length(m2r)
length(m2runiq) % => bits differents donnent meme syndrome
u=1;
for k=1:length(m2r)
num=ismember(m2r,m2r(k,:),'rows');
if (sum(num)>1)
double(:,u)=find(num==1)' % lignes identiques ?
solution(double(1,u),:) % position 1er bit errone'
solution(double(2,u),:) % position 2nd bit errone'
u=u+1;
end
end
Cela prouve-t-il que RDS, contrairement à notre affirmation, ne sait pas corriger deux fautes dans le message ? L'erreur vient de notre lecture superficielle de la documentation technique, qui précise bien ([3], p.14) :
The error-protecting code has the following error-checking capabilities:
a) Detects all single and double bit errors in a block.
b) Detects any single error burst spanning 10 bits or less.
c) Detects about 99.8% of bursts spanning 11 bits and about 99.9% of all longer bursts.
The code is also an optimal burst error correcting code [5] and is capable of correcting
any single burst of span 5 bits or less.
Ainsi, la norme RDS n'affirme pas pouvoir corriger toutes les erreurs doubles sur les blocs transmis, mais uniquement détecter ces erreurs, et corriger des séquences de bits erronés séparées de 5 bits ou moins. Par exemple, une erreur sur les bits 3 et 8 (séparés de 6 bits donc) fournit le même syndrome qu'une erreur sur les bits 15 et 26. Il y a 9 cas où une double erreur est attribuée de façon erronée à une autre séquence de bits (m2runiq contient 316 éléments), sur les 325 cas possibles. Le taux de succès sur la correction de doubles erreurs est donc de 1 - 9 / 325 = 97,2 %.
J.-M. Friedt
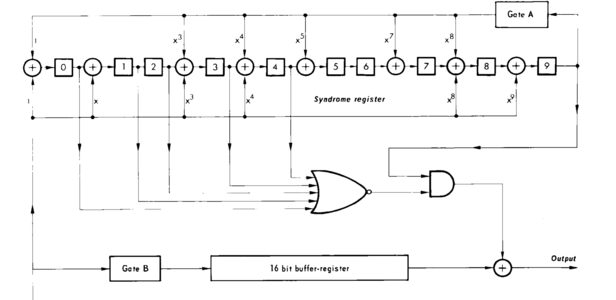
Le code de correction suivant suit d’assez près l’implémentation matérielle proposée dans [3] (voir figure 2) et est inspiré de [5]. Il est placé dans https://github.com/gilles1728/trapping-error-rds :
/* d'après http://www.the-art-of-ecc.com/3\_Cyclic\_BCH/RBDS.c */
#include<iostream>
#include<bitset>
using namespace std;
const unsigned long gen = 0x5B9;
const unsigned int gdeg = 10;
const unsigned int mlen = 26;
bool echec = 1 ;
unsigned long int divise(unsigned long mot, unsigned long ini) {
// voir code de division précédent
{
unsigned long int corrige(unsigned long message) {
int decale ;
const unsigned long trap= 0x1f;// piège
unsigned long prem = 0x31b;// x^9+x^8+x^4+x^3+x+1
unsigned long reg;// =x^325 mod gen
reg=divise(message,prem) ;// ini=prem
for (decale=16 ; decale>0 ; decale--) {
reg=divise(reg,1) ;// syndromes successifs
if ( (reg & trap) == 0 ) {
echec = 0 ; break ;
}
reg=(reg << 1);
}
reg= (reg << decale );
reg = message ^ reg ;
return(reg) ;
}
int main(void) {
unsigned long entree,sortie ;
cout << "Entrer le message, exemple 9726E0" << endl;
cin >> hex >> entree ;
sortie=corrige(entree);
if (echec) cout << "pas de piégeage" << endl;
else {
cout << "le message estimé est " << hex << sortie << endl;;
bitset<26> binaire(sortie);
cout << binaire << endl;
}
return 0;
}
Fig. 2 : Implémentation matérielle [3].
Les décalages à gauche (sens horaire sur la figure 1) que l'on opère ne doivent pas faire sortir un mot à corriger m’ de la situation de piégeage (m’ et S(m’) dans un arc de longueur 26). Pour éviter cela, on le décale circulairement 325 fois sur sa gauche, c'est-à-dire qu'on pré-multiplie par x325 le polynôme correspondant du code 341 (et on prend le reste modulo cycle). Pour calculer le syndrome correspondant, il suffit, comme dans [5], de pré-multiplier au préalable par le polynôme prem = S(x325) = x⁹ + x⁸ + x⁴ + x³ + x + 1 puisque S(x325*m’) = S(S(x325)*m’) = S(prem*m’).
On multiplie les monômes de m’(x) par prem et on les traite de la même manière que dans l'algorithme de calcul de syndrome, ce qui revient à initialiser les boucles de division par ini = prem au lieu de ini = 1. Si l’erreur est une petite salve b sur les bits forts (poids de 21 à 25), on la pousse dans le piège par le décalage de 325bits et elle devient une salve c identifiée par c = S(c) = S(prem*b) = S(prem*m’) . Une petite salve placée de manière quelconque est piégée par des décalages supplémentaires lors d'une boucle. La propriété de Kasami garantit que le syndrome n’est dans le piège qu’au moment où l’erreur y est poussée, ce qui permet de trouver la position de b.
On peut tester la fonctionnalité de la correction sur toute modification par une petite salve d'erreur d’un mot de code. En particulier, toute modification d'un chiffre hexa est corrigée. Bien sûr, tout peut arriver avec des erreurs plus « rusées ». D’une part, le piégeage peut ne pas fonctionner. Mais le procédé de correction peut donner aussi des résultats surprenants. Par exemple, en radioguidage le message « Voie(s) de dépassement fermée(s) »de code 0x100A69A perturbé par seulement 2 bits d’erreur aux poids 20 et 1 se déforme en 0x110A698 qui se corrige en 0x110AE98 signifiant « Gros animaux sur la route ». Les couples de bits pouvant donner lieu à ce phénomène sont assez nombreux (25 sur 325). Notons qu’une erreur indétectable donc non corrigée comme celle sur 3 bits 0x2010040 peut donner lieu aussi à des quiproquos : « Manifestation importante, Trafic en accordéon » se déforme en « Match de boxe »(oui ça existe !).
Conclusion
La correction d’erreurs RDSest bien adaptée aux petites salves d’erreurs. Comme elle peut fournir des résultats incorrects, des précautions supplémentaires sont bienvenues. Par exemple, dans certaines sociétés de radioguidage TMCun groupe d’information est émis trois fois, et on n’affiche le message que si deux des trois résultats de décodage sont identiques (un groupe consiste en quatre mots de code, l’un indique comme on l’a vu l’avertissement routier, les autres, en particulier, la localisation de l’événement et la station de radio utilisée).
Remerciements
Je remercie J.-M. Friedt et F. Royer pour des échanges fructueux.
Références
[1] FRIEDT J.-M., « Radio Data System (RDS) analyse du canal numérique transmis par les stations radio commerciales, introduction aux codes correcteurs d'erreurs », GNU/Linux Magazine n° 204, mai 2017, p.12 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-204/Radio-Data-System-RDS-analyse-du-canal-numerique-transmis-par-les-stations-radio-FM-commerciales-introduction-aux-codes-correcteurs-d-erreur
[2] BLOESSL B. : https://github.com/bastibl/gr-rds .
[3] Standard RDS : http://www.interactive-radio-system.com/docs/EN50067_RDS_Standard.pdf
[4] KASAMI T., « Optimum shortened cyclic codes for burst-error-correction », IEEE Trans. Inform. Theory, vol. IT-9, pp. 105- 109, Jan.1963.
[5] MORELOS-ZARAGOZA R.H., « The Art of Error Correcting Coding », Second Edition, John Wiley & Sons, 2006 : http://www.the-art-of-ecc.com/3\_Cyclic\_BCH/RBDS.c