La transformée de Hough propose un passage de l’espace bidimensionnel de l’image acquise par un capteur optique (caméra) vers l’espace des paramètres représentant des structures géométriques recherchées dans l’image – droites, cercles, et coniques dans les exemples qui sont abordés. Cette méthode de traitement d’images, généralisable à tout motif paramétrable par un jeu d’équations, est présentée sur trois cas concrets d’utilisations sur des images réelles.
De nombreuses applications de traitement d’images nécessitent de trouver des motifs géométriques dans une image, qu’il s’agisse du cas trivial de lignes (navigation d’un véhicule sur une chaussée marquée de lignes), ou plus complexe tel que nous l’illustrerons ici, de cercles ou de coniques. La transformée de Hough [1][2] vise à convertir une image dont les pixels représentent une distribution spatiale d’intensité lumineuse (sortie d’un capteur d’intensité lumineuse derrière un montage optique de focalisation) vers un espace représentatif des paramètres de la structure géométrique recherchée. Par exemple, une droite dans l’espace (x, y) s’exprime par
: la transformée de Hough dans l’espace des paramètres de la droite passe de (x, y) vers (a, b). Le cas de la droite est simple, car nous passons de deux dimensions à deux dimensions, facilement représentable sur une image. Le cas du cercle ou de la conique sera à peine plus complexe puisque l’espace d’arrivée est à plus de deux dimensions : pour un cercle, nous aurons les coordonnées de son centre (xc, yc) et son rayon R. Une façon d’ajouter cette troisième dimension consiste à réaliser un film dans lequel Révolue dans le temps.La philosophie de la transformée de Hough est de partir de l’espace d’arrivée – celui des paramètres du motif géométrique recherché – et de tester de façon exhaustive si les pixels de l’image d’entrée sont distribués sur le motif recherché. Pour chaque série de paramètres, la somme des intensités des pixels issus du capteur optique est assignée au point correspondant au jeu de paramètres en cours : la somme ne deviendra significative que si les pixels sont « convenablement » distribués le long du motif. Cette opération peut devenir très fastidieuse si nous testons tous les pixels possibles : pour une image de N x N pixels, nous devrons sommer les N2 pixels pour N2 valeurs des paramètres. Un motif ne concerne cependant que les bords de l’objet détecté : une balle n’est ronde que parce que sa circonférence représente un cercle, tandis que le motif de la balle elle-même est sans intérêt. Il est donc classique de précéder la transformée de Hough d’une détection de bords, dont l’implémentation la plus simple est le gradient. En effet, un « bord » se définit comme une rupture entre un premier motif (couleur de fond) et un second motif (couleur de l’objet), donc une dérivée significative. Une dérivée spatiale est un gradient, que nous calculons selon les deux directions de l’image X et Y, pour en déduire le critère de bord de l’image pour chaque pixel P :
. Un seuil permet alors de ne sélectionner que les pixels pertinents et de réduire considérablement le temps de calcul, et la robustesse de la détection, en ne conservant que le pourtour des objets à détecter.Nous allons appliquer ces concepts à trois cas concrets : la détection de droites dans les images utilisées notamment pour diriger un véhicule (détection des bandes de signalisation sur une route), la détection de cercles dans les images de gouttes d’eau déposées sur des surfaces dont l’énergie est représentative des fonctions chimiques en contact avec le solvant (méthode de l’angle de contact pour caractériser une surface), et finalement détection d’hyperbole dans les images issues de RADAR dont l’antenne se déplace linéairement au-dessus d’une cible ponctuelle.
1. Détection de droites
Nous allons nous familiariser avec un cas trivial de détection de droites dans une image réalisée spécifiquement à cet effet (voir figure 1). Formatés que nous sommes à penser en coordonnées cartésiennes, il semble naturel d’exprimer l’équation d’une droite sous forme
et rechercher les couples (a, b) qui correspondent le plus probablement aux droites visibles sur une image. Une mise en pratique démontre rapidement les faiblesses de cette approche : alors que le coefficient b, l’ordonnée à l’origine, est en unité de pixels et s’intègre naturellement dans le traitement, le coefficient a varie dans le premier octant de à 1 (une variation peu favorable au calcul sur des entiers), puis dans le second octant de 1 à (cette seconde borne étant très difficile à atteindre en pratique)... l’expression de a comme pente de la droite ne s’exprime pas simplement dans une distribution linéaire de valeurs du paramètre sur un nombre fini d’échantillons discrets le long d’un des axes dans le domaine de la transformée de Hough. Une façon plus intuitive [3] consiste à exprimer l’angle que fait la droite considérée avec l’axe des abscisses : évidemment a et sont reliés par le fonction tan(), mais cette fonction allant de à p de façon non-linéaire, il sera plus simple d’exprimer – distribué régulièrement de à selon l’axe des abscisses du domaine de destination (de Hough) que d’exprimer a. La seconde variable dans l’expression polaire de la droite est , la distance de la droite à l’origine. Dans ce contexte, une droite de la forme s’exprime aussi et le domaine de Hough consiste à transformer l’ensemble des points remarquables (x, y) vers les valeurs les plus probables de définissant les droites selon lesquels les points d’intérêt se distribuent.Fig. 1 : De gauche à droite : image d’une route (avenue de l’Opéra) avec sa signalétique ; identification des droites remarquables dans une image synthétique représentative des caractéristiques de la photographie originale.
Nous nous familiarisons dans un premier temps sur des images synthétiques (voir figure 2) avant d’appliquer ce traitement à une image réelle (figure 1). Dans ce premier exemple, nous nous sommes efforcés d’indiquer par un cercle les points caractéristiques dans le domaine de Hough des paramètres polaires
représentatifs de(s) droite(s) visible(s) en blanc sur un fond noir. Le premier cas montre bien un unique point de forte probabilité dont l’abscisse représente la pente et l’ordonnée la distance à l’origine. Le second cas démontre la pertinence de l’analyse puisqu’une seconde droite parallèle à la première indique un second jeu probable de paramètres représentatifs des structures géométriques, à la même abscisse (même pente), mais d'ordonnées différentes (distance à l’origine différente). Les troisième et quatrième cas démontrent que l’abscisse des paramètres est bien la pente de la droite puisque changer cette pente fait varier l’abscisse d’un des jeux de paramètres probables.Fig. 2 : De gauche à droite : divers cas de droites avec pentes (abscisse dans la transformée polaire de Hough) et distance à l’origine (ordonnée dans la transformée polaire de Hough) variables.
En manipulant une structure de données contenant une image codée en tons de gris sur un octet (*p) et ses dimensions (xet y) :
struct image {unsigned char *p;int x; int y;int bpp;};
Alors, le gradient de l’image d’entrée s’obtient dans une nouvelle structure de données par :
01: pictin=(struct image*)malloc(sizeof(struct image));
02: pictin->x=pict->x;pictin->y=pict->y;pictin->bpp=255;
03: pictin->p=(unsigned char*)malloc(sizeof(unsigned char)*pictin->x*pictin->y);
04: for (x=0;x<pictin->x-1;x++)
05: for (y=0;y<pictin->y-1;y++) // calcul du gradient : P sur 1 octet donc P*P/255\in[0..255]
06: {pictin->p[x+y*pictin->x]=(((pict->p[x+1+y*pict->x]-pict->p[x+y*pict->x])*\
07: (pict->p[x+1+y*pict->x]-pict->p[x+y*pict->x]) \
08: +(pict->p[x+(y+1)*pict->x]-pict->p[x+y*pict->x])*\
09: (pict->p[x+(y+1)*pict->x]-pict->p[x+y*pict->x]))/255);
10: if (pictin->p[x+y*pictin->x]>max) max=pictin->p[x+y*pictin->x];
11: }
12: for (x=0;x<pictin->x-1;x++)
13: for (y=0;y<pictin->y-1;y++)
14: if ((float)pictin->p[x+y*pictin->x]>((float)max*0.01)) // sature le gradient
15: pictin->p[x+y*pictin->x]=255; else pictin->p[x+y*pictin->x]=0;
Puis, ayant obtenu cette image des gradients saturée qui indique les points significatifs, nous appliquons la transformée de Hough elle-même, en exploitant une table de sinus et de cosinus pré-calculée puisque les angles pour lesquels se fait la recherche sont déterminés par le nombre de pixels en abscisse de l’espace d’arrivée :
01: float dtheta,theta,*smat,*cmat,tmp;
02: dtheta=M_PI/(float)(psize);
03: smat=(float*)malloc(sizeof(float)*psize); // x*cos(th)+y*sin(th)=rho
04: cmat=(float*)malloc(sizeof(float)*psize); // th selon l’abscisse : precalcule sin() et cos()
05:
06: tmpi=(int*)malloc(sizeof(int)*psize*psize); max=0;
07: for (i=0;i<psize*psize;i++) tmpi[i]=0;
08: i=0;
09: for (theta=0;theta<M_PI;theta+=dtheta) {smat[i]=sin(theta);cmat[i]=cos(theta);i++;}
10: for (i=0;i<psize*psize;i++)
11: {if (pictin->p[i] == 255) // ne garde que points significatifs
12: {for (x=0;x<psize;x++) // % : modulo = x et / : division entiere = y
13: {tmp=(float)(i/psize-(psize>>1))*smat[x]+
14: (float)(i%psize-(psize>>1))*cmat[x]+(float)(psize>>1);
15: if (( (int)rint(tmp)<psize) && ((int)rint(tmp)>0) )
16: tmpi[(int)rint(tmp)*psize+x]++; // note de chaque couple de params (th,rho)
17: }
18: }
19: }
Ici psize est la grandeur maximum entre la hauteur et la largeur de l’image d’entrée.
Comment ces figures dans le domaine de Hough ont été obtenues ? Dans un premier temps, les points remarquables sont identifiés, ici trivialement par seuillage puisque nous sommes dans un cas idéal sans bruit, avec des droites blanches sur fond noir. L’espace de destination est une nouvelle image, initialement vide (initialisée à ), de la même taille que l’espace de départ (par homogénéité avec les paramètres exprimés en pixels), mais cette fois dont l’ordonnée représente
et l’abscisse . Pour toute valeur de (boucle sur l’axe des abscisses), et pour chaque point remarquable de l’image d’entrée, nous ajoutons une unité à l’ordonnée tel que . Nous prenons bien sûr soin de vérifier que est positif et inférieur à l’ordonnée maximale de l’image d’arrivée pour éviter d’accéder à une zone non-allouée de la mémoire. Cette accumulation de paramètres probables est itérée pour toutes les colonnes de l’image d’arrivée (boucle sur ) et pour chaque point remarquable de l’image de départ. À la fin, l’image d’arrivée présente des pixels d’autant plus clairs que le jeu de paramètres correspondant est plus probable : un seuillage dans cet espace d’arrivée donne les paramètres des droites identifiées dans l’image de départ.Le cas d’une « vraie » image est rendu à peine plus complexe par l’étape de prétraitement qui doit permettre d’identifier les pixels distribués le long des droites avant d’en extraire les paramètres par transformée de Hough : dans ce cas, les bords des bandes qui nous intéressent sont détectés par des gradients (passage du blanc au noir) selon les directions des abscisses et des ordonnées. Le critère critique dans l’identification des bandes est le seuil sur le gradient : ici ce seuil est sélectionné manuellement, et un algorithme robuste de seuillage en illumination naturelle est complexe à identifier [4]. Dans ce cas particulier, le résultat est convaincant, et une comparaison entre la transformée de Hough du gradient de l’image et un cas synthétique dans lequel les droites ont été tracées manuellement sur un fond noir (cas idéal non-bruité) permet de retrouver quelle droite correspond à quel jeu de paramètres dans l’espace de Hough (voir figure 1, droite).
Nous verrons que ces calculs deviennent d’autant plus longs que l’espace des paramètres est grand. Ici, seuls deux paramètres
sont recherchés, mais sur une image de résolution typique d’un capteur actuel (8, 10 Mpixels), le calcul prend déjà plusieurs secondes, un délai inacceptable dans de nombreuses applications de navigation. Notre choix s’est donc porté directement sur une implémentation en C au lieu d’un prototypage sous GNU/Octave comme nous le verrons plus loin (cas des hyperboles) : les sources permettant de lire une image au format BMP, calculer les gradients en abscisse et ordonnée, seuiller puis calculer la transformée de Hough, sont disponibles sur http://jmfriedt.free.fr/hough.2. Une surface propre est une surface qui mouille
2.1 Paramètres du cercle représentant au mieux une calotte sphérique
Ayant compris le concept sous-jacent à la transformée de Hough – à savoir accumuler les valeurs les plus probables des paramètres représentant les courbes selon lesquelles s’agencent les points remarquables d’une image – nous pouvons étendre le principe à la recherche de cercle. Un cercle est caractérisé par son centre (xc, yc) et son rayon R, reliés par l’équation (x-xc)2+ (x-xc)2= R2. Un ensemble de points de coordonnées (x, y) supposés distribués sur la circonférence d’un cercle doivent respecter cette équation, donc nous recherchons les valeurs communes de {xc, yc, R}. S’agissant de trois paramètres (donc un espace à 3 dimensions dans lequel nous recherchons une solution optimale), il n’est pas facile de le représenter sur une image (de dimension 2). Nous nous proposons donc d’explorer l’espace (bidimensionnel) des centres possibles du cercle (xc, yc) pour un paramètre qui évolue dans le temps qu’est le rayon R. Ainsi, pour chaque valeur de R, la transformée de Hough consiste à accumuler les valeurs possibles de
avec xc l’abscisse dans le domaine de Hough et yc son ordonnée, pour chaque point remarquable (x, y). La valeur de R qui permet de maximiser un couple (xc, yc) fournit le triplé des paramètres caractérisant le cercle recherché. Mais pourquoi rechercher un cercle dans une image ?Une application concrète de cet algorithme est proposée dans le contexte de l’analyse de l’énergie de surface d’un substrat, mesuré par l’angle de contact
de solvants déposés par la surface. L’angle que fait une goutte de solvant déposée sur une surface est en effet déterminé par cette énergie de surface, qui définit donc la propension d’une surface à se « salir » (interagir avec son environnement) [5]. Nombreuses sont les études visant à fonctionnaliser les surfaces pour en faire varier l’énergie, que ce soit pour les rendre adhérentes (lors d’un vernissage ou d’un dépôt de peinture par exemple) ou au contraire répulsives (surface d’une poêle qui ne doit pas accrocher les aliments)[6][7]. Au niveau du contact de la goutte avec la surface, trois interfaces cohabitent : la surface solide, la surface du liquide et le gaz environnant. Ces trois interfaces possèdent chacune une énergie de surface, et la condition d’équilibre impose (équation de Young) :Donc déterminer v.png permet de déduire les propriétés de la surface considérée
. Une valeur faible de tension de surface correspond à une faible mouillabilité et donc une surface fortement hydrophobe (par exemple le teflon), tandis qu’une valeur élevée correspond à une forte affinité à interagir avec l’environnement et donc une surface hydrophile. Les traitements de surface visant à rendre les surfaces mouillables (par exemple pour les enduire d’une couche de vernis), soit en les chauffant soit en les irradiant, augmentent donc l’énergie de surface gamma.png avant fonctionnalisation.L’énergie de surface est dominée par les groupements chimiques en surface de l’objet considéré [8], forte pour des groupes tels que carboxyle (
20–60° [9]) ou alcool ( 70° [10]), mais faible pour le methyl ( 112°) et surtout les groupes chlorés ou fluorés ( 118°, voire 108–110° pour le teflon), avec une contribution relativement secondaire de la longueur de la chaîne carbonée qui relie ces groupes terminaux à la surface [9].Concrètement, tout le monde connaît empiriquement les conditions pour une surface « propre » (voir figure 3). Une surface « propre » est une surface sur laquelle une goutte d’eau s’étale, une surface « sale » (par exemple, grasse) est une surface sur laquelle une goutte d’eau reste sous forme de goutte.
Au-delà de cette approche qualitative intuitive, nous pouvons formaliser ces concepts pour les rendre quantitatifs au travers des énergies de tension de surface qui définissent l’angle de contact d’un solvant avec une surface. Un paramètre amplificateur de cet effet est la rugosité dont nous discuterons plus loin.
Fig. 3 : Exemple de surface d’ustensile de cuisine encore couvert d’une couche grasse, ne permettant pas aux gouttes d’eau de s’étaler sur la surface d’acier inoxydable. Les groupes acides carboxyliques, hydrophiles, s’orientent vers l’oxyde métallique présent en surface de la casserole, exposant les groupes hydrophobes qui expliquent l’angle de contact élevé observé.
Le montage expérimental pour mesurer une énergie de surface au travers de l’angle de contact
consiste à déposer une petite [11](<10µl) goutte de liquide sur la surface à analyser, prendre une photographie en contre-jour de la goutte (voir figure 4), et analyser son angle de contact avec la surface. L’angle de contact se détermine en ajustant un cercle sur la circonférence de la goutte – supposée suffisamment petite pour que la gravité soit négligeable sur les forces de tension superficielles et que la goutte soit donc de forme cylindrique – et en calculant l’angle à l’intersection avec le plan formé de l’échantillon qui supporte la goutte. Pour notre part, une webcam munie d’un objectif compatible avec une mesure en macrophotographie [12]et commandée par vlc permet d’acquérir films et captures d’écran pour un traitement des images présenté ci-dessous.Fig. 4 : Montage expérimental de prises de vues – une webcam munie d’un objectif dont la distance focale est compatible avec des applications de macrophotographie – avec une illumination en contre-jour pour saturer en blanc le fond de l’image et faire apparaître la goutte en sombre sur fond clair. Nous constatons (droite) en prenant une photographie de papier millimétrique gradué l’absence de déformation significative par l’optique de prise de vue.
La séquence de traitements que nous vous proposons de suivre pour identifier l’angle de contact d’une goutte avec une surface est :
1. Identifier le plan de la surface, supposée horizontale, comme maximum du gradient
selon l’axe vertical. En effet, le plan présente une rupture nette en se déplaçant verticalement le long de l’image ;2. Identifier les limites de la goutte, en particulier ses bords haut, droit et gauche, pour circonscrire la zone d’analyse, et réduire les risques de trouver des cercles qui ne correspondent pas à la goutte étudiée. Ces bords se déduisent du plan qui a été identifié dans la première étape, en faisant l’hypothèse que la goutte se trouve au-dessus du plan la supportant, et que ses bords droit et gauche correspondent au maximum du gradient
selon l’axe horizontal ;3. Partant d’une hypothèse « raisonnable » sur le rayon probable de la goutte compte tenu des considérations géométriques précédentes, nous appliquons l’algorithme de Hough aux trois paramètres que sont le centre du cercle et son rayon ;
4. Ayant identifié le centre du cercle (xc, yc), son rayon R, et l’ordonnée du plan yp sur lequel repose la goutte, l’angle de contact
se déduit trivialement par .Le résultat de ces traitements est illustré sur les figures 5 et 6, avec en bout de chaîne la superposition du cercle identifié comme représentant au mieux la forme de la goutte, la tangente au point d’intersection avec le plan supportant la goutte, et par conséquent l’angle de contact.
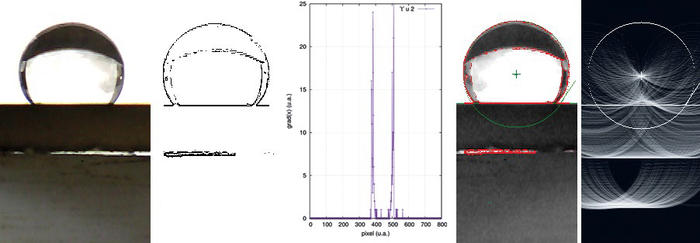
Fig. 5 : Séquence de traitements pour identifier l’angle de contact de deux gouttes d’eau sur des surfaces de polymères. De l’image brute, les points remarquables de la circonférence de la goutte sont identifiés par détection de contour (gradient selon les deux directions de l’image), puis transformée de Hough sur des itérations des divers rayons du cercle avec recherche, pour chaque rayon, du centre du cercle le plus probable. Finalement, le calcul de la tangente au point d’intersection de la goutte avec le plan qui la supporte donne, dans le cas du haut, 44,3° et dans le cas du bas, 83,4°.
Fig. 6 : De gauche à droite : image originale acquise par caméra connectée sur port USB ; gradient sur la zone identifiée comme contenant la goutte ; évolution du gradient le long de l’axe des abscisses, illustrant clairement les deux maxima lorsque les bords de la goutte sont parcourus ; somme des contributions des pixels dans le domaine de Hough des paramètres du centre du cercle, pour la valeur du rayon maximisant la somme des intensités des pixels ; identification du cercle représentant la goutte (cercle vert) et tracé de la tangente au point de contact (droite verte). Noter le choix peu judicieux du support de la goutte qui ne couvre pas toute la largeur de la photographie, se traduisant par un gradient parasite dans la direction horizontale. Dans cet exemple, l’angle de contact est de 123,4°, une valeur élevée, mais qui n’est pas aberrante pour une lame de verre silanisée avec une terminaison fluorée.
2.2 Fonctionnalisation d’une surface
Une approche opposée à la surface propre parce qu'hydrophile consiste à dire que toute saleté en solvant aqueux doit être repoussée par l’objet que nous voulons maintenir « propre ». Pour ce faire, une surface hydrophobe propose les propriétés requises. Un exemple trivial est la poêle recouverte de teflon pour empêcher les matières grasses de s’y fixer. Cependant, de même que le teflon ne veut pas que les matières grasses s’y fixent, une couche de teflon tend à se détacher de la surface qu’elle est supposée protéger. Une approche alternative consiste à générer une surface d’hydrophobicité médiocre, mais stable, et d’amplifier l’effet d’hydrophobicité par une rugosité aux échelles micrométriques et en deçà [13]. Cette approche est celle mise en œuvre dans les sprays « anti-salissants » à la mode, qui consistent à déposer des nanoparticules sur les surfaces à protéger (par exemple UltraTech Ultra-Ever Dry).
En effet, la rugosité de surface tend à amplifier la propriété d’hydrophobicité (ou d’hydrophilicité) selon l’équation de Wenzel qui affirme que pour une surface de rugosité r, l’angle de contact
est relié à l’angle de contact de la même surface lisse par .Un mécanisme pour rendre une surface hydrophobe est de la couvrir de suie de bougie ou d’un solvant organique (voir figure 7) [14] : les nano-particules ainsi déposées sont couvertes de sites hydrophobes (
) qui rendent la surface répulsive pour la goutte d’eau. Dans le cas des surfaces super-hydrophobes, la goutte reste sphérique sous réserve que son diamètre soit nettement plus petit que la longueur capillaire (donc avec une contribution négligeable de la gravité devant la tension de surface), et l’algorithme de détection de cercles de Hough fonctionne parfaitement.Fig. 7 : Haut, gauche : fonctionnalisation d’une surface de verre « propre » par de la suie produite par une flamme de solvant organique (isopropanol) [14]. Droite : image au microscope électronique à balayage de la surface de verre couverte de suie. Aucune particule de dimensions micrométriques ou supérieures n’est observée, la structuration de la surface se fait sur une échelle de quelques dizaines à la centaine de nanomètres. Bas : séquences d’un film visant à déposer une goutte d’eau sur cette surface super-hydrophobe. Non seulement la goutte refuse de se détacher de la micropipette, mais une fois libérée de l’embout, la goutte roule pour s’enfuir rapidement du champ de vision de la caméra.
Le lecteur désireux de ne pas développer ses propres implémentations des algorithmes, mais de se contenter d’expérimenter avec la détection de cercles et de droites pourra avantageusement exploiter la fonction houghtf()fournie avec la bibliothèque de traitement d’images de GNU/Octave.
3. Traitement d’images issues de RADAR à ouverture synthétique
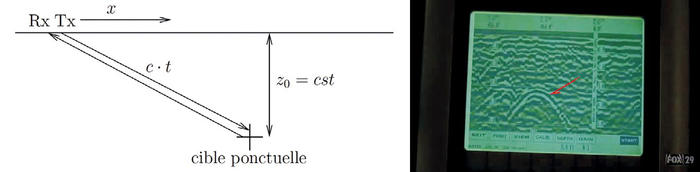
Le dernier exemple que nous proposons est le cas d’un réflecteur ponctuel sondé par un dispositif mobile illuminant cette cible et observant les signaux réfléchis – cas typique d’un RADAR mobile, qu’il s’agisse de RADAR de sol (Ground Penetrating RADAR– GPR) ou RADAR à ouverture synthétique (SAR) dans lequel une antenne d’ouverture équivalente immense est synthétisée en déplaçant l’instrument le long d’une trajectoire supposée rectiligne [15]. Dans ce cas, pour une cible placée à une distance z de la trajectoire (profondeur z dans le cas du GPR qui se déplace à la surface du sol), le temps de vol de l’écho t en fonction de la position x de la source RADAR – en supposant une célérité de l’onde électromagnétique de c – vérifie
(voir figure 8). Ainsi, un réflecteur ponctuel de profondeur z sous terre se traduit, pour une mesure GPR, par une hyperbole dans le plan (x, t) puisque avec z constante est l’équation d’une hyperbole. Dans ce cas, la transformée de Hough se doit d’identifier quatre paramètres ; le décalage en abscisse et en ordonnée (x , y ), le centre c et la pente des asymptotes pou en d’autres termes les coefficients a et b de l’hyperbole (la relation entre ces quatre termes étant p = b / a et c2= a2+ b2 : . Ce problème est donc très similaire au cas du cercle, si ce n’est que a et b sont moins intuitifs que R le rayon du cercle.Fig. 8 : Gauche : schéma justifiant de l’observation de réflecteurs ponctuels comme hyperbole dans un RADARgramme de RADAR à ouverture synthétique ou RADAR de sol (GPR). Rx et Tx sont l’émetteur et le récepteur du RADAR dans une configuration bistatique. Droite : capture d’écran de l’épisode 7 de la saison 1 de la série télévisée Bones (34 minutes, 11 secondes du début de l’épisode) illustrant la distribution hyperbolique des réflexions de l’objet enterré (flèche rouge), observée par GPR par l’héroïne de la série.
L’application du même algorithme que précédemment, mais cette fois en choisissant les points remarquables le long des hyperboles (x, y) et en cherchant à maximiser la note [16] du jeu de paramètres (x , y , a, b) en balayant (boucles) a et b et en traçant pour chacun de ces couples l’image dans le domaine de Hough fournissant la note de chaque couple (x , y ) s’obtient par y0.png. Dans ce cas, x correspond à l’abscisse dans l’image de Hough et les y correspondants s’accumulent pour donner le résultat de la figure 9. Comme nous pouvons nous y attendre, la précision sur les valeurs de a et b est peu précise, mais avec une valeur maximale cohérente lorsque a = b qui correspond à une pente de l’asymptote parallèle à la première bissectrice, et une note qui chute rapidement lorsque a
b.01: clear all;close all
02: x=[-10:0.1:10]; a=5; b=5; % params de l’hyperbole tracée
03:
04: % on fabrique une image avec une hyperbole
05: y=-a*sqrt(1+x.^2/(b*b)); % y^2/a^2-x^2/b^2=1 ie y=+/-a*(1+x^2/b^2)
06: plot(x,y);hold on
07: y=-a*sqrt(1+(x-3).^2/(b*b))+4; % 2eme hyperbole décalée de x0=3,y0=4
08: plot(x,y);axis off;colormap gray
09: print -dbmp hyperbole.bmp
10:
11: % on lit une image avec une hyperbole
12: entree=imread(’hyperbole.bmp’); % relit l’image generée
13: entree=entree(1:4:end,1:4:end,2);% trop grand : ne garde que 1/4 de l’img
14: figure;imagesc(entree); colormap(gray)
15: [y,x]=find(entree>0); %figure; plot(x,y) % points remarquables
16: % a=5;b=5;
17: for a=1:7 % recherche des couples (a,b)
18: for b=1:7
19: [sy,sx]=size(entree); espace=zeros(sx,sy);
20: for x0=1:sx % recherche du centre pour chaque (a,b)
21: for k=1:length(x)
22: tmp=y(k)-a*sqrt((x(k)-x0).^2/(b*b)+1); % (y-y0)^2/a^2-(x-x0)^2/b^2=1
23: tmp=floor(tmp); % ie y-y0=a*sqrt([1+(x-x0)^2/b^2])
24: if ((tmp>0) && (tmp<sy)) espace(x0,tmp)=espace(x0,tmp)+1;endif
25: end % ^^^ note de chaque jeu de params
26: end
27: figure;imagesc(espace');
28: m(a,b)=max(max(espace')) % note max = probabilité d’avoir les bons params
29: [yt,xt]=find(espace'==m(a,b));yy(a,b)=yt(1);xx(a,b)=xt(1);
30: title([num2str(a),' ',num2str(b),' ',num2str(m(a,b))])
31: end
32: end
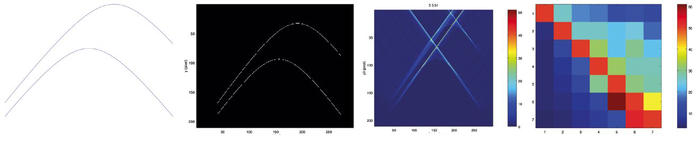
Fig. 9 : De gauche à droite : l’image originale considérée comportant deux hyperboles ; l’identification des points remarquables, ici par simple seuillage puisque dans ce cas synthétique les données ne sont pas bruitées ; la transformée de Hough présentant la probabilité de (x , y ) d’être le centre de la parabole pour une paire de a et b égaux (cas le plus favorable dans cet exemple) ; et finalement la note maximale de la transformée de Hough en fonction des valeurs de a (en abscisse) et b (en ordonnée).
Conclusion
Le traitement d’images n’est pas une fin en soi, mais répond à des besoins : nous avons illustré une méthode classique d’identification de structures géométriques dans des images – la transformée de Hough – dans trois cas concrets d’utilisation. Dans un premier temps, nous avons recherché les paramètres représentant les droites visibles dans une image, et validé le concept sur l’identification de bandes signalétiques sur route. Une deuxième application porte sur l’identification de cercles représentant des images de calottes sphériques, et ce en vue du calcul d’angle de contact de gouttes déposées sur des surfaces. Le cas particulier des surfaces super-hydrophobes illustre le cas des cercles observés lorsque la goutte, repoussée par la surface, reste sphérique. Finalement, le dernier exemple porte sur l’identification de coniques, et en particulier d’hyperboles telles qu'observées dans les images RADAR où les antennes se déplacent par rapport à une cible fixe. La méthode de Hough se généralise à toute courbe paramétrable, avec un calcul d’autant plus long que le nombre de paramètres est élevé. L’étape préliminaire d’identification des points remarquables – par exemple par détection de contours ici illustrée par de simples gradients dans les deux axes de la photographie – permet de considérablement réduire le temps de calcul. Le lecteur est encouragé à étendre ces concepts à ses propres problèmes, et en particulier pour des structures géométriques différentes de celles abordées ici.
Remerciements
L’inspiration de la nanostructuration de la lame de verre par la suie de bougie vient d’une présentation, « Hacking Atoms », par Thomas Deits à la conférence OMH2013 (Hollande). Les références bibliographiques qui ne sont pas librement disponibles sur le Web ont été obtenues sur Library Genesis (http://gen.lib.rus.ec). Les ressources – images et programmes – associées à cette prose sont disponibles sur http://jmfriedt.free.fr/hough.
Notes & Références
[1] HOUGH P. V. C., « Method and means for recognizing complex patterns », brevet US3069654 (18 déc. 1962)
[2] HART P. E., « How the Hough Transform Was Invented », IEEE Signal Processing Magazine, pp.18–22 (nov. 2009)
[3] R.O. DUDA R. O. et HART P. E., « Use of the Hough Transformation to Detect Lines and Curves in Pictures », Comm. of the ACM 15(1), pp.11–15 (1972)
[4] KUMAR A. M. & SIMON P., « Review of Lane Detection and Tracking Algorithms in Advanced Driver Assistance System », Int. Journal of Computer Science & Information Technology 7(4), pp.65–78 (2015).
[5] DE GENNES P.-G., F. Brochart-Wyart, D. Quéré, « Gouttes, bulles, perles et ondes », Belin (2002)
[6] BALL P., « Made to measure – the materials for the 21st century »(1997) et en particulier l’étude des fonctionnalisations de surface par angle de contact au chapitre 10
[7] TABELING P., « Introduction à la microfluidique », Belin (2003) et son chapitre 7 sur les effets capillaires
[8] BAIN C. D., TROUGHTON E. B., TAO Y.-T., EVALL J., WHITESIDES G. M. et NUZZO R. G., « Formation of Monolayer Films by the Spontaneous Assembly of Organic Thiols from Solution onto Gold », J. Am. Chem. Soc. 111(1989), 321–335
[9] BAIN C. D. et WHITESIDES G. M., « Depth sensitivity of wetting : monolayers of
-mercapto ethers on gold », J. Am. Chem. Soc. 110 (1988), 5897–5898[10] HOLMES-FARLEY S. R., REAME R. H., McCARTHY T. J., DEUTCH J. & WHITESIDES G. M., « Acid-Base Behavior of Carboxylic Acid Groups Covalently Attached at the Surface of Polyethylene : The Usefulness of Contact Angle in Following the Ionization of Surface Functionality », Langmuir 1, pp.725–740 (1985)
[11] Petit devant la longueur capillaire [5] donnée par
avec la tension superficielle, rho.png la masse volumique du fluide et gla constante de gravité – pour l’eau, =70 mN/m et la longueur capillaire est 2,7 mm, donc une goutte de 10µL ou de rayon 2 mm respecte la contrainte de négliger les effets de la gravité sur la forme de la goutte[12] http://www.conrad.fr/ce/fr/product/191251/Camera-_microscope-_numerique-_USB-_plat-_20-_MPix-_zoom-_x-_65-_et-_x-_250-_Conrad pour 80 euros
[13] CARRÉ A. et K.L. MITTAL K. L. (Ed.), « Superhydrophobic Surface », VSP (2009), ou SENEZ V., THOMY V. et DUFOUR R., « Nanotechnologies for Synthetic Super Non-Wetting Surface », Wiley (2014) et en particulier son chapitre 5 intitulé « Characterization Techniques for Super Non-wetting Surfaces »qui met en garde contre les techniques triviales présentées ici
[14] DENG X., MAMMEN L., BUTT H.-J. et VOLLMER D., « Candle soot as a template for a transparent robust superamphiphobic coating », Science 335(6064), pp. 67–70 (2012)
[15] GOLOVKO M. M. et POCHANIN G. P., « Automatic Measurement of Ground Permittivity and Automatic Detection of Object with GPR Images Containing a Response from a Local Object », dans « Ultrawideband Radar : Applications and Design »édité par J.D. Taylor, et en particulier le paragraphe 7.3 (p.234) titré « Use of the Hough Transform for Detection of Hyperbolic Curves »
[16] Le nombre de pixels vérifiant une distribution le long d’une forme géométrique d’équation donnée, valeur sommée dans chaque pixel de l’espace de Hough