Le défi que la cryptographie en boîte blanche vise à relever consiste à mettre en œuvre un algorithme cryptographique en logiciel de telle manière que les éléments cryptographiques restent sécurisés même en cas d'attaque en boîte blanche.
1. Introduction
L'objectif initial de la cryptographie a été de concevoir des algorithmes et des protocoles pour protéger un canal de communication contre l'espionnage. Cela a été la principale activité de la cryptographie moderne dans les 30 dernières années et a produit de nombreux algorithmes de chiffrements (comme AES, (T)DES, RSA, ECC) et de nombreux protocoles. Les éléments source et destination sont supposés sûrs (boîte noire) : l'attaquant a seulement accès aux entrées/sorties de l'algorithme. Pour se conformer à un tel modèle, l'algorithme doit être exécuté dans un environnement sécurisé. L'activité de recherche dans ce domaine comprend des chiffrements améliorés et à usage spécifique (par exemple, le chiffrement par blocs légers, des schémas d'authentification, les algorithmes à clé publique homomorphiques), et leur cryptanalyse. Toutefois, du point de vue industriel, le problème principal est le déploiement pratique. Des protocoles déployés dans le mauvais contexte, des algorithmes mal mis en œuvre, ou des paramètres inappropriés peuvent offrir un point d'entrée pour les attaquants. Le déploiement de la cryptographie dans la pratique est devenu un enjeu en soi.
Le problème empire lorsque le modèle d'attaque en boîte noire n'est plus satisfait. Au cours des dix dernières années, nous avons assisté à l'apparition d'un grand nombre de techniques de cryptanalyse nouvelles qui exploitent la présence d'informations additionnelles qui peuvent être observées lors de l'exécution d'un algorithme de chiffrement sur des canaux auxiliaires (side channel attacks en anglais) ; informations telles que le temps d'exécution, le rayonnement électromagnétique et la consommation d'énergie. Pallier ces attaques par canaux auxiliaires est un défi, car il est difficile de décorréler cette information des opérations sur des clés secrètes. De plus, la plateforme de déploiement impose souvent des contraintes de taille et de performance qui rendent difficile l'utilisation de techniques de protection.
Aujourd'hui, nous sommes confrontés à un nouveau modèle d'attaque, pire encore, car la cryptographie est déployée dans des applications qui sont exécutées sur des appareils ouverts tels que PC, tablettes ou smartphones, sans utiliser d'éléments sécurisés. Dans ce contexte, on parle d'attaque en boîte blanche. Ainsi, un attaquant en boîte blanche a un accès complet à l’implémentation logicielle d'un algorithme cryptographique : le binaire est complètement visible et modifiable par l'attaquant et celui-ci a le plein contrôle de la plateforme d'exécution (appels CPU, registres mémoire, etc.). Par conséquent, l'implémentation elle-même est la seule ligne de défense.
Les implémentations logicielles qui résistent à ces attaques en boîte blanche sont notées implémentations en boîte blanche (white-box en anglais). Elles sont la pierre angulaire d'applications où une clé cryptographique est utilisée pour protéger des biens, comme par exemple dans le domaine des DRM. Dans de tels cas, l'utilisateur du logiciel a une incitation à rétroconcevoir l'application et à en extraire la clé. Des attaques similaires peuvent se produire à l'encontre de l'intérêt de l'utilisateur, par exemple quand une application bancaire est exécutée sur un dispositif infecté par des logiciels malveillants ou sur un système multi-utilisateurs où certains utilisateurs ont des privilèges élevés. Dans de telles situations, lorsque les opérations cryptographiques sont implémentées au travers de bibliothèques cryptographiques standards comme OpenSSL ou que les clés cryptographiques sont stockées simplement dans la mémoire, la clé secrète sera découverte sans trop d'efforts, et ce quelle que soit la force de la primitive cryptographique utilisée.
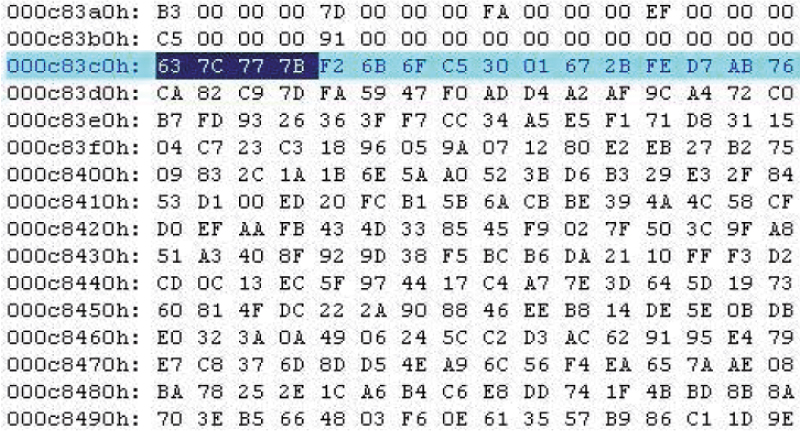
Pour illustrer ces attaques en boîte blanche, nous présentons l'attaque Key Whiteningde Kerins et Kursawe[Kerins06]. Cette attaque peut être déployée sur la plupart des implémentations de l'AES, y compris dans OpenSSL. On observe que l'AES utilise une opération de masquage par la clé du dernier tour comme étape finale de l'algorithme, afin de protéger l'itération finale de l'algorithme de chiffrement (voir figure 1). L'avant-dernière opération consiste en une consultation de table. Comme les spécifications de l'algorithme sont publiques, la table est connue et est accessible par un attaquant boîte blanche. En effet, avec un simple éditeur hexadécimal, cette table peut être située dans le binaire, et remplacée par des zéros. En conséquence, la sortie de l'avant-dernière opération sera zéro, et l’exécution de l'opération de masquage va simplement afficher la sous-clé finale, à partir de laquelle la clé d'origine AES peut être calculée.
Cet article aborde le large spectre de la cryptographie en boîte blanche. Nous allons introduire les premières implémentations en boîte blanche qui ont été présentées et décrire les principaux résultats de cryptanalyse. Les questions existentielles qui ont été soulevées à la suite de ces cryptanalyses, comme les preuves d'existence et les limites, sont étudiées dans la branche théorique de la recherche sur la cryptographie en boîte blanche ; nous n'aborderons ce sujet que brièvement. Enfin, nous allons couvrir des aspects plus pratiques : comment les implémentations en boîte blanche sont attaquées dans la pratique, quels mécanismes de sécurité additionnels peuvent être déployés pour atténuer les problèmes pratiques, et quels sont les défis du futur.
2. La cryptographie en boîte blanche
Le principe de la cryptographie en boîte blanche a d'abord été publié par Chow et al.[Chow02DES] et s'intéressait au cas des implémentations à clés fixes du DES. Le défi consiste à coder en dur la clé symétrique dans l’implémentation du chiffrement DES : une implémentation implique une clé (on parle aussi d'algorithme boîte blanche statique, à la différence d'algorithme dynamique où la clé est paramétrable). L'idée principale est d'intégrer à la fois la clé fixe (sous la forme de données, mais aussi sous la forme de code) et des données aléatoires instanciées au moment de la compilation dans une composition dont il est alors difficile de déduire la clé d'origine.Un des principes fondamentaux de la cryptographie est le principe de Kerckhoffs, qui dit que la sécurité d'un système doit se fonder uniquement sur la confidentialité de la clé secrète, tous les autres aspects pouvant être publics. La cryptographie en boîte blanche aspire elle aussi à résister à une telle exposition publique : un attaquant a accès à l'implémentation, il connaît l'algorithme implémenté, ainsi que les techniques de protection en boîte blanche mises en œuvre ; la sécurité s'appuie sur la confidentialité de la clé secrète et des données aléatoires. Ceci est tout différent de l'approche de la sécurité par obscurcissement, généralement obtenue par offuscation du code, qui vise à prévenir la rétro-ingénierie d'une application de façon que l'attaquant ne puisse pas trouver facilement un point d'attaque ou divulguer de la propriété intellectuelle.
2.1 Implémentations en boîte blanche
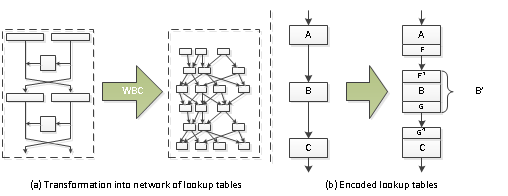
Les premières implémentations en boîte blanche ont été présentées par Chow et al. [Chow02DES][Chow02AES] en 2002 sur le DES et l'AES. Leurs techniques en boîte blanche transforment un chiffrement en une série de tables dépendant de la clé (voir la figure 2 (a)). La clé secrète est codée en dur dans les tables et protégée par des techniques de randomisation. L'un des procédés employés est l'injection de codages aléatoires annihilants qui sont fusionnés avec les tables de façon que les tables et le flux de données soient aléatoires, tout en conservant la fonctionnalité sémantique globale de l’implémentation. Ceci est représenté dans la figure 2 (b), où F et G sont des codages aléatoires injectés entre A et B, puis B et C respectivement. La fonctionnalité globale (entrée A - sortie C) reste la même.
Figure 2 : Chow et al. implémentations en boîte blanche
Les techniques pour transformer un chiffrement par bloc en un réseau de tables peuvent être facilement étendues à d'autres chiffrements par réseaux de substitution-permutation (SPN). Très grossièrement, les étapes sont les suivantes :
- Réorganiser le chiffrement de sorte que les opérations boîte-S et l'opération exploitant la clé de tour soient contiguës, puis coder en dur la clé secrète dans la boîte-S, par exemple Tk (x) = S(x) + k.
- Injecter les opérations affines annihilantes dans la couche affine du chiffrement. De cette façon, les boîtes-S peuvent être ré-ordonnancées et l'opération affine (généralement conçue pour être aussi efficace que possible) peut être rendue moins creuse. (Ceci est référencé comme l'introduction de bijections de mélange dans les articles de Chow et al.).
- Décomposer toutes les opérations affines en une série de tables, implémentant même l'opération XOR en une table.
- Injecter des codages aléatoires annihilants dans la séquence de tables.
Il s'agit d'une technique très ad hocd'implémenter une primitive cryptographique et il est difficile d'en quantifier la sécurité. La seule affirmation de sécurité pouvant être faite concerne « la sécurité locale » : lorsque B est une bijection et F et G sont choisis aléatoirement, la fonction B' ne laisse pas fuir d'information. En effet, étant donné B', toute bijection B avec un nombre équivalent de bits en entrée et sortie est un candidat car il y aura toujours une paire (F, G) telle que B' = GBF-1. Par conséquent, l'attaquant est obligé d'analyser également d'autres composants de l'implémentation, l'objectif étant que l'attaquant doive prendre trop de variables en compte, ce qui finalement rendrait son attaque impossible. Malheureusement, il n'existe pas de preuves de sécurité qui soutiennent cette déclaration ; dans la section suivante, nous montrerons même comment l'approche de Chow et al. peut être vaincue.
Comme des opérations très efficaces (telles que le XOR) sont transformées en tables, il y a un important surcoût en performance et en taille.
|
Implémentation |
Taille |
Référence |
|
WB-AES [Chow02AES] |
770 KBytes |
14.5 KBytes (OpenSSL 1.0) |
|
WB-DES [Chow02DES] |
4.5 MBytes |
8.25 KBytes (OpenSSL 1.0) |
|
WB-DES [Link05] |
2.3 MBytes |
|
2.2 Cryptanalyse en boîte blanche
L'implémentation en boîte blanche du DES [Chow02DES] a été la première prouvée non sûre. Sa vulnérabilité est due principalement à la structure de Feistel du DES qui peut être distinguée dans une représentation en table. Les premières techniques de cryptanalyse en boîte blanche trouvent leur origine dans des attaques par canaux auxiliaires telles que la corrélation de la propagation des fautes [Jacob02] ou les attaques deviner & déterminer (guess and determine) [Lin05]. Néanmoins, ces techniques font des hypothèses sur l'implémentation qui peuvent facilement être contournées [Link05]. Ce n'est qu'en 2007 que l'implémentation en boîte blanche du DES a été complètement cassée grâce à l'utilisation de la cryptanalyse différentielle tronquée par Wyseur et al.[Wyseur07] et Goubin et al. [Goubin07].
L'implémentation en boîte blanche de l'AES a été cassée par Billet et al.[Billet04] en utilisant une technique de cryptanalyse algébrique. La technique algébrique présentée s'est montrée très puissante car elle cible directement la stratégie de randomisation des tables. Sans entrer trop dans les détails, l'idée de l'attaque est la suivante :
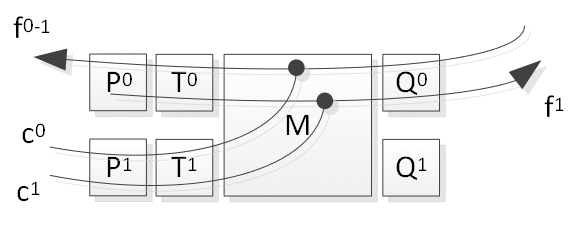
- Isoler l'ensemble des tables qui représentent une itération (codée) de l'implémentation AES sous-jacente. Ceci est trivial, puisque les transformations employées sont connues (àclé secrète et aléa près). La figure 3 illustre la composition d'une telle itération, où P et Q sont des codages internes, Ti des boîtes-S avec les clés codées en dur, et M représente la partie linéaire de l'algorithme de chiffrement (comme l'opération MixColumns).
- Définir les fonctions fi comme des fonctions bijectives entre un octet à l'entrée et un octet à la sortie de l'itération ; les entrées vers les autres octets sont constantes mais différentes pour chaque fi.
- Étant donné que ces fi sont bijectives et opèrent sur 8 bits, elles peuvent facilement être inversées et donc les fonctions composées hij = fj . fi-1 peuvent être calculées.
- De l'ensemble des fonctions hij, la composante non linéaire de Q0 peut être obtenue. Ceci est dû au fait que ces fonctions hij ne dépendent que de Q et des constantes Ci et Cj ; elles ne dépendent pas de P et T .
- L'information sur Q conduit au P de l'itération suivante (puisque ce sont des codages annihilants - inverses les uns des autres). Par conséquent, répéter les étapes 1 à 4 sur plusieurs itérations conduit à une implémentation de l'AES qui est seulement protégée par des codages linéaires. Il suffit alors de résoudre les équations restantes pour obtenir la clé secrète dissimulée.
Figure 3 : Analyse d'une ronde de l'implémentation en boîte blanche d'AES
Michiels et al. [Mich08] ont démontré que cette technique de cryptanalyse algébrique peut être exploitée sur n'importe quel algorithme de chiffrement qui a des propriétés similaires à celles de l'AES (i.e. chiffrements SPN avec des matrices de code MDS). En fait, ils ont montré que ce sont précisément les propriétés qui ont été sélectionnées du point de vue de la sécurité boîte noire qui rendent le chiffrement vulnérable aux attaques en boîte blanche. Dans [Wyseur09], nous avons montré comment les attaques algébriques peuvent être utilisées contre toute la stratégie d’implémentation en boîte blanche basée sur les tables : toute table avec perte (ce qui est inévitable dans les implémentations en boîte blanche à base de tables) laisse fuir de l'information qui peut être exploitée.
Les techniques de cryptanalyse algébrique ont conduit à la conception de nouvelles constructions dépassant la stratégie des tables, vers des implémentations basées sur des équations algébriques randomisées [Bil03] et l'introduction de perturbations pour casser la structure algébrique qui permet de monter des attaques algébriques [Bri06wbc]. L’implémentation de Billet et Gilbert [Bil03] a été cassée en raison d'un résultat de cryptanalyse sur la primitive sous-jacente qui a été utilisée. Des tentatives de résolution du problème ont été introduites par Ding [Ding04] en incluant des fonctions de perturbation pour détruire la structure algébrique. Cela a conduit à un schéma amélioré de chiffrement traçable [Bri06trace] et a finalement été appliqué à des implémentations en boîte blanche d'AES [Bri06wbc]. Néanmoins, même ces nouvelles constructions améliorées ont été démontrées non sûres par De Mulder et al.[Dem10].
En dépit de toutes les nouvelles constructions qui ont été présentées, la sécurité de la cryptographie en boîte blanche est très floue. La quasi-totalité des constructions présentées ont été prouvées non sûres dans des articles de cryptanalyse publiés par des universitaires. Seules quelques constructions restent « non cassées », mais ce ne sont que des variantes mineures de constructions existantes - donc les attaques existantes pourront être appliquées avec peu d'efforts.
Considérant l'état de l'art actuel de la cryptographie en boîte blanche dans le domaine académique, les questions suivantes demeurent :
- Existe-t-il des implémentations en boîte blanche « fortes », et quellesécurité est atteignable en boîte blanche ?
- Quelle est la difficulté d'exploiter les attaques dans un scénario du monde réel ?
Nous abordons ces questions dans les sections suivantes.
2.3 Approches théoriques
La cryptographie en boîte blanche est souvent liée à l'offuscation de code, puisque toutes deux visent à protéger les implémentations logicielles. Toutes deux ont été reçues avec un scepticisme similaire quant à la faisabilité et à l'absence de fondements théoriques. La recherche théorique sur l'offuscation de code a pris de l'ampleur avec le papier fondateur de Barak et al. [Barak01] qui a démontré qu'il est impossible de construire un offuscateur générique, c'est-à-dire un offuscateur qui peut protéger n'importe quel programme. Barak et al. ont ainsi construit une famille de fonctions qui ne peuvent pas être offusquées en exploitant le fait que le logiciel peut toujours être copié tout en préservant sa fonctionnalité. Néanmoins, ce résultat n'exclut pas l'existence d'offuscateurs de code sûrs : Wee [Wee05] a présenté un offuscateur prouvé sûr pour une fonction de point, qui peut être exploité dans la pratique pour construire des fonctionnalités d'authentification.
Des approches théoriques similaires à l'offuscation de code ont été conçues pour la cryptographie en boîte blanche [Sax09]. La principale différence est que la sécurité des implémentations en boîte blanche doit être validée par rapport à des notions de sécurité. Une notion de sécurité est une description formelle de la sécurité souhaitée pour un système cryptographique. Ainsi, un système est considéré comme sûr du point de vue CPA (attaque à clair choisi ; Chosen Plaintext Attack en anglais) s'il n'est pas possible pour un attaquant ayant accès à un oracle de chiffrement de déterminer le messageclair correspondant à un message chiffré donné sans connaître la clé ; ou encore un système est dit KR-sûr (Key Recovery) s'il n'est pas possible de retrouver la clé secrète.
Il est sain de définir la cryptographie en boîte blanche avec la même approche, car celle-ci correspond à la réalité. En effet, en pratique, il n'est pas suffisant de s'assurer qu'il ne soit pas possible d'extraire des secrets cachés dans une application. Par exemple, pour créer en logiciel l'équivalent d'une fonction AES dans une carte à puce, il ne suffit pas que l’implémentation en boîte blanche résiste à l'extraction de sa clé, mais elle doit aussi être difficile à inverser. Saxena et Wyseur ont démontré que certaines notions de sécurité ne peuvent pas être satisfaites avec une implémentation software (par exemple la notion IND-CCA2), et ils ont proposé une construction dite à « securité prouvable » par rapport à la notion de sécurité IND-CPA [Sax09].
Il résulte d'une analyse théorique que la cryptographie en boîte blanche peut être perçue comme un pont entre la cryptographie symétrique et la cryptographie asymétrique. Un système à clé publique d'un nouveau type peut ainsi être élaboré, où l'opération privée est effectuée de manière efficace par un chiffrement par bloc instancié avec une clé symétrique, alors que l'opération publique est l’implémentation en boîte blanche de la fonction de chiffrement avec la même clé symétrique incorporée dans son code. Notez que ceci est plus difficile à réaliser que la seule protection contre l'extraction de la clé secrète. Par exemple, sans considérer les résultats de cryptanalyse, l’implémentation en boîte blanche originale de l'AES peut facilement être inversée puisque chaque itération peut être décrite comme quatre opérations parallèles de 32 bits dans 32 bits ; chacune d'elles peut être inversée facilement.
3. Cryptographie en boîte blanche dans la pratique
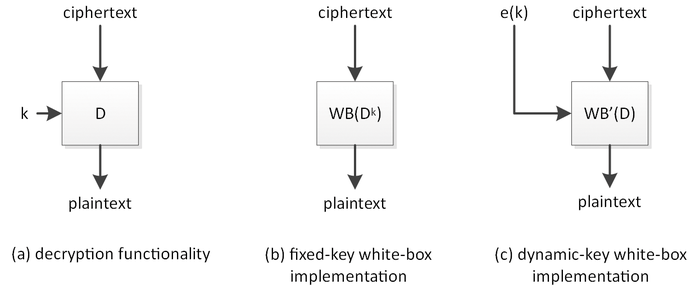
La cryptographie en boîte blanche est utilisée dans plusieurs produits. Des entreprises telles que Microsoft, Apple, Irdeto, NAGRA, Sony, Arxan, et de nombreuses autres ont annoncé le déploiement de techniques en boîte blanche, ont déposé des brevets et/ou ont montré qu'ils ont déployé cette technologie. Jusqu'à présent, nous avons surtout discuté d'implémentations en boîte blanche à clés fixes, dans lesquelles la clé secrète est codée en dur. Dans la pratique cependant, des implémentations en boîte blanche dynamiques sont plus adaptées. Ce sont des implémentations qui ne sont instanciées avec une clé qu'au moment où elles sont appelées. Dans ce cas, ce n'est pas la clé originale qui est présentée (ce qui conduirait à une divulgation facile), mais une version protégée de la clé. L’implémentation en boîte blanche dynamique effectue ensuite une opération de chiffrement/déchiffrement en exploitant la version protégée de la clé de telle sorte qu'aucune information sur cette clé ne soit exposée.
Figure 4 : Types d'implémentations en boîte blanche
Les principales préoccupations avec la cryptographie en boîte blanche sont d'une part la pénalité en termes de performance et de taille, et d'autre part la sécurité. Les problèmes de performance limitent son exploitabilité dans les usages à haut débit ou très contraints, tels que les systèmes mobiles. Cela peut être résolu en utilisant des implémentations en boîte blanche spéciales qui peuvent exploiter des accélérateurs matériels.
En ce qui concerne la sécurité, pour autant que nous le sachions, aucune implémentation en boîte blanche dans un produit réel n'a souffert d'une attaque de récupération de clé, en dépit des résultats de cryptanalyse qui ont été publiés. Cela montre qu'il existe un écart évident entre la théorie et la pratique, et que même des implémentations en boîte blanche faibles peuvent avoir leur utilité. Pour avoir une idée de la difficulté de monter une telle attaque dans la pratique, nous avons lancé quelques défis publics sur des implémentations en boîte blanche faibles. Ils ont récemment résulté en deux exploits de récupération des clés. La conclusion de ces attaques est que casser une implémentation en boîte blanche en pratique est un travail dédié et très coûteux en temps. Les attaques sont très dépendantes de la construction de l'implémentation en boîte blanche et des propriétés de l'algorithme de chiffrement sous-jacent. Par conséquent, des attaques largement applicables sont difficiles à déployer et il n'existe pas d'outils automatiques pour casser systématiquement des implémentations en boîte blanche.
3.1 Code lifting
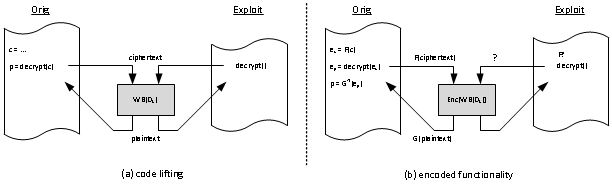
Le principal problème dont souffrent les implémentations en boîte blanche dans la pratique est le « code lifting ». Dans cette attaque, l'attaquant ne cherche pas à extraire la clé secrète à partir de l'implémentation, mais utilise l'ensemble de l'application comme si elle était une grosse clé. De telles attaques ont été utilisées dans la pratique à plusieurs reprises, où une bibliothèque de sécurité n'est pas rétroconçue, mais où sa fonctionnalité de déchiffrement est directement exploitée.
Figure 5 : Code lifting
Le code lifting peut être combattu en poussant à la limite le principe de l'implémentation en boîte blanche. Ceci peut être réalisé en appliquant des codages externes au système original, et notamment les codages annihilants à d'autres endroits dans l'application principale. Par exemple, des codages annihilants peuvent être incorporés dans la fonction qui appelle l'opération de déchiffrement. Ainsi, la fonctionnalité (G D_k F-1) est implémentée, et sans la connaissance de G et F, l'attaquant sera incapable d'utiliser l'opération de déchiffrement en dehors du contexte prévu. Il faudra alors utiliser des techniques d'offuscation ou d'isolation de processus dans un environnement sécurisé afin de s'assurer que les fonctions G et F ne peuvent pas être extraites de la fonction appelante. Par conséquent, nous avons aussi une méthode pour associer une opération cryptographique à un composant sécurisé ; nous pouvons donc faire du node-locking. Ceci est un exemple de technique de protection préventive des logiciels.
3.2 Software fingerprinting
Une autre direction consiste à déployer des stratégies réactives : être capable de détecter qui a partagé le code au moyen d'une clé embarquée. Dans [Mich07], Michiels et Gorissen présentent une technique pour insérer des fingerprints dans des implémentations en boîte blanche. L'idée principale repose sur l'observation que les codages annihilants internes peuvent être choisis de façon que les tables en boîte blanche qui en résultent contiennent une valeur arbitraire prédéfinie. Cette valeur peut être une empreinte qui sera utilisée pour identifier le logiciel ou introduire un droit d'auteur via des clés cryptographiques. Cette même approche peut également être utilisée pour permettre une forme de résistance aux modifications des logiciels : lorsque les tables contiennent des valeurs qui représentent du bytecode ou des instructions assembleur, toute modification de cette représentation conduirait à une modification des tables en boîte blanche, et donc de rendre la fonctionnalité de l'algorithme de chiffrement sous-jacent incorrecte. Ainsi, le logiciel dispose d'une double représentation. La sécurité de cette approche est cependant contestable. Tout d'abord, cela dépend de la sécurité des implémentations en boîte blanche, ce qui est déjà discutable. D'autre part, une telle approche peut être assez facilement contrée puisque l'attaquant peut insérer de nouveaux encodages internes qui détruisent l'empreinte, il peut exploiter une attaque par clonage qui distingue l'exécution du code de l'exécution de l'implémentation en boîte blanche sous-jacente.
Une meilleure stratégie réactive a été présentée par Billet et Gilbert [Bil03] qui ont proposé une implémentation en boîte blanche intrinsèquement traçable. Ils ont ainsi présenté une nouvelle construction d'un chiffrement par bloc, à partir de laquelle plusieurs instances peuvent être générées ; chaque instance est fonctionnellement équivalente, mais identifiable par inspection du code. Malheureusement, le bloc de base sur lequel ce chiffrement a été construit a été cassé. En introduisant des perturbations, Bringer et al.[Bri06trace] ont renforcé ce chiffrement traçable.
Conclusion
La cryptographie en boîte blanche est un élément nécessaire à toute stratégie saine de sécurisation globale du logiciel. Elle est la pierre angulaire de la protection des primitives cryptographiques des applications qui s'exécutent sur des plates-formes hostiles. Les techniques en boîte blanche initiales ont été présentées en 2002, avec des implémentations du DES et de l'AES. Depuis, la cryptographie en boîte blanche a pris de l'ampleur : plusieurs résultats de cryptanalyse et à de nouvelles constructions ont été publiés et de véritables fondations théoriques ont été formulées.
Aujourd'hui, la cryptographie en boîte blanche est utilisée dans des applications réelles, principalement des applications de DRM. Malgré la publication d'attaques académiques, aucune attaque contre les implémentations commerciales en boîte blanche n'a été observée à notre connaissance. Les attaquants se concentrent plutôt sur d'autres parties du système et exploitent la fonctionnalité cryptographique sans l'attaquer. Mais la cryptographie en boîte blanche offre des possibilités de combattre également sur ce front : les attaques par code lifting peuvent être évitées par le verrouillage des implémentations dans l'application et d'autres fonctions de sécurité telles que la traçabilité peuvent être ajoutées aux implémentations en boîte blanche.
Remerciements
La version originale de cet article a été écrite en anglais, et peut être téléchargée à l'adresse suivante : http://www.whiteboxcrypto.com. Nous tenons à remercier Jean-Bernard Fischer et André Nicoulin pour la traduction de l'article.
Références
[Barak01] Boaz Barak, Oded Goldreich, Rusell Impagliazzo, Steven Rudich, Amit Sahai, Salil Vadhan, and Ke Yang, On the (Im)possibility of Obfuscating Programs, in Advances in Cryptology - CRYPTO 2001, volume 2139 of Lecture Notes in Computer Science, pages 1–18, Springer-Verlag, 2001
[Bil03] Olivier Billet and Henri Gilbert, A Traceable Block Cipher, in Advances in Cryptology - ASIACRYPT 2003, volume 2894 of Lecture Notes in Computer Science, pages 331–346, Springer-Verlag, 2003
[Bil04] Olivier Billet, Henri Gilbert, and Charaf Ech-Chatbi, Cryptanalysis of a White Box AES Implementation, in Proceedings of the 11th International Workshop on Selected Areas in Cryptography (SAC 2004), volume 3357 of Lecture Notes in Computer Science, pages 227–240, Springer-Verlag, 2004
[Bri06trace] Julien Bringer, Hervé Chabanne, and Emmanuelle Dottax, Perturbing and Protecting a Traceable Block Cipher, in Proceedings of the 10th Communications and Multimedia Security (CMS 2006), volume 4237 of Lecture Notes in Computer Science, pages 109–119, Springer-Verlag, 2006
[Bri06wbc] Julien Bringer, Hervé Chabanne, and Emmanuelle Dottax, White box cryptography: Another attempt, Cryptology ePrint Archive, Report 2006/468, 2006
[Chow02DES] Stanley Chow, Philip A. Eisen, Harold Johnson, and Paul C. van Oorschot, A white-box DES implementation for DRM applications, in Proceedings of the ACM Workshop on Security and Privacy in Digital Rights Management (DRM 2002), volume 2696 of Lecture Notes in Computer Science, pages 1–15, Springer, 2002
[Chow02AES] Stanley Chow, Philip A. Eisen, Harold Johnson, and Paul C. van Oorschot, White-Box Cryptography and an AES Implementation, in Proceedings of the 9th International Workshop on Selected Areas in Cryptography (SAC 2002), volume 2595 of Lecture Notes in Computer Science, pages 250–270, Springer, 2002
[Dem10] Yoni De Mulder, Brecht Wyseur, and Bart Preneel, Cryptanalysis of a Perturbated White-box AES Implémentation, in Progress in Cryptology - INDOCRYPT 2010, volume6498 of Lecture Notes in Computer Science, Springer-Verlag, pp. 292-310, 2010
[Ding04] Jintai Ding, A New Variant of the Matsumoto-Imai Cryptosystem through Perturbation, in Proceedings of the 7th International Workshop on Theory and Practice in Public Key Cryptography (PKC 2004), volume 2947 of Lecture Notes in Computer Science, pages 305–318. Springer-Verlag, 2004
[Goubin07] Louis Goubin, Jean-Michel Masereel, and Michaël Quisquater,Cryptanalysis of White Box DES Implementations. In Proceedings of the 14th International Workshop on Selected Areas in Cryptography (SAC 2007), volume 4876 of Lecture Notes in Computer Science, pages 278–295, Springer-Verlag, 2007
[Jacob02] Matthias Jacob, Dan Boneh, and Edward W. Felten, Attacking an Obfuscated Cipher by Injecting Faults. In Proceedings of the ACM Workshop on Security and Privacy in Digital Rights Management (DRM 2002), volume 2696 of Lecture Notes in Computer Science, pages 16–31, Springer, 2002
[Kerins06] Tim Kerins and Klaus Kursawe, A cautionary note on weak implementations of block ciphers, in 1st Benelux Workshop on Information and System Security (WISSec 2006), page 12, Antwerp, BE, 2006
[Link05] Hamilton E. Link and William D. Neumann, Clarifying Obfuscation: Improving the Security of White-Box DES, in Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC 2005), volume 1, pages 679–684, Washington, DC, USA, 2005, IEEE Computer Society
[Mich07] Wil Michiels and Paul Gorissen, Mechanism for software tamper resistance: an application of white-box cryptography, in Proceedings of 7th ACM Workshop on Digital Rights Management (DRM 2007), pages 82–89, ACM Press, 2007
[Mich08] Wil Michiels, Paul Gorissen, and Henk D.L. Hollmann, Cryptanalysis of a Generic Class of White-Box Implementations, in Proceedings of the 15th International Workshop on Selected Areas in Cryptography (SAC 2008), Lecture Notes in Computer Science, Springer-Verlag, 2008
[Sax09] Amitabh Saxena, Brecht Wyseur, and Bart. Preneel, Towards Security Notions for White-Box Cryptography, in Information Security - 12th International Conference, ISC 2009, volume 5735 of Lecture Notes in Computer Science, pages 49–58, Springer-Verlag, 2009
[Wee05] Hoeteck Wee, On Obfuscating Point Functions, in Proceedings of the 37th ACM Symposium on Theory of Computing (STOC 2005), pages 523–532, New York, NY, USA, 2005, ACM Press
[Wyseur07] Brecht Wyseur, Wil Michiels, Paul Gorissen, and Bart Preneel, Cryptanalysis of White-Box DES Implementations with Arbitrary External Encodings, in Proceedings of the 14th International Workshop on Selected Areas in Cryptography (SAC 2007), volume 4876 of Lecture Notes in Computer Science, pages 264–277, Springer-Verlag, 2007
[Wyseur09] Brecht Wyseur, White-Box Cryptography, PhD thesis, Katholieke Universiteit Leuven, Bart Preneel (promotor), 169+32 pages, 2009



 Ajouter à une liste de lecture
Ajouter à une liste de lecture