La cryptographie standardisée et utilisée actuellement s’appuie essentiellement sur deux problèmes mathématiques : la factorisation et le logarithme discret. Mais les chercheurs s´intéressent à trouver des alternatives crédibles qui, par exemple, pourraient résister à l’avènement de l’ordinateur quantique. L’une de ces alternatives, basée sur la géométrie des réseaux euclidiens s’est clairement démarquée durant cette dernière décennie de recherche, offrant de nouvelles perspectives comme le chiffrement dît homomorphe.
Comme souvent en cryptologie, les réseaux euclidiens ont été utilisés en cryptanalyse avant d’être un outil pour la cryptographie, c’est-à-dire qu’on s’est servi de ces objets mathématiques pour essayer de casser certains cryptosystèmes avant de se rendre compte qu’ils pouvaient aussi servir à en construire de nouveaux.
Ce sont les travaux fondateurs de Miklos Ajtai [2] qui démontreront que les réseaux euclidiens peuvent servir de base solide à la cryptographie. Précisément, il démontre qu’il n’y a pas d’instances faibles pour les problèmes de réseaux : contrairement à RSA où certaines propriétés des nombres premiers choisis peuvent rendre la factorisation facile (et doivent donc être soigneusement proscrit), les réseaux euclidiens sont tous aussi difficiles à « résoudre » les uns que les autres. Un autre intérêt en terme de sécurité est que cet objet mathématique apparaît dans de nombreux problèmes d’informatique, et le fait que 40 ans de recherches dans un cadre bien plus large que celui de la cryptographie n’ait pas permis de résoudre ces réseaux efficacement est une garantie rassurante. Enfin, on ne connaît pas d’attaques même en présence d’ordinateurs quantiques, contrairement à RSA ou au logarithme discret [3].
Très rapidement, des cryptosystèmes inspirés des idées d’Ajtai verront le jour, et un premier brevet est déposé par l’entreprise fraîchement créée NTRU Cryptosystems. Mais l’entreprise bute à plusieurs reprises sur la création d’un schéma de signature digitale [4], et subie plusieurs attaques. Durant les années 2000, les chercheurs prendront le temps de résoudre les nombreuses embûches théoriques liées à ce nouvel objet, laissant temporairement de côté les questions d’efficacité et d’implémentation.
Cette étude théorique permettra de découvrir tout le potentiel de cette cryptographie nouvelle, reproduisant d’abord les cryptosystèmes à gestion fine de droit d’accès (voir article 1) puis les dépassant [5]. Mais c’est surtout l’invention du chiffrement pleinement homomorphe [6] qui surprendra la communauté, car cette invention résout des problèmes véritablement paradoxaux : le chiffrement homomorphe permet d’effectuer n’importe quel calcul sur des données chiffrées sans pour autant devoir les déchiffrer. En théorie, cela permet par exemple de faire une recherche en ligne sans que le moteur de recherche ne connaisse le contenu de notre requête, ou de faire filtrer ses courriels sans que le service de filtrage ne puisse comprendre le contenu de nos courriels. Étonnant non ?
Depuis peu, la question de l’efficacité et de l’implémentation de cette cryptographie nouvelle est redevenue pertinente, des prototypes open source apparaissent [1,7] et le NIST envisage la standardisation de cette cryptographie nouvelle [8], mais c’est un processus qui s’étale sur plusieurs années. Une qualité intéressante de cette cryptographie est qu’elle émerge d’un effort de recherche collégial, ce qui la rend, peut-on espérer, plus difficilement brevetable.
Dans cet article, nous allons présenter les principes de base de cette cryptographie nouvelle, et en particulier la construction de ce fameux chiffrement homomorphe.
Les techniques et méthodes présentées dans cet article sont inspirées de travaux de recherches récents, et ont été simplifiées dans un but pédagogique. L'auteur déconseille vivement l'implémentation et le déploiement de ces techniques sans intervention d'un expert du domaine. L'auteur ne saurait être tenu responsable d’un quelconque dommage résultant de l'utilisation des techniques présentées dans cet article.
1. Une géométrie labyrinthique
Éliminons tout de suite toute confusion possible : ce que les mathématiciens appellent “réseau” ou “réseau euclidien” n’a rien à voir avec la notion de réseau en informatique. Ainsi, pour que cela soit plus parlant, dans cet article nous utiliserons le terme de treillis en lieu et place de “réseau euclidien”. Attention cependant, en dehors de cet article, le terme de treillis est utilisé en mathématiques pour d’autres objets.
1.1 Définitions
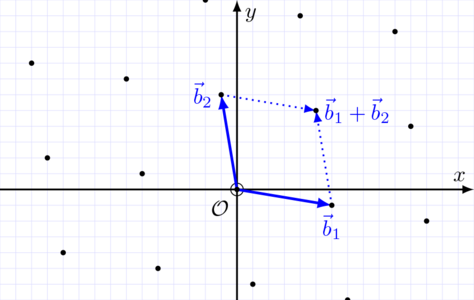
Formellement, un treillis est défini comme “un sous-groupe discret d’un espace vectoriel euclidien”. Pas de quoi s’inquiéter ! En réalité il ne s’agit que d’un “ensemble de points arrangés régulièrement”. Pour visualiser les choses, observons un treillis de dimension deux en figure 1.
Fig. 1 : Un treillis dans le plan Euclidien (ensemble des points noirs), et un exemple d’addition dans ce treillis.
Pour être plus précis, lorsque nous disions “arrangés régulièrement”, nous parlions de la structure additive de cet ensemble de points : un treillis est un ensemble de points du plan (ou d’un espace à plus grande dimension) dans lequel on peut faire des additions et des soustractions (c’est ce qu’on appelle formellement un “sous-groupe”). La propriété d’être discrète s’oppose à la continuité ; par exemple une droite passant par l’origine aurait aussi cette même structure additive, mais la droite est un ensemble continu, elle n’est donc pas un treillis. Enfin, un espace vectoriel euclidien est simplement un espace “droit”, comme le plan, ou l’espace à trois dimensions auquel on est habitué. Cette précision s’oppose aux espaces courbes qu’on trouve dans la théorie de la relativité par exemple.
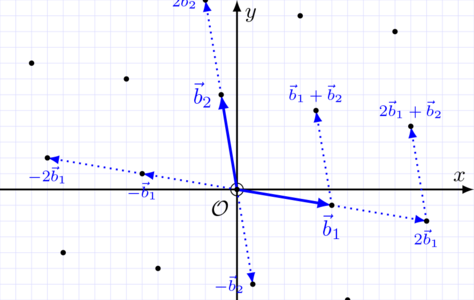
Pour décrire un treillis, on ne peut pas donner la liste complète de ses points, car elle serait infinie. On décrira plutôt un treillis en en donnant une “base”, c’est-à-dire un ensemble de points qui engendrent entièrement le treillis, comme décrit en figure 2.
Fig. 2 : Une base générant le treillis.
On peut maintenant expliciter n’importe quel point du treillis en utilisant une telle base comme un système de coordonnées. Il y a deux différences essentielles avec le système de coordonnées (O, x, y) du plan: dans un treillis les coordonnées seront toujours des nombres entiers (positifs ou négatifs), par contre son système de coordonnées (O, b_1, b_2)n’est pas nécessairement rectangle (les angles ne sont pas droits). En fait, à part pour certains treillis très simples, il n’existera aucune base rectangle. Mais certaines sont plus rectangles que d’autres : en effet les treillis admettent plein de bases différentes !
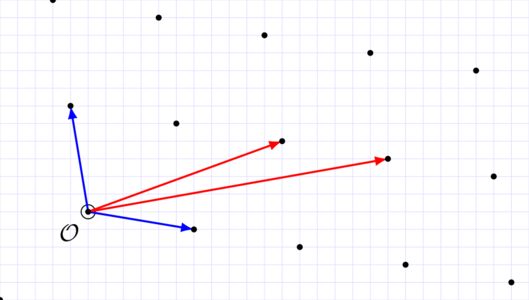
Fig. 3 : Deux bases d’un même treillis. La bonne base en bleu, la mauvaise en rouge.
Intuitivement, la base bleue de la figure 3 semble meilleure que la base rouge, elle n’est pas parfaitement rectangle, mais elle est plus rectangle que la base rouge. Nous allons voir pourquoi cette base bleue est “meilleure”. Par contre, il y a une tâche qui est aisée même avec une mauvaise base, c’est tirer un point aléatoire du treillis : on choisit aléatoirement des entiers r_1, r_2 …, r_n (pour un treillis en n dimensions) et on retourne le point p = r_1 * b_1 + r_2 * b_2 + … + r_n * b_n. En Sage (une extension de Python pour mathématiciens) cela s’écrirait comme suit :
def tirage_treillis(B):
r = vector([randint(-1000,1000)]) // la valeur 1000 est arbitraire
p = B * r
return d
L’entrée B du programme est la base sous forme de matrice : chaque colonne de cette matrice est l’un des vecteurs de base b_1, …, b_n.
1.2 La correction d’erreur et les treillis
Pour comprendre en quoi la base bleue est “meilleure” que la base rouge, il faut expliquer à quoi peuvent servir les treillis, en particulier dans les modems. Lorsque l’on souhaite utiliser un canal analogique pour des communications numériques, il y a forcément du bruit qui vient perturber ce signal. La communication étant numérique, on souhaite transmettre une donnée discrète, on peut donc faire correspondre cette donnée à un point dans un treillis. L’espace complet dans lequel se plonge notre treillis correspond à la donnée analogique transmise, par exemple par modulation de fréquence et d’amplitude. En supposant que l’erreur soit suffisamment petite, on peut retrouver la donnée numérique transmise : il s’agit du point du treillis le plus proche de la donnée analogique reçue.
Pourquoi se compliquer la vie avec des treillis tordus alors qu’un treillis carré ferait l’affaire ?
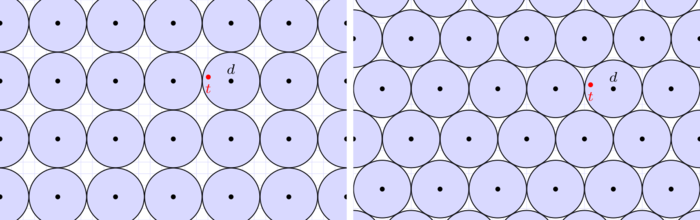
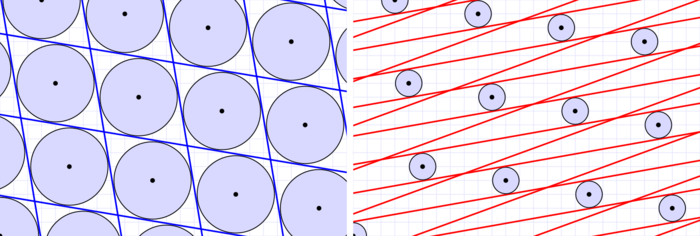
Fig. 4 : Correction d’erreur utilisant deux treillis différents : le treillis carré et le treillis hexagonal. Le modem émetteur cherche à transmettre le point d, mais les erreurs analogiques le transforment en t = d + e pour une petite erreur e. Le modem récepteur retrouvera le point d : c’est le point du treillis le plus proche de t.
Eh bien, car comme nous le voyons en figure 4, le treillis carré (à gauche) laisse beaucoup d’espace inutilisé (en blanc), seulement 78% de la surface est utile. À l’opposé, le treillis dit hexagonal (structure en nid d’abeille, à droite) est optimal avec une densité de plus de 90%. Ainsi le treillis hexagonal permettra un meilleur débit pour le modem tout en garantissant la même correction du bruit analogique.
1.3 Bonne base et mauvaise base
Mais les bases dans tout cela ? Eh bien les bases servent à découper l’espace pour retrouver le point le plus proche. Souvenons-nous que pour effectuer la correction du bruit dans le modem, il faut, étant donné le point e, retrouver le point d, lepoint du treillis le plus proche de t. En deux dimensions, cela semble faisable aisément en dessinant quelques cercles… ce qui peut se traduire par un algorithme efficace. Mais si l’on se place dans un treillis avec plus de dimensions, on va devoir faire des compromis pour que l’algorithme reste efficace : on ne pourra pas corriger des erreurs trop grosses.
Précisément, il existe divers algorithmes dus à Laszlo Babai pour retrouver rapidement un point proche, et ces algorithmes utilisent une base du treillis. Précisément, ces algorithmes “pavent l’espace” en fonction de la base, et chaque point du treillis est au centre de l’un de ces pavés. Comme on le voit en figure 5, la tolérance aux erreurs – définie par le plus grand cercle inscrit dans le pavé – dépend de la forme du pavé
Fig. 5 : La correction d’erreur avec une bonne base (à gauche), et une mauvaise base (à droite).
Si l’on dispose d’une librairie qui fait du calcul matriciel, l’un des algorithmes de Babai est plutôt simple à coder. Il prend en entrée la base, sous la forme d’une matrice B, dont chaque colonne représente un vecteur de la base :
def Algorithme_de_Babai(B, t):
B_inv = inverse(B)
v = B_inv * t
w = vector([round(x) for x in v])
d = B * w
return d
L’idée sous-jacente est très simple : le vecteur t est donné dans le système de coordonnées naturel et on commence par le convertir vers le système de coordonnées du treillis (en multipliant par l’inverse de la matrice B). On arrondit toutes ces coordonnées, et on reconvertit vers la base naturelle en multipliant à nouveau par B. le résultat d = B * w, est un point du treillis, car w est un vecteur constitué de nombres entiers.
1.4 Le labyrinthe multidimensionnel
Lorsque le nombre de dimensions est petit (deux, trois), trouver une bonne base d’un treillis est aisé (on dit “réduire un treillis”), même à la main. Avec des algorithmes un peu malins [9], on peut s’en sortir raisonnablement jusqu’à des dimensions plus grandes, 30 ou 40 en quelques secondes. Mais ces algorithmes de réduction de treillis s’avèrent exponentiels, ainsi, pour la dimension 80 il faut y mettre un certain effort, et les records [10] sur clusters atteignent péniblement 130 dimensions. Ainsi, on estime qu’avec 200 ou 250 dimensions, la réduction de treillis est impossible à moins de milliards d’années de calculs.
2. Chiffrer avec les treillis
Nous n’avons pas encore parlé de cryptographie dans la première section, mais tous les ingrédients sont déjà présents : les treillis présentent des problèmes qui sont résolubles seulement si l’on connaît une bonne base, mais qui sont difficiles sinon. Ainsi on peut espérer se servir d’une bonne base comme d’une clef secrète. Voyons cela plus en détail.
La cryptographie à base de réseaux euclidiens (ou de treillis) ne fait intervenir que des calculs simples, n'implique pas de nombres premiers ou de structure complexe. En fait, ces calculs sont si simples qu'ils peuvent être traduits en un jeu vidéo qui ressemble à Tétris.
Ce jeu, Cryptris [11], a été conçu en collaboration avec l'INRIA, et réalisé par Digitalcuisine. Le jeu est open source, et fonctionne entièrement en HTML5. Il est accompagné de deux articles de vulgarisations scientifiques, qui peuvent servir d'introduction intuitive à cette cryptographie nouvelle. Nous sommes à la recherche de sponsors pour financer l'internationalisation du code source ainsi que la traduction du jeu et des articles.
2.1 Cacher un message dans le labyrinthe… et le retrouver
L’idée est la suivante : on va interpréter un message à chiffrer comme un petit vecteur, comme une “erreur”, et ajouter cette “erreur” à un point aléatoire du treillis. De cette façon, quelqu’un connaissant une bonne base pourra retrouver cette “erreur”, ce message, mais sans une bonne base il sera difficile de le retrouver.
En fait, cette idée simplifiée (c’est ainsi que nous présentons les choses dans Cryptris et les articles de médiations associés [11]) n’est pas tout à fait suffisante, car les messages sont un peu trop prédictibles. Il faut leur ajouter de l’aléa. Supposons que l’on veuille chiffrer juste un seul bit : m = 0,ou m = 1. Il faut transformer ce message en un petit vecteur aléatoire (ses coordonnées ne seront que des 0, +1 et -1). Pour pouvoir facilement enlever l’aléa, on va faire en sorte que le message soit le XOR de toutes les coordonnées. Ainsi on définit :
def ajoute_aleas(m):
a = [randint(-1,1) for I in range(n-1)] // tire toutes les coordonnées aléatoirement sauf une
b = sum(a) % 2 // Calcule le XOR de toutes les coordonnées sauf la dernière
c = (b + m) % 2 // Calcule la dernière coordonnée de telle façon que le // XOR total soit le message
if (randint(0,1) == 1):c = -c // Transforme 1 en -1 avec probabilité ½ (ne change pas le XOR) total
return vector(a + [c])
def enleve_alea(e):
return sum(e) % 2
Pourquoi une procédure si compliquée pour rendre les messages aléatoires ? L’une des raisons sera évidente plus tard, pour le chiffrement partiellement homomorphe.
Maintenant que nous savons inclure de l’aléa dans nos messages, nous allons pouvoir les chiffrer. La procédure est plutôt simple, étant donné une base quelconque (qui sert de clef publique, donc notée P) nous allons tirer un point du treillis au hasard, et y ajouter le message randomisé :
def chiffre(P, m):
d = tirage_treillis(P)
e = ajoute_alea(m)
t = d + e
return t
Il ne manque plus qu’une fonction pour déchiffrer. Cette fonction aussi nécessitera une base, mais pas n’importe quelle base ; pour être sûr que le déchiffrement fonctionne correctement, il faut une bonne base, celle qui sert de clef privée (secrète, et donc notée S):
def dechiffre(S, t):
d = Algorithme_de_Babai(S, t)
e = t - d
m = enleve_alea(e)
return m
Pourquoi le déchiffrement fonctionne-t-il correctement avec une bonne base ? Eh bien, comme “l’erreur” e ajoutée au point d est petite, l’algorithme de Babai retrouvera correctement le point du treillis d choisi lors du chiffrement. Au contraire, avec une mauvaise base, l'algorithme de Babai se trompera presque à tous les coups (d'autant plus que le nombre de dimensions est grand).
Fig. 6 : Le chiffrement et le déchiffrement. Les messages chiffrés (0 ou 1) deviennent des points proches de l’un des points du treillis. Leur position par rapport à ce point proche du treillis correspond à la valeur du message (0 ou 1). Le déchiffrement fonctionne avec une bonne base, car le carré de 0/1 ne déborde pas des pavés bleus. Il échoue parfois avec la mauvaise base (pavés rouges), car cette fois-ci le carré déborde, et avec plus de dimensions cela échouera toujours.
Il manque un dernier élément essentiel à notre cryptosystème : comment créer la paire de clefs (S, P), la bonne base S servant de clef privée, et la mauvaise base servant de clef publique P. Pour la clef privée, cela n’est pas très compliqué, il suffit de la choisir ! En effet, plutôt que de définir un treillis et de chercher une bonne base, on peut simplement choisir une bonne base, et cette base définit un treillis. Mais une fois la bonne base S choisie, il faut aussi dériver une mauvaise base P servant de clef publique. Pour ce faire, on peut essayer de “mélanger” aléatoirement la clef publique, comme dans Cryptris [11]. La vraie bonne solution est un peu plus subtile [12], nous ne la détaillerons pas ici…
2.2 Calculer des XOR… sans déchiffrer les données
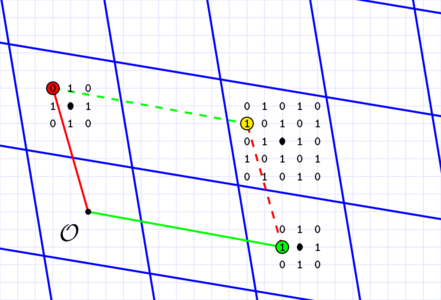
Cette méthode de chiffrement à une propriété étonnante : si l’on ajoute deux messages chiffrés, et que l’on déchiffre le résultat, alors le résultat sera le XOR (le ou exclusif) des deux messages chiffrés. En effet, comme on le voit en figure 7, la somme de deux messages chiffrés suit le même motif que le XOR de ces deux messages (si ce n’est que les carrés de 0/1 sont un peu plus grands)
Fig. 7 : En rouge et vert, deux messages chiffrant respectivement 0 et 1 et en jaune la somme de ces deux chiffrés qui, en effet, chiffre la valeur 1 = 0 XOR 1. Si l’on change les deux chiffrés rouge et vert, leur somme est modifiée comme prévu par la loi du XOR.
Dans notre figure 7, il semble qu’effectuer un XOR soit la limite : si l’on essaye de répéter cette opération, alors le carré de 0/1 grandit à chaque fois. Au bout d’une deuxième opération, on sortirait du pavé bleu : on ne pourrait plus déchiffrer correctement. C’est comme si dans le cas du modem, l’erreur était plus grosse que prévu et donc non corrigeable. Cependant cette figure en deux dimensions est un peu trompeuse, en vérité on peut concevoir des treillis qui pourraient supporter plein de XOR d’affilés, mais il y a toujours une limite.
2.3 Tout calculer sans déchiffrer : le chiffrement homomorphe
La propriété que nous venons de voir est appelée un “homomorphisme partiel”. Homomorphe signifie “qui préserve la forme/la structure”, ainsi le chiffrement que nous venons de présenter préserve la structure additive modulo 2 (car le XOR peut être vu comme une addition modulo 2). En fait cet homomorphisme partiel n’est pas si surprenant compte tenu que d’autres cryptosystèmes comme RSA [13] avaient eux aussi des homomorphismes partiels.
Cet homomorphisme est dit partiel, car seule la structure de l’addition est préservée. Le tour de force viendra de Craig Gentry [6] qui réussira à faire en sorte qu’en plus des additions, on puisse aussi faire des multiplications sans déchiffrer les messages : voici donc le premier cryptosystème entièrement homomorphe. Pourquoi est-il si remarquable de pouvoir faire ces deux opérations d’addition et de multiplication ? Eh bien, modulo 2, la multiplication correspond au “et” logique, la porte logique AND. Et vous le savez sûrement, cet ensemble de deux portes est universel : n’importe quel programme peut être exprimé sous forme de circuit qui n’utilise que des portes logiques XOR et AND. On peut donc construire des “circuits logiques” de XOR et de AND, mais qui au lieu de fonctionner comme dans un processeur sur des données en clair, fonctionnent sur des données chiffrées ! Ainsi, on pourrait en théorie faire travailler un ordinateur sur des données qu’il ne peut pas comprendre…
À part la beauté théorique de la chose, quel est l’intérêt du chiffrement homomorphe ? Eh bien, le chiffrement homomorphe pourrait permettre de résoudre de nombreux problèmes liés à l’externalisation du stockage et traitement de données : le fameux cloud.
En effet, imaginons que je souhaite stocker une base de données sur un serveur à qui je ne veux pas faire confiance, je serais alors tenté de chiffrer mes données. Mais alors, le serveur ne pourrait plus calculer pour moi des statistiques sur mes données. Le chiffrement homomorphe résout ce problème. Il me suffit d’utiliser ce chiffrement pour ma base de données. Lorsque je souhaite récupérer une information statistique sur mes données, disons une fonction f de mes données D, il me suffit d’exprimer ma fonction f sous la forme d’un circuit C, fait de portes logiques XOR et AND. J’envoie ce circuit au serveur, qui l’exécute “homomorphiquement” sur mes données, et il peut me renvoyer le résultat chiffré, résultat que seul moi peux déchiffrer.
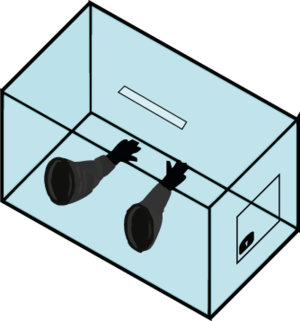
Une métaphore pratique pour comprendre le fonctionnement et l’utilisation du chiffrement homomorphe est celle de la “boîte à gants”-- pas celle de la voiture, mais celle qu’on trouve dans les laboratoires de chimie ou de biologie pour manipuler des produits sans risque de fuite [14]. Ainsi le chiffrement à clef publique usuel peut être vu comme « un coffre-fort à clef, avec une fente » : tout le monde peut insérer des messages dans le coffre, mais il faut la clef pour sortir ces messages. Le chiffrement homomorphe est une boîte similaire, mais avec en plus “une paire de gants” dans une paroi, qui permet de manipuler le contenu de la boîte, sans pour autant pouvoir sortir ce contenu, comme en figure 8.
Fig. 8 : Une métaphore pour le chiffrement homomorphe. Tout le monde peut chiffrer des messages (glisser un papier dans la fente), tout le monde peut manipuler les données chiffrées (utiliser les gants), mais seul celui qui a la clé privée peut ouvrir la boîte et lire les données.
Muni de cette métaphore, on peut entrevoir le coup de génie de Craig Gentry : sa technique nommée bootstrapping. La construction du chiffrement entièrement homomorphe se heurte à un problème : lors des multiplications (porte logique AND) le “bruit” (la taille de carré de 0/1 de la figure 7) augmente énormément : on ne peut effectuer que quelques opérations homomorphes, après quoi le résultat ne serait plus déchiffrable. On ajoute ainsi à la métaphore que les gants “durcissent” à force de manipuler les objets à l’intérieur de la boîte, limitant la quantité de manipulations faisables.
Pour résoudre cette limitation, Craig propose d’utiliser plusieurs de ces boîtes. La deuxième boîte contient la clef de la première, la troisième la clef de la seconde, etc. Ainsi, lorsque les gants de la première boîte ont durci, on met la première boîte dans la seconde – oui, la boîte, bien qu’impénétrable est pliable, de sorte à pouvoir passer dans la fente d’une autre boîte. Dans cette seconde boîte, on peut ouvrir la première boîte grâce à la clef qu’on a soigneusement placée ici. On récupère ainsi, à travers la seconde boîte, le contenu de la première, et l’on peut continuer à manipuler nos éléments. Lorsque les gants de cette seconde boîte durciront à leur tour, on passera le tout dans la troisième boîte et ainsi de suite.
Conclusion
Voici donc présentées les idées les plus récentes de la recherche en cryptographie, et en particulier cette idée prometteuse du chiffrement homomorphe. La révolution du cloud par le chiffrement homomorphe n’est cependant pas pour demain, car l’efficacité des calculs homomorphes n’est pas encore raisonnable pour de grosses bases de données. Mais du progrès a été fait depuis l’invention initiale de 2009. À l’époque, le bootstrapping (voir encadré) n’était que théorique, et on estimait qu’il faudrait plusieurs mois pour effectuer un tel calcul. L’état de l’art permet aujourd’hui d’effectuer ce bootstrapping, et permet d'évaluer entre une dizaine et une centaine de portes logiques par seconde [15]. On est encore loin d’émuler un processeur complet, mais on peut déjà faire de petits calculs de façon homomorphe. Il y a sûrement des applications pour lesquelles de tels calculs simples pourraient suffire…
Références
[1] Ducas L. et Lepoint T. (2013): Une implémentation open source du schéma de signature BLISS : http://bliss.di.ens.fr.
[2] Ajtai M., "Generating hard instances of lattice problems", 1996 : https://www.cs.cmu.edu/~yiwu/doc/ajtai-worst-avg.pdf.
[3] Algorithme de Shor: https://fr.wikipedia.org/wiki/Algorithme_de_Shor
Scott Aaronson (2007) sur l’algorithme de Shor: http://www.scottaaronson.com/blog/?p=208
[4] NTRUsign et les attaques subies: https://en.wikipedia.org/wiki/NTRUSign
[5] Gorbunov S., Vaikuntanathan V., et Wee H., "Attribute-Based Encryption for Circuits", 2013 : http://eprint.iacr.org/2013/337.pdf
[6] Gentry Craig, "A fully homomorphic encryption scheme", Thèse de Doctorat, 2009 : https://crypto.stanford.edu/craig/
[7] Halevi S. et Shoup V., "HElib, software library that implements homomorphic encryption", 2013 : https://github.com/shaih/HElib
[8] NIST : Workshop on Cybersecurity in a Post-Quantum World, 2015 : http://www.nist.gov/itl/csd/ct/post-quantum-crypto-workshop-2015.cfm
[9] Algorithmes LLL et BKZ : https://fr.wikipedia.org/wiki/Algorithme_LLL
[10] Records de réduction de réseau : http://www.latticechallenge.org/svp-challenge/index.php
[11] Cryptris et son code source:
https://inriamecsci.github.io/cryptris/
https://github.com/InriaMecsci/cryptris
Articles de médiations autour de Cryptris :
http://images.math.cnrs.fr/Cryptris-1-2-Comprendre-une-des.html
http://images.math.cnrs.fr/Cryptris-2-2-Les-dessous.html
[12] Micciancio D., "Improving Lattice based cryptosystems using the Hermite Normal Form", 2001 : https://cseweb.ucsd.edu/~daniele/papers/HNFcrypt.html
[13] Ducas L., « Démocratiser la cryptographie », GNU/Linux Magazine n°177, décembre 2014.
[14] https://fr.wikipedia.org/wiki/Bo%C3%AEte_%C3%A0_gants_%28laboratoire%29
[15] Dernières avancées sur le chiffrement homomorphe et le bootstrapping:
Ducas L. et Micciancio D., "FHE Bootstrapping in less than a second", 2014 : https://eprint.iacr.org/2014/816
Halevi S. et Shoup V., "Bootstrapping for HElib", 2014 : https://eprint.iacr.org/2014/873