De la Scytale à Enigma, la Cryptologie est restée pendant longtemps un art secret, réservé aux militaires et diplomates. Elle devient une science dans les années soixante, et cette ouverture permet la naissance de nombreuses idées nouvelles. Mais beaucoup reste à faire pour la mise en pratique et la démocratisation de la cryptographie moderne.
Enigma est sans doute la méthode la plus emblématique de la cryptographie, pour son rôle historique durant la Seconde Guerre mondiale et c’est la cryptanalyse du chiffre Enigma qui motivera Turing et son équipe de mathématiciens à réaliser les premiers ordinateurs. C’est pour la cryptologie que naît l’informatique : d’abord la machine mécanique, puis la machine à transistor.
L’informatique trouvera très vite des applications commerciales, motivant des progrès théoriques comme l’invention des premiers langages de programmation (ex. FORTRAN, 1954), et des avancées pratiques avec la miniaturisation des machines et des circuits. Mais la cryptographie restera confidentielle jusqu’aux années 70, chaque état développant secrètement ses propres méthodes pour une utilisation interne.
La création du réseau ARPANET viendra bouleverser ce statu quo : il devient nécessaire de standardiser les méthodes de chiffrement à une échelle internationale. Un appel à candidatures est lancé, et attirera l’intérêt de scientifiques universitaires, mais aussi d’entreprises comme IBM. La Cryptographie s’ouvre et se transforme en discipline scientifique. Des théories longtemps considérées pures, comme l’arithmétique modulaire, se voient appliquées avec des retombées politiques et économiques majeures.
L’ouverture de la cryptographie permettra à de nouvelles idées d’apparaître, en particulier le domaine de la cryptographie dite asymétrique ou comment communiquer de façon chiffrée sans partage préalable d’une clef secrète. Naîtra aussi un combat pour la libre utilisation de la cryptographie, avec des logiciels open source comme PGP et OpenSSH. Mais il faudra attendre l’année 2004 pour voir l’usage privé de la cryptographie légalisé en France. L’actualité, avec des affaires comme celle de Lavabit [1], montre tout de même que la confidentialité des communications face aux injonctions étatiques n’est pas encore un droit véritablement acquis.
1. Un premier Standard, le DES
Jusqu’à la fin des années 60, les techniques cryptographiques restent secrètes, développées indépendamment dans chaque nation pour les applications diplomatiques et militaires. Avec l’arrivée des réseaux informatisés dans les entreprises, et bientôt ARPANET, le bureau états-unien des standards lance un appel à candidatures pour la standardisation en 1973. L’entreprise IBM proposera alors l’algorithme de chiffrement par bloc Lucifer, développé deux ans plus tôt, notamment par Horst Feistel. Quelques modifications furent apportées, et le DES, Data Encryption Standard, fut adopté en 1976. Cela marque le début de la recherche académique en cryptographie.
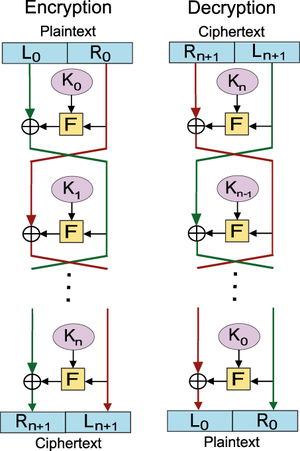
La contribution majeure de Feistel sera souvent réutilisée par la suite. L’idée derrière sa construction est qu’il est facile de concevoir une fonction qui a l’air aléatoire, mais beaucoup plus compliquée si l’on ajoute la contrainte que cette fonction doit être efficacement réversible. Il propose ainsi une transformation qui augmente une petite fonction quelconque en une plus grosse fonction réversible, à l’aide de quelques XOR (voir figure 1).
Il est aujourd’hui avéré que la NSA a influencé le NIST dans les modifications apportées a Lucifer pour définir DES [2]. L’une des modifications internes du schéma a augmenté la sécurité du DES, empêchant des techniques de cryptanalyse qui n’ont été découvertes par le milieu universitaire que plus d’une décennie plus tard. Mais l’autre modification a fait baisser la sécurité du schéma, et ce de façon peu subtile... la taille de clef a été réduite de 64 bits à 56 bits, réduisant ainsi le coup d’une attaque exhaustive par un facteur 2^8 = 256. Les esprits mesquins pourront essayer d’en déduire un encadrement de la puissance de calcul de la NSA en 1976.
Le DES sera remplacé par le triple-DES, puis en 2001 par l’AES qui reste le standard le plus répandu aujourd’hui. Des instructions AES sont implémentées en dur sur les processeurs modernes, permettant de chiffrer les données à des vitesses comparables au flux du bus RAM.
Fig. 1 : La transformation de Feistel : F est une petite fonction pseudo-aléatoire (quelconque), et la fonction totale est aussi pseudo-aléatoire, mais réversible. Image sous licence CC BY-SA 3.0, utilisateur Amirki, Wikimedia commons.
Quelques acteurs
Le GCHQ (Quartier général gouvernemental britannique des télécommunications)
Agence en charge de l’espionnage et du contre-espionnage. Célèbre pour la cryptanalyse d’Enigma durant la Seconde Guerre mondiale, ayant accueilli les fondateurs de l’informatique comme Alan Turing. Les récentes fuites concernant la NSA révèlent la collaboration du GHCQ avec la NSA sur des programmes de surveillance massive comme UPSTREAM [3].
Le NIST (Bureau national états-unien des standards technologiques)
Agence Nationale américaine, du département du Commerce. Travaillant de concert avec l’industrie pour promouvoir le développement économique et technologique. Notamment en charge de la mise en place de standards pour les fonctions cryptographiques. Son indépendance a été mise en doute récemment avec l’affaire des backdoors dans le standard Dual EC-DRBG [4].
La NSA (Agence nationale de sécurité états-unienne)
Agence en charge de l’espionnage et du contre-espionnage informatique. La fuite de documents classifiés en 2013 a soulevé une forte controverse sur la légalité et la légitimité de leur méthode de surveillance électronique [3], incluant la collaboration (sous pression judiciaire) de nombreuses entreprises.
Lavabit
Société fondée en 2004, fournisseur de services de courriels chiffrés. En 2013, sous pression judiciaire la société décide de fermer son service plutôt que de livrer les clefs maîtresses de leurs serveurs [1].
L’EFF (Electronic Frontier Foundation)
Fondation à but non lucratif ayant pour but de défendre la liberté d’expression sur internet. Outre son implication judiciaire et politique dans de nombreuses affaires, l’EFF se lance aussi dans des missions techniques, avec des projets comme le DES-cracker, ou de calcul distribué de nombres premiers.
L’IACR (Association internationale des chercheurs en cryptologie)
Elle organise les conférences majeures du domaine. Elle a en particulier négocié auprès des éditeurs de journaux que les cryptographes gardent presque tous les droits sur leurs publications. En mai 2013, elle s’exprime sur les affaires récentes avec la « résolution de Copenhague » [5].
L’ANSSI (Agence nationale pour la sécurité des systèmes d’informations)
L’agence a pour mission la surveillance et la protection de réseaux sensibles, notamment des réseaux interministériels. Elle joue aussi un rôle de conseil, établit des standards et délivre des labels. Enfin, elle est censée informer régulièrement le public sur les menaces provenant des réseaux informatiques.
La CNIL (Commission nationale de l’informatique et des libertés)
Commission indépendante, munie d’un pouvoir de contrôle et de sanction, dont la mission est de veiller à la protection du droit à la vie privée et des libertés individuelles et publiques dans le cadre des réseaux et fichiers informatiques.
Alice et Bob
Protagonistes canoniques des aventures cryptographiques. Le choix des noms reflète simplement l'ordre alphabétique. Ainsi, si plus de parties sont en jeu, on invitera aussi Charly, Denise, Eve, Frank... Alice et Bob sont généralement les deux parties légitimes voulant communiquer. On réserve le prénom Eve pour un attaquant écoutant les communications, en raison de la consonance en anglais avec le terme Eavesdropper [6].
2. La crypto asymétrique connue et utilisée
Toutes les techniques de chiffrement inventées jusqu’ici nécessitent que les parties voulant communiquer de façon confidentielle partagent au préalable une clef secrète ; cette limitation semblait naturelle à bon nombre de cryptologues. En 1970, James H. Ellis affirme dans une note interne au GHCQ qu’il est concevable d’effectuer des communications confidentielles sans secret partagé au préalable ; ouvrant la voie de la cryptographie dite à clef publique ou asymétrique.
2.1 L’échange de clefs
Le problème principal de la cryptographie symétrique est logistique : avant de pouvoir communiquer secrètement les deux parties doivent connaître à l’avance un secret commun, la clef.
Plutôt que de s’attaquer directement au chiffrement, Merkle s’affaire à un problème plus simple. Deux parties communiquent à travers un calcul non confidentiel, mais veulent s’accorder sur un secret commun aléatoire. Théoriquement ce n’est pas possible, car toutes les informations connues par les deux parties sont aussi connues par l’attaquant. Mais Merkle veut faire en sorte que l’attaquant doive faire plus de calculs que les deux parties légitimes. On retrouvera bien plus tard son idée de puzzle dans les « preuves de travail » que constituent les block-chains de Bitcoin.
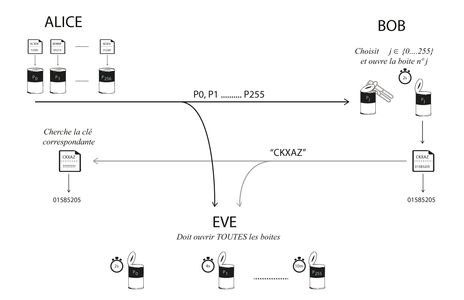
Prenons n’importe quel chiffrement, par exemple l’AES, mais rendons-le cassable en réduisant la taille des clefs à 32 bits (en complétant avec des 0) : cela prendrait environ deux secondes à casser sur une machine moderne. Alice a ainsi 256 petites clefs de 32 bits k[0] … k[255], et chiffre des paires indices/grandes clefs aléatoires (I[0], K[0])...(I[255], K[255]) qu’elle envoie à Bob, son correspondant : chaque message chiffré est un « puzzle » résoluble en y mettant un certain effort de calcul. Bob, choisi l’un de ces puzzles (disons le puzzle numéro j) et le résout, retrouvant ainsi I[j] et K[j]. Bob renvoie à Alice alors la valeur de I[j], et ils peuvent utiliser la grande clef commune K[j]. Un attaquant voulant retrouver cette même clef devra essayer de résoudre les 256 puzzles (ce qui lui prendra environ 10 minutes) pour retrouver quel puzzle contient I[j] et en déduire K[j]: l’attaquant a dû fournir un plus gros effort que les participants légitimes. CQFD. Le protocole de Merkle est résumé en Figure 2.
Fig. 2 : Le protocole de Merkle. Ici les puzzles sont représentés par des boîtes de conserve : c'est plus facile à ouvrir qu'un coffre fort, mais ça requiert un effort. Les indices I[0] … I[255] sont ici des chaînes de caractères alphabétiques, et les grandes clefs K[0]...K[255] des chaînes numériques. Crédit Pratik Shah.
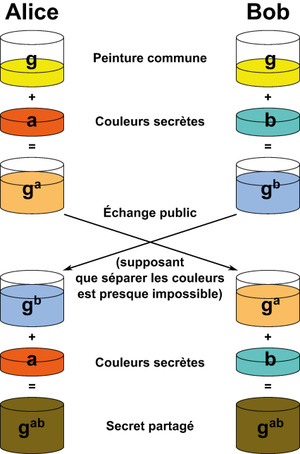
Néanmoins, cette solution est loin d’être idéale, on voudrait un beaucoup plus gros écart entre l’effort de calcul des participants légitimes et l’attaquant. Il ne faudra attendre que deux ans avant que cette idée soit améliorée pour obtenir enfin un écart exponentiel entre le temps de calcul nécessaire aux parties légitimes et l’attaquant, avec le protocole d’échange de clefs de Bailey W. Diffie, Martin E. Hellman. L’idée novatrice est de s’appuyer sur une structure mathématique algébrique ; jusqu’alors toute forme de structure était évitée en cryptographie de peur qu’elle ne mène à des cryptanalyses. Cette structure algébrique permet en effet des attaques plus rapides que la recherche exhaustive, mais l’essentiel est que ces attaques restent exponentielles.
Soit p un nombre premier, et g < p un entier quelconque (ou presque), établi à l’avance, mais ne nécessitant pas d’être secret. Le protocole se déroule ainsi :
|
Alice |
|
Bob |
|
choisit a aléatoirement |
|
choisit b aléatoirement |
|
Calcul A = g^a mod p |
|
Calcul B = g^b mod p |
|
|
→ A → |
|
|
|
← B ← |
|
|
Calcul K = A^b mod p |
|
Calcul K’ = B^a mod p |
|
K = |
g^(a*b) mod p |
= K’ |
|
|
|
|
Une version plus graphique de ce protocole est proposée en figure 3.
Fig. 3 : Le protocole Diffie-Hellman expliqué avec des mélanges de peinture. La métaphore veut qu’il soit facile de mélanger les peintures (ainsi on peut calculer A=g^a connaissant g et a), mais difficile de les séparer (retrouver a connaissant g et A). Image dérivée de Wikimedia, non éligible au copyright.
À la fin du protocole, les deux parties se sont mises d’accord sur une clef commune K = g^(ab). L’attaquant a seulement eu accès à A=g^a, et B=g^b, et peut certes calculer certaines combinaisons, telles que A * B = g^(a+b). Par contre, pour retrouver g^(ab) la seule méthode connue est de retrouver a à partir de A = g^a (ou symétriquement b à partir de B = g^b) c’est-à-dire résoudre le problème du logarithme discret ; les seuls algorithmes connus pour résoudre ce problème sont (presque) exponentiels.
Ce protocole est toujours d’actualité par exemple comme sous-protocole de SSL, mais au lieu d’utiliser l’exponentiation modulaire, on utilise aujourd’hui les courbes elliptiques (ECDHE) : les calculs restent similaires, mais la signification du symbole ^ est changée. Malheureusement, c’est un sujet difficile à aborder sans un lourd bagage mathématique.
2.2 Fonction à trappe, Chiffrement et Signature
En 1977, Ronald Rivest, Adi Shamir et Leonard Adleman proposent le premier algorithme de chiffrement à clef publique RSA. L’échange de clefs vu précédemment ne permet à deux parties que de s’accorder de façon confidentielle sur une clef commune aléatoire, qui servira de clef privée à la suite des échanges ; le chiffrement à clef publique RSA permet directement la transmission d’un message confidentiel, et ne nécessite pas d’interaction après la publication de la clef publique. Plus précisément, Alice souhaitant pouvoir recevoir des messages confidentiels, choisit deux grands nombres premiers p et q, qui constituent sa clef privée. De ces nombres elle déduit la clef publique N = pq, en calculant un simple produit. Ainsi retrouver la clef privée à partir de la clef publique est exactement le problème de la factorisation, pour lequel aucun algorithme efficace n’est connu, et ce malgré des décennies de recherche ; il est raisonnable de croire qu’aucun algorithme efficace n’existe !
Cet entier N sert de paramètre à une fonction dite à trappe : f_N(x) = x^e mod N, pour une valeur de e partagée par tous, disons e=17. Ainsi, connaissant N, il est possible à tous de calculer y = f_N(x) pour n’importe quelle valeur de x, mais inverser la fonction, c’est-à-dire retrouver x à partir y = f_N(x) ne semble être possible (au sens calculable efficacement) qu’en connaissance de la trappe : la factorisation de N en nombres premiers p et q. En effet, pour un entier p, il est possible (grâce au « petit Théorème de Fermat ») d’inverser la fonction f_p(x) = x^e mod p en calculant d l’inverse modulaire de e, c’est-à-dire un entier vérifiant e*d = 1 mod (p-1), car on a alors x^(e*d) = x mod p. Ainsi, en inversant séparément f_p et f_q, on peut inverser complètement f_N en utilisant le « Théorème des restes Chinois ».
On peut aussi utiliser ces fonctions à trappe pour faire de la signature électronique, par exemple pour émettre des certificats X.509 dans le protocole TLS. On utilise la trappe pour trouver une signature s telle que f_N(s) = m, où m est le message. N’importe qui connaissant juste N mais pas la trappe peut vérifier que F_N(s) = m.
2.3 Les preuves de sécurité
Il reste cependant une question essentielle : la difficulté de factoriser N suffit-elle à garantir la confidentialité de ce schéma de chiffrement ? Ou, au contraire, existerait-il une façon de casser RSA sans pour autant factoriser N ? Cette question reste un problème ouvert : aucune méthode autre que la factorisation n’est connue à ce jour pour s’attaquer à ce chiffrement, mais les seules preuves établissant formellement un lien entre la confidentialité du schéma RSA et la difficulté de la factorisation ont été établies dans des modèles de calcul restreints.
Heureusement, deux ans après la publication de RSA, Michael O. Rabin propose un autre cryptosystème, cette fois-ci vraiment basé sur la factorisation au sens où il prouve mathématiquement que s’il existe un algorithme efficace compromettant la confidentialité de ce nouveau schéma, alors il existe un algorithme efficace de factorisation [7]. De telles preuves mathématiques sont appelées réductions, ou plus simplement preuves par l’absurde : on suppose l’existence d’un attaquant efficace, et l’on construit un algorithme (appelé un simulateur) qui fait appel à cet attaquant comme une sous-routine, par exemple ici pour résoudre le problème de la factorisation.
Fig. 4 : Le simulateur interagit avec l'attaquant, en prétendant être le vrai schéma de Rabin (mais en fait ne connaissant pas la clé privée). Il envoie donc une clé publique et un challenge c, un message chiffré (dont il ne connaît en fait pas le contenu). Le simulateur se sert de la réponse m de l'attaquant, pour résoudre le problème de la factorisation : retrouver p et q.
En d’autres termes, Rabin construit une fonction à trappe F_N (différente de celle de RSA), telle qu’il existe un algorithme (la réduction) qui ayant accès à une méthode pour inverser F_N (l’attaquant) permet de factoriser N. Et comme factoriser N semble être quasiment impossible, inverser F_N doit aussi être tout aussi impossible.
Une façon d’interpréter une preuve de sécurité est de considérer que l’algorithme de réduction « hack » l’attaquant : l’attaquant ne fait que déchiffrer des messages, pourtant la réduction s’en sert pour un autre usage, résoudre des problèmes mathématiques supposés difficiles. Pour les lecteurs familiers de la notion de problème NP-complet, les méthodes de preuve de NP-complétude [8] sont tout à fait similaires.
3. Les nouvelles primitives
3.1 Le chiffrement à gestion de droit d’accès
Bien que ces outils cryptographiques suffisent à répondre aux problèmes principaux de sécurité sur un réseau non sécurisé, certains scénarios requièrent de nouvelles fonctionnalités. Une restriction est que le chiffrement ou la signature seule n’intègrent pas de façon native de structures hiérarchiques permettant une gestion fine des droits d’accès; si l’on veut chiffrer un message pour plusieurs personnes, il faut le chiffrer séparément pour chacune d’entre elles. Dans bien des cas, il serait beaucoup plus efficace de chiffrer le message une seule fois, en l’associant à une règle qui définit une règle d’accès. Avec un tel outil, on pourrait imaginer garantir les droits et les interdictions en lecture sur un système de fichiers, non pas par les verrous imposés par l’OS (parfois contournables), mais par une telle primitive cryptographique. Certes il est déjà possible de chiffrer ses fichiers, voire l’intégralité de son répertoire /home/~, mais cela n’offre pas la même finesse que la gestion des droits à la UNIX (root > user > group > all).
Le premier pas dans cette direction a lieu en 2001, lorsque Dan Boneh et Matthew K. Franklin proposèrent un schéma de chiffrement basé sur l’identité [9]. Leur construction s’appuie sur les courbes elliptiques et le couplage de Weil. Pour ces travaux, Boneh, Franklin et Joux ont reçu en 2013 le Prix Gödel.
Cette première version n’offre pas encore de structure fine d’accès, mais simplifie les échanges entre les autorités de certification et les parties par rapport à l’infrastructure à clefs publiques. Le point essentiel pour la suite est que les clefs ne sont plus choisies complètement indépendamment les unes des autres, mais toutes générées par une autorité unique, ce qui permet d’intégrer des structures de gestion de droits au sein même des clefs. La première évolution sera le chiffrement basé sur l’identité hiérarchique, permettant de chiffrer un message de telle façon qu’il soit déchiffrable par une entité précise, mais aussi par tous ses supérieurs hiérarchiques. Ont suivi de nombreuses variations offrant de nouvelles règles d’accès de plus en plus fines : grâce au couplage de Weil on peut exprimer essentiellement des règles d’accès sous forme de regexp (expression régulière). Très récemment, sont apparues de nouvelles solutions basées sur un autre objet mathématique, le réseau euclidien, et permettent cette fois-ci d’exprimer n’importe quelle règle qui serait calculable par un programme quelconque.
3.2 Le partage de clef et les multi-autorités
Le partage de clefs est une idée simple qui s’avère très utile dans de nombreux scenarii. Imaginons que l’on souhaite pouvoir déclassifier des documents (par exemple militaires) si deux autorités (disons judiciaires et législatives) s’accordent sur la déclassification de ces documents. Si la clef de chiffrement de ces documents est k, alors on peut partager cette clef, en choisissant un masque aléatoire a, et les deux parts du partage sont alors k1 = k XOR a, et k2 = a. Si les deux autorités s’accordent, elles peuvent retrouver k = k1 XOR k2. Par contre, en ne connaissant que k1 (ou k2), on n’apprend aucune information sur la clef k elle-même, car le masque a est aléatoire. Pour une application plus courante, cela permet de pouvoir retrouver sa clef en cas de perte sans pour autant donner tout le pouvoir à une seule personne.
Il est possible de rendre le partage de clefs plus subtil en utilisant un peu d’arithmétique. Précisément, on peut partager la clef en N parts, et faire en sorte que n’importe quel sous-ensemble d’au moins M parts permette de reconstituer la clef partagée. On peut ainsi garantir que la déclassification soit possible si et seulement si une majorité des partis vote en faveur de la déclassification. La technique utilise l’interpolation de Lagrange pour les polynômes [10].
L’idée du partage d’autorité peut s’appliquer aussi à la gestion fine de droits d’accès. En effet, l’un des problèmes des schémas présentés dans le précédent paragraphe est l’existence d’une autorité centrale capable de tout déchiffrer, et qui décide unilatéralement des droits de chaque utilisateur. Cela peut correspondre à une certaine hiérarchie interne en entreprise ou en agence gouvernementale ; mais une telle autorité centrale à l’échelle globale d’internet serait tout à fait inacceptable autant d’un point de vue de la sécurité (la fuite de la clef maîtresse compromet toutes les communications) que d’un point de vue politique. Par contre, si cette autorité était partagée entre différentes entités basées dans divers pays avec des antagonismes prononcés, cela pourrait être acceptable.
3.3 Le Chiffrement Homomorphe
Une autre direction de recherche ouvrant de nouvelles applications est le chiffrement dit homomorphe, c’est-à-dire un chiffrement qui préserve certaines structures arithmétiques entre les clairs et les chiffrés. L’exemple le plus simple est en fait le chiffrement RSA vu plus haut : le produit de deux chiffrés est un chiffré valide du produit des deux messages clairs. Dans beaucoup de contextes, notamment en présence d’attaques actives, cette propriété est considérée comme une faiblesse, car la préservation de structure peut permettre à un attaquant d’extraire de l’information ; des contre-mesures brisant ces structures sont ajoutées.
Cependant, cette structure peut aussi être un atout considérable pour de nouveaux scénarios cryptographiques, car elle autorise un tiers à effectuer des opérations sur des données chiffrées sans qu’il soit pour autant capable de les déchiffrer. Un exemple d’application est le vote électronique [11] : chaque vote est chiffré puis publié, on additionne le contenu de tous les bulletins sans les déchiffrer ; calcul qui peut être publiquement vérifié pour éviter certaines fraudes. C’est seulement ce résultat final qui sera déchiffré, révélant uniquement le résultat de l’élection, mais pas les votes individuels. Et pour limiter les risques d’utilisation frauduleuse de la clef de déchiffrement, on peut inclure du partage de clef.
Outre RSA qui autorise la multiplication, d’autres schémas, comme celui de Pascal Paillier [12], permettent l’addition. Il faudra attendre les travaux de Craig Gentry en 2009 [13] pour voir apparaître un schéma crédible de chiffrement qui autorise à la fois l’addition et la multiplication ; et le fait de pouvoir conjointement utiliser ces deux opérations autorise en fait d’effectuer n’importe quelle opération sans déchiffrer les données ! Cela rend par exemple possible pour deux personnes d’optimiser un partage de ressources, sans révéler à l’autre ses propres préférences ; ou encore – paradoxe ultime! – d’effectuer une recherche sur internet, sans que le moteur de recherche n’apprenne le contenu de notre requête.
Ces nouveaux cryptosystèmes sont basés sur un outil mathématique récemment introduit en cryptographie : le réseau Euclidien. Un prochain article sera consacré à ces nouvelles techniques. Ces derniers résultats furent d’abord très théoriques, dans la mesure où les calculs et les tailles des messages chiffrés semblaient astronomiques ; mais les améliorations successives pourraient permettre à une telle technologie d’être appliquée dans un futur proche.
Conclusion
Cet état des lieux révèle une situation paradoxale : la théorie semble offrir un arsenal de solutions cryptographiques à des scénarios d’utilisation assez complexes, mais en pratique nos données sont extrêmement mal protégées sur Internet. Le fait est que les implémentations de la cryptographie sont essentiellement motivées par les applications commerciales, et de ce fait disponibles en interne pour les entreprises, et mises à la disposition des utilisateurs uniquement dans le cadre très restreint du protocole HTTPS.
Quid de Tor et de GPG ? Il existe en effet des solutions libres permettant de garantir son anonymat et la confidentialité de ses communications, mais elles restent difficiles d’accès aux utilisateurs qui ne seraient pas des power-users. Pour paraphraser Dan J. Bernstein [14], il est temps de développer un logiciel de chiffrement suffisamment simple pour qu’un journaliste soit capable de s’en servir. Mais le problème n’est pas que l’interface logicielle : il y a un énorme effort d’éducation et de sensibilisation à faire et mon avis est qu’il est nécessaire de comprendre les notions de base de la cryptographie pour en faire bonne utilisation. C’est l’objectif du jeu vidéo Cryptris [15] par exemple : démystifier les principes de la cryptographie asymétrique.
Un autre challenge est celui d’imposer la cryptographie là où elle serait bénéfique à l’utilisateur, mais pas forcément aux acteurs du net. Les nouvelles techniques comme le chiffrement homomorphe pourraient permettre de garantir à la fois l’utilisabilité des données mises dans le cloud tout en préservant leur confidentialité, mais on ne peut pas vraiment compter sur des acteurs dont l’intérêt est de connaître ces données. Rappelez-vous « si c’est gratuit, c’est que vous – et vos données – êtes le produit ».
Ainsi, un véritable challenge à long terme est de réussir à faire collaborer le monde de la recherche en cryptologie directement avec les communautés open sources. Contrairement à d’autres communautés scientifiques, l’IACR a réussi à imposer l’open-access [16] aux éditeurs, et l’on voit apparaître des prototypes de cryptosystèmes innovant en open source. Mais les chercheurs ne sont pas armés pour la mise en pratique et le déploiement : il y a un effort de transfert à faire. Il faudrait certainement imaginer des structures plus rigides qu’à l’habitude pour des projets open source afin d’éviter des mésaventures comme celle de Debian/openSSH [17]. Néanmoins, une telle collaboration semble être la seule bonne voie pour développer des solutions pour l’intimité des utilisateurs de la toile.
Un problème majeur serait le financement de telles collaborations. Il n’est pas clair que le crowdfunding soit adapté en termes d’échelle et de durabilité. La recherche en cryptologie, et plus généralement en informatique ne souffre pas trop des difficultés de financement des autres sciences [18]. Le financement par projet proposé par les agences nationales et internationales (ANR et ERC) favorise de facto ce domaine (et plus généralement l’informatique). En effet, ces agences apprécient particulièrement les projets incluant une branche transfert, ce qui est bien plus direct en informatique que dans d’autres sciences. Cela pousse les laboratoires à collaborer avec des entreprises et la recherche publique est ainsi détournée vers les intérêts privés, transformée en brevets. Dans le cas particulier de la cryptographie, on favorise ainsi les technologies qui protègent les entreprises (chiffrement en interne, DRM ...), mais on ne développe rien pour protéger les individus. Dans le cas plus général, on prétend favoriser l’économie nationale ; on oublie peut-être qu’une technologie libre et gratuite peut contribuer grandement au bien commun – ce qui est rappelons-le le but premier de la recherche publique, telle qu’elle à été définie par la loi Française [19] – y compris à l’économie [20] et aux finances publiques [21].
Tout en arguant pour un changement politique d’envergure, serait-il possible de composer avec le système actuel pour laisser de nouveau aux chercheurs la possibilité de s’attaquer à des problèmes d’intérêt public ? Pourrait-on imaginer que des structures à but non lucratif montent de tels projets types ANR en partenariat avec les laboratoires ? L’idée qu’en République [22] l’impôt finance la recherche, mais aussi son transfert et son déploiement dans des produits gratuits et open source semble après tout assez défendable.
Références
[1] Affaire Lavabit (2013) : https://www.eff.org/deeplinks/2013/08/lavabit-encrypted-email-service-shuts-down-cant-say-why
[2] La NSA et le DES : https://en.wikipedia.org/wiki/Data_Encryption_Standard#NSA.27s_involvement_in_the_design. La page Wikipedia (EN) offre de nombreuses références, notamment American Cryptology during the cold war (p. 232), recueil de documents déclassifiés. Disponible sur le site de la NSA : https://www.nsa.gov/public_info/_files/cryptologic_histories/cold_war_iii.pdf
[3] Things the NSA doesn’t want you to know and why you should know about it : https://www.nsa-observer.net/
[4] Dual EC DRBG : https://projectbullrun.org/dual-ec/index.html
[5] IACR Statement On Mass Surveillance, Copenhagen resolution, mai 2014 : http://www.iacr.org/misc/statement-May2014.html
[6] Munroe Randall, xkcd 177, Alice and Bob, 2006 : http://www.explainxkcd.com/wiki/index.php/177:_Alice_and_Bob
[7] Rabin Michael, « Digitalized Signatures and Public-Key Functions as Intractable as Factorization », 1979 : http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TR-212.pdf
[8] La NP-complétude : https://fr.wikipedia.org/wiki/Probl%C3%A8me_NP-complet
[9] Boneh Dan et Franklin Matthew, « Identity Based Encryption From the Weil Pairing », 2001 : https://eprint.iacr.org/2001/090
[10] Partage de clef de Shamir : https://fr.wikipedia.org/wiki/Partage_de_cl%C3%A9_secr%C3%A8te_de_Shamir. Une implémentation open source est disponible sur http://point-at-infinity.org/ssss/
[11] Projet open source de vote électronique cryptographique : https://vote.heliosvoting.org/
[12] Pailler Pascal, « Public-Key Cryptosystems Based on Composite Degree Residuosity Classes », 1999 : http://www.lamsade.dauphine.fr/~litwin/cours98/Doc-cours-clouds/Pai99pai.pdf
[13] Gentry Craig, « A fully homomorphic encryption scheme », Thèse de Doctorat, 2009 : https://crypto.stanford.edu/craig/
[14] Bernstein Dan J. , Lange Tanja, et Heninger Nadia, « The year in Crypto », at Chaos Communication Congress, 2013 : https://www.youtube.com/watch?v=G-TM9ubxKIg
[15] Cryptris : un jeu vidéo sur la cryptographie. Présentation vidéo : http://vimeo.com/105507991. Jeu : http://inriamecsci.github.io/cryptris/
[16] Rauzy Pablo, « Le libre accès à la recherche : une introduction », 2014 : http://pablo.rauzy.name/openaccess/introduction.html
[17] Schneier Bruce , « Random Number Bug in Debian Linux », 2008 : https://www.schneier.com/blog/archives/2008/05/random_number_b.html
[18] Mouvement Science en Marche, 2014 : http://sciencesenmarche.org/fr/
[19] Points b) et c) de l’article 112-1 Code de la recherche : http://www.legifrance.gouv.fr/affichCode.do?cidTexte=LEGITEXT000006071190
[20] Groupe de travail Européen, « The impact of Free/Libre/Open Source Software on innovation and competitiveness of the European Union », 2006/2007 : http://www.flossimpact.eu/
[21] Le libre et l’administration publique : http://www.adullact.org/, http://www.journal-officiel.gouv.fr/mimo/
[22] République, du latin Res Publica : Le bien commun.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture