Vous avez aimé les machines de Mealy [1] et de Turing [2] ? Vous voulez passer à la pratique ? Vous aimerez le langage Brainfuck.
Comme son nom l’indique, ce langage fait des nœuds au cerveau, mais il oblige à un minimum d’organisation si on veut écrire un programme même tout simple. Pour quoi faire ? Vous pouvez répéter la question ? Bon, d’accord : pour que Bolosse 31 puisse parler avec Toto, son petit robot iDiot qui ne comprend que ce langage. Pas de chance, Toto ne comprend pas le Python ni même le C, mais vous pouvez aider Bolosse 31 et simuler son comportement histoire de ne pas l’envoyer dans les limbes d’une boucle infinie.
1. Présentation du langage
Brainfuck (ou BF) est un langage de programmation minimaliste qui contient exactement huit instructions. Nous allons utiliser un dialecte qui en comprend quatre complémentaires, deux pour manipuler les nombres entiers et deux pour déboguer. BF est un langage Turing-complet, ce qui veut dire que théoriquement, vous pouvez coder ce que vous voulez avec. En pratique, c’est une tout autre affaire.
1.1 Le cadre
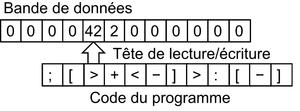
Brainfuck est une variété de machine de Turing simplifiée constituée :
- d’un ruban de cellules fini, mais non nécessairement borné (des deux côtés dans cet article) sur lequel se déplace une tête de lecture/écriture. Les cellules contiennent des nombres entiers, ici relatifs et sans limites a priori ;
- d’un programme, le code BF exécuté pas à pas ;
- d’une entrée et d’une sortie standards.
Fig. 1 : Représentation de BF. Toto est la flèche, la figure ne présente pas l’entrée et la sortie standards.
Certains dialectes de BF comportent en plus une pile (et deux instructions pour empiler et dépiler) ou quelques autres raffinements, parfois des interdictions qui lui enlèvent son caractère Turing-complet. Le langage n’est pas standardisé même s’il existe un paquet pour Debian (hsbrainfuck) ou un autre pour insérer du code BF dans Perl (libacme-brainfck-perl).
1.2 Les instructions
Les huit premières instructions sont celles de BF « standard », les deux suivantes viennent du dialecte BF++ [3] et les deux dernières de la littérature. Oui, Toto ne sait faire que ça.
Pour les exemples, on se basera sur le schéma de la figure 1 :
- , (virgule) : Insère le code ASCII de l’entrée standard dans la cellule courante.
- . (point) : L’inverse du précédent, affiche donc « * » (42 en ASCII correspond au caractère *).
- + : Ajoute 1 à la cellule courante (qui deviendra 43). Toto dépose un petit clou sur la cellule.
- − : L’inverse (41, donc).
- > : Déplace le pointeur d’une cellule vers la droite, donc vers la cellule qui contient 2. Toto avance d’une case.
- < : L’inverse, vers le 0 immédiatement à gauche.
- [ : Si la cellule courante est nulle, va juste après le ] correspondant, sinon passe à l’instruction suivante. Toto déroule son rouleau d’instructions.
- ] : Retourne au [ correspondant. Les boucles sont construites avec ces deux seules instructions.
- ; (point virgule) : Insère la valeur du nombre (entre deux espaces) de l’entrée standard dans la cellule courante en écrasant la valeur présente.
- : (deux points) : L’inverse, affiche « 42 ». Toto répond à LA question. Formidable !
- ! (point d’exclamation) : Affiche l’état de la bande et la position du pointeur par des crochets, utile pour déboguer.
- # : Commentaire, ce qui suit n’est pas interprété jusqu’à la fin de la ligne.
Les deux commandes ; et : permettent de coder plus rapidement des programmes d’arithmétique élémentaire et de s’initier aux subtilités du langage sans devoir comprendre comment utiliser la table ASCII pour traduire une entrée standard numérique en nombres. Nous verrons comment, finalement, nous en passer.
Si vous vous êtes intéressé aussi aux machines de Turing, vous avez dû remarquer qu’il est facile de transformer un code en BF en table des transitions alors que l’inverse est loin d’être évident. On peut traduire les trois états d’une machine de Turing (blanc, 0 et 1) en BF en 0, 1 et 2 ou −1, 0 et 1.
2. L’interpréteur en Python
Le code est un énorme switch, plus quelques traitements préliminaires qui vérifient l’emboîtement des crochets ou suppriment les commentaires éventuels.
Le programme en Python utilisera en entrée deux fichiers : le premier sera le code en BF et le suivant, les données éventuelles de l’entrée standard.
2.1 Les vérifications préliminaires
On commence par vérifier si un code en BF est bien envoyé en entrée :
001: #!/usr/bin/python3
002: # -*- coding: utf-8 -*-
004: from sys import exit,argv
006: try:
007: codebf=argv[1]
008: except IndexError:
009: print("Usage: brainfuck.py code.bf [donnees.txt]")
010: exit(0)
On continue par une petite analyse syntaxique du code : les crochets doivent être correctement emboîtés et on teste la présence de commandes nécessitant un fichier de données ligne 26. On supprime aussi tous les caractères inutiles, que ce soit ce qui est écrit après un # ligne 23 ou les caractères qui ne sont pas des instructions. Les instructions sont stockées dans code.
012: code=""
013: entree=False
014: commandes={",",".","+","-",">","<","[","]",";",":","#","!"}
015: sep={"\n","\t"," "}
016: nbo=0
018: with open(codebf,"r") as bf:
019: for l in bf:
020: for c in l.strip():
021: if c not in commandes:
022: continue
023: if c=="#":
024: break
025: code=code+c
026: if c in {",",";"}:
027: entree=True
028: if c=="[":
029: nbo+=1
030: elif c=="]":
031: nbo-=1
032: if nbo<0:
033: print("Crochets incorrects.")
034: exit(0)
036: if nbo!=0:
037: print("Crochets incorrects.")
038: exit(0)
S’il y a plus de crochets fermants qu’ouvrants en cours de route ligne 32 ou l’inverse à la fin du traitement ligne 36, on arrête tout.
Si le code nécessite des entrées, on les stocke dans entrees s’il y en a, sinon on s’arrête :
040: if entree:
041: try:
042: entree=argv[2]
043: except IndexError:
044: print("Votre code nécessite un fichier de données.")
045: exit(0)
046: with open(entree,"r") as en:
047: entrees=[]
048: for l in en:
049: entrees=entrees+list(l.strip())
2.2 Toto fait ce qu’on lui demande
Le code est maintenant nettoyé et prêt à être exécuté par Toto, il reste donc à écrire le switch géant.
dp est la position de Toto sur la memoire. Si Toto cherche à dépasser les bornes du ruban à droite ligne 63 ou à gauche ligne 68, on ajoute un 0 où il faut : on ne bloque pas l’exécution du code, on crée ad hoc la memoire nécessaire.
p est la position de l’instruction courante sur son rouleau. Noter que l’instruction virgule ligne 81 ne prend qu’un caractère de l’entrée alors que le point virgule ligne 87 vide les séparateurs éventuels puis construit le nombre jusqu’au séparateur suivant avec l’algorithme de Horner qu’on reverra plus loin.
J’ai ajouté le compteur c pour ne pas planter Toto dans une boucle infinie.
051: p=0
052: dp=0
053: c=0
054: memoire=[0]
056: while p<len(code):
057: c+=1
058: if c>=10**6:
059: print("Limite max. Votre code semble tourner en rond.")
060: break
061: elif code[p]==">":
062: dp+=1
063: if dp==len(memoire):
064: memoire.append(0)
065: p+=1
066: elif code[p]=="<":
067: dp-=1
068: if dp==-1:
069: memoire=[0]+memoire
070: dp=0
071: p+=1
072: elif code[p]=="+":
073: memoire[dp]+=1
074: p+=1
075: elif code[p]=="-":
076: memoire[dp]-=1
077: p+=1
078: elif code[p]==".":
079: print(chr(memoire[dp]),end="")
080: p+=1
081: elif code[p]==",":
082: memoire[dp]=ord(entrees.pop(0))
083: p+=1
084: elif code[p]==":":
085: print(memoire[dp],end=" ")
086: p+=1
087: elif code[p]==";":
088: while entrees[0] in sep:
089: entrees.pop(0)
090: while entrees and entrees[0] not in sep:
091: try:
092: memoire[dp]*=10
093: memoire[dp]+=int(entrees.pop(0))
094: except ValueError:
095: print("Entrée non numérique.")
096: exit(0)
097: p+=1
098: elif code[p]=="[":
099: if memoire[dp]!=0:
100: p+=1
101: continue
102: nbo=1
103: while nbo!=0:
104: p+=1
105: if code[p]=="[":
106: nbo+=1
107: if code[p]=="]":
108: nbo-=1
109: p+=1
110: elif code[p]=="]":
111: if memoire[dp]==0:
112: p+=1
113: continue
114: nbf=1
115: while nbf!=0:
116: p-=1
117: if code[p]=="]":
118: nbf+=1
119: if code[p]=="[":
120: nbf-=1
121: elif code[p]=="!":
122: for i in range(len(memoire)):
123: if i==dp:
124: print("["+str(memoire[i])+"]",end=" ")
125: else:
126: print(memoire[i],end=" ")
127: print()
128: p+=1
130: print()
Le code en Python est du type âne qui trotte, mais même Toto ne le comprend pas. Essayons néanmoins de communiquer avec lui.
3. Quelques exemples de codes en BF
L’interpréteur est en Python, on utilise donc son arithmétique, ce qui veut dire que les entiers sont relatifs et sans limites a priori. Attention, BF n’a aucun moyen de savoir si un nombre sur le ruban est positif ou négatif, c’est à vous de prévenir Toto.
Les codes en BF seront expliqués par des commentaires au bout de chaque ligne.
3.1 Arithmétique élémentaire
+++:
Ce code écrira le nombre 3 en sortie.
++++>++++++[<+>-]<:
Ce code effectue 4+6=10. En détail :
- dans la première cellule, on part de 0 et on effectue ++++ donc on stocke la valeur 4 ;
- > : on se déplace d'une cellule vers la droite ;
- ++++++ : on stocke le nombre 6. On a donc la cellule précédente qui contient 4 et la suivante (cellule courante) qui contient 6 ;
- [ : début de boucle qui s'arrête si la cellule est nulle, ce qui n'est pas le cas pour l'instant. La boucle effectue :
- < : retour à la case précédente et ajout de 1 (+). Donc les cellules valent 5 et 6 ;
- > : passage à la cellule suivante et on soustrait 1 (-) . Les cellules valent 5 et 5 ;
- ] : retour au début de la boucle.
- < : retour sur la première cellule qui contient le résultat ;
- : : affiche le contenu de la cellule.
On vide la cellule de droite petit à petit, regardez la sortie de ce code, c’est le même avec un point d’exclamation qui affiche l’état du ruban et la position de Toto :
++++>++++++[!<+>-]<:
> ./brainfuck.py code.bf entree.txt
4 [6]
5 [5]
6 [4]
7 [3]
8 [2]
9 [1]
10
Et voici comment multiplier 6 par 7 :
++++++[>+++++++<-]>:
C’est presque le même code, mais on ajoute 7 à la deuxième cellule chaque fois qu’on décrémente la première. Avec le point d’exclamation pour afficher l’état de la bande, on a :
++++++[!>+++++++<-]>:
./brainfuck.py code.bf
[6]
[5] 7
[4] 14
[3] 21
[2] 28
[1] 35
42
Toto donne LA réponse, sans tricher et en moins d’un million d’années.
Mais comment multiplier deux nombres qui viennent de l’entrée standard ? Commençons par les additionner :
Si l’entrée contient deux nombres, ce code les ajoute et affiche leur somme.
;>;[<+>-]<:
C’est le même code que pour ajouter sauf qu’on ajoute deux nombres de l’entrée standard et non deux nombres codés en dur. Pas de chance, le code précédent de la multiplication ne fonctionnera pas à cause du multiplicande dans la boucle.
Pour multiplier, on a besoin de planifier l’occupation du ruban pour Toto, c’est malheureux, mais il ne le fera pas pour nous ni même pour son maître, Bolosse 31. Voici :
|
Premier facteur |
Stockage du deuxième |
Copie temporaire du deuxième |
Produit |
Nous allons utiliser la technique de la duplication :
++++[>+>+<<-]!
Ce code déplace deux fois la première cellule dans les deux suivantes :
> ./brainfuck.py code.bf
[0] 4 4
;>;< # Stockage des deux facteurs
[
>[>+>+<<-] # Duplication de la cellule 2 vers les n°3 et 4
>[<+>-] # Déplacement de la sauvegarde qui est temporaire vers la cellule 2
<<- # On décrémente la cellule 1
] # Et on recommence tant qu’elle n’est pas nulle
>[-] # On vide la cellule 2
>>: # On affiche le produit
Il faut veiller à anticiper la position de Toto sur le ruban pour qu’il arrive où il faut avant le crochet fermant. En gros, entre une paire de crochets, sauf exception, on veillera à avoir autant de > que de < et surtout, Toto doit arriver à la cellule qu’on teste avant le crochet fermant. Il faut absolument contrôler à tout moment la position de Toto, sinon il va tourner en rond ou partir dans le décor. Usez et abusez de la commande !
Regardez ce que fait ce code :
+[>+]
Toto avance, puis dépose un petit clou sur la cellule courante. Elle n’est donc pas nulle, il recommence et ne s’arrête jamais. Vous avez intérêt à prévoir un ruban jusqu’à la Galaxie d’Andromède voire jusqu’à Zotra plus une réserve de clous qui entre dans le TARDIS.
La division est plus complexe, vous commencez à deviner pourquoi. On le verra plus loin.
3.2 Bonjour tout le monde
Comment faire parler Toto, par exemple lui faire dire « Bonjour ! » ? Il suffit de lire une table ASCII et de construire les nombres qui vont bien. Cela dit, sans l’astuce précédente pour multiplier, c’est vite infernal.
Les codes ASCII sont, respectivement 66, 111,110,106,110,117, 114, 32 et 33. Nous allons donc construire 32=4×8, 64=2×32 et 96=3×32, puis décliner le reste en fonction de ces trois-là.
++++[>++++++++<-]> # Construit 32
[>+>++>+++<<<-] # Construit 32, 64 et 96
>>++.-- # Affiche « B » et rétablit 64
>+++++++++++++++.-. # Va à 96 et affiche « on »
----.+++++.++++++. # Affiche « jou »
---.------------------ # Affiche « r » et rétablit 96
<<.+.- # Va à 32, affiche l’espace et le point d’exclamation, rétablit 32
C’est plus simple avec une ou deux astuces, non ?
3.3 Les carrés
On peut utiliser l’idée du code erroné de la fin de la section 3.1. pour faire recopier le même nombre autant de fois que l’entrée standard le dit. Observez ce code sachant que l’entrée est 7 :
;[[>]+[<]>-!]>!
> ./brainfuck.py code.bf entree.txt
0 [6] 1
0 [5] 1 1
0 [4] 1 1 1
0 [3] 1 1 1 1
0 [2] 1 1 1 1 1
0 [1] 1 1 1 1 1 1
0 [0] 1 1 1 1 1 1 1
0 0 [1] 1 1 1 1 1 1
La cellule n°2 est en fait la cellule qui contient initialement 7. [>] oblige Toto à aller à la première cellule nulle tout à droite. La suite lui ajoute 1, retourne juste une cellule à gauche de là où il y a le 7, revient sur le 7 et décrémente. On recommence jusqu’à ce que la cellule 2 soit nulle.
Avec ceci et l’identité remarquable (n+1)²=n²+(2n+1), on peut construire la suite des carrés par récurrence.
;[[>]+[<]>-]>: # Construction du tableau de jeu, placement des 1
>[++>]<[<]>> # Suite de la préparation, on ajoute 2 à tous les 1 sauf le premier
[
<[>+<-] # On ajoute le carré à gauche au nombre suivant
>>[++>] # On ajoute 2 à tous les nombres à sa droite.
<[<]>:> # On se place sur le carré à afficher, on l’affiche
] # Et on rembobine
Voici ce que ça donne si on remplace les deux points par un point d’exclamation :
> ./brainfuck.py code.bf entree.txt
0 0 [1] 1 1 1 1 1 1
0 0 0 [4] 5 5 5 5 5 0
0 0 0 0 [9] 7 7 7 7 0
0 0 0 0 0 [16] 9 9 9 0
0 0 0 0 0 0 [25] 11 11 0
0 0 0 0 0 0 0 [36] 13 0
0 0 0 0 0 0 0 0 [49] 0
On pourrait sûrement factoriser le code (on a deux fois >[++>]<[<]>), mais le code fonctionne et Bolosse 31 est déjà bien content de s’être fait comprendre par Toto.
3.4 Factorielle
La factorielle de 7 est 7!=1×2×3×4×5×6×7=5040.
Reprenons l’astuce précédente pour écrire la suite décroissante des entiers de 5 à 1 (si l’entrée vaut 5) :
;[>[+>]+[<]>-!]>!
> ./brainfuck.py code.bf entree.txt
0 [4] 1
0 [3] 2 1
0 [2] 3 2 1
0 [1] 4 3 2 1
0 [0] 5 4 3 2 1
0 0 [5] 4 3 2 1
Nous allons utiliser deux cellules à droite pour le stockage temporaire, comme dans la multiplication.
;[>[+>]+[<]>-] # L’initialisation
>[>]<:< # Placement à la fin et affichage de 1
[ # La boucle principale qui va construire le produit par la droite
[ # La boucle qui multiplie les deux nombres à droite
>[>+>+<<-]
>[<+>-]
<<-
]
>>>!
[-<<<+>>>] # On déplace la factorielle intermédiaire à droite du facteur suivant à multiplier
<<[-]<< # On supprime un résidu du produit sinon ça pourrit le produit suivant
]
Regardez comme Toto fait de belles choses :
> ./brainfuck.py code.bf entree.txt
0 0 7 6 5 4 3 2 [1] 0
0 0 7 6 5 4 3 0 1 0 [2]
0 0 7 6 5 4 0 2 0 [6] 0
0 0 7 6 5 0 6 0 [24] 0 0
0 0 7 6 0 24 0 [120] 0 0 0
0 0 7 0 120 0 [720] 0 0 0 0
0 0 0 720 0 [5040] 0 0 0 0 0
Étonnant, non ? Remplacez chaque ! par un : et vous obtenez la suite des factorielles. Remarquez le résidu des deux cellules à gauche de Toto qu’on supprime avec [-] à l’avant-dernière ligne.
Notez qu’avec des additions au lieu de multiplications, on peut calculer les nombres triangulaires.
3.5 La suite de Fibonacci
Je rappelle qu’une suite de Fibonacci est une suite linéaire récurrente d’ordre 2, c’est-à-dire que si les deux premiers termes sont uO=1 et u1=3, u2=uO+u1=4 et u3=u1+u2=3+4=7. De manière plus générale, si n est un nombre entier positif, un+2=un+1+un ; on a besoin des deux premiers termes uO et u1 de la suite pour calculer les autres de proche en proche, autrement dit, par récurrence.
L’entrée contient le rang du dernier terme à afficher, le premier terme uO et le deuxième u1 de la suite. Voici le tableau du ruban :
|
n |
Tampon |
Tampon |
un |
un+1 |
Et le code :
;->;>>>;<<<< # Dans l’ordre, n−1 (sinon on affiche un terme de trop),
# uO puis u1 deux cellules plus loin
[
>>>>
[<+<+>>-]<<< # On duplique un+1 entre sa position et un
[>>>+<<<-]> # On déplace un
[>>+<<-]>>! # On calcule un+2=un+1+un
<[<<+>>-] # On déplace un+1 en vue de l’étape suivante
<<<- # On décrémente n
]
Voici :
> cat entree.txt
7 1 3
> ./brainfuck.py fibonacci.bf entree.txt
6 0 0 3 [4]
5 0 0 4 [7]
4 0 0 7 [11]
3 0 0 11 [18]
2 0 0 18 [29]
1 0 0 29 [47]
Comme d’habitude, remplacez le point d’exclamation par les deux points pour afficher les termes de la suite.
La longueur de ce code n’est pas optimisée, on peut la ramener à 31 instructions.
3.6 La division
Commençons par la division euclidienne par 3, qui affiche le quotient entier et le reste. Voici la disposition des variables dans la memoire :
|
Dividende |
Accumulateur borné par le diviseur |
Copie de cet accumulateur |
A-t-on soustrait le diviseur (booléen) ? |
Quotient |
La cellule appeléeaccumulateur est décrémentée de 1 à chaque fois que le dividende l’est. Dès que l’accumulateur atteint 0, le quotient augmente de 1 et l’accumulateur revient à 3.
;> # Entrée du dividende
++< # C’est le diviseur−1
[ # Tant que le dividende n’est pas nul
!>>>+<< # Le booléen vaut 1 (enlever le point d’exclamation)
[>+>[-]<<-]> # Si l’accumulateur ne vaut pas 0, le booléen est annulé
# et l’accumulateur est déplacé à droite
[<+>-]> # On déplace la copie de l’accumulateur s’il le faut
[<<+++>>>+<-] # Si l’accumulateur est nul, on incrémente le quotient
# et on rétablit l’accumulateur à 3
<<- # On décrémente l’accumulateur
<- # Et le dividende
]!
>>>>:<<<< # On affiche le quotient
++> # Le reste vaut diviseur−1−accumulateur=2−accumulateur dans notre cas
[<->-]<: # On affiche le reste
Voici ce que cela donne :
> ./brainfuck.py div.bg entree.txt
[7] 2
[6] 1 0 0
[5] 0 0 0
[4] 2 0 0 1
[3] 1 0 0 1
[2] 0 0 0 1
[1] 2 0 0 2
[0] 1 0 0 2
2 1
Le quotient de la division euclidienne de 7 par 3 est 2 et le reste vaut 1 car 7=2×3+1.
Oui, mais si on veut que le diviseur vienne aussi de l’entree ? Bolosse 31 sait comment faire : il lui faut une copie de sauvegarde du diviseur (par exemple une cellule à gauche du dividende) qu’il dupliquera à chaque fois qu’apparaissent dans le code des +++ ou des ++ (auquel cas il soustraira 1 immédiatement). Il n’oubliera pas de rétablir la copie de sauvegarde à sa place, car la duplication la vide. Je vous laisse faire.
3.7 Pour aller plus loin
Autrement dit, comment revenir au BF pur, sans : ni ; ?
Voici, en pseudo-code pythonique, l’algorithme qui remplace les deux points, il s’agit de l’algorithme de Horner pour l’évaluation des polynômes :
Tant que le caractère entré n’est pas l’espace :
Multiplier par 10 la cellule courante
Lui ajouter le code ASCII du caractère entré−48
Le code ASCII des dix chiffres est 48+chiffre.
Voyons ce que ça donne en BF. Il sera déjà bon de sauvegarder quelque part les valeurs de 32 et de 16, pour ne pas saturer le code d’un nombre illisible de + successifs. Voici la disposition des cellules :
|
32 |
16 |
Code ACSII du caractère courant |
Tampon à sauvegarde |
Nombre voulu |
Voici le code :
++++[>++++<-] # Calcul de 16
>[<<++>+>-] # Calcul de 32 et déplacement de 16 (pas besoin de 48)
, # On fait entrer le premier caractère
<<[>>>+>+<<<<-] # On duplique 32
>>>>[<<<<+>>>>-] # On déplace une des copies de sauvegarde
<[-<->]> # On soustrait 32 au caractère pour lancer la boucle
[ # On peut commencer la boucle
<[->->+<<] # On soustrait 16 sur l’ASCII en le déplaçant sur la sauvegarde
>>[<<+>>-] # On rétablit 16
>[<++++++++++>-] # On multiplie par 10
<[>+<-] # On replace le résultat à sa place
<[>>+<<-]! # On lui ajoute le chiffre en cours
, # On insère l’ASCII du chiffre suivant
<<[>>->+<<<-] # On soustrait 32 à l’ASCII en le déplaçant sur la sauvegarde
>>>[<<<+>>>-]< # On rétablit 32
]>>! # Et on recommence
Voici le résultat :
> cat entree.txt
4057 51
> ./brainfuck.py dp.bf entree.txt
32 16 [0] 0 4
32 16 [0] 0 40
32 16 [0] 0 405
32 16 [0] 0 4057
32 16 0 0 [4057]
Et pour l’affichage avec le point, c’est l’algorithme réciproque, on a besoin de la division euclidienne par 10.
Voici l’algorithme en pseudo-code :
Tant que le nombre à afficher est non nul:
On stocke le 48+reste de la division euclidienne par 10
On recommence avec le quotient
On affiche les chiffres à partir du dernier calculé
Il peut se terminer par l’affichage d’un espace.
Il s’agit à peu de choses près de l’algorithme de division, mais emboîté dans la boucle de stockage. Vous savez aussi comment stocker un nombre à la fin d’une file de nombres non nuls (ils le seront, car on a ajouté 48). Faites-le vous-même !
Conclusion
Voilà, Bolosse 31 a quelques techniques pour rendre Toto utile. Il aura du mal à lui faire résoudre un sudoku, mais il pourra tout de même lui faire faire quelques tâches élémentaires.
Si vous voulez écrire des programmes en BF plus élaborés, vous pouvez écrire votre propre langage [4] constitué de macros ajoutées au BF. Vous accélérerez l’écriture du code en utilisant par exemple :
- DUP(a,b,c) qui duplique la cellule a sur les cellules b et c,
- MUL2(a,b)=DUP(a,b,b),
- PLUS(a,b) qui déplace la cellule a sur la cellule b (si b=0), sinon qui ajoute a sur b,
- MUL(a,b,c,d) qui multiplie les cellules a et b, stocke le résultat en c et utilise comme tampon la cellule d.
Et ainsi de suite. Le code ainsi créé sera probablement moins joli qu’un autre écrit à la main, préparé aux petits oignons. Attention, les lettres dans les macros désignent des coordonnées relatives à la position de Toto au début de la macro.
Voici quelques algorithmes en BF que j’ai vu passer sans les avoir codés moi-même (je ne suis pas fou à ce point) : la factorisation en produit de facteurs premiers d’un entier, l’algorithme de Syracuse, des quines (code qui écrit son propre code sur la sortie standard), rot13 et même un décodeur de DVDCSS et interpréteur de BF en BF. À quand Nethack ?
Et pour finir, voici un cadeau de saison sur Ideone [5].
Références
[1] Prcovic N., « Les machines de Turing », GNU/Linux Magazine n° 174, septembre 2014, p. 24 à 31.
[2] Raynaud M., « Apprenez à programmer avec une machine de Turing ! », Bulletin vert de l’APMEP n°510, septembre-octobre 2014, p. 471 à 484. Voir aussi le site http://www.machinedeturing.org/ où l’auteur présente sa machine physique fonctionnelle.
[3] Page sur BF++ de Code Abbey : http://www.codeabbey.com/index/wiki/brainfuck.
[4] Colombo T., « Créez votre langage de programmation », GNU/Linux Magazine n° 175, octobre 2014, p. 24 à 36.
[5] Programme en Brainfuck : http://ideone.com/nLwtdt. Ne le lancez pas depuis Ideone, mais dans une console. La version commentée est ici : http://ideone.com/L5lJjP.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture