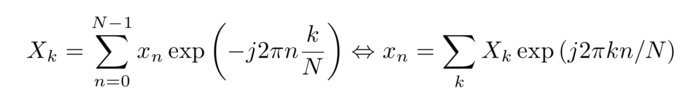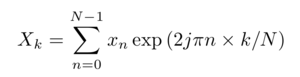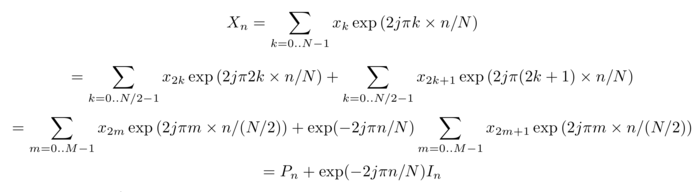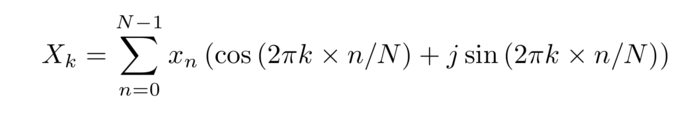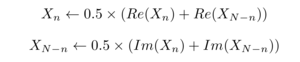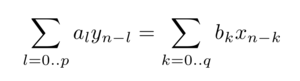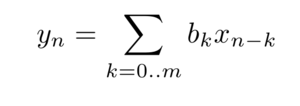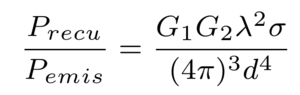Le travail dans le domaine spectral n’est pas nécessairement intuitif puisque nous appréhendons en général l’évolution temporelle d’un signal : un convertisseur analogique-numérique échantillonne périodiquement (i.e. à intervalle de temps réguliers) la valeur d’une tension pour fournir une grandeur numérique comprise entre 0 et 2p-1 avec p le nombre de bits de conversion (12 bits dans le cas du STM32 qui va nous intéresser dans les applications, soit de 0 à 4095). L’aspect fréquentiel devient évident pour les signaux périodiques qui sont caractérisés par trois grandeurs : leur amplitude, leur fréquence et éventuellement leur phase. Un intérêt dans une de ces trois grandeurs justifie l’exploitation de la décomposition en série de Fourier. Cependant, la complexité calculatoire de cette opération mathématique doit aussi inciter à se rappeler qu’il existe souvent des méthodes alternatives de calcul qui, sans être nécessairement aussi générales, peuvent se montrer plus efficaces pour un problème particulier. Ainsi, un filtrage pourra être implémenté de façon plus efficace dans le domaine temporel que dans le domaine spectral.
1. Rappels de quelques concepts de la décomposition en série de Fourier
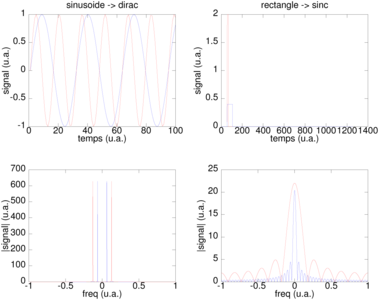
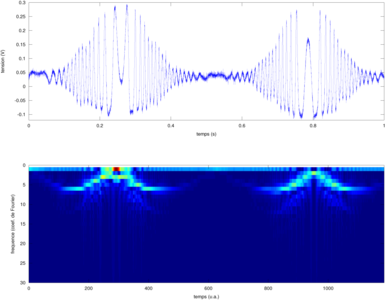
Figure 1 : Haut : signaux caractéristiques, à gauche sinusoïdes de fréquence variable, à droite des rectangles de largeur variable (et donc de hauteur variable pour conserver l’énergie correspondant à la surface de ces rectangles). En bas, décomposition en série de Fourier de ces signaux. Plus la fréquence de la sinusoïde est élevée, plus le « pic » sur le graphique en fréquence s’éloigne de l’origine. Plus le rectangle est fin, plus sa transformée de Fourier en sin(x)/x (aussi nommé sinc()) est large. Asymptotiquement, un rectangle « infiniment » fin (fonction de Dirac) présente un spectre constant sur toute la bande spectrale analysée.
Pour des pas de temps discrets (dates des échantillonnages), il est connu [2] [3] qu’il existe une bijection entre la représentation des données dans le domaine temporel, et leur représentation dans le domaine spectral (des fréquences). Ainsi, l’information contenue dans une séquence de points xn=x(nx T) échantillonnés aux dates nT (T pas de temps constant, n entier positif) et la décomposition en série de Fourier Xk est la même, mais les deux représentations des informations permettent de faire ressortir des propriétés différentes des signaux. La relation entre les Xk (coefficients de la décomposition en série de Fourier) et xn (échantillons dans le temps) est
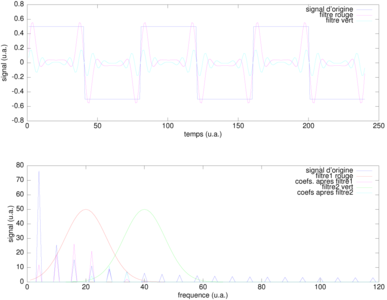
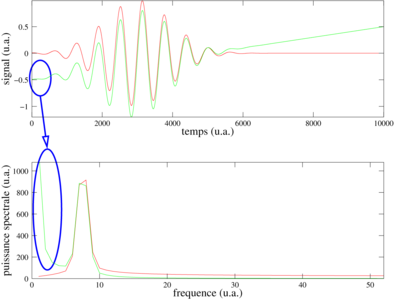
Figure 2 : Exemple de filtrage par pondération des coefficients de la série de Fourier. En haut, en bleu, le signal d’origine en forme de crénau est analysé dans le domaine spectral (en bas) sous forme de coefficients de la série de Fourier (la pondération de ces coefficients est en 1/n avec n l’indice en abscisse du coefficient). En traçant des filtres dans le domaine spectral (gaussiennes rouge et verte, en bas), nous sélectionnons certaines composantes fréquentielles du signal, dont l’information temporelle est ensuite retrouvée par transformée de Fourier inverse (en haut, en magenta et cyan). Nous observons clairement que plus les filtres sont décalés vers les hautes fréquences, plus les variations « lentes » du signal sont éliminées pour favoriser l’observation des évolutions « rapides ». Cette approche du filtrage, bien que gourmande en ressources de calcul, est intuitive car permet de graphiquement déterminer les propriétés spectrales du filtre.
où j2=−1. L’expression de gauche permet de calculer les complexes Xk connaissant la séquence acquise xn (réelle ou complexe), et l’expression de droite permet de remonter à la séquence temporelle, connaissant les coefficients de la série de Fourier. Ainsi, un signal temporel échantillonné à des temps discrets (supposés équidistants) nT=n/fe, peut être représenté par la suite des coefficients Xk qui représentent, en amplitude, la contribution de chaque pulsation (donc de chaque fréquence). Le graphique représentant ces coefficients en fonction de k (qui représente donc une fréquence, puisque k apparaît dans les expressions exp(j2π kn)=cos(2π kn)+jsin(2π kn)) est nommé le “spectre du signal”, et permet d’identifier rapidement un certain nombre de caractéristiques spectrales d’un signal [2] [3]. Les développements théoriques autour de ces concepts sont très riches et bien au-delà de la contribution de cette présentation (et de la compréhension de ses auteurs). Nous nous contenterons ici de proposer d’exploiter (Fig. 1) une bijection entre une série de N données temporelles et N coefficients dans le domaine spectral permettant une représentation nouvelle de ces données qui permet d’en déduire une information “différente” (Fig. 2). Deux hypothèses fondamentales de ces développements sont d’une part lapériodicité de la séquence xn (signifiant notamment que x est supposé proche de xN−1), et d’autre part l’absence d’évolution “rapide” du signal, i.e. que le signal ne présente pas de variation significative dans un intervalle de temps inférieur à T. Sans formaliser ces divers points, nous allons illustrer ci-dessous l’impact de ces aspects et les artefacts induits s’ils ne sont pas respectés.
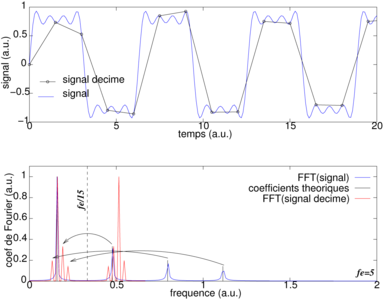
Figure 3 : Un signal rectangulaire (en haut) est caractérisé par une somme infinie de sinusoïdes pondérées par un coefficient de magnitude inversement proportionnelle à la fréquence : rectangle(t)=Σn=0N cos((2× n+1)ω t)/(2n+1). En bas, la série de Fourier du signal n’incluant que les 3 premiers termes (n=1, 2, 3) en noir (valeurs théoriques) et en bleu les valeurs calculées par transformée de Fourier du signal de durée finie. En noir (haut) et en rouge (bas), le signal est décimé : réduire d’un facteur 15 la fréquence d’échantillonnage induit un repliement spectral sur une fréquence d’échantillonnage représentée par la ligne pointillée sur le graphique du bas. Le signal résultat s’apparente à une sinusoïde (pic principal rouge) avec des parasites que sont les transposées de facteurs fe (fréquence d’échantillonnage) des raies du signal original. Ce phénomène est le repliement spectral (aliasing en anglais).
Un aspect du traitement du signal que nous ne pouvons manquer de présenter est le concept de fréquence d’échantillonnage fe qui conditionne toute la suite de cette présentation. Le signal temporel échantillonné aux dates n/fe est dit échantillonné à la fréquence fe, et son spectre distribue N coefficients dans la gamme [−fe/2;fe/2]. Ce point est fondamental pour l’analyse quantitative des spectres. Par ailleurs, l’hypothèse de périodicité de la séquence temporelle se traduit par la périodicité du spectre : toute composante de fréquence supérieure à fe/2 est ramenée dans cet intervalle par transposition d’un nombre entier de fe (Fig. 3). Ce phénomène est nommé repliement spectral ou, plus classiquement, par sa nomenclature anglophone d’aliasing. On évite les problèmes de repliement spectral soit en s’assurant que le signal analysé ne comporte aucune composante au-dessus de fe/2, soit en précédant le convertisseur analogique-numérique d’un filtre passe-bas de fréquence de coupure inférieure à fe/2 (théorème d’échantillonnage de Nyquist [4]).
L’approche naïve du calcul des coefficients de la série de Fourier nécessite N2 multiplications, puisque chacun des N (k∈[0..N] ou k∈[−N/2..N/2]) termes en sortie nécessite lui-même N multiplications [6, p.607].
Le calcul de la transformée de Fourier rapide (Fast Fourier Transform, FFT [5] [6]) exploite les symétries de la formule vue ci-dessus pour utiliser autant de fois que nécessaire les mêmes termes xkexp(−2jπ k× n/N) qui apparaissent plusieurs fois : on notera [6, p.609] la relation suivante entre les termes pairs (gauche) et les termes impairs (droite) de la transformée de Fourier Xn
en posant M=N/2, et avec Pn le calcul sur les indices pairs et In le calcul sur les indices impairs. Le calcul des N termes Xn s’est donc transformé en la somme de deux termes de longueurs N/2, le second étant multiplié par exp(−2jπ n/N). Chaque calcul d’un terme de la FFT nécessite donc N opérations, mais ceci le long d’un arbre binaire de longueur log2(N) au lieu de N alternant les termes pairs et impairs de la somme. La complexité du calcul est donc passée de N2 à Nlog2(N). Ce calcul implique que N est nécessairement une puissance de 2 : si ce n’est pas le cas, la série temporelle est complétée de 0 jusqu’à la puissance de 2 supérieure à N la plus proche pour respecter cette condition.
L’expression de la série de Fourier
fait clairement apparaître les éléments pairs (en cos) et impairs (sin) de la série de Fourier. Pour des coefficients xn réels, nous allons en déduire des relations de symétries qui seront utiles pour optimiser l’occupation mémoire du microcontrôleur. Notamment, nous constatons que la partie réelle de la transformée de Fourier est égale pour les termes d’indice −k et k (puisque la fonction cosinus est paire), et que la partie imaginaire de l’élément −k est l’opposé de l’élément k (puisque le sinus est impair) : en termes complexes, l’élément k est le complexe conjugué de l’élément −k si la série temporelle xk est réelle [7], et de la même façon nous démontrons que si xk est purement imaginaire, alors le terme k est l’opposé du complexe conjugué du terme −k (car j2=−1).
Ces relations ont aussi pour conséquence que pour les signaux qui vont nous intéresser par la suite (signaux réels), seule la moitié positive (k∈[0..N/2]) est exploitée, puisque par symétrie les coefficients négatifs contiennent la même information que les coefficients positifs.
Par ailleurs, une hypothèse qui n’est pas forcément explicite dans les relations vues plus haut est que le signal analysé est périodique. Une conséquence est que la valeur initiale du signal (début de la série temporelle) doit être proche de la valeur finale (fin de la série temporelle) afin de permettre le raccord des séquences pour respecter l’hypothèse de périodicité. En l’absence de cette condition, la rupture entre la dernière et la première valeur crée une composante haute fréquence (artefact) dans la transformée de Fourier qui s’observe comme du bruit sur la séquence caractérisant le comportement spectral de la séquence temporelle. Une façon classique de résoudre ce problème consiste à “fenêtrer” le signal afin d’imposer des valeurs nulles en début et fin de séquence sans excessivement affecter la réponse spectrale (Fig. 4). Bien que ces concepts puissent paraître triviaux lorsqu’ils sont énoncés explicitement, ils sont la cause classique de dégradation du rapport signal à bruit lorsqu'une séquence continue de mesures est découpée en sous-ensembles traités individuellement (analyse temps-fréquence par application de la transformée de Fourier sur une fenêtre glissante) tel que nous le ferons par la suite.
Figure 4 : Effet de la discontinuité entre le début et la fin d’une séquence temporelle (haut) analysée par transformée de Fourier (bas). Bien que ces deux séquences soient de valeur moyenne nulle, la discontinuité induit des artefacts qui pourraient aller jusqu’à cacher le signal utile. Le fenêtrage, qui multiplie la séquence temporelle par une fenêtre pondérée de façon à annuler les termes en début et fin de séquence, sans induire de rupture brute dans la séquence, vise à éliminer ces artefacts.
2. Implémentation pratique dans un système embarqué
Avec la disponibilité d’ordinateurs aux puissances de calculs quasi-illimitées, le calcul des coefficients de la série de Fourier devient omniprésent sous une forme aussi simple que la commande fft() de GNU/Octave (utilisée pour illustrer toutes les figures jusqu’ici). Il est néanmoins intéressant de se remémorer que le ticket d’entrée pour accéder à cet outil est cher. La STM32F10x_DSP_Lib de ST Microelectronics [8] propose par exemple des implémentations en assembleur de la FFT pour divers compilateurs propriétaires et pour gcc, certainement optimum en termes d’exploitation de ressources, mais peu portable. Cette bibliothèque est utilisée dans le projet stm32harmonicmeasure hébergé à http://code.google.com/p/stm32harmonicmeasure.
Heureusement, une note d’application de Maxim [9] fournit les outils de base pour implémenter la transformée de Fourier rapide sur à peu près tout microcontrôleur. Cette note d’application est intéressante car en plus de fournir un exemple concret d’application de la FFT sur un microcontrôleur aux ressources réduites, elle fournit les générateurs de code en C permettant de pré-calculer les tables (LUT) de cosinus et de sinus ainsi que les indices des éléments des tableaux à échanger dans l’algorithme en papillon. Par ailleurs, elle rappelle quelques notions de base sur le calcul en virgule fixe et les conditions pour ne pas atteindre de dépassement de capacité de stockage des short (16 bits). Bien que ces conditions soient quelque peu pénibles à valider théoriquement quelle que soit la nature des signaux acquis, un point fondamental à mémoriser est que l’élément d’indice 0 de la transformée de Fourier (fréquence nulle, donc composante constante) est représentative de la puissance moyenne du signal. Cette information de puissance moyenne étant sans utilité pour nous dans la suite de cette présentation, nous prendrons toujours soin de retirer la valeur moyenne de tous les signaux analysés afin de minimiser les risques de dépassement de représentation des nombres en virgule fixe telle que proposée dans cette note d’application (Q8.7). Cette notation signifie que nous allouons, par convention dans l’ensemble de nos calculs, 8 bits pour la partie entière du nombre que nous représentons (avec un bit additionnel pour le signe), et 7 bits pour la partie décimale. Ainsi, les valeurs en entrée devront être comprises entre 0 et 255, tandis que la partie fractionnaire est exploitée au cours du développement du calcul pour améliorer la précision. La maîtrise de la gamme des valeurs d’entrée est importante car le moindre dépassement de capacité des registres 16 bits (short) utilisés lors des calculs se traduit par l’ensemble du calcul erroné puisqu’il y a propagation des termes le long de l’arbre de la FFT.
Nous avons vu les relations de symétrie entre les termes d’indice positif et négatif lorsque les signaux d’entrée sont tous réels purs ou imaginaires purs. Une FFT est conçue pour accepter en entrée deux tableaux de N éléments (partie réelle et imaginaire de chaque xn), et renvoyer en sortie les N coefficients de Fourier (complexes).
Dans toutes nos applications, les signaux d’entrée seront réels, rendant cette conception inefficace : nous fournirions en entrée un tableau de valeurs nulles (les N parties imaginaires), et savons déjà qu’il y a redondance de N/2 informations en sortie par symétrie du spectre. Lors du traitement de N données réelles, nous exploitons des tableaux de N éléments réels et N éléments imaginaires (2N cases mémoire) pour n’exploiter à la fin que N/2 coefficients de la série de Fourier Xn puisque XN−n=Xn*. Il est donc judicieux d’optimiser l’occupation mémoire en calculant la FFT sur 2N points réels en entrée, et ce en plaçant la moitié des données initiales dans le tableau de la partie imaginaire des données en entrée : alors l’intégralité de la transformée de Fourier est exploitée, et les relations de symétrie entre transformée de données purement réelles (XN−n=Xn*) et purement imaginaires (XN−n=−Xn*) permettent d’identifier quelle partie de chaque coefficient de Fourier vient de quelle donnée initiale. En fin de calcul, nous réorganisons les N données du spectre en sortie (cette fois toutes pertinentes puisque 2N données réelles en entrée) par (n=[0..N/2]) :
La limitation la plus contraignante pour l’application de la FFT sur microcontrôleur aux ressources réduites est la disponibilité d’une quantité de mémoire suffisante : dans notre implémentation, pour obtenir N coefficients de Fourier exploitables, nous allons remplir un tableau de 2N éléments réels (i.e. pas de partie imaginaire) codés sur 32 bits issus d’un convertisseur analogique-numérique (résolution 12 bits), puis allons transférer ces données dans un tableau de 2N éléments réels codés sur 16 bits après retrait de la valeur moyenne des signaux acquis (nous verrons que ce premier tableau de 2N éléments codés sur 32 bits est imposé par le transfert par DMA depuis le convertisseur analogique-numérique vers la RAM sans intervention explicite du processeur). Enfin, l’algorithme de la FFT lui-même nécessite deux tables de constantes (tables précalculées des coefficients de cosinus et sinus) de N/2 éléments chacune, codées sur 16 bits. Les données en entrée étant écrasées lors du calcul, aucun tableau intermédiaire additionnel n’est nécessaire. En conclusion, l’application de la FFT sur N points réels nécessite 2N octets en mémoire volatile (codage sur 16 bits), et 2N octets en mémoire non volatile. Pour N=256, nous sommes bien en-deçà des capacités du STM32 [10].
Un point fondamental concernant l’exploitation des données acquises et converties par FFT en série de coefficients de Fourier consiste à appréhender l’axe des abscisses. Nous avons vu que les N coefficients de Fourier s’étendent de −fe/2 à fe/2. Par ailleurs, nous avons vu que tout signal variant à plus de fe/2 se retrouve dans cet intervalle par repliement spectral. Nous avons donc deux contraintes quant à la paramétrisation de la FFT :
1. maximiser fe afin d’être le moins possible limité par le repliement spectral et le risque de “rater” une composante représentative de variations rapides du signal ;
2. minimiser fe afin de réduire l’occupation en mémoire (N) d’un échantillon acquis pendant une durée déterminée.
Sachant que la résolution de la FFT est de fe/N (intervalle en hertz entre deux points de la FFT), une résolution donnée s’obtient au détriment de l’occupation mémoire si fe est choisie trop grande. Dans l’exemple qui va suivre, nous allons voir que pour une application connue (par exemple mesure de vitesse d’un véhicule dont nous pouvons faire l’hypothèse de la valeur maximale), le signal échantillonné ne peut théoriquement pas dépasser une certaine borne fm. Dans ce cas, il est inutile de choisir fe>> 2× fm car nous savons que toutes les composantes de Fourier entre fm et fe/2 seront proches de 0. Par contre, pour fe déterminée par la physique du phénomène observé, nous constatons que maximiser N (i.e. la durée de la mesure et par conséquent l’occupation en mémoire) améliore la résolution spectrale fe/N.
3. Échantillonnage périodique de signaux
Le point clé de tout traitement numérique [3] du signal est la fréquence d’échantillonnage. Les ouvrages de traitement du signal présentent des axes de fréquences gradués entre -1/2 et +1/2, en considérant implicitement que la fréquence d’échantillonnage est normalisée à 1. Notre premier souci lors d’une implémentation pratique consiste donc à déterminer, ou mesurer, la fréquence d’échantillonnage d’un signal, i.e la vitesse à laquelle ce signal est numérisé lors de la conversion analogique-numérique.
La première approche, naïve mais pragmatique, permettant d’identifier la fréquence d’échantillonnage consiste à effectuer la mesure d’un signal périodique de fréquence connue f par une conversion analogique-numérique temporisée par diverses méthodes (délai par boucle vide, timer) et de mesurer a posteriori la position de la raie associée à la transformée de Fourier du signal acquis. Étant donné que la fonction fft() de GNU/Octave convertit un signal temporel de N points en un signal spectral de N points s’étendant de −fe/2 à fe/2 avec fe la fréquence d’échantillonnage, alors si la raie du signal s’observe à l’abscisse M, nous en déduisons que fe=f× N/M. Plus f est grand (i.e. N/M s’approche de 1), plus la mesure sera précise.
Une façon plus rationnelle d’aborder le problème de la fréquence d’échantillonnage consiste à l’imposer. À peu près tous les microcontrôleurs permettent de déclencher une conversion analogique-numérique sur une condition de compteur périodique (timer), ou au pire la conversion peut être amorcée dans le gestionnaire d’interruption du timer. Dans le cas particulier du STM32, le mécanisme est encore plus puissant, puisque non seulement une source de déclenchement de la conversion peut être la condition de dépassement d’une valeur prédéfinie d’un compteur (Capture Compare), mais en plus un mécanisme d’accès direct à la mémoire (Direct Memory Access, DMA) place le résultat de la conversion dans un tableau d’emplacement prédéfini par l’utilisateur en mémoire sans soliciter le processeur. Ainsi, nous aurons dans notre cas une boucle dans le programme principal qui se contente d’effectuer la transformée de Fourier des données contenues dans un tableau et communiquer le résultat à l’utilisateur, et ce en étant informé du remplissage du tableau contenant les données à traiter par une interruption (Fig. 5). La DMA remplit un tampon de façon circulaire : une fois plein, l’adresse dans laquelle la donnée suivante sera stockée est automatiquement replacée en début de tableau.
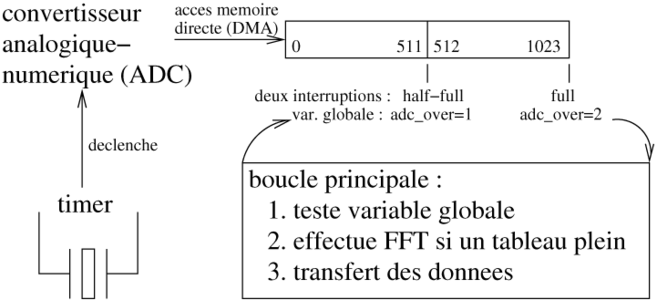
Figure 5 : Principes généraux de l’implémentation de l’échantillonnage périodique sur STM32, libérant le programme principal de tous les détails de la gestion des conversions pour se focaliser uniquement sur le traitement numérique des données acquises. Deux interruptions sont déclenchées par le gestionnaire d’accès direct à la mémoire (DMA) qui transfère les données échantillonnées par le convertisseur analogique-numérique vers la RAM : moitié-plein et plein. Ces deux informations sont utiles pour garantir que le traitement (FFT) n’est effectué que sur un tableau déjà rempli et dont les valeurs ne changent pas au cours de l’analyse. La conversion ADC est elle-même cadencée par un timer programmé pour déterminer le rythme de remplissage du tableau de données. Ainsi, le programme principal se contente d’attendre un signal associé à une des interruptions, et traiter les données suffisamment rapidement (choix de la fréquence d’échantillonnage et de la taille des tableaux) pour garantir la fin du calcul avant la prochaine interruption.
Dans la séquence des initialisations, il faut d’une part lier le déclenchement de la conversion analogique-numérique (ADC) sur la comparaison entre la valeur d’un compteur et une borne prédéfinie, et d’autre part lier la sortie de l’ADC à un tableau qui se remplit automatiquement par accès direct à la mémoire (DMA).
Lors de l’initialisation ADC, nous lions la source de déclenchement externe au compteur 2, et annonçons que la sortie des données se fera par DMA.
void init_adc(void)
{ u8 channel_array[16];
rcc_peripheral_enable_clock(&RCC_APB2ENR, RCC_APB2ENR_ADC1EN);
gpio_set_mode(GPIOA, GPIO_MODE_INPUT,
GPIO_CNF_INPUT_ANALOG, GPIO3 | GPIO0);
ADC_CR2(ADC1) &=~ADC_CR2_ADON;
ADC_CR1(ADC1) = 0;//1<<5;
ADC_CR2(ADC1) = ADC_CR2_TSVREFE|(ADC_CR2_EXTSEL_TIM3_TRGO<<17);
ADC_SMPR2(ADC1) &=~(0x07<<0); // config CHAN0
ADC_SMPR2(ADC1) |=(0x00<<0);
ADC_SMPR2(ADC1) &=~(0x07<<9); // config CHAN3
ADC_SMPR2(ADC1) |=(0x00<<9); // 1.5 cycles, 0x03 pour 28.5 cycles
ADC_CR2(ADC1) |= ADC_CR2_ADON;
ADC_CR2(ADC1) |= 1<<20;
[... calibration ...]
ADC_CR2(ADC1) |= 1<<8; // dma
adc_on(ADC1);
channel_array[0] = 3; // channel : 3 pour snd, 0 pour RADAR
adc_set_regular_sequence(ADC1, 1, channel_array);
}
Lors de l’initialisation de la DMA, deux conditions d’interruption sont définies lors du remplissage cyclique du tableau contenant les données à traiter, moitié plein et complètement plein. Ces deux interruptions sont distinctes et le message est transmis au programme principal (afin de savoir quelle moitié du tableau traiter) au travers de la variable globale adc_over. La configuration de la DMA nécessite par ailleurs de définir la nature de la source (ici un périphérique), de la destination (ici la mémoire) et de la taille des données à manipuler (bien que nous travaillons sur des données issues de la conversion sur 12 bits, le registre de sortie de l’ADC est sur 32 bits qui impose la taille des données transférées).
volatile char adc_over = 0;
void SetupDMA (void);
#define TxBufferSize1 512*2
int32_t TxBuffer1[TxBufferSize1]; // ADC est 32 bits
void dma1_channel1_isr (void)
{if ((DMA_ISR (DMA1) & DMA_ISR_TCIF1))
{DMA_IFCR (DMA1) = 1 << 1; //clear intr
adc_over = 2;
}
if ((DMA_ISR (DMA1) & DMA_ISR_HTIF1))
{DMA_IFCR (DMA1) = 1 << 2; //clear intr half transfer
adc_over = 1;
}
}
void SetupDMA (void)
{ nvic_enable_irq (NVIC_DMA1_CHANNEL1_IRQ);
nvic_set_priority (NVIC_DMA1_CHANNEL1_IRQ, 0);
rcc_peripheral_enable_clock (&RCC_AHBENR, RCC_AHBENR_DMA1EN);
DMA_CCR1 (DMA1) |= 3 << 12 /* Set the channel priority: very high */
| 2 << 10 /* Set the memory size: 32bits */
| 2 << 8 /* Set the peripheral size: 32bits */
| 1 << 7 /* Enable memory increment mode */
| 0 << 6 /* Disable peripheral increment mode */
| 1 << 5 /* enable circular mode */
| 0 << 4 /* Set transfert direction: Read from peripheral */
| (2+1) << 1; /* Enable half & full transfer complete interrupt */
DMA_CNDTR1 (DMA1) = TxBufferSize1; // Total number of data to be transfered
DMA_CPAR1 (DMA1) = (uint32_t) (&ADC1_DR); // Set the peripheral register address
DMA_CMAR1 (DMA1) = (uint32_t) & TxBuffer1; // Set the memory base address
DMA_CCR1 (DMA1) |= 1;
dma_enable_channel (DMA1, DMA_CHANNEL1);
}
}
Finalement, il nous reste à définir la source de déclenchement de la conversion analogique-numérique, à savoir le dépassement (overflow) du compteur 3. La valeur chargée dans le registre TIM_ARR détermine donc, connaissant les facteurs de division de l’horloge chargée de cadencer le compteur, la période d’activation de la conversion. Dans notre cas, nous désirons déclencer une interruption à 4 kHz sur une horloge qui a été divisée pour atteindre 36 MHz : TIM_ARR(TIM3) = (36000000/4000);
void timeBaseInit()
{ TIM_CR1(TIM3) = TIM_CR1_CKD_CK_INT /* clockdivision*/
|TIM_CR1_DIR_UP
|1<<2; // under/overflow only declenche interrupt
TIM_PSC(TIM3) = 1; // 72/(TIM2_PSC+1)MHz = 36 MHz // Set the Prescaler value
/* Set the Autoreload value */
TIM_ARR(TIM3) = 4500*2; // 36e6/(4500)=8000 Hz, on veut 4 kHz
// seule cette valeur definit le retour a 0
TIM_EGR(TIM3) = 0x01; // Generate an update event to reload the Prescaler value immediatly
}
void rcc_init()
{rcc_peripheral_enable_clock(&RCC_APB1ENR, RCC_APB1ENR_TIM3EN);}
void setupTim3(void)
{
rcc_init();
timeBaseInit();
TIM_CR2(TIM3) = 2<<4;
TIM_EGR(TIM3) = 1<<0;
}
void enableT3() {TIM_CR1(TIM3) |= 0x0001;}
void disableT3() {TIM_CR1(TIM3) &= ~0x0001;}
Ces initialisations effectuées, le programme principal peut maintenant se concentrer uniquement sur le traitement numérique des signaux transmis dans les tampons qui se remplissement automatiquement par DMA, en amorçant l’analyse des données chaque fois que l’interruption de remplissage (moitié ou complet) est déclenchée. Une fois les données traitées, elles sont transmises à l’utilisateur par liaison asynchrone (RS232). Afin de garantir un flux continu de données contigües, nous devons sélectionner un ensemble de paramètres de mesures et de traitement qui permette un temps d’acquisition plus long que le temps de traitement et exploitation des informations.
#define TAILLE 512
void
clock_setup (void)
{ rcc_clock_setup_in_hse_8mhz_out_72mhz ();
rcc_peripheral_enable_clock (&RCC_APB2ENR, RCC_APB2ENR_IOPCEN);
}
void moins_moyenne (int32_t * t, short *sortie)
{ int k, somme = 0;
for (k = 0; k < TAILLE; k++) somme += (int) t[k];
somme /= TAILLE;
for (k = 0; k < TAILLE; k++) sortie[k] = (t[k] - (int) somme)/8;
}
int main (void)
{ uint16_t temp; int i;
short sortie[TAILLE]; // ADC est 32 bits, mais FFT veut 16 bits
adc_over = 1;
clock_setup ();
SetupUART (USART1, 115200);
init_adc ();
SetupDMA ();
setupTim3 ();
enableT3 ();
adc_over = 0;
while (1)
{ while (adc_over == 0);
put_int(USART1,adc_over,4);usart1_put_string(" ");
if (adc_over == 1)
moins_moyenne (TxBuffer1, sortie);
else
moins_moyenne (&TxBuffer1[TAILLE], sortie);
fft_fast (sortie, &sortie[TAILLE / 2]); // TAILLE puissance de 2
for (i = 0; i < TAILLE/4 ; i++) // 4*256 chars a 115200 bauds = 89 ms
{ // mais 512 points a 4 kHz = 128 ms
put_int (USART1, sortie[i], 1); usart1_put_string (" ");
put_int (USART1, sortie[TAILLE/2+i], 1); usart1_put_string (" ");
}
usart1_put_string ("\r\n");
adc_over = 0;
}
}
Ayant acquis des séquences de points échantillonnés périodiquement suivant un intervalle de temps imposé par la configuration du timer, il nous reste à mettre en œuvre le contenu de la note d’application pour calculer en temps réel les coefficients de Fourier par la fonction fft_fast() contenue dans le main() ci-dessus. Un aspect intéressant de l’étude de la note d’application AN3722 est de constater la génération automatique de code pour précalculer un certain nombre de constantes. Ainsi, la réorganisation des données pour passer de la transformée de Fourier classique à la FFT est générée automatiquement, ainsi que les tables contenant les fonctions trigonométriques pré-calculées. Par ailleurs, cette génération de code automatique est très sensible à la nature des données manipulées. Les casts successifs (long sur 4 octets et short sur 2 octets) sont nécessaires pour le bon fonctionnement de ce code :
resultMulReCos=((long)cosLUT[tf_index]*(long)x_n_re[b_index])>>7;
resultMulReSin=((long)sinLUT[tf_index]*(long)x_n_re[b_index])>>7;
resultMulImCos=((long)cosLUT[tf_index]*(long)x_n_im[b_index])>>7;
resultMulImSin=((long)sinLUT[tf_index]*(long)x_n_im[b_index])>>7;
x_n_re[b_index] = x_n_re[a_index]-(short)resultMulReCos+(short)resultMulImSin;
x_n_im[b_index] = x_n_im[a_index]-(short)resultMulReSin-(short)resultMulImCos;
x_n_re[a_index] = x_n_re[a_index]+(short)resultMulReCos-(short)resultMulImSin;
x_n_im[a_index] = x_n_im[a_index]+(short)resultMulReSin+(short)resultMulImCos;
#include <stdlib.h>
// 23 secondes de TF devient 5 par FFT et 4 par FFT_fast
//
// on a deux tableaux de N donnees, pour R et iR
// mais les donnees initiales sont reelles => X(N-n)=X(n)^* ou` X
// est la transformee de Fourier de x (X1=TF(x1), X2=TF(x2))
// si on concatene x1 (dans R) et x2 (dans iR), alors on retrouve X1 et X2 par
// Re(X1)= (ReX(n)+ReX(N-n))/2
// Im(X1)= (ImX(n)-ImX(N-n))/2
// Re(X2)= (ImX(n)+ImX(N-n))/2
// Im(X2)=-(ReX(n)-ReX(N-n))/2
/*
********************************************************************
* maxqfft.c
*
* July 01, 2005
*
* Paul Holden (Paul_Holden@maximhq.com)
* Maxim Integrated Products
* NOTE: All fft input/outputs are signed and in Q8.7 notation
* Copyright (C) 2005 Maxim/Dallas Semiconductor Corporation,
* All Rights Reserved.
[... copyright dans la note d'application de Maxim]
*/
#include "maxqfft256.h"
void main_fft(short *x_n_re,short *x_n_im)
{
/* 4.0. Variable Declaration and Initialization */
short i; // Misc index
int n_of_b = N_DIV_2; // Number of butterflies
int s_of_b = 1; // Size of butterflies
int a_index = 0; // fft data index
int a_index_ref = 0; // fft data index reference
char stage = 0; // Stage of the fft, 0 to (Log2(N)-1)
int nb_index; // Number of butterflies index
int sb_index; // Size of butterflies index
int resultMulReCos;
int resultMulImCos;
int resultMulReSin;
int resultMulImSin;
int b_index; // 2nd fft data index
int tf_index; // The twiddle factor index
/* 4.2. Perform Bit-Reversal: Uses an unrolled loop that was created with
the following C code:
#include <stdio.h>
#define N 256
#define LOG_2_N 8
int bitRev(int a, int nBits)
{
int rev_a = 0;
for (int i=0; i<nBits; i++)
{rev_a = (rev_a << 1) | (a & 1);a= a >> 1;}
return rev_a;
}
int main(int argc, char* argv[])
{ printf(" unsigned int i;\n");
for(int i=0; i<N; i++)
if (bitRev(i,LOG_2_N) > i)
{printf(" i=x_n_re[%3d]; " ,i);
printf("x_n_re[%3d]=x_n_re[%3d]; ",i,bitRev(i,LOG_2_N));
printf("x_n_re[%3d]=i;\n" ,bitRev(i,LOG_2_N));
}
} */
i=x_n_re[ 1]; x_n_re[ 1]=x_n_re[128]; x_n_re[128]=i;
i=x_n_re[ 2]; x_n_re[ 2]=x_n_re[ 64]; x_n_re[ 64]=i;
i=x_n_re[ 3]; x_n_re[ 3]=x_n_re[192]; x_n_re[192]=i;
[... beaucoup de lignes pour le papillon ...]
i=x_n_im[ 1]; x_n_im[ 1]=x_n_im[128]; x_n_im[128]=i;
i=x_n_im[ 2]; x_n_im[ 2]=x_n_im[ 64]; x_n_im[ 64]=i;
i=x_n_im[ 3]; x_n_im[ 3]=x_n_im[192]; x_n_im[192]=i;
[... idem pour Im ...]
/* 4.3. FFT: loop through the 0 to log2(N) stages of
the butterfly computations. When the FFT
begins, the input samples (x(n)) are stored
in x_n_re/x_n_im. When the FFT is done,
the spectrum (X(n)) has replaced the input
stored in x_n_re/x_n_im. */
for(stage=0; stage<LOG_2_N; stage++)
{
for(nb_index=0; nb_index<n_of_b; nb_index++)
{
tf_index = 0; // The twiddle factor index
for(sb_index=0; sb_index<s_of_b; sb_index++)
{
b_index = a_index+s_of_b; // 2nd fft data index
resultMulReCos=(short)(((int)cosLUT[tf_index]*(int)x_n_re[b_index])>>7);
resultMulReSin=(short)(((int)sinLUT[tf_index]*(int)x_n_re[b_index])>>7);
resultMulImCos=(short)(((int)cosLUT[tf_index]*(int)x_n_im[b_index])>>7);
resultMulImSin=(short)(((int)sinLUT[tf_index]*(int)x_n_im[b_index])>>7);
x_n_re[b_index] = x_n_re[a_index]-resultMulReCos+resultMulImSin;
x_n_im[b_index] = x_n_im[a_index]-resultMulReSin-resultMulImCos;
x_n_re[a_index] = x_n_re[a_index]+resultMulReCos-resultMulImSin;
x_n_im[a_index] = x_n_im[a_index]+resultMulReSin+resultMulImCos;
if (((sb_index+1) & (s_of_b-1)) == 0)
a_index = a_index_ref;
else
a_index++;
tf_index += n_of_b;
}
a_index = ((s_of_b<<1) + a_index) & N_MINUS_1;
a_index_ref = a_index;
}
n_of_b >>= 1;
s_of_b <<= 1;
}
}
void fft_fast(short* xre,short *xim)
{int monxre,monxim,monyre,monyim,i;
main_fft(xre,xim); // fft(x)
for (i=0;i<N/2;i++)
{monxre=((int)xre[i]+(int)xre[N-i])/2;
monxim=((int)xim[i]-(int)xim[N-i])/2;
monyre=((int)xim[i]+(int)xim[N-i])/2;
monyim=-((int)xre[i]-(int)xre[N-i])/2;
xre[i]=monxre;
xim[i]=monxim;
xre[N-i]=monyre;
xim[N-i]=monyim;
}
}
Listing 1: Calcul de la FFT tel qu’implémenté dans l’AN 3722 de Maxim. Noter la génération automatique de code pour l’organisation des données en mémoire.
/*
********************************************************************
* maxqfft.h
* July 01, 2005
* Paul Holden (Paul_Holden@maximhq.com)
* Maxim Integrated Products
* NOTE: All fft input/outputs are signed and in Q8.7 notation
* Copyright (C) 2005 Maxim/Dallas Semiconductor Corporation,
* All Rights Reserved.
[... copyright de la note d'application de maxim]
*/
#ifndef __MAXQ_FFT_H__
#define __MAXQ_FFT_H__
/* DEFINE STATEMENTS */
#define N 256
#define N_DIV_2 128
/*
cosine Look-Up Table: An LUT for the cosine function in Q8.7. The
table was created with the following program:
#include <stdio.h>
#include <math.h>
#define N 256
void main(int argc, char* argv[])
{printf("const int cosLUT[%d] =\n{\n",N/2);
for(int i=0; i<N/2; i++)
{printf("%+4d",(int)(128*cos(2*M_PI*i/N)));
if (i<(N/2-1)) printf(",");
if ((i+1)%16 == 0) printf("\n");
}
printf("};\n");
}
*/
const short cosLUT[N_DIV_2] =
{
+128,+127,+127,+127,+127,+127,+126,+126,+125,+124,+124,+123,+122,+121,+120,+119,
+118,+117,+115,+114,+112,+111,+109,+108,+106,+104,+102,+100, +98, +96, +94, +92,
+90, +88, +85, +83, +81, +78, +76, +73, +71, +68, +65, +63, +60, +57, +54, +51,
+48, +46, +43, +40, +37, +34, +31, +28, +24, +21, +18, +15, +12, +9, +6, +3,
+0, -3, -6, -9, -12, -15, -18, -21, -24, -28, -31, -34, -37, -40, -43, -46,
-48, -51, -54, -57, -60, -63, -65, -68, -71, -73, -76, -78, -81, -83, -85, -88,
-90, -92, -94, -96, -98,-100,-102,-104,-106,-108,-109,-111,-112,-114,-115,-117,
-118,-119,-120,-121,-122,-123,-124,-124,-125,-126,-126,-127,-127,-127,-127,-127
};
/*
sine Look-Up Table: An LUT for the sine function in Q8.7. The
table was created with the following program:
#include <stdio.h>
#include <math.h>
#define N 256
void main(int argc, char* argv[])
{printf("const int sinLUT[%d] =\n{\n",N/2);
for(int i=0; i<N/2; i++)
{printf("%+4d",(int)(128*sin(2*M_PI*i/N)));
if (i<(N/2-1)) printf(",");
if ((i+1)%16 == 0) printf("\n");
}
printf("};\n");
}
*/
const short sinLUT[N_DIV_2] =
{
+0, +3, +6, +9, +12, +15, +18, +21, +24, +28, +31, +34, +37, +40, +43, +46,
+48, +51, +54, +57, +60, +63, +65, +68, +71, +73, +76, +78, +81, +83, +85, +88,
+90, +92, +94, +96, +98,+100,+102,+104,+106,+108,+109,+111,+112,+114,+115,+117,
+118,+119,+120,+121,+122,+123,+124,+124,+125,+126,+126,+127,+127,+127,+127,+127,
+128,+127,+127,+127,+127,+127,+126,+126,+125,+124,+124,+123,+122,+121,+120,+119,
+118,+117,+115,+114,+112,+111,+109,+108,+106,+104,+102,+100, +98, +96, +94, +92,
+90, +88, +85, +83, +81, +78, +76, +73, +71, +68, +65, +63, +60, +57, +54, +51,
+48, +46, +43, +40, +37, +34, +31, +28, +24, +21, +18, +15, +12, +9, +6, +3
};
#endif
Listing 2: Tableaux associés à la FFT : noter la génération automatique de code pour les tables contenant les valeurs de cosinus et sinus, stockées en mémoire non volatile (préfixe const)
La portabilité de ce code est excellente puisque son utilisation a été validée sans problème majeur (si ce n’est pour les castset l’importance de la taille des données manipulées) sur MSP430 (architecture 16 bits) et STM32 (architecture 32 bits).
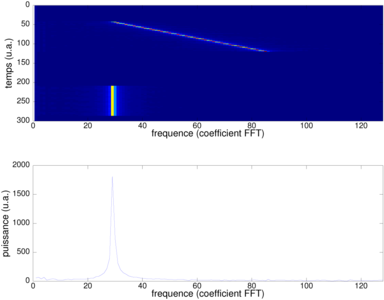
Figure 6 : Calibrage de la fréquence d’échantillonnage, en émettant un chirp linéaire entre 400 et 1320 Hz (durée 10 s) puis une sinusoïde de fréquence fixe à 440 Hz (durée 10 s), sur la carte son utilisée comme synthétiseur de signaux au moyen de audacity, et acquisition par le STM32 exécutant le programme décrit dans le texte. Nous constatons (en bas) que la sinusoïde se trouve à l’abscisse 28±1 pour une FFT sur 256 points, soit une fréquence d’échantillonnage de 4020±120 Hz, en accord avec nos attentes compte tenu de la configuration du compteur en charge de cadencer les conversions analogiques-numériques.
Supposons que dans le cas qui va nous intéresser, nous voulions échantillonner à la fréquence de 4 kHz, et que nous remplissions un tableau de 512 valeurs, alors il faut 128 ms pour remplir le tableau. Ce temps va nous permettre d’effectuer le calcul et transférer les données. Nous mesurons un temps de calcul pour une FFT sur 512 points de l’ordre de 4,5 ms, incluant les quelques pré-traitements tels que retrait de la valeur moyenne. Par ailleurs, communiquer en 115200 bauds sur une liaison asynchrone (RS232) le résultat du calcul, à savoir les 256 coefficients utiles (par symétrie de la FFT d’un signal réel) codés chacun sur 5 caractères ASCII en moyenne, résulte en un temps de communication de 111 ms. Ainsi, le temps de calcul et de communication est bien inférieur au temps d’acquisition, et le flux de données sera continu. Nous pouvons nous convaincre par analyse d’une séquence d’acquisitions sur un signal variant dans le temps (chirp) que la fréquence d’échantillonnage est celle prévue, et de la continuité des signaux analysés (Fig. 6). Dans cet exemple, le logiciel Audacity est exploité pour générer un signal sur la carte son d’un ordinateur personnel, se comportant ainsi comme un générateur de signaux de forme arbitraire échantillonnés à 44100 Hz (carte son d’un Asus eeePC 701).
Néanmoins, nous devons prendre soin de ne pas travailler sur un tableau en cours de remplissage, sous peine de traiter des données qui n’ont pas été acquises de façon contiguë. Nous exploitons un mécanisme de DMA pour remplir directement un tableau qui contient les informations à traiter, et ce de façon circulaire. Le STM32 fournit un mécanisme pour alterner entre deux tableaux : une interruption est déclenchée lorsqu’un tableau est à moitié plein (et une autre interruption lorsqu’il est plein). En déclarant un tableau de taille double du nombre d’éléments à traiter, et en identifiant la nature de l’interruption, nous garantissons de calculer sur une série de données qui restera inchangée au cours du traitement, tandis que l’autre moitié se charge de nouvelles informations. Ce double tampon était déjà la méthode classique pour éviter les clignotements sur carte VGA programmée en mode 0x13 sous DOS, avec remplissage d’un tableau tandis que l’autre était en cours d’affichage (et attente de l’interruption de synchronisation verticale pour commuter entre tampons) [11].
4. Exemple d’utilisation : application au RADAR à onde continue (CW)
Une application classique de l’exploitation de la transformée de Fourier rapide sur des séquences échantillonnées est l’analyse de la voix. Cependant, l’intervalle de temps entre la transmission de deux spectres doit alors être inférieure à quelques millisecondes, trop court pour la liaison asynchrone (RS232) que nous expoitons ici1. Nous allons par conséquent nous intéresser à une autre application, les RADAR (RAdio Detection And Ranging) à onde continue (CW, Continuous Wave).
Il existe deux grands types de RADAR [12] [13] : ceux fonctionnant dans le domaine temporel et ceux fournissant une information spectrale. La première solution est toujours lourde à mettre en œuvre en termes d’instrumentation car identifier une position de cible à 1 m près se traduit par un échantillonnage du signal avec une résolution de 3 ns ou une fréquence de 300 MHz. Même en exploitant diverses astuces de traitement du signal, une électronique d’échantillonnage fonctionnant à plusieurs dizaines de MHz est fastidieuse à mettre en œuvre. Nous allons voir qu’au contraire, l’information dans le domaine spectral est très simple à obtenir, au détriment de la résolution spatiale. À ces fins, nous expérimenterons avec des RADAR développés par Microwave Solutions en Angleterre (http://www.microwave-solutions.com/) et en partie distribués en France par Lextronic2.
4.1 Le RADAR CW
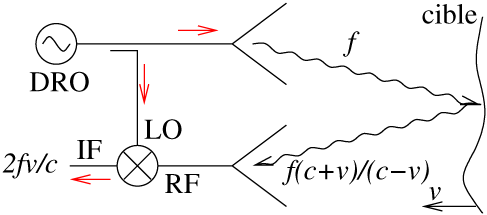
Figure 7 : Schéma de principe d’un RADAR à onde continue (CW) : un oscillateur (DRO – Dielectric Resonator Oscillator dans lequel une onde électromagnétique est confinée dans une céramique de permittivité élevée pour définir la fréquence d’un circuit oscillant basé sur un amplificateur à transistor à effet de champ (FET) génère une onde hyperfréquence de fréquence f. Une fraction de cette onde est couplée vers un mélangeur afin que l’onde émise (antenne du haut) et reçue après réflexion sur une cible mouvante (antenne du bas) soit mélangée avec le signal d’excitation pour fournir un battement basse fréquence dont les propriétés sont liées à la vitesse de la cible tel que décrit dans le texte.
Un RADAR CW génère un signal radiofréquence, l’émet sur une antenne, et mélange l’information retournée sur une seconde antenne (configuration bistatique dans laquelle émetteur et récepteur sont séparés afin de ne pas saturer la réception par le signal émis) pour la ramener dans une fréquence basse accessible au microcontrôleur (Fig. 7). Le principe du mélangeur est d’exploiter le point de fonctionnement non linéaire de composants afin d’effectuer le produit entre un signal de référence (Local Oscillator, LO) et un signal à analyser (Radio-Fréquence, RF). En effet, le produit de deux sinusoïdes donne cos(a× t)×cos(b× t)=1/2×(cos((a−b)× t)+ cos((a+b)× t)). Le filtrage par un filtre passe-bas de fréquence inférieure à a+b permet d’éliminer le second terme et de ne conserver que le battement entre les deux fréquences a−b. Nous avons donc effectué une transposition de fréquence.
Figure 8 : Haut : signal temporel expérimental lorsqu’une cible est éloignée (dates 0,1-0,2 s et 0,6-0,7 s) et approchée (dates 0,3-0,4 et 0,7-0,8 s) du RADAR, illustrant clairement la présence d’oscillations avec une fréquence dépendante de la vitesse. Bas : transformée de Fourier (fonction fft() de GNU/Octave) sur fenêtre glissante sur des échantillons de 512 points successifs, permettant d’illustrer l’évolution de la vitesse de la cible (en ordonnée) en fonction du temps (en abscisse).
Le RADAR CW a pour vocation de mesurer la distance et la vitesse d’une cible. La première information est une grandeur caractéristique du domaine temporel (au travers de la célérité de l’onde électromagnétique dans le milieu) que nous allons abandonner dans un premier temps (section 4.2), la seconde est une information spectrale. En effet, une onde réfléchie par une cible mobile voit sa fréquence décalée d’une quantité appelée le décalage Doppler fD tel que fD=2×fv/c avec f la fréquence émise par le RADAR, v la vitesse de la cible et c la célérité de l’onde électromagnétique (3× 108 m/s). Cette formule se déduit de la relation générale reliant la fréquence reçue f′ lorsqu’une cible se rapprochant à vitesse v réfléchit une onde électromagnétique incidente de fréquence f : f′=f×c+v/c−v et en tenant compte de l’approximation v<< c, nous déduisons l’expression de fD=f′−f=2× fv/c. Cette fréquence caractérise le signal issu du mélange (IF, Intermediate Frequency) du signal émis (LO) et du signal retourné (RF) par la cible. Cette relation explique pourquoi un RADAR CW doit fonctionner en hyperfréquence pour mesurer la gamme de vitesses (0 à quelques dizaines de mètres par seconde) qui nous intéresse le plus souvent : plus f est grand, plus fD est élevé pour v donnée. Pour avoir des ordres de grandeur, un humain qui se déplace à 1 m/s induit, pour une porteuse à 9,9 GHz, un décalage Doppler de 66 Hz. Un véhicule se déplaçant à 36 km/h (10 m/s) induit un décalage de fréquence de 660 Hz, parfaitement mesurable avec un microcontrôleur échantillonnant un signal à quelques kilohertz (Fig. 8). Nous avons vu qu’il faut choisir la fréquence d’échantillonnage telle que fe/2 se trouve au plus près de la fréquence maximale du signal à observer : étant donné qu’il est peu probable que nous ayons à observer une cible se déplaçant à plus de 110 km/h (30 m/s) (Fig. 9), nous choisissons fe=4 kHz afin que le décalage Doppler de 2 kHz soit observable. Cette vitesse correspond aussi à celle du bout de pale d’un ventilateur de 25 cm de rayon tournant à 19 tours/s. Afin d’obtenir un signal exploitable et filtré, la sortie du RADAR CW est traitée par le premier étage du circuit proposé sur le site web de Lextronic (encadré 1), permettant d’obtenir un signal propre pour une cible métallique plane de surface 10× 10 cm2 (Fig. 8) ou en plaçant le RADAR dans une orientation presque parallèle à la route devant un véhicule (Fig. 9).
La perte de l’information de distance peut sembler a priorirédhibitoire, mais de nombreuses applications s’intéressent exclusivement à une mesure de vitesse sans contact avec la cible, sans requérir l’information de distance (par exemple [14]). Dans la même veine, parmi les exemples d’utilisation de RADAR capables de ne mesurer que la vitesse, l’application de mesure de vitesse de déplacement de véhicules (RADAR de contrôle de vitesse, Fig. 9) sont les plus connus, mais la mesure de vitesses de balles (de tennis ou de baseball [12, p.36]) est une autre application moins connue de ce genre d’instrument.
Il est remarquable de mentionner que bien que ce qui est abusivement nommé RADAR de recul sur les automobiles (à l’exception des modèles haut de gamme) soit un SONAR, leur fonctionnement autour de 40 kHz induit des variations de fréquence du même ordre de grandeur par décalage Doppler, compte tenu de la célérité d’une onde acoustique dans l’air : c=~ 340 m/s et pour f=40 kHz, nous avons un quotient f/c égal pour une onde acoustique à 40 kHz et une onde électromagnétique à 2,55 GHz.
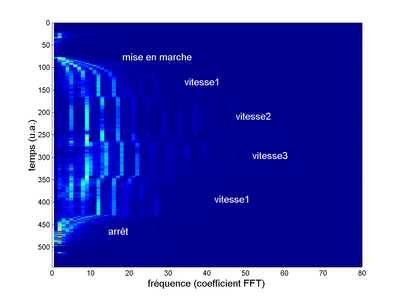
Figure 9 : Afin de déterminer, sans contact mécanique avec l’extérieur, la vitesse de translation d’un véhicule, nous le munissons d’un RADAR CW illuminant la route selon un angle rasant (gauche). Le véhicule sort de sa place de parking en marche arrière (dates 100-180), se positionne en bout de parking (dates 200-250), puis accélère. Cette séquence est répétée (dates 280-400), puis les données acquises sont traitées entre les dates 620-1100, avant de retourner sur une place de stationnement. On notera notamment que le RADAR CW muni d’un simple mélangeur ne peut pas donner le signe de la vitesse : une marche arrière ou marche avant fournissent des signaux identiques.
Compte tenu du nombre de messages observés sur les forums de discussion s’interrogeant sur le bon fonctionnement du circuit proposé sur le site web de Lextronic et de son utilité, une rapide analyse sous ngspice [15] permet d’intuiter son fonctionnement et l’influence des divers composants passifs mis en jeu :
* analyse du circuit de Lextronic pour RADAR CW
Ve 1 0 dc 0 ac 1
Valim 3 0 dc 5
R1 1 2 10k
R2 2 3 100k
Cr 99 98 10n
Rr 99 98 1meg
Rm 98 4 4.7k
Cm 4 0 10e-6
Co 99 5 10e-6
X1 2 98 99 opamp
Ro 5 6 4.7k
X2 88 6 89 opamp
Crr 6 89 1n
R11 6 89 1meg
R12 88 0 100k
R13 88 7 10k
X3 8 7 100 opamp
R14 7 3 100k
Ror 89 8 100k
Cor 8 0 22n
.subckt opamp 1 2 3
* +in (=1) -in (=2) out (=3)
rin 1 2 2meg
e 4 0 1 2 100k
rbw 4 5 0.5meg
cbw 5 0 31.85nf
eout 6 0 5 0 1
rout 6 3 75
.ends opamp741
.control
ac dec 1000 0.01 1Meg
plot vdb(100)
.endc
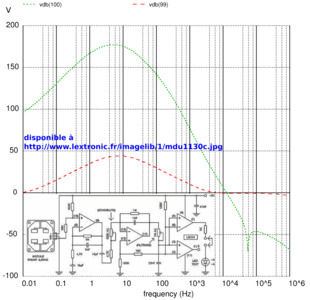
Nous constatons que les deux étages se comportent comme des filtres passe-bande, avec une fréquence de coupure autour de la centaine de hertz, et un gain nul pour le premier étage aux très basses fréquences (pour éviter de saturer la composante continue lors de la seconde amplification) pour atteindre un gain de 50 dB à 10 Hz (i.e. pour une cible se déplaçant à 0,15 m/s=0,5 km/h). Pour les exemples fournis dans cette présentation, seul le premier étage de ce circuit a été utilisé (gain de 50 dB).
Tableau 1 : encadré 1 : analyse du circuit de mise en forme des signaux basse fréquence issus du RADAR hyperfréquence de Microwave Solutions, proposés par Lextronic.
Au-delà de l’information de vitesse de la cible obtenue par transformée de Fourier du signal décalé en fréquence par effet Doppler, la visibilité par intermittence de la cible peut aussi fournir une information de signature sur la nature de la cible [17] [18]. Prenons pour exemple concret un hélicoptère : la section visible des pales par le RADAR varie au cours de la rotation des hélices. Chaque aéronef fournit ainsi une signature qui peut être caractérisée et aider à son identification. Il est bien connu qu’un hélicoptère n’est ni plus ni moins qu’un ventilateur dont les pales sont orientées parallèles au sol (?!). Exploitons donc ce concept de signature RADAR sur un ventilateur dont les 3 pales sont couvertes de scotch métallique : le signal associé au mouvement (lent) du ventilateur au-dessus du RADAR est accompagné de composantes à haute fréquence dues au passage par intermittence du réflecteur sur chaque pale devant le faisceau du RADAR. Non seulement cette signature peut être identifiée comme liée à un ventilateur, mais en plus l’indication de vitesse de rotation des pales se retrouve dans la signature spectrale (Fig. 10).
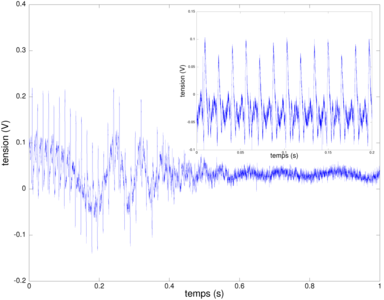
Figure 10 : Haut : signal temporel acquis lorsqu’un ventilateur est placé devant le RADAR CW. La variation lente du signal sur la première moitié du graphique correspond au mouvement lent appliqué à l’ensemble du ventilateur s’approchant et s’éloignant du RADAR, tandis que les pics rapides – zoom dans l’insert en haut à droite – sont représentatifs de la vitesse de rotation des pales (passage d’une pale devant le faisceau RADAR pour réfléchir l’onde électromagnétique. Bas : analyse spectrale des signaux découpés par paquets de 512 échantillons. Nous observons clairement la phase de mise en route du ventilateur, l’accélération de la vitesse de rotation alors que la puissance électrique est incrémentée 3 fois, avant de revenir à la vitesse initiale puis de couper l’alimentation du ventilateur.
4.2 Le RADAR FMCW
Nous avons vu qu’un RADAR à onde continue ramène par mélange un signal de fréquence très élevée (hyperfréquence) dans une gamme de fréquences accessibles par un microcontrôleur de puissance de calcul réduite. Ce mélange fournit un battement dû à l’effet Doppler et ne permet aucune mesure de distance. Une alternative à la création d’un battement par effet Doppler est de balayer la fréquence de la source. Dans ce cas, l’onde qui met un temps non nul dt pour se propager de l’antenne émettrice à la cible puis revenir au récepteur, est mélangée avec la source de fréquence qui s’est décalée du fait du balayage de fréquence. Si l’excursion (décalage volontaire de la fréquence de la source) de fréquence est de Δ f pendant un temps Δ T, alors la cible située à distance dt est détectée sous forme d’un battement de fréquence df=2dtΔ f/Δ T. Si par exemple la cible se trouve à 15 cm, alors le temps de vol de l’onde est de 1 ns, et si la source de fréquence est balayée sur une plage de 4 MHz en 100 µs (10 kHz, fréquence fournie par une carte son par exemple), alors le battement doit s’observer à une fréquence df=40 Hz. Plus la cible est loin, plus le battement est à fréquence élevée et sa détection aisée (Fig. 11, gauche).
Nous avons tenté de mettre en œuvre ce concept avec le RADAR CW ajustable en fréquence, référence MDU1100T chez Microwave Solutions (une centaine d’euros incluant les frais de douane et d’expédition). Cependant, l’absence de signal exploitable est expliquée par l’absence de linéarité entre la tension de commande de l’oscillateur et la fréquence générée par le DRO [19] : dans ce cas, alors que nous avons induit le balayage de fréquence par une rampe linéaire de tension sur la broche d’ajustement de fréquence de la source, le délai dt n’induit pas un battement de fréquence constante df au cours du balayage de fréquence, et le signal analysé n’accumule pas de façon cohérente des signaux de composante df exploitable (Fig. 11, droite). Cet échec mérite donc un effort additionnel3, à savoir la qualification de la dérive de l’oscillateur hyperfréquence en fonction de la tension de polarisation (qui n’est donc pas linéaire), le calcul de la séquence de tensions qui permettrait de générer une rampe linéaire de fréquence, et la programmation du convertisseur numérique-analogique avec cette séquence : une autre belle opportunité d’exploiter la fonction de DMA du STM32. Cette opération s’appelle “linéariser” la source de fréquence, telle que mentionnée par les ingénieurs de Microwave Solutions, en complément de la fourniture d’une note d’application concernant la mise en œuvre de ce module dans un mode de sauts de fréquences (FSK) que nous n’avons pas approfondie.
Figure 11 : Principe du RADAR à balayage de fréquence FMCW : à gauche le cas idéal d’une source à modulation linéaire de fréquence, à droite la conséquence d’un balayage non linéaire de la fréquence (la fréquence de battement due à un retard constant dt associé à la propagation de l’onde électromagnétique jusqu’à la cible n’est pas constante au cours du cycle de balayage).
Le RADAR FMCW présente donc un signal issu du mélangeur dont la fréquence peut être décalée par deux causes : le temps de vol dt induisant un mélange entre le signal émis à date t à la fréquence f(t) et le signal retourné, arrivant sur l’étage de réception à t+2× dt et donc mélangé avec l’oscillateur local de fréquence f(t+2dt), pour induire un battement que nous avons vu égal à df=2dtΔ f/Δ T. Par ailleurs, si cette cible est en mouvement, alors elle induit un décalage de fréquence additionnel par effet Doppler. La solution pour séparer ces deux contributions consiste à remplacer le signal de balayage de la source de fréquence en dents de scie par un signal triangulaire. Dans ce cas, l’information de distance se traduit par un signal alternativement décalé de ± 2dtΔ f/Δ T (de signal déterminé par la pente du triangle), tandis que le décalage Doppler induit un décalage de fréquence qui est toujours de même signe quelle que soit la direction de la rampe. Un peu de traitement numérique des signaux acquis en phase croissante et décroissante permet donc de séparer les deux contributions.
5. Exemple d’un signal complexe : les composantes I et Q
Au cours de cette étude, nous avons toujours exploité des signaux temporels réels car issus d’une mesure unique (sortie de la carte son comme source de signal, sortie du RADAR CW), et par conséquent nous nous sommes contentés d’extraire l’information d’amplitude de la transformée de Fourier. Il peut être intéressant de mentionner dans quel cas ces concepts s’appliquent en pratique à des signaux complexes.
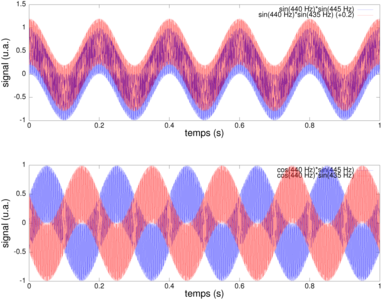
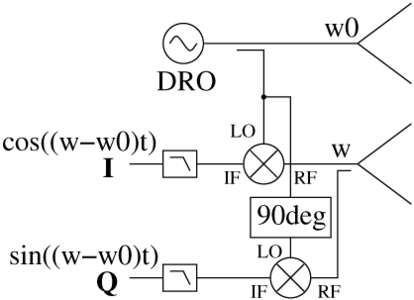
Un signal complexe M×exp(j×ϕ) se caractérise par un module M et une phase ϕ. La notion de phase n’a de sens que lors de l’analyse de la position d’un signal périodique relativement à un signal périodique de référence. Lors de l’émission d’un signal par une carte son, le récepteur (microcontrôleur STM32 dans nos exemples) n’a pas de référence de fréquence commune avec la carte son émettrice, et la notion de phase n’existe pas. Au contraire, dans le cas des mélangeurs exploités par les RADAR, nous avons vu que le même oscillateur sert pour la génération du signal émis et, par mélange, pour former IeIr×(cos(2ω t+ϕ)) et, par filtrage passe-bas, IeIr×(cos(ϕ)). Si par malheur ϕ=π/2, alors la sortie du mélange est nulle, quel que soit Ir. Afin d’éviter ce cas pathologique, un composant nommé démodulateur I/Q (Fig. 12, droite) génère deux signaux I=IeIr×(cos(ϕ)) et Q=IeIr×(sin(ϕ)). De cette façon, si ϕ annule un des deux termes, il maximise l’autre. On trouve donc que IeIr=|I+jQ| et que ϕ est la phase du complexe I+jQ. Physiquement, Q s’obtient en décalant (déphasant) de 90° le signal retourné par le RADAR puisque cos(θ+π/2)=−sin(θ). En pratique, lorsque le signal analysé est, comme dans le cas du RADAR CW, référencé à un oscillateur local fournissant un signal périodique de fréquence, alors le complexe I+jQ fournit une information riche pour extraire la phase en plus de la magnitude.
Évidemment, si nous reprenons toutes les applications décrites auparavant sur le complexe I+jQ, alors les optimisations dues aux symétries lors du travail sur des réels sont perdues, et l’encombrement mémoire de l’algorithme est double. Cependant, la richesse de l’information complexe, et en particulier l’exploitation de phase qui en découle, mérite largement le coût additionnel (en mémoire du processeur mais aussi sur la théorie associée) en ressources.
Figure 12 : Haut : exploitation des composantes I et Q pour compléter l’information de magnitude de la différence de fréquences par une information de phase. Nous pouvons ainsi déduire si le battement ω−ω se fait par une fréquence inférieure ou supérieure à la fréquence émise (i.e. donner un signe à la vitesse de la cible), ce qu’un simple mélange sur une seule voie (haut) ne permet pas. Bas : mise en œuvre expérimentale pour l’obtention des composantes directes (Identique) et en Quadrature permettant l’extraction de magnitude |I+jQ| et phase arg(I+jQ).
6. Sources d’incertitude
Nous avons vu que, au travers de la transformée de Fourier, nous pouvions fournir une information de vitesse sur la cible illuminée par un RADAR à onde continue. Néanmoins, quelle est l’exactitude de cette mesure, et quelle confiance pouvons-nous donner aux résultats obtenus ?
1. La résolution de la mesure est donnée par la durée de l’acquisition. En effet, nous distribuons N échantillons sur une gamme spectrale de fe la fréquence d’échantillonnage, soit une résolution de fe/N=4000/512=7,8 Hz qui se traduit en vitesse par 0,12 m/s=0,5 km/h,
2. L’exactitude de la mesure est déterminée d’une part par la connaissance de la fréquence émise par le RADAR, et d’autre part par la connaissance de la fréquence d’échantillonnage lors de la conversion entre indice de Fourier et fréquence. Ces deux paramètres sont déterminés dans notre exemple pour le premier par le comportement mécanique et thermique d’un résonateur diélectrique filtrant à plusieurs GHz, et pour le second par la compréhension du mécanisme d’échantillonnage lors de la conversion analogique-numérique et par la fréquence du résonateur à quartz utilisé pour cadencer l’horloge du microcontrôleur. Il suffit de manipuler un peu le RADAR devant un analyseur de spectre pour se rendre compte que le résonateur diélectrique est excessivement sensible aux contraintes mécaniques. Par ailleurs, sa sensibilité thermique est indiquée dans la datasheetdu composant. Pour une dérive thermique de l’ordre de 15 MHz autour de 9,9 GHz sur la gamme de températures d’utilisation, l’erreur sur la vitesse mesurée est de l’ordre de 0,15%.
Notons que la disponibilité de sources hyperfréquences ultrastables fournit les outils pour tester la validité de théories physiques sur des gammes de résolution inaccessibles par ailleurs [20] : une fréquence est la grandeur qui peut être générée et donc mesurée avec la meilleure stabilité (quelque 10−15 relatifs) parmi toutes les grandeurs physiques.
7. Alternative au passage dans le domaine spectral
Après cette longue présentation d’un outil aussi puissant que la FFT, il semblerait que tout traitement du signal soit accessible par cette méthode. Cependant, sa lourdeur de mise en œuvre nous incite à ne pas oublier que le passage dans le domaine spectral nécessite une puissance de calcul importante, et que parfois rester dans le domaine temporel peut s’avérer utile, voire efficace. Nous avons présenté des exemples volontairement choisis pour expliciter l’utilité de l’information spectrale : pour le RADAR CW, les raies contenant l’information en fréquence du signal sont représentatives des diverses composantes de vitesses caractérisant le déplacement de l’objet illuminé.
Dans bien des cas, le passage dans le domaine spectral est utilisé pour filtrer un signal dans le domaine temporel (Fig. 2). Dans ce cas, deux FFT sont effectuées : une première pour passer du domaine temporel au domaine spectral, dans lequel le filtrage est effectué par multiplication des coefficients issus du calcul par le gabarit du filtre, puis FFT inverse pour retourner dans le domaine temporel (noter que le même code est utilisé pour la FFT directe et la FFT inverse, simplement en prenant le complexe conjugué des signaux, puisque exp(−iω t) est le complexe conjugué de exp(iω t)). L’alternative consiste à rester dans le domaine temporel, et d’appliquer le filtre comme convolution entre les signaux acquis et les coefficients du filtre. Cette approche, historiquement utilisée pour l’analyse des signaux RADAR par exploitation de batteries de filtres analogiques montés en parallèle [21, p.322], est bien entendu exploitable dans l’application du traitement numérique de signaux. À titre d’exemple, pour engager la réflexion et, là encore, encourager l’expérimentation plutôt que prétendre à une rigueur mathématique, nous proposons la démarche suivante pour la mise en œuvre pratique d’un filtre à réponse impulsionnelle finie.
7.1 Conception d’un filtre de réponse finie (FIR)
De façon générale, le filtrage linéaire d’une séquence de données d’entrée xn pour générer une séquence de sortie yn s’exprime par
qui traduit le fait que les sorties dépendent des entrées passées ainsi que des valeurs passées des sorties du filtre. L’opération liant les coefficients du filtre et les données issues de la mesure est une convolution, et sa relation à la série de Fourier devient apparente lorsqu’on identifie le fait qu’une convolution dans le domaine temporel (coefficients xn) est un produitdans le domaine spectral (coefficients Xk) [22]. Il peut néanmoins sembler utile d’identifier la capacité à exploiter en pratique l’équation ci-dessus sans passer par toute l’implémentation de la FFT, et ceci nécessite d’être capable de fournir dans le code implémenté dans le microcontrôleur les coefficients a et b. Historiquement, avant l’avènement des systèmes numériques sur-puissants et des capacités de calcul associées, l’analyse spectrale se faisait en alimentant une batterie de filtres passe-bande par le signal à analyser [21], chaque filtre fournissant en sortie la puissance correspondant au contenu spectral du signal d’origine dans une bande passante donnée (l’équivalent de notre fe/N dans les calculs qui ont précédé) [12, chap.3.4].
Dans la pratique :
- Un filtre de réponse impulsionnelle finie [2] (Finite Impulse Response, FIR) bm est caractérisé par une sortie yn à un instant donné n qui ne dépend que des valeurs actuelles et passées de la mesure xm, m<= n :
L’application du filtre s’obtient par convolution des coefficients du filtre et des mesures, sans rétroaction sur les valeurs passées de sortie du filtre.
- Un filtre de réponse impulsionnelle infinie (IIR) a une sortie qui dépend non seulement des mesures mais aussi des valeurs passées du filtre. Il s’agit donc d’une rétroaction sur les sorties du filtre qui peut engendrer des instabilités numériques de calcul.
- GNU/Octave (et Matlab) proposent des outils de synthèse des filtres FIR et IIR. Par souci de stabilité numérique et simplicité d’implémentation, nous ne nous intéresserons qu’aux FIR. Dans ce cas, les coefficients de récursion sur les valeurs passées du filtre (nommées en général am dans la littérature) seront égaux à a=1.
Le calcul d’un filtre dont la réponse spectrale ressemble à une forme imposée par l’utilisateur (suivant un critère des moindres carrés) est obtenu par la fonction firls(). Cette fonction prend en argument l’ordre du filtre (nombre de coefficients), la liste des fréquences définissant le gabarit du filtre et les magnitudes associées. Elle renvoie la liste des coefficients b.
L’application d’un FIR de coefficients b (avec a=1) ou de façon plus générale d’un IIR de coefficients a et b sur un vecteur de données expérimentales x s’obtient par filter(b,a,x);.
Tout filtre se définit en termes de fréquence normalisée : la fréquence 1 correspond à la demi-fréquence d’échantillonnage (fréquence de Nyquist) lors de la mesure des données.
Au lieu de boucler sur des fréquences et observer la réponse du filtre appliqué à un signal monochromatique, le chirp est un signal dont la fréquence instantanée évolue avec le temps. Ainsi, la fonction chirp([0:1/16000:5],40,5,8000); génère un signal échantillonné à 16 kHz, pendant 5 secondes, balayant la gamme de fréquences allant de 40 Hz à 8 kHz (Fig. 7.2).
7.2 Exemple de programme et résultats :
L’exemple ci-dessous propose une implémentation d’un filtre à réponse impulsionnelle finie dont les coefficients ont été calculés sous GNU/Octave pour répondre au gabarit recherché dans le domaine spectral. Après mise à l’échelle pour travailler sur des entiers sans induire de dépassement de capacité de représentation des short, la fonction filtre() applique la convolution entre le tableau des coefficients et le tableau des données (Fig. 7.2).
long filtre(unsigned short *in,long *fil,long nin,long nfil,long *sortie)
{unsigned short k,j;long s=0,max=-2500;
if (nin>nfil)
{for (k=0;k<nin-nfil;k++)
{s=0;
for (j=0;j<nfil;j++)
s+=((((long)fil[j]*(long)in[nfil-1+k-j])))/256;
s=s/256;
sortie[k]=s;
if (max<s) max=s;
}
}
return(max);
}
int main (void)
{
unsigned short tableau[NB],k=0;
long sortie[NB],max;
// a=(round(firls(60,[0 500 700 900 1000 32768/2]/32768*2,[0 0 1 1 0 0])*65536)')
long fil200[NBFIL]={-384,-543,-695,-836,-964,-1074,-1164,-1229,-1270,-1283, \
-1268,-1224,-1153,-1054,-930,-783,-616,-433,-237,-34,173,379,578,767,941,\
1096,1228,1334,1411,1459,1475,1459,1411,1334,1228,1096,941,767,578,379,173,\
-34,-237,-433,-616,-783,-930,-1054,-1153,-1224,-1268,-1283,-1270,-1229,-1164,\
-1074,-964,-836,-695,-543,-384};
[...] // acquisition des donnees dans tableau
max=filtre(tableau,fil200,NB,NBFIL,sortie);
}
fe=16000;
ffin=4000;
fdeb=40;
b=firls(160,[0 600 700 900 1000 fe/2]/fe*2,[0 0 1 1 0 0]);
x=chirp([0:1/fe:5],fdeb,5,ffin);
f=linspace(fdeb,ffin,length(x));
plot(f,filter(b,1,x));
freq=[fdeb:150:ffin];
k=1;
for f=freq
x=sin(2*pi*f*[0:1/fe:1]);
y=filter(b,1,x);
sortie(k)=max(y);
k=k+1;
end
hold on;plot(freq,sortie,'r')
xlabel('frequence (Hz)')
ylabel('magnitude (u.a.)')
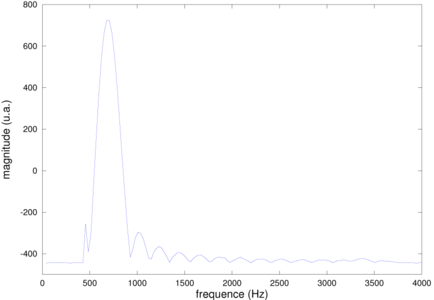
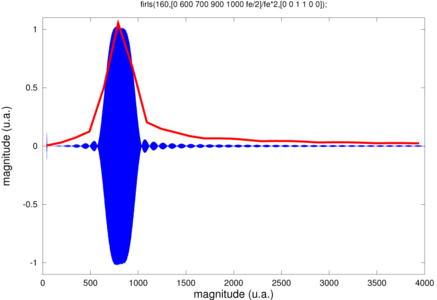
Figure 13 : En haut à gauche : mesure expérimentale de la réponse d’un FIR passe-bande conçu pour être passant entre 700 et 900 Hz. La mesure est effectuée au moyen d’un chirp de 40 à 4000 Hz en 30 secondes généré par une carte son d’ordinateur contrôlée par audacity. En bas à gauche : modélisation de la réponse d’un filtre passe-bande entre 700 et 900 Hz, en bleu par filtrage d’un chirp, en rouge par calcul de l’effet du filtre sur quelques signaux monochromatiques. Ci-dessus : programme GNU/Octave de la simulation.
Conclusion
Nous avons présenté les diverses étapes permettant l’analyse d’informations spectrales issues de séquences de mesures acquises à des temps discrets. Après un bref rappel théorique sur la décomposition en série de Fourier d’un signal périodique, visant en particulier à mettre en garde contre les artefacts apparaissant si les conditions sur le signal acquis ne sont pas respectées (fréquence maximale du signal inférieure à la moitié de la fréquence d’échantillonnage, périodicité du signal) et illustrant le comportement de signaux dans le domaine temporel et fréquentiel, nous nous sommes engagés dans l’étude d’une implémentation sur microcontrôleur 32 bits STM32. Un cas d’application idéal est le RADAR à onde continue dont l’information de sortie est une fréquence, mais dont la richesse du spectre permet de pleinement tirer profit de tous les coefficients de la série de Fourier lors d’une identification de cible. Ce RADAR nous a donné l’opportunité d’explorer quelques aspects associés à la source hyperfréquence nécessaire à son fonctionnement, en particulier l’influence du bruit de la source sur la portée de la mesure et la capacité à balayer une source de fréquence pour retrouver l’information de distance qui est a priori perdue lors de l’illumination d’une cible par une onde continue. Finalement, nous avons bouclé l’utilisation de la transformée de Fourier à des fins de filtrage par une illustration d’une méthode pour identifier les coefficients d’un filtre à réponse impulsionnelle finie appliquée dans le domaine temporel, nous affranchissant de la FFT pour effectuer quelques calculs simples de filtrage qui sont souvent suffisants pour obtenir un signal exploitable.
Les perspectives de ces activités sont nombreuses, et cette brève présentation avait plus prétention à identifier des voies de développement futures que d’exaustivité. À titre d’exemple, il semble pertinent de vouloir étendre la portée de fonctionnement du RADAR CW en plaçant le module, dont nous avons illustré l’utilisation, au foyer d’une parabole. Les antennes de réception d’images satellite fonctionnent à peu près dans la gamme de fréquence qui nous intéresse (11-12 GHz au lieu de 9,9 GHz) pour des gains supérieurs à 30 dBi (diamètres typiques de 60 ou 80 cm). Dans ce cas, les gains des antennes en émission et réception passent de 8 dBi à 30 dBi, soit une portée multipliée par (10002/62)0.25≃13. Au-delà de l’analyse spectrale, l’exploitation de la FFT pour le calcul d’intercorrélation [22] n’a pas été abordée bien qu’il s’agisse d’une méthode classique d’extraction d’un signal aux propriétés connues d’une séquence bruitée, par exemple enregistrée par l’étage de réception d’un RADAR impulsionnel.
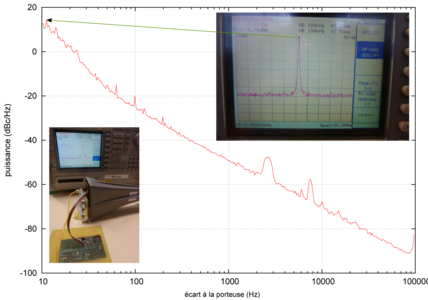
Le bruit de phase de l’oscillateur local [16] est un élément clé dans la détermination de la limite de détection du RADAR CW. En effet, nous avons vu que le signal mesuré est le mélange entre le signal issu de l’oscillateur, et le signal réfléchi par la cible et décalé en fréquence. Si l’oscillateur présente lui-même des fluctuations de fréquence (thermique, mécanique ou tout autre mécanisme qui fait fluctuer la fréquence de résonance du DRO) à cette fréquence, nous serons incapables de distinguer le signal renvoyé par la cible des fluctuations autour de la porteuse de l’oscillateur. C’est pourquoi la première caractérisation fondamentale d’un RADAR consiste en la qualitification de son oscillateur local. Cependant, cette mesure nécessite du matériel professionnel [23] qui n’est pas à la portée de l’amateur : une telle mesure, gracieusement effectuée à titre éducatif par les collègues des auteurs, est proposée sur la figure ci-dessous.
Cette figure présente la puissance relative à la puissance de la porteuse (dBc, le “c” signifiant carrier) observée autour de la fréquence supposée fixe de l’oscillateur, intégrée sur une bande passante de 1 Hz. Ainsi, l’abscisse 0 correspond à une fréquence de porteuse proche de 9,9 GHz, et l’abscisse présente l’écart à cette porteuse en Hz (équivalent au mélange que nous effectuons pour identifier la fréquence décalée par effet Doppler). En ordonnée, la puissance relative à la puissance émise par la porteuse. En effet, cette normalisation se justifie par le fait que plus la puissance émise est importante, plus la puissance reçue est importante, et ce dans la limite technologique et des normes d’émissions radiofréquences.
Les sources des pertes de la liaison radiofréquence sont résumées dans une équation dite du RADAR qui comprend le gain des antennes en émission G1 et réception G2, les pertes de propagation pour une propagation à une distance d, la section efficace RADAR (σ, i.e. la capacité de la cible à réfléchir une onde électromagnétique) : le signal reçu de la cible doit se situer au-dessus du bruit intrinsèque de l’oscillateur, faute de quoi il sera noyé dans le bruit. Ainsi, le ratio de la puissance reçue à la puissance transmise est
Il est intéressant de noter quelques subtilités dans l’interprétation des termes :
- Nous voyons apparaître la longueur λ de l’onde électromagnétique émise par le RADAR. Les pertes ne sont pas dépendantes de la longueur d’onde (en l’absence d’un milieu dispersif qu’est l’air), mais ce terme traduit que la cible se comporte comme une source ponctuelle qui devient, une fois illuminée par l’onde incidente, la source d’une nouvelle onde sphérique. Le terme λ2 correspond à l’intersection de la surface de l’antenne représentative de la cible (de l’ordre de λ2) avec la surface de 4π stéradians sur laquelle se distribue la puissance incidente.
- Étant donné que la puissance incidente se distribue sur une sphère de surface proportionnelle à d2, et que la cible est une source ponctuelle qui ré-émet elle-même une puissance qui se distribue sur une surface évoluant en d2, les pertes dans l’équation du RADAR ne sont pas en d2 comme nous en avons l’habitude en transmission radiofréquence, mais en d4=d2× d2.
Inutile de préciser que compte tenu du coût du DRO équipant le RADAR de Microwave Solutions, la courbe présentée ici illustre les performances d’un oscillateur très médiocre et n’est en rien représentative des performances des oscillateurs de qualité équipant les RADAR pour des applications plus “sérieuses”. La datasheetdu RADAR MDU1100 indique que le gain des antennes G1=G2=8 dBi=6 (i.e. relative au rayonnement isotrope), nous avons λ=3 cm, σ≃ 1000 cm2 pour un réflecteur métallique de 10 cm de côtés dans un cas idéal [24]. L’effet de la propagation de l’onde électromagnétique dans l’air pour se réfléchir sur une cible à distance d, en mouvement, avant de revenir sur l’étage de réception est une perte de cohérence de la source pendant le temps de vol 2×τ=d/c, avec c=3× 108 m/s (célérité de la lumière dans le vide). Pour des distances de mesures allant de 0,15 m à 150 m, τ=1 ns à 1 µs soit, en fréquence 1/τ, des écarts à la porteuse de 1 MHz à 1 GHz pour lesquels le niveau de bruit de l’oscillateur devient insignifiant, en dessous de SNR=−100 dBc/Hz. Ainsi, pour Precu/Pemis=10−10=−100 dB, et une transformée de Fourier qui travaille sur une bande passante de 4 kHz/256 points≃16 Hz, la portée de la mesure est de d4=6× 6× 32× 1000/((4π)3× SNR× 16) ⇒ d=560 cm. Dans ces conditions, et pour un facteur de qualité du résonateur du DRO supérieur à 4500, seul le bruit d’amplification en sortie du mélangeur (voir encadré 1 sur l’amplificateur avec fonction de passe-bande) détermine la capacité du RADAR à fonctionner sur une telle portée. Cette analyse nous permet néanmoins d’établir une limite intrinsèque à la portée de fonctionnement indépendamment de tout gain ou traitement du signal effectué sur le signal issu du mélangeur. Notons par ailleurs que les gammes de fréquences des caractéristiques en bruit de phase d’oscillateurs typiques, 103-105 Hz, correspondent à des distances de mesure de 150 km à 1,5 km. Dans ces conditions, le décalage Doppler de l’ordre de quelques dizaines de hertz à kHz est négligeable devant l’inverse de la durée de propagation de l’onde vers la cible. Cette analyse est primordiale pour déterminer les limites physiques du RADAR sur sa portée qu’il sera impossible d’améliorer, en l’absence de stabilité accrue du DRO, quel que soit le traitement du signal effectué sur la sortie IF, mais indique aussi la contribution de la bande passante d’analyse et du gain des antennes.
Remerciements
Nous remercions nos collègues du département Temps-Fréquence de l’institut FEMTO-ST d’avoir patiemment répondu à nos multiples requêtes de clarifications sur divers points concernant la RADAR CW, l’implication de la stabilité de l’oscillateur local sur la portée de la mesure, ainsi que pour la mesure de l’(im)pureté spectrale du DRO. Toute omission ou erreur est néanmoins uniquement attribuable aux auteurs de cette prose. Le matériel utilisé l’a été dans un cadre ludique et pédagogique.
Références
[1] D. Roddier, Distributions et transformation de Fourier – à l’usage des physiciens et des ingénieurs, Ediscience (1993)
[2] A.V. Oppenheim & R.W. Schafer, Discrete-Time Signal Processing, 2nd Ed, Prentice Hall (1999), et le cours disponible en ligne à http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-341-discrete-time-signal-processing-fall-2005/. Les vidéos associées à http://www.youtube.com/course?list=PL8157CA8884571BA2 ne sont pas jeunes, mais le fond du sujet reste toujours aussi passionnant.
[3] J.G. Proakis, D.K. Manolakis, Digital Signal Processing (4th Ed.), Prentice Hall (2006)
[4] H. Nyquist, Certain Topics in Telegraph Transmission Theory, Trans. AIEE, 47 617-644 (1928), republié dans Proc. IEEE, 90 (2), 280-305 (2002), et disponible à http://www.ieee.org/publications_standards/publications/proceedings/nyquist.pdf
[5] E.O. Brigham, The Fast Fourier Transform and its applications, Prentice Hall Signal Processing Series (1988)
[6] W.H. Press, S.A. Teukolsky, W.T. Vertterling & B.P. Flannery, Numerical recipes – The art of scientific computing 3rd Ed., Cambridge University Press (2007), disponible à http://www.nr.com/oldverswitcher.html
[7] W. Appel, Mathematics for Physics and Physicists, Princeton University Press (2007) est la traduction en anglais du livre du même auteur Mathématiques pour la physique et les physiciens !, H&K (2008)
[8] UM0585 User Manual – STM32F10x DSP Library (Juin 2010) décrit des implémentations de FIR, IIR et FFT, disponible à http://www.st.com/internet/com/TECHNICAL_RESOURCES/TECHNICAL_LITERATURE/USER_MANUAL/CD00208762.pdf
[9] Application note 3722, Developing FFT Applications with Low-Power Microcontrollers, Maxim, (2005).
[10] STM32F101xx, STM32F102xx, STM32F103xx, STM32F105xx and STM32F107xx advanced ARM-based 32-bit MCUs Reference manual (RM0008), ST documentation ID 13902 Rev. 13
[11] A. Lamothe, Teach Yourself Game Programming in 21 Days, Sams Publishing (1994)
[12] M.I. Skolnik, Introduction to RADAR Systems 3rd Ed., Mc Graw Hill (1980), ou les vidéos des cours de http://ocw.mit.edu/resources/res-ll-001-introduction-to-radar-systems-spring-2007/
[13] M.I. Skolnik, Radar Handbook 3rd Ed., McGraw-Hill Professional, (2008)
[14] T. Younos, Advances in Water monitoring research, Water Resources Publications, 2002, p.211 pour la mesure de vitesse d’un cours d’eau
[15] J.-M Friedt, Introduction à SPICE3 : simulation de circuits électroniques, et au-delà, Open Silicum 1 (Janvier-Mars 2011)
[16] E. Rubiola, Phase Noise and Frequency Stability in Oscillators, Cambridge Univ. Press (2008), ou http://www.femto-st.fr/~rubiola/pdf-slides/2006T-ifcs-leeson.pdf
[17] P. Tait, Introduction to RADAR target recognition, The Institution of Engineering and Technology (IET RADAR, SONAR and navigation series 18) (2005)
[18] J.S. Jaffe & P.L. Roberts, Acoustic reflections on marine populations, Phys. Today 64 (9), 76 (2011)
[19] F. Chebila, Lecteur radar pour capteurs passifs à transduction radio fréquence, thèse de l’Institut National Polytechnique de Toulouse – INPT (2011), disponible à http://hal.archives-ouvertes.fr/
[20] horloge ACES/PHARAO décrite à http://smsc.cnes.fr/PHARAO/Fr/GP_science.htm et http://smsc.cnes.fr/html-images/basic_physics2.htm et références associées
[21] Y. Blanchard, Le Radar – 1904-2004, histoire d’un siècle d’innovations techniques et opérationnelles (Ellipses, 2004)
[22] J.-M Friedt, Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées, GNU/Linux Magazine France 139 (Juin 2011)
[23] P. Salzenstein, J. Cussey, X. Jouvenceau, H. Tavernier, L. Larger, E. Rubiola, G. Sauvage, Realization of a Phase Noise Measurement Bench Using Cross Correlation and Double Optical Delay Line, Acta Physica Polonica A 112 (5) 1107-1111, (2007), disponible à http://przyrbwn.icm.edu.pl/APP/PDF/112/a112z562.pdf
[24] le calcul des sections efficaces RADAR est complexe : pour une surface plane conductrice, nous prenons la formule disponible à http://www.microwaves101.com/encyclopedia/absorbingradar2.cfm
1 http://cnx.org/content/m0505/latest/
2 http://www.lextronic.fr/P1455-tete-hf-hyperfrequence-mdu1130.html
3 un exemple de système fonctionnel est décrit à http://ocw.mit.edu/resources/res-ll-003-build-a-small-radar-system-capable-of-sensing-range-doppler-and-synthetic-aperture-radar-imaging-january-iap-2011/projects/ et en particulier les transparents décrivant la réalisation du RADAR à base de composants discrets et le compte-rendu en bas de page